economist_brexit.ipynb

{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Using statsmodels lowess\n",
    "\n",
    "Copyright 2019 Allen B. Downey\n",
    "\n",
    "MIT License: https://opensource.org/licenses/MIT"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 77,
   "metadata": {},
   "outputs": [],
   "source": [
    "%matplotlib inline\n",
    "\n",
    "import numpy as np\n",
    "import pandas as pd\n",
    "\n",
    "import random\n",
    "\n",
    "import matplotlib.pyplot as plt"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "[This article](https://medium.economist.com/mistakes-weve-drawn-a-few-8cdd8a42d368) suggests that a smooth curve is a better way to show noisy polling data over time.\n",
    "\n",
    "Here's their before and after:\n",
    "\n",
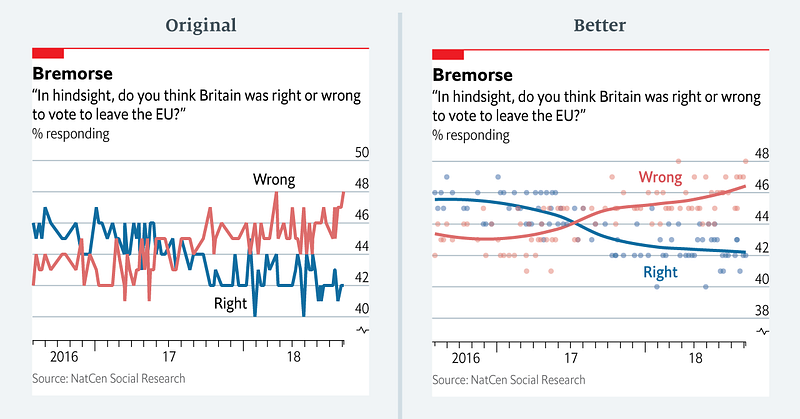    "![](https://cdn-images-1.medium.com/max/800/1*9GzHVtm4y_LeVmFCjqV3Ww.png)\n",
    "\n",
    "And here's their data:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 78,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>Date</th>\n",
       "      <th>% responding right</th>\n",
       "      <th>% responding wrong</th>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>Date</th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>2016-02-08</th>\n",
       "      <td>2016-02-08</td>\n",
       "      <td>46</td>\n",
       "      <td>42</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2016-09-08</th>\n",
       "      <td>2016-09-08</td>\n",
       "      <td>45</td>\n",
       "      <td>44</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2016-08-17</th>\n",
       "      <td>2016-08-17</td>\n",
       "      <td>46</td>\n",
       "      <td>43</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2016-08-23</th>\n",
       "      <td>2016-08-23</td>\n",
       "      <td>45</td>\n",
       "      <td>43</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2016-08-31</th>\n",
       "      <td>2016-08-31</td>\n",
       "      <td>47</td>\n",
       "      <td>44</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "                 Date  % responding right  % responding wrong\n",
       "Date                                                         \n",
       "2016-02-08 2016-02-08                  46                  42\n",
       "2016-09-08 2016-09-08                  45                  44\n",
       "2016-08-17 2016-08-17                  46                  43\n",
       "2016-08-23 2016-08-23                  45                  43\n",
       "2016-08-31 2016-08-31                  47                  44"
      ]
     },
     "execution_count": 78,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "df = pd.read_csv('Economist_brexit.csv', header=3, parse_dates=[0])\n",
    "df.index = df['Date']\n",
    "df.head()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 79,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>Date</th>\n",
       "      <th>% responding right</th>\n",
       "      <th>% responding wrong</th>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>Date</th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>2018-08-13</th>\n",
       "      <td>2018-08-13</td>\n",
       "      <td>43</td>\n",
       "      <td>47</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2018-08-14</th>\n",
       "      <td>2018-08-14</td>\n",
       "      <td>43</td>\n",
       "      <td>45</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2018-08-21</th>\n",
       "      <td>2018-08-21</td>\n",
       "      <td>41</td>\n",
       "      <td>47</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2018-08-29</th>\n",
       "      <td>2018-08-29</td>\n",
       "      <td>42</td>\n",
       "      <td>47</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2018-04-09</th>\n",
       "      <td>2018-04-09</td>\n",
       "      <td>42</td>\n",
       "      <td>48</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "                 Date  % responding right  % responding wrong\n",
       "Date                                                         \n",
       "2018-08-13 2018-08-13                  43                  47\n",
       "2018-08-14 2018-08-14                  43                  45\n",
       "2018-08-21 2018-08-21                  41                  47\n",
       "2018-08-29 2018-08-29                  42                  47\n",
       "2018-04-09 2018-04-09                  42                  48"
      ]
     },
     "execution_count": 79,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "df.tail()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The following function uses StatsModels to put a smooth curve through a time series (and stuff the results back into a Pandas Series)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 80,
   "metadata": {},
   "outputs": [],
   "source": [
    "from statsmodels.nonparametric.smoothers_lowess import lowess\n",
    "\n",
    "def make_lowess(series):\n",
    "    endog = series.values\n",
    "    exog = series.index.values\n",
    "\n",
    "    smooth = lowess(endog, exog)\n",
    "    index, data = np.transpose(smooth)\n",
    "    \n",
    "    return pd.Series(data, index=pd.to_datetime(index)) "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Here's what the graph looks like."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 81,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXgAAAEICAYAAABVv+9nAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzsvXl8ZEd59/st9apu9aJ914zGs49mNDMez2oM3sEMZrmAHTAJW3xDkgsvTnDgk9yb9+aGN3CTcB0SIDEQQsJitmASMCQGYwzj8cxoNs/u2bXv6kW9L3X/qJbU0rSWbu2t+n4+rVafU6fqqaqjX5fqVD2PkFKi0Wg0mvyjYLEN0Gg0Gs38oAVeo9Fo8hQt8BqNRpOnaIHXaDSaPEULvEaj0eQpWuA1Go0mT9ECr9FoNHmKFniNRqPJU7TAazQaTZ5iXMzCy8rK5OrVqxfTBI1Go1l2HD9+vF9KWT5dukUV+NWrV9PS0rKYJmg0Gs2yQwhxcybp9BSNRqPR5Cla4DUajSZP0QKv0Wg0eYoWeI1Go8lTcn7IKoQwAC1Ah5TyoBDiXuCvUV8aw8D7pZRX5sZMjUazLPF2QMcJCPaDrQxqd4KrdvLjmjllNiP4jwEX0j5/CXivlHI78C3gz2ZjmEajWeZ4O+DScxAPQlGFer/0HLQfz3zc27HYFucdOQm8EKIOeDPwlbTDEnCmfncBnbMzTaPRLGs6ToDVCRYniAL1bnXC+R9lPt5xYrEtzjtynaJ5CngScKQd+zDwnBAiBPiAvZkuFEI8DjwO0NDQkGPxGo1myRPsVyP0dMxF4OuChj23Hh/uXTjbVghZj+CFEAeBXinl8QmnPg48JKWsA74GfC7T9VLKp6WUu6SUu8rLp92IpdFoliu2MogOjz8WHQZndebjtrKFs22FkMsUzQHgYSHEDeAZ4B4hxE+AZinlkVSa7wD758ZEjUazLKndCWEfRHwgk+o97IPNb818vHbnYlucd2Qt8FLKT0kp66SUq4FHgReAtwIuIcT6VLL7Gf8AVqPRrDRctbDhITDa1PSL0aY+192e+bheRTPnzIkvGillXAjxu8APhBBJYAj44FzkrdFoljGu2szCPdlxzZwyK4GXUr4IvJj6/YfAD2dvkkaj0WjmAr2TVaPRaPIULfAajUaTp2iB12g0mjxFC7xGo9HkKVrgNRqNJk/RAq/RaDR5ihZ4jUajyVO0wGs0Gk2eogVeo9Fo8hQt8BqNRpOnaIHXaDSaPEULvEaj0eQpWuA1Go0mT8nZm6QQwgC0AB1SyoNCiF8zFsKvAjgqpXzbHNio0Wg0mhyYjbvgj6GCejgBpJSvGzkhhPgB8KPZmZb/dHlCnG73MBiIUmI301znptpduNhmLTq6XabB26ECVAf7VZi72p25+Vafq3wWg9naPt316ecRIISKPpX++zJos5ymaIQQdcCbga9kOOcA7gGenZ1p+U2XJ8Tz53sIRROUFVkIRRM8f76HLk9osU1bVHS7TIO3Ay49B/GgCmgdD6rP3o7FyWcxmK3t012ffl4YoO0VaD0MId/Y78KwLNos1zn4p4AngWSGc28HfiGl9OVs1QrgdLsHh9WIw2qiQAgcVhMOq5HT7Z7FNm1R0e0yDR0nwOoEixNEgXq3OtXxxchnMZit7dNdn35+6DrYStSr49jY70PXl0WbZS3wQoiDQK+U8vgkSX4L+PYU1z8uhGgRQrT09fVlW3zeMBiIYreMnyGzW4wMBqKLZNHSQLfLNAT7wVw0/pi5KDWVsAj5LAaztX2669PPR3xgLASjFUKDY79HfNmXuwjkMoI/ADwshLgBPAPcI4T4BoAQohTYDfxksoullE9LKXdJKXeVl5fnUHx+UGI3E4jExx0LROKU2M2LZNHSQLfLNNjKIDo8/lh0WB1fjHwWg9naPt316ectToiHIB6GwpKx3y3O7MtdBLIWeCnlp6SUdVLK1cCjwAtSysdSp98F/FhKGZ5DG/OS5jo3/nAcfzhGUkr84Rj+cJzmOvdim7ao6HaZhtqdEPapEaRMqvewTx1fjHwWg9naPt316eeLGyE4qF61d4z9Xty4LNpMSClzv1iINwB/LKU8mPr8IvAZKeXPZnL9rl27ZEtLS87lL3f0apHM6HaZBr2KZsWvohFCHJdS7po23WwEfrasdIHXaDSaXJipwOudrBqNRpOnaIHXaDSaPEULvEaj0eQpWuA1Go0mT9ECr9FoNHmKFniNRqPJU7TAazQaTZ6iBV6j0WjyFC3wGo1Gk6dogddoNJo8RQu8RqPR5Cla4DUajSZP0QKv0Wg0eUrOQbeFEAagBeiQUh4UQgjgL1E+4RPAl6SUn58bMzUajWYFExyE9hboaFHvMyRngQc+BlwAUqFNeD9QD2yUUiaFEBXTZXCp288HvnaU/beVsn9tGesqHJiN+ftPxUz8nM+1L/T58K0+XZ5TnU8/J5CQ+jmdbdm2XXre2ZSTFXPgT31J+77PVD+YvQ/5hfJDP5NyJvP7PhO7svEpP11+6WktLjAXgqdViXn7MRUDFlQMWWctlXYxozBSOfmDF0LUAV8HPg08kRrBHwXeI6W8MtN8nPUbZNXvPEU0rmJ3mw0FrKssYkuNk83VTrbUuthU7aTIMpvvoaVBlyfE8+d7cFiN2C1GApE4/nCc+zdXjhO/6dLMdZlznedU54HRc5F4gmM3hpASdjeWYDEWTGpbtm2Xnvf6yiIu9w7PqJys8HbApedU0GVzkQrdFvbBhodmLFbz0T9zRqb6DbWqc8UNOdd5LtptzspJTxOLQOvL6njDfjBZprZruvxnWk8pofUVOPGvMNytRH3oBiRTYSsd1VB7O9TtAvdq8HVAUTmle3/rykAwuW66ZshVOZ8CngQcacduAx4RQrwd6AM+KqW8PFUmVS4r//DoDq73D9M7HMFoKOB8p4+fX+jluy3tgPpCXV1qZ3ONky01TrbUuNhc7aTcYcnR9MXhdLsHh9WIw2oCGH0/3e4Z/WOeSZq5LnOu85zqvPqszl2+OYy70AxC0joYYGdDyaS2Zdt26XmfbPNQ57bNqJys6Dih/nhHYnOOvHecmLFQzUf/zBmZ6jcyyq1qGjs2knam4jwH7TZn5aSn6T0KNnVvMHQd6ndPbdd0+U92/tpLUFQ+NtXScVwF8wYwWKCkEda/UeVRvhl2vX+szPP/qa61OIGZDcyzFnghxEGgV0p5PBWybwQLEJZS7hJCvAP4Z+B1Ga5/HHgcoLJuNQUFgsbyIhyFJt6zZxUAUkp6fBHOdXo51+njXKeX020efvJq12g+FQ7LqOCPvNeXFKIeBSw9BgNRyorGfynZLUb6hyNZpZnrMuc6z+nOj5zzR2I4U4LmC8emtC3btkvP2xOMsra8aEblZEWwH4omzEKai2C4d8ZZzEf/zBmZ6peI3ZouyzrPRbvNWTnpaSI+sLoBCWHv9HZNl3+wHwqLYeCKevVfgYHLMNyTSiygfCNsfAjiUajZAe4GKDCo0zJ5a9mZypyGXEbwB4CHhRAPAVbAKYT4BtAO/CCV5ofA1zJdLKV8GngaYH1TswQIROKU2M2jaYQQVLmsVLms3LupcvS4NxjjXJeX850+znf6ONfp46XL/SSS6tvMYTGyKW2kv6XGydqKIkyGxZ/XL7GbCUTio6M0uLXeM0kz12XOdZ7TnR8557CYCMeSICQOq3FK27Jtu/S83TbzjMvJCluZ+rd7ZGQG6rNtRlOjM67XopGpfgYTMGEAlWWd56Ld5qyc9DQWJ8RD6vjINVPZNTF/mYSBq2pq5rlPwJVfgOfm2FRLYTG4V0Hj62Hn+6B6uxrhgxqZx4Nj4j5Z2ZnqNA1ZC7yU8lPAp2Bc0O3HhBCfAe5BjdxfD7w2fWbgD8fwh+PsXVM6bXKXzcT+28rYf9tYxcOxBJe6/aMj/fNdPr59tFX9UaPm9ddXFbGl2sWWWiX+G6uc2Bd4Xr+5zs3z59W3d/p8a3q9Z5Jmrsuc6zynOz9yrqG0cNwc/FT3QbZtl573jnr3uDn4bO63KandqeZYYcIc650zzmI++mfOyFS/EcGJ+HKu81y025yVk56muHH8HHzEN7Vd7gY4/jU1yva2KnGPBdU5kx0qt4C7Hso3QEUTGM0Q8Wee059pm6Snm/hFOwmzCrqdJvAHhRBu4JtAAzAM/J6U8vRU16/ZtE1+8Xv/NecrBxJJyfX+4ZTo+0anejzBWMpuWFdRxLY6N831bprrXGyscs77Ch69ikavosmlXouGXkWj0kf80HVazZd3HFfpvW3qelEAjioo2wC33QNr71OiXmDIfRXNVGlT6ap2v/Vm93By9XRNMCuBny27du2SLS0zX9M5G6SUdHnDnOv0cbbDy6vtHk63exkMRAE10t9U46S5zkVznZvmehdryoooKFiac/oajWYeiEeh99yYkHecgL6LjD7UdK9S4lu7S61uqd4GZvuCmymEOC6l3DVtupUi8JmQUtI+pEZQr7arB7lnOrwEowlAzek31brYVu9ie52bbfVualzWJfsgV6PRZEEyqR6Adp4YE/TuM5BIPeQeGUnX3g41O9Xv9jl+VpAjWuBzJJGUXO0b5lSbh1dTwn+hy0csodqprMhCc50rNb2jRvvFS+GhmEajmRwpwduuhLwzNTLvOq3m2kHNm9dsV6tZam9XL3eDmrJZgmiBn0PCsQQXu/2cbvOMjvav9qkHdwANJTa2jU7tuGmqdWIzL//NWRrNsiUwMCbkI6Ie6FPnCkxqLf/IqLxm59i8+TJhpgKvVWgGWE0Gtte72V7vHj3mD8c40+HldJuazz/Z6uHHqXX6BQLWVzrYlhrpb693s6HKsSSWa2o0eUc0CN2vpj0EPa52gwIgoGw9rL0/Nd2yEyqbwLi8Nkrmih7BzyF9/oh6eNumHuC+2u5hKLVyx2wsYEuNc/QB7vb6YlaX2vR8vkaTDckE9F1KCXkLtB+H3vMg1XMzXPWpaZaRufMdYHFMnecyRE/RLAGklLQNqoe4p9vU1M6ZDi+hmLoZ3TbT6H8GIy+3Tc/nazSjDPelhPyYenWchKhfnbO4xoS8bpeaanFUTp1fnqCnaJYAQggaSm00lNp4S3MNAPFEksu96iHuqVYPp9o8/Oq1y6Pz+WvK7Gyvd7Ojwc32+mI2VuupHc0KIRGDnrPQdgzaj0LbUbUbFKDAqDYPNT+Segi6C0rXQoH+25gKPYJfAvjDMc60eznZpgT/ZKtn1B+JxVjAtjpXSvSL2dHgptq1RDbCaDSzITioRLztiHrvPDG2G9RRDXV3qFf9bqhuBpO+70fQUzTLGCklHZ4QJ1tHBH+Isx0+ognlfqHSaWFHfXFqlO9ma51Lr9rRLG2kVNv5215R7nHbjkB/yptJgRGqtkL9Xqi/A+p2g6tuyS5RXAroKZpljBCCumIbdcVjUzuReIILXX5OtQ5xMjXK/9m5bgAMBYKNVQ52NLjZ2VDMjgb9AFezyCRi0PWq8u/SmhL1YL86V1gM9Xug+VEl6jU7wGxbXHvzFD2CX8YMDEc41ebhROvQ6Jx+ILULtzj1AHdE8JvrXeO8Fmo0c0rErx6Ctr4CN19Wvs5HvDMWN0LDPmjYowS9bL2eO58legS/AigtsnDvpspRl8qJpORyr5+TrWpa52Srh19eUps7hID1FQ52rlJz+Tsbirmt3K5H+Zrc8PdA6+HU6Pyw2uIvE8r5VtVWuP390LBXvRxVi23tikWP4PMcbyjG6dQo/0RK+P1h5aPabTOxs6GY21cpwd9e76bQvHx282kWCClh8JoambceVu8jMUKNhWqJYsM+WLVPPRTNw3XnS415H8ELIQxAC9CRchf8Lyg/8KlwKLxfSnkq1/w1c4Or0MRd68u5a305AMmUr50TrUOcuOnheOsQL1xUkWOMBYItNU5uX1XC7sYS7lhdTGnRytjxp0kjFlZ+WtpTyxVbXxmLRFRYosT8jg+p96ptyte5ZkkymymajwEXgPTwIp+QUn5/diblP5l8gAM5+QXP1p94QYFgndXHOvtpHlndz+BqJ4fCqzk2YKHXF6bbF+GbR27yz4fUCO22cju7G0vZ4IxRPXwed6wbk6OC2i0HqKy/bVobetqu0nHuEL6BLvqlg2BpMxX1a2ZXPzGY0U/54OVX6OxoYwAnyeodbFy/8da0zhrwdU7q/7vHF6bj3CFi/t5b6jktufr/zuSHHODy80poQTnCWnsfXbKE0+0eQv2trApfYo0tjLusenqf6pPZNrK6paOFwLVXiLW24PBcwCBTkYjcDdB4F6zarwJhjMyfj+R3/SUIeaDQDaXrpve5PrFdZuKPfbLrsz2eLdPZnaF/5sWv/SzIaYpGCFEHfB34NPBE2gj+x9kI/EqcounyhHj+fA8Oq3E0ik/7YBAKBHXuwnGRfe7fXDmlCGbKa9rr0qK9D8bMnLvegYMg3lUPMGgowx+O8/r15fQHIhy5Psix64Mcuz7AcDS1RNOaYLMjxObCIR66525KqhomtaHA38n1Q98jbLBz019AoQxhiQ8TXvNGIvaqnOoXH2rnAcNxXCVlY9FvhlrxhuO86ndgLHRgFxGSQQ9thZu4y946ltbTCq1H1IM+s218BB+TBV/nFS73BUg66zEWOoiH/CRCXhoPvGt6kU9r1/FReTJE8ElPG4vcYgdDrSouaLBfCScCQkN4bav4b+PdFFmMrBr4FQFs+JMWdlSZKTaEMpc1sTyDRW3t7z6r1px3nR4N+hwzFOJxNzFc1kyPcxutti28bseWW/toJL9kHHovKsFPJqF8ExgM4+2Yql1g6nYI+9Tu1M4Tt16f7fHJ2iaX/gQ49S0YvDqufyi5Dba/Z0FEfr6naJ4CngQmTrZ9WgjxfwG/AD4ppVwC0YOXFqfbPTisxtEVLQ6ricGgCjqyqco5emwk7VQCmCmvaa9Li/Z+vXsQo82FQVhwDZ0lVnc/ABe6fbyxqZrbV5XAG+DYT/+V60NRXgsXc2bIwLEhO7/sK+IL/3KFGlc7ayuK2NFQzPqKonE2VLQfwlDoYiBgxGJKYjS6SUQLMPedxFz6lpzqZw9f5DpGtlenRasP9jPYH8RYuptCs5EkZgxCsK7/Ba6zcSztcC/YiiHQAwHAVqKOD12H+t0M9HXjlJKAXf1HZUq9d5w7NL3Ap7XrqF0jxyf+waen7T16ix0E+2HwOpStBVNq+aAQDPZ2UldykcKEkYTZiclURGE0zjW/4PYqZ+ayQh5o+WfoOafyH7gKyVTw7KIqJVj1u/lNeBV91kYchdbRS03hWOY+GrG/9yJY7MrGWFC1a8XG8XZM1S4wdTsAnP8RVG259fpsj2dqm6mYzu5gv7I3rX8IDmRfzjyTtcALIQ4CvVLK46mQfSN8CugGzKig2n8C/EWG6x8HHgdoaGjIweTlzWAgStmEeW3la378f1J2i3F0N2s2eU17XVpk9uFwHGehiQQ2zOH+Sa9PDveyrqyK9QVRDjZAQsJ1H5zoDHE0uoaXrw7w0uV+jAWCDZUOmmpd1BVbKfb3YnZVEfL4xzZimeyIYB+2HOvnTHjol67xCRMxotEwVtPYA+KE0UZptI+e+LaxdBEfWN1jPsCtbkCq0TIQi4SxmAwE0rI2FjqIeruntBPIHPHeXKS+VKZKO2JTmh0kYmrZoTFNWI1WotE+nAkPIimIWlXgCavJgC8UA7M7FR+0fWxly83DarSOBGGAktWw7gHlGrdsHcQjsOsDALQeuUmZdYb30oj9o7Yr+wh7b63zdO0yVTuYi8DXpZZXTrw+2+OZ+mEqprM7EVOfRzBa1ZfpyFr/JUIuI/gDwMNCiIcAK+AUQnxDSvlY6nxECPE14I8zXSylfBr1BcCuXbsWbwnPIlFiNxOIxMetSTcZBBOD6AYicUqmCSSSKa9pr0uLzF5kNRKOJSgSYaKW0kmvNzkqiIf8oyNag4BVRg9r1tm5q24D3mCMbl+Ys50+zrR7+U6LildZW7ie3SXDrLFZMYgoFpMBYgGkrTTn+vkMblxMEB2DCbPZymAsQWHqi8QQD+Izl+MyRsfSWZwQ9oyJ0sg67dTozGSxEp0wZRkP+TE5JvyhZyJTxPv0QNWTpbU4b7EDg0mtRImHxkaI8bCqo8FNocmIIR4kYbQhvO2sDl6DQ6nR+Y//h0pvLlIrWra8Tc2zO6vBXj5mQ8Q3zras7qV0+0dsjIfV54l1nq5dpmqH6LCyO9P12R7P1A9TMZ3dBtMt/YPBnH0580zWuw2klJ+SUtZJKVcDjwIvSCkfE0JUAwi1sPptwNk5tTRPaK5z4w/H8YdjJKXEH45RYjNTUmQZd8wfjo8+fM0mr2mvq92p5hIjPhpLbcSDXhKBIbzFTZNeX7vlAImQl1jAg0wmiAU8JEJearccoLnOTSSepKHExrtur+NP3riB/3HvOp64fz01pQ6e7XDyt5cr+OvLlfyo1UybJ0G4bHvO9Wu3bqTRHlcCJZOjQlVSUUM86CUUiVIQ9ZMIDHG55J7xaYsqIDgE9kq1+SY4qF7FjRDxUVpehU84M9ZzWtLaddSusG/sgelkaTPYga1MPcwMDipRiQYgOEhJeTXepA3TwCXqL/8bW458gu1n/xerrj0DPedVvm/8DDz+K/iTm/Dbz8Lrn4Qdj6nR+hS2ZXUvjdhfVAGRgJqaiARUu06s81TtMl07hH2w+a2Zr8/2eKZ+yLU/a3eqPprQP9hKsy9nnpnVOvjUFM0fpx6yvgCUo4aip4Dfk1IOT3X9SnzICou7igYYtzpgECenk2vokiVTXj+yGibT6pKpbLj42iWe/c0pftMpOT9cRBKB22bi/k2VvPuOem5vKJ4ysPmKX0Uz4lExHoKhm6NTABGTi6BjDZbKddga98D6N4K7bla2ZXUvjeQ3cFmvooEFX0WjnY1plhzeUIwXLvbw3JlufvVaH9F4kkqnhYe2VvOW5hp21Lv1ztoROk/Csa/CuR+qUaK9Qi1XHHkVr9bOuFYwWuA1S5rhSJxfXOjhJ6928WJK7OtLCnlrcy1v21HD2ooVuBsyEVOrQI78k9pgZLKrKYfdv6sccmlB16TQAq9ZNvjCMf77XA8/OtXBoSv9JCU01Tp59I4G3rajliJLnrtM6r8Mp5+Bk9+A4W4oWQO7H1drqq2u6a/XrDi0wGuWJb3+MP95uovvH2/nQpePIouRd+ys5X17V7GuMo9G9dGAEvVT31Ih6UQB3HavEva192lvi5op0QKvWdZIKTnR6uEbr9zkJ692EU0k2X9bKb+9bxX3bqpcvmEMA/1w9Gn1Cg1BxRbY/luw9V3a66JmxmiB1+QNA8MRnjnWxreOtNLhCVFqN/O2HbW8a1cdG6uc02ewFBi8Doe/oKZh4iHY8GY48FHlTlejyRIt8Jq8I55I8qvX+vj+8XZ+fqGHWEKyrc7Fu26v4+HmWly2JRjQpPMUvPx5tRpGGFTQ6P0fVbtJNZoc0QKvyWsGA1F+dKqD77aouXqzsYAHt1TxyK569t9WOuXa+nlHSrj2Szj0d3DtRbUbctcHYM9H1E5LjWaWaIHXrBjOdnj5Xksbz57qxBuKUV9SyKN3NPCuXXVUOKzTZzBXJOJw/lk49JSKcFRUBXs/osRdr4bRzCFa4DUrjnAswX+d6+aZo20cvjaAsUBw36ZKHtu7an5H9ZFhOPlvcPiL4G2Fsg1qfn3ru8CoA6Zo5h4t8JoVzfX+AM8cbeV7x9sZDERZU2bnfftW8cgd9WOeLWeLtwOOfRlavqacmDXshwMfUx4b9TJHzTyiBV6jQY3qf3q2i389fJOTrR6KbSY+eKCR3963OveHsm3H4MiX4NyzgISNb1YPTkd8mGs084wWeI1mAi03Bvnii1d54WIvRRYj79nTwIfubKTSOYN5+hE3Aq98SW1Msjhh52+rjUnFq+bfeI0mDS3wGs0knOv08o+/usZPXu3EWFDAO3bW8nuvv43VZfZbE/s64dQ34dg/g79ThWXb83tqc5Ilj3bWapYVWuA1mmloHQjy5V9f47stbcQSSR5uruEP7l7LulIzXPqp2pR09RfKfe2aN8De34e19+v5dc2iM98xWRFCGIAWoENKeTDt+N8DH5BSFk168SKRk+/0+WQmvrCzyWOG16W3Q7UYpLngGiX4GArFaR8KEYxEs/eFnoOdXbKE0+0eetquYh94laK4h2Gjm2BpMxX1a27pn6l80s+kriV2M9VOK12+MIOBKALJ5moHT9y/jpYbQ1w918Kvzn6WavMhipI+cNTAnU/AjvcqB2BZMJ2t6XYJJKR+TunzPq1f5+VenuW9lMmOXO1Mb7+IuZhBVxMSWBW+xBpbGHdZ9Xjf/mn25nKf5Cs5j+CFEE8AuwDniMALIXYBHwPePhOBX8gRfJcnxPPne3BYjdgtRgKROP5wnPs3Vy6OyKdHbZ8sovx0keCnivw+yXXp7VCS6Md187/xY2OVy0Dk2iFMBYLhqt2EkkYSIS+NB941+z+ODHZ6B/v578TtJJKSwmv/hVcW0hE0UmdL4BRBwmveSMReNdo/PW1XuX7oexgKXRgLHcRD/mntm9jn7UNBjt/wsGt1MYXmAo7dGMIcD/J2y1HWtv87JUOnSQgjv5C3883oGyhYezd/cM8Gdq0uyaq609mablcknuDYjSGkhN2NJViMBcSH2nnAcBxXSVnGfp2Xe3mW91ImO3K1M739QsJKa3cf7kg39SU2okW1+JMWdroCuPuPQ/1eKK4ftbfPsYWrp1/K6j5Zjsx0BJ/T/5pCiDrgzcBX0o4ZgL8Gnswlz/nmdLsHh9WIw2qiQAgcVhMOq5HT7Z7FMSg9avvQdRWh3Vaifrc41bmRCO4zyUMUzOi69HZwDZ3FYC/GaHPRdvU8FBaDvRRboB2T3Y2h0EXHuUNzW9eUndcDRurCF7H0niZhcTIsCrGaDQwLKwmrE3PfyXH903HuEIZCFya7G1FgmJF9E/u83x/FbTcy6PNhvvwzPtj1F/zF5bey+8yfY04EOLPlE7x48CX2fvIn7L7/3ZzuGOad/3iYR/7pMIeu9DPTwdB0tqbb1ToQwl1opthuonUwgMNqoi58kesB46T9Oi/38izvpUx25Gpnevv1DccxFrooNfiJ+now2d1TFKFuAAAgAElEQVQUWkz0d7eCrRgCPePs9Z38Qdb3ST6T6xTNUyghT3/K9IfAf0gpu6aKyiOEeBx4HKChoSHH4rNnMBClrGiGUeMXgvSo7ZNFlJ8uEvx0kd8zkN4O5sgAUWsZVgT+sJcCdzVJAcaoDwBjoYOotzuX2k1rpzdupkx46AkNI23lRIfDWIwFROJJMNkRwT5saf0T8/dido33tjidfeP6XCYpGWjhAd/PWT/wc2wJP0GjmzMVD9PivI812+8mCfQPR3BaTfzB3Wv5wIHVfPtoG0+/dJX3fuUIuxtLeOL+9exdUzpldaezNd0ufySGMxXo2heOAeBMeOiXE3a+pvXrvNzLs7yXMtmRq53p7ReKxbGZjViIE40lMQFWk4FkyAsVtepvJ81e4e/EWLZjXH5zdh8vQ7IWeCHEQaBXSnk8FZMVIUQN8C7gDdNdL6V8Gnga1BRNtuXnSlZR4xeC9Kjtk0WUny5C+3SR3zOQ3g5RSymGeJBhacVgdZGMBjEZDcRNKr94yI/JUTFpXjMmg50uYxQfbmShFaIBzCYjkVgSq6kAYgGkrXRc/5gcFcoe+1gQ6Cntk5K6ZCeO116hevAYJb0vc19kiGiBlcslr+d86Rt5zb6LZIEBi7EAhCAQjo27H2xmIx+6s5H37mngO8fa+MIvr/Do069wYG0pH79v/aRTN9PZmt4HDouJcCwJQuKwqj9Hn8GNiwkimNav83Ivz/JeymRHrnamt1+hyUg0niSCEWMqm3AsgaPQpTaXWdOCgkeHkY6a7O6TPCeXKZoDwMNCiBvAM8A9wDlgLXAlddwmhLgyV0bOBVlFjV8IZhJRfroI7VNFfp+E9HbwFjeRCAwRD3qpv22z8k8eGCBoryMW8JAIeandcmBu65qys9Eep926kUhFM4aIjyIZIhxNUCTDGMI+ouU7xvVP7ZYDJEJeYgEPMpm41b6IH24cUg6+vvMY/M067vqvN7Lj9P/E1XuU/qq7eLHpf/HJ1f/O0e2fJXHbvQyGkwwFYjSU2Ke8H6wmA7+zfzUvPXk3/+fBzVzq9vPOfzzM+756hBOtQ7dWdxpb0/ugobQQTyg6zo5260Ya7fFJ+3Ve7uVZ3kuZ7MjVzvT2Ky8yEg95GUg4MDsriQU8hCIxyqoaIDgE9spx9jp3/G9T3ycrjFktk0yN4P84fRVN6vjwUnvICnoVzQjLfRVNwtOGsyBCjcOII9gGXadU2DtS93LxamjYBw176S3eyYlAGYPBWMZVNLesXpnB/RCMxvnGKzf5x19dYzAQ5e4N5Txx/wa21o1Nq+hVNLOzU6+imZoFWQe/3ARes0wZ7oUbv1aud28cgsGrY+ccNVCzXQWlrk69F5UviFmBSJyvH77BP/3qGt5QjAe3VPLE/RvYUKU3QGnmF73RSbM8SSbBcwO6XoUbv1HC3ndRnbO6YNWdKTHfpgTdUbmo5oJ6OPrPv7nOV399neFonIPbavgf963jtvIltxVEkydogdcsfSLD0HNW+U7vPgM956D3AsQC6rzJrkLaNb4OVt+lRuoFhsW1eQo8wSj/9NI1vv7yDcKxBG/bXstH712X2QWCRjMLtMBrlhahIRW+ruv02GvwGqPz5oXFUNmUem2Gyi1QtQ0MSzAM3zT0D0f4p19d5V8P3ySelLxzZx3/x71rqSu2LbZpmjxBC7xm8YiF1ci844TyvNh+LCXmKVwNqSmWZiXiVU3grFUPmfOIXl+YL754lW8daUUieeSOev7w7nVUuRYwypQmL9ECr1kYkknof02JeMdx6DwBPechqTbtUFQFdbvUCoeRB6G27Lb+L3c6PSH+4ZdX+O6xNgoKBO/d08BH3nDbwoYT1OQVWuA180NwUIl521H13nlybDehxTW2oqV2J9TsBFdd3o3Mc6VtMMjnf3GZfz/Zgckg+J19q/nQnY1UzMQfvUaThhZ4zeyRUq0vb3sF2o5A6xEYuKzOCYOaJ6/bBXV3QO0uKF2rXenOgOv9Af7u56/xo9OdGITgwS1VPLZ3FXvXlDCVmw+NZgQt8JrsiYXVFEtrStDbjqiHowCFJVC/B+rvUO81O8CsV4fMhhv9Ab555CbfbWnHG4qxodLBH9yzljdvrcYwXwHCNXmBFnjN9Az3pYT8FTU67zw5Nndetl7FGK3fq5Yqlq7VUy3zRDiW4D9Od/L0S9e40jvMmnI7f3j3Wh5ursFo0P8RaW5FC7xmPCMPQ9teUfPnra+M7Qg1mNV8ecMeJej1e8A+tcdEzdyTTEp+erabv3/hMhe7/awqtfHBA408ckc9VtPSXf+vWXi0wK90IsNquqXtCLQdU+/hlB9uW2lqumWP8tlSsx2Mlqnz0ywYyaTk5xd6+OKLVznV5qHSaeHh5hoe2lrN9nq3nqfXaIFfUUgJnptjQt52RO0KlQl1vnyjehDasFeN0Etv09Mty4RDV/r5yq+v8Zsr/cQSklp3IW9qquKejRXcvroYi1GP7FciWuDzmYhfzZe3t6hXRwsM96hz5iKovT01Qt+tVrkUFi+uvZpZ4w3GeP5CDz8908WvL/cTTSSpcKiR/RubqtjZUEyBfjC7YtACny8kk9B/Sa05HxH0vgvKrTBAyW1KxOt3K1Gv2Lyk/bVoZo8vHOPItUG+fbSV36TEvqzIwv2bK3lwSyX7byvDbNQPZ/OZeRf4VAzWFqBDSnlQCPFVVBBuAbwGvF9KOTxVHlrgM+DvUTtCO0ZG5ycg6lfnrC613rzujtTu0NtX3K5QzXj84Ri/vNTHf53r5sWLvQSiCRxWI/dsrODBLVW8fn05dkuukTk1S5WZCvxsev5jwAVgJMbXx6WUvlThn0PFaP3MLPLPP0YCKgxchpAHTIUqYHA8AoNX1Dlvm0orCsBVDxvfDGter0S95LbsNxLlEMRhXpnKnontU+hW6++FgODA6LHBwlWcTq6hS5aMDyIxFwFUJpBN8Ii5DsKRMb8JgUActTt5uLmWh5trCMcSHLrSz3+d6+bnF3r50alOLMYCXreunAe3VHLfpkqKFytE5RwwsT1MAo7eHKLHF6bSaeWhpmqaG4pH013rG8YbiuEuNNNYbs+qP7o8IV681MPZTh9SwtZaF2/YUDF6/WIFDxopt8DmniaepyKnEbwQog74OvBp4In0gB9CPeL/InBDSvnZqfJZUSP4/itw/GvqYWjPeSVY4bTo8q56qNqqdohWbISKTZCMq7BpGx7KTZS9HXDpObA61dx8dHh2+c2WqewBdS4Zh96L6oss5Euty5dgsIDVQSAU5UysBqvZhHfVAwwayvCH4zxYn6Cy6wWVdywCrS+rPBv2g8mSU7172q5y/dD3MBS6MBY6iIf8JEJeGg+86xaR7/KEeP58Dw6rEbvFSCASxx+Oc//mypz+8DPlFx9q5wHDcVwlZdP2ZzyRpOXmED87281/n+um0xvGUCDYtaqY+zZVcs+mimXlr35ie5zr9PDz832sryyi2mXFG47hCcR5x45qOrwR4skkl3uGKShQs5zrKx0YCsSM+qPLE+L7LW3cGAzisppASDzBOI3ldt65sw5gTvs6lzZ454FNVxIh/7rprsl1BP8U8CQwLnSNEOJrwEPAeeCPcsx7+RMNKm+KnSdTLnJPpebNU1+mpkIViahsvfKi2Hinii0JEA+OD3wMasSWiyB3nFCCN5LfyHuu+c2WqewBda73IljsYLKpcGwqmh3Eo1Cymh5vH26GiNk34Bo6S6zufpXFuZeorEnl3Xt0bOpq6Lp6PjFSThb17jh3CEOhazSA88h7x7lDtwj86XYPDqtxNMD0yPvpdk9Of/SZ8rOHL3IdI9urp+9Po6GAvWtK2bumlD9/y2bOdvhSI/sePv3cBT793AUay+zcs7GC160rY0d9MS7b0nXNPLE9LnYN47IZicQTFBQUUGxTy3y/09LOm7ZWc7lnGJvZSKHZQCgWp284zLoKx4z643S7h8FgFHehmUKzep4lhGBwOMLpdjUom8u+nikT22AmZC3wQoiDQK+U8ngqZN8oUsoPpObm/x54BPhahusfBx4HaGhoyLb4pUcsBN0pMe86pQS97+LYEkV7ufKg6KpTvs79XUrcCwrU9EHYC45qFZYOoGhC9Hdz0di5bAn2z21+s2U6e4oqlOMyayooczKu3tP+yQwmjDgIEDbaMIf7AbBbjMT8vWDepBKN5iFV+04sZ4bE/L2YXVXjjhkLHUS93bekHQxEKSsav5fAbjHSPxzJqsyp8nMmPPRL1/iEM6iXEIKtdS621rn44wc30D4U5JcXe/n5hV7+7fBNvvqb6wCsKbOzvd7N1joXm6qdbKp24ipcGqI/sT08oSglhSaCscToMZfVxNkOL3aLEX8khjMlhFajAV84NuP+GAxEiSUkrsKx6VCr0YA3FGUwEAWY076eKZnuienIZQR/AHhYCPEQYAWcQohvSCkfA5BSJoQQ3wE+QQaBl1I+DTwNaoomh/IXj1hIrS9PH5n3XhgTc1uZ2jS08aGx+KDOGjUXfP4/1egcIBGGAhvEw2oUFh1W14L6PX0En34uW2xlc5vfbJnOnpFz8ZAawRcYx0bwqTvFZogTwo4hHiRqUbttA5E4ZY6KsetH8oCxsnKot8lRQTzkHx25A+qzo+KWtCV2M4FIfNzoKhCJU5LjnHem/HwGNy4miEgO9aortvG+fat5377VBKNxTrV6ONnm4WSrh5cu9/PvJztG09a6C9ne4GbfmlL23VbKmjL7omy0mtge7kIz3kgMd9oXkDcco9JhVeksJsKxJIVmA+G4evA80/4osZsxGcTo9QDheAKToWD0+rns65mS6Z6YjqwFXkr5KeBTMBZ0G3ifEGKtlPJKag7+LcDFbPNeUsTCKTE/MTYyHyfmpUrA179xzEXuVEEraneqOeaiCjUNEQupycHyhtQ86p0q3aXn1Pu4OdY7c6vDSJlzld9smc6eie1jKho/Bx8coNIc50ysAmtgCO+qO/CHY/jDcWq3HICuF1Q+xY3j5+AjvpzqXbvlANcPfQ9g3Bx8w84HbknbXOfm+fNqL0L6vOzeNbm5fMiU35B1Iw8Yjqv6zFF/2sxG9q8tY/9a9SUhpaTPH+F8l48LXX7Od/k4dn2Qn7zaBUCl08LeNaVsr3ezpcbF5honRQuwSmdie2ysLuLn5/uodFhJJpOjc/CP7KqjwxuhzGHmcs8w4XicZBLq3LYZ90dznZvL3X5uDAaRcvwcfHOd+rKfy76eKeltMFNmtQ4+TeAfBn6NWlEjgNPAR0ZW1UzGknnIGgtDb9rIvDM1Zz4yRVBYogS8ZvvYyDwXP+eZVomUrsu8kmSuVr3oVTR5vYpmIfpTSsmNgSCHrw5w+NoAr1wboM+v/pMQAtaWF7Gtzs221DTQ5mrnvPjO0atoxsp9857NNxOBodXTpV95G53ikbFplq5T6r03XcyLxyIPjYi6q15v7ddoUkgp6fVHONfp5dX2kZeH/mE1P20oEKyvdLCt1kVTnYtttS42Vju0W4U5RO9kBUjE1APPzpNq1NN5Uon7iEtcq3tMxEdE3d2gxVyjyRIpJd2+MK+2eznT7uVMhxL9oaD6WzMZBBuqHGytTY30a12sr3ToHbc5svIEPplQ0Yc6T6ZeJ6D7jHqQCalwcs3KLe6IoLtXaTHXaOYJKSUdnpAS/ZTgn2n34gur/5bNhgI2VDloqlWCv7XWxfqqIj3SnwH5LfDJpFrfPCLmHSeg6zTEAuq8yQ7VzWOBnmt2qAdvOpycRrOoSClpHQxypmNspH+2Y0z0jQWCdZUOttQ4aapxsqVWLdlciAe5y4n8EXgp1fb9kSmWkQehkdT6ZqNV7QCtSRPzsnXa4ZZGs0wYEf1znT7OdHg51+njXIeXgdSac4DVpTY21zjZXO1kc41ao1/ltK5Y3/gL4YtmfvB1jU2xjAh6cECdKzCpQM9N7xgbnZdvBMPS2Iyh0WiyRwjBqlI7q0rtPLS1GlCi3+OLcLbDy4UunxL9Th/PnRnbZFZsM7GxSon9xioHG6sdrKtwjK5d1yy2wCfjcPn58Q9Bh1MdKAzKH8uGN42Nziu36MhDGs0KQAhBlctKlcvKfZsrR4/7wzEudvu50OXjQpeP811+vnX0JuGYcp9dIGB1qZ2N1Q42VDrZUOVgY5WD+hLbigxkvrhTNDUG2fJ4ESCUX5aaHWMj88omMNsWzTaNRrM8SCTVFM/FLh8Xu/1c7FbvrYPBUfdPVlMB6yocrK9Ugr++ysGGSgeVTsuynOZZHnPwGxtky8++DdXbwOKY/gKNRqOZIcFonNd6hnmtx89r3X4u9fi51O2n1z/m7sFpNbK+Ugn++ooi9V7pyNrny0KzPAR+qexk1Wg0K4ahQJTXepTgK/Ef5lKPH28oNpqmxG5mXUURG6ocrKtUo/31lUW4bUvDn/7yfciq0Wg080ix3cyeNaXsSfMdM+KDR4n+MJdTXwD/fqKD4Uh8NF25w8L6yqLR6Z4NVUWsq3SMeq5camiB12g0Kx4hBBVOKxVOK69bVz56XEpJlzfMaz1+Lveokf7lHj/fbWkjGB1zVVzltLKusig10newrlIJ/2Kv39cCr9FoNJMghKDGXUiNu5A3bBhzE51Mql26r/X4udw7zGvdfl7r9fONI2MrekC5W15fmZrbr3CwocrB2oqieXHGlgkt8BqNRpMlBQWC+hIb9SU27t00towzkZS0DQbHhD/1YPfQlQGiCSX8QsCqEpt6uFs5tqKnscw+5755chb4VOSmFqBDSnlQCPFNYBcQA44C/7uUMjZVHhqNRpNPGAoEq8vsrC6z88CWsePxRJIbA8HRuf3XUnP9v7jYSyKpFroYCwSNZfZRwVdz/A4aZrGGfzYj+I8BF1A+4AG+CTyW+v1bwIeBL02ZQ7BfRTpaKB/lS803+nJlYjs6a1T81Mk+T9bOc9gfU/rnnqd+nxOf4JPYdrp1iOfOdt3i6zzXcjNdA+ScTza+1qcqOz0ft80ICCTMu4/1TPWYSfnpdfEGI3R4wgxH4rf00WT1ftPWat6U2q0LEIknuNYXSAm+n0vdw5zt8PLcma7RNfwWYwHrKouU4KdG/DMlp2WSQog64OvAp4EnpJQHJ5z/OFAmpfzTqfLZ1bROtnzrL3OKeJ813g4VMcjqnDYivWYKJrajpxVaj0D9Xiiuv/XzZO08h/2RHm3+lij3YnBe+n3KMmcqSpO0wbmiA3zxRBi33YjLahqNVvT4XY1UOK1Zl5vJ1vbBIBQI6tyFWecTTya53DNMQYHy+7e+0oGhQGS8dqqy7WbDaD7+UJxYUlJoMrC7sQSLsSD79pwhmeoxk/LT69LjC/HTsz2YDIJN1U6SUo720UjQkdncH8FonCu9w1zqVsJ/MfXe41Nr+G9+9uC8LpN8CngSuOWrRAhhAt6HGuFPzxSR4eeUjhPqD2mkvIUqN9+Y2I7DvWArhkAPlKy69fNk7TyH/TEx2vy4KPcF89PvU5Y5U0GapA0unHgRt/1Oim1qs83I+3Nnu9jRUJx1uZlsHQwqR16bqpxZ53O5Zxib2Uih2UAoFqdvOMy6CkfGa6cqO2QyjubT7Q0jgBq3ldbBADsbSrJvzxmSqR4zKT+9Lj8724270IzZKBgYjrCmXEnhc2e7aG4onvX9YTMbU1Gy3OOOe4JRXusZZs9nZ1bXrGf0hRAHgV4p5fFJknwReElK+etJrn9cCNEihGjx+VIR/cxFqTBr80iwX5WTzkKUm29MbMeITwVOifgyf4bM7TyH/TEYiGKfsBzNbjEyGIjOW79PWeZMmcS2uL8P14R11S6riR5fOKdyM10TS0hiieS4YzPNxx+JYTUp6bAaDfjD8Umvnars9HziCUksmRzNbyb25Eqmesyk/PS6eEJRbOYCTIYCgjG1XHKkjyar91zUx20zs7uxZMbpc3lkewB4WAhxA3gGuEcI8Q0AIcSfA+XAE5NdLKV8Wkq5S0q5y+nMPeJ91tjKVDnpLES5+cbEdrQ4IewZPwpN/wyZ23kO+2Mk2nw6o1Hu56nfpyxzpkxim9FRjjc8fn2CNxyj0mnNqdxM15gMApNh/J//TPNxWEyjSwHD8QQOq3HSa6cqOz0fo0FgKigYzW8m9uRKpnrMpPz0urgLzQSjSWKJJLbUkseRPpqs3vNVn6nIWuCllJ+SUtZJKVcDjwIvSCkfE0J8GHgQ+C0pZXLKTNIZiXhfuzNbU7KjdqcqJ+JTgZgXqtx8Y2I7FlVAcAjslZk/T9bOc9gfzXVu/OE4/nCMpJT4wzH84bh6mDdP/T5lmTNlEts27XwDnkCcoWCEZDLJUDCCJxBXD/FyKDfTNSU2MyVFlpzyKXOYCUaVfcFIgvIi66TXTlV2ej52sxGT0cBQIEZDiT239pwhmeoxk/LT67KjwYUnFGUoGKW0yDKujyar93zVZypm5YtGCPEG4I9TyyTjwE3Anzr971LKv5jq+l2bV8uW7/+9XkWz3NCraKYvc6boVTQrahXNXNVHOxvTaDSaPGWmAq+DlGo0Gk2eogVeo9Fo8hQt8BqNRpOnaIHXaDSaPEULvEaj0eQpWuA1Go0mT9ECr9FoNHmKFniNRqPJU7TAazQaTZ6iBV6j0WjylCUXkzUWi9He3k44HF5sU5YEVquVuro6TCbT9Ik1Go0mjSUn8O3t7TgcDlavXo0QucUhzBeklAwMDNDe3k5jY+Nim6PRaJYZS26KJhwOU1pauuLFHUAIQWlpqf5vRqPR5ETOAi+EMAghTgohfpz6/IdCiCtCCCmEmFU0BS3uY+i20Gg0uTKbKZqPAReAkdA9h4AfAy/O0ibNSmGu/bRrf//Lgvn0kz4fLIS981VGTiN4IUQd8GbgKyPHpJQnpZQ3Zm3REsBgMLB9+3aampp4y1vegsfjAaCzs5N3vvOd015fVFSU8fizzz7L+fPn59TWZYu3Ay49B/GgigIVD6rP3o6lkZ9mXujyhHj+fA+haIKyIguhaILnz/fQ5QkttmkZWQh757OMXKdongKeBGYemm8ZUVhYyKlTpzh79iwlJSV84QtfAKCmpobvf//7OeerBT6NjhNgdarYraJAvVud6vhSyE8zL5xu9+CwGnFYTRQIgcNqwmE1crrds9imZWQh7J3PMrIWeCHEQaBXSnk8lwKFEI8LIVqEEC19fX25ZLGg7Nu3j44ONQq8ceMGTU1NAASDQd797nezbds2HnnkEfbs2UN6dKo//dM/pbm5mb1799LT08PLL7/Mf/zHf/CJT3yC7du3c/Xq1UWpz5Ih2A/mCf/pmIvU8aWQn2ZeGAxEsVvGzwzbLUYGA9FFsmhqFsLe+Swjlzn4A8DDQoiHACvgFEJ8Q0r52EwullI+DTwNKmTfVGn/7/88x/lOXw4mTs7mGid//pYtM0qbSCT4xS9+wYc+9KFbzn3xi1+kuLiYV199lbNnz7J9+/bRc4FAgL179/LpT3+aJ598ki9/+cv82Z/9GQ8//DAHDx6c0TRP3mMrg+iwGmmPEB1Wx5dCfpp5ocRuJhCJ47CO7esIROKU2M2LaNXkLIS981lG1iN4KeWnpJR1UsrVwKPACzMV9+VCKBRi+/btlJaWMjg4yP33339Lmt/85jc8+uijADQ1NbFt27bRc2azmYMHDwJw++23c+PGjQWxe1lRuxPCPoj4QCbVe9inji+F/DTzQnOdG384jj8cIykl/nAMfzg+Goh7qbEQ9s5nGXO20UkI8VHUvHwV8KoQ4jkp5Ydnk+dMR9pzzcgcvNfr5eDBg3zhC1/gox/96Lg0UwUrN5lMo8sbDQYD8Xh8Xu1dlrhqYcNDao58uFeNtDfcmfuql7nOTzMvVLsLuX9zJafbPfQPRyixm9m7pnTJrqJZCHvns4xZCbyU8kVSyyKllJ8HPj9ri5YQLpeLz3/+87z1rW/lIx/5yLhzd955J9/97ne5++67OX/+PGfOnJk2P4fDgd/vny9zlx+u2rkV4LnOTzMvVLsLl6ygZ2Ih7J2vMpbcTtalxo4dO2hubuaZZ54Zd/z3f//36evrY9u2bXz2s59l27ZtuFyuKfN69NFH+eu//mt27NihH7JqNJp5R0w11TDf7Nq1S6avPAG4cOECmzZtWiSLZk4ikSAWi2G1Wrl69Sr33nsvr732Gmbz3D8sWi5totFoFgYhxHEp5a7p0i05Z2PLhWAwyN13300sFkNKyZe+9KV5EXeNRqPJFS3wOeJwOJj434dGo9EsJfQcvEaj0eQpWuA1Go0mT9ECr9FoNHmKFniNRqPJU7TAT+DjH/84Tz311OjnBx98kA9/eGxD7h/90R/xuc99bjFM02g0mqzQAj+B/fv38/LLLwOQTCbp7+/n3Llzo+dffvllDhw4MPo5kUgsuI0ajUYzE7TAT+DAgQOjAn/u3DmamppwOBwMDQ0RiUS4cOECXq+Xu+++m/e85z1s3boVgM997nM0NTXR1NQ0+h/AjRs32LRpE7/7u7/Lli1beOCBBwiFlBP/Y8eOsW3bNvbt28cnPvGJUTfEGo1GM1cs7XXwP/0kdE/v4yUrqrbCmz4z6emamhqMRiOtra28/PLLo/7gDx8+jMvlYtu2bZjNZo4ePcrZs2dpbGzk+PHjfO1rX+PIkSNIKdmzZw+vf/3rKS4u5vLly3z729/my1/+Mu9+97v5wQ9+wGOPPcYHPvABnn76afbv388nP/nJua2jRqPRoEfwGRkZxY8I/L59+0Y/79+/H4Ddu3fT2NgIKNfBb3/727Hb7RQVFfGOd7yDX//61wA0NjaO+oofcR3s8Xjw+/2jeb3nPe9ZhFpqNJp8Z2mP4KcYac8nI/PwZ86coampifr6ev72b/8Wp9PJBz/4QQDsdvto+qn8+VgsltHfDQYDoVBoyvQajUYzV+Q8ghdCGIQQJ4UQP059bhRCHBFCXBZCfEcIsWwdsxw4cIAf//jHlJSUYDAYKCkpwePxcPjwYcZe87oAABBQSURBVPbt23dL+rvuuotnn32WYDBIIBDghz/8Ia973esmzb+4uBiHw8Err7wCcIunSo1mKdDlCfGzs11868hNfna2a0kFxl7Kti0lZjNF8zHgQtrnzwL/n5RyHTAE3BrnbpmwdetW+vv72bt377hjLpeLsrJbQ8Dt3LmT97///ezevZs9e/bw4Q9/mB07dkxZxle/+lUef/xx9u3bh5RyWlfDGs1C0uUJ8fz5HkLRBGVFFkLRBM+f71kSQrqUbVtq5OQuWAhRB3wd+DTwBPAWoA+oklLGhRD7gP8ppXxwqnyWs7vg2TI8PExRkQoS/ZnPfIauri7+7u/+LmPaldImmqXDz852EYomxsUJ9YdjFJoNvLGpehEtW9q2LRTz7S74KVR4PkfqcyngkVKOxKZrBzKG1hFCPA48DtDQ0JBj8cufn/zkJ/zVX/0V8XicVatW8S//8i+LbZJGM8pgIEpZkWXcMbvFSP9wZJEsGmMp27bUyFrghRAHgV4p5XEhxBtGDmdImvFfAynl08DToEbw2ZafLzzyyCM88sgji22GRpOREruZQCQ+bpQciMQpsS/+o7WlbNtSI5c5+APAw0KIG8AzwD2oEb1bCDHyhVEHdOZqlF5lMoZuC81i0Fznxh+O4w/HSEqJPxzDH47TXOdebNOWtG1LjawFXkr5KSllnZRyNfAo8IKU8r3AL4F3ppL9DvCjXAyyWq0MDAxoYUOJ+8DAAFardbFN0awwqt2F3L+5kkKzgf7hCIVmA/dvrlwSwbKXsm1LjblcB/8nwDNCiL8ETgJfzSWTuro62tvb6evrm0PTli9Wq5W6urrFNkOzAql2Fy5Z0VzKti0lZiXwUsoXgRdTv18Dds/WIJPJNLpDVKPRaDS5o10VaDQaTZ6iBV6j0WjyFC3wGo1Gk6fktJN1zgoXog+4OctsyoD+OTBHl7u0ylyscldSXRer3JVS5nyWu0pKWT5dokUV+LlACNEyky27utzlVeZilbuS6rpY5a6UMhez3BH0FI1Go9HkKVrgNRqNJk/JB4F/Wpebl2UuVrkrqa6LVe5KKXMxywXyYA5eo9FoNJnJhxG8RqPRaDKwLAReCJHJHXFeouuav6yk+uq6Lg2WhcADboA0d8TzjhDiPUKI5tTvC9mBo64jl/KNM0cseL+myltxfSuEWOi/9aJUuYaFKlAI8bAQ4raFKi+N0Toutb/ZJS3wQgiXEOK/gZ8BpEWMms8y7xNC/Brl435Hqtx5f1AhhHhACPEy8A9CiPcuYLlvE0L8P/NdzoQyF7xfU+WutL59WAjxxHyXk1aeEEJUCCFeBL4CIKVMLEC59wkhDqM82C5YzD4hxJuFEM8DnxNC3AUL06/ZsKQFHgijAng3CSHeBfMzIkjdmIVCiO8Cfwb8JfB9wDZfZU4ovxz4C+D/Bb4FPCKE+FTq3Jz3Uaq+BiHEh4G/AT4phHjdXJczBQvSr6l8V1TfpvI1CiH+BPg88DdCiO1SyuR81zUlbuHUa5sQ4k0pe+brHi4SQvwnql//DHgFWDVfZU4ofzUqJvXfAxeAx1N/T4vx39LkSCmX5Av1b08l8HHgINCddk7MU5lvTfv9MeDwAtRTAE3AP6Ud2wwMAGXzXN83oOLq/i7wYr726wrt27fx/7d37sFWVXUc/3y5ICIvYZBSfKAC6iDCmCn5AIowTNMMyNJMEivNR2k6pYOS5uRjGscMUWI0H41O5ivDlGp8kJIKmuJjTJ1wfOSrURNRSOHXH791vNvbBc45d5/HPfv3ndlzztp7nf3Zv7X2Wc/fXtuHhH4APFinvO2R7DsfOKROaXxY5vvxwA11snUyMDd93zT9lx4DBtUyXyvdmqamkXSSpAWSjpYk867dO8CBZrYQWC7pLEm7mpnlMdaVYX4bwMx+n/a3ASuAJyVt01VOJ9yjJE1JTAPeBfaWNDjtewr4Hd46yJNbsveYtOteM1tpZguAvpJmpXi53ReNyNcO3CLl7fmSvpp23W5mq83sYmCopMNTvF7rP0vVzGkAZrYOf1XnKOB+4BVJx0oaWQPmjMT8bdrfBrwNvCip94bOUSV3uqS9MrteAqZJ6p3S+R5gCXBm3uwuqdE1TKrtZuLdq6nAvcAZwI7AUODcFOdo4ENgWQr3qgFzh8zxMcBSoH+Odg7ChwdeAZYDbZlj1wDXdoj7ILB9jdL4dGDHzPEDgCdJLZDumq9Fy1u8l3AyXqBOx4cLZgJDM3EOBV7O0db1MQcDewBzUrxTgVXAH1K4Zw2YW2Ti7A08nZed6ZxD0z30L+BWoEeHfL04c31j0z3wiTyvoStbs7TgJwMXmNmdwA/xLs8M4H3ggDQhdxJwF+2rT3Z1Yq4jcxO86w6AmT2e+F/rIucjmdlbwJ+AXYCHgbMyh08Apkr6dAqvwrt8/80J31kaH5G5tjtoH0vsX2oh1YBZ63ztjNuyeWteunwWmG1mN+KF4FjgC5k4twDPSDoVfFKyBsxxwBTgVWCCpD8C38IL5H+mn1Y94boBO6dm4iwBXpJ0cLWcTriv4++XnopX3t/NHD4HOEjS6HR9q4GVeK+tKdTQAj4zFPB3fDwWM1uGd3W2B/YF/gw8ZGbjzGx/YJKk7VOC5sl8ANhK0j4pnvA/7KY5DQeVznGNmb0NzAO+Imm7dA3vAGcDZ0o6Cp802pUu3iwbsPdvZOxN+hFwHvAs8MkaMGuWrxvhtkTedrzWjL3LgP0S607gGWC0pJ0y0Y8DLpT0KjCsBsx/ALvhBf2LwFIzG41XopMkDSs3b6uwc+cUbwDwNPBBufaVyf0l8BR+zxwoact0Dc/hnjvzJO2LNyKGAuuq4ddCdS3gJY2W9JEvsPmYHXgt30PJ1QgfKngZnwA8y8xmZ06zrZmtqAHzCbyG3irFMzyzVlVT6HTCtfS5On0uBe7AZ+JLcebiLnyfwr0BppvZfyrk7qOML3C59koagRdMtwK7m1nZY8QVMHPL1wq5eedtR25d8hb42FumM/Y+B/SXNCaF7wUG4umMpHHAAuAmPG+vrgFzMTAAeAM41szmpPhvAvuY2cs1YJbs7JfivQNsjU/iV6NOuWb2gbkr7xK8Avl+Js55eCE/C9gJmGVm71fJz1/1GAfCa/b7gFuAYZn9PdLnYHy87lLS2CVwOXBa+t5GZuyrhszLSswU3iRHW9XRBmBbvHU5Gr8pR5TsrYK7O97CWIP/iSuyF9gCGFkHZpfyNQ9bu5C36+PWOm/H44Xzr4H9Mzb1TJ8jcM+VUzL7bsMLWoBtgDF1ZrZRoSdJV5kpvGmO6ausDcmmCcDNeEUylHavmYrvp3ps9WrBzwZuNLNDLdXkktqsvWZeCfwVHyv9eZrp3xx3J8PM1mbi1pI5qMRM3GrGSNfHNXNf5D6SSi2OF/CK4HG8NTKgZG+5MEm9JM3HV627BFiEu2xVZK+ZvWFmz9aBWXW+5mVrYpedt2Vwa5K36fyT8J7VzfgwyDeAQZJ6WHpAzHyoYCleAP44/XQNaV7DzF40n3eoB/P5kp2WSr56MVOc1eUyy+CamZmk3slbZq2ZLcZ7ok/g+TokcfOaK8tXtaw98CGgHYErM/um4H/yUg18Lu42tjP+FNpVeMtnPtW1durOrID7U/xG2i2Fv47/CS+kSu8RvHt6BNAnhWfi3fGemThn55zGdWd2A+6cvPM2neckkh893mq8nkwrNd3LVwDDk8234ZO886mid1QkZpncc4BrgeEpfCzwOnBBV/K1Xlv+J/TuzqhMuD8+aXcQPr67CHcvOj1l1nWk7muK34MK3dcawcyJO54qXOWyXDp0g/GxwMtLx/Aho+v4uEtkl9K4Xsxuzu1y3qbwOOBNvAJ5DbgHuBI4DHcL7HhP9QM2D2bNuJ/Phpt9y+9E3lK9He8ezwb6Zo6dATwCHJzCE3DXo89k4lQzFlt3Zk7caluSnXLJjAHj3dfX6OSJujzTuJbMbs7NK2/7ZY7tiRc601J4Ft6DGJtz3rYkMyduVfna6C3PMfi+eIv1xPR9QubYQrwFOziFl+H+sqvB3ZGs8jH2RjHz4FbrD9wp11zrklvX8ynOxNKxDDe3NK4xsztz88rbj9YGMrOH8Enw0rMCd+EF1lsZbh5526rMPLg1XzStFupSAS/pm5ImShpgPqH4K+AGvDDbS9IwADNbDpwGHC9pCD6RMYb2ybZKJtrqzmxybsnNUencJdfMUoWiSrmNYAZ3g9zeuIve99JPJ+MNiJJbZi3ytlszG8ltJlVcwMu1paS7gaPwyafLJA0xX5PhPeAvuNfC50q/M7Mr8AmMnwDTgGPMPQ2aktnduGZmyaPjXXw4YXxpf7Myg7tR7uR0/jX4pGI/SYvxCdwTzJ+yDGYTcJtWVtk4Vsk/dBTwm/S9J/6k180d4p6Mz3wPJDPJRYUzz41gdlPuZg1I46qZwS2buznt3jt9yKypE8zm4DbzVm7C9QR+hrsGTQS+BFydOS78ScGJmX398Cf3HsInpLaqMLPqziwat0i2dmPu0sQdFszm4naHrZzEm4gvjHQZvm74YnzhnReAPTPxjgPuzoQPwxdTWkBmZbsyM6zuzKJxi2Rr0bhFYTaS2122chJwP+DITHheSqyZwMNpXw98caobaH8g4BBgQlUX1QBm0bhFsrVo3KIwG8ntLls5CbgZ0Jv28a0jgPPS90eBE9P3PYDrc7moBjCLxi2SrUXjFoXZSG532TbqRWNm75nZGmv3A52CrxgHvt7zLpIW4l4jj8D/L7tZqRrBLBq3SLYWjVsUZiO53UYV1JRteFfnDtpXxhuBz0LvSw0mKRrBLBq3SLYWjVsUZiO5zb5V4ge/DugF/Bt/Y/pC/P2D68zsPqtsvedmZhaNWyRbi8YtCrOR3OZWhbXkeDwh78MXtq95DdQIZtG4RbK1aNyiMBvJbeZNKWHKkqStgSOBi8yf/qq5GsEsGrdIthaNWxRmI7nNrIoK+FAoFAp1HzX0pduhUCgUqp2igA+FQqEWVRTwoVAo1KKKAj4UCoVaVFHAh0KhUIsqCvhQYSRpraRHJT0p6TFJp8hfwbeh3wyXdHi9rjEUylNRwIeKpPfNbJyZjcbXLPkiMGcjvxkORAEf6pYKP/hQYSTpXTPrlwnvgL/wYQiwHXAt/kJm8Fe2LZH0ALALsAK4GrgEOB+YhK9ieKmZza+bEaFQBYoCPlQYdSzg0763gJ2Blfi6JasljcSXlt1D0iTgVDM7KMX/Dv6CiHPlL2u+H5hhZivqakwoVIZ6NvoCQqEGq7R0bC9grqRxwFr8vZ6daX98MavpKTwQGIm38EOhplIU8KHCKg3RrAVex8fiXwPG4nNTq9f3M/wlEovqcpGhUBcUk6yhQkrSFsDlwFzzccqBwCtmtg5fsKotRV0J9M/8dBFwnKRe6TyjJPUlFGpCRQs+VCT1kfQoPhzzIT6pelE6Ng+4SdIM4G5gVdq/HPhQ0mPAVcAvcM+aR9Kbgd4AvlwvA0KhShSTrKFQKNSiiiGaUCgUalFFAR8KhUItqijgQ6FQqEUVBXwoFAq1qKKAD4VCoRZVFPChUCjUoooCPhQKhVpUUcCHQqFQi+p/eT9LWnlZ2kEAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "options = dict(marker='o', linewidth=0, alpha=0.3, label='')\n",
    "\n",
    "df['% responding right'].plot(color='C0', **options)\n",
    "df['% responding wrong'].plot(color='C1', **options)\n",
    "\n",
    "right = make_lowess(df['% responding right'])\n",
    "right.plot(label='Right')\n",
    "\n",
    "wrong = make_lowess(df['% responding wrong'])\n",
    "wrong.plot(label='Wrong')\n",
    "\n",
    "plt.legend();"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.7.2"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 1
}

Nice! Loved her article!

Thanks for this! For my use case I needed a slightly more sensitive smoothed line so I made a tiny addition to the function to add a variable which passes to the frac parameter for the original lowess function, this means you can alter the 'wobbliness' each time you call the function as required.

Makes sense. Glad it was useful!

…

On Fri, Jul 26, 2019, at 4:51 AM, Tom Bush wrote: Thanks for this! For my use case I needed a slightly more sensitive smoothed line so I made a tiny addition to the function to add a variable which passes to the `frac` parameter for the original `lowess` function, this means you can alter the 'wobbliness' each time you call the function as required. — You are receiving this because you authored the thread. Reply to this email directly, view it on GitHub <https://gist.github.com/818f6153ef316aee80467c51faee80f8?email_source=notifications&email_token=AAOLP3KC3TNLURUYYFUTU33QBK3JPA5CNFSM4IHB2BFKYY3PNVWWK3TUL52HS4DFVNDWS43UINXW23LFNZ2KUY3PNVWWK3TUL5UWJTQAFV7G6#gistcomment-2981487>, or mute the thread <https://github.com/notifications/unsubscribe-auth/AAOLP3KCN5QUXDIJDIVP3IDQBK3JPANCNFSM4IHB2BFA>.