Skip to content

Instantly share code, notes, and snippets.

@GuiUzeda

GuiUzeda/tensorflow-2-0-deeplearning-workshop.ipynb

Created October 2, 2019 16:08
Show Gist options
  • Save GuiUzeda/7e5723f690e96e3c36ada59429f5e0a4 to your computer and use it in GitHub Desktop.
Save GuiUzeda/7e5723f690e96e3c36ada59429f5e0a4 to your computer and use it in GitHub Desktop.
Download ZIP
Tensorflow 2.0 & DeepLearning Workshop
Display the source blob
Display the rendered blob
Raw
tensorflow-2-0-deeplearning-workshop.ipynb
{
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"name": "Tensorflow 2.0 & DeepLearning Workshop",
"provenance": [],
"collapsed_sections": [],
"include_colab_link": true
},
"kernelspec": {
"name": "python3",
"display_name": "Python 3"
},
"accelerator": "GPU"
},
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "view-in-github",
"colab_type": "text"
},
"source": [
"<a href=\"https://colab.research.google.com/gist/GuiUzeda/7e5723f690e96e3c36ada59429f5e0a4/tensorflow-2-0-deeplearning-workshop.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "84tt9mnsk9E2",
"colab_type": "text"
},
"source": [
"# Tensorflow 2.0 & DeepLearning Workshop\n",
"\n",
"Este material apresenta alguns conceitos básicos de Deep Learning juntamente com uma introdução ao Tensorflow 2.0, portanto tem como objetivo ser um ponto de partida para quem está estudando e quer aprofundar seus conhecimentos em Deep learning tanto práticos como teóricos. Não é objetivo desse material esgotar todo este tema e, por isso, muitos aspectos teóricos mais complicados foram deixados de fora. Materiais mais avançados serão referenciados no decorrer deste material por meio de Links. \n",
"\n",
"Este notebook foi projetado para rodar no Google Colab, em caso de execução local ou em outro ambiente lembrar de checar se as dependências estão corretas, incluindo o Tensorflow 2.X. \n",
"\n",
"O TensorFlow é uma plataforma de código aberto de ponta a ponta para aprendizado de máquina. Possui um ecossistema flexível e abrangente de ferramentas, bibliotecas e recursos da comunidade que permite que os pesquisadores desenvolvam o que há de mais moderno em ML e os desenvolvedores construam e implantem facilmente aplicativos com ML.\n",
"\n",
"\n",
"![Tensorflow](https://i1.wp.com/sourcedexter.com/wp-content/uploads/2017/05/tensorflow-1.gif?resize=800%2C445&ssl=1)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Hgyx89Z4lPzh",
"colab_type": "text"
},
"source": [
"## 1. Importar Bibliotecas\n",
"\n",
" \n",
"\n",
"A primeira coisa que é preciso fazer é importar as bibliotecas necessárias para este código. Como queremos lidar com o Tensorflow 2.0 basta selecionar no Google Colab a versão 2.x. Vale lembrar que se esse notebook não for usado dentro do Colab o Tensorflow 2.0 precisa ser instalado manualmente.\n",
"\n",
" \n",
"\n",
"Fora a biblioteca do Tensorflow também usaremos o `matplotlib` para visualização de imagens e `datetime` para medir o tempo total de treinamento da nossa rede neural.\n",
"\n",
" \n",
"\n",
"O Tensorflow 2.0 utiliza o `Keras` como interface primária e por isso precisamos importar as `layers` que vamos utilizar bem como a classe `Model`. As layers que iremos utilizar nesse workshop são:\n",
"\n",
" \n",
"\n",
"* **Dense**\n",
"\n",
"* **Flatten**\n",
"\n",
"* **Conv2D**\n",
"\n",
" \n",
"\n",
"### Dense:\n",
"\n",
"Essa camada é uma das camadas mais simples que existem e é chamada de densa, pois todos os neurônios que a constitui recebem todos os inputs e produzem outputs agregados de acordo com a sua função de ativação. Ou seja, a conexão entre os neurônios é densa e pode ser representada segundo a seguinte imagem:\n",
"\n",
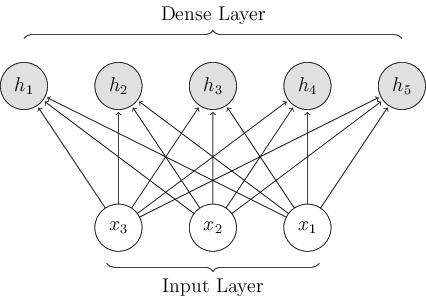"![Camada Densa](https://slugnet.jarrodkahn.com/_images/tikz-be0593f4dad31d763e7f8371668007610e7907c1.png)\n",
"\n",
" \n",
"\n",
"### Flatten:\n",
"\n",
"Essa camada é na realidade uma operação de reestruturação de um tensor. Como uma camada densa só consegue lidar com tensores unidimensionais essa operação se faz necessária para transformar tensores de n dimensões em uma dimensão apenas. No nosso caso, estamos lidando com imagens que podem ser interpretadas como tensores de dimensões i por j, então quando aplicada a operação da camada Flatten teremos um tensor de uma única dimensão $i \\times j$. Assim, essa operação pode ser representada por:\n",
"\n",
"![Camada Fallten](https://sds-platform-private.s3-us-east-2.amazonaws.com/uploads/73_blog_image_1.png)\n",
"\n",
" \n",
"\n",
"## Conv2D\n",
"\n",
"Essa camada é chamada de Convolucional e dá o nome as Convolutional Neural Networks. O funcionamento desta camada é um pouco mais complexo do que as camadas densas, entretanto uma das suas principais características é o fato de ser uma camada esparsa que economiza bastante memória e, portanto, permite a criação de redes realmente profundas. As camadas convolucionais conseguem abstrair informações muito precisas sobre o tensor em questão e durante o treinamento conseguem se especializar em reconhecer determinados tipos de padrões.\n",
"\n",
"Em linhas gerais essa camada é constituída por um núcleo (Kernel) que é um tensor de tamanho i por j que vare o tensor de input agregando os valores em um output. A explicação em profundidade desse tipo de camada está além do escopo desse workshop, mas um artigo muito completo e rápido sobre o assunto pode ser encontrado [aqui](https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53). Assim, as camadas convolucionais podem ser representadas visualmente da seguinte maneira:\n",
"\n",
" \n",
"\n",
"![alt text](https://miro.medium.com/max/790/1*nYf_cUIHFEWU1JXGwnz-Ig.gif)\n",
"\n",
" \n",
"\n",
"Por fim, a classe `Model` servirá de ponto de partida para nossa rede neural. No Tensorflow 2.0 podemos utilizar essa classe como classe-mãe para a nossa classe Modelo e a partir daí definir quais são as camadas e como elas se relacionam entre si."
]
},
{
"cell_type": "code",
"metadata": {
"id": "ZNG8M4Te8Goh",
"colab_type": "code",
"colab": {}
},
"source": [
"# Selecionar a versao do Tensorflow\n",
"# Funciona somente no Colab\n",
"try:\n",
" %tensorflow_version 2.x\n",
"except Exception:\n",
" pass"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "code",
"metadata": {
"id": "WiQRjRTJ8JLk",
"colab_type": "code",
"colab": {}
},
"source": [
"import tensorflow as tf\n",
"\n",
"from tensorflow.keras.layers import Dense, Flatten, Conv2D\n",
"from tensorflow.keras import Model\n",
"\n",
"import matplotlib.pyplot as plt\n",
"from datetime import datetime"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "9PGA-KKQlXLr",
"colab_type": "text"
},
"source": [
"## 2. Preparar os dados\n",
"\n",
" \n",
"\n",
"Os dados que iremos utilizar para esse experimento são imagens de dígitos de 0 a 9 escritos a mão que compõem um dataset chamado de MNIST. Esse dataset é muito utilizado para introduzir de forma amigável o tema de redes neuras, pois é um dataset fácil de entender que não requer preparo prévio. Normalmente, em um projeto de I.A. algo entre 70% e 90% do tempo seria gasto para entender, tratar e preparar os dados para treino, entretanto dado a limitação de tempo e escopo vamos limitar essa seção para ter apenas um conhecimento superficial dos dados.\n",
"\n",
" \n",
"\n",
"O dataset MNIST, como dito anteriormente, é composto por imagens de 28 por 28 pixels que contém um único dígito escrito a mão de 0 até 9. Cada imagem tem apenas 1 canal, ou seja, é uma imagem em preto e branco e pode ser representada num tensor de formato `[28, 28]`. Cada valor desse tensor é, portanto, um único pixel que pode variar entre 0 e 255. Assim, se o pixel for branco seu valor será 255 e 0 caso o contrário.\n",
"\n",
" \n",
"\n",
"Normalmente, imagens de texto como no MNIST tem um fundo branco com os caracteres em preto, porém isso representa um problema para nós. Conforme dito anteriormente, o preto é representando por 0 enquanto que outros tons são representados por valores maiores que 0. Se o fundo da imagem é branco quer dizer que existem vários valores altos que não ajudam a resolver o problema que precisam ser filtrados pelos neurônios da rede, por exemplo, as bordas da imagem. Isso dificulta o treino da rede neural e, por isso para resolver esse problema utilizamos as imagens com as cores invertidas. Dessa forma, o mais importante, o dígito, vai conter os valores mais altos e as demais partes da imagem vão estar com valores 0.\n",
"\n",
" \n",
"\n",
"Esse dataset pode ser encontrado dentro do keras, já com as cores invertidas. Por isso vamos fazer só mais uma alteração nas imagens. Redes neurais são muito sensíveis a valores extremos por isso vamos limitar o valor das imagens em um intervalo entre 0 e 1. Basta dividir a imagem por 255.\n",
"\n",
" "
]
},
{
"cell_type": "code",
"metadata": {
"id": "rU2HE3L28K_Q",
"colab_type": "code",
"colab": {}
},
"source": [
"# Carrega o dataset\n",
"mnist = tf.keras.datasets.mnist\n",
"\n",
"# Divide os dados entre treino e teste\n",
"(x_train, y_train), (x_test, y_test) = mnist.load_data()\n",
"x_train, x_test = x_train / 255.0, x_test / 255.0\n",
"\n",
"print(\"Quantidade de treino:\", len(x_train))\n",
"print(\"Quantidade de teste:\", len(x_test))"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "code",
"metadata": {
"id": "b8iQsuUrPVWJ",
"colab_type": "code",
"colab": {}
},
"source": [
"# Mostra a classe e o tamanho da primeira imagem\n",
"print(\"Classe da Imagem:\", y_train[0])\n",
"print(\"Formato da Imagem:\", x_train[0].shape)\n",
"\n",
"# Cria uma visualizacao da primeira imagem\n",
"plt.figure(figsize = (10,10))\n",
"plt.imshow(x_train[0], \"gray\")"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "KCuwUiBpma3u",
"colab_type": "text"
},
"source": [
"No Tensorflow temos a possibilidade de colocar os dados dentro de uma classe chamada `Dataset`. Essa classe já tem várias funcionalidades para manipulação de dados prontas que facilitam na hora de criar um modelo. Uma das funcionalidades mais importantes desta classe chama-se `batch`. Essa função agrupa os dados em grupos de tamanho $n$ que são utilizados no treinamento. Outra função importante é `shuffle` que embaralha o dataset e repete os dados $n$ vezes. Além disso, a classe `Dataset` é especialmente boa quando os dados não cabem todos na memória, pois ela possibilita a leitura do disco sob demanda. Mais sobre como trabalhar com dados dentro do Tensorflow 2.0 pode ser lido [aqui](hhttps://www.tensorflow.org/beta/guide/data#parsing_tfexample_protocol_buffer_messages)"
]
},
{
"cell_type": "code",
"metadata": {
"id": "MwOVctzzPt-c",
"colab_type": "code",
"colab": {}
},
"source": [
"# Carrega os dados dentro de um dataset do tensorflow.\n",
"train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train))\n",
"test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "tlbjBveQ216c",
"colab_type": "text"
},
"source": [
"## 3. Definindo e Treinando o Modelo\n",
"\n",
" \n",
"\n",
"Uma das formas mais diretas e rápidas de definir um modelo no Tensorflow 2.0 é utilizando a classe `Model` que carregamos anteriormente. É possível fazer toda a construção e treinamento de uma rede neural utilizando uma biblioteca mais simples como `numpy`, afinal de contas redes neurais são operações matemáticas e o Tensorflow é um pacote de programação diferencial. A grande vantagem do Tensorflow é que muitas operações e procedimentos já estão prontos, então não existe a necessidade de ficar programando cálculo de gradiente e back propagation.\n",
"\n",
" \n",
"\n",
"Antes de definir o modelo é preciso definir alguns conceitos de redes neurais que até aqui ficaram de fora. Primeiro uma rede neural é uma estrutura matemática modelada com inspiração no cérebro humano. O cérebro humano é composto por uma infinidade de células chamadas neurônios, em linhas gerais essas células servem como moduladores de sinais eletromagnéticos, ou seja tem a função de receber um sinal eletromagnético e amplificar ou reduzir esse sinal para os neurônios subsequentes (esta explicação ilustrativa aplica-se apenas para o estudo que estamos fazendo aqui, não necessariamente é uma interpretação biologicamente correta). Da mesma forma, os neurônios matemáticos servem para modular um sinal, que ao invés de eletromagnético é puramente matemático. Ou seja, um neurônio artificial pode ser representado pela seguinte função $y=\\sum_{i=0}^{n}x_iw_i+b_i$. No qual $w$ é o que chamamos de peso e $b$ o viés. Assim, quanto maior forem $w$ e $b$ maior o sinal de saída ($y$) e quanto menor forem menor o output. Dessa forma, podemos comparar as duas estruturas abaixo:\n",
"\n",
" \n",
"\n",
"#### Neurônio Humano\n",
"\n",
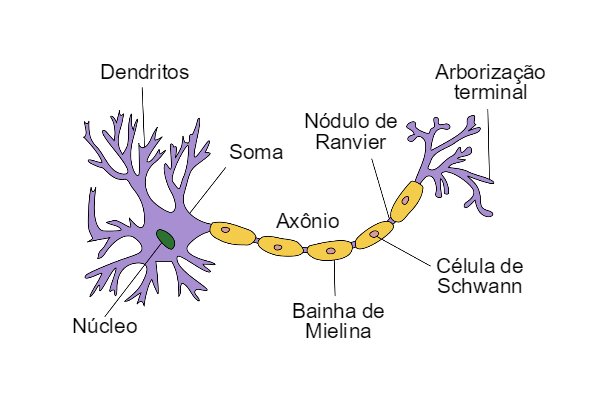"![Neurônio Humano](https://static.significados.com.br/foto/partes-neuronio.jpg)\n",
"\n",
"#### Neurônio Artificial\n",
"\n",
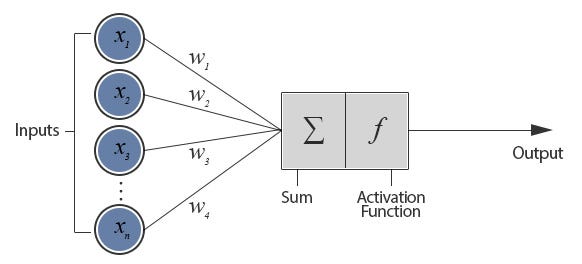"![Neurônio Humano](https://miro.medium.com/max/1164/1*nRRXhhjSjKNpGn-T3yF2Ew.jpeg)\n",
"\n",
" \n",
"\n",
"Como podemos ver na imagem acima existe também uma função chamada de função de ativação. Essa função serve para limitar ou até mesmo determinar qual o sinal que um determinado neurônio vai passar para frente. O input da função de ativação é a soma que foi apresentada anteriormente. Existem inúmeras funções de ativação e algumas delas são:\n",
"\n",
" \n",
"\n",
"![Funções de Ativação](https://miro.medium.com/max/1192/1*4ZEDRpFuCIpUjNgjDdT2Lg.png)\n",
"\n",
" \n",
"\n",
"Agora já é possível definir um modelo simples para identificar os dígitos. Um modelo inicial pode ser um modelo de apenas duas camadas:\n",
"\n",
" \n",
"\n",
"* Operação Flatten\n",
"\n",
"* Camada 1: 128 neurônios com ativação Relu\n",
"\n",
"* Camada 2: 10 neurônios com ativação SoftMax\n",
"\n",
" \n",
"\n",
"A segunda e última camada vai ser nosso identificador de classe, ou seja, se o neurônio 0 ativar isso quer dizer que a rede está classificando a imagem como dígito 0 e assim por diante. Essa camada tem uma ativação especial chamada de SoftMax. Essa ativação é dada por $\\sigma(x)_i = e^{x_i} \\div \\sum^k_{j=1}e^{x_j}$ e tem como objetivo transformar o resultado da rede em uma distribuição de probabilidade. Assim, no resultado final a ativação dos neurônios estará restaria a um valor entre 0 e 1 e se o neurônio 9, por exemplo, resultar em um valor 0.85 quer dizer que a rede tem 85% de \"certeza\" que a imagem input é o dígito 9.\n",
"\n",
" "
]
},
{
"cell_type": "code",
"metadata": {
"id": "ADJGdMHK18DJ",
"colab_type": "code",
"colab": {}
},
"source": [
"class MyModel(Model):\n",
" # Inicia a Classe com as definições\n",
" def __init__(self):\n",
" super(MyModel, self).__init__()\n",
" # self.conv1 = Conv2D(32, 3, activation='relu')\n",
" # Define a operação flatten\n",
" self.flatten = Flatten()\n",
" # Camada 1 com 128 neurônios e ativação Relu\n",
" self.d0 = Dense(128, activation='relu')\n",
" # Última camada com 10 neurônios e ativação Softmax\n",
" self.c = Dense(10, activation='softmax')\n",
"\n",
" # Funcão de Predição com a definição das camadas\n",
" def call(self, x):\n",
" # x = x[..., tf.newaxis]\n",
" # x = self.conv1(x)\n",
" x = self.flatten(x)\n",
" x = self.d0(x)\n",
"\n",
" return self.c(x)\n",
"\n",
"model = MyModel()"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "T8zUkFHnUyqd",
"colab_type": "text"
},
"source": [
"Com a rede definida, precisa-se definir a função de perda (loss) e a função de otimização. A função de perda que utilizaremos aqui é a chamada Sparce Categorical Crossentropy e a função de otimização será a Stocastic Gradient Descent. A função de perda simplesmente calcula o erro entre o resultado da rede e a classe esperada. O objetivo da rede é justamente minimizar o valor dessa função, encontrando os pesos e viés que melhor descrevem os dados. Já a função de otimização tem o papel de apontar para qual a direção a rede deve ajustar os pesos e viés para que o erro seja o mínimo.\n",
"\n",
" \n",
"\n",
"O processo de treinamento da rede neural ocorre pela busca dos pesos e viés que compõem uma função que melhor descreve os dados fornecidos. A maneira pela qual se atinge esses valores ótimos pode ser descrita como um processo de tentativa e erro, onde a rede tenta calcular o melhor resultado possível para um batch, avalia o erro desses resultados e ajusta os pesos de acordos com o gradiente desse erro. O gradiente, portanto, é o fator (derivada parcial em cada neurônio) pelo qual os parâmetros da rede são ajustados a cada iteração. O tamanho desse ajuste é controlado pela taxa de aprendizado. Essa taxa dita o tamanho dos ajustes na rede, por isso o ideal é que seja uma taxa pequena se não o otimizado pode sobre ajustar a rede e nunca convergir para uma resposta aceitável. Esse processo de ajuste chama-se back propagation, entretanto este tema está fora do contexto desse workshop e pode ser compreendido mais com [este material](http://neuralnetworksanddeeplearning.com/chap2.html)\n",
"\n",
" \n",
"\n",
"No nosso caso a função de perda escolhida se encaixa perfeitamente no tipo de classicação que se deve fazer. A Cross Entropia é dada por $-\\sum^n_{i=1}y_n\\log(\\bar y_n)$, onde:\n",
"\n",
" \n",
"\n",
" * $n$ representa o número de classes\n",
"\n",
" * $y_n$ é uma representação binária (0 ou 1) se a classe $n$ é a correta\n",
"\n",
" * $\\bar y_n$ é o resultado da rede neural para a classe $n$\n",
"\n",
" \n",
"\n",
"Uma vez que a ativação da última camada é SoftMax os valores de $\\bar y$ pertencerão à uma distribuição de probabilidades (entre 0 e 1) e o valor do logaritmo na função resultará em um valor entre $- \\infty$ e $0$, por isso a função é multiplicada por $-1$. A Cross Entropia que utilizamos aqui é categórica, pois permite a utilização de mais de 2 categorias, e esparsa, pois aceita apenas um dígito ao invés de uma lista de probabilidades.\n",
"\n",
" \n",
"\n",
" "
]
},
{
"cell_type": "code",
"metadata": {
"id": "mFEqXFSdtu4L",
"colab_type": "code",
"colab": {}
},
"source": [
"# Define a Loss como Cross Entrepia Categorica\n",
"loss_object = tf.keras.losses.SparseCategoricalCrossentropy()\n",
"# Define o otimizador como SGD\n",
"optimizer = tf.keras.optimizers.SGD(learning_rate=0.001)"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "MoQc0_74-Cz1",
"colab_type": "text"
},
"source": [
"Para que se possa avaliar melhor o modelo a ser treinado vamos definir duas métricas. A primeira é uma média direta da função de perda e a segunda é uma medida de acurácia. Aqui a média é usada, pois estamos usando os dados em batch, ou seja, treinamos a rede simultaneamente para mais de um dado, e por isso precisamos agregar o erro e a acurácia para todos os resultados. Vale lembrar que acurácia é a quantidade de acertos dividido sobre a quantidade total de predições e não se deve confundir com precisão.\n",
"\n",
" "
]
},
{
"cell_type": "code",
"metadata": {
"id": "cvOyYOAptv5b",
"colab_type": "code",
"colab": {}
},
"source": [
"# Define as métricas de Treino e Teste\n",
"train_loss = tf.keras.metrics.Mean(name='train_loss')\n",
"train_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(name='train_accuracy')\n",
"test_loss = tf.keras.metrics.Mean(name='test_loss')\n",
"test_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(name='test_accuracy')"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "imHJ-lVeHMhZ",
"colab_type": "text"
},
"source": [
"Agora é necessário criar as rotinas de treino e teste e para isso utilizamos o decorador `tf.function` do Tensorflow 2.0. Decoradores são funções especiais do Python. Essencialmente um decorador é uma função que estende uma outra sem alterar o comportamento original da função inicial. Pode-se pensar em um decorador como um \"corta caminho\" de uma função para outra. No caso do tensorflow registramos duas funções em seu decorador, uma para treino e uma para teste, ambas as funções recebem como input um conjunto de imagens e suas respectivas classes. Utilizar esses decoradores é especialmente importante no Tensorflow 2.0, uma vez que o modo eager está ativado por padrão. O que esse decorador faz na realidade é registrar todas essas operações em um Grafo do Tensorflow. Esse Grafo é o que contém o registro de todas as operações que devem ser executadas em um nível inferior ao Python, e por isso devem ser registradas de antemão. Para o Tensorflow conseguir rodar em GPUs e de forma distribuída essa estratégia de registrar antes as operações é especialmente importante. Mais sobre esse comportamento pode ser encontrado [aqui](https://www.tensorflow.org/guide/function)\n",
"\n",
" \n",
"\n",
"Tanto na função de teste quanto na função de treino primeiro fazemos uma predição do modelo e depois calculamos o valor da loss. Na função de treino fazemos isso utilizando uma classe do Tensorflow chamada de Tape. Essa classe tem como principal função calcular as derivadas parciais do modelo para que o gradiente possa ser aplicado de forma correta. Por último, nas duas funções registramos os valores de loss e acurácia nas métricas que criamos acima.\n",
"\n",
" \n",
"\n",
" "
]
},
{
"cell_type": "code",
"metadata": {
"id": "lIWrfruZ8i_L",
"colab_type": "code",
"colab": {}
},
"source": [
"@tf.function\n",
"def train_step(images, labels):\n",
" # Abre o contexto de um tape\n",
" with tf.GradientTape() as tape:\n",
" # Gera predições com o modelo\n",
" predictions = model(images)\n",
" # Calcula a Loss\n",
" loss = loss_object(labels, predictions)\n",
" # Calcula os gradientes para cada variável do modelo\n",
" gradients = tape.gradient(loss, model.trainable_variables)\n",
" # Aplica os gradientes com o otimizador\n",
" optimizer.apply_gradients(zip(gradients, model.trainable_variables))\n",
" # Registra loss e acurácia nas métricas\n",
" train_loss(loss)\n",
" train_accuracy(labels, predictions)\n",
"\n",
"@tf.function\n",
"def test_step(images, labels):\n",
" # Gera predições com o modelo\n",
" predictions = model(images)\n",
" # Calcula a Loss\n",
" t_loss = loss_object(labels, predictions)\n",
" # Registra loss e acurácia nas métricas\n",
" test_loss(t_loss)\n",
" test_accuracy(labels, predictions)"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "i3FBluaPIeVJ",
"colab_type": "text"
},
"source": [
"O último passo antes de treinar o modelo é criar as batchs a partir dos datesets. Treinar o modelo por batch é uma prática comum, pois facilita o treinamento, uma vez que se torna possível acumular erro para um grupo de exemplos ao invés de se diferenciar a função para todos os exemplos do dataset. Adicionalmente usar batches facilita o que chamamos de generalização. [Generalização](https://cbmm.mit.edu/sites/default/files/publications/CBMM-Memo-067.pdf) é a capacidade da rede se adaptar e prever corretamente dados que nunca foram vistos antes, mas que estão no mesmo domínio dos dados de treino, por exmplo, a imagem do dígito 5 de ponta cabeça. Aqui nessa etapa também utilizados shuffle para repetir os dados de treino 100 vezes e embaralhar eles entre si, isso é feito para se obter uma composição de batches mais variada aumentando a probabilidade de chegar em um bom estimador."
]
},
{
"cell_type": "code",
"metadata": {
"id": "X6xvZn0t80Xm",
"colab_type": "code",
"colab": {}
},
"source": [
"BATCH_SIZE = 32\n",
"train = train_ds.shuffle(100).batch(BATCH_SIZE)\n",
"test = test_ds.batch(BATCH_SIZE)"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "Z37V9odFLlup",
"colab_type": "text"
},
"source": [
"Por fim o treinamento do modelo é feito utilizando um loop por um número definido de épocas. Consideramos uma época um loop por todo o dataset de treino, portanto se forem utilizadas 10 épocas o modelo vai ter \"visto\" 10 vezes o dataset de treino inteiro. Ao final de cada época é preciso limpar o estado das métricas, para que estejam prontas para agregar os resultados da próxima época sem interferências.\n",
"\n",
" \n",
"\n",
"O resultado de cada época será impresso durante o processo de treinamento e é nesse resultado que podemos avaliar a performance do modelo. A abordagem que usamos aqui nesse workshop foi de dividir os dados em duas partes uma parte de treino e uma de teste. A parte de treino utilizamos para treina o modelo e a parte de teste apenas para validar sua acurácia. Essa separação é feita para que se evite algo chamado de Overfitting.\n",
"\n",
" \n",
"\n",
"Overfitting acontece quando o modelo se ajusta muito aos dados de treino tendo uma acurácia muito boa para esses dados. Entretanto, para qualquer outro dado o modelo tem uma queda de performance isso é especialmente verdade para os dados reais em produção. Overfitting pode ter várias causas, mas em geral ele acontece em virtude de o modelo estar muito bem adaptado aos dados de treino, seja porque o modelo é muito complexo ou porque foi treinado por muito tempo nos dados. abaixo temos um exemplo visual de Overfitting:\n",
"\n",
" \n",
"\n",
"![overfitting](https://miro.medium.com/max/1125/1*_7OPgojau8hkiPUiHoGK_w.png)\n",
"\n",
" "
]
},
{
"cell_type": "code",
"metadata": {
"id": "bWK2zpOO8oKP",
"colab_type": "code",
"colab": {}
},
"source": [
"EPOCHS = 10\n",
"\n",
"for epoch in range(EPOCHS):\n",
" # treina a rede e acumula as métricas\n",
" for images, labels in train:\n",
" train_step(images, labels)\n",
"\n",
" # Testa o modelo e acumula as métricas\n",
" for test_images, test_labels in test:\n",
" test_step(test_images, test_labels)\n",
"\n",
" # Imprime as métricas para controle\n",
" template = 'Epoch {}, Loss: {}, Accuracy: {}, Test Loss: {}, Test Accuracy: {}'\n",
" print(template.format(epoch+1,\n",
" train_loss.result(),\n",
" train_accuracy.result()*100,\n",
" test_loss.result(),\n",
" test_accuracy.result()*100))\n",
" \n",
" # Reseta as métricas para a próxima época\n",
" train_loss.reset_states()\n",
" train_accuracy.reset_states()\n",
" test_loss.reset_states()\n",
" test_accuracy.reset_states()"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "gyMtN9wA4Ubt",
"colab_type": "text"
},
"source": [
"## 4. Melhorando o Modelo\n",
"\n",
" \n",
"\n",
"Um modelo de Redes neurais pode ser melhorado de muitas formas. Se nada foi alterado no modelo original temos uma acurácia de aproximadamente 88% nos dados de teste. Esse valor já é bom para um modelo inicial, entretanto, para um modelo em produção esse número deve chegar cada vez mais perto de 100%. Para melhor um modelo podemos aumentar o número de neurônios por camada, fornecer mais dados, alterar o número de épocas, alterar a taxa de aprendizado, mudar função de ativação ou utilizar modelos profundos com mais camadas.\n",
"\n",
" \n",
"\n",
"Essas alterações podem ser feitas de forma rápida, porém cada uma delas pode ter um efeito diferente no modelo final. Para entender o efeito que uma alteração tem numa rede neural acesse o [Tensorflow Playground](https://playground.tensorflow.org)\n",
"\n",
" \n",
"\n",
"### Desafio:\n",
"\n",
" \n",
"\n",
"Tente alterar um pouco o modelo inicial e veja quais são os resultados. Não se esquece de rodar todas as células após a alteração do modelo para que tudo esteja registrado corretamente dentro do tensorflow. Veja se é possível chegar a 98% de acurácia nos dados de teste fazendo alguns ajustes no modelo.\n",
"\n",
" "
]
}
]
}
Sign up for free to join this conversation on GitHub. Already have an account? Sign in to comment