Principe de la datation absolue ou radio-chronologie
Télécharger au format zip depuis Github
Télécharger avec git:
git clone https://gist.github.com/e4d0315fbf3b2b67859aba84c8d9c352.git
Télécharger avec wget:
wget https://gist.github.com/YannBouyeron/e4d0315fbf3b2b67859aba84c8d9c352/archive/15f7064b79d8f640a0c5e223133bdfa4d406a139.zip
unzip 15f7064b79d8f640a0c5e223133bdfa4d406a139.zip
Le fichier chrono.py doit ensuite être placé dans votre repertoire de travail pour pouvoir être importé avec python.
Si vous êtes dans jupyter:
import matplotlib.pyplot as plt
%matplotlib inlineSi vous travaillez en console linux sans interface graphique:
#import matplotlib
#import os
#if "DISPLAY" not in os.environ:
#matplotlib.use("Agg")
#import matplotlib.pyplot as pltModification de l´apparence des graphiques pour permettre l´export depuis Jupyter en html / markdown dark theme, tout en conservant les axes visibles.
plt.style.use('seaborn-white') # blanc
#plt.style.use('dark_background') # noirAttention le fichier chrono.py doit se trouver dans le même repertoire que celui à partir duquel vous avez lancé python.
from chrono import Chrono
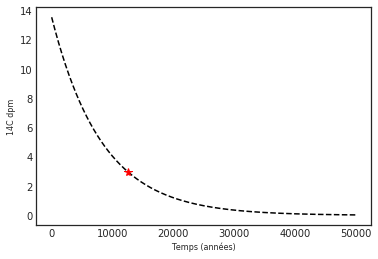
c = Chrono()On mesure une concentration en 14C de 3 dpm dans un échantillon.
On utlilise alors la méthode c14(dpm) pour retourner l'âge de l'échantillon et la courbe de désintégration du 14C avec la position de la mesure.
age = c.c14(3)age12467.041271439173
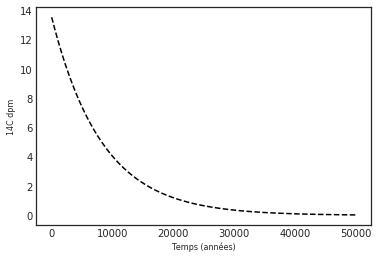
On peut aussi simplement afficher la courbe de désintégration du 14C:
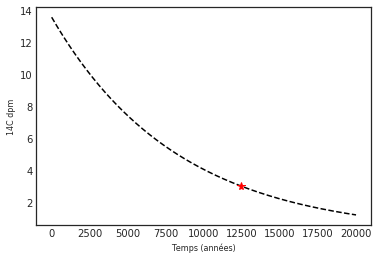
c.c14()L'argument facultatif xmax permet de restreindre l'axe du temps en fixant un t max pour la représentation graphique:
c.c14(3, xmax=20000)12467.041271439173
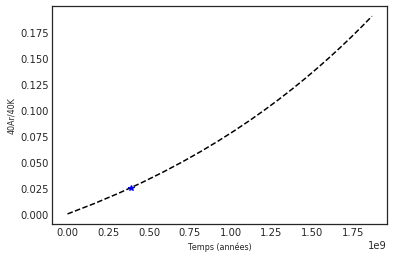
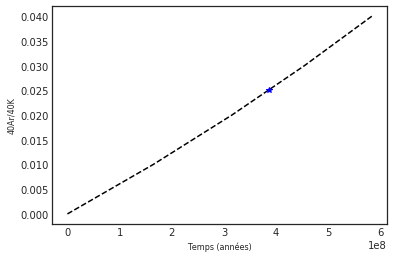
On utilise la méthode kar(k, Ar) avec k la concentration en 40K et Ar la concentration en 40Ar mesurées sur l'objet à dater.
age = c.kar(0.008, 0.0002)Attention, sur le graphique le temps est bien en années , ici en x 109
age385910162.54356444
L'argument facultatif ymax (rapport k/Ar max) permet d'ajuster la représentation graphique:
c.kar(0.008, 0.0002, ymax=0.05)385910162.54356444
Premier exemple:
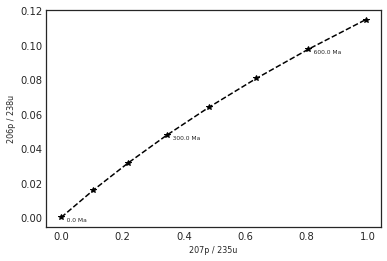
On commence par tracer la concordia sur l'intervalle de temps présumé avec la méthode concordia:
help(c.concordia)Help on method concordia in module chrono:
concordia(ti=0, tf=1000000000, incre=10000000, dotlabel=True, labelincre=3) method of chrono.Chrono instance
Arguments:
ti: age présumé inférieur à réouverture
tf: age présumé superieur à age roche
incre: incrément de temps pour la construction de la concordia en années
dotlabel: si True (defaut): indication age sur concordia
labelincre: icrémentation des labels des points de la concordia pour ne pas surcharger trop
Return: array des points de la concordia.
c.concordia(ti=0, tf=800000000.0, incre=100000000)(array([0. , 0.01562075, 0.0314855 , 0.04759808, 0.06396234,
0.08058223, 0.09746174, 0.11460491]),
array([0. , 0.10349785, 0.21770751, 0.34373762, 0.48281158,
0.63627939, 0.80563079, 0.9925097 ]))
On ajoute ensuite nos mesures effectuées sur les zircons de l'échantillon de la roche:
pb206U = [0.06231448, 0.06247915, 0.06264385, 0.06280857, 0.06297332, 0.06313809,
0.06330289, 0.06346772, 0.06363257, 0.06379744, 0.06396234]pb207U = [0.46827978, 0.46972653, 0.4711747, 0.4726243, 0.47407533, 0.47552779,
0.47698168, 0.478437, 0.47989376, 0.48135195, 0.48281158]c.concordia(ti=0, tf=800000000.0, incre=100000000, labelincre=2)
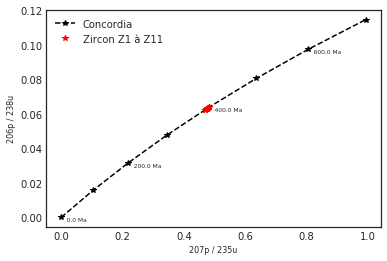
plt.plot(pb207U, pb206U, "*r", label="Zircon Z1 à Z11")
plt.legend()<matplotlib.legend.Legend at 0x6d262250>
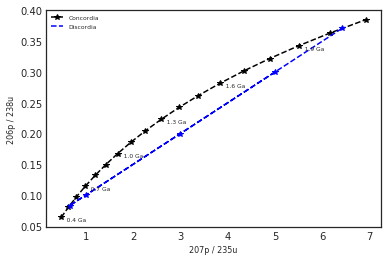
On observe que les mesures des rapports pb/u effectuées sur les zircons (ici en rouge) s'alignent sur la concordia. Il n'y a pas eu de réouverture du système. L'âge de la roche est l'âge du plus vieux zircon lisible sur le graphique, soit 400 Ma. Il n'est donc pas nécessaire d'afficher la discordia.
Deuxième exemple:
On dispose des mesures suivantes effectuées sur 3 zircons d'une roche:
pb207U = [5, 3, 1]
pb206U = [0.3, 0.2, 0.1]On affiche la concordia et on place nos mesures sur le graphique:
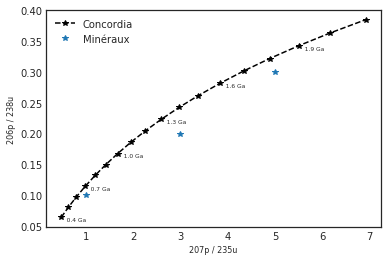
c.concordia(ti=0.4*10**9, tf=2.2*10**9, incre=100000000)
plt.plot(pb207U, pb206U, "*", label="Minéraux")
plt.legend()<matplotlib.legend.Legend at 0x6d271530>
On observe que les mesures effectuées sur les minéraux ne sont pas alignées sur la concordia. Il y'a eu une ré-ouverture du système. Il faut donc afficher la discordia avec la méthode upb :
help(c.upb)Help on method upb in module chrono:
upb(p207, p206, ti=100000000, tf=2500000000.0, delta=100000, incre=100000000, dotlabel=True, labelincre=3) method of chrono.Chrono instance
Arguments:
p206: liste valeurs 206Pb/238U mesurées (Y)
p207: liste valeurs 207Pb/235U mesurées (X)
ti: age présumé inférieur à réouverture
tf: age présumé superieur à age roche
delta: precision du calcul des intercepts en années
incre: incrément de temps pour la construction de la concordia en années
dotlabel: si True (defaut): indication age sur concordia
labelincre: incrémentation des labels des points de la concordia pour ne pas surcharger trop
Show: graphique concordia discordia
Return: {coeff correlation discordia, intersup, interlow, a, b}
dico = c.upb(pb207U, pb206U, ti=0.4*10**9, tf=2.2*10**9, incre=100000000, delta=1000)dico{'R': 1.0,
'sup': 2033986000.0,
'low': 514235000.0,
'a': 0.05000000000000001,
'b': 0.049999999999999954}
La méthode retourne un dictionnaire avec l'âge de la ré-ouverture du système correspondant à l'intercept inférieur: low = 515093000 +/- delta années; l'âge de la roche correspondant à l'intercept supérieur: sup = 2033278000 +/- delta années. La précision des âges obtenus dépend du paramètre "delta" passé en argument de la méthode upb.
Attention un delta faible augmente la précision, mais augmente aussi le temps des calculs.
On utilise la méthode rbsr()
help(c.rbsr)Help on method rbsr in module chrono:
rbsr(rbsr, srsr) method of chrono.Chrono instance
Arguments:
rbsr: liste rapport 87Rb/86Sr
srsr: liste rapport 87Sr/86Sr
Show graphique isochrone
Return equation droite reg, age (en annees)
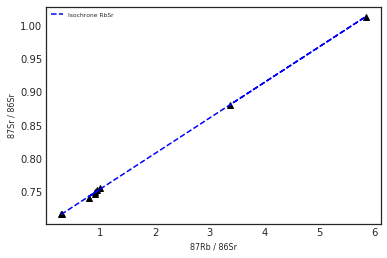
rbsr = [0.288, 0.31, 0.996, 0.787, 0.898, 0.945, 0.901, 5.84, 3.36]
srsr = [0.7165, 0.7171, 0.7556, 0.7413, 0.7471, 0.7521, 0.7495, 1.0133, 0.8807]y , a = c.rbsr(rbsr, srsr)# fonction de la droite isochrone
print(y)y = 0.05354693x + 0.7
# age
print(a)3673415678.371164
La méthode creatRbsr(age) permet de créer des couples de valeurs rbsr et srsr fictifs en fonction de l'âge désiré.
help(c.creatRbsr)Help on method creatRbsr in module chrono:
creatRbsr(age, n=5, b=0.7, out='') method of chrono.Chrono instance
Création de données RbSr en fonction de l’age.
Arguments:
age: age désiré
n: nombre de couples SrSr, RbSr
b: ordonnée à l’origine = Sr/Sr à t0
out: path en .xlsx ou en .json pour sauvegarder les données crées
Show graphique isochrone
Return RbSr (liste), SrSr (liste)
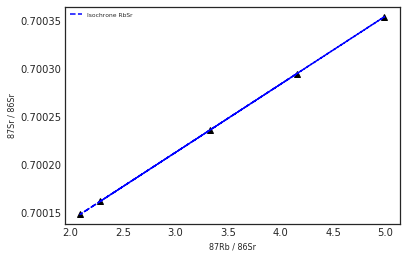
rbsr, srsr = c.creatRbsr(5000000)rbsr[2.282978862971912,
4.988633011174326,
3.3254901343712717,
2.091505108366786,
4.1554292953511585]
srsr[0.7001620972536554,
0.7003542055179406,
0.7002361181816367,
0.7001485021344575,
0.7002950459539775]
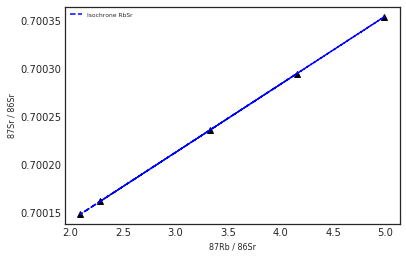
On peut vérifier l'âge en ré utilisant la méthode rbsr():
y , a = c.rbsr(rbsr, srsr)a4999999.999987198