Created
December 29, 2020 06:36
-
-
Save ahhzaky/79358cb554945191700d1e1353c54fe9 to your computer and use it in GitHub Desktop.
svm-tutorial-2.ipynb
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| { | |
| "nbformat": 4, | |
| "nbformat_minor": 0, | |
| "metadata": { | |
| "colab": { | |
| "name": "svm-tutorial-2.ipynb", | |
| "provenance": [], | |
| "collapsed_sections": [], | |
| "authorship_tag": "ABX9TyPAW7WmevWBEnJYKti9b5qJ", | |
| "include_colab_link": true | |
| }, | |
| "kernelspec": { | |
| "name": "python3", | |
| "display_name": "Python 3" | |
| } | |
| }, | |
| "cells": [ | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "view-in-github", | |
| "colab_type": "text" | |
| }, | |
| "source": [ | |
| "<a href=\"https://colab.research.google.com/gist/ahhzaky/79358cb554945191700d1e1353c54fe9/svm-tutorial-2.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>" | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "S_R-JgfnHWLa" | |
| }, | |
| "source": [ | |
| "### SVM Machine Learning Tutorial – What is the Support Vector Machine Algorithm, Explained with Code Examples\n", | |
| "\n" | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "mw4g-HoUHlRv" | |
| }, | |
| "source": [ | |
| "### Supervised vs Unsupervised learning\n", | |
| "\n", | |
| "### Apa itu supervised learning?\n", | |
| "Supervised learning adalah saat Anda melatih model pembelajaran mesin menggunakan data berlabel. Artinya Anda memiliki data yang sudah memiliki klasifikasi yang tepat terkait dengannya. Salah satu penggunaan umum dari supervised learning adalah membantu Anda memprediksi nilai untuk data baru.\n", | |
| "\n", | |
| "Dengan pembelajaran yang diawasi, Anda harus membangun kembali model Anda saat mendapatkan data baru untuk memastikan bahwa prediksi yang dikembalikan masih akurat. Contoh supervised learning adalah memberi label pada gambar makanan. Anda dapat memiliki kumpulan data yang didedikasikan hanya untuk gambar pizza untuk mengajari model Anda apa itu pizza.\n", | |
| "\n", | |
| "### Apa itu unsupervised learning?\n", | |
| "unsupervised learning adalah saat Anda melatih model dengan data tidak berlabel. Artinya, model harus menemukan fiturnya sendiri dan membuat prediksi berdasarkan cara model mengklasifikasikan data.\n", | |
| "\n", | |
| "Contoh pembelajaran tanpa pengawasan adalah memberikan gambar model Anda tentang berbagai jenis makanan tanpa label. Dataset akan memiliki gambar pizza, kentang goreng, dan makanan lain dan Anda dapat menggunakan algoritme yang berbeda untuk mendapatkan model untuk mengidentifikasi gambar pizza saja tanpa label apa pun." | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "XRdIgJPkIbds" | |
| }, | |
| "source": [ | |
| "### Apa itu SVM?\n", | |
| "Support vector mechine adalah sekumpulan metode pembelajaran yang diawasi yang digunakan untuk klasifikasi, regresi, dan deteksi pencilan. Semua ini adalah tugas umum dalam machine learning.\n", | |
| "\n", | |
| "Anda dapat menggunakannya untuk mendeteksi sel kanker berdasarkan jutaan gambar atau Anda dapat menggunakannya untuk memprediksi rute mengemudi di masa mendatang dengan model regresi yang sesuai.\n", | |
| "\n", | |
| "Ada jenis SVM tertentu yang dapat Anda gunakan untuk masalah pembelajaran mesin tertentu, seperti dukungan regresi vektor (SVR) yang merupakan perpanjangan dari klasifikasi vektor dukungan (SVC).\n", | |
| "\n", | |
| "SVM berbeda dari algoritme klasifikasi lain karena cara mereka memilih batas keputusan yang memaksimalkan jarak dari titik data terdekat dari semua kelas. Batas keputusan yang dibuat oleh SVM disebut pengklasifikasi margin maksimum atau bidang hiper margin maksimum." | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "pxngEHulI8IK" | |
| }, | |
| "source": [ | |
| "### Cara kerja SVM \n", | |
| "Pengklasifikasi SVM linier sederhana bekerja dengan membuat garis lurus antara dua kelas. Artinya semua titik data di satu sisi garis akan mewakili kategori dan titik data di sisi lain garis akan dimasukkan ke dalam kategori yang berbeda. Ini berarti jumlah baris yang dapat dipilih tidak terbatas.\n", | |
| "\n", | |
| "Apa yang membuat algoritme SVM linier lebih baik daripada beberapa algoritme lain, seperti k-neighbourhood, adalah ia memilih baris terbaik untuk mengklasifikasikan titik data Anda. Ini memilih garis yang memisahkan data dan yang paling jauh dari titik data lemari mungkin.\n", | |
| "\n", | |
| "Contoh 2-D membantu memahami semua jargon machine learning. Pada dasarnya Anda memiliki beberapa titik data di kisi. Anda mencoba untuk memisahkan poin data ini dengan kategori yang harus mereka cocokkan, tetapi Anda tidak ingin ada data di kategori yang salah. Itu berarti Anda mencoba menemukan garis di antara dua titik terdekat yang memisahkan titik data lainnya.\n", | |
| "\n", | |
| "Jadi dua titik data terdekat memberi Anda vektor pendukung yang akan Anda gunakan untuk menemukan garis itu. Garis itu disebut batas keputusan.\n", | |
| "\n", | |
| "### Contoh linear\n", | |
| "\n", | |
| "\n", | |
| "## Conton non-linier menggunakan kernel RBF.\n", | |
| "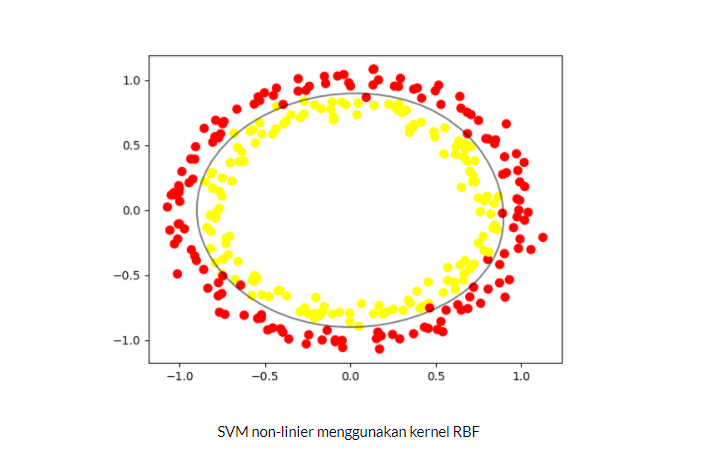\n", | |
| "\n" | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "9XIor0kyJmiN" | |
| }, | |
| "source": [ | |
| "### Contoh SVM Linear\n", | |
| "Kami akan mulai dengan mengimpor beberapa pustaka yang akan memudahkan untuk bekerja dengan sebagian besar proyek pembelajaran mesin." | |
| ] | |
| }, | |
| { | |
| "cell_type": "code", | |
| "metadata": { | |
| "colab": { | |
| "base_uri": "https://localhost:8080/", | |
| "height": 265 | |
| }, | |
| "id": "qTeWV50zJ0pf", | |
| "outputId": "9394f82a-8157-41fa-d80c-603b8dafb301" | |
| }, | |
| "source": [ | |
| "import matplotlib.pyplot as plt\n", | |
| "import numpy as np\n", | |
| "from sklearn import svm\n", | |
| "\n", | |
| "# linear data\n", | |
| "X = np.array([1, 5, 1.5, 8, 1, 9, 7, 8.7, 2.3, 5.5, 7.7, 6.1])\n", | |
| "y = np.array([2, 8, 1.8, 8, 0.6, 11, 10, 9.4, 4, 3, 8.8, 7.5])\n", | |
| "\n", | |
| "# show unclassified data\n", | |
| "plt.scatter(X, y)\n", | |
| "plt.show()" | |
| ], | |
| "execution_count": null, | |
| "outputs": [ | |
| { | |
| "output_type": "display_data", | |
| "data": { | |
| "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAD4CAYAAAD1jb0+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAO5UlEQVR4nO3dbWydd3nH8e9FEsRJeDAjXtW43dwXk7WpkebOYkC3ChFYYERtFE1QpCJWDWWTEGvZFNTwpuJVNgUheIUUpUARpV3XhmyaqqaIhwEvlsmJM6U0zbRBW+KkxAhMKfPWNFx74XOS1E0cn3Nu+77/Pt+PFMW+fXKfn3KSn4+v++EfmYkkqTyvqTuAJKk3FrgkFcoCl6RCWeCSVCgLXJIKtXYln2zjxo05Ojq6kk8pScU7cuTITzNzeOH2FS3w0dFRJicnV/IpJal4EfHs5bY7QpGkQlngklQoC1ySCmWBS1KhLHBJKtSKnoUiSYPk4NQ0ew+d5PTsHJuGWuzaOsb28ZHK9m+BS9IyODg1ze4Dx5k7dx6A6dk5dh84DlBZiTtCkaRlsPfQyQvl3TF37jx7D52s7DkscElaBqdn57ra3gsLXJKWwaahVlfbe2GBS9Iy2LV1jNa6Na/Y1lq3hl1bxyp7Dg9iStIy6Byo9CwUSSrQ9vGRSgt7IUcoklQoC1ySCmWBS1KhLHBJKpQFLkmFssAlqVAWuCQVygKXpEJZ4JJUKAtckgplgUtSoa56L5SI+CKwDTibmTe2t/0G8A/AKPAM8IHM/PnyxZTUBMu9RJi6s5R34F8G3rtg2z3ANzPzd4Bvtj+XtIp1lgibnp0jubhE2MGp6bqjDayrFnhmfhf42YLNtwH3tz++H9hecS5JDbMSS4SpO73OwK/JzDPtj58HrrnSAyNiZ0RMRsTkzMxMj08nqW4rsUSYutP3QczMTCAX+fq+zJzIzInh4eF+n05STVZiiTB1p9cC/0lEXAvQ/v1sdZEkNdFKLBGm7vRa4P8MfKT98UeAf6omjqSm2j4+wp4dmxkZahHAyFCLPTs2exZKjZZyGuGDwDuBjRFxCrgX+Dvg4Yj4C+BZ4APLGVJSMyz3EmHqzlULPDM/dIUvbak4iySpC16JKUmFssAlqVAWuCQV6qozcEnSRU26H4wFLklL1LkfTOeWAp37wQC1lLgjFElaoqbdD8YCl6Qlatr9YCxwSVqipt0PxgKXpCVq2v1gPIgpSUvUOVDpWSiSVKAm3Q/GEYokFcoCl6RCWeCSVChn4JIaqUmXrDeVBS6pcZp2yXpTOUKR1DhNu2S9qSxwSY3TtEvWm8oCl9Q4TbtkvakscEmN07RL1pvKg5iSGqdpl6w3lQUuqZGadMl6UzlCkaRCWeCSVCgLXJIKZYFLUqEscEkqlAUuSYWywCWpUH2dBx4RnwA+CiRwHLgzM/+3imDSSvCWpavDoL6OPb8Dj4gR4K+Bicy8EVgD3F5VMGm5dW5ZOj07R3LxlqUHp6brjqYuDPLr2O8IZS3Qioi1wHrgdP+RpJXhLUtXh0F+HXsu8MycBj4DPAecAX6RmU8sfFxE7IyIyYiYnJmZ6T2pVDFvWbo6DPLr2M8I5c3AbcANwCZgQ0TcsfBxmbkvMycyc2J4eLj3pFLFvGXp6jDIr2M/I5R3Az/KzJnMPAccAN5RTSxp+XnL0tVhkF/Hfs5CeQ54W0SsB+aALcBkJamkFeAtS1eHQX4dIzN7/8MRnwY+CLwMTAEfzcz/u9LjJyYmcnLSjpekbkTEkcycWLi9r/PAM/Ne4N5+9iFJ6o1XYkpSoVyRRyrAoF5pqMVZ4FLDda407Fys0rnSELDEB5wjFKnhBvlKQy3OApcabpCvNNTiLHCp4Qb5SkMtzgKXGm6QrzTU4jyIKTXcIF9pqMVZ4FIBto+PWNh6FUcoklQoC1ySCmWBS1KhLHBJKpQFLkmFssAlqVAWuCQVygKXpEJZ4JJUKAtckgplgUtSoSxwSSqUBS5JhbLAJalQFrgkFcoCl6RCWeCSVCgLXJIKZYFLUqEscEkqVF8FHhFDEfFIRDwdESci4u1VBZMkLa7fVek/DzyemX8WEa8F1leQSZK0BD0XeES8CbgF+HOAzHwJeKmaWJKkq+lnhHIDMAN8KSKmImJ/RGxY+KCI2BkRkxExOTMz08fTSZIu1U+BrwVuAr6QmePAr4B7Fj4oM/dl5kRmTgwPD/fxdJKkS/VT4KeAU5l5uP35I8wXuiRpBfRc4Jn5PPDjiBhrb9oCPFVJKknSVfV7FsrHgQfaZ6D8ELiz/0iSpKXoq8Az8xgwUVEWSVIXvBJTkgplgUtSoSxwSSqUBS5JhbLAJalQFrgkFcoCl6RCWeCSVCgLXJIKZYFLUqEscEkqlAUuSYWywCWpUBa4JBXKApekQlngklQoC1ySCmWBS1KhLHBJKpQFLkmFssAlqVAWuCQVygKXpEJZ4JJUKAtckgplgUtSoSxwSSqUBS5JhbLAJalQa/vdQUSsASaB6czc1n+k1eng1DR7D53k9Owcm4Za7No6xvbxkbpjSSpY3wUO3AWcAN5Ywb5WpYNT0+w+cJy5c+cBmJ6dY/eB4wCWuKSe9TVCiYjrgPcD+6uJszrtPXTyQnl3zJ07z95DJ2tKJGk16HcG/jngk8Cvr/SAiNgZEZMRMTkzM9Pn05Xp9OxcV9slaSl6LvCI2Aaczcwjiz0uM/dl5kRmTgwPD/f6dEXbNNTqarskLUU/78BvBm6NiGeAh4B3RcRXK0m1yuzaOkZr3ZpXbGutW8OurWM1JZK0GvRc4Jm5OzOvy8xR4HbgW5l5R2XJVpHt4yPs2bGZkaEWAYwMtdizY7MHMCX1pYqzULQE28dHLGxJlaqkwDPzO8B3qtiXJGlpvBJTkgplgUtSoSxwSSqUBS5JhbLAJalQFrgkFcoCl6RCWeCSVCgLXJIKZYFLUqG8F4pUEZfN00qzwKUKuGye6uAIRaqAy+apDha4VAGXzVMdLHCpAi6bpzpY4FIFXDZPdfAgplSBzoFKz0LRSrLApYq4bJ5WmiMUSSqUBS5JhbLAJalQFrgkFcoCl6RCWeCSVCgLXJIKZYFLUqEscEkqlAUuSYWywCWpUD3fCyUirge+AlwDJLAvMz9fVbAOl6mSpMvr52ZWLwN/m5lHI+INwJGI+EZmPlVRNpepkqRF9DxCycwzmXm0/fEvgRNApa3qMlWSdGWVzMAjYhQYBw5f5ms7I2IyIiZnZma62q/LVEnSlfV9P/CIeD3wKHB3Zr6w8OuZuQ/YBzAxMZHd7HvTUIvpy5R1r8tUOU+XtJr09Q48ItYxX94PZOaBaiJdVOUyVZ15+vTsHMnFefrBqemK0krSyuq5wCMigPuAE5n52eoiXbR9fIQ9OzYzMtQigJGhFnt2bO7pXbPzdEmrTT8jlJuBDwPHI+JYe9unMvOx/mNdVNUyVc7TJa02PRd4Zn4fiAqzLKuq5+mSVLeBuRKzynm6JDXBwKxK3xnDeBaKpNViYAocqpunS1ITDMwIRZJWGwtckgplgUtSoSxwSSqUBS5JhbLAJalQFrgkFcoCl6RCWeCSVCgLXJIKZYFLUqEscEkqlAUuSYWywCWpUBa4JBWq8fcDPzg17SIMknQZjS7wg1PT7D5w/MJq8tOzc+w+cBzAEpc08Bo9Qtl76OSF8u6YO3eevYdO1pRIkpqj0QV++jKryC+2XZIGSaMLfNNQq6vtkjRIGl3gu7aO0Vq35hXbWuvWsGvrWE2JJKk5Gn0Qs3Og0rNQJOnVGl3gMF/iFrYkvVqjRyiSpCuzwCWpUBa4JBXKApekQlngklSoyMyVe7KIGeDZHv/4RuCnFcapirm6Y67umKs7qzXXb2fm8MKNK1rg/YiIycycqDvHQubqjrm6Y67uDFouRyiSVCgLXJIKVVKB76s7wBWYqzvm6o65ujNQuYqZgUuSXqmkd+CSpEtY4JJUqMYXeER8MSLORsSTdWe5VERcHxHfjoinIuIHEXFX3ZkAIuJ1EfHvEfEf7VyfrjtTR0SsiYipiPiXurNcKiKeiYjjEXEsIibrztMREUMR8UhEPB0RJyLi7Q3INNb+e+r8eiEi7q47F0BEfKL9b/7JiHgwIl5XdyaAiLirnekHVf9dNX4GHhG3AC8CX8nMG+vO0xER1wLXZubRiHgDcATYnplP1ZwrgA2Z+WJErAO+D9yVmf9WZy6AiPgbYAJ4Y2ZuqztPR0Q8A0xkZqMuAImI+4HvZeb+iHgtsD4zZ+vO1RERa4Bp4A8zs9cL9KrKMsL8v/Xfy8y5iHgYeCwzv1xzrhuBh4C3Ai8BjwN/lZn/VcX+G/8OPDO/C/ys7hwLZeaZzDza/viXwAmg9huX57wX25+ua/+q/bt0RFwHvB/YX3eWEkTEm4BbgPsAMvOlJpV32xbgv+su70usBVoRsRZYD5yuOQ/A7wKHM/N/MvNl4F+BHVXtvPEFXoKIGAXGgcP1JpnXHlUcA84C38jMJuT6HPBJ4Nd1B7mMBJ6IiCMRsbPuMG03ADPAl9pjp/0RsaHuUAvcDjxYdwiAzJwGPgM8B5wBfpGZT9SbCoAngT+OiLdExHrgT4Hrq9q5Bd6niHg98Chwd2a+UHcegMw8n5m/D1wHvLX9Y1xtImIbcDYzj9SZYxF/lJk3Ae8DPtYe29VtLXAT8IXMHAd+BdxTb6SL2iOdW4F/rDsLQES8GbiN+W98m4ANEXFHvakgM08Afw88wfz45Bhwvqr9W+B9aM+YHwUeyMwDdedZqP0j97eB99Yc5Wbg1vas+SHgXRHx1XojXdR+90ZmngW+zvy8sm6ngFOX/PT0CPOF3hTvA45m5k/qDtL2buBHmTmTmeeAA8A7as4EQGbel5l/kJm3AD8H/rOqfVvgPWofLLwPOJGZn607T0dEDEfEUPvjFvAe4Ok6M2Xm7sy8LjNHmf+x+1uZWfu7I4CI2NA+CE17RPEnzP/YW6vMfB74cUSMtTdtAWo9QL7Ah2jI+KTtOeBtEbG+/X9zC/PHpWoXEb/Z/v23mJ9/f62qfTd+UeOIeBB4J7AxIk4B92bmffWmAubfVX4YON6eNwN8KjMfqzETwLXA/e0zBF4DPJyZjTptr2GuAb4+/3+etcDXMvPxeiNd8HHggfa44ofAnTXnAS58o3sP8Jd1Z+nIzMMR8QhwFHgZmKI5l9U/GhFvAc4BH6vyYHTjTyOUJF2eIxRJKpQFLkmFssAlqVAWuCQVygKXpEJZ4JJUKAtckgr1/7jhHhWthgEnAAAAAElFTkSuQmCC\n", | |
| "text/plain": [ | |
| "<Figure size 432x288 with 1 Axes>" | |
| ] | |
| }, | |
| "metadata": { | |
| "tags": [], | |
| "needs_background": "light" | |
| } | |
| } | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "-ACB5IRaJ90e" | |
| }, | |
| "source": [ | |
| "Beriku data sederhana yang dibuat.\n", | |
| "\n", | |
| "Setelah itu kita akan menempatkan data mentah ke dalam format yang dapat kita gunakan untuk melatih model SVM." | |
| ] | |
| }, | |
| { | |
| "cell_type": "code", | |
| "metadata": { | |
| "colab": { | |
| "base_uri": "https://localhost:8080/" | |
| }, | |
| "id": "MB7uwRDMKPyO", | |
| "outputId": "25c71d26-f66a-45fb-bdf4-4cc68f093d38" | |
| }, | |
| "source": [ | |
| "# shaping data for training the model\n", | |
| "training_X = np.vstack((X, y)).T\n", | |
| "training_y = [0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1]\n", | |
| "\n", | |
| "# define the model\n", | |
| "clf = svm.SVC(kernel='linear', C=1.0)\n", | |
| "\n", | |
| "# train the model\n", | |
| "clf.fit(training_X, training_y)" | |
| ], | |
| "execution_count": null, | |
| "outputs": [ | |
| { | |
| "output_type": "execute_result", | |
| "data": { | |
| "text/plain": [ | |
| "SVC(C=1.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,\n", | |
| " decision_function_shape='ovr', degree=3, gamma='scale', kernel='linear',\n", | |
| " max_iter=-1, probability=False, random_state=None, shrinking=True,\n", | |
| " tol=0.001, verbose=False)" | |
| ] | |
| }, | |
| "metadata": { | |
| "tags": [] | |
| }, | |
| "execution_count": 2 | |
| } | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "k1XUPwL3KYVy" | |
| }, | |
| "source": [ | |
| "Begitulah cara Anda membuat model untuk proyek pembelajaran mesin apa pun. Kumpulan data yang kami miliki mungkin kecil, tetapi jika Anda menemukan kumpulan data dunia nyata yang dapat diklasifikasikan dengan batas linier, model ini masih berfungsi.\n", | |
| "\n", | |
| "Dengan melatih model Anda, Anda dapat membuat prediksi tentang bagaimana titik data baru akan diklasifikasikan dan Anda dapat membuat plot batas keputusan. Mari kita plot batas keputusan." | |
| ] | |
| }, | |
| { | |
| "cell_type": "code", | |
| "metadata": { | |
| "colab": { | |
| "base_uri": "https://localhost:8080/", | |
| "height": 282 | |
| }, | |
| "id": "AiALXtOwKbvP", | |
| "outputId": "2f93ef86-286a-4495-c146-5e3b03f10fb3" | |
| }, | |
| "source": [ | |
| "# get the weight values for the linear equation from the trained SVM model\n", | |
| "w = clf.coef_[0]\n", | |
| "\n", | |
| "# get the y-offset for the linear equation\n", | |
| "a = -w[0] / w[1]\n", | |
| "\n", | |
| "# make the x-axis space for the data points\n", | |
| "XX = np.linspace(0, 13)\n", | |
| "\n", | |
| "# get the y-values to plot the decision boundary\n", | |
| "yy = a * XX - clf.intercept_[0] / w[1]\n", | |
| "\n", | |
| "# plot the decision boundary\n", | |
| "plt.plot(XX, yy, 'k-')\n", | |
| "\n", | |
| "# show the plot visually\n", | |
| "plt.scatter(training_X[:, 0], training_X[:, 1], c=training_y)\n", | |
| "plt.legend()\n", | |
| "plt.show()" | |
| ], | |
| "execution_count": null, | |
| "outputs": [ | |
| { | |
| "output_type": "stream", | |
| "text": [ | |
| "No handles with labels found to put in legend.\n" | |
| ], | |
| "name": "stderr" | |
| }, | |
| { | |
| "output_type": "display_data", | |
| "data": { | |
| "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAD4CAYAAAD1jb0+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAdfklEQVR4nO3de5SU9Z3n8fe37zeguYkIIiiKoqBIc782mh0MbCS7J9nEMTc1bDZOzGTiZJMxs9HdY+IkMTO5zCRhNasz8WQ2Y0zM5MRJHOkW5CagKIIXQERbEJpbA32rrqrv/lFNLdUX6Ws99VR9Xud4uvup6q6Pnubjw6+e5/c1d0dERMInL+gAIiLSNypwEZGQUoGLiISUClxEJKRU4CIiIVWQzhcbNWqUT5w4MZ0vKSISetu3bz/q7qM7Hk9rgU+cOJFt27al8yVFRELPzA50dVxLKCIiIaUCFxEJKRW4iEhIpXUNXEQk17W1tVFXV0dLS0unx0pKShg/fjyFhYU9+lkqcJEc4fFGiL4KeZVYweSg4+Ssuro6hgwZwsSJEzGz5HF359ixY9TV1TFp0qQe/SwVuEgOiDf+E5z+DlgBeBQvmIQNX4Pljwk6Ws5paWnpVN4AZsbIkSOpr6/v8c/SGrhIlvPWzXD6u0AL+JnEx+gb+InVQUfLWR3L+3zHu6MCF8ly3vQo0NzhaAyi+/Ho3iAiyQBRgYtku9jRro9bAcRPpjeLDCgVuEi2K6kGijsf9xgUXJX2OJJ4w7I3x7ujAhfJclZ2K+SPIrXES2HI3VheeVCxclZJSQnHjh3rVNZnr0IpKSnp8c/SVSgiWc7yhsLIJ/Gmn0NLDeSPxMo+jRXPDTpaTho/fjx1dXVdXm1y9jrwnlKBi+QAyxuKVXweKj4fdJScV1hY2OPrvM9HSygiIiGlAhcRCSkVuIhISKnARURCSgUuIhJSKnARkZBSgYuIhJQKXEQkpFTgIiIhpQIXEQkp3Uov0gvuUWjbBVYIBVf1egN+kYF03jNwM/uZmR0xs1fOOTbCzJ42sz3tH4cPbkyR4HnrevzIfPzEp/Hjt+D1S/G23UHHkhzWkyWUR4DlHY59FXjG3S8Hnmn/WiRreew9/MSd4CfBG8GbIH4IP/4p3DtPFxdJh/MWuLuvA453OHwz8Gj7548CqwY4l0hG8eZfA/EuHolCa02644gAfX8Tc4y7H2r//D2g29HWZrbazLaZ2bbeTFsWySixo0Ck83GPQfxE2uOIwABcheKJsRLdzgFy9zXuXuXuVaNHj+7vy4kEwooXAGVdP1g0O61ZRM7qa4EfNrOxAO0fjwxcJJEMVLwECqcCpeccLIXSm7CCyUGlkhzX18sIfwt8Cnig/eOTA5ZIJAOZ5cOIR/Cmx6HlSaAIK/svULIi6GiSw85b4Gb2C2ApMMrM6oBvkCjuX5rZ7cAB4KODGVIkE5gVYeW3QPktQUcRAXpQ4O7+8W4eumGAs4iISC/oVnoRkZBSgYuIhJT2QhHJEh47iJ/5IbRuhLwRWPlnoeQm7deSxVTgIlnAY+/hR28GPwPEErf5N3wNYvuxijuDjieDREsoIlnAGx9O7NFC7JyjzXDmp3j8TFCxZJCpwEWyQWQLEO183Aogui/tcSQ9VOAi2SB/PNDFWre3Qf4FaY8j6aECF8kCVn4HUNzhaBEUzcLyxwYRSdJABS6SBazoehj2LbBKEvu1FEHxYqzyB0FHk0Gkq1BEskRe6Qq8ZDnE3oW8oVheZdCRZJCpwEWyiFk+FEwIOoakiZZQRERCSgUuIhJSWkIRSSP3SGKGZuwwFF2PFV4TdCQJMRW4SJp49E382C1Aa+L6bPLx4nlY5Y8w0x9F6T0toYikiZ/4AviJ9lveI0AztG7Em34RdDQJKRW4SBp4tA5ib9N5/ncLNP8yiEiSBVTgImkRpds/bt6W1iSSPVTgIumQfwnkjejigWIo/VDa40h2UIGLpIGZYZV/C1ZOcs8SK4OCyVj5ZwLNJuGlt75F0sSKroPRz+BNv4H4IaxoFhQv0xUo0mf6zRFJI8sbgVXcFnQMyRJaQhERCSkVuIhISKnARURCSgUuIhJSKnARkZBSgYuIhJQKXNLO3fG2N/C2nbhHg46TUTx2EI/swONngo4iIdCv68DN7EvAHSR26NkJfMbdWwYimGQnj+7FT3wO4vUkzh8KYNi3sZLqoKMFyuOn8ZN3QWQbWCF4G17xOaz885hZ0PEkQ/X5DNzMxgF3AVXufg2QD3xsoIJJ9nFvw49/EmLvgDcntlX1BvzkF/HoO0HHC5Q3fAUiW0nsFX4m8fHMGmh5KuhoksH6u4RSAJRa4l7gMuBg/yNJ1opsSBR3py1VY3jzvwSRKCN4/CS0riexR/i5mvHGh4KIJCHR5wJ393eB7wJvA4eABnf/Y8fnmdlqM9tmZtvq6+v7nlTCL3aczuUN0Abxw+lOkzniDST+AtvVY8fSGkXCpT9LKMOBm4FJwEVAuZnd2vF57r7G3avcvWr06NF9TyrhV1QFHuvigTKsaHHa42SM/PFgJV09AMUL0x5HwqM/Syg3Avvdvd7d24AngPkDE0uykRVMgNIPA6XnHC2Bgkuh5D8EFStwZvkw9H8AJcDZNywLwYZgFXcGmEwyXX+uQnkbmGtmZUAzcAOwbUBSSdayofdB0ZzEHEhvhpIVWPktmBUGHS1QeaUr8PyL8Mb/DbF3oWgOVn47lj8m6GiSwfpc4O6+xcweB14gMS/qRWDNQAWT7GRmULoCK10RdJSMY0UzsKJ/CDqGhEi/rgN3928A3xigLCIi0gsa6CBZyb0Fb/oltPwbWDlWdkvO3ywk2UcFLlnHPYIf+zhE9wGJG4O97Xk88knyhn452HAiA0h7oUj2afk9xN7kbHkDiTdMmx7BYzl8vblkHRW4ZB1vWdt+x2cHVpDYa0QkS6jAJfvkjabbOxvzKtMaRWQwqcAl61jZx4CO15UbWBkUzQ0iksigUIFL1rHCy2HYN8HKwSoSxZ03DhvxaOKuR5EsoatQJCvlla7ESz4AbS8nCrxgqvbVlqyjApesZVYMRbOCjiEyaLSEIiISUipwEZGQCsUSyre//W0OHjxIdXU1ixcvZvjw4UFHEhEJXCjOwPfu3ctPf/pTVq1axciRI5k5cyZ33303v/vd7zh16lTQ8UREAmHuXY24GhxVVVW+bVvf7oRrbW1ly5Yt1NbWUlNTw6ZNm2htbSUvL4+ZM2dSXV1NdXU1CxcupKKiYoCTi4gEx8y2u3tVp+NhKfCOmpub2bx5MzU1NdTU1LBlyxba2tooKChg1qxZLF26lOrqahYsWEBZWdmAvKaISBCyrsA7amxsZOPGjckz9K1btxKNRiksLGTOnDnJM/R58+ZRUtLV/EERkcyU9QXe0ZkzZ3juueeSZ+jbt28nHo9TXFzM3Llzqa6uZtmyZcyePZvi4uK0ZBIR6YucK/COGhoaWL9+PWvXrqW2tpYdO3bg7pSWlrJgwYLkGXpVVRWFhbk9n1FEMkvOF3hHx48fZ926dckz9J07dwJQXl7OokWLkmvo119/PQUFobjaUkSylAr8POrr63n22WeTa+i7d+8GYOjQoSxatCh5hn7ttdeSn68NkUQkfVTgvXT48OFkmdfU1PDGG28AUFlZyZIlS5Jn6NOmTSMvLxSX04tISKnA++ndd99NFnptbS379u0DYOTIkSxZsiR5hj51qna9E5GBpQIfYG+//XbKGfqBAwcAuOCCC5Jn59XV1VxxxRUqdBHpFxX4INu/f3+yzNeuXcvBgwcBGDt2bLLMq6urufTSS1XoItIrKvA0cnf27t2bLPSamhoOH05MQ7/44ouTZb506VImTpwYbFgRyXgq8AC5O6+99lqyzGtrazl69CgAEydOTDlDHz9+fMBpRSTTqMAzSDweZ/fu3clCf/bZZzl+/DgAkydPTjlDHzt2bMBpRSRoKvAMFo/Hefnll5OFvm7dOhoaGgCYMmVKSqFfcMEFAacVkXRTgYdILBZjx44dyUJfv349p0+fBuDqq69OFvqSJUsYOXJkwGlFZLANSoGbWSXwEHAN4MBt7r6pu+erwPsmGo2yffv2ZKE/99xzNDU1ATB9+vRkoWtakUh2GqwCfxRY7+4PmVkRUObuJ7t7vgp8YEQiEbZu3Zos9I0bN9LS0oKZMWPGjGShL1q0iKFDhwYdV0T6acAL3MyGATuAS72HP0QFPjhaW1tThlts3ryZSCRCfn5+p2lF5eXlQccVkV4ajAK/DlgD7AauBbYDX3T3xg7PWw2sBpgwYcLMs3csyuBpbm5m06ZNKdOKotEoBQUFzJ49O1no8+fPp7S0NOi4InIeg1HgVcBmYIG7bzGz7wOn3P2vu/senYEHo7GxkQ0bNiQLfdu2bcRiMYqKipg7d27y1v+5c+dqWpFIBhqMAr8Q2OzuE9u/XgR81d1XdPc9KvDMcPr06ZRpRS+88ALxeJySkhLmzZuXPEOfPXs2RUVFQccVyXmD9SbmeuAOd3/dzO4Fyt39L7t7vgo8M508eZL169cnC/2ll17C3SkrK0tOK1q6dKmmFYkEZLAK/DoSlxEWAW8Cn3H3E909XwUeDmenFa1du5aamhpeeeUVACoqKli4cGHyDH3GjBmaViSSBrqRR/qsvr4+Zevc1157DUhMK1q8eHHKtCINtxAZeCpwGTCHDh1KGW6xZ88eAIYPH54y3OLqq69WoYsMABW4DJq6urqUM/T9+/cDMGrUqJRCv+qqq7QXukgfqMAlbQ4cOJCyF/o777wDwJgxY1KmFV1++eUqdJEeUIFLINydN998M+UM/ey0oosuuih5hYumFYl0TwUuGcHd2bNnT8pwi66mFVVXV3PJJZcEnFYkM6jAJSO937SiSZMmpeyFrmlFkqtU4BIK8XicXbt2pUwrOnEicWvBudOKqqurufDCCwNOK5IeKnAJpVgs1mla0alTpwC48sorU87QR48eHXBakcGhApesEI1GefHFF1OmFTU2JjbAvOaaa1KmFY0YMSLgtCIDQwUuWamtra3TtKLm5mbMjGuvvTZ5hcvixYuprKwMOq5In6jAJSdEIhGef/75lGlFra2t5OXldZpWNGTIkKDjivSIClxyUktLC1u2bOlyWlFVVVWy0BcsWKBpRZKxVOAiQFNTU8q0oueff17TiiTjqcBFunDmzJnktKLa2tpO04rOFvrcuXMpLi4OOq7kKBW4SA+cOnWq07Qid0+ZVrRs2TJmzZqlaUWSNipwkT44efIk69atS5lWBFBWVpYy3GLmzJkabiGDRgUuMgCOHTvGs88+myz0Xbt2ATBkyBAWLVqUvGxxxowZ5OfnB5xWsoUKXGQQHDlyhNra2uRui2enFQ0bNixlWtH06dM13EL6TAUukgbnTiuqqalh7969AIwYMSI53GLp0qWaViS9ogIXCUBdXV3KTovnTis6d7jFlVdeqb3QpVsqcJEM8NZbb6WcoWtakfSEClwkw5ydVnTu+LlDhw4BMG7cuGShL1u2jEmTJgWcVoKkAhfJcO7OG2+8kbLkcuTIEQAuueSSlDP0CRMmBJxW0kkFLhIy7s7u3btThlscO3YMgEsvvTRluMVFF10UcFoZTCpwkZCLx+O88sorKYV+8uRJAK644oqU4RZjxowJOK0MJBW4SJaJxWK89NJLKdOKTp8+DcBVV12VUuijRo0KOK30hwpcJMu937SiadOmJQt98eLFmlYUMipwkRzT1tbGtm3bkm+IdpxWdG6hDxs2LOi48j5U4BkmFovx9u46ikqLGDd5bNBxJAe837Si66+/PlnoCxcu1LSiDDNoBW5m+cA24F13X/l+z1WBJ2x/+iUeuPUHtDZHiMfjXDjxAu799VcYf7mKXNKnpaWFzZs3p0wramtrIz8/n1mzZqVMKyorKws6bk4bzAL/C6AKGKoCP7/33jrCHdf8Ba1NrcljZsaIsZU89taPyS/QDnYSjKamJjZu3Jgs9K1btxKNRiksLGTOnDnJQp83bx4lJSVBx80p3RV4v3bTMbPxwArgof78nFzy1MPPEItGU465O82nW3jh318OKJVIYo/zG2+8kfvvv5+NGzdy4sQJnnrqKb70pS/R2trK/fffz7Jly6isrGTp0qXcd999rFu3jtbW1vP/cBkU/d2B/u+ArwDdLpiZ2WpgNaC7x4D6d44RjcQ6HY/H4xx/72QAiUS6VlFRwfLly1m+fDkADQ0NKdOK7rvvPu69915KS0uZP39+8gy9qqpK04rSpM8FbmYrgSPuvt3Mlnb3PHdfA6yBxBJKX18vW1x/43TW/2ozLY2pZy3xWJyr508JKJXI+Q0bNowVK1awYsUKAE6cOJEyrejrX/86oGlF6dTnNXAz+xbwCSAKlABDgSfc/dbuvkdr4BBpbeMLc75G3Z5DRJojAJSUF7Pko/O5++HPB5xOpO+OHj2aUugdpxWdLfTrrrtO04p6aVAvI2w/A79bb2L2THNjC7/+we+p/ecNFJcV86H/9ifccOsibfAvWeXw4cMp4+def/11ACorK1OmFU2bNk2/++ehAheRQB08eDBlL/R9+/YBMHLkyOS0ourqaqZOnaq90DvQjTwiklHeeeedlL3QDxw4AMDo0aNTts6dMmVKzhe6ClxEMtr+/fuTt/3X1NRQV1cHwNixY1MK/bLLLsu5QleBi0houDv79u1LOUN/7733ABg/fnxyl8Xq6uqcmFakAheR0HJ3Xn/99ZQz9Pr6eiAxrejc4RYXX3xxwGkHngpcRLJGx2lFtbW1HD9+HIDLLrssZS/0bJhWpAIXkawVj8fZuXNnyrSihoYGIDumFanARSRnxGIxduzYkTLc4uy0oqlTpyYLfcmSJaGYVqQCF5GcFY1G2b59e7LQn3vuOZqamgCYPn16ynCL4cOHB5y2MxW4iEi7SCSSnFZUU1PDhg0baGlpwcyYMWNGcrll8eLFDB06NOi4KnARke60trayZcuWZKFv2rSJSCRCXl4eM2fOTJlWVFFRkfZ8KnAJrVg0xtuv1lE+rIwLJowOOo7kgObm5pRpRVu2bKGtrY2CgoKUaUXz589Py7QiFbiE0vpfbeZvV/+EaDRGrC3GpdMv4RtP/CWjLtJUdUmfxsbGTtOKYrFY2qYVqcAldN58+QB3zf8rWpsiyWN5+XlMuHIca15+MOdup5bMcfr0aTZs2JAs9O3btxOPxykuLmbevHnJQp8zZ86ADLdQgUvoPPjZH/PHR2qJx+Ipx0sqSniw5l6umHlZQMlEUjU0NLB+/fpkoe/YsQN3p7S0lAULFlBdXc3tt9/e52vQuytwjcmQjFX/9tFO5Q2Ql2ccP6Txc5I5hg0bxsqVK1m5MrGj9vHjx1OGW9xzzz3ccsstA/66KnDJWFV/ch2vbHgtZQkFoC0SZcrsyQGlEjm/ESNGsGrVKlatWgXAsWPHGDly5IC/jsZgSMa66Y4bqBw9jMLi/3+eUVJezIfv+iDDLxgWYDKR3hmM8gadgUsGKx9axj9s/xsef/Bf2fDkVioqy/lPd32QxR+ZF3Q0kYygNzFFRDJcd29iaglFRCSkVOAiIiGlAhcRCSkVuIhISKnARURCSgUuIhJSKnARkZBSgYuIhJQKXEQkpFTgIiIhlfMFfvrEGd58+QBNp5uDjiIi0it93szKzC4G/hEYAziwxt2/P1DBBlu0LcoP7nyIf/+ndRQWFxCNxFj1heXc8cCtmvQiIqHQnzPwKPBld58KzAXuNLOpAxNr8P3snl+w9rH1tLW20XSqmUhLhCf//g/85oe/DzqaiEiP9LnA3f2Qu7/Q/vlp4FVg3EAFG0zxeJx//fEfaG1OHRTQ2tTKL7/z24BSiYj0zoDsB25mE4EZwJYuHlsNrAaYMGHCQLxcv0XbYkQ6lPdZp46d7vb7Ii0Rnn/qRZpPtzDjhmsYNW5wNmkXEemJfhe4mVUAvwL+3N1PdXzc3dcAayCxH3h/X28gFBUXMvayC3l3z6FOj11R1fWg3N2b3+Cvbrofdyced+LRGB/72of5xF9/ZLDjioh0qV9XoZhZIYnyfszdnxiYSOnxhR/dTnFZEWffr8zLM0rKivnc9z7d6bltkTa+vvJbNDY00XSqmZYzLURa2vi/f/MkO9e/mt7gIiLt+lzglrhU42HgVXf/3sBFSo+ZH7iWB2vuY+5/rGLc5WNZ/JF5/HDLt5jSxRn4S7W7iUVjnY5Hmlt56uFn0hFXRKST/iyhLAA+Aew0sx3tx/7K3UNzGceUWZP5n7/57+d9Xnfr5e7QcqZloGOJiPRInwvc3Z8DcuKC6WuXTiXa1vkMvKS8mCUfnR9AIhER3YnZI+XDyvmzH95GcWkRefmJ/2QlFSVMW3QVC//znIDTiUiuGpDLCHPBTbfdwFVzruAPj9Rw5vgZ5q+azZwV15OXp/8HikgwVOC9MPHqi/mv3/lk0DFERAAtoYiIhJYKXEQkpFTgIiIhpQIXEQkpFbiISEipwEVEQkoFLiISUipwEZGQUoGLiISUClxEJKRU4CIiIaUCFxEJKRW4iEhIqcBFREIqp7eTPXOykaf/sZYDu+uYPONSbvjThZRWlAYdS0SkR3K2wOveOMhd8+8h0hKhtSlCSXkxP/9f/8KPnn+AUReNCDqeiMh55ewSyvc++xPOnGiktSkxsLilsZUThxv46ZcfDTiZiEjP5GSBR9ui7NrwOu6ecjwei7P5d9sDSiUi0js5WeBmhuVbl48VFObsqpKIhExOFnh+QT7zP1RFQWF+yvHC4kJu/MTigFKJiPROThY4wBd/vJpxl4+ltKKE4rIiSipKmDxjIrd985ago4mI9EjOrhcMGzWUNS8/yEu1u3h3z3tMmjaBqfOuwKzrpRURkUyTswUOkJeXx4xl05ixbFrQUUREei1nl1BERMJOBS4iElIqcBGRkFKBi4iElApcRCSkrOPt5IP6Ymb1wIE+fvso4OgAxkknZQ9GWLOHNTco+2C5xN1HdzyY1gLvDzPb5u5VQefoC2UPRlizhzU3KHu6aQlFRCSkVOAiIiEVpgJfE3SAflD2YIQ1e1hzg7KnVWjWwEVEJFWYzsBFROQcKnARkZAKRYGb2XIze93M9prZV4PO0xNmdrGZ1ZjZbjPbZWZfDDpTb5lZvpm9aGa/CzpLb5hZpZk9bmavmdmrZjYv6Ew9ZWZfav99ecXMfmFmJUFn6o6Z/czMjpjZK+ccG2FmT5vZnvaPw4PM2J1usn+n/XfmZTP7tZlVBpmxJzK+wM0sH/h74CZgKvBxM5sabKoeiQJfdvepwFzgzpDkPtcXgVeDDtEH3wf+zd2vBK4lJP8OZjYOuAuocvdrgHzgY8Gmel+PAMs7HPsq8Iy7Xw480/51JnqEztmfBq5x9+nAG8DX0h2qtzK+wIHZwF53f9PdI8A/AzcHnOm83P2Qu7/Q/vlpEiUyLthUPWdm44EVwENBZ+kNMxsGLAYeBnD3iLufDDZVrxQApWZWAJQBBwPO0y13Xwcc73D4ZuDR9s8fBValNVQPdZXd3f/o7tH2LzcD49MerJfCUODjgHfO+bqOEBUhgJlNBGYAW4JN0it/B3wFiAcdpJcmAfXA/2lf/nnIzMqDDtUT7v4u8F3gbeAQ0ODufww2Va+NcfdD7Z+/B4wJMkw/3AY8FXSI8wlDgYeamVUAvwL+3N1PBZ2nJ8xsJXDE3bcHnaUPCoDrgR+7+wygkcz9a3yK9vXim0n8T+gioNzMbg02Vd954hrl0F2nbGb3kFgCfSzoLOcThgJ/F7j4nK/Htx/LeGZWSKK8H3P3J4LO0wsLgA+Z2VsklqyWmdnPg43UY3VAnbuf/dvO4yQKPQxuBPa7e727twFPAPMDztRbh81sLED7xyMB5+kVM/s0sBL4Uw/BTTJhKPCtwOVmNsnMiki8qfPbgDOdlyWmIz8MvOru3ws6T2+4+9fcfby7TyTx33utu4fiTNDd3wPeMbMp7YduAHYHGKk33gbmmllZ++/PDYTkDdhz/Bb4VPvnnwKeDDBLr5jZchLLhh9y96ag8/RExhd4+5sKfwb8gcQv8y/dfVewqXpkAfAJEmevO9r/+WDQoXLEF4DHzOxl4DrgmwHn6ZH2vzU8DrwA7CTx5zNjb+82s18Am4ApZlZnZrcDDwAfMLM9JP5G8UCQGbvTTfYfAUOAp9v/vP4k0JA9oFvpRURCKuPPwEVEpGsqcBGRkFKBi4iElApcRCSkVOAiIiGlAhcRCSkVuIhISP0/cfDaapb860UAAAAASUVORK5CYII=\n", | |
| "text/plain": [ | |
| "<Figure size 432x288 with 1 Axes>" | |
| ] | |
| }, | |
| "metadata": { | |
| "tags": [], | |
| "needs_background": "light" | |
| } | |
| } | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "DCMH0UPeKdsR" | |
| }, | |
| "source": [ | |
| "### Contoh SVM Non-Linear" | |
| ] | |
| }, | |
| { | |
| "cell_type": "code", | |
| "metadata": { | |
| "colab": { | |
| "base_uri": "https://localhost:8080/", | |
| "height": 265 | |
| }, | |
| "id": "M-cKg_VJKmN1", | |
| "outputId": "f732d69e-3d5d-41d5-d6d2-40abcd5484ea" | |
| }, | |
| "source": [ | |
| "import matplotlib.pyplot as plt\n", | |
| "import numpy as np\n", | |
| "from sklearn import datasets\n", | |
| "from sklearn import svm\n", | |
| "\n", | |
| "# non-linear data\n", | |
| "circle_X, circle_y = datasets.make_circles(n_samples=300, noise=0.05)\n", | |
| "\n", | |
| "# show raw non-linear data\n", | |
| "plt.scatter(circle_X[:, 0], circle_X[:, 1], c=circle_y, marker='.')\n", | |
| "plt.show()" | |
| ], | |
| "execution_count": null, | |
| "outputs": [ | |
| { | |
| "output_type": "display_data", | |
| "data": { | |
| "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAD4CAYAAADvsV2wAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOydd5QURdeHn+rJmyNZBMGACogioKioiDln0NecxYQRBcx+CmZRFBExR1QwixFRUEEFyTnDBjaHiX2/P3rZAJt3ZmM953DYnq6uuj27c6f61q3fVSKCRqPRaFo/RlMboNFoNJrGQTt8jUajaSNoh6/RaDRtBO3wNRqNpo2gHb5Go9G0EexNbUBVpKSkSLdu3ZraDI1Go2lRLFiwIFNEUis712wdfrdu3Zg/f35Tm6HRaDQtCqXUhqrO6ZCORqPRtBG0w9doNJo2gnb4Go1G00bQDl+j0WjaCNrhazQaTRtBO3yNRqNpI2iHr9HUk1AoxJTR7zBy4D18NvFrTNPkl4/m8s3UHyku9Da1eRrNbjTbPHyNprnz5Svf89kLX+Er8rNh6Wbmf/svC39eggh8NvFrJi0Yj1Kqqc3UaErRM3yNpp5sXbMNX5EfABFh0eyleAt9+Ip8bFi6mfysgia2UKOpiHb4Gk09Oemq44iK8xAV5yEmIZo+R+2P0+3AZjdI6phATGJ0U5uo0VRAh3Q0mnqyZ68uvLX2Rbas2k63A/fAZjOY8eI3FOYUcfqNJ2AYej6laV5oh6/RNIC4pFjiBsaWHp93++lNaI1GUz16CqLRaDRtBO3wNU2OaZqs/mcdaRsymtoUjaZVExaHr5SaqpRKV0otruK8Uko9r5RarZRapJQ6OBzjalo+IsJ9p/wftx01liv2v5Uf3v21Qf0VF3rZsHQTfl8gTBY2HNM02bxqG4W5hZWeX/7nKma+9C1bVm9rZMs0bY1wxfCnAROBN6s4fxKwd8m/gcCkkv81bZzt69L5b/ZSfMVWeuPbD33M0BFH1qmPUDDEWw99xMKfl7Bm4XpEID4llpfmP0FcUmyFtot/W87/XfwcZtDkztdv5ODj+oTtXqqy7c6hD7JywRqUYfDEt2PY/7B9S8///f0ixp35BGIKNruNl/+ZQKceHSJqk6btEpYZvojMBrKqaXIG8KZYzAMSlFIdwzG2pvmSvimTj56cya/T5yEilbaJTYqBks1JNruNTj3a13mcDyfM4OOnP2fxnOUU53vxFnjJSc9lzvQ/dmv74LlPkr4hk8wtWTxw9oQq7QoXS+euZPU/6/AV+fEWeHnrwY8qnJ/z2Z/4ivz4vQFMU1j0y9KI2qNp2zRWlk5nYFO5480lr1V4hlVKXQNcA9C1a9dGMk0TCQpzC7n+4LsoyivC7rSzZfU2Lrz7rN3axSRE8+gXo5k65l1SOiVx80tX13mstYs2lG6A2olSiuROibu19ReXtQv4g4hIRHfDxqfGYYZMAOxOOyldkiucP+joA/hu2s/4inyAsO+hPerUv4ggIjoFVFMrmtVfiYhMFpH+ItI/NbXSkoyaJkJEWDxnGUvnrazVrHjD0s0EA0GCgRDeQh+/ffZXlW37Hn0Az815lLEf3k58SlydbTv9hhNxRbmIivXgjnbRZZ+OnH/XGQw4efelopsmXondacfusHH905fWy1EGA0E+emomk0ZNY/Oq6uPuXffrzI0vXEGXfTsx8OR+XPvkJRXOH3XuYdzz1k2cd8dpPP7tWLr33rPWdvz1zT+cHvc/Tom6iJdvf4O8rPw634umbaHC9UirlOoGfCEiB1Zy7hXgZxF5r+R4BXC0iFT5aenfv7/omrbNhycum8ic6fMAOOmqodzwzOXVti/IKeSSniMpyivC4XJw4d1nctGYcyNmX9qGDDav3EqvQfsQFeuptq3f60dEcHlc9Rrruesn892bvxDwBoiOj+LdjZPwxFQ/ZiQ4r8NV5KTnlh7HJsUwedFTpHRKanRbNM0HpdQCEelf2bnGCunMBEYqpd7HWqzNrc7Za5oXoVCIH96ejZjW5ODLyd/X6PBjEqJ5af4T/PTeb3To3o6jLzi8zuOKCB9OmMHcz+fTb2gftq1NIz8rn8sfGU7Pg7pXaNt+z1Ta71n2VBgKhbDZbJX263Q762xLeRbNXloaGgoFQ6RtyKTbAXs0qM/6YLNVfDrxFvmYO3M+p113fKPbomkZhMXhK6XeA44GUpRSm4H7AQeAiLwMfAWcDKwGioDqvYWmWWGz2UjtkkzG5h0opWq9sNqhWzuGj949bl9bZn80l7cf/hhvoY+lc1eilMIMmSz5bQUfbp+C0+XY7Zpta9O4/ZgHyNyyg+MuPoo7X78x7DH64/43hHcfnQ5AQrt4OvXsgK/Yh2EzcDh3tylSjH73Fsae9jjFBZYUs2EY7LFvp0YbX9PyCIvDF5HhNZwX4MZwjKVpGp786QFeG/0ONrudq5+4qFHG3LomjUBJPr2YgmA9YfiK/RTmFuFsF7/bNa/d+w6ZW3YgpvDr9HmcfNVQDjyiV1jtGn7PWexzyF7s2JrN4DMP5ZNnv2DauA+w2QzGfXQ7A085JKzjVUXfIQcwI/dNPnxyJnOmz2Ovvt3odmDDnjR2bMvmvlMfY8vKbZx67TCumXCJlnhuRTSrRVtN86Vj9/aMeX8Uo9++mZTOyTVfEAaOGT4YT6ylRun0OHG6Hbhj3Bw8tDcJqZUv7trs9goOyrBXHtZpKIcM68vxlx6NYTOYNu4DQoEQfm+AZ66bHJHxqkIpRcfu7Vi3eCM/vTeHq3vfTn52/WWZp4x+h/WLNuIt9PHFK7NYNm9lGK3VNDVaPE3TbOnQrR1vrp7IhiWb2POAPcjckkVhbhG9Bu1d5azz6icuYu2i9Wxdk8ZJVw2l18C9w26XBFZAcA24BmGzx2AYBiFCALg9DVsfqA/fTP2xNC1VGYrlf6zi0BP71auvgC+AuTORQykC/mC4zNQ0A7TD19SL9I0ZzP92Id377BkRp7qT2MSY0pBMbGJMje1TOifz6qKnI2aP+H5Bsm8CZQNcOFK/ZvQ7t/D8ja/iiXZz3/u3RWzsqjjwiP1YNHsZviIfZsika68u9e7rikeGs3jOcrK2ZTPo1EPofWTdw2GmabLuv43EJkbTrqtOr25OhC0tM9zotMzmy+vj3ue9Rz9BKbC77Iz94HYGndo4ceumxsweCb7vSo5cEDsGI/qCprXJNJnx4jesXbiek646jv0H7dOg/kSEUDCE3VH9fPDTF75i5ovf0LPfXoyach2eaDciwtjTH2fhz0swTWHUq9fVWSpD0zCaQ1qmppWw7I9VfDR+RskOT/AXB/jp/TltxuHj6Ae+XwCf9S//McR1CMres8lMMgyDs246OWz9KaVqdPYr/lrNa6PfwVfkJ21DBildkrh2wiWkbcjgnx8Xl6atvvXgh9rhNyP0om0zQkRYu2hDrVQTZ388l6v7jOL+s8aTt6PxdljmZeZVWAg1bAZ9huzfaOM3NSr6cnAOKveKFyn6LOLjilmABFcj0ngx9bQNGdx+zP1c3XsU879bWOFcdlpu6S7lgC9IxuYdAMSWK+uolCK1S/0W+AtyCvn+7dn89+uyelqvqQzt8JsR4y9/kZsPv49r+t7BJ89/WWW79E2ZPHHJC6xfvIk/vvqb5294tdFs7HdcH7r37orDZcfhsnPZwxdy8lXHNdr4kUYkVO15pQxU9MXAzi89geL3EPFFzqbASiTjKGTHOciOMxEpjthY5XlsxLP89+sy1i/ZxP1njacov2zcg449gKg4D8pQON0Oht9j7bdwRbmwO8rem0Cg+vezMnzFPq7tdwfPXT+Ze09+lJmTvg3H7WjQDr/ZUJhXxE/vzsFX5MNf7Oe9Rz+psm1eZj5GyS7LUCBE2sbMxjITp8vBc789wuvLn+fTrGkMv+esVpGnLcGNmOlDkLT9MXPuqlYvSLmGgCq3B0ACEEqLnG1Fr4EUghRDaAv4ZkdsrPJkbcsu3V0tplm6wQtg1pu/UJBThJiW+Jzfa+2XKMwtKv1ZBLbUoDVUGesXb6IgqxBvoQ9voY9vpv4YhrvRgHb4zQZ3lAt3tKXtYhiKdl1TqmzbvU9Xeg3aB1eUC1eUk8seatxFQ8MwaL9nar21aJojkv8UmGmAWIuygQXVXxB1PigP4AFbR7BFcIer0REoSfcUE4zGyXy56vGLcbodON0Ojhl+BMkdy9RH1y7cUKLwaaWCblq+BYC45Fj6HLU/nhg37mgXp19/Qp3GNE2TgtxCTNNEKXB5nPSpR6aQpnJ0lk4zYsX8Nbxy+xtExUdx84tX0W6Pqp2+aZpsXrmN+JTYOitM5mTk8tGTMzEMg/PvOqM03fGT57/kw/Ez6LJPJ+57/zYSK9nJGg5ETMCPUu6I9F8fzJzbwfsVEAI8qKQ3UM6DqmwvIuD7GcwscJ+AMmpOGa0vIl4kdxwEFkHUBRjRjadMkpuZR1F+MR26tavwJLf8z1XcOfRBS07C5eDVRU+R2D4BsPSF/vlxMVFxnjpnDD103pP89c2/hIIh9unfg8FnDuDsW07BFqENdK2R6rJ0tMNvg1zdexSbVm5FoejRrxsT5/0fG5Zu4sZD78FX7MdmNxhy/uGMfvuWsI8twTXIjotAcsB1IirhaZSK3IOmmNkQygB7D5Sq2mlIaDuSdSWENkLUhajYe1tFqCqSpG3IYMPSzew3sOdulcXqQ25mHhd2vpZgwFqYTuqQwAdbG299qrWg0zI1pZimyYZlm0tjs2sXrges2KvauS4QNMnbUfft+SIhCCwGIxFlr7yAjeQ/BZINCPh/hsA/4IxMSqf4/0Kyr7IO7PtA0rsoVbm4mbJ1QKVWvVBeod/AUjDzwNkfpZrmIySh7ZYN9qp3HUeaXRVKG4oloeEgGAhisxl0rEf1M0316Bh+G8MwDAac1A93tLVmMPjMAQDsN3Bv+g7ZH7vTTnR8FFc8Wq0e3m6ICJJ9BZJ9KZJ5KmbRp5U3VB5K/+xEIIJhHSl4yVrolGIIrobAvw3u0yx4FdkxHMm5Dsm+OuIlEiu1ofhLJGMYsuM8JOfGJrEhEjicDsZ/fz/9hvZm8FkDGPfR7U1tUqtDh3TaIMFAkN9n/IUyDA4/o3+pbryIkJORR3R8VKXSw9UhwY1I5qlASSaHrRtG6ne7twulI9nXQWg9RF2KERv+sNFOzNwxUPwpEADcqJQZKHv3mi6rvs/0I8BMLzlyolJ/RtmqXmuJBGbG8db7B4ALlfIVyt74evya5okO6WhKMU2Tb6b+xKYVWzjx8mMqFAlRStV7oVZUglWMXADsYOtWaTtla4dKqTrltLS/4Fqk6GOUfU/wnFevOL+KvQeRQmt2H3V1g509APYe4M8CgtbTiVH5grmYuUjuWAhtQMWMBFtHxPsNynEgyn1iw2ywdYbQJqwFZgOMhIb1F2FM0+Tn938jc0sWQy8+qkK2j6Zx0TP8ZkxtNU3qwlsPfcQH42fgK/LhiXHzxqoXSrMr6otZ8AoUPGeFa4yu4NgLFTcGZdTvgy1mDpJxrJV7jguiL8OIHWWFjQqeA++34DoSFXv3bguxIn4IbgBbZ5QR1aD7qtK2/Alg5qBibkY59q20nZkzyrKTgHUPKKynHw/EPYARVf/CMBLKRPLGQCgDFXs7ylWfamJmRBfLyzNl9Dt89sLXBANB4pJieXPNRNxRrSelt7lR3Qxfx/CbKav/Xcc5qVdwStRFvHTb62Hr958f/6uQP72xJH+6vkgoEwpeAIIg+aBCGAlP1dvZAxBcv7N3wAu+361D33dQ+DqE1kDR+yXhmnK2mDlI5glI1nlIxtFIcFPt7yOwFPH9UfNOWyMBI/5RjMQXq3T2AIQ2Yzn7nfexk2Lwz6m1XZXaYEvBSHwZI2V6nZ29mFmYmacgab0ws65GJFDzReWvDyzHzLkNM+8JxCyq1TXzPp+Pr8hHKBDCW+Rl25rtdRpTEz60w2+mvHjTVPKzCjBDJl9N/p5NKxrmmHcy7H9DSjZsuXC6nfQ8qFutrhMzHzPrSsz0wZgFL5Q7s2uGSBgyRux7lyzuuq3/PadZr4fSALOkUcDKVCmP9xsI7QApAslDij+o1XBlC7HXhm0hVsXcVGa/fX+sj5oL8ICrgSGdBiCFr0FwHVaW1F/gnVX7a81CJGsEeL+EoreQvPtqdd2g0/rjinJhc9hwR7np2KNDPa2vPSLCl6/O4vH/Pc8fX/0d8fFaCjqG30xxuK3KTTtVKesa1gmFQqz+ex2xSTF0KvcBO+nKoXTq2YGtq7cz6LT+RMdHV9NLGVLwHPjnAQEomII4D0M5+6NsyUjsKMh/Bow4VPxjdbKzMpQRDckzwTcLbF1QriOsE55TofBV60kCNyrqnIoXGu0p+8Jxomwdazdg0TSg2JqI+/+wNlPZykS/xPsDkv802Dqg4p+o1SKtch0JqT+BmQn2nkhwM+Q/auX5h1YjclwTpVPaKH2PFCW6/rXEzIBS8TY/+BdW23wnVzw6nO4HdmXH1iyOvejIiIZz5n2xgOnPfoHNbmPxr8vwFfuZ8+mfPPXzg+zbv0fExm0paIffTLll0jWMOe1xdmzN4qIx59Jxr9rnJIsI953yfyz5bTmmKdz80lWccOkxpef7DjmAvkMOqPQ6JBdUzO755WYuUPJhVwrMMoVOI/oKiL6iTvdXE8qWDFEXVnzNSILU760YvX0PlPJUvMh1NMRcDcVfWoqWnlpKTth7gD8bayHWA0bZJiIJ7UBybgV8EFqL5I5GJdVuM5CyJZd9cQQXI/4/gGIoeBns3cB9Uo19iARBvGHbyauir0T8cyGwDJxDwFUH4TvbHtZifGgFIGCmIf6/UM5Dq73MMAyGXhR5ieTNq7bxyIVP4yvyY9gMzJD1NBgKhZj7+Xzt8NEOv9nSuWdHXl/2XL2u3b4+nf9+XVaqSf7eo59UcPiVIRJCcm4A36+gYiDpHZSjrJKVirkB8c22FlLtB4BrcL1sayhKucBR+XZ9pZSVERMzsm59JjyH5I8HMxcVcwtKlStTKLmUPTWEwKxn/LlCTD9giaDVgASWIFmXgBQh7lNQ8RNq9VQgwY1I7p2WU8cPjkNQSVNQyoMy4lHJH9XrFpSyIbG3Qc7NWPUAAkjBFFRS9Q4/3ORl5fP1lB9weVycfPVQnG7r95W+IQOjJOvMDJkoQyGmEPQF+WjCDHoN6NloBeabKzqG3wqJS47FMCzHYHfY6Lx3LUIbgQVWOIMgSC5S8EyF08reHdVuDiS9A2YuknE0ZtH0CFjf+CgjESP+/zASX9p9IdbWHVxHAG7AjYqt52Ygz2nWF+nOf+5TarxE8p8oCV+FrPBWsHba8JJza8kmMy9gQmAhFNXPye+KtYN655eOy3pSaUREhNuOHMu0cR/w6t1v8ciFZX+n+x++L8kdE/DEenBFuTj56mE43NZ+Er83wA/v/NqotjZH9Ay/mZKdlkN2Wi57HtClQq58bYiOi+Kxr+5j2tj3SOqUxMjnaxFuUTGWEiMAtkrzy5VyWE4otAoQyLsfcQ1p9I1HjYlSChJehNAGMOLrnX2kbJ0g9Qer+Lm9Z+1CNCoaa05mgphI8Uwk5yawH4iK/7+q007NHVTMDAofyt4DiX/cypZy7IeKbdwavt5CL5tXbisN1yz6ZWnpOXeUi5f/mcDyP1bTvlsqQX+Q79/6xToX7aL3UVp1U+fhN0MWzFrI/WeORxmKHgd146mfHmwUtUCzYBIUvgH2vVCJE62Y+a5tMk+H4PKSIwOwWTnvSa+jbJ0jbmNbQkLbkewbrXCQ+xTwTrdkInCW7E24o9LrzOIvIfcewA8IOA4tDem0dESEG/rfzcblW1BKcdhph3Dfe1V/6Sz+bTk/vPMr+x3ak+MvO7rSkFjAH+D7t2YT8AUZdslRBPxBxp7+BOsWbWDoxUdx84tXtSghPa2W2cK47aixLJ5jOVV3jJsJ349jvwF713BV+JHQNisO7OiNslkiWeL/E8m+GsRf0qpkt6drGEbiC1X2pWkY4p1lxeWlCFDgORMj/omq25vZ1mJvbTOVWhDFBcV8/9ZsXFEuhl50ZIMnQ/efNZ4FsxYhInQ/sCv7H7YPn0/6lmAghDvaxf3T76T/8X3DZH3k0dIKzZDstByevHISO7ZkccVjIxhwUr/Scx26t2P5n6sJ+oOYIbPBO2HrgwRWIFkXYM3iFSTPQNm7oJwDoN1fiP8fyL4G2Fn2ru6l7DR1wHWUlSETXAvKiYq+utrmDdr41gzJ2p7NIxc8w7a1aVw05hxOq2Nhler4+/tFpZsRV85fw1599sQsUZNVShHw1W1zWnNGL9rWgoKcQj6b+DU/vPMroVB4HNv4y15kwXcLWbNwPQ+d+yR5WWVpjjc+dwWDzxpAz37duefNm+otQSv+BZhZV2HmjkXMuskdi/frEqXJAhAf+MrKzCnltBy/5wwsLZcOqNh76mWjpnYo5UIlT0elfIlq9yvK3rOpTWpUXhj5Gkt/X0HmliwmjXqDrWHcrdv7qP1xup04XA726rMnF487l5TOSShDceCRvSpMxlo6eoZfA6FQiJsGjSZ9YyaGzWDxnGXcMumaBvebsSmTULDsy6Mgu7C0iERMQjRjqolL1gYxc5HsK0pjviL5qIRna329su+D4MaawdtgFwejlELFP4TEPdii4pstGaVs0ExUMSWwBMl/0lrIjh0T8YX7vMx8QiULtYahKMytnaxDbXhg+h18NeUHAr4gJ191LNHx0by97iUCvkBpymdrQc/wayAnPY+0jZn4vQG8hT7mfh6edYXLHr4Qp9uJK8rJIcf3rdPGqlphZpQ78ENgVd2ud58EsXeDayjEPVSlZot29s0DCSxCfL9ZG7UiPZb4rf0B/t/A+y2Sc3PEx7zy8YvwxHpwuOz0P+EgetRSEqQ2ON1Ozhx5EufdflrpznOlVKtz9qBn+DWSkBpHYvt4dmzNxm630W9o77D0e8RZA3l73YvkZRXQdb/O4Xectu5WlafgapAQ1BDz3RWlFCp6BESPCK9dmrBjFkyydu8qBY6+kDgtsl/EUgBSUveAkJWyWp9uAssgtBUxUlH+eeA4AFXFhr79B+3Dx2lTKMwtapI1rdaCdvg1YLPbmPjH43w95XtiE2M46aqhYes7sX1CxP54lbJB0rtWCUEjGWXX28pbLUVvU6YFtMDKw49kiEUlgmuINcMXgejqQ5wSXI3kPQrYUHHjUPaumEUzIW9sSQsvggE4kPjxGJ7KxeWcbmernHU3Jtrh14LEdvGMuPecmhs2M5RygHNAU5uhiTT2fcCfQ5kWUOVFWcKFtRltIgT+AyO6xgVkybrUEpFDIdlXolJnQfFblGV4gZXlFbKSA6pw+JqGox1+hPAV+/ji5Vn4in2cet3xpQuyGk24UQnPWsXhzVxUzMiKWkCRGlMZ4Kw5N13ELLfzV0okrgFHHwgsx9LkgVL5aNfumk9iZln3J0WW1lEjyzm0JrTDjxAPnvsUC39ajGma/PjuHKYstjQ/fp/xFz++N4e+R+/PqdceH5FYq5hZSPZIK2c7+lKMmOvDPoam+aCMeFT8QxEdQyQEgUVWVo59r1pfp5SBRF0MRR9aL5SoqqrYuxEVa2nzu45FmVtLYvhH7T529vXW0wQm4p8Hqb81WrWu1oZ2+BFi8Zzl+L3Who2Ny7fg9/pZs3ADj130LL4iP398uQB3lJthlwwJy3gixZZme3AjECwRzwpCwfOYtu5VxkU1mpoQEST7SutvSkwkbgxG1Pm1vl7F3gee80DZSsM/SjlRsbfWroPgGkqluc0cK9VY1a6Og6Yi+muyAZimSfrGDPyV7MQbcHI/3NEuXFFO9u3fA6fbybr/Npae9xb6WPn32nqPLWJiFr6LmTsO8S9E8h62yv75f7IW03Z+QAhB7t21Lken0eyGudVaDJYiwAuFr9TpcqUUyrFv/TeLeYYDHlBR4BpiFcipJ9lpObxy55u8PvY9CnML691PSyUsM3yl1InAc1jldKaIyOO7nL8MmADsFAGfKCJTwjF2U+Er9nHrEWPZuHwL7igXz899lM49y3RLRr91Mz++Owe/18/Qi63H1ENPPAiH04HNZiMUMjl2+BH1Hl8Kp0LhCyDFiHcGGF0oi4c6S37eqZNkWnn5xp71Hk/ThlEJVmUsAbBbKb+NiBF3O+Ieas3sG5iEcNtR49i+Lg1lGPw3exlP/xLZUFhzo8EOXyllA14EhgGbgb+UUjNFZOkuTT8QkbpVpmjGzPvibzav2oa/2E/AG+CjJz/n1pfL0tNsdttu4ZrULsm8tvQZlvy2gr367lnhC6LO+P8s2UULYLPS5Io2WR9MWxdwnQKFLwEG2Ltar2k09UAZ0ZA4DSl4FoxUVNy9jW+D86AG9xHwB9i6entJzWKTVQ14wm6phGOGPwBYLSJrAZRS7wNnALs6/FZFXHKMlYMM2J12EtpVnQqXvimT5294laL8Yq598lKOPGdQww3wnFVSY1YBTlTMNRB1tpUF4eyPUi7ENcBKh3MdZeXlazT1RDkPQiVNa1IbRPxI/gQILIaoizE8NReRKY/D6eCgYw9k2R8rQeCIcHwOWxjhcPidgU3ljjcDAytpd45S6ihgJXCbiGzatYFS6hrgGoCuXbuGwbTIkb4xk9jkWJRh0H9YHy6856wq2z5w1gTW/LsO0xTuHvYQ0zOmNljS1fCchNg6QWgNOI9CGQlgJFTQvFHOgxs0hkbT1IgIBP+zfi7+Hoo+ALyQuwSx99y9QlkNPPrlaH779E8cLgeHnV6pgnCN7Hyy7967a4uTFmmsLJ3PgfdExKeUuhZ4Azh210YiMhmYDJYefiPZVmeWzlvJCyNfw1fkw+Vxsv/h++KOclXZPn1jZqncqrfQh6/YT1Rsw4tRKGdfoOXodGs0dUXyHgTvp9aBSsUq24gVugxtgTo6fIfTwdEX1L8e80dPzWTauA9QSnH0hYdzx5Qb6t1XUxCOLJ0tQHkJvy6ULc4CICI7RGTniuIUoEVXEt6+Ng1VUjPWV+xn04rqC1KPGHM2To8TV5SLY0ccERZnr9G0FsQ3DzP3bszC99itIFPxByUy3cVgbrF2EqtoMJLBWVkgIbK899in+JSAckYAACAASURBVIv9+Ip8zHrjF7xFvpovakaEY4b/F7C3Uqo7lqO/EKiguKWU6igi20oOTwdqV425mdL/xIOIiY/CMBRmSDj12uOrbX/2zacw8OSD8RVZj4HhQsQqYadU1U8XGk1zRoKrkexrsGbu3yCIJdq3E6Oj5ehRJaU037FKPjoOQCl3o9vbrmsKhbmFmKYQFevG4WpZW5kabK2IBJVSI4FvsdIyp4rIEqXUQ8B8EZkJ3KyUOh0rOTwLuKyh4zYlcUmxTF32LKv+XkeXfTqS1KHm6kINysgpQfzzkZxbLKVC95nW7AcTiR2DoVUtNS2RwHLKAg3FEPibnfNF8f1uZZ8FV4CRhIq9B2VrD7YwS4mXICK8du+7/PT+HPocuT+3vXodTpejQpuHZtzF8zdOwVvo47qnLsVma1nJELqmbQvCTB8C5rZKzthR7Rfr7eaaFoeEMpDMk0ECgIlKnIRyDUZ8c5Hsa7Fm/m5U0lsla1aRY94XC3h0+DN4C3043Q4ufegCzrntVMQU7I6WM5OvrqZtm/YQfq+fbevSaixb6PcF2LxyK36vv9p2kaeK4hbKiZWeqdG0LJQt1SrbGP8wKvnDUj188c+nbCNhCAKRn/zlZubtzLQm6A+y/I/VnBF/CadGX8yHT86I+PiNQZt1+FvXbGd41+u4+sBRXNfvTooLvZW2y8nI5bJ9buL6Q+7if3vdSObWrEa2tAwV/xjgBuzgucKKbxrtUAkTW1x6mEazE2Vrh/KchnLsV/aaazDgwto1bgPnYRG348hzBtF+zxRcHidxKbEs+X0FviI/oWCI1+97j6L84po7aea0nOeUMDP92S/I31GAiLB9XTpzZ86vVOrgx3fnkJOeR8AXIOAL8t20nxlx79lNYDEo1xBo/y/WQq0NqFg4XIKrLRlZFVUS76xf8XONpqlRzoMh+W3w/w3OgShHr4iPGRXrYfKip8jYtIOkjolc03tUmT1KYdha/vy45d9BPUnqkFBhhT0htfKdsontE7DZrbfJ7rST1CGy5dUklIkElllytJWglFHprlkRE9lxsVVAwvsVkn1dRO3UaCKNcvRBRV/WIGcvIpa4oH/h7imflWCz2ejQrR1Ol4PR795Ku64pxCbFcMe0G6vda9NSaLMz/HNHncaGpVtYNnclwy4dQt9jDqi03ZDzD2PV32v4fcZ8Dj3xIIZdGh4548oQ32+W9jcKHPtB0jsoVctfkXhBcrEUrupfZ1SjaU1I3oNQXLJxy3M2Kv7+Wl+7b/8evLN+UoQsaxrafJZOdloOtx9zP5tXbGPQqYdw//Q7Gix7UF/MHSPKFqdUFCrxDXD0qXV83sy+GfyzS+qMXokRe3MErdVomj/m9l5Y5RMB7BgdWrXEF6CzdKrlvcc/LVXQ+/enxcz9vAlTQW17ACV5vxJCcm5F0nph5txdq8dRlfAsKvE1VPJ72tlr2hQifsy8xzF3XIJ4vy87YeuM5eYMsHWKyNhfv/YDF3W7njuGPkB2Wk5ExggXbTaksxOb3VY6gxakyWb3ACpuDELAKvtGFAQXACb4vgX/2eCqfiu5VWe0RatWaDT1QgpehKJ3AS+S8y+kfIKy90QlTkPynwCssorhZtvaNCbeNBW/18+Ordncd+r/0a5rCoPPHMCw/w3hj6/+5vkbXsUT6+G+d2+he++mrUnR5h3+8NFn8d/spaxdtJEjzhzIwFOaTmFSGbGohKcBMHPvhuDf5U7qtEuNpkqCK6korLYZ7D1R9i6oxBciNmxBTiGGzfpshoIhVv+zjlUL1rLgu4VExXl4bMRz+Iut/TsPn/80U5c9FzFbakObd/hxSbFM/OPxmhs2AiIC3q8gtAmMPbA2UylwHgOOQ5vaPI2m2aKiLrWkGJQBKhZR0SAS8f0pPQ7qxsHD+vDX1/8iIoSC1npBwBdk3aINpccAhXlNn8ff5h1+c0IKX4GCSVg7DM2SVxWY6XpjlUZTDco1CFK/RvIngvdzyLoKcZ+AShgf0XENw+CB6XeStT2HrO053D5knKWkK3D0BYMJhUzef/wzlKEY+fwVEbWlNrT5LJ1wIsGNVjUeZz+Ure5iaeaO8yCwcPcT9r0xUr4Mg4UaTevGTOsPkldyZKDa/4NSjSdHnrF5Byvnr2Gf/j1I7ZIMWGEfm8OGJ7px1D2ry9LRM/wwIYGlSNZwShOfkmeg7JVLIYtZiOSMguAicJ9u7YpVClzDrFik+LGERwWwoWLvtUSmCp4BCaFib0FFKONAo2nR2LpAcDlggorDkmdoPFK7JJc6+p3EJEQ3qg3VoR1+mBDvN+WKijvB9zPYL6m8beGr4P8N8FsSx67BVt3Z6KvBvqe14OQ+GZQLlAelPJiZp0NwFSBI4C9U6o+NdGcaTfNCJGRl3vh/B/fJqOjrS0OeKvFlJO8RkCJU7N1aQXYXtMMPE8pxAKI8JU7fBtVtBzfzqKB8aRZYfSgF7hMqvya4jtINJKEtiJj6j1nTNin+CIreB7xQsAnsvcB9DADK1gGVOLFCcwllAv4an4rFLALlKpUu+eOrv9m4bAtHnjOQDt3aReJOGh3tMerI3M/nc/0hd/HguU+StyO/9HXlPgFi7wf3KRA/HuWsOqtGxVwJRgrgAPve4B5a88Ces0rKu0VZsxrt7DVtFAltBXZKlZtgbq+yrVn0AZJxNJJxAmbeY5X3J4KZey+SfgiSPgAJLOHLV2fxyAVPM/W+d7mu351kp+eG/0aaAD3DrwObVm7l4fOfslKuFm9EKcW4j24vPW9EnQ1RNStpKltnSP3FWlxSCbXKwFFxD1pfJgQbRSpWo2muKM+5SNF7QBBUbNVPxQD5T1P65VD0FhJ72+6LuMFVUPwlEALJR/Ie49fpvfAWWnr8TreD1f+s49ATDorE7TQqeppYjqzt2dx9/EOcHv8/ruo9ig1LN5Wey9yyg5sPu5eAzwrFhAIhtq9Pr/dYStlQRmKt0y2VUijXQJRrsJ7da9o0yt4VlfoTKuk9VOp3KCOp6sZGEqXFgZSLUumSCh26KEuDNkBFMeiUg3FHuTBKUix79G3aHbLhQs/wyzHuzPGs+HM1ABuWbOL+syYwbcXzAMz+aF7pNz5YkgyXPnhBk9ip0bR1lBEDxn41t0t8CckdDVKIiru/UvVZZd8TiR0FBS+BrRMq/kHOGNmRpI6JbFy2hSHnH1arutUtAe3wy7Fl5dYKx3mZZTH6Dt3bYXfYCPqDONwOrp1wCQNPbjoZBo1GUzPK3h2V/H6N7YzoyyH68gqvHXVu6wud6thAOc6+9dRS8TRlKK6ecHHpucNO78/F485jv4F7M/yeszj9hmrihlUg4keCaxGpvJyiRqMJL2bx95jpgzEzjkMCS5ranCZH77TdhdX/rCNtQwYHDN6XhNT4sPUrZhaSeRZIjqV1n/wpytYhbP1rNJqKiPiRtEMoLYZu2wMj9Ycmtakx0Dtt60DPft3p2a97+Dsu/hLMLMAH4keKPkbFjgz/OBqNpgSTsuInlNsYGT5EBDNkNqmsel3QIZ3GwpZK2dvt0AXGNZoIo5QbYm7Fmte6IPbBsPa/Yv4azkm5nJM9I5h815th7TtSaIffWLhOgKiLwbYneM4Bz7lNbZFG0+IREcyCVzEzz8TMm4CIWeG8EXMNqv0CVPsFGJ5hYR174sgp5GcXYoZMZkz8hm1r08LafyTQIZ1GQimFirsTuLPC69YaSgClnE1il0bTovH9DAUTgWIIrrW0qKLOr9AkUmqZDpcDpawS0gA2R/MP6+gZfgQRkWpr0UooA8kchqT1sWpxir/KthqNphLMbZRtmvIjoS1hHyI3M4+lc1dQXFBxDeC2ydfSsUcHomI9XP7IcNrtkRL2scNNm5rhf/z058yY+A179d2Tu9+8iajYyOlki/8fJPsakEIk5kaU5/zd4vZSOBVCWwATAovAOws8p0TMJo2m1eE6AYwXSxZkDZTnbMziWVA4GRw9UbFjUEb95YnXL9nELYffBwqiYj288u+TxCXHArDHvp15Y2XkyidGgjYzw18xfw3Txn3A9vXp/PXNP7w+tuJmjPRNmXw15QeW/7kqLONZu/tygSAUPIdkHI2Z92TFRspJhV+Balztbo2mpaNsyaiUWaikN1CpPwEKcm+H4EIo/ry0gHl9+XLyLIryiynKK6Ygu5DfZ7asoky70mZm+HmZeZYuBla9yext2aXnMrdmcU2f2wkGQoAw5v1RDDr1kAaOuOt3aQCKXkNiR1rZA4CKvhrxL4DgEnCfCK5jGzimRtP2UEYUGL0BkOByq4i5APghuKE0rFob3SoJZYB/Dth7oBx96Lx3R1xRTnxFfgTo2L1lyyS3GYd/0LEH0q13V9b+ux67086I+84pPbf412WYpomvyNqg8dP7cxrs8FXCE0j2dWBmUvLXVzKjL3vLlRGDSn67QeNoNJpyOPqCrRuE1oGY4DgYSesLCBL/BIbn5CovtTZHngriLWn/JKddfzw7tmTx789LGHbJEPoefUBj3UlEaFM7bU3TJH1jJgnt4nFHufB7/Tx47lP8+9N/BP0hzJCJO8rFdc9cSpe9O/HttJ/Y99AenHb9CRhGzdEvERMpehMCC1Gec1GuwUhwNZJzF0gxKu4BlGtgWO9Jo2mNSHAzkjcWpAAVex/KWXtpYpEABJeB0QHJPAGksOSMG9V+YZUzffH+iOTeXtbeNRQjcVK97PcV+xhz6uP8N2cZvY/sxSOf34PLU3nIVkTI25FPTGI0NlvDM330TtsSDMOoULnm69d+5N+f/sNfHMDhstPnqF4cf9kx7HtoD27ofw++Ih+zP56HGRLOurnqmcFOpOhNyH8GKEa8P0DKJyh7T1TKJxG8K42m9SE5N0JwBWAi2ZdDu78qVbqsDKUc4Ohj9YMqf6L6C+17W08FAHjAWanPrBXfTP2JpfNWEgqEWDp3Jd++/nOl+lvFhV5uO3IsG5ZuJqlDAs/PfYzkjpFT5mwzi7aVEfAFSn+/SikGnzWQYf8bwvrFm7DZrLfGV+Rjye8ratnhQqAkdUvZILg6/EZrNG2BUBql6ZbiLQmz1AN3uYJEnsurjeMr+x6opDfAcyHE3oOKurzKtjUhppQl6Itgmta9eIt83HHM/ZzkupB7TniYH9/5lc0rtxH0B9mxNYsZL35T7zFrQ5t2+CddNZSuvTqjlKLbgV054bKjAegzZH/sLjueGDeuKGfp6zWhPOcCblDRgAucAyJlukbTuom5CXABbvCcY+nf1xGRIBS/V/ZC+Z+rQDkPwoh/CCN6eIMKDZ1wxTHsfUgPlKHYp38PTrzCSsj46tXvWfbHKoKBEIvnLGfV32tLHzxsdhsxCVH1HrM2tKmQzq5Ex0Xx8t8TCPgDOJxllXASUuOZsvgZ/vnhP7odsAd79aldtRvlGgwpn1gze+eA6ivxaDSaKjGiL0Lcx1gze1t9xQwVVAjpNN5OWE+0m2d/fRgRqfBUIaaUTfyBvfp0QxkGcz6Zx4GDe3HmyJMialdYFm2VUicCzwE2YIqIPL7LeRfwJnAIsAO4QETWV9dnU8kjNxUS2m7V6VQJqOiLtNSCRhMGzOKvIG8M4EQlPNfkSRPFBcXcffwjLP9zFb2P6MVjX99b5WJufalu0bbBDl8pZQNWAsOAzcBfwHARWVquzQ1AHxG5Til1IXCWiFRbH7AtOXyRIJJxTEkKpx3cx2EkPNPUZmk0mgix68w/nFTn8MMRwx8ArBaRtWKJwbwPnLFLmzOAN0p+/hgYqiJ1ty0RMwvMbCztbh/4/2pqizSaNoGIWKnToe2NOm5Tub9wOPzOwKZyx5tLXqu0jYgEgVwgedeOlFLXKKXmK6XmZ2RkhMG05oFZ/AVm+hDMjDMwA5Vk7hgplsofbsAD7rqXT9RoNHVHckchmWcjGcMwi2Y0tTkRp1ll6YjIZBHpLyL9U1NbR4EQMbMh9x5L1S+0DHacglk0vUIbpQxU0geouLGohPGo2DFNZK1G03aQULolWIgX8EHBs01tUsQJh8PfAuxR7rhLyWuVtlHW7ol4rMXb1o/4qJApgEDe7pV3lBGDijoP5T6hyR73NJo2hYrByjMBMMDWsSmtaRTC4fD/AvZWSnVXVmrJhcDMXdrMBC4t+flc4EdprpoOYUbZOoDn7F1e1KqYGk1To4woVOIrYD8QnEegEp5uapMiToPz8EUkqJQaCXyL9XU5VUSWKKUeAuaLyEzgNeAtpdRqIAvrS6HNYMQ/iOk6AvIeAhQqfkJTm6TRaADlGoRyNUz65M+v/2Hziq0ccfYA2nVt3qHoNiWe1tSICPhng5kDrmGWrKtGowk7ZuHrVulDox0q8RWUvWt4+jVNfp3+B4U5hRx94WB+fG8OL496AzMUwhXlYtqK54lPiQvLWPWlTYmnBQNB1i/ZRLs9Ukor05RHRPj5g99JW5/OsSOOaNRvZCl4BoretDQ27K9C8gxUI+7+02jaAhLcDPlPAz4IFSJ5Yy2NnDAw8abXmPXmL4gI05/9ErvTKJVVd7gcrP5nHYcM6xuWsSJBq3L4vmIfIweOZvt6K6Vzwvfj2G/A3hXavPPIx3wwfgYBX4CPnprJm6snEh1f/xJodaJ4BkiR9XNwA5hpYOvUOGNrNG0GP2WJEmb9hdcq4bdP/8RbaDn4jcs3Yy9fuFyotQxLU9Gs0jIbyr8/LiZtQwbeAi/eAi8fTtg9r3bu5wvwFvoIBU2CgRAbl29tPAOdB2MJQhmWwJrR/IseazQtDWXfC6LOxfqcxaHixoat795D9sfpdmCUqOkG/SEAkjsmMvHP/yOxfULYxooErWqGn9IlGTNkyZA63Q46dm+/W5vDzziUjcs2EwyEsDvtdO216x6xyKHiH0fsr4OZhYr6n9bL0WgihBE3Dom9G3BUUL00i2dBwVNga4+KH4+y7e4jquOuaSP5fNK3ZG7J4vOXvsNX7MPpdjDotEPYY9/G8yX1pdUt2n7z+o989sLX9Dy4Oze9cOVuwkQiwuyP55G+IYOjLxxMapfdNvxqNJpWiOmbA9lXYulUGuA8HCNpar37WzpvJR8/NZOOPTpwyf3nhV0Erb5EVDwtUrTGLB2NRtN0mGn9QfLKXrDvg5HyRdMZFCEiLZ6maQQktA1zx0WYGScg3u+b2hyNpkUhImUJEyWo2DubyJqmQzv8FoLk3AmBBRBah+Tchpg5TW2SRtNiUEpBzC2AE3BAzK0o15CwjrH4t+WMv2wiHz/9OaFQKKx9h4tWtWjb3BApRnJHg/9fiDoPI+bG+ndmZlJa4xNACoHmnRGg0TQnjJhrEc85gELZwrt2t21dGvec8Ai+Ih+uKCd+r58R954T1jHCgZ7hRxApmAze78HcCoWTEd+8evelYu/GSul0gftEMHT+vkZTHhGxKseZBVW2UbaUsDt7gE3Lt2KzW+7UV+Rn6dyVYR8jHGiHH0nMTCBQcqCsQiflT3t/xEw/DDP9SMS/oNqulPsYVLvfUKnfWelkWlFToylFRKxQZ8ZxSPrhiO+3Rh1//8P2weVx4Ylx44pyctKVQ/nsxa85LfZiRux5HWsWrm9Ue6pCZ+lUw6y3fuGLV2ZxwOH7cMWjI7A76hYBk+B6ZMf51k4/ezdU8gco5bHOiYmkHYSlxQ0YqRjtGvePVKNpLUhwLZJ5JqWfJ3svjJTwFzQxCyaDdyY4B6JiR2OpvVvk7chnwaxF7LFfJ1I6JzGi6/UEfNaEr2e/bkxa0DiiiW1KS6c8G5ZuYsypj5OTkcslD5zPebefTnFBMb/PmE9CuzgOPq5PlTPlFX+t5rnrX8VX5GPNP+uITYph+D1nV9q2KpS9G7T7FUIZYOu4i26OCQTLDsVf5/vTaDQlqFis/HoAW9h3sUtwA+L73RJkwwvBjYitKyr60tI2ccmxHHPhYACy03LK2QPBgElzoFWHdJ6+5hXSNqTjLfQxbez7bF+Xxk2D7uXZ617hgbMn8PbDH1d57fZ16RiG9WXgK/azqZ4SDEq5UPYuKGVDQmlI0TuI7zdrZhA7Bus71wlxD1e4TkKZmLn3YGbfggTX12tsjaatoGypEP842LqC4xBU/GNh69ssnIpkngb5j1AWovVBqGqfkNg+gRH3nYPNbhCTEMVtk6+t1VjZaTk8e90rPHXlS6Rvymy48bvQqmf4oUCI8hGrtI2ZbF+fUapuN+vNX/jfuPMqvbb/CX2JTY5BKYVpCmfceGKDbBEzF8k8vSQX2EBiR2NEj0BKND/KPxoCSPa1EFwGmEjgL0j9TcftNZpqMDyngOeU8HdcMInSUBEAHlAOVNTwSpsXFxTz/uOfUZBTyNTlz9Gxe/vSz25BTiEZmzLZY7/OlYaI7z35Mdb9twERWPjLEt5c/WJYb6VVO/ybX7qK0Sc+SkFOIefcdir7DeiJy+PEX+zH4bJzwOH7Vnrd5y9/y5xP/uDMG0+k16B96NSzA0kdEhtmTGAZ1uzA+rLB+wVEX1i1nk5oHaUhHzMLSwGweWzd1mhaKhJYhWRfCeYOiL4OI/ammi+ydYJgPmBaoaPEN1D2bigjptLmj1z4DP/88B+hQIg5n/7JuxsnYbPZWLNwPaOGjMM0hXZ7JDPxz8fxRLsrXLtx2RZCQSv8s31dBqFQCJstfBLqrdrh73NIDz5Ofw3TNEvftOfnPsqnz39FUsdEzr3t1N2umfv5fCbf+RbeQh9L567krmkjOfCIXg03xt4TK6anADe4jqy+vWc4FL9ttXceiaplWUQxC5CcGyGwGNynoOIeqCAepdG0ZSRvHJjbrYPCyYjnTJR9j2qvUYmTkNwHQIpQcaNRjgOqbJu1PZv/Zi8j4LMma3k78inMKSIuOZaPn/6corxiADI27WD+tws58uyBFa4fdslR/PDuHAAGnNQvrM4eWrnDB2uHXfk3rXPPjox8/soq229esZWg3/pl+b0BNi7ftR57Pe2wpUDyR0jxDJS9O7jPqra9EXcn4j7eyvBxHlrrcaTwVfDPBwJWNoHrGHAf00DrNZrWSs1ZisrWCZU0ucZ2+dkFXNPnDnxeKwHD4XLQ8+DuxCZZTwLt90zF6Xbg9wYQU0jpnLRbH7dMuoYh5x9OKGhy8HG963gvNdPqHX5liAgLf15CflYBA085GKe7LKxyxDkDeefR6ThLgv9Dzj88bOMqe09U7O21b++sR+UcKaJ0R64AUlz3PjSaVoqKe6AkpJMF0VeFrfQhwKoFawn4A5glIZnOe3fkyR8fKI3fj7j3bDK3ZrHiz9Wceu0weg3ce7c+lFL0Ozb8jn4nbdLhv/ngh3z81OcopdijV2demPsYhmGFPTp2b8+0lc+z5t/17NVnz2Zf0GBXVPSViHeWVU3LcQC4j2tqkzSaZoNy7ItqNycifXfdvwtiWhNFV5SLY0ccgdPlKD3vdDu5Y8oNERm7trTJjVfD97iWzC3Wrlen28Ebq14gpXPr0cXfqQyojEYq3ajRNAHim43kjAIE4sdjuIc2tUmsWbie76b9xJ4HdOXEK44pnUg2Jm1241VV7HtoD3Iz8wj6Q7hj3MSnNm2V+XCjlLJKKGo0rRjJuQ0k3zrIHYW4/m3y1OUefbtx/TOXN6kN1dEmHf7db93Me499Qk5GHhfcdQYOp6Pa9ukbM5j+7JfEJEZz3u2n447S6ZEaTdNTXj1Wyv0YQnLvBt8ssB+ISnylyhTKtkabdPieaDdXPDqi2jahUAjDMDBDJjcNupecjDxsdhur/17Hg5/eFVH7RAKAvclnKxpNsybuCci9Ayuk83jZ58X3vfVPiiHwL1I4FRV7c5Oa2lxokw6/OkSEF2+ZysyXviU+JY6xH4wiP6sAM2RihkyWzQuv7KmICcElVgjG1g3JuRV834LRHpLeRdm7hHU8jaalIxICFIbneMS9EKDi5EgC5Wb8grVpUQOtXEunPqxfsolvpv6ImEJuRi5vPfwR3Xp3xR3twh3t4tiLatgwVUck52Yk639I5plI3sPgnw0ImOlIwbNhHUujaemYRR8haX2QtL6YxbNQSu3+JOw+Hhx9AQW2Lqio8MXUs7Zn88lzX/LrJ3/QXBNeqkPP8HfBZreV7cVQCofTzjOzH+K3T/8kOiGaASf1q3OfZvFXkPcgGNGohBdKd+qJmQW+nygVZPJ+QdngBtRyd61G0xYQCUHeA5R+XvLuBc+w3dop5UQlv4mIv2rpknpQXOjl+oPvIj+7EMOmmDW0D0POP5yjLzjc8hstAD3D34Wu+3XmvDvPwB3tonPPDox84UpcHhfHjjiSgScfXOe4uogXcu8CyYbQ5pI0shJUTDmnbgNbD/CcB8oD9n1RMbeF78Y0mhaPAso5VlX1fFVEkMJXMNOHYGbfhJhFVbatLVtWbaO40EfAF8BX5GfeFwt49rpXeOLSiQ3uu7HQM/xyFBd6WTxnOUNHHMGlD5wfnk4lSMVsgjLVPaWckPQGkj8BVAIqbqwl8xo3JjxjazStCKUMJP5pa2av7Kj4Z6pu7P8DCqdYC7e+HUjhZFTsrQ0av1OPDjhcdryFCjEFEcFb6OOPL6uvVtec0A6/BG+Rj+sOupPs9BzMkMmY90cx6NRDGtyvMmKQmFug4FnAgYqvqHuvHL1RSW9Weq1IEIo/A8kFz1koY3ftDY2mLWF4jgNPLXaPSw7WEwFAwFLHbCBRsR4mzX+Cb9/4mS9e/o68zAIMm+KAwfs1uO/GQjv8EpbNW0lOei7F+dYM/JPnvgyLwwcwYq5Foi8DbLvp3leH5D0AxZ8DQSh8C1K/r9P1Gk2bxXU02LpDcDUoDyq6asHEmpj11i9MvvMt4pJjuX/6Hfxv7HmcccOJzJz0LS6Pk9OuPyF8dkcY7T1K6LhXe0IhK/Ti9DjpcVC3sPZfW3njCvhmAyXiZ+YOMK1SiRqNpnqUckPydEsK2Uip9+JtXlY+z1zzCgFfgNyMXMZfOpGJf/wfccmxXDzm3DBbHXn0om0JHbq1gw/hxQAAIABJREFU46HP7mLgKQdz9i0nc/kjlVezaVRcQwAP4ARbKhipNV4iUowEN1v5/RpNG0Ypw5I2bkCmjiWVbmXOiUBRfstWn9UzfGDBrIW8eMtUYhKiufvNm+jcs+ZZtN/rJzczn+ROiRETSFJxD4CzH5i54DmzxnCOBFYiWcOtjSeOfayNW2FMS9No2hpJHRI5Y+SJfPrc19iddm6aWP/QUHOgzTt8X7GP+88c///tnXd4FNXawH/vbHY3vUASQKQqKoh0UcECdlFRxIKVq1gQ5VqwK4INELGABfunePVauHpFxasgUiyg0kGUauiEFNKzbc73xywhSPpudpPs+T3PPpnZOXPOu5PZd8+85y24StyICE9e8TzTl06u8pyM37dx1yljcZW4ObJnB6Z8P77afDx1QcQGMZfUuL0qfPlAMinPWpRrEdIAMghqNFWhPOtReQ8AHiTxccRR+1iX+sA0TSZcNZWFM3+mZYd0npn7KC3apYdbrICIaJPOX2u3MXbw07j9FWqUUuzbm1fteR9M+JTCfUW4Sz1sWb2VZXNW1beoNcPcW27HB57fwyaKRlNTVO5I8K4B75+o3BENJoJ16ZxVLJm9DGUqdm3aw8je97NywdpwixUQASl8EWkmInNEZIP/b4WVvkXEJyIr/K9ZgYwZLJRS3HP6eFbMW22l3RCwR9u5afK11Z6bnJZElMN6ODJNRULzhHqWFpR3I2bWUMysC1DuSvx+7X054IoWhdha1LtcGk3AqH3ltotRRdNR3q3hk8ePYRwcZFmYU8gjF0zE4/aESaLACXSG/wDwnVKqE/Cdf78iSpRSPfyvwQGOGRS8Hi8F2QVlOZai46L5cPtrnD7s5GrPve6xy+lzTg/S26ZyzdihdDnxqHqWFlTureBdDd71qNwbK1yUlfjhYOsIGFa1q5gL610ujSZg4scADix1ZEDhi6jsIVbqkTDS68xunHbZSQe953F7cZc2XoUfqA3/ImCAf/tdYD5wf4B9hgS7w85Zwwew4OOfUEpx2ZgLSWxWs5l6XGIsj/83xB/TzD2wrUoBL9aX5ABipCBpX6OUq25uoBpNGDDirkZFn4vaNwo8y/3vKlTJF+Dsj0QdGRa5RIR73hrFcad2ZuqtbyDAeTeeQVxibFjkCQYBlTgUkX1KqWT/tgC5+/f/1s4LrMDSUpOUUv+tru/6LHG4H6UUG5Ztxu6006Fr8IoZ1wdm8YeQ/6S1E3c9RsIYlPKgCl8Ez1qIvRwx80FsEH0hIsFfRNZo6hOzaAYUPIuVHE1hTWgUJDyIERdeN+nczDzcJW5atKveNTrcVFXisFqFLyJzgZYVHHoYeLe8gheRXKXUIXZ8EWmtlNohIh2BecAZSqlNFbS7GbgZoG3btr0zMjKqlC3SUL5swIPYrH+HWTDNyhdCKdbjsN366+yHkTI9fIJqNOVQ3m2oopeAeCThn4iRVHE7pcA1F+VZA0VvUZbH3miNkf59yORt7ARU01YpVWniChHZIyKtlFK7RKQVkFlJHzv8fzeLyHygJ3CIwldKvQ68DtYMvzrZIg2x/a3QuvcPLGUPVoI2l7Xp+iGEUmk0laOUicoZ5s9lY6C8fyDN3z9w3Cy2kgf6/kLibkaizwLnyajiGaDcQBREdazT2PP+vYj/vPAVnXp24Nbn/4EzRps5A120nQUM928PBz7/ewMRSRG/QVlEUoH+gPYXDAISey0QbaVZJsr/coC9R3gF02j2o4rBzMGakHgtpwPPOpRnnXW44Eko+QTcP6JyR6J8mYjEICnvgONkiD4fSZ5S62G3rNnKcze9yvpfNzFnxgJmjPu47FjWjmw2r8rANCMvGj3QRdtJwMciMgLIAC4HEJE+wEil1I1AZ+A1ETGxfmAmKaWavMLP2pnDk5c/x56te7lu3OWcNyL4AVDiPAlSvwLfVpTtSCj9L2BDYquu16vRVIdZ+BIUvQ221kjK60glOZyUWQDiqNxJQOLAcRJ4lln7tjao7MsBD0pSwUimzHQjAuYesKUjju5Is7frLH/W9mwMmzWfdZd62L5hFwALPvmZyf94CcMQup3ahSe/fDCiakcHtGhbn4Ri0bY+GTt4Er98vRzTZ+KItvP2uqmNYsFHo1GeDajsoZStDTlPx0h55ZB2Zv7TUPwuEIWkvIw4Ky7/qZQXXItAYlG512P5buwnEXBbzga2tkjzmUFxOHCVuLjt+AfI3JqFUoqJ/3uErv2PYcSxd7J13Q7ASpL4+sopNUql0pgIyIavqRv52QWY/uybYhgU59e94k5+TgHRsU4c0cHPi6NcP6KKPwL7cUjcDVY6B02E47Jm2wpAWUVE/obyZUPxDCzl7UXlP4akza2wN5EoiB5onWe0BHN7uaPFSOrX1sze3iNo3mXOGCevLJ3MllUZpLdNJaVFMq4SFwkp8Rg2wfQpRCAxBEGTDYmITq1Qn9w0+Vpi4qOJckRx0oW9KdxXzLDDb+HS9Bv46fNfa9SHUoopI17hilY3MTRtBKsWBtcSprybrIAu1/+g8CVU0VtB7V/TSIk6FqLPw4raVuD+GbPwjYPbiIMDUd0CUrHiVEphFn+CmTsas+QLpNk7YGuPpXocEHcLEtUOcfQNeqI/h9PO0ccfSUqLZApyC7mhy51sWpWBiEH7rm157LP7SEiJD+qYDR09ww8y2zfs4udZv3FE93Z8sudNigtKSUlPYtjhN5O90wqeeurK55lV8B42W9Wz6R0bdzP/wx/xenx4PT5eHfMur/z6dPCE9W6xHqUVQAl4Vgevb02jRUSQpEmYrt/A3AqYUPgCKvbyMpdKMRJQSZOhYAIYyZUvrLq+9cePlFj1HVKmY6R9i/JuAxQSFZr4l59n/UZ+VgGlRS4Q6DHwWHqf1T0kYzcktMIPInu3Z3Nbn/txuzzYomyMefNWBg7rj2malBYdqGXr85n7U2xXSXScsyyRlBhCQkpcrWVSnt9ReVaNXEl6ErF3OXDQcbxVMB1A+ZDYK2rdv6YJc4h55WCDgBEzCGIGHfSeMgvBNc8qOuLsh/Ks54DrsA+8f4KzHxLVpt7Eroi0Ngdcmp3RDlq2j8z1NG3SCSJ/LNkAWEUTXMUufvhsCUopHrlgUln+DcNmcNvU67FFVW8rTz2sGaNfvpHmh6XQqVdH7n7j1lrLpHJv9GciXGNtl0OMJCR1NpI0GUn9DHFWn0dIEzlI8jNgtLQ8bRLHIUbV9m6lPKjsoaj8R1H7bsUsfA2JPtuaVEi89QPiDE+67p6nH8c/nhjGEd3bM+imM7l49KDqT2qCaC+dILL7r0xuOu5uXMVunDEObn95BF1OPIpbe9+Hq9hyPWvZIZ1nvx9PetvQzDDM3cdihaoD2DFaVp/eVSmFyn8cSmeB/Vgk+eVqv+wajfJuRmUPObDIa+uAkfYNyrfDSv9h71YWJR4IXo+XhTMXg1KcetlJRNm1oaI82ksnRLRsn860nyfww6dLOKJ7e/pddDx5WfkHmW8yt2ZxQ+c7Gfvx3ZxwfnCKpFdJ/D+h8EX/9u01O8f9A5R+ZgXNuJeiil5FEu6t0alKuVH77vE/1ichya8gjsizlUYkRkus/Del1l9HLwDE1hpsrYM2zOOXPsvyedZ603cfLOKpLx8KWt9NHa3wg0yHrm0PSsSWlJrIozPvYfpd/8fOTXswfSauEjcfTvpvSBS+EX8LKuZigJrnxz/IDc8HZlHFzcw867jEAQqRaFTBs5bXD4C5F5U7CmnxY53l1zQexIiF5h+jit4FW0sk7oZ6GeeXr5fj8/oA+O2blSil6j14KuP3bXzx6re0bJ/OxaPPa7RPFY1T6kZG3/N60r5rG2445g5cJW7sTjttjjksZOPXuhCKcwBEdQPPr2CkIfG3HNLELP4I8h/HCplXgIFKGHtolS1Vt/gD5d2IKvnCSo0bfUFERUM2ZiSqA5I0vl7HOLJnezattBIrdujapt7vjcJ9RdzR7xGK8otxxjjI3JrFqBeur9cx6wut8ENEeptUHp15D/+e+Cltj2nNyOeGV39SmBBxIM1noMwikNiKv1AFkziwNgBgQsGTkPwi7FtKWTRl4rhaj698majsy6zqR0SDubfeZouaxsekb8by6dSvQMGQO+p/8XXX5j2Y/rVOV4k76PEwoUQr/BDS97ye9D2vYRRorgliVOEGKomg/mbqESfiHAipX6G8m8HRC8OosOpl1XjXUxb0Qwm4FqFir0UVTAPPSoi9CiPm3Nr3q2kSxCfHcd24y0M2XtvOrUloFofyJ1s7+x8DQjZ2sNEKX1MnJGU6Ku8+8OWBygcMSHzSehqI6oBEdah75/YugA1rAdAG0eejit70520phbwVqKh2iL1zUD6LRlMVzhgnry57hsVfLCWtTXN6DOwabpHqjPbDb6S4XR42rthCQW5hWMYXexeM1C/B3gnwAaVQ8HSFtXarQymFmf8k5u5umFmDQXmR1FlIwn1IyisYsZf6Z/3+AB6xgW9bMD9OxKDMAqsgSQN1x64tSineGfchwzvdzpQbX6m3AuMJKfGcdd1pjVrZg57hN0pKCksYdfwDZO/IQUR4dsFjHNkjgBl1IHhWU5be1sy0FmmllvlJPMusnOiUgncDqvBZjKSnIe66siYSew2qdJ6l7CXBSrkbZJRZ6E/1G/wkdQ0B5VqMyr0FMMHZD5KnI9Iw53xej5fNqzJIO7w5KS0OqZpaxi+zl/Gf576ktMhF1s5c2ndpw6V3XxhCSRsXDfO/ramS375ZSfaOHEoKSykuKOHTF74KnzDRg0BigViwd/e7aNYS5eVAIi4F6tBZmjh6I2n/s/z6U2cHPRDMzH8aldkXtacPytU03UhV4bNACeAC92L/U1Mt+1AmyrUQVToPs+gTzKxLMfOfQCl30OR0uzyMPvEh7hk4nmuPuJ2VCyoPFszNzC97WvG6POTs3hc0OZoieobfCEk9vDmmad3kjmgHLTukh00WSRwPztOsmX302XVzkXMcD87TofQrMFog8XdVPJatFZQrxKHMfFTR24APibseMZrV6TMoX1YFqX6/rVNfwUB5VvnzHwmS9BRiD5IZwUjH+sp7QZlQSW3ZKmXLfwRKZ4PyYXlpmeD9E2U0Q+JvC4qYv//0Jzs27qKk0DLhfTjpM7qfdmyFbU8ZegIfTvqMrB05RMc6uPDWs4MiQ1NFK/xGSOcTOjHy2ev4Yvq3dD6xE8MeGBKUfpUyUQUTrShZx6lI4iPV5scXEYg+PaBxRQwk+TmUmmzlTq+pvLk3gWcNoFCu75DU2XUU4O+pfsObMlfl3ATKyqyqcm9G0n8KSr+S+Dgq717wbYf40ZVWsaqSki85kAxtPy4r82oQKC4oYfl3q/G4rKc8uzOKw46oPB1DXGIsb655jj0Ze0lt3UzXra0GnUtHU4YqmYXKH+uPtI1BEh9FYoeGW6xKMXd3pWz9AEFarKuzTdos+RIKJoKRAvH3IvjA0QcxEgOWUyk3mHlWBslqnoCUUqg9XTkQ4+DAaLkmgLE9qKI3wLseib0GcVSYYqXGmFlDwbsOhQkIItGAQpq9h9iPC6hvgFF97ifj922YpsIZ46D/kBO4/cUbiImLDrjvSKGqXDraht+EWfTpEoZ3up07+j/Mnoy91Z9gZvsf1QE81n5DJvpM//pBDDhODmgB0oi5ACP9RyThQdg3GpU3BpU1CGXmBySi8m5EZfZH7R2IyrkaVcH6RHlEBOLvxHJJdUDCmMDGL5gGha9C6WxUzgiUb2dA/UmzN9m2bSCz32vOiJOP5ofvRyJp84Ki7N0uDxuXb8Fd6sHr9uLzmdz79iit7IOIVvhNlPycAiZdM5Wdm/awbskGnr7uxepPirkIjOZADBjNICY4pqL6QpKeRZImWXbulFcrbad8uzGzLsbc0wezsPJ2AKr4A6DUCipTReCuWXWySvsrfMUfp+AG7+/gthaElfJh5j2CmXky5r4HrLqvfoz4m5C0BUjaAoy4AEP4vas4yJ3VmxFQd2KkcMc5hUy7/zB2bLYzcfj3mKr2awEV4XDa6di9HXanHWeMgx4DKrbba+qOtuGHGaUUpcWuoM9iSgsP2FmVqdi3N6/ac8RoBmlzwLfbSn7VAN0TlW83qngmYkuHmKFIdPURtyr/SfD+gVW56RWU8wzE3qnixvbjrILblFpPO4EEkIFlIiIKy0SjQPzKsXQWlHwBlFiLoI5eEHsgelRszSvorA7EXAXuFSCG5c5q7xZwl85oB0VYOZJs9igMI3jzxmfnP8Y3b3+P3RnFOTcEtjakORSt8MNI5rYs7jplLFk7cuh2Whcmfv1w0LLwNWuVQv+L+/LDZ0sQw+CWKTXL3SPigBCVnastSpVa+dbNfSjsll068ZEanFiMleQNrMXZvy86HkDibrKyWXtWI7FXIlEdA5JZ4u9EeTOsH5zYqxCHP7WGmY8VsIb117R+kJV3O6roJcCJJNxRZ8+j/Rgx56Ci2oNvKzhOrDpdRg0Z+8kYJlz1Aj6Pj3veHhXU5GVxibFccuf5QetPczBa4YeR/e5kps/kz182svjLpZw85ISA+921ZQ//7PcwhblFdOjWjgmzHyI5NfDFx7Dj2+5fUPZZL9eiQ5oo7zZU8QwwmluumuJEEu5H5awBVQDRZ0NU5W6OIjYkfmTQRBYjAWn25qFyOgdA0auW4relQ+xQa8E25yorgA1QJZ+gHCcgyS+U1ZKtkwz2o8F+dJ3P/ztd+x/DBxlVm8Y0DRNtww8j0XHRGDbrX6AAZ2xwXMo+nvw5eXvz8bq9bP9jB6sXrqtzXysXrOXdcR9VGfwSMmxt/SYRJxAD0eccdFgpl5Vls/g9KHwZlWcVxhD70Uj6YiR9KUbyM9V7yriWYO45AXNPT8t7J8gosxhyrgGzGLBB7M3+mbzbr+xN/8sL7iVWjYEI5POXv+aKw27ijv4Pk7UzJ9ziNAm0wg8jVz10Ccf2O5q4pFjOuu40+pwdnMpQccmxRNkt/3mlFHFJsXXqZ80P63h40AT+9cRMHh40gdWL6v7DEQxEHFbt3YR7keSnDw3Q8u0tZ75xgXtZuXMNq0BHDVB5Yyw/eFUEeQ9U61lTa7x/+DONlgClUPpfv4xOqxYB5X/4fWDmBnf8RsCOjbt4/b5/kbN7H3/8spGXbj/0KUlTe7RJJ4zEJ8cxZd74oPd71UND2bJqK+uXbuLsfwyk5+nVR2p6PV4+mzabzK1ZXHTbuRx+1GGs+eEPvB7Le8Tj9rJ60TqOOyW8GSrFaHZQjp2DsLWCqDbg3W7tx1xUx1HKJ4CrhziVqPbl+o0G+wGXaUl+GeVaCIVTrdQHEofEjw6+DA2QZd+t5oVbXsMRbefqh4diGNaTmOkzKcipuOqapnbowCsNAFNvfZ1vZyzAXeomPimO9zOms+2PHYwZMA7TZ2LYDKZ8P55j+lbi3RIkcjPzmHDl8+zYsJurHr6EC26pXai8MovANcdyK3WcUqcFReVahNo32srpkzgeI/ayWvdR7RiedajiD61U0rHXHBJhrJSy4iCMxFp5SynvRnD9aBUMdzSe2gs+n4+Lk4ZTWuwCoEX7NI7p24kf//sLDqedp+eMrfd7r6mgi5hrqmXVonW4S6yoVa/Xx56MvRx9/JE8t/BxVi9cx3Gnduao3kfUuD+lFMvmriJvbz4nDe5DTHxMjc57+Y63Wb1oHT6vyfS736XH6cdxeKeapwAQIw78NXzrijhPgfTl1nY9lc8Te2ck6bHKj4uALbVWfSrvZlT2UH/wnAEp0xFn/4Dk/H3xeqbc8DIA9/7f7XQ+oWZKNz+7gG/emU98cixnDx+ALarqFB3KVAelNi7OL+GRD+8iP7uAmIRo7A573T+Epgyt8CMIn89H3t58ktISsdkO/gKefd1p/OuJmQCkpCfR2q9kj+p9RK0U/X7ee/wTPpkyC0T4YMKnvLZiSrVfeoC8vfn4vJZJxTCEon3heZSvjaJX3q2ogsmAgSTej9ha159gVeH+BZRif7oJ5fq+UoXv8/kwfWa1inTs4EnkZxWUbc/c81a1Yvh8Pkaf+CB7t2VjRNlY88Mf3Pt/VSdWi7JHcd34y3nv8ZmIUFYCNLF5cLOiRjpa4UcIhfuKGH3ig+zJyKJZy2Re+mUiyWkHXP2uuO9iOvXqSPbOXPpd1AeHM7AZ1ZwZCygtsh7Pd/+VSea2LFp1qL6Y+g1PXcX9Zz+B1+2hx+ld6dQ7MD/4UKByrgNzt3/7TyTtm/AIYi9vwolGKqkZsHTOSsYNeQav28vwxy7nygcvqbTLkoKSsu3CfUWMGzKZ9se24ZpHL630xyJvbz57t+fgcXvB7eW3b1bUSPyrHhrK4FHnYtgMYhNq9kSoqR1a4UcIc/+1kMytWXhcHrJ35vD1W/O48m9ZNnudGXgU5n6O7Xc0Obty8bi8OGOcNG9Vs9q2nU/oxCe736BwXzHNWibXm0klWFi29t2ULfT6doRNFrEfDc1moFzzEUcPxDmgwnbP3/IaLr+tfMZjnzB41DnEJVUckHXj09fyxn3voZRCRPjp819Z+u1KPG4vN0++tsJzktISSTu8OXu3Z2HYbBxfizrO8cmBB4ZpKkcr/AghPjmuzOffFmWr9y/W3W+MpG3n1uTs3seQfw7CEV3zhUdnjLNBpblVnjWoffcBXiRpwkEZJ0UEFXMplHzB2t+i+WlOb44dsCQoAXR1QRw9EEePKtuU/1+IUHZfVMQl/xzEWdeeyupF63j6uhfxur24StxsWLa50nNsNhsvLpnAnHcXEJccx1nXnlr7D6KpF7SXToTg8/mYNuoNFn+xlF5ndmPMW7cGLY0DWDPd4oISYhNiGvysvLaYmaeAucfakXgkfelBn1EpxZblc/nnqf+Hq9iDM9bJfe/cxqmX1q4M4/5ZdH2zYdlmHrt0CiUFJYyaegNnXHVKteeUFJVyS7cx7MvKx/SZPPTBnfQbfHy9y6qpPdpLR4PNZuOu10bCa8Hvu6SolDEDxrF55V+0aJfG1J+eoiC3iJnPfUH2jhyGPTCErv2PCf7A1bD7r0w2r8qg84lHkZIeQEZHVVBuuxTLfHNgAVpEWL/CVpae2VXsYsX8tTVW+Eopnr1pOt++M5/0tqlMmTeelu3rr4pZp14d+dfmV2p1TkxcNK+tnMLqRX/QskM6bY8J08K0JiC0wtcEzPf//pGt63bg85rs2ZrFQ+c9xcYVf6H8ZRhXzl/Lv7a8QlII8/msX7qJMQPGYdgMDJvB6yufJe3wOmagTHgQ8h+3tuPvrLAKWLfTuiAiOKLtiCGcfHHfGne/9qc/WfDRTyhTkbk1izcffJ9H/l1xmcdQsmPjLjYs3UyXfkeT3iaVmPgY+tbCHq9peGiFrwmY6Dgn+y0RhiFsWplRpuzBmgFn7cgJSOHP/+hH5n/8E33O7s75N59Vrelj3geLyryEnLEOfpm9jPNvPqtOYxuxV6CizwNMxEiusM1hR7TklaWTWTZnFUf16VirIKH9EaVgXavK0g3/vng9bz/0Acnpidw2bURgTy3VsGHZZu4+7VHEEARh+rLJVZYa1DQOtMLXBMxpl5/E0m9X8tOsX+l84lGs/H4tbp/lC24YQutOrWh/bJs6979ywVqmjJiOq9jF0m9WEp8cx4Arqg4oOqJ7B5yxzjJvlHYBjA/UqNTh4Z1a1SpIbD+dTzyKc64fyFevz6VVxxbcOOnqsmNfvj6HH/6zmJ5nHsf7T/yHksJSbFEGeVkFPDN3XK3HqikL/7O47AfT7rTzy+zlXDz6vHobTxMaAlL4InIZMB7oDPRVSlW4yioi5wJTsQyfbyqlJgUyrqZhYbPZDgqs+eXr5bw65h0cMU6G3nU+p13Wr0ZBV5Xx15ptKNNyeywtdrFpZUa1Cv/Ma0+lKK+I5d+t4fSrTwnLGkJlmKbJnr/2ktIymehYJyLC7dNGcPu0EQe1WzJ7Ga+NeZfSIpeV18hr5c/3eU0y1m7j3XEfcdypXeh1RuDlBf/OUb06lv1gGjbhiB7tgz6GJvQE5KUjIp2xVrBeA+6pSOGLZfBcD5wFbAd+Ba5USv1eVd/aS6dpopRi7nsLWfvTHwy88mS6n1Z9Gbvdf2Uysue9KKUwfSbPL3qCI3sEWInqb7x2z7t8Nu1rmrduxtPfjq3TTL0muEvd3HXqo2Ss3UaUI4rnFz1B606tyM8uoHmrlINMVf95/kveevB9PG4vItC602Fk7cjG5/Vh+hQ+rw9nrIPHP3+gXpT+tzPms2zOKk6+5ISwuZlqak9VXjpBccsUkflUrvBPAsYrpc7x7z8IoJSaWFWfWuE3Tb5553teGv0WpUUunLEOXlw8kQ5dq6+wlb0rlz+WbOCIHu2D7sGyZXUGo096CFexGxGhz7k9mPDVQ0EdYz8/f/EbE6+eSklhKSLQd1Avfv/pT0qL3RzT90gmz320zF12T8ZeRva8F9M0QcG0xU9RWuTmx8+WMPPZL6xIVuCasZcy/LEr6kVeTeMj3G6ZrYFt5fa3AxVOF0TkZuBmgLZtG2aZPU1grFm0rsw2LIbB5pUZNVL4zf0lGxs7SWmJmP4F7SiHnZ2bdlO4rwilYOPyLSz/bjXHn2t5wrRol8Y766excfkWOnZrR0oLa8E4ym7j06mzsWMFTfUOUh0FTdOn2gIoIjJXRNZU8KprsvFKUUq9rpTqo5Tqk5aWFuzuNQ2AgVeejDPWQXScE5vNoNtpXcItEh2Oa8eFI8/GFmUjrW0qo164vt7G6nLiUQx/7HJadkjnpAt70+3ULtj8M3rTVCQ0iz+ofVJqIr3P6l6m7AGO6N6eqT8+yYiJVzPl+/ENan1C07DRJh1NyNm4YgubVvxFzzOOI71N7VIANzWK8oqYcPU0Nq/8i4tuP5dh9w+p/iSNpgrCbdL5FegkIh2AHcAw4KoQjKtpoBzZo0PQF11ritvl4fmbX2XVwt8ZcEV/bpxouUAu/nIpOzfdBlFnAAAFW0lEQVTu5pShJ5DeNnRPl3FJcTz15YMhG08T2QTqljkEeBFIA74SkRVKqXNE5DAs98tBSimviNwOfIPllvm2UqoBVMTWRCKzXv4fCz/5GXeph1kv/49j+x1NZsZe3nroA7weH+8/OZN3NrxIYjOdh13T9AhI4SulPgM+q+D9ncCgcvuzgdmBjKXRBIN9mXl4PZY/u1KK/KwCFn26pGwh2Yy2s2XVVroPqN5ddH8fTTVpnKbpUe2irUbTlBg86hwSmyfgjHGQ1iaVUy49kb6DehEd57TSBIvQvmvNonJLCku4tfd9DE29nuuPuYO8rPx6ll6jCQydWkETUaS3TeP9jOnk7Mol7fDm2KJsXH7PYNLbpLJz424GDOtX45w/373/A9v/3Gkljfsrky9fm8PVDw+t50+g0dQdrfA1EYfDaT8oeEtEGDis9sW+o+OciD/xmWGzERMfHTQZNZr6QJt0NJo6MnBYf04ecgLxKXH0Oac7F9xSt2ycGk2o0DN8jaaO2KJs3D9jdLjF0GhqjJ7hazQaTYSgFb5Go9FECFrhazQaTYSgFb5Go9FECFrhazQaTYSgFb5Go9FECFrhazQaTYQQlHz49YGI7AUy6qn7VCCrnvpu7OhrUzX6+lSOvjZVE6rr004pVWGO7war8OsTEfmtsgIBkY6+NlWjr0/l6GtTNQ3h+miTjkaj0UQIWuFrNBpNhBCpCv/1cAvQgNHXpmr09akcfW2qJuzXJyJt+BqNRhOJROoMX6PRaCIOrfA1Go0mQogIhS8il4nIWhExRaRStygROVdE/hSRjSLyQChlDBci0kxE5ojIBv/flEra+URkhf81K9RyhpLq7gMRcYrIR/7jS0SkfeilDB81uD7/EJG95e6XG8MhZzgQkbdFJFNE1lRyXERkmv/arRKRXqGULyIUPrAGuARYWFkDEbEBLwPnAV2AK0WkS2jECysPAN8ppToB3/n3K6JEKdXD/xocOvFCSw3vgxFArlLqSOB54OnQShk+avE9+ajc/fJmSIUML+8A51Zx/Dygk/91MzA9BDKVEREKXym1Tin1ZzXN+gIblVKblVJu4EPgovqXLuxcBLzr334XuDiMsjQEanIflL9mM4EzRERCKGM4idTvSY1QSi0EcqpochEwQ1ksBpJFpFVopIsQhV9DWgPbyu1v97/X1GmhlNrl394NtKikXbSI/CYii0WkKf8o1OQ+KGujlPICeUDzkEgXfmr6PRnqN1nMFJE2oRGtURBWPdNkatqKyFygZQWHHlZKfR5qeRoSVV2b8jtKKSUilfnptlNK7RCRjsA8EVmtlNoUbFk1TYIvgH8rpVwicgvW09DpYZZJQxNS+EqpMwPsYgdQfiZyuP+9Rk9V10ZE9ohIK6XULv+jZWYlfezw/90sIvOBnkBTVPg1uQ/2t9kuIlFAEpAdGvHCTrXXRylV/lq8CUwOgVyNhbDqGW3SOcCvQCcR6SAiDmAY0KS9UfzMAob7t4cDhzwNiUiKiDj926lAf+D3kEkYWmpyH5S/ZpcC81TkRDBWe33+ZpMeDKwLoXwNnVnAdX5vnROBvHIm1fpHKdXkX8AQLFuZC9gDfON//zBgdrl2g4D1WDPXh8Mtd4iuTXMs75wNwFygmf/9PsCb/u1+wGpgpf/viHDLXc/X5JD7AHgcGOzfjgY+ATYCvwAdwy1zA7s+E4G1/vvle+CYcMscwmvzb2AX4PHrnBHASGCk/7hgeTlt8n+X+oRSPp1aQaPRaCIEbdLRaDSaCEErfI1Go4kQtMLXaDSaCEErfI1Go4kQtMLXaDSaCEErfI1Go4kQtMLXaDSaCOH/AZH4+jslvy+DAAAAAElFTkSuQmCC\n", | |
| "text/plain": [ | |
| "<Figure size 432x288 with 1 Axes>" | |
| ] | |
| }, | |
| "metadata": { | |
| "tags": [], | |
| "needs_background": "light" | |
| } | |
| } | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "YbHNIyI1Kswf" | |
| }, | |
| "source": [ | |
| "Sekarang Anda dapat melihat bagaimana data dipisahkan, kita dapat memilih SVM non-linier untuk memulai. Dataset ini tidak memerlukan pemrosesan awal sebelum kami menggunakannya untuk melatih model, jadi kami dapat melewati langkah itu. Begini cara model SVM akan mencarinya:" | |
| ] | |
| }, | |
| { | |
| "cell_type": "code", | |
| "metadata": { | |
| "colab": { | |
| "base_uri": "https://localhost:8080/", | |
| "height": 265 | |
| }, | |
| "id": "o7dYrMVpKvQu", | |
| "outputId": "3bd92197-1ca5-4868-e438-7fe3ef67f90c" | |
| }, | |
| "source": [ | |
| "# make non-linear algorithm for model\n", | |
| "nonlinear_clf = svm.SVC(kernel='rbf', C=1.0)\n", | |
| "\n", | |
| "# training non-linear model\n", | |
| "nonlinear_clf.fit(circle_X, circle_y)\n", | |
| "\n", | |
| "# Plot the decision boundary for a non-linear SVM problem\n", | |
| "def plot_decision_boundary(model, ax=None):\n", | |
| " if ax is None:\n", | |
| " ax = plt.gca()\n", | |
| " \n", | |
| " xlim = ax.get_xlim()\n", | |
| " ylim = ax.get_ylim()\n", | |
| " \n", | |
| " # create grid to evaluate model\n", | |
| " x = np.linspace(xlim[0], xlim[1], 30)\n", | |
| " y = np.linspace(ylim[0], ylim[1], 30)\n", | |
| " Y, X = np.meshgrid(y, x)\n", | |
| "\n", | |
| "\t# shape data\n", | |
| " xy = np.vstack([X.ravel(), Y.ravel()]).T\n", | |
| " \n", | |
| "\t# get the decision boundary based on the model\n", | |
| " P = model.decision_function(xy).reshape(X.shape)\n", | |
| " \n", | |
| " # plot decision boundary\n", | |
| " ax.contour(X, Y, P,\n", | |
| " levels=[0], alpha=0.5,\n", | |
| " linestyles=['-'])\n", | |
| " \n", | |
| " # plot data and decision boundary\n", | |
| "plt.scatter(circle_X[:, 0], circle_X[:, 1], c=circle_y, s=50)\n", | |
| "plot_decision_boundary(nonlinear_clf)\n", | |
| "plt.scatter(nonlinear_clf.support_vectors_[:, 0], nonlinear_clf.support_vectors_[:, 1], s=50, lw=1, facecolors='none')\n", | |
| "plt.show()" | |
| ], | |
| "execution_count": null, | |
| "outputs": [ | |
| { | |
| "output_type": "display_data", | |
| "data": { | |
| "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAD4CAYAAADvsV2wAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOydd5QUxRaHv+rJM5sjOSNIziBKUiQoBkSEpxjAnHPOmPVhjhgwAwaCD0UFJeccJWcW2MDmydP1/uhh2TAzO4uLgPR3zh6Y6e6q6t2ZW9W37v1dIaVER0dHR+ffj3KiB6Cjo6Oj88+gG3wdHR2d0wTd4Ovo6OicJugGX0dHR+c0QTf4Ojo6OqcJxhM9gHCkpKTIBg0anOhh6Ojo6JxSrFixIltKmRrq2Elr8Bs0aMDy5ctP9DB0dHR0TimEELvDHdNdOjo6OjqnCbrB19HR0TlN0A2+jo6OzmmCbvB1dHR0ThNO2k1bHZ2TneW/r+HHN6dxaFcWjdrUo+/VvTi4IxOf10+Hvq1p3LbBiR6ijk4ZxMkqntapUyepR+nonKx8/MjXTH33VzxOT5n3DSYDQoDBaKBtr5Y8PelBzBbTCRqlzumIEGKFlLJTqGO6S0dHp4rsXLebqe9Mr2DsAQK+AH5vAI/Ty+rZ6xn7wJcnYIQ6OqHRDb6OThX57YvZ+Lz+Ss/zunz8+tmfeFwVJwYdnROBbvB1dKpIfnYhakCN6lyhCHIP5R/nEenoRIdu8HV0qki73i2xxVijOjcQUIlPiT3OI9LRiQ7d4OvoVJHew7pjjbGiKCLieSazkXMGd8UWY/uHRqajExnd4OuccIrzi1k9az2blm5FVaNzlZxILDYLby14nkZtG2CxmbHH2RCKQFEEIjgJ2GKt1GlWi7veu+EEj1ZH5yh6HL7OCUNVVT5++Gt+eu9XTBYTqqpitVt46Is76dSv7TG1mbUvh+z9h6nRMI3EtPhqHvFRajZM54MVr7Jn036y9x+mdpN0Dh/MZ9aE+fjcPrpc0IEuF7THYDDgKnKxd3MGsUkx1GyYXqYdt9PDgslLydqXQ70za9P1gg4YjIbjNm6d0xs9Dl/nhPHZ498y6a1fKoQ3WuwW3l74Ao3a1I+qnTWzN/D9mJ9YO3cjHqcHi92C3xug6wUdeGDcbTji7AAc2HmIL57+jkVTlyGlpPPA9lw3ehh1m9Wu9nsDCPgDjH3wS34eOxODyYDfF6Bus1o8+vVd1G9Rl1V/ruPpwa8CWkSP2WbCHmvjv38+Q50zah2XMen8+4kUh18tBl8I8RkwCMiUUrYKcVwAbwEXAE7gOinlykht6gb/1CYQCLD819VsXLyV2EQHvYd1J6V2cslxt9PD5WnXh4xlF4qgx5BuPDnxvkr7+fCBL5j24YyQ7ZgsJpp2bMib857nwI5D3Nb5YVyF7pIIG6EIrA4Lby14gYat6v2Nuw3NGzd/xB/fzMXj9Ja8JwQ44h28MW80d3Z7DHdx2XELAcm1k/h65/sYDPpKX6fq/BOJV58DAyIcHwg0Df7cBHxQTf3qnIQcPpjL9S3u5YUr3+TbF37ks8fHc23TO/nxzWkl5+zbnIHBGPrjJ1XJ+vmbKu1n46LNYY09gM/jY8ea3Wxauo2PH/4aZ4GrTDilVCWuQjfv3z2uindYObmZ+cz4ak4ZYw8gJXjdXt6/exyqWnGxJSUU57tYOWNtVP14PT68bm/lJ+roUE0+fCnlXCFEgwinXAJ8KbXHicVCiAQhRE0p5YHq6F/n+FOUV8ya2RsQiqBdn1bYY8NHnoweOoaDOw8R8GvG1efxATDuiQk079KUlt2b4Yi34/cFwrbhiK88smXa2Bl4XZGNnd/rZ928jSyetgIZwsACrJ27Ea/HF7UEwubl25nx5WyK8orp2Lctva44C7PVXOacTUu2YjIb8bl9Fa73un1sW70r7Nj9Xh97N2fQeUD7sGPYvmYXH9z7Oevm/YWUkvT6qVz15OUMuK5PVPegc3ryT23a1gb2lnq9L/heGYMvhLgJ7QmAevWq/xFbp+pIKfny2e/57tUpGM3axyXgC3Dtc8MYet/FFc7fv+0AW1fuLDH2pfG6PHw/5idadn+Qmo3SqdUonV0b9lY4z2I3c9Et/Sod2+EDeVTmkjSYjNhibJUmSkWTSCWl5K3bPmbmV3Pxub2oqmThlGV89sR43l74Aql1jrqsKovTt8fZcBe5Q2bsmsxGUuumhL1298a93NvjSVxF7pL3Du7MZMyo9/nulSn8d9YzJNVIrPR+dE4/TqqwTCnlWCllJyllp9TUkCUZdf5hfh47gx/++xNetw9ngQtngQuPy8sXT33HnO8WVjj/4M5MTObQ6wgpYe/mjJLXj3x9F/Y4G0bzUV+11W6hUZv6XHhzPzYu2szooWO4sfV93NH1EW7t9BB3nvUY3740iYKcQtr0PBOzNfKqXKoq51zWlZbdm4U9p0HLuljtlsp+FcyftIQ/vp6Lx+kpcce4itwcPpDLC/95o8y5rc5pjmII/fWyOiwMve8iRJjjBqOBboM6hB3Hp499W8H3f4S9mzN44NxnK50IdU5P/imDvx+oW+p1neB7OicxUkq+Gv097hA+co/Tw+dPT6zwfnqDNPxhdGaEgDpNa5a8bty2AR+ve51Lbh9IvTNr06xzE257ayRjZj/L/z74jYfOH828Hxeza8NeNi/bzraVO9m0ZCvfPP8jo868m4792pY8dYSj20UdSUiN48ZXr8ZiN1c4brGZuXnMtZX9KgD44fX/hTS0akBly/Lt7Fx3tJSo0WTkoc/vwGI3o8UsaFjtFpp3acqgW/px/ye3YLaZMQVdSVa7BXusjed/fgyTOfxEtuL3NRENetbebFb9uT6qe9I5vai2sMygD39amCidC4E70KJ0ugJvSym7RGpPj9I58TgLXVyWPJKAP7SvXQjBb/6JZQwawF3dH2Pzsu0V3CQWu4WXpj9O6x5nRuw3c282I5vdhTeE//sIiiJo3bMFN712NU9f+ipFecXaxFTu42y1W7j8gYu59pkrWDt3I+/e+Sn7NmeAEKTXT+H2t6+POub/qga3krknO+xxg9FAk/YNuOv9GzmjY2MAtq7cwbcvTOKvJVuJTXJw8W0DGHj9uRhN2kSVvT+H3z6fzcGdmTRqW59+1/TCEe+IOI5BjqvwRNi7EIrg+hevYthDl0R1X0dwFbn4avQPTP/kD5yFLuo2q8W1o4fT47KuVWpH58TyT4Rljgd6AynAIeBpwAQgpfwwGJb5LlokjxMYKaWMaM11g3/iCfgDXBR7dcmma3nssTam5leU/83OOMy9PZ4kP7sAV6Ebk9mIUATXPDuMYQ9WboQmvjqFL56aWKkipcliZPzej4hNiuHjh79m6rvT8XkqXmO2mpiY8TExCZohzcvKR6qSxPSESsdSmscueIFlv66u9Dyrw8q7S16kfou6lZ57LIy+YgzzflxcYXI7ghCCW16/lsvuvjDqNr0eH3d2e5S9mzLK/L0tdgsjnx/OkHsG/d1h6/xDHPewTCnlf6SUNaWUJillHSnlp1LKD6WUHwaPSynl7VLKxlLK1pUZe52TA4PRQM+hZ2E0VYwHN1mM9B8VOiIkpVYSn29+m0e+vIuhD1zENc9ewbhNb0Vl7AEKcgqjkh82mowU5RWjKAqbl20LaewBjGYja+dsLHmdkBpfZWMPMPyRwTjijXQ9P58BV+bQtI0z5Hkep4cvQri7qotRL1yJ1RF+U1hKyazx86vU5pyJC8nYdrDC5O5xehj3+Hicha5jGqvOyYUuraATkVtfv5YNCzaRl5lf4r+2OizEp8SRkBrHn9/Oo/ulXSpsehqMBrpf0pnul3Sucp9ndjsDW6wVV6E74nlCEaTV06JZFCXy2kVUInQWDa27FjBxzUa8Hg+KAZCSvdusPHFVI/IPH/0qSSlZ/tuav91fOOo0rckHy1/hrrMeozC3OOQ5O9ftYffGvVE/Zcz4ak7YjWCDycDqWevpfnF0f8viAifbVu3E6rDStEPDSv82Ov8c+l9CJyLxKXGMXTuGm167hja9WlC/ZR38Xj+Hdmcx7okJvHb9+wxNv55lv1Xu6oiWsy7qRFxSbNgoF9BcDZffd1HJ5mbfET2xOkJH2gR8Adr2bvm3xiQDB5F5N2Myu3DEqtjsKjaHpFELF6O/2l7h/OOth1PnjFrUPbNO2OMGk4FdG/ZF3V5Vw1Y3Lt7CExe/zPA6N3Fz+wf4ddwsfD4fnzz6DcNq3sjTl7zCg+c+w/A6N7NixvGb/HSqhm7wdSrF5rBy0S39OP+a3uzZuK9MwpTf48dd7OGZy14ja19OtfRnMBp4Y95zNGnfEIvNjNmmGXVFUbDFWDFZTAy6qS9XPTGk5JpzrzyH9PqpmCxlH1otdgvXPjcsYqJYNEjnNyArbl4bTdCsrZuzBhwtcnLEFXa8Sa+fWmHD/AhSlSTXij4Wv9fQs8KGpvq9ftr0alHy+o9v5/FQ32dZ+vMKcjJy2bFmN+/d9Sk3tb6fKe9Mx+PyUlzgwlXkJvdgHk8Pfo3ta3ZV6d50jg+6eNpJhKvYzZbl2zGZjTTr3CTsKnH3xr2Mf3kK6+ZuxBFv56Jb+jHg+nMjhvJVx9iGpI4KmTkKYDAqDHvoUkY+/59q7XfPpv0c3JlJSp0k8g7l43X7aHHWGcQlVywqUlzg5PMnJ/D757NxFrqo3bQmwx68hHbntcJd5MZZ6MZd7Mbv9RPwq/h9fvy+gFaH9sj//Udea+9JVaIYFITnB4S6G6GAwSARCigCFINECPB5YezoWkhpwOawcOd7N5BaJwWzzYzVbsZsMwcnr+C/VnNYYx0KGciAQBYYGyAUTQV0w8LNPNzvuZDSEql1k/lm1wdR9+EqdnNj6/vI3n+YQOkMaKFN+L2uOIvhjwwmuVYSQ9OvD+v+CYVQBOdc1pWnvrs/6mu2rdrJhoWbiUlw0O2ijiUCeDqVc9yjdI4Hp5PBl1Iy/qVJfPviZIwmA1KVGEwG7vnwJnpeXnaluGb2Bh4f9BI+j6/kMdtit9CkfQNe++Pp42b0509ewktXvRUxVLLLBe15Ydpjx6X/8ng9PgpyCinILqQ434mz0BU06trK0lXkLmu4ghiMBoxmI0aTAYPRgMFkwGgyYDQZMRjBYFIxGO2YzEYMJiOKIlBVSaDgE1T3IqQKqgqqKkr+L1WB3w8zv0/Dq7aj4/ltMJlNEX9XQmjCbY54O44EBzEJdmISHDgSHDji7cQk2DGZTUj/XmT+/eD7C4QJpA+sFyLin0UIC1888x3fvzYVn9ePGlCx2M0YzUbGzHqWxm0bVOl3mpeVz/t3j2PepCUVcikUg4LFZuaaZ67gq9Hf4yyo2iZuYno83x34pNLzigucPDHoJbau3Kl9D4wKakDlnrE30/eqnlXq83QlksHXN21PAqa+O53xL07G4/RQet306rXvkpAWT5ue2uO0qqq8dPXbFVZ0HqeHbat28cfX8xgw6tzjMkavy6tlTkWgZqP0iMeriqqqFOc7KcgpJD9bM+5H/u8qFzVitpqwxlixx9pIrZOMLdaGLcaKPdaKNcYa/L8Nk8VUYdUr1cPIgpfAPR1QQUkExx0I+/CSc6XvJmTOTCC8/k/fK2JR0p4vM36v26f9XV1evC4vniM/Tg+uIjfFeU4OH8hl76b9FfzkZqvEYfwYR2whjjgz8Ul+ElJUElJ+wSzzEIkfcu0zV3DO4C788skf5GQcptXZzek/sg+xiTFV/n0npMbz2Lf3MO6pCdokUirqSQ2ouIrcTHrr50r1i0IRiLIG8Msj3g4ZcfXmzR9Rr3ntkvwGnWNDN/gnmEAgwFejfwidzery8sVTExkz+1lAe8x15ocPBZw2dsZxM/itzmkeMbtTMSpcdGv/Y24/4A+Qk3GYzL055GTkUpBdQEFOUZmkL7PVRFxKHLUapxOXHEtcSizxKbHEJDhKEpmqilSdyJzLIXAQCBoZNQsKX0aqWYjYuwAQptZI89ngnRu+MTUDGchBGDRNHUVRsNotUck2SClxFroozndSnFesTXQHf6b4kJuCwwoZu2wEfEcnKkf8RpIaTiKhZlMS0+MZ8eTlxCXHVIuk8swv5oQNcc09kIc/TCJeJMIl75Ume38OK2asCdm31+3ju9em8sSEyiWzdcKjG/wTzOEDeWHlfQG2rDgaAeIqdEeMXInmMTsQCLDk55XMm7QEIaDX0O50HtCODQs28+Wz37F1xQ4c8XYuvPl8htxzIRabZqzS6qXS47JuzPtxcchErBtfHkH9CFEjpZHSRXFeDln7A2TvO0zWvsMcPpBbssKNSXSQkBpHzcY1iE+JLTHuVrulSn7vqMbimgKBHEqMfQkuKP4Y6bgOocQBIBJeRWZ2C9+YsGqThSE5/DnhLhUCR5xd81UHhdPU3DfBk6mNU0JRvoG8bGPwx05e1hb27wiUqIAqBoX4lFgS0hNIqpFAat1kkmslVnkSCLX4OII8xl9/KDG9Mu1KydiHvg470UhVsn317pDHdKJHN/gnGFuMNeLjbukEmybtG4TNejWajHQ8v03EvlzFbh7o8wx7N+0vUVqc/+MSkmsnkbknC69La7s438k3z//IwilLeX3ucyWywQ+Ou434lFh+/ngmUpUEfH6Sayfx6Nd3R5RLCAQC5B7MI3PXNrK2jSVr9xaKC4wgTBjsnUmpfx4tzjqD1LrJpNRJxhYhqaiqSP8OUPPA2KTEcJfB/QsQZqIUJvAuAev52kslCWloBIEd4ToDQzVWqhJHN6aFgNiEALEJAeo28YAAEd8W1diP/OwC8jILyD2UR15mAYd2ZbJzrWYcDSYDKbWTSK+fSlq9FFLrJle6z9O2dwvmT14aVk76WGjUOrL67cRXpzB/8pKI56TWrfpEqlMW3eCfYGISHLQ6uxlr5mys8AUzWUwMKJXN6oh3cNEt/Zg2dmaFpwKT1cjl910Usa9PH/2Gnev2lJk0XEVuTVumHF6Xl90b9zF7wgL6Xdsb0CaV294cycjnh3NwVxbxKbFlZHilmge+9SBsePwtyNiWyd7NGWRsO4jXXQzOb3DEFpJay0OLTj5SanpJTDuEIS4ZJbZ6H9WlbxMy714IZIAwgvQibYMRcU8iRGmDV1lkcrnVceyDkHcXUH7itYB1QOhJ5RgRtiFIz0yQIdx40ocUsSiKm6QaicG/w9GSkK4iF5l7ssnck82h3dmsm6vp5gtFkFQjgbTgBJBWL6XCBDviyaEsnb46ZOnJTv3bsvy3NSGfSo0mA0JRKixKLHYLI54aGvY+/T4/E16eEjYCDLRkvyH3RC8VoRMaPUrnJCBj+0Hu6Poo7mJPyZfFYjeTXj+Vtxe9WCYkLRAI8Omj3/DTe79hMBkI+FVS6yTxyNd306xT+A0tVVW5JP6aKoXTgea7f2PucxHPkTKALHyJwozv2bfDzr7tJg7tsyDN52OPb06dZrVIr7mI1PhPccSG2oOwINIWVJuxlIFMZPZAkIXljljBegFKwstHz3X+iCwcDTLUKt+KSFuIULQNUNU5GQqf1VbyHNm4VAAzmNohEj9EKNUXPiilRObfB54/Q4zPBMKijcVxHSLm3ojuLq/HR9beoxNAzv7DJX71uJRYajWuQZ0zapLeIBWDwcCaORv476j3yT2Uj8GggIART17OgFHnck3jOyjKK5vhazAaqHdmbVqcdQa/fzFHk8gWmivnltevZdBN54cd24Edh7ip7f0RP5uX3jGA294aVe0uvX8jeljmKUBuZj5T3/mF+VOWYjKb6D+yD/1H9gnr3nAWutjz1z4c8XbqnFGr0i+Cq9jN4MRrK/WllueMjo14b9krIY9JKcnJOMyelW+yd+Mc8rK0z1J8sp+6TTzUaQyprb5CMbdEzRkGvlWhOxExiPj/IqzVs+GsFr4BxZ9y1CiXxoxInYUwpAbvwYPMuQz8u8udb4XYe1Aco7TzPIuRuTcB5eUeTGC9FCXhhWoZe3mkVME9DVn8OagHQT0MlP8b2iDmRpSYO6Jut2STPDgBHNyZScAfwGQxUatxOnWa1aJWkxpk78vB4/RSr0WdEtfe9jW7ePLilynKLQahRfA0aFmX5356hMT0BHIO5LJu7kbMVjPt+7au1EVXkFPI8Do3hfXfx6fG8cOhT6O+t9Md3eDrIKXk8vTrKcguv+oNj9lq4j+PXcaIJy4v0072/sPsWLOLPZsycBYWIIo/Ia2OkzqNPdRp7CEu8UhEhgKW81ES30HNGQG+paE7EjGIhDcRlp7BPjzgno70LgUlEWEbjDA2iXrcavYQ8K8L31e5yUWqRciit8D1g+Y+MTRAxN6DsA482mbE8TsQaUsQwhwcvw9cU5DOb0EWgKk9GBqAeggMNRC2IQhDjajvp2QMuXeD5zcqGnxA2INjqDwiKBR+n58DOw6xb8sB9m05gKvQhRCC1Hop1Gtei7rNa5cJ9ZRSsmHBJnIycql3Zm0atq4ftu2DuzKZPXEhxQVO2vQ4k4792lbQ17m/z9NaucZybk2z1cR/Hh3MiCfDu4R0yqIb/FMUr9uL1+3DEW+vlkfZh/uNZuXMiobQYFQQQpSRTBCKIDbRwWd/vUV8Shxet5cda3ezdcUO7THfZKB2kxrUrr+S2mnvYbWHeXJQUlHSFkR2nQgbIm0xQtiQ/n3Iw8NBFgV91wbABI5RCHNnZPHH4N8JhjoIxw0Ia1nFThnI0VbiYQ2+A5HwIcISWuNdShnyd60e6hjCRXSkTTsieSrCWB8pfcjDI8G3jtCbwWZAQNwzKPYhIY6HR808W4sCCjkGByLpW4Qpcq0B0FxwSLc27hD3KqUk50Au+zZnsHfTfnIPabIRienx1G1em3pn1iYxPSGqz+TXz33P+Jcmo6oSv9ePLcZKWr0Uxsx+lviUoy68jO0HuaPbo3iKPSUJa1aHhdpNa/LGvOeqdSP/345u8E8xDu3O4t27PmP5r6tACBLT4xn1wn/oO6LXMbe5du5GHh34QsikmZgEB4PvuYAfx0xDVVUC/gDNuzbl/k9uxWQ2smXFDnZv3EfAFyC5ViJNOzaiQat6GNWZkP8QEGFfwNAYJXV60HUyFPw7qOg6eQzFMRwANXsw+P+i4irWBIiy1wob2EagxD2ordLzHwbPHDS/ehilTZGg+eVFaXVLD3gXg/SAuRNCSapwmZrZB9RwRdrMiLR5CCUR6ZqEzH+WsJE/pe5bpExFGBtWcl6pMWT1g8CuMEctiJRfEMbw6phSdSILx4D7B5BeEHHguF6bOEX4zevC3CL2btrPnr+2k7ljPtK3i8R0G00696dRx4ux2kMb4+W/r+HZIa9V8M0bTQba9WnFS78+Ueb9vKx8pr73K4t+Wo7ZambAqHPpO6JHhQLxOpHRDf4pRF5WPje0vJfC3OIymZcWu4UbX7mKS24fGOHq8Dwz5DUWTllKqD+31WHhjXnPUb9FHTL3ZGOymMjef5itK3aQn1WA0aLQoOk2mjafQXJqLhibguM2KHgU1PAVoDRj/iCK42oApFqMLP4QnN9pK3hjU0TM3SWrdOnfgcy+lLDGOiQWSJ6ijcW3kdB+eziyuSoS3y1xHQGozilQ+Awl0TrSB/ahiNgnyhhBtehjKHonxNgUMHdBSdIKwag5Q8EXjTqkEewjUOKil6JQiz6FordCjAEwNEVJ/TnstVIGkDlXgH8LZSdoG9gGocRH3oOQ/j3InCtwF7vZvUWybZ2Nw5l2DOa61Gt/M007NKZGw7Qyq/4H+z7L6jClFs1WE19se5eUWhUn1+pg91/7mPbB7xzYeYgmHRox6Obzj1tfJxu6tMIpxOS3fsFZ6K6QZu9xevjssfEMvKFvyeZZJIryitm8bBtWh5XmXZtwcGdmSGMPWoRF1t4cYhNj2LF2D3s27iPgD5BSJ5luF3Wgfu3RmFgNuLUqS75VkHc7YUsuHcHUEmEfVvJSKA5E7P0QG0ZEK3AgqBdTFYMfgOJPwLeZ0MZegEgEy9kIx80I0xklR6RnMRQ8RQUD6vwRKRIQsXdpk1DRR+BddOSmOBqSaQXFgYh/6ei1alGU4/ZrrqkqIBxXId3TwL+91JhNIMyIhNciX+yZA4HtVHwac4HrJ6TjVoQxfOKczH8AZB5Wu0qzdtCsnYvDmQVsW+di519/sGv9PmISHTRu14Am7RrgiHeQse1g2PZMFhOHdmVVqxE+sPMQk9/6hfmTl5C9/zACUFXJypnr+GHM/xg95SE69I2cq/JvRzf4JxnzJi0Jm1yFgK0rdtCye7Ow16uqytgHvuR/H/6OyWJCVVXMVjON2tRHMSghdc89bi9bVmxny4qtmC1emrRrTNNOLUmqkYh0/4nMW0vFVWUleioiHpH0ZbmY90owNtBcDVXCH3RzhIvhlmDtixL/fMUjIVfsAC5wjkM1d4Hcm9Hu9cj+hglwgLEZWM9H2IeWDSc1nwWuPRHGU3oAlYfISrUQZDEoqQhhheQJSOcP4Jqo7YeYeyBirkcYaoe+XvoAI9LzW+h4fgCEJhlhvDJ0G4EDmnhbOTdbUpqfLufl0KHPPPbnXMPWlTtZM2sDa2dvpGbjdJJqJoStAezz+EhvkFrp/UfL2rkbefzCF/F5/SWieUeWI0e+T88MeY3vD35Skj1+OqIb/JOMSNIJyEqOA+OeGM+0sTPxun0lm1+uQjcbFmzCYKpo8BVFkJQeT0L8Wlq0+ZP6zZwYjQEwd0EGXkS6JqGVIQ6FIPQq3wS2y6pm7AFhqI00dwTvMqIymADCobmYfBuoKI8AoJTJWC2D/6/w7Uo1uD9R3hfvAwxgG4jiuDbEcEYh3ZM011Bl+FYiAwdDRuxI/15kwRPgXa71J2zImNsQ9mtQHFeB46owwy5EFn8Gzq+Cm8wSiIEIvv3gyMMfUnOCT16hJyijspsGLew0bN2bwtwitq3ayfbVu6jdpCbbVu4sEwwAmg+/dY8zj2l1L6Vk9az1LJ2+CqPJQM/Lz6JR2/qMHjqm0hwTV6Gbb1+YVO0S3qcSusE/yeh7VQ++eu77EpmD0hhMBs7o2CjstW6nh8lvTw+ZBenz+GnasRE71+9BCPB7AwhFkJgWz9NfJdK4yTSEKGXcvIu0+HRj0wijlWgfodKGVm387D8AACAASURBVNFCHx03VHqvoRAJbyAPXweB3cGNRZNmfEUSyGzKTgRGUFLAcTu4Jodp0YywhamlK+K0vYSQ+DRJhpC4tX2IUAbfWAcSv9AkjdWsYJJWBOPv/hkc15d5S6qHNUE3mY+2qvZpbq7C15GyCBFze8impFqAzBkMgf2UXY0XgX8r2j5FqGgqCZbQ9YkBLaQ04pOXQDq/RcTeTWxiDO3PbU3b3i3J2H4Ir8dXsnekBlSsMRbS66Xy6Dd3R2gvNK5iN4/0e44d6/bgLnIjFMHkt3/hzG5nRMzSLc13/53KoFv6kVrn9JRp0CtenWRcdGs/ElLjMRjL/mksNjN3vntDxNJ5+7ce0LIiQyCl5OCuTK57dhid+rXjnMFdeWjc7Xy98wWaNP1fWWMPQADUYiAOqKRalFIHbYVoAssARMrkksSmqiKURETyFETix4jY+xCxjyHS5iJSfwLzOYA5uGK3gLkzImkCijEdYu+rOE5h0zZgTc1Dd2a/EggVYaKAsbkmyRAOGbqWLIAwt0WkzEAk/QDWARHu1qvJUVRo+uug+6W8cXZB0VuoWRcgnd9r4ZVlrvs4qPoZyqgfmZTLPXUJG9iHRcwLEEoMmEPuAQZRwbuwzDuKolCnaU2e+u5+3l36MueN6EnrnmfS/ZIuXPfc8GOqMfzR/V+wddVO3EEdKKlKPE4v6+dvwu+rvOg9aCJ0P3/0e5X7/regr/BPMvZtORD8Mhz9QsSnxvLQF3fSZUD7iNfGJDgif/ClxGwzM+rFK6nXvDZCCKR7JlKYw6zgXFp2pxIPqpvQ7hs/qPvAegXEPoBiSIjmNiMihABzZ+2n9PtJHyEDWRDYB4aaZYyU4hiJNJ6JLB6rbWoaaiEco8DSN3w/juuQnj/Bt4mjbittI5aE/0L24DBXGsByduX3YGoK1guQnj9C+8+FA2HqUPF9zwwihroGtiELngfPLEh472hkjGsykV1hKhjbQ2Cb9vSg1ATHLQj78Ij3AoB9lCYkF64egBK+nGKTdg15aNztuIpcrF+wmS3LtrNz3R4at2tAm54tiElwVNq91+Nj5ldzQ67k/V5/RI9UaQK+AFtWlBW/27VhL4t+Wo4aUGnXpyUrZq7lp/d/oyi3mFpN0rn6qSvoMzzy3/tUQTf4JxGHdmfx4HnPlihZHsFd7GHR1GWVGvz0+qnUbVabHWt3VYjIMZgM9Lu2Dxff1r9slmNlfnbphLjRkHcnEY2QexL4liCTp1arnkx5hCEVwjw9CEs3hCWCfHH584UZkr4C9+9I1w+a28TSt2QjVnWMguLPqODHFxaE48boOrH01txOgf2UNZYGUFKhVIjoUaLZ+3Bpq2rvwqOTT6XRTQIsXVFix4dNMAt7paU7UsQE3UzlD9qjmjRsMTY6929Hy+7NWD9/E1tX7GD76l00ad+QNj3PxBEf3vAXHi6KGBMmhMBkMUasMgbaHtiRQj2qqvLfUe8z5/tFBHwBpKryxTPaeUcyfvduymDMDR+wf2vGvyLbV3fpnAC8bi+T3/mFG9vcz9WNbueNmz8iY/tBfnxzWkg9EY/Ty2+fz6Ygp3JZhIe/uhNbrK2MS8hsNXFGh0aMfOE/FVLaMXcltAsgSGAP5N1N6A3R0vghkKnpy59CCGFC2C5ESRqHkjweJeb6o/r3MXeCY5Tm9hAxgA0M9RGJnyOMDaJs34BI+hZMbQFr0B1l1cTWkr5BiBAuOttlhHY1lUM6tYnqCOYuRF7qWhDW84LjqppLRQgjIuGN4LhKj9kO5t5gjj4p0B5ro8vA9lx610DO6NSY7at3Mfnt6Sz5eQXFBRWfhNxODz+PnYHXHX4fIa1+Kp36t8NkNWGPC++CNJqNDLqlHwBT3/uVuT8sxuvyEvAHUFWJDP6UxuP0MP6lyVF9/0529MSrSpBSsnHRFlb/uR6z1cQ5Q7pSs+Gxl/LzuDzc2+NJ9mzaj8epfYANRgWT1UxiWhwHdmSGvM4Rb+fJ7+6j4/ltI451z1/7mDVxIevnraB+47/od0U2iTXTSGxwI0bHwJAGRnX+AAWjiZzwFC4ipxymDijJEyo/7xRCShf4t2kRQYaGxyxzIf27g+6oughjeH14KV3apm0FQbcQmHujJI3VrvP9hcwZTugsXyNYeqIkfnhMYy8Zm3+7FgXkXQlKMsJxNVjOj5ipWxnF+cWsm7eJrSt3oCgKLc9uRqtzmmM0GfG6vdzV/XH2bsoIa/CtDgu3vjGSC244j8w9WWxfs5u8zHw+uO9z1ICKx+nFYDJgMBi44ZWrGHznBQBcWe8WsvblRDVGW4yVuz+4ifOu6nHM9/lPoSdeHSOuYjePDXyBbat24nV5UYwGPn9qApfeOZAbXh5xTF/8aR/+zp6/9uMpJXEQ8KsEitzkRCgDpwZU7HHhXSXF+cUs+WUV+zZnkJzu4+E3ZpOc7kQzGDlQ/ATSOwUSPywjKwCg2C9HGmoii94OhjeG+mJFuzA4ORcQfwchbGBq/ffbMdYHY3iRsTL9JU3U9iOcE0CGixayaS6jI9eZzoSkj5F5j2h7LyVPZVZw3IiIueXv3gLC2Bhi79eE4dwzkcXjEGoh0nZxiXhcVXHEO+g2qCMtz27G6j/Xs3bORnas2U3H/m1ZM3sD+7ccCGvsTRYj543oycDrNTG8tHqppNXTXH7nXNaV3z+fxaZl20mtk8wFN5xHnTOOFqjJOZBbhVHKqMo0nuzoK/wIvDryXeZMXFjBL2h1WHjg09vodUX3Krc5qsU97N0UWpPFaDaiGETIkMykmomM3/thBZeMqqpsXradVX+sQ0pJuz6taNb4PhS5NUQPNkTcU4gIol1q/jPg+jbMUQEiDeShMMet2sat45qw7etUHTX3zqBGUOknMEVbYaf8DkIBzyLAA6ZOwT2D3SDdSENdRBiRtGNBk1gYGtyEDu7pCBsYGiGSv9Umq7/JwV2ZLJu+itxD+cz4ag4Hd4Z+6jVZjDw47o5j3lAdXvdmcvYfjupck8XEl9veIaX2yR/OGWmFr/vww+AsdIU09qBtoo5/OVzcd2TKb8iWxmwx0bBVPayOo5mAikHBYrfw6Nd3VTD2hblF/DZuFsumryKtXgoX39afFl0sKHJvuN6Rzq8jD9CQRthNQ2FFxN6uxb1X8DEbwZCMsF0WuX2dKiMSxoDtUsAS3Eswg6kjIvl7pPsX5KFuyPwHkPmPIbP6IAue1txGpuYoiqNai4bI/MeCG7elNvCDLi9ZPC76dqQX6Z6F6vwRtXgcauHryOKvkWoeNRqkceHN59N5YPuI9Z5NFhMJacdeNOfyewdhiaLAvMVuof91vU8JY18ZuksnDIcP5AZj3kPv+h/cFXrVURlte7dk1vj5ISUOVFXl1ZlPM/eHxfzvg98oyi2idc8WXPHgJdRrXjZ1fue63SyethIhtEfXhq3raWGW3m2R9WjUyI+xwnYpsuiD0AelCtaBKEo8qqGeJuSlHgSMYL0QEfdwSXUonepDCDMifjQy9iFtD0BJQhjSkJ4FUPAcJRpHR3BNRSqJiNh7q3UcUs0F32pCb/J7NPdTzG3lrskPun+mAwKsF4OhJhQ8oX2eSmVxS6xQ+Coy/jUUW3/O7NqUviN6Mumtn0MW7gn4AjTrHH2dhPIMvvsC/lqylSU/r8Dr9iFVidVuwRprpSi3GCEEFruZKx64mGEPX3rM/ZxM6AY/DIk1EiqkhJfmWDP1/vPoYOZPWhKyXujQBy7GHmtjwMg+DBgZOvPR6/GxbPoqtq/eRWrdZHoM6VY2jtnYOEJWpALmyKGdwlALGfsoFL6M5stX0T4mRoh/GaHEay3ZByNtl6Kt9Eyho010qhWhxIByNIlMFr1LeC2gL5Axtx+zXz0kaiEVavyWplzWsgxkatnaaqkngqLtaIuoUK7k4L3kP4g0t0IYanP5/Rcx/bM/tepapTDbzAy5dxD22GN3IRkMBp6ceB9bVmxnweSlBPyB4F5Cc3xeP65CFzGJDgyGf89nWzf4YXDE2el+SWcWTlmKz1s2JNHqsHDFg2HS9dGiZTYt3ca8Hxfh9wXoNqgT7c9thRCC+mfW4aXpj/PKte+Qn1VQImg25L5BXB2h0DNAdsZh5v2wmKLcYtr0akGbXi0quHmEEou0XRZMwilvDMwIx02V3rviuBJp7oh0fgX+XWBshnCMqKDdrrkK9MIUJwz/lsjHAwchQjRQlTHUDBaED3Pc1LLMS1nwvKbDUyb/IBpxvADSOQERez+J6TG89ef5jLnpf2xZHQgmJRroNqgjQx+8+NjuoxxndGzMGR3L1oM2W0xRqdKeaugGPwL3fnQT+7ZkkLHtIK4iN4pBwWQ2cu5VPeg7IlTCjFZk/Plhb7D8t9V4nF6klEz/9E8atq7Hg5/dxm/jZrFt9S46929Hx35tSaqZSMPW9Sqt6LN15Q6W/LwSq8NCv+t6k14/dPKRlG5t066EYJFtYUHEvxpVRSQAYWqGCKEwqXMSIeLCV+GSfqimovBwxJ2zFqwDwfU/KoZ+WhExdx09X/rB8wdhM3Mj4gP/VqR0Iw+PoE76Nt6Y6iQv20hRvp38vHjWrkph2oczOOuijtRvUZkwnM4R9CidSlBVlRUz1rLi99VY7VZ6DetOw1bhV00/vP4/Pn9qQkmM/RGMJgOqKlEMCn6vH8WgYDQbufHlq7g0GBccikAgwPLf1rB56TZqNk6nx5BuWMttNEmpgmeO5iv1LkN7fC6X1RnzGErM1cfwG9A5WQlfEMUA5m4oSdFvooZDygCy8EVNLO6IkB1+QEJJ/VwBcc+h2I5+jqXqRGZ25NgMvgkcIwEzFH9MxQxvIwXFvVj45xCy9x/mzG5N6XB+m3+V6+XvoFe8Ok64ilwc2p1NQlocCamab/s/dW8mO8pQL9CyYMeuHUPtJjUrtl/sZu73izi0K4sW3ZvRoW/rEheO9G1Fur7XHtv9u7QwvMrK6qX8imIMr7apc2ohpVdTFvVvLKXVY9OKsiRPOqZC6eVRC/6rSS1X+GxZIPYBhLE5mDtUkMKWUiKz+oCacQy9WhEpvyAPDw26hEJhRk1ezMqZW9m0ZCtp9VLoOfSsiD79gD/A4mkrmD95CQajgd7Dzi7znfq3oCdeVTNej48P7/uc3z6fjdFowOf106bnmTz4+R3kZobQGomAGlD59bNZXP9i2eITuYfymDV+Aa4iN2cP7kLjtg2OXlP0PhR9iLb5VYUVVO4dkPpLlcanc/KiaQF9CZ4/kM4ftfBIa1+EbUi1REtJ6Q5j7AG84F2ECCERrY1NIGPuDVYUK3+9gmZ6yvvzzdqx+FcQxjrIiNXDBAbFSZeB7Umtk8TCn5bz80cz6Dn0rJDuTmehi/t6PVXingWY8/0izuzShBd+eQyT+d/nrw+FbvCPgRevfJPlv67G6/KWfGRXz1rPnd0eJaV2Eod2ZUXdlt8XIGtf2apA2ftzmPnVXAwmI/1Hlo3/ld41QWNflTKAQQK7whbc0Dk1EcII1v4Ia//qb9y/W0vqCukEkJXW7lXsl6DKPCh6g6MpPxJiHkEY6yNd30EgG5QkLdTU2ABsg44WkTc2Cl+kRli064CGreuTkJ7AnIkLmfnVXHoN606dpmWfmD+8/wv2/LWvjFaVu8jNxkVbmPjKlH+FMFo0VMuzjBBigBBisxBimxDikRDHrxNCZAkhVgd/jq06xknAvi0ZLJu+qow0AmjyCEW5xbTu0aKCjz0SVruF5l2OFhnJ3JPFjC/nYraZGXj9uRWSPbTEqaqWATyCBdTo3U06pzlKfLCASxhE5ZvCiuNaRNpiROKHiMSPEGlLUBzDEJZuKAmvoyR/iZL4Jkr8UwjHNUeNPSBi7iZ0FJgAQ31N2C9IYlo8A64/l4S0OGZPWMDuv/aVHPP7/Pzx9dzQwoQuL1Pf+7XS+/i38LcNvtACsN8DBgItgP8IIVqEOHWilLJd8OeTv9vviWLtnI1ho9JcRW5cRS76XtMLs9WE0Vz5A5TBZOD8q7WInwM7DzHz63nYYqz0H9kntE54YB8R1S0j4geDHtGgEx3CUCNY8SxUpq41WEAminaEFWHugjB3rlJegLCeCzF3ozkiSpsqCf6NyOxLkZ45R0dkt3D+Nb1IrpXI3O8XsXPdbkBz56hq+L3KgpxoC89rk8f6BZtYM3sD7ghZwCcr1bHC7wJsk1LukFJ6gQlA+CD1U5yd6/eELacmhCb9evf7NzJ27Rhadm8WtgatYlBIrJHAa388jSPewf5tB/jzm/k44u30H9kbRzihNFNLotNLL48FbJcglDD1XXV0QiASXg1KOpc21DYwtUTYj29t2KNRSEYqLnICgBuZdx+yVKKh2Wqm79U9SauXwvxJS9m2aieOeDsWe/iJJtpi6rMmLGBo+g08fuGLPHXpKwxNv54Jr0zmZA18CUV1GPzaQGnxln3B98ozRAixVgjxgxAi5DJTCHGTEGK5EGJ5Vlb0fvB/Clexm+mf/hH2uMli4vxrNF3w2k1qsmvD3pASCgAI+GT96zTt0Ih9WzKYNX4BcSmx9LuuN7aY8JEGwn4N4bMdlaDWypEVkRWt7J8FLL0QcU9VfpM6OqUQxiaIlF/BcSMYW4KpMyJ+NCLpy2rJ4pXqYdSiD1Bzb0UteA7p3waA6pwCRW+j7VVF2q+qWF7RZDZx3lU9qNk4nYVTl7F1xQ6G3DMopNG32C1c9Vh4McEjrPpzHWNueJ+ivGKcBS6cBS7cxR6+fu5Hfh47owp3fGL5pzZt/weMl1J6hBA3A18A55Y/SUo5FhgLWljmPzS2qFkybUXYFTtoipbt+rQqee0uDv9BNZqMeF1edm/cy9wfFpNUI4G+V/fEYovs/xfGepDwFjI/qJMiAyAMYKgDjts1XXJTG82/6p0LqhPMnTRpXh2dY0AYUhCxd0Ns1QuPR0J6VyJzR2mfYTyAQavVG3sPFIeLDgqBWlDhLaPJSJ/hZzP3h8Us/WUV7c5txYEdh5jz3UIQQosiUlUuvq0//a7rXWkXnz9ZMbcGtOIoXzz9HRfc2PeUCO+sDoO/Hyi9Yq8TfK8EKWXpYNpPgFerod9/nMLcYtQQIk5HaNyuQRllwqYdGrF+/qaQ59ocFvKzC1k4dRkptZM476oemK3hV0zSvwdZ+JpWxxQ/2iN28AMokiDmERTrOWUvsg6M8s50dP5ZpPQhc28pV+s3oP0UvkHUgQnSH7ZWgcFooOfQbiyYvJTVf66n/3V9uOqJIaycsRbFoND1wg5lgiKWTl/F+JcmsXfTfpJrJ3H5fRfRd0RPhBBsXbkz7BCcBU7yMvNJqhG+ru/JQnUY/GVAUyFEQzRDPxwos5sjhKgppTwQfHkxECbW6uSmWefGmqM+BFaHpczqHuC654bz+IUvVlgZWOwWBt3an4VTl5FaN4Vzrzwnom6HpkE+GGQxR32ZpZ4e1AOQdxsy8SOE5axjuTUdnX8Wz3zCF1z3El0hHQuYu1TQeCqNwWDgnMu6YjAaWDN7Ax36tuaiWyuGsE58dQpfjf6hRNQwP7uQt2/7mOW/reaOd67H6rDg84Qer6pKbDGnhqbU334GkVL6gTuA39AM+XdSyg1CiNFCiCPqRncJITYIIdYAdwHX/d1+q4PczHx2rN0dso5mafKy8tmyQqua06hN/QrRN0KU9d8foW2vljw47g5ik2Kwx9mwx9mwOiwMufdCLDYzCalxlRp7AFn0ZjljHwo3svCliO3o6Jw0qJlBmYZQVGbsjWj7Uj0QCW9X2pWiKHS/pDMNWtVl1R/rydh+sMzx3EN5fPnMdxUUbN3FHv78dj5D065HVdWgXHr5tgXt+7SKuO92MnFaSivkHMjl1WvfZd28vzBZjPi9fs67qgd3vHN9GbdKUV4xr418j2W/rsZkMeLz+GnVozkBX4BNS7ZispgI+AOk1E7imckPUf/MOiH7C/gDbF62DZ/XT6M29fnz2/m4iz1ceFPf0KGX5VAPtSv36BsOAyJ9ZbVUHdLROZ5I7ypk7sgoP9elEPEQ9yzC3B5hqChHEgmf18evn/5JcYGLC2/qS2yilo3889gZfHDfFxGLrWh9a3sD/qB6rtlqwhpj5b2lL1OjQVrV7uM4oksrlMLr9nLXWY+Rk3GYgF8teUz745t5HD6Yx/P/exTQtEAe7Pssu9bvxe/1l5y3bs5GajWpwdi1Y9i35QDJtRJp3Las7748BqOBFmc1Q0rJrAkLKMgp5PxrekVl7LXBRBt3ryIPX4PEolWesg2qXj10HZ3qwtQODLXBv4MqyYPYhpcRaatSl2YTvYZ155exM5k9cSEDrz8Xo8mIx+lFDUQxBgk2h5X0lqn4fX7Ouawrl9w+oERH61TgtDP4c75bROHhogoVdLxuH6v/XM/ujXup36JuSfFkfzktfL8vQNbeHPZtzqDrhR2r1PfqWevZtzmDLhe0D7kikFJqGueyAIxnlBQbwXJOUGq2sqcxUZLuLv3rwPk5JE1AKOGLn+vonAiEEJD4mbbKD2RoixphCEbsSCoqZALCjjCdUaV+pFqkKcgKAabOxCXFcs6Qbsz6dj6Lp63g7Eu70KZ3i4jRd6XxuDw899PDp2y5w5M/jqiaWTp9Zdi6slJK1s7ZCMC6uX/hChNW6Spys2rWhir1u3vjXtbN/Ysm7RuGLMsmfWuR2X2Rh69A5t6MzDwbNf9ppPQhYu/TCkVXSqlJTLrAvxNZ/GGVxqmj808hDOmI5J8RiZ8i4h5DxL8GqbO1IishMYG1X9Ttq0UfIzO7I/Pv1xK0Ms9CLfqEOk1r0qZ3C3as2c3mZdto0q4hLbs3w2ytPKFRSkL68k8VTjuDb4uxhgu0wev2sWbOBlRVxRpjxWQK/cEzGA3Y46Lflc89lMeCKctIqZNM1ws7VHD/yEAG8vA1ENirGWpZBHjBNRlZ8BQYGiOSxoOpM1rSlRLMfrQGf8K5kzyajrmOzkmKEAJh7oiwD0dY+6IYkhCJH2sJhMIOCO1fEY9IGocQ0elUaYlbwRKQsij4nXJD0Tuozqm06dmCOmfUZNmvq8nck8XoqQ/Te/jZmiSKKbxBr920BonpCdVy7yeC087gn39N74iV6hdPW8G7d35Kr6HdguXUKmIwKvQZdnZU/bmdHmZNWIDJYqL3sO4hVwey+PMwdWjd4PoRmXkO0rcOkfQ1In0VIm0FSvoKlBprEal/UDbtvXzj0euE6OicDAhzJ0TaAkTcM4iYuxBxzyPS5iNMrUKeL6VEeuaiHr4JNXswav5zUDSG0IlbLih+CyEE51zWlZgEB3O+W0TAr/LgZ7fz3cFPeOGXx4hJdFRw81jsZu5678Yy721aupXHB73IZSkjGdHoNia8PBmP6+TV2DntonSklLx41VssmLwkpHoeaCGWn295m18/+5PvXvupzO691WHholv7c9Or0VWPmjdpCbs37KX/yD5hC5+r2YMqr0+KDRyjUMplO0oZQGaeBTIv9GXGVigpk6Iaq47OqYaUElnwZLmyi0a05MRwCET6BoQwkpuZzy8fz6Rus1r0vPxoDkvmnizGPTmB+ZOWEPAHaN2jBaNevJJmnY7Wvl08bQXPD3sdr9vLETOqGBQsNjPnjehBt0Gd+P2L2ayYsQajUcv8vfLxy477E4Je8aocqqpyd/cn2LR0a8jjVoeFW98YyQU3nMeSX1Yy8dUpZGw7SI0GaVzx4CV0v6RzVP0c2HGIGV/OoXXPM2l/buhsQAA150rwRXOvFm2lo5SNClCLP4PCtwhZZzTxbYSld1Tj1dE51ZCeRci8WzRXaNRYEOlrS1yrq2etZ+2cjQwY1Ye0etEJqQUCAa6oeSMF2WFqCgsqxFgYTQZik2P5aNVrx9XoRzL4p51LB7REjJqN0ys5R/swdL2gA6/PHs2EfWN5c/7zURv7gD/Akp9XEpsUQ+sekQuHC/twNJGzShBG8C4Kcf1IsF8DWIK+z6D/M+5x3djr/KuRzglVNPYmTTW21D5ay7ObYYu1sfy3NVErX25eug1/GA+BNrCKb/l9AQpyCvlq9PdVGG/1cloafIA+w88Omw4d8Kt0Htj+b7W/fv4mCnIK6XphB4xhNn9LsF4AhsgTEKCFCITYoBVCoMTdr63+4/+LSHgTkbYYxT7s2Aavo3OqoGZXckJpE2cDQy1E7ANlzjCZTXTo25rs/YfZsXZ3VN16XN6we3yRCPgCzJ64sPITjxOnrcHvckF7GrapXyEUy2K3MPiugSTXrJoQkpQBpGcB0vk9eRlzWDtvIw1b16NW4yjKCfrWQOBA5efhAXN4rRyhxCOs5yIsPRHi1ND20NH5W5i7EjFoAQFKXTB1gthHESk/IZSK7pRGbeqTXCuRVX+sw+cNp/FzlDM6Na6QoxMtvmO8rjo4bQ2+wWDgtZlPMeTeQcQkOkBAev1Ubn9rJDe8PKJKbUnfJmRWL2TeHaj5z7Pkxycwej+n43kVN2ml9KMWf4GadS7qoXao2ZciC18mOnVAgcy7B+mchJQnbySAjs4/hbD/B0Sk+PkAUIxI+hrFMTys7IgQgs4D2uEscLFxYWUBFOCIs3PZPRdGjPgL3Q+07xM62uif4LTctA2FlDKiPELY61QnMqsXyHwAdmy0suCXeLqeX8QZ7WMRqX9qhaaDfci8W8C7uJzfMcQOTySEHZR0RPJ3FTZwdXT+zUgpwTMb6fwM/Pu1QufWvlAQqbiPBZE6C2FIqbT9Od8vYt+WDC69c2D4qnOlxvLti5OY+OoULZkziq+wxW7hrQXP07htg8pPPkZ0LZ0oOBZjD4D7Z5DaI6DXI1gxO5aUmj6atikOZojPBWuw1ot3EXiWUDGapoqTrnRCYB+y8GVEvK6QqXP6IAtfAdf4owsm7z5NOgELIeUYAAgg/XtBiUeEeRqQUgU1m/bnNmLf5gwWTllKcYGLguxCmnZsRJcL2mMwlM2hEUJw1eNDGPrAxayZtYE3b/2IwlL1ca0OIm1YFwAAIABJREFUC1JKXIVuVFVSu2kN7v3o5uNq7CtDN/hVYN/WA0x8dQprZ2/AHmdn0M3n03fwOkxoin9b19pwOxV6X5qnZfNKF/g3c6S4l3RPBaqoDhgWH7imIeOeR6sjr6Pz70b6toLzWyqWPHShZaCbCK2xr0LeKCQGZMwDKI7hR9uUEukcD8XvgFpEDCopSU358D4DLqcFn9uHLdZGXFIMr88dTVrdik8JZouJzgPa8fWO99mwcDMHdhyiVuMatDjrDKSUZO3NwWg2Vnlf8HigG/woWb9gE4/0ew6f14ca0FbkH9z3BTM+t/LKBDOK4mXjcgc16ntJrXXkQ2cBpdQHJKLf/cifQnD0Q1uZq8cP0g0iStVNHZ1TGG3BFG5D1aTJjchCKk4IarCeBFD4EqqwoNgHa20WfwzF75VxsbbrtoV+w1KZ/k0SPrcRV6ELj9PDkxe9zEer/xt2fEIIWp3dnFZnNy/zXnr96GL7/wlO203b8ng9Pr4f8xPDat3IQMtwLk28lvfvHUd+dgGHD+byUN9n8bi8JcYetHqW29a5mPl9Ats32HAXK7TuWlyqVVmmzKCwnBfUBwmFAf7P3nmHSVEtffg9PXlmI7tLjpIzkkRRREFABBEx4zVgxHTNOUeMV7yGz3TNAUVMYECJouScM0tcYHOa2H2+P3p2YZjp2VlAgaXf5+HR7T59unt3prq6TtWv0j9BJN8FntGQ+iZk/AxKrH7wYZT0OPOZmNQwtGKMpZRD4LkMkh8AW2fA6HvhhdKXdc9eeqOMPUBW/RB1Gwdo32Pfd1lTNXZsyGHDEuNWh8cCpocPeMt83NzjPrat2Vm5LVRUzrdjf2Lal39itdsMZRj8ZQEmftqW/iPWklkvRJ1GAfRXSwsi7T8IJWnfYOdAKH0N1B1Eln47wdEXxdENHN0iMu21pNvDC1IHxv1d4Lnp4NceTEyOMYS9F9L7AzHDosKOsPdC2LuB51K0HOPKdrQiPX9f3YIeCoqmbddytqyJTG22WBV2bsihRRfjlopHO6aHD3z53LdsXxs7D75wdxH5O/PjHl+Ub6E0MJIOffsjHH3AczUi62eEs1/EOCHsiIxx4DgTPXfYpcseuy9FpL0cc27FPQySbkSvovWEwzcOcF+OcI+s/s2amByrOPuDkka0kbaBpTnYuu7bFFdVUwPhRPd3Y4dMm7T2oSiR+zRVo26zo6ez1cFgevjApHd+j1tSranxO07VbpxFet2mNO56fVyPW2r5oO5ApDwGYgxoBWCpXaXkq5I0GukeCYG/9EYRjl4IpVb8mzIxqWEIYYeMccjC2yG4AoRdXxez90akvRj53XMOA+/nxAwB2boglGSkrSNGJlANwZ7t+wq6hCKo3TiTll1POLw39Q9jGnygvKQ6WhyRWGwWWnZtRodT2xgae6mVIIvuB/+M8Ic0APaTwh/SxAo3hJICzkEHfZ0mJjUBvWnKF0h1p16dbmmEsMTwup1ngPfT2JMk3arPJazIlCeg6H72X+hVVSu5ORaWz9NrXBxuO0lpHp7+8YFjPoRqhnSAZh0bxd0f7288dPQA6jatTdMOseeQUiLzr9KNPYF9zU0Cs5F5lyLlkSuzNjE5VhGW+nrjlFjGHqDkZWKHayzg+7HyJ8U1GJH+Tjgc5ACRhiX5StyNJ3LpAyM5sV8H+o3swyeb3qDeCdF6VwFfgLKisoRF1440psEHrnryEiwGXW6sNgvn3zEEh9sR8XS3OW386/GLSM1IoUn7RiiKwa8yuADUDURLJ4RA2w3+6YflHkxMTHSkVhinv4QKvp8jtghHL5SML1HqLkepMw8l5T4yGzbh4nvP45L7hpPVMCPKs9+1eTcPDXmWYalXMKL2NVze7CamfvHH33RHhw/T4AM9Bp3IbW9ci9VujRCjdKe4ePKH+7nxpSt54fdH6T28J43bNeTkc7sz5peHOfW8nmiqRpN2DY0nDywwzr+X5Uj/nMN7MyYmxxEysAit4Ca0vWeh5Y9C+v8EGcK47ScYp3ZGU7tJFpqqsXd7XuW2/JwCbu55Pwt+WUIoqKIGVfZszeWV6/6PSe/+dvA38w9gxvDDDL62P/1GnsaSqSvI2bKXNie1oFW35pVP9na9WvHY+EhZ1enj/sSd4iKzQZwFVOFC/zXHEkezgHDpi7ki1ayYNTGpBlrZZ1DyPLqkggQ1GxlYCO4rwVIb1O0xjhJgPyXhc9RupHv3e7JzqddMD+mMf2UivrBcwv74ywO8e++nDLzqjKol0Y8Qpoe/Hw6Xg5PO6cawmwfRunuLuAs0wUCQHRtyaNSmgfFirQwhHWdg7G1IKP8AuacPck9PtJLXkDJx78PE5HhFqnlQMgZ9sXV/w+uF8g/APQqIJRHuRCT9O8b22NiddqTUmDNpIbuz9wLo7VENJI41TWPj0sQ09Y8ER+dj6G9gxazVfPrUeDYs2UJqZjLn3TqYwdf2i9lUPBF2bshBDaoxwzkylI0sfgYCf6Dn/Kbo6ZQRZeEVD4Gw5y8DUPYeUt2GSHvxoK7JxOS4wf8rxo5UAEpeA6W+3utZlgISrK30xui2NgbHRbJzYw5PjHiJbWt3AILvX/+ZTn3axT9IgsVy9PrRx4XB//3TGbx647uVzciL9hbz9t0fM/uH+Tw98QEAlkxdweblW0mvm8Ypw3rgrELneuvqHTjcDmo3jhRTkupOZN6I8IcsnL8flk7WQzgeUDJA3Um0up8PfL8gQ7cirI0P7aZNTGoyWgnGujoSKAStEHCCvSekvohiie5PYYSv3M+/ez9MUW4xcr/QzdIZq0jNTMHmsMasvre77DTrdPR+d2u8wfeV+xk7ep+xr8Bf7mf5rDVM/nAaXzz3LQW7iwgFQlgdVl694W0eHX833Qd0jjmnqqpsX7eLJu0bRmXnyNK3dPliYhVrqbonr9QC1UiTQ0BgFlgvq/7NmpgcL9hP1KtpZVXqsz4ILNSlyV1D4o6UUkJwIQRXM/WTPHxlvghjDxAKhCgtLMOd4qassIxQcF8I1uGyc9sb10bJKB9NHL3vHoeJRb8vQzF4xfKV+njj9g/I2bIXb6mPYCCEt8SHt9TH4+e/GLEyvz/FeaUE/UHqNo2RA+z/nUidnKizQnBVnP0CI30PExOTMLYeYGmCrltVFV4ouhMt72JkYGnMEVLdi8wbiiy4FlnyAkt++wVfWezsOk3VGH7bYAZcdQauJCcWq0LrHi148of76XNBZAtSVT261uRqvIfvLw/ELYrwlcb+owb9Qe7p9wTdzurEkBvOolnHJpX7CncXApBeN7I3pgyuAq2UqgkCLqIF0QBUcPRNYA4Tk5qJ1Ep1jXrvt0AQHP0QnqsRln2FT0IIqPUhsvCucAMUhdjfp/0ILkbm/wtqfYKwR769y4LrIbSRipTN1AwfiiUJTY1eJ7DaLNRulMnIh0Zwx9s3RO1XQyrjXviOb16dRHFuCamZyZx/+zlcfO95MdcM/V4/+TmFpGam4E6O3YLxcFHjPfwOp7ZBDVb/KaupGjvW72Li279xa68H+fL5byv3FewuQrEopGTsU8LUSt9E5l1CYr1pAVsnorMIXOC+MuKDbWJyPCG1YmTe8LCq7AZQs6H8E2TuOchQZBhUKOkotf6HyPoVUp8nMW/fhyyJ7BIng6sgtIn98/MHXJyPzR7bUVRVjVOGxewgCMBTF7/C589OoDi3BICi3BI+f3YCT1/yn8oxmqYR8Af57y3vMSJzFNd3uosLal/DM5f+h9LCMqOpD5kab/CzGmbQ54KTcbjjdbY3RlM1/N4Anz45vlILu2B3EalZKZWxOhlcCaX/R3SKWCwE2E5E1HpfV8FUMgGr/nqa8jgi+e4qjjcxqbnI0rd0jZyIhIYgyBJk0SMxjxGW+iiuQeHeE7FSMQ8guAQp91vwDW0EEWkKm7f3ce7VuThc+x4CQuhx+jvevh5PauymQ2sXbGTBr0vxl0c6fv7yAPN+XsTYm95lRNbVDLRezLCUfzHpnd/xewP4yvwE/UFmfTuP20975G8LBdV4gw9w1/ujGXxtfxwuO+4Ul2FMPx7BQIgf35oMQMHuQtLr7GseLsu/JDHPXs/SEalPIIQdJekmlNp/odRdhZL1G4p7+DEvzmRickh4JxD7uyT1kIxWbHioSH0WnIPRpcerYr/vmcEb9bUP7+Kx/22lx1luajfOpEmHxrwy80n6X3664axzJy4g4IttCwLeID+/N4XicN/bUFBFDUUa9lAgxJ7svcydtCiBe6g+x4XBt9qs3PTq1Xy9531e/eMpho4eGL/yOgaaqrFn61585X7Ki72k19kvfq/uJHZWDoBVz8NXssA1ApHxPcLa4mBvxcSkZiMPbE+4P5a4WTlC2FHSxiBqz0Rvam40MAUh9lu+tHUHkRRzaLfTAzwz8R4e+epOTht+Eo1a1497+VoVImoHGvhYeEt9zJ20sMpxB8NxYfArcHmcNOvYhL4XnVxlnv2B2Bw2WndvTuEePad+fw8fWxcMvQphQ9T6EKX2nyipTyOs0aqaUoaQvsloRY+gFT+DDC6r1rWZmNQYbHE6VSkeUBJpQGInbqacjEysEEJBpL+t98SlYtHUAjgh6RaErQOuJD1U5C2N90CCk4d0x+48uPBx5fUoAoerevYpUY4rg19B+95taNOzJXZX5B/G7rLjStbTrA7EYlUYcuMAivP0hZjUzOTKfcJ9MYhYCU9WsJyAsHUwvBapFSJzhyKL7gPvOCj/GJn3L7TCe5AyfuMVE5Oahki+g9hxeBd4bkOIw2GyojNlhK0dImsaJN+hrwW4/4XInICSdD1Apa0I+IyKvXRa92hBlzM74DjAtlQnjOxw2Tnj0lMTHl8dDovBF0IMEkKsFUJsEELcH2O/QwgxLrx/rhCi6eE478EihOCZSQ8w5IazcCY5sTmsuJKdDLt5IO8tf4Um7Rrh9DhwuB24k12VzQ8yG2QQCmto2Bz7MgKEpTYi/T0QaeE2hG5dNM3aWt8eB1n0MKhbQVaszEvAC77J4bQ0E5PjB2Hvhkj7j16NLjx6qEV4IPnfKJ5LE5tDSQJrW4O9SkTas5ReZGCxnqkjklA8V6GkjUVJeTAi9KqGdOcrESmWx7+5mwvvPhdPmhvFouBJczPgitNxeqr22h1uXc+rTc+/J+wrDlW4X+gSj+uAs4DtwHzgUinlqv3G3AR0klLeKIS4BBgupbw43rzdu3eXCxYsOKRrSwQ1pFJWVI4n1V35x5RSsnruejYvyya9Tho9zu6Cza4b+GUzV7Fk6gpGPjIiqqJOyqDehlDNBVtrhK0DMrgKWfpaOFfYDq7BiKTbEEqqnoK25xQMF3wtLVCyfvob797E5OhEShVCa0AGwdY24c5wlccHliDzr2D/TlYg9KSJjG/A0hRZ9iaUvYPu8WsgkhGpYxCO3lHzZa/axoyvZjN09IDI9bu49yAJ+AKVIZ4HBz/D8pmr8Xv3fd+tdit2pw0pJbXqpDHizqGcc31/4/4aCSCEWCiljJk3ejgKr3oCG6SUm8In+xIYBuxfTjoMeDz8/+OB14UQQh4FbWIsVgspGckR24QQtOvVina9WkWNDwVVhCJilk8LYQPHvhV86Z+LLLiOiA9d+SfI8i+Qaa8jrM30UJA0MPjanoO6JxOTYx0hLGBrf/DH27tAxufIkhcgMI8Kz14k342wNkMrfRdK3yGiWEuWIwtGQ8aXCFukSFqFhIJRo6TY9xAZi3/y+/v45Mmv+eGNX/GW+nAnuxj+78GMfGjEQYs4VpfDYfAbANv2+3k7cJLRGCllSAhRBGQAufsPEkJcD1wP0Ljx0SlAFAqEEtK6llIiix8k0sOonAUKb0GmvwPx5JAtR+fvwMTkWEDYOiBqfVxZaV+R8ixlAMreInZlrh9Z+joi/c2IrRXZNYeic2+z2xj19GVc/dSllZ7/P52GfVQt2kop35FSdpdSds/KyjrSlxOTUDCkd8aqCjVbD+0YzwSlY8E1jNgpZC5E0o0HeZUmJiYVCCEiDau6DeM0aqmLrR1AhYdvrYaHH+96HC7HEam5ORwe/g5g/1zDhuFtscZsF3oCbCoQW5nsKEcNqon90aWfKpP9g8sg/UO9M09gEXppdzie6LkG4RxwyNdrYmJyAMIT/81auKM2qQYhnaLcYmZ8NZvivBJadm1G90Fdjmq1zMNh8OcDLYUQzdAN+yXAgdq+PwBXArOBC4CpR0P8/mAIJWrwrSdQ9QuUghAuRK0PdXmGwBzAAc7+CEvdw3C1JibHH9I/B1n6CgRXgnCC8zxE8q0IRV9sFZa6SGtzCMVSrXWA+8KorcFACCEEuTvy+eu7+QR8QXzlPr564XuEEPh9AVweJ2m1U3llxhNkNkhce/+f5JANfjgmfwvwK7p7+j8p5UohxJPAAinlD8D7wCdCiA1APvpD4W+hKLeY7FXbSa+TSqPWDaL2787ey7QvZ1GSX0r73m046Zyu1XoiW+2xGx8ciBA2ZPKdUPI0hq+PIhVdOdOBsLU/pEUqExMT0Ly/QNG9VK6dySB4v0QGpkHGD3rKJiBSxyDzLw2/iVd8n51gbYRwXxk1b0l+Kcv/XF0poqiGtKiqWW+pD783wCPnPs9bC1/4m+7w0Dgs8shSyp+Anw7Y9uh+/+8Doh+bh5GAL8B/rn+bmeNnY3PYCAVD1DuhDg+Pu5MmbfU2hONe/J6PHxuH1CTBQAjX/00mvXYqr8x8iox66Qmdx53spLzEi5Syyhic4rkcTc2H8tdjD5ClyOInEanPVOteTUxMopFSheLHiE6UCIK6F1n+OSJcSCVsbSBzIrL0fQjM1N8EXBcg3BcjRLRE8YJfl7Dij9VVOnuaqrFt7U42L8+OkFQ/WjiqFm0PhWdHjmXm+NkEfEHKisrxlwfIXrmN2099mOK8EpbNXMUnT3xNwBesbEDsLfGxO3svT174csLncSU50VTNUCDpQJSU28Bq1AczAN4fkAlp6JuYmMQltBJjEUM/eL+L2CIsDVBSH0XJ+h0lcyKK56qYxl5VVeb+tCihN3vQq/K3r8+p5sX/M9SIBii7Nu9m/s+Lo8qepYSgL8hP701h1V9rCXijm52oIY2Nizezc2MO9ZtXHTd3hRsUlJf4Ete7UHca7xNW0HJAMQXVTEwOCakSN1FCetEK74LAXL0S3nUhwn05QolepN2f4rxSSvITd8o0VaNes0Q0f/55aoSHv3rOesOCCL83wMLJS9m+bidGy8RWu5WczYkVOVV0pPGWVNFdZ38scVJMZVDvcWtiYnJo2Npj3I/CCtoO8P2oFzSq2VD6GjL/YqSM/10u3FNUrU5UdZpk0bxL04TH/5PUCIPvSXHFjacn10qiUZsGGA0JBvR4fyK4knVhp/JqGHzhHsU+Fb79sYK9F8I0+CYmh4wQdki6g+jvmkJs9cwAhLYgyz6PO2/B7iLa926dUBMlq83KUz/cf9T2tagRBv/E/p0MH+zOJCdnX9uPC+8aij1GCMZitdCqe/PEDX5YJtVXhUxq5EHDwXkm+gcx/EEQbrDURaSOqfJwqZWilb6Jtrcf2p7eaIV3IUMbEj+/iclxguK5AlIeC8so2wFbWPbYCD94v447Z+GeIrr278Sp5/fCEUdW3eawcc+HNydsS44ENcLg2x027vv4VhxuO4qy78nq9DjoNaQb3Qd0psOpbbnqqYuxO22VSpeuZCd1m9XmkXF3JHwum92Gw+2o7FqTCEIoiNRXELX+B66LwXkuIuUpROYvCEtm3GOlVobMuwBK39IrBLW94JuEzB2BDPw9XXFMTI5lFPf5iKw/9EYotedE6d9HoRk3VZFSkrcjn4x66dz/8a28PP0JzrridKx2a0Q9jsNtp1HbBkz7Yhav3vgO6xdtOly3c1g5ZLXMv4uDUcvcuHQL457/jrXzN5BWJ43ht55NnwtPjlCe27s9j+nj/qK0oJR2J7c6qMq4aV/+ScHuQs7/9zmGY6TUwDsBWf6BLrFgbYlIugnhOKVa59JK34LSN4ns8RnG0gSROfmofX00MTnSSBlA7u6EsZQC4ByBkvZczF17tuXyy/tTOW3ESRFplkW5xUx693cW/74cocCq2etBSvzeAIpFwWa3MuLOIVz9VGKSzoeTeGqZNcrg/1OsmrOOBb8sYcQd58RsZiylRBbeBv6ZRAo0uSD5XhTPyITPpe3tr+vlx8SJyPwRYT368n1NTP5ppAxAKBsUN8Kyr+hS23s2qBsNjhK602TwHVr421JWzV7HxfcOi9nJStM0Lms8mryd+VH7HG4HY359mA692xzU/Rws8Qx+jQjp/NPUbapn3ezONhBHC8zVizmi1Pi8UDIGqZUgg+vQ8m9Ay+mIltMJrfAOZCiGYY/X41NYoIoMAxOTmo6UEq30beSek5D5FyH3DkLLHaLLlQAi+V5id9ESkPxQXIdp29qd1G1W27Bt4co/11JeEjsk5C/3c8dpj3CO+zLGXPFfcnccefmw48LgH8xbzJaV23hp1Btc3+kuHjznWeb/srhynvQ6adhddnK2xE7llL5v4xhqK7L8E2T+RRCYjh6q8YHvZ2Te8Gijbz8F4z+TCGv2mJgcv8iyN/WwpywLd47zQ2gdMn8kMrQN4TwDUseAkqnn3+MAkQGpr+uLvAYU5RZTnFtS2bhcBhbqTtqeM9HyRiJ9U8jbmY+oQiQx4Asy7YtZjO52HwW7Cw/jnVefGlF4FYv8nAL+99AXTP/yTwL+IM27NOXa50ZSq146y2aswulxcPK53UmpFb2C/9f383l25KsE/SE0VWPziq0sn7mKQaPO5OaxoxBCUKdJFru37I19cq0M43xgPbaPPNAr0ECWIUteQqS/VrlVJN2I9E+OMd4Fnpv0VDQTk+MUKX3hrlUx3nRlAFn2HiL1CRTXYKRzEKibAAGWZlX2x922Rhf9bdiqNlrx81D+CZWVvNp2ZOEKmjQbSigUR3kzjKZqlBaWMe7F77nxpWitnn+KGhnDL84r4frOd1G4pzhC4EhRBIpFQbFYUCwCTdW47oV/cd4tZ1eO8Xv9XFjn2pjd6R1uBy/8/ijterVi1ey1LPh1KSPuHIInJbJST5Z/gyx+Coj1qheWPzZ8IDgQdRbqHr/3W5AhsHUA/1RQc/QwDgI8NyM8o8wFW5PjGhlYiiy42jgTR2mIUnvqQc3903tT0PxLGXzBZyBLDEY5uWNEf9Yt2FmpmR+PzIa1+GLr2zH3hYIh/vhmLlM//wNNk/S96BROv+hkw3CSEX93i8Ojjgmv/URxXkmUmp2mSTRNhf3+MO/d/xmN2zaka7+OAMz7abFhgVbAF+Dn96fQrlcr6jTVS6d3bdpNiy7NIge6ztGbm2h+dI37/anqQ6Ei8y6C0GYqvZbgclDSoNYnCOEEazPTszcxAV30LF4GjoiO3etOrqa3UTSgrLicvdlL6dJtXBxjDxDgic9SefhiO9mrtqOpMq7OVigQYuVfa2nYqh6pmSmV271lPu48/VG2r9tVWeOzbMZKPn9uAv+d/SxJadHJIQdDjYzhT/t8VsJCR/5yP188O6Hy503LsiOaDO+P1CSFu4sAqFU3jaR0DxsWb4kaJ4QTkfE12HuiF39U49es1IXQRiJfUb16/n3Zewhba9PYm5hUYG0VlhmPhRPcF1X+JNU9etHi7g7I3e3Q9p6N9MX2/tfO24AIzqFpm+IqLkAjJa2M1+eO4cUpj1G/efyiq+K8Uh4651kua3wjz10+Fn9Y3+vjx78ie+X2iIJOX5mfnM17+L+7PqriGhKnRhp8KeM88WOQvUpvyfvz+1MY98J3qKHYxzvdDrqc2QHQ25S17tGCPdl7KdhTFDVWWOqg1PpI72iV8IuUC7QiYubcEwL/VD1maYCUQbTSd9D2nIaW00H/QHsnJnhuE5NjDyEEIvV59Cyc/c2ZA6yNEe6LAZBaATJvOPh+Qu9BIUHdiCy8Ha3824g5Q8EQ6xZuomGz7SSnVfFGLtyVtTUr/lzDjg3xVTI1VaOsqJyAL8isCXN56qJXAPj5vSkE/cGo8aFAiGlfzIqKVhwsNdLgn3p+L2yJ9J0Nk1E/nYLdhbx+6/vGbwYCbE4bA686o3JT8y5NsVgtrJtvLHMgZBGIqlQ1rWDVGy7Hbnq+30VELd7qSKkhC66H0tdB2w0E9A900UNoJa9WcX4Tk2MX4eiFyPgKHANAyQBLI0i6GVHrq0q5Y1n2SdiZOtBw+qDkWaTc973fuDSbgDdAu+5VrW8qIFLAeTYFuwt5//7PYhptIwK+IIunLGfrmu2UFxunV6uqZhh1qC410uBfeNdQXMkuFEvVt2d32Rlxx1Cmj/sr7rjUjGT+M/PJiFia0+2gaYdG+gfE6A9tqU9s4SYAAY7+iNpzUTInIOydwdrc+CKE2/j1NTAbgouJfmB4oew9pGqQUWRiUgMQtjYo6a+h1J6NkjUFJenGSNlj3ySMtfLVynaHUkpWz1lHRv10slqehx6SjXlGsHVGZIxDCAePDX8xoUXbA1EsCqtmr6denFBQcnpSpYbXoVIjDX56nTTemD+GkwZ3xWKzYLFaqN0kk+RaSVgP8PxDgRCzf5hPXk5hlJ7+/vS/4nSatGsUtb11j+aEAiE2L8uOeZywtQWlIbF/1Q6E5zqEsi81VCTdRswiEeGCpBsMF5qk7wdD7x9hAf/02PtMTI5hpJQHVWdzwCxUaKfv2JBDcW4JbXu1Qkm6CSwNiPw+2nUxtvRPUTLGISz1yF69nU3LthzUmRVFwZ3s5F+PXhhTmM3pdnDZQ+cftmy8GpmlA1C3aW2e/P4+goEgoUAIV5KL2T8uiOpupakacyctovMZHXAlO/GWRIdUXMlO2p7UKuZ5MurXIqN+Omvnb6RV9+Yx/zAi/S1k/iW6QZbl6L92CyTdgrCfGDnW2R+ZfDeUvBROwUTXzHddFpZZNkDGeZWUEuO3DBOTYw8ZXIsseV5/swWk/SRaJwhFAAAgAElEQVRE8n26gxUL59lQ9h6xvXxLZT/p1XPW4Up20aR9Q4RigYxvkd6vwfut/h1zDkR4Lo+QNN+2ZgcWq3HGjxC6Jx9rbVBVNXqcfSIuj5Oczbv5/LlvK0XZQgGVIaMHRKSNHyo11uBXYLPbsNl1dcxxL3xHKBBt+PzeAEunrSA1MwV/eQBN3feHURSBJ8VN7/N6xJy/YvH2r+/nszt7L3WbRne6EdbGkDVNz60PLAQlA+EabljSrXiuQLpG6BINBMHeE6HE77krnGeFMw5iefkS7L3jHm9icqwgg2uR+RdHvtEG/tKdqlpfIGzRLUWF5wqk9yvQCoiM4zsh+QGEsFKwp4hdG3dzYr+OlYKKQnEjPFeCx7hYKqthRoTNOJDMhhm0792aOT8uxFemJ2QIIbC7bNzxzg24PPobxOWPXMi5Nw9i0W/L0DTJif06kl7bKAPp4KiRhVdGDM+4itKCspj7XMlOnvz2Xt668yN2bMjBYlXQVI06jbM454b+rJm3AYfbQb+Rp9GpT7sITz4UDPHtaz+TlOZm0Kgzj0gxlJRBZO4wvZMP+3v7TnCehZKWeN9eE5OjGS1/FARmxd5p7QHu86Ds//TWokoauC9HeK4DLV9/K/BNBkJ6tW3yXQjnWYCugrtzYw4j7hiCM47u/YFIKbm6zW3s3JAT1VXP7rTz4pRHadurFTO++osJYyeRn1NIixObcen9w2nd4/C3NjXVMsOMavtvtq2N3V/W5rDx5fa3SclIZsOSzWxZuZ30rBT+e8t75OcU4i31IYRebdvtrM488vWdEbLKa+dvYO6kRZx+0ckxY/2JIqWmF3oIV7Xz7aVWjCx+Eny/6huEFdz/QiTdhhA1/mXO5DhASg25ux1xi61wEVnH4gB7N0T6BwghwmnboYjv144Nu5jy6R907d+RDqcahIXisHXNDu7o8wgBbwBfmR+LVV87HPnw+Vz24Ihqz3coHHeVtkYMv20wb9/zCf7yyDx3i1Whc9/2pGQk89snM/jw4S/J25Vf+ZpW8UyUUi+GWDh5KT+98ztDRw+snKNltxNYt2AjCycvo0HLelhtif1qpVYCwWVIbHpFbdk74TJxgXQORKQ8XGU4pwKhpCDSXkLKp0ErBiUdIWwJHWtiUnM4MMXRD8ElerzfcUpYQ2efsVdDKvN/XkJKRjJte8Veq6uKxm0a8OnmN5n2+SyW/7mGWnXSGHj1GTRu06Dqg/9BjisPX1VVHj//JZZMW1FZ0eZMcpJSK4nXZj/LjK/+5H8PfYG/vOqc1wYt6/Hh2tcituVs2cPkD6fTuW97OvdtH/d4KSWy9D9Q9gEIG0g/kaEYACtY6iEyJ1bmE5uYHK9I/1xkyTMQWhNnlMBQp8p1EUrq01GbV8xazaLfl9Pv8tNo0KKe8fmlZPHUFaz6ay3uZBd9LuxFZoOM6t3EP4Dp4YexWCw8+d29LJ66gskfTcdb6uXkoT044xK9Uu6DR8YlZOyBmDKndZvWpmmHRqyYtYbmXZqSlOZBBlciS16GwHw9xOIciEi6Hen9Aco/AvxhYx+LkN4tyzsR3Bce5F2bmBz7yMA8ZMF1xC9MtKIbfKOMteiEjbLicpbOWEWjNg3iGvvivBLuPvNxcjbv0UM2Ngvv3Psx3QedyE3/uYr6zetW426OHMeVwQd9dbxrv46VYmkVLJ2xMqIfblU0bFU/5vZuAzqzbe1OFvy6hNOHO5H5V1P5IZV+8H6P9E0DGSCmpGsUXqRvEsI0+CbHMbL4aeIae1sXcI+ConsMBtjB0T9q68LJS0FCj0Fd4p7/2cteZduaHZXFVRXZfnMnLmTh5KUMvrYft/z3mqNevbZGFl4dDIqioGmJafA43A5GPhx7IcaT4qbz6e3YunoH25c8RvSHVAVZHGN7PKrXc9fEpCYhtTIIrY8zwoKS8RWKaxA4BwCx1q2CUD4hokhr1+bdbFmxjQ6ntYmrRrl3ex7L/lhtWEkbCoSY/NF0fn7/4GSY/0lMgw94S718/twEfKVGoRWwWC04PQ7sThsjHx7BKefGzssHaNurFcnpMH9yEQF/rCe+StUyyRXYQNiQ/j8PQ0WhickxSBWNSiLMWPLDxM7gkRD8q7JQKxgIMnfSIpLSPbQ/pXXc2XM278HuiJ/84Cvz8+WYb+OOORo47kI6sXj2srEsnbYy5j6LzUJ6Virn3zmE5DQPvYZ2Iy0rfjGExWqh15D2/Pa2hb9+SeX0cwtjaOxb0BeXqnqrCOoqmYE5YGkKtT5FKEmJ3ZiJSQ1ACBfS1imsFXUgCjj2CRqKwB9InECMehtZjvR+B/aTmTNxESV5pfT/V5+4GXVr52/gg4e/oKzIQLZkP/ZsM+hxfRRx3Bv8nC17WPT7MkOVu8Zt6vPS1CdIyYhuhRiPuie0o2tfCwunOlg5z0OHk/b/ACpgPxWCS8NNyCveLGzsW3Q6wJuX5RDagCx6CJE+tlrXYmJyrCNSHkHmjUQPhVZ8NxRdnjj5rn0DpY+4TpQsY93CTWxelk3nM9pT7wRj0bJFU5bz6LAxCSdyHO6q2L+D4z6ks2lpdpSg2v7YHPZqG3vQF4fb9r2Ppm1UlsxKYueW/YqohBORcj8i6xfwXAfWtrryXspjentDq1HhRwD8U5CacVMGqe5BBtfocU8TkxqCsHVAZHwJ9tPQHSN9EVZkTEBY9+s4Z++JocEXbvLzezH/58XUb1GXTn2iJRgqkFLyn+v+L2Fj73DbGXHHkITv50hx3Hv4AV8g7h+1Vt20mNsL9hRRnFtMnaa1DcuwLe4B9LpQUvj2WP6YKBh8eT7JWe0QKY8jwjLIIvk2SL4t4jip7jC+YGEDbQ8oKRGbpboDWXiPXrwlbCBDSPeFiOT7zeIrkxqBsLVF1Hov/hhrU6SjL/hnEJkYYcHvS2HGj0m4kmycev5JcTNqdm7MiZl6HXU+IXC47XQb0Jnh/x6c2I0cQY5rg79h8WZevvYtw24yTo+Dc28aGLFtz9a9vHDVG6yavQ6r3YqmapxzXT+ue+FfMWOBjtSB9L3mFH5650dmTkvi7GsHV12Fa2kIoeguWoCu2KdEvoZKrRSZdwFo+ehSr+EQUfkXSLUQkW7q6JgcnUgtH1n2PngnAarutSddj7AY58RXhUh7GVn8LHgn6IqzMoi0deev3y/AW+Jj4NV9qtTKCQZCqHEE0ZLTPZw58jSsNiunX3QKbXq2OOpTMuE4NvglBaU8PPS5SvW6A7HYLPS9uDfdB+7Lzy0v8XJrrwcp3FuMpmqVcf9J7/xOcV4p9318a8y5UjOSOe2CM5j2+SzmTFxI7/N6xv1wiKTrkUX3h+P7+2MH51kR+vkAsnxCWAXwwCyeEPgnIdW7EJbYdQMmJkcKqe5F5g3TZUAqZIu945C+HyFjPMLa9KDmFcKOSH0cmXwPaLtAqcWKWTns2LCCnoNPJKth1dWxv/xvakxlXQChCHqffxK3vHbNQV3fkeS4jOHn7shjVNvbydtZYDjG5XFy57s3RhjmyR9Np7zYGyWF6vcGmDl+dtxV+oYt69Gpbzs2Lc1mzTzjlogAOAaB6xLAwb5nshWQ4J+HVvQ4Ut21b7zvB4wXqjSk99f45zMxOQLI0ldAKyRSoz4EshhZeBsyXo+HBBCKB2FtwY4NPpZOW0mzTk0SUqcs2F3ID28Yf2ekJukz4uRDurYjxXFp8F+/9X8U55XEHSOljPLC50xciK/c4I3AamH5zNVx5+zUpx0NW9dnwS9L2Lh0i+E4IQRKygOIzB/Bcy1Q0aotCHIveL9C5g5BhjbpmzWD8E8FobXx95uYHAl8P2HYmCe0Brm3H1KNrW6bKLuz9zLj69mk103j5KHdEgq7LJ6yvLIJiRGfPvX1IV3XkeKQDL4QopYQ4jchxPrwf2PKOgohVCHEkvC/Hw7lnIdKwBdg7k+L4jYsEIKYK/jx+koKRWB3xZczFkLQ54Je1G1Wm7++m88mg7aIleOtTcOhmgCRX4wQyFJk8eP6j/tnKcTCoNGKickRRVaRAaPtRuZfcdCe/p5tuUz57A88qW76XX5awgq2MYpmoli3cFOVTuPRyKF6+PcDU6SULYEp4Z9j4ZVSdgn/O/cQz3lIGHno+2N32bniiYuitg+4si9OA6OvhjS6D+xc5dxWm5UzLu1NnaZZ/PntPDYvj2/08U0kthckITAPLX80qFvjnRGxX2GKiclRg61TFQMkqFuRu3ugeSdXa+rcnflM+fQPXElOBlzZt7KrVCJ0O6tTlQ3JLRYlIVtytHGoBn8Y8FH4/z8CzjvE+f52ktOTSE43rlS12q08M/FBWnSJ9ppPOqcrHXq3xuGO9OQdbjs3j7064Q+V1WblzMtOpU7TLGZNmMf6RZuMB8f1gjQITAHV6Hg7OPoibG0Sui4Tk8ONlD5k+Xi0/OvQCm5G+n5DSt2YiuS7iWwQbkQ5FN2NDCxJ6Jz5OQX8/slMHG47A648HXdy9aTFUzNTuOiec+OKKbpTXGQ2qGW4/2jlUA1+HSllxephDmBUtuYUQiwQQswRQhzRh4IQgisej90h3u6089j4uw217BVF4ekfH+D6F66gYev6JGck0blve56Z+CBnX9OvWtdRYfTrt6jL7B8WsGq2QZzdVvVbgyG2bog0syrX5MggtXxk7mBd6TIwA/y/IYvuQeb/CykDYOsG7qvRq8urwo8sfaPKUQV7ivjt45mUFJSyZt56bu31IHf1fYw/vplTLS2qK5+4mMseGhHz0hxuO1c/cymKcuwtgVbZAEUI8TsQS+z5IeAjKWXafmMLpJRRcXwhRAMp5Q4hxAnAVKCflHJjjHHXA9cDNG7cuFt2dhXhjoNESsnnz07gi2cnYKlYnJFw4ytXVttwHyqqqjJrwjyyV26j0+nt6Ny3fcTCkgwsQOaPonrqmmGUOii1/zh8F2tiUg20glvBP4XokKQNnEP0ZIPAHKBqnRoARDpKnbmGu4tyi5n84XS2rd3JlM//IBQIVa7VOT0OTj63O/d/chublmbjLfXRvEvTKr3/hb8t5aVr3qS0oAyhKCiKYNQzl3LuTYMSu+YjwN/W01YIsRboK6XcJYSoB0yXUsaVnhNCfAhMlFKOjzfu7+h4dSDeUi+rZq9DsSi0792mSkW8hOct8zH+5R/56b0peEu9tOvVmisev5A2PVvGHK9pGnMmLmTDos20OaklPQZ1iTT6/hnIokf0L4gQ4TCPQXZDBAJRZ80xURBicvQg/TOQJf+B0DoQbnCNQCTdEl3/ITXQdoNwIJTI8IbUypF7ehKZcnmIWJqgZP0Wc1dxfgm/fjAdNRTiy+e+o6w4+iFid9pwehwE/SEUiyAUUBl269lc8+xlcb11KSVbV28nGAjRtH2jxBd/jxB/Z8erH4ArgTHh/34f4+TpQLmU0i+EyAR6Ay8c4nkPC64kF93OOoSQSQx85X7+fcpD7Fi/i4BPzy6Y/8tils1cySPj7uSkc7pFHaMoCicP7Y7NYWP17HV4S32cMqw7Nrv+ABKO0yFrhh6rlyrSNwnK3qfKL5OoZRp7k2qhlX8DxU+wr2lPMZR/ivTPgMxvK1ttauXfQumLoJUCKtLaGpH6NMLWbt9xhzXr2wmuS2PuKdhTxJRPZ6KpGnWa1kYatDgM+IKV38kKvn/9F6xWC1c/HXtu0MPATdo1OvhLP4o41L/IGOAsIcR6oH/4Z4QQ3YUQFaIXbYEFQoilwDRgjJRy1SGe96jl5/ensHNjTtQHy18e4KVr3kJVY6/+CyHoPqAzXc/qxNZV2/np3SkU7i1CVVV2bd5NUW4xwtocYWuFcI/U2yXGxQmeK+KOkOputJKxaPlXoRXdjwwsrc6tmtQwpAxASazOUkFQd+kV3VQ8FB4DLTc8NgihFcj8y5ChzfohSqau6XTQ7H+sC2ztEJ7Lo0bt3JjDL+9PRUo464o+esi9GkELf7mfCWMnHZMZNwfDIXn4Uso8ICroLaVcAFwb/v+/gI4Hjqmp/PrBNEMxtsI9RQzxXE7X/h255tmRnNApMj9eCEGH3m3IqJ/OzPFzeOmat1jxxypCQQ0tpNL8xGbc/f5o3dtI/whZeDPI0hiSsC5wnITwXGt4nTKwAFlwLcgQ+puCgvT+hPRcjZJ8xyH/HkyOQQKLMF5A9UL5x0j3JVDyAjHXlKQPWfoWIu0FhLAiPVdD6dvsk/9OFDu4r9Dj+8Ktt/d0Do4SAVy3cCNzJy0iLSuFMy87FU+qh9Y9WxAKJhLu3IdiUdi6ejutujWv5nUeexzdwahjjFAwROFeY+li0Nuhzf95MctmrOKlaU/Qunv0h6xeszoE/QEWTl4aoeexdt56bjvlId5d/gq1G3WGrJkQXIhU83XBtNByQEE4B4LtRMNwjpQhZMHNusZ+JRrgg7IPkI4zEfbDG+oyORaoogubugVZ9jnGBlwD/8x9P4raJLbWtD9OcA5CSbnX+DJCKvN+Xsz6hZuo36IufS48uXL9rV6zOvQYdCLzf1kc9ZZtOF9QxZPqrnpgDeDYyys6StmxYReXN7uJoioMPoCUeku0N257P+b+gC/AVy/8ECXeJCUEvEG+fkkvVhZCQdh7oLgGorjPRUl5SJdksHdFCIFUc9FKXkDb01f/VzwGqeaGMyOM4v8BpPfz6ty6SU3B1iX8xmeEhLK3QMZ7MAhk+WdoZR9CyZMk3spToIsD9kekPm04qqyojF8/mMb6hZvocFpbzrzs1Khkiwc+u41TzuuJzaEv0lZFnSZZNGhx8OqcxxKmwT8MSCl54OxnyM8pNFTYi8W6BZvwlh6oiAmblmUjDIo+QsEQcyYurPqa1F3I3HOg7CPQdur/yj9B5p6DDG3AONCpgZqT8D2Y1ByE4oGkG+MPkiWgZBnNALIQWTwGSl4k8QwdG3huQGRNQUl7BSFiS5Ts2rybSe/8TuHeYk6/+BS69usYM7vG4XLw0Oe389mWNxl41RlxGxxZrAr3fRJb5bYmYhr8w8DKP9dQuLsIqVU/xTWWpo/NYUOLM5caUquMU8riMSCL0NslVhDUt/lmgDTSErKDSELLPQctpwPanlPRSv9PX9AzqfEIz2j2ifUZkHwPeoXs/k6JQHciVPSQTyLhFBuQDClPoSTfibDErtuUUrLyr7X8/vFM7C473c7qxOLfl/Ptaz+xY8OumMcApNdJo1X35nHTKM+87LTjInZfgWnwDwM7NuRUq4qvgqxGGXhSPVHbm3VsjMegIMRqt9KodX0m/t9v7N2eF3OMlBr4fyO2ZLIGwblga03sJRwJ/j8gtB4I6N21St9E5l+rzxsHKSVa+Vf6QyKnDVpOe7TC2yOlnE2OaoQQ4BoOGKhFWuognIP0doOOviCSQKSRWLVsxUk8kHwvIuMLRJ05KO7zDYcGfAFmjp/DwslLadimPusXbebO0x/l3fs+4b37P+X6Tnfx0jVvommxP5unDOthKJTocNsZftvR36XqcGIa/MNA3aa1DUMw8cjbVcCuzbujtiuKwl3vj8ZxgPqmzWGjTpMsbnjpSkLBEL+8P5XZPy6IkVKmET92qkLam2BrDzj14hrhAZGK7qUdmIHhg9AyCOyr2pVSIkNbkaEtaGouWigXWXgTFD+sPyTQgCD4fkLuHRy/baPJUYVIuhFECtHmwYlIeQIhBMLWDiX9bZQ6ixC13tc/QwmhgEhGuK9C2DrFbb+5a9NufnxrMltXbafrWZ3I25nPjK/+qsynr/g3fdxffPPKxJhzJKV5uOW/o3C47RFJDE6Pg7NHnUnLridUecW+cj+//G8qz458lf/e+j7rFkaJBBwzHFKl7d/JP1Fpe7jQNI3Lm91M7vZcqvPrtNosDLlhADe/Nirm/jXz1vPxY1+xcvZanB4HA686g4vvHYYn1UPAH2Tp9JWsmbsem8NG1/4dadn1hMoPtZZ7TthLj3XiliiZkwCQwdUQWgNKJlLdDcVPY1jq7hyCkvYK0v8HsuhR0Paiv7pLdOMQ5w3AcS5K+kuJ/FqQ0g++n5GBxaBkIVzDENaaUfhyrCDVXciSl8A3GQiCrQsi+R6EPbpwUKo5yL39MY7ZCwgXbKHURqS/h7A2Njx3MBBk0e/LWTtvAykZyfQe3pOshhlcVO86wz6zqVkpfJ3znmFm2qo56/jqhe/ZvGIrtRtlcv7t59BrSNX6+Ls27+bfvR/GW+LFV+ZHUQQ2p41Bo87k5rGjjsrCxr9NWuHv5Fgy+ADZq7dz1+mPEfAF8Jb6sNqtCS3gNuvQmHeWHXzP2YLdhcz9aTF7sveS2aAWPc/pSmb9Wkj/dGTBbUR7605E+msIR9+ouWT517rQFdELyQA4BiI8Vx6kto8dpe6KKkfJ0BZk/qV6e0dZjh7nVSD5LhTPVdU8p8k/hZZ3GQQXE/1m6QLPKN3AW5rETRcGXcP+z2/nUZJfStteLTmxX0esNitqSOVsxyWGDpWiCH4s++ywyaNUcHPP+9iwaHPUmprT4+DBz2/n5KEx7eoR5e+UVjAJ06RtQz7f+hYzx89h/cKNZDSoReO2DXn6olfwe40XPFMykw33JUJ6nTQGXtWXTcuyWTh5KT+/O4VW3U+gy5knY0t9Tq+crOiNK1yQ/HBMYw+A/WQMQ0HCjXAORJa8yEEJucXz/sNIKZEFN+xrxg5ULv6VvITm+01/CNi6IDxXIczGLkcNIu0VZN5FuqSCLEeP6TvBNQiRdFuVnrDf62fJ1BWsW7AJT6qbAVf1pW7T2pX7FYuCO8VNWVHst0+Hx4EtTjbOwbBjwy6yV26PmUDhK/Mz4dVJR6XBj4dp8A8jdqed/pf3of/lfSq3vb30JW448W78ZdFG3+lxMHT0wEM+rxCC5p2b0qh1fZZMW8naeRvIXrWdrv070azTTBQtrJdvbYEQxq3bhLUh0nUOeH8m0qjbQKkDzgFQdM/BXaStS9VjQit0Ma6YKaMBCM4Pj1uL9H4D6a8jHH1ijDX5pxGWupA1Gbw/IQMz9Ti9a3iVHr2maaxftJnFU5YT9AVp3bMFXc7sEOWpCyEYOnoAE8ZOIuCNzACyO20MuWHAYQ+v5O7Ix2q3Gjps8XpYH62YIZ1/gJV/reX+QU8T8gcrO+k4PQ5O7NeRx765G4slfv/MWBTsKWL72p2k102jYcvIopH8nALmTlrE3m15pGal0OWM9jRu2zChL4SUKrL0dSj/CGQ4Pu8cgEh5FKGkoeV0pPql8goiYzzC1iH2Ob0/IUvHgrqFagmhiCRE7TmGedsm0cjQNj2X3noCQiTeBervYM/Wvcz7eQn5uwqo0zSLnmefSHqdNMPxAV+ABwY9w7pFm/CV6g6J3WnD5rBhc9rIapjBBXcO5YxLeh8W45+7M58rmt9C0B+dYiqEoPfwnjw2/u5DPs/hxozhHwXs2rybCa9OYun0laRkJDN09EBOG3FStZso+Mr9vHzNm/z5/XzsDhuhQIiGrevz8Lg7Iwx/haTr4qkrKM4tIaN+Ol3O7ED95nUTNPxBvZ+ukhJhGLTCe8JtFxOsoBQeSHsDxXFKzN1a6ftQ+hqG6wZx505CpL6McB56C0dd6ncPCHuU1G9NQAZXIYvuhVB2WNRMA/fViKRbEeKfTdYrL/Gy8LdlbF6WjTvFRbcBnWnavlHE57Iot5gtK7aRkpFE0w6NK/dJKVk8ZTkzx89m07JsNizeEmGQnR4HfS/uzV3vjT4s1/rosOdZMHlplNF3uO28NPVxQ8nzI4lp8GsQDw5+hqXTV0bohAhFkFwriY83vI4nJTI9TtM0Ni3LZtn0VZQWlpHVKIOOp7WlQct6B+UFSTUHmXseyPw4o6yQ/CDYO6PYjHXzpFaK3HMy1X9jCCPc+puHyziPOxF0qd+XQCsBVLC2CUv9tj2keY8WpLpTr7qWZQfscYH7XygpiXupUs2DwExkaBeEVkFoI1hqI9xXgOPMuJ+pYCDIqtnrWPnnWjRVo90prel4WptKGXCAgD/I2BvfYfq4P7E5bKghlYz66Tz85Z20OHFf29GCPUVc3nR0TL0ch9vBy9Nj61RVl7Lich4e8hzrF21GUzUsVgVNk9z6+jUMuvrMQ57/78A0+DWErWt2MLrbvQRixBSdHgejnr2M4bfGLiRRVZUNizaz8s+1lBaWkV4nlQ6ntqFJ+0bVfsuQ6l7k3j4Ye/lORNZvhpWTlfP4fkMW3acrfhpixViAywaOM0BJQjgGgqNP3DWKWETpv1cg3IiM7//xhWGp7kaWvgP+cNNu5yCE5zqEpXb8A+OgFT8F5V8Q+/foRNT+C6EY93mG8IJ66dhwHwZJVAqmcIFzKCLlqSijr4ZU1i3cxPKZq/CV+WnctgFdz+pESq3ohIVnR47lr+/mRcXN3Sku/rd6LBn19IZ6k975jbfu/Ah/DFljoQiG3TyIm8fGTnc+GNYt3Miq2evwpLg5ZVj3mAWTRwtmlk4NYdXsdYaNlX1lfhZOXmpo8C0WC617tKBF12ZsWbGNFbPW8Mc3c1kybSXte7emeeemKKHpyLK3Qd0GloYIz3XgOCvqCywsWUjrCcZ5/sICSlSnyxhoxI3ZK43AMxJK/gsc6J0KQK00jNL3C1iaQ61PEEpiRUBSqvGlfsveRKQ+n9BchwMZ2o7MOz/8AAwb5/LPkd4f9OYjlvoHN7F/FoYPTWGF0Gqw94h/bd7voOwDDN/GpBe8P4JrWOVcakhl84qtlW+XdZvV5sR+HclqmBFzir3bc5k5fjZqMNqRCPpDfP/6z4x65jJA/7xrodgOh9Qk5cUHESKMQ6tuzWuEBINp8I8h3MlOQ29cCEiuFd9LA93wN+/clBM6NWHrmh2s+GM1c35cyJJf36J1u1mc0L4QT7IGWh6y8B5wX4pIuT/6fJ6bkEUPEh17d4JrZGILqfaecdQZXeC5HsVzMdLeC1lwE8hCwBJO+5NEpHrKcgitQ5a8hEh9tOpzA6jZxJX69U2D1MSmiofUCkArBEt9hI4TtkUAACAASURBVDBWb5Qlz4U7Re2fwqrrH8niMYj016p/7sDCcJqrEdq+oqh4lL1B1essPmT5eHzBjqxbsJF18zfiLfVRq146/Yd2o94JdQxDPgF/kIeHjolp7AGC/iCLpyyHZ/SfO53eDsVqgRi1Lq4kJ90HJpAVdhxiGvxjiB5nn2ioGeJwOxg0al9MccvKbXz61HiWTFuBw2Vn4NVnMOKOIZUxfiEETdo2pHGbBuxav5Tlv45lySwbS//MosEJflp09NLgBC9K+WdI90UIa2QJunCFVTfL3tU9einRM3r6IZJvT+h+hJKOdF8F5R8TaUysYMlEuM/Vx9naQdY0CC4DLVdffJQlMWb0g3c8MuWhBEM7tjgicoAsRMu7FJH+FkIxzh4xPFzNQRY9AIH54Q5lEukaiUi+E3FAxzIpVfBPw1D/yP87UsqE112klMiSZ8D79b46jFiIJLC2q3pCdVuVQwr2Wli9NIfsLZNQQyoNWtajba+WcQ19Bf978HO2ro4vv5Gcsc+hadn1BNqc1ILVs9dFxPEtVgupmSmcen7PKq/3eMQ0+McQLo+TO98dzcvXvknAF6xU53R6HJw2ohed+uhf3BWzVnP/oGcI+gKVRSPjnv+OqZ/P4o35YyIWdoUQ1Ks/n7oXFlJcoLFhuYuNK11s3+jAlaTRvH2A5j1/IK1JtBFXkv+NdF8WNlQhsJ+CsDat1j2J5DuRljq6B6kVAQo4z0akPFjZP7XiOrF31kXqYhr7CkJ6BzChx1ilVoosewvKx+uLlrY2iKTbEY5TwdIQLLVB3Wo8XXAZsmA0IuOLat2X1MqQeReAlgeo4cbz6P1htXxwnIYsewfU7WCpD+5RxC9OU8P7E1yjCMyuwtgrgAOR+nxiWToiJay+GomUsGOTndULPeRsdWPxNKBlz6a0OaklqZkpCV2qGlKZ9M5vcSvTnUlOzrnurIhtT/1wP6/e8A5/fDMHm8NK0B+i42ltue/jWyIWgk32YS7aHmH8Xj9lReWkZqZgsSb2ZV63cCPjnv+O9Ys2U6teOuf/ezCnjeilNz2Rkqta38bODdGa9nanjcseOp+RD10QsV0rGRt+ZddRVdixycGG5S52bnYgrV2p3/Z8WnRtRuM2DRK+zuqgG/JSEE5DQS0pQ+Cfjiy6+4BuXfsh0hC154Z/Fz5k3gg9FTFikdEJKU+guIcjA/OQ+dcSv3rYGa4jaJXw/Whln4XXB2IZXAu6ZMT+53SBsMc0qgBY26Jkfp/4+QtuAv/vxgPsJyOSH0DY2iQ2X8nLBP+/vTMPj6rI/vdbvXc6IQuEJARI2FcBFRAFBEEFGQREUNRB5Ic7buOIuDuDitvgDCjCADKI+gUXVBQBFRFFkUUR2RECBAiBELIvvdfvj9sJCX07dEASJPU+Tz/pvvf27erK7XOrTp3zObmzMVu0m5LHLUjbZmPnLw4K84zYI320u9hAq36fYHOE0svXp+B4IaMa36Ub715Gz2HdeOajR3RdmoW5RRxNP0ZcYgxxieGsHZ3fqCidc5CCnEKmPzCX1YvWIYSmhDn8ob9wy1PXn1YiVhkZezK5q8sjIevqJjVPYP6eNyptk661yLy7dY1ocVEke9MnkLalHkV5xVjsFlp0TqFFl1RiE2JqTDxK+nOQx0dpgm1B4YVl2CHyHgyBIh7+4gVQ+BK6RrdC0pb0bEPmjA2sEeggHJpKpH1I2O3154wF949hH69RNuE+eaRr09xK1p7hf372cC1zWQ8RpY3sbVeGfT4pnWxf2oOYeA+H91rZsyUCl0tQP9FDy44lWK2SRhcvxFavQ9jnLMPn9TEsdgzOYv31lKi4SD7Keqva0WR1FRWlc47hcXt4sOdTHNmXVT6NdTs9fPDqYrLSj/HI3PGnfe7sjBw8rtBTY900ccslYEwF7x4qj4TNOGIa0anFjXTqJ8jce5TdG/exa0MaO9buJioukiZtk2nathENGtc/qz9Imfd3zf2hG20SEFizDQBDEv68RzSXjnsDVS40ujeCtQfC3AFp7QPOzwgZNWTQjywJSTgLoUF40XXZWK4+ZRRNEOYumgqqXn9JN5jCn60U5BSyf+tBJg5vTWLTUpq1L6VhsofcLCM7N0aw+K0GHEpzsDi/ZfXaGMBoMjLojitZMvNr3M7K16c1wspfnx6hjP0fhDL4tcDqRes4npET5LN0lbhZufBHRj97Awkp1ZsWg5Z6/urY6SELPhiMBi6+qlPQdiEExL2jLTC6VgVcC268hktZ8fEA0rbMpUmbZPrf0ps+Iy/FWeIiffshDu7MYOe63Wxfo8k3N2mbTJO2ySQ1a/iHun2kLwvcPxMytNCQCDFTIP9hLUyzXLzrVJw4n4i4Gen8Cv0bhEG7KVYDYR+OdK0hpNR0SHSiVNxfIHMOQ9z8oMXekJ/vGKPpDQX1mQUs3aqUJwYoyitm/7aDpG87yPHDuQA069SMPRv3cigtWJKh0+VtsdpPXT82FOMm38y+LQfYsfZ3nCWu8pmj1+3l/VcWU5hbxA2PDMEeeTo3UkUZyqVTC0waOYXVi9bq7rM5rNz7n7FcM65/tc/79fzvmDZ+dsipsTXCwsyNr9K4deh4bunPBV8mW9bk8uS1M5F+iavEVV5AYtLiiVzY70T2rNvlIWN3Jgd3ZpCx+wgelweTxURyqySatksmuWUiFtuZad1I92/I3LGhE7QMCWBqFSjOHm5N4eCEI3/eU+D8QOdYCyLubV0t+JBtlj5k7jhtFlHJV19WCrCaiAhE9EsI28Dw2+D6AZn3IOUhrNIP5k6BqKPgpKeSwlLStx9i/9YDHDuoVVNrkBxHascmpLRvTMHxIu7p+iilBaXlwQBCCKwOK/9Z/RwtOqdW/3tVbK+U7Fj7Ox++9jk/Ld6Az3ti4GKxmUlulcTrayef0Y2lLqBcOucYVRVVRogqa3BWxY+L14c09kIIrn9ocEhjv2vDHr56exVFecV07NWOWRPmVzpX2ZrAM8NeYeGh/5ZH+lisZpp1bEqzjk3xeX1k7svi4M4MDu06TPq2gxiMBhKbNaRRy0QSUuKJTYiu/vTc2PhElEuo/e71hG/s7RB5R3B2qSxE3yC7kQWTENVYNBXCCLGzkSXvQck7gTj8ZpocQdjtrNi2EmTJomoZfGHtBQ1/AteP2vqEqSPCfEL7RUpJfnYBR/Zlkb79EFnp2UgpiU2I5sL+F5DSoXGlbFhHtIMZv7zCvGfe56fFG/D7Jd0GdOG250eR0q5x9b9TBTL2ZPLOpI9Yv3QjRblFQbr3bqeHw2lH+Wreqj9EYbauogx+LdD/lt5aacKi4MgQv9dH90EXntZ5Ty6JWBGbw0pTnR+llJKp985ixTurcTvdSL9k9aK1IdcBpF/y7YIfGXzXVUH7jCYjjVsl0bhVEv6/+MnOyOHgzgwO7jzMz8s3AdridHyT+iSkxJOQ0oD6jeLK3T+uUhefTFvGkplfUVJYSptuLRn97Eja92iNtPbWau0GVVWyg20IeHdVcVMoi/oxaL79yPGIiL8GH+b6lpCjb+9upL8AYQgv1BBACDPCcRsECrdI12pk3kOnCCutgqri6UErNO9aCd69mpvLNgBhcEBAXK7cwO8/xtH9WRzdf4zSwDVYr0EUnfq0J6VDY2LiQ2ebJTVL4PF3Hji99odg39YDPNjzSVzFLl3t+TJcJS6W/+9bZfDPAGXwa4FuA7vQpmsLdqzbXUkXx+qwMurRoWHHL5/MlaP7sGbxBt1Rvi/EjeSHj9fxzburK2mSVLnoW+Iic29wyOfJFOUVs2nlVpzFLrr060h84ziyDmRzND2brAPZWtYk2k2ifnIc9RvFMmvCO2TsycQTSKT5+ctNbPl+O4+9+wA9h76MzLkNfHu1OPsyIx55L8J+LbJwcujGmDsjYmdrvn1D/dNUhzxNV0xFDAlVZBZD1WUi7VBFVI307EbmjAZcgRuDDVkwiSL5GkcPp3B0/zGO7D9GaaF207BH2UlsnkBiajwJqfFExUYGRVxlHczm/174mB8/WQdAz+su4eYnh9OwSYMqv6aUkt9WbWPjis1Y7BYuH3EpTdsmhzz+9fFzKC0Mr6jOyYu6iuqhDH4tYDAYeHH5k3w45XMWv7GcwpxCGrVIZPQzI+lzg76McDhcfFUnLujdjs3fb68UlmmNsDLmnzdgMhs5tDuT2ITocpfMR699HtINpIfNYaVJm9A/XoBPX1/KrInvYjQaApnBgs592vPsokdodoEmRuYscQVuAMc4diCbz2d8ycGdGfhO0kdxlbqZcvsMLr32LQz1F2lFUNw/a0WzbQO1whuAtA+G0iUESyXYEZH3aiNdTiF4Ze0Frm/QNeymZghD8MhX+ouRpZ+A8wtAaAJiEcMqJY2VIcytkcZk8KXpfIYNLL3AvZJgo28AgwNhv1632VJ6kbljcJfmkpttIjfLRvYRM0cPmikpeh4ixhARFUtCajyJzRqSmNoQo9mIz+vTNfSgFRC/t9tESgud5f+T5XNX8v2Ha5i+4WWSmusL45UUlvLoVZNI334IZ5ETo8nIgskfc824/oyfFlwDtrSolO1rf9c918mYreY/XYWpcw21aHue4fP6+OzN5Xw8dSn52YU0adOIGx8dyrqlG1m18EeMJiNer49ew7rz4Mw7ubPT38k6EH7lHke9CBZk/Be7Q794xsYVm3lm2CtBKoYWm5krburFI2/dq/u++3s8wc71+mJsJouJQbf3p/2lbYhNiNYeiTHUqx9Vvh4gpROZe1/Aly9BGLRFyqi/YXCEp5oovXu07NigfAQbInYWwtqj8vH+HO1433FORPfYwZiAqP+h/g3Cu0/LJ5DOwHsMgAUibsZQ7zH83iNQ+M+A+8oI+MByMSL6xXLxNCklhblF5B7JI/doPjkHfyAnfSHF+SdulrYIPwlN3CQ0ESS0HUNsyr0IIdi7OZ1p4+ewc/1uBIL4pvW5+19juGxo5bDPZ4a9zNolv5Rnc1ekfqNYJs6/ny5XdAwy4C/f+jrffbgmaJZoc1h5aOZd9L+ld6XthblF3JB4e3lhoFAIgyAyxsFb2/5dZZEUhUq8qtNIKfl732fZtWFPJc0Rs9VESvsmxCZEsyHgX9fD5rDiLHFhd9gwGA1MXvYk7XuEjuF+pN8/+G3VNt19FpuZDzJn60rL3n3hBNJ+26/7PmuEhZF/H0JcYgz52YXlYadGk5Ho+HpEx9fDER1BZEwEDsdRHPbtOGLqYYq6strFTKRnl6ZB416vbTC102QedOLg/XmPBorBnOymMYN9JIbof+h/hr9YU8D0rAURh4gYgTBXTljy+124iw9SUmSmpNBMUV4xeVkF5B7VjHxZSK8Qgnr1thAT9RUx8S7i4j3ExHuJiPRTbottQzHEvMqh3w+Xj9orYo2wMPHt++l9fY/AZ/sZZLupUpTMydgirPT7a28emnFnudEvKSxlZMI4XY16gGYXNGXWb1Mq94WUjGl9P5lpR3XfIwwCk9lI2+6teHjOPUHV3RTBqCidOsz2n35n98a9QT9Cj8tLxu5M+t/SK8gFBNr0ufugC+k9vAeH046Q1DyB3tdfcsqQuPTth0LuM1lMHE3PpnmnYIPfY/BFHNiZoZteL/2SEQ8PxhHtwOfzUZBdSE5gdJt7JI9jB7LZX1BSYTSqrYHYHKuJjHHgiHGcuCFER2CNsGKxmbHYLFhsZowmY7nREuY2iLj52gIogD8XWTQTmfeANmOwXYlw3APGJHAupczYF+Ub+GZRLGlb7SQ2dXP1qM9p2OUfuv0gseM1Xo/TNZji/BKK95VQUrBde17hcXKehsVmJiYhhpYXNiuf5cTE18Poi0Lmfx4iA9kCAX2jdyZ9qJuB7SpxM+PhefQafokmSeGX+H1VDwSdJS5WvreaXtddQreAMmXOkbzAAry+wT+aHjyTFEJw16u38uJfpwa1zRph4bH5D3DB5e1Oe11LURll8M9zNq3cGrIIc2mRk+zDudw9ZQwz/jYPg8mI3+tDGARtu7di4tv3hZ3o4nZ5KMguIC4xmrwsfT0Yj8tLbIJ+BMjQ+65h8Ztf4nV7qTjrtEVYGTJ+QPmswGg0EpsQEzSt9/v9lBaWUpRXQlFeMcX5gb95JeQeyePQrsNB6wNlGIwGrHYL5go3AYvNjNlSiKn0Bc3FI3wIAUJ8CWIVot6TUGhFCDPpv9uY81wSfh943EaMJj/v/RsG3TGHNt1a4nF58Li82l+3V1ckTCIxW0xExUUS3SCKRi0ScERHEFFPu0k5oiOwR9p0/e3S1I/QP2UDwq5pJ61f9mvIpLyC7EKOHcymYdN4jCYjzTunkLZpf4hzajiLXXw2fXm5wY9LjAnZxwAJKfqLvT2HdefRefcx42/zKMwpQkpJfJMGPDTzTrpcoV8HWXF6KIN/nlM2gtUzMgajAZvdyuC7rqbPDZexZvEGSguddOzVtlI5uapwuzy89fh7LJ29AumXeL0+hFEgTxohGoyCjr3ahvS/xibEMG3NC7w69k32/LoPk1kbdY985FpuflJ/sbLS+Q0GHNEOHNEOElLi8fv9bFm9g9JCJ+0va03LC5vhLHZRUlCCq9SN2+nB7fTgcborvXY73bhL3RTlFuPMXYS31A9YQVIeGy6lAMN7SF8CPm8RH82Mx+M6Efnj82rPv5i9goTUeOonxREVZ8JsNWOymLBYzZitJix2CxH1Ili75Gc+ePUzcgMj5H439+LOV0frVoTSQwgLxM4JJKf50NYGrICA6H+VVx4zGENHJ/ml1PTlA9z56q08M+SlkIOFMnIyc8ufR0TZufyGy/ju/TVBMzWbw8qoicNCnufyEZfS+/oeHE0/htFkpEFyXI3pNNUllME/z+l5XXfmPbNQd5/JYqLPDZcCEBUbyYDbql8MfNKIf1U5iyhD+mHUY9dVeUyTNslMW/MCOUdyKc4vISG1IRZr9WVu921J58m/vEhRfnHgsyVJzROYvPQJGiSHr4njPzKB4Lj/MrIh6llWL3wdo0ni0Ql0MghBSaGTGx7pHbwzwLvPfcj7Ly/GGVjk9vv8fPPu92z5fjv//W0KtojwskqFpTPEf48s/VzLSTA2RtivQxhPfN/LR/Rg2ZyVuqPwxNR4GjQ6sd7RuW97bnzsOha99jnF+fryECazkfaXtam07YE3xnFo12H2bz2As9iF0WTEaDYycOwVXHFTr6q/gxAkpp5+KUfFqVEG/zynUYtEhowfyJKZX1UKv7Q5rPS7uVd5mOTpsGfTPjZ9e2pjD9ri3PQH3uKtbf855bFxibGVZG4Ppx1h8fTl7NucTnKrJIaMH0izjvpaMCWFpTzc91mKciv7s9O3H2JC/38yd8fUsEaOmlvpFBmx9mvJPr4Fn2en7m6P28vhPZkh316cX8yCFz8Nii33enwcz8xjxTvflye45RzJ5dPXl7F2yS9YI6wMur0//f96eaUbojBEIhw3hfy8W54aweqP1lGUV1RpQdYaYeXBGXeWv077bT9PDJpMaVEpfq8fg0HoJkSZzCaGP/iXyl0SaWfamhfY/N12Nn6zBavdTO/re5wylFdRMyiDXwe485XRtOnagoUvfULmvmPEN6nPjROGcuXoy8/ovBu/3hyyJJ0eR9OzSd9xqFpp+Ks/XsfLt07D5/Hh9fj47bvtfDX/O+55bQyD77o66Phv3lut677y+/wcP5zLryu3clH/C4L2n4wQAmnuBJ4QEUzGVAwGB00uGIHJ8hoed3DikMVuoXmn1JCf8dt32zFZjOi8FVeJi6VzVrBr/W52/ZzGwZ0ZIET5d9u/5QBfzPqaKav+Gba2TINGcczY+Arznl7I6kVr8Xq8dOzVjnGTb6ZNN03psrTYySP9/hF0wyzDHmVDIDCajTz9wcO68fhCCDr37UDnvtWXSlacXZTBrwMIIeh7Y0/63hi+nno4mMwmzS8cptE3mY0UZIcvK1CcX8zLo6dVmkH4fX7cpW5m/G0e3QZeGKQqun3t7yETyTxuD2mb9oc0+F6Pt3LETtQEZM44gouj2BD1JgJw8dWdcMRE4Cx2cXKIs8EgGDA22E1WUlhK5t6jFOaEEIMLsOfXfaRt2q+70OoscbF74z6ev/HfTPjfeOrVD8/fH9+4PhP+N54J/9OX4P52wY8hK09ZHRYG33U1Xa/uTOe+Hc5KIRzF2UWJTCtOm8uGVU+j3ePyYLaamfXoOzx342t88Opi8rMLQh6/etE6hEHf/SL9kq/mrwra3iA5DpNZ3xCZLWZiGgaH9333wRrGtL6fQbab+UvEzbxy2xvkHctHWLohYt/UxNmwaQ9DorYQau0LaFFDr654lrikGOxRdowmI/ZIG/YoO8999hixDU9EJXncHqaNn83IhNt5uM8zTL1ndpWSAlp4ZOhYeL/Pz9ovfuGW1HvY8GXoXIrqsPuXtNA3zFIPkTEOLrqykzL2f1LOaIQvhBgJ/ANoB3SXUupmSgkhBgJT0VIH50gpXzqTz1WcGySmNuTae67mi1krTinPYDQZaXFhKn+/4ln8Xs09s27JL7z73Ee8uPwpOpy0+AeQezQ/ZBKPx+3leEZO0PaBY6/g4/98oTvrkH5Jr+sqF7dePH0Zsye+Wx4D7nF5WbngB35btY1Zm6fgqNcLGnwDvgzAD8YmQWsAjVs34r39M1i/7FcO7MigQXIcPa/rHrTg+sqYN/jps5+1SKAqpGMMZZIU4eRESi08ctKIf/Fe+oywI3tCEd+0QXl92JOx2K3EJaos1z8zZzrC3woMB74PdYAQwghMB64B2gM3CSHan+HnKs4R7vrXGB548w6atGmEyWJEdz1UQJcrOpD2637cpe7yNHpXqZvSIidPX/siXk+wgWneOQVrhL4CqM1ho233VkHbk1smMW7yTVjtlvIwRJPZhDXCwhMLHqqUV+AqdTHn8f8LSvjxeXzkHytg6WytJqwQAmFqjDA1DbngazQZufTartz46FD639I7yNgf2Z/FmsUbwlrgjox1VFunTfolK94N+TMMm6tG9wn5HaWU9B7RQ3ef4s/BGRl8KeUOKeWuUxzWHdgjpdwrtfTFhcDQM/lcxbmDEIKrRvdh7o6pLHMuZO6OqVx1ax9iE2OITYyh742XMXvzFFI7Ng2Zqu/z+lm/7Neg7V0HdA7o5VQ2QEKAxWai7yj9NYnhDw5m6poXGDD2Cjr37cDQ+wYwe/NrQcJbO9buDjp3Ga5SN98u+CGcLgiLLat3hO0GKc4rweaoXpEPV6mbw7tDRwSFS3zj+jzw5h1Y7BaMAdeY2aLdMJ9a+Ldy0T3Fn5OaWLRNBg5WeH0I0K0XJ4S4E7gToGnTqkuwKc5NGrduxKPz7gvafmRfVsgsTJ/XV15GryJGo5Ep3/6TJwa9QNaBbG3kKSAyJpLJS5+oMka9RedUHp519+l/kT8Ym8MWcj3iZMxWE7YIK26np0offuXzW2narsmZNLGcAbddQYeebVky80sO7cqkeecUBt91FQ2bVr/spuLc4pQGXwixAkjU2fWklDL8EkBhIKWcBcwCTTztjzy3onZpdXEzNiz/VdcnbzAaaNpOP047ISWeOVv/zc71ezj0+2ESUuLp2KvtaRW1llLyzXur+XDKZxzPyKFRy8TQESl2yykThapD1wGdqxQjq4jBYOD/Tb6FxdOXcej3TIwmA36fn/qNYjl+OFd3vUQYBP1v+ePa27hVEndPue0PO5/i3OCUBl9KGbrqQnhkABWHHo0D2xR1iEG3X8nClz4N2m4wGohLiqXT5aGXdYQQtLukFe0uCfbZV4cpt8/guw/WlBvM/OzCkKPuyFgHg+4400v/BHaHjfvfGMfr983RFTCriM/np++oy7hmXD/2bk4nY88RElPjaXlhM/b8uo+JVz+H1+2ltNiJPTBzeGHJ47oqpApFRWrCpbMBaCWEaIZm6EcBN9fA5yrOIWITYnh+yeM8O+wV/H6JLxDzHpsYwytfP33WdVN2bdjDqvfXBOn06+m9CyGIaRgdlr+6TDQuKi7ylAlQA267gkYtEnnvhUWkbdqPs9iJ1+PF6z7h6rJGWBg/bWx5vYHmnVJo3ulENnSri5qz8NB/+eGT9WTsziQxtSG9R/QIW4JBUbc5Iz18IcR1wOtAPJAHbJJSDhBCNEILvxwUOG4Q8B+0sMy5UsoXTnVupYd/fuJ2eVi35BeOZ+aS2qEJnft2qBGRrDcf+h+fvrFM18DrYbVbmL7hJVLa6/vF3S4PsyfMZ9ncb0FKJNBvVE/unTo2bIVRr8fL5zO/4tPXl1FwvJDmnVIY/cxIpRCpOCNUARRFnWfK7TNYPndl2MdH1LPz2DsPhCyp9/jA59m8ejvu0opFZcw079SUaT9NPq01BoXij6Aqg6+uSkWdoOuALtgj9csy6uHz+klspq/cuOvnNLb8sKOSsQctkzh9R0Z5gXaF4lxDGXxFnaDnsG7EJsaElF2oiMFoILlVYkhFzl9XbMark4kK4Cxysm7pxjNqq0JxtlAGX1EnMJlNTP3xeS66qjNmq5mIenYsNjOtuzYPVLfS4hfskTbikmKY9OnEkOcymk2IEMVEhEGUn0uhONdQV6aizhATH80LSx4nP7uAnCN5NGxSH0e0g6wDx/jmvdXkHSugfY/WXDasG2ZL6MIrPYd1Y97TC3T3WWxm+txw2dn6CgrFGaEMvqLOEd2gXqWi2A2bxnPT48PDfn+jFokMur0/y+d+W16pCrRCIpcO6Urri1v8oe1VKP4olMFXKE6De6f+P1pe1JyFL31K1oFjxCXFMuLhwVx7z4DabppCERIVlqlQKBTnESosU6FQKBTK4CsUCkVdQRl8hUKhqCMog69QKBR1BGXwFQqFoo5wzkbpCCGOAeln6fQNgOyzdO4/O6pvqkb1T2hU31RNTfVPipRStzzZOWvwzyZCiJ9DhS3VdVTfVI3qn9Covqmac6F/lEtHoVAo6gjK4CsUCkUdoa4a/Fm1hRYsUwAAA11JREFU3YBzGNU3VaP6JzSqb6qm1vunTvrwFQqFoi5SV0f4CoVCUedQBl+hUCjqCHXC4AshRgohtgkh/EKIkGFRQoiBQohdQog9QojHarKNtYUQIk4I8bUQYnfgb2yI43xCiE2Bx2c13c6a5FTXgRDCKoR4P7B/nRAiteZbWXuE0T+3CSGOVbhebq+NdtYGQoi5QogsIcTWEPuFEGJaoO82CyEuqsn21QmDD2wFhgPfhzpACGEEpgPXAO2Bm4QQ7WumebXKY8A3UspWwDeB13qUSim7BB5Daq55NUuY18E4IFdK2RL4N/Byzbay9qjG7+T9CtfLnBptZO0yDxhYxf5rgFaBx53AjBpoUzl1wuBLKXdIKXed4rDuwB4p5V4ppRtYCAw9+62rdYYCbweevw0Mq8W2nAuEcx1U7LOPgP5CCFGDbaxN6urvJCyklN8DOVUcMhSYLzXWAjFCiKSaaV0dMfhhkgwcrPD6UGDb+U6ClDIz8PwIkBDiOJsQ4mchxFohxPl8UwjnOig/RkrpBfKB+jXSuton3N/J9QGXxUdCiCY107Q/BbVqZ86bEodCiBVAos6uJ6WUi2u6PecSVfVNxRdSSimECBWnmyKlzBBCNAdWCiG2SCnT/ui2Ks4LPgcWSCldQoi70GZD/Wq5TQrOI4MvpbzyDE+RAVQciTQObPvTU1XfCCGOCiGSpJSZgallVohzZAT+7hVCrAIuBM5Hgx/OdVB2zCEhhAmIBo7XTPNqnVP2j5SyYl/MAV6pgXb9WahVO6NcOifYALQSQjQTQliAUcB5HY0S4DNgTOD5GCBoNiSEiBVCWAPPGwA9ge011sKaJZzroGKfjQBWyrqTwXjK/jnJJz0E2FGD7TvX+Qy4NRCt0wPIr+BSPftIKc/7B3Admq/MBRwFvgxsbwQsrXDcIOB3tJHrk7Xd7hrqm/po0Tm7gRVAXGB7V2BO4PllwBbgt8DfcbXd7rPcJ0HXATAJGBJ4bgM+BPYA64Hmtd3mc6x/XgS2Ba6Xb4G2td3mGuybBUAm4AnYnHHA3cDdgf0CLcopLfBb6lqT7VPSCgqFQlFHUC4dhUKhqCMog69QKBR1BGXwFQqFoo6gDL5CoVDUEZTBVygUijqCMvgKhUJRR1AGX6FQKOoI/x+u4dw7FWwz3wAAAABJRU5ErkJggg==\n", | |
| "text/plain": [ | |
| "<Figure size 432x288 with 1 Axes>" | |
| ] | |
| }, | |
| "metadata": { | |
| "tags": [], | |
| "needs_background": "light" | |
| } | |
| } | |
| ] | |
| }, | |
| { | |
| "cell_type": "markdown", | |
| "metadata": { | |
| "id": "yrbR-SKsK80j" | |
| }, | |
| "source": [ | |
| "Berikut hasil yang didapat untuk non linear." | |
| ] | |
| } | |
| ] | |
| } |
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment