Demonstration of Uber's H3 DGGS which I did at the Palmerston North Regional GIS Forum (May 2022)

chalet-demo-may-2022.ipynb

{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# H3 Demonstration\n",
    "\n",
    "h3-py: Uber's H3 Hexagonal Hierarchical Geospatial Indexing System in Python\n",
    "\n",
    "## Installation\n",
    "\n",
    "From PyPi (conda is an option, too):"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "pip install h3"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Basic usage\n",
    "\n",
    "What's the cell ID for The Chalet?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import h3\n",
    "theChalet = (-40.36733404184009, 175.62988653271506)\n",
    "resolution = 12\n",
    "cellId = h3.geo_to_h3(*theChalet, resolution)\n",
    "cellId"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Do the reverse: what's the coordinate of the centre of that cell?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "h3.h3_to_geo('8cbb2b66e3723ff')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
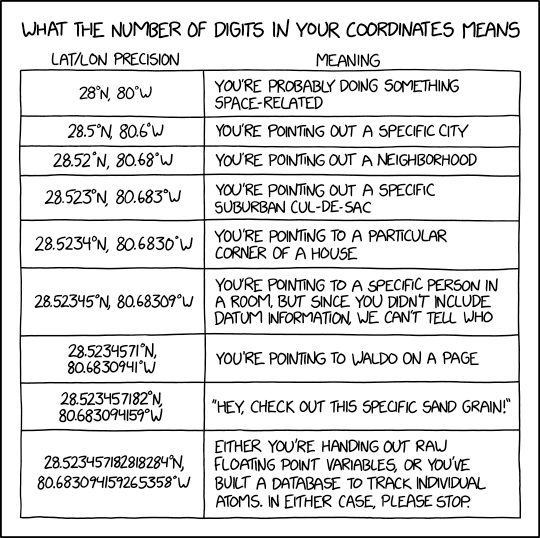
    "This is not the same as the original, so we have **lost information**. However, perhaps what we have really done is **discarded useless information**? Do we actually know the original precision of `theChalet`? I just clicked on Google Maps to get it. I never wanted the precision of my mouse click recorded to **thirteen decimal places**.\n",
    "\n",
    "![40 digits: You are optimistic about our understanding of the nature of distance itself](https://imgs.xkcd.com/comics/coordinate_precision.png)\n",
    "\n",
    "The DGGS _resolution_ allows us to be explicit about the claim we're making of a geographic object's precision."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Add some extra dependencies just for visualiation purposes — these are not strictly required for working with a DGGS.\n",
    "- `shapely`: geometry\n",
    "- `pandas`: data analysis library\n",
    "- `geopandas`: geospatial datatype extensions for `pandas` (uses `shapely`)\n",
    "    - `folium` interactive maps in a Jupyter Notebook\n",
    "    - `mapclassify`, `matplotlib` other dependencies for geopandas to show interactive maps, get colours, etc."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "pip install shapely pandas geopandas folium mapclassify matplotlib"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "What does that DGGS cell of the Chalet look like?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "from shapely.geometry import Polygon\n",
    "import geopandas as gpd\n",
    "\n",
    "gdf = gpd.GeoDataFrame({\n",
    "    'thing': ['The Chalet'],\n",
    "    'cellId': cellId,\n",
    "    'geometry': Polygon(h3.h3_to_geo_boundary(cellId, geo_json=True))\n",
    "}, crs=\"epsg:4326\")\n",
    "gdf.geometry[0].wkt"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "gdf"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "scrolled": false
   },
   "outputs": [],
   "source": [
    "gdf.explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Polygons in H3\n",
    "\n",
    "Points can be represented as a cell (at a specific resolution).\n",
    "\n",
    "What about polygons? I have roughly traced the Chalet's building footprint from OpenStreetMap and copied it here. Then I do Python magic to convert it to a GeoJSON object for use in GeoPandas.\n",
    "\n",
    "Again, note the absurd coordinate precision."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "chaletPolygon = Polygon([\n",
    "    [175.62980128436485, -40.367208360351114],\n",
    "    [175.6298267653505, -40.36723901433664],\n",
    "    [175.62987035124698, -40.36721755654824],\n",
    "    [175.62991728990474, -40.36722113284678],\n",
    "    [175.62998970954814, -40.36730696395485],\n",
    "    [175.62989516168037, -40.367360097443175],\n",
    "    [175.62983347087302, -40.36735294486065],\n",
    "    [175.62980530767837, -40.36732739991685],\n",
    "    [175.62977513282695, -40.36734425958085],\n",
    "    [175.62970874815383, -40.36733812879443],\n",
    "    [175.62962023525634, -40.36726302661556],\n",
    "    [175.6297496518413, -40.36720325135217],\n",
    "    [175.62980128436485, -40.367208360351114]\n",
    "])\n",
    "chaletPolygonGeoJSON = gpd.GeoSeries([chaletPolygon]).__geo_interface__['features'][0]\n",
    "chaletPolygonGeoJSON"
   ]
  },
  {
   "attachments": {
    "Screenshot%20from%202022-04-28%2010-12-26.png": {
     "image/png": "iVBORw0KGgoAAAANSUhEUgAAApAAAAFCCAYAAABGq+3pAAAABHNCSVQICAgIfAhkiAAAABl0RVh0U29mdHdhcmUAZ25vbWUtc2NyZWVuc2hvdO8Dvz4AACAASURBVHic7N17XFTV3vjxDzPA4G1UUBQBNRA163jXx5TfyfIe4hXEu+ZRRFQUL3k0zaPmLcUUVKqTmpmWWGpHDZIw7ahloeQVL4kgIIKKcVUYh/n94cN+HBgug3ipvu/Xq1ey99prrb32Xnu+s/baeyycnJwMAAaDAQsLC4r+WwghhBBCiEepnnUFhBBCCCHEH4sEkEIIIYQQwiwSQAohhBBCCLNYVmQjg8FQ2fUQQgghhBDPQEWeeykzgJRgUQghhBDiz8tUrFdWUFliAFmYWdH/CyGEEEKIP6eigWNJgaRl0QSPBowGgwFra2s0Gg0WFhbyah8hhBBCiD+pwtgvLy+P/Px8o7ivaAxoWXTDRzOoUaMGKpU8ZyOEEEII8WdXOFhYpUoVNBoNWVlZyvKi7wgvFh0WBo9arVaCRyGEEEKIvyCVSoVWq1XiwmLrC/9RmKBw5FFuVwshhBBC/HVZWFhQo0YNoxixkNEQY+GcRxl5FEIIIYQQKpUKa2vrYqOQKsAoqtRoNE+/dkIIIYQQ4rlUGBs+Gi8WG4GUW9dCCCGEEKJQ4UM0jyo2B1ICSCGEEEIIUagwgCxxDqQQQgghhBBlkQBSCCGEEEKYpdgcSCGEEEIIIR5VbA6kBI1CCCGEEKK8DAaD3MIWQgghhBDmkQBSCCGEEEKYRQJIIYQQQghhFgkghRBCCCGEWSSAFEIIIYQQZpEAUgghhBBCmEUCSCGEEEIIYRYJIIUQQgghhFkkgBRCCCGEEGaRAFIIIYQQQphFAkghhBBCCGEWCSCFEEIIIYRZJIAUQgghhBBmkQDSDL179+b48eMcP34cFxeXZ10dIYQQQohnQgJIIYQQQghhFgkghRBCCCGEWSwcHR0NAAUFBej1emxtbZ9YYZaWlvTp04cePXrQpEkTatSoQWZmJqdPn+aLL77gzJkzRul79+7NO++8A8CwYcNwc3PDx8cHV1dX9Ho9sbGxbN++nRMnTpgsr0mTJgwfPpx27dpRq1YtsrOz+fXXX9m+fTsXLlwwSmtvb8/evXsBWLVqFceOHWP8+PF06dKFTZs2MWvWLJNlfPLJJ3z00UfFtt+zZ49Ruk6dOrFmzRoApkyZwqlTpwCYN28effv25e7du3h4eNCnTx+8vLy4ceMGCxYsULa3srJi0KBB9OjRg8aNG6NWq7l+/TpRUVHs3LmTvLy8ch0DIYQQQghzpaeno1arUakejj1aPq2CHR0dWblyZbG5g7Vr16Zr1668+uqrLFmyhIiICJPb+/r68tprrxkta9++Pe3btyc4OJgvvvjCaF3//v2ZNWsWarXaqKzXXnuNV199lffff5+vvvrKZFkvv/wy/v7+VKtWrSK7WiEWFhYsXryY7t27A3Dr1i1lXe3atQkKCqJ58+ZG27i5ueHm5kb37t2ZNm0ad+/efWr1FUIIIcRf11MLIB88eEC9evW4du0ae/bs4fLly6jVatq0acPo0aOxtrZm+vTpREZGotfri23/2muvcfz4cSIiIsjJyaFDhw54eXlhaWnJlClT+PXXX7l48SIAHTt2ZPbs2ahUKs6dO8emTZtISkrC3t4eHx8f/v73vxMYGEhcXBwxMTHFyurTpw/37t1j//79XL9+nV9++YVJkybRsWNH3nzzTQAWL15MSkoKN2/erJT2qVWrFt27d+fixYscPXqUa9euAQ8Dy2XLltG8eXPy8vL45JNPOH78ODqdjtatWzNx4kSaNGnCokWLCAgIqJS6CCGEEEKU5qkFkKmpqUyZMoXffvvNKECMiYnh/v37TJkyBa1WywsvvMBvv/1WbPt169axc+dO5e8ff/yRa9euMXfuXFQqFT4+PixatAiAgIAAVCoVV69eZfLkyeh0OgCSk5OJiYlh9erVdO7cGV9fXyZNmlSsrMuXLzN79myjUcDExEQcHByM0sTFxT1+w/wvg8FAUFAQu3fvNlretWtXWrVqBcCyZcuIjIxU1sXHx3P58mU++ugjZTQ2Ojq60uokhBBCCGHKU32IJjExkWHDhrF06VJWr15NQEAAbm5uXL58WUlTo0YNk9v+9NNPxZYdOHCApKQkANq2bQtAo0aNlNvke/bsUYLHRxXeum7ZsiW1atUqtv7rr782Ch6fht9//71Y8Ajw+uuvA3D37l2j4LHQhQsXlJHXv//970+2kkIIIYQQPMURSFdXV4KDg6ldu7ayrHPnzvj4+HDs2DFlmYWFRbnzLCgo4MqVKzg5OWFnZ4eFhQXOzs7K+lmzZpX48EthWU5OTvz+++9m7s3T4+TkBDycB3n8+PFS0zZs2PBpVEkIIYQQf3FPLYCcOXMmtWvXRq/Xs27dOr799lsePHhAu3btmD59eqWV82gAmpycTFZWVqnpDQZDpZX9JBTuT15enjIvsiRpaWlPo0pCCCGE+It7KgGkWq2mZcuWABw8eJAvv/xSWXf06FH0ej1BQUFm56tSqXBzcwPg9u3bGAwGEhMTlfUHDx7k3//+92PW3nxWVlaVlldSUhJNmzbFwsICf39/7t+/X2l5CyGEEEJUxFOZA6lSqZT3BmVmZhZbb2qeYlGdO3cutqxfv37KLd7C9yrGx8dz/fp1AAYOHIi9vX2x7SwsLKhTp075d8CEokHio4FdYVD7aHmm6l8eR44cAcDa2pp//OMfJtPUrVu3QnkLIYQQQlTEUxmB1Ol0XLlyBTc3N3r37s2+ffuUJ5hr1qzJsGHDysxj6tSptGvXjsjISHJycmjfvj2DBw8GQK/XGz2hHRISwnvvvUetWrX4+OOP2bRpE2fPniU/Px83Nze8vb2xs7Nj9OjRZr2AOyMjQ/n3yJEjiYyMRKfT8eOPP5KZmUl2djbVq1end+/e/P7775w5cwatVkvfvn2VJ6nNFRUVhY+PDy1atGDEiBHUq1ePvXv3cuPGDWrXro27uztDhgwhODiYffv2VagMIYQQQghzPLU5kOvXr2fNmjXUrFmTrVu3EhcXx4MHD2jSpEm53qW4f/9++vbta3Ikb/369Vy6dEn5+9ixY6xevZoZM2ZQp04d5syZU2ybjIwMGjZsyJUrV8q9DxcuXCAnJ4dq1arRrVs3unXrxpkzZ/jxxx8B2L17N6NHj0atVjNixAhGjBgBPHzYJyoqim7dupW7rEIFBQXMnj2b1atX8+KLL9K9e3flZeOPevnllyWAFEIIIcRT8dQCyMKXcY8fP55WrVrRsGFD4uLiWLduHUlJSaxdu7bU7bdv387Ro0cZMWIETZs25cGDB8TGxvLZZ5/x888/F0u/Z88efv31V4YOHUqHDh2ws7NDp9ORmJjI8ePH+fLLL83+5ZaMjAzmzp3LlClTaNSoERkZGfz666/K+k2bNnHv3j369OlDvXr1yMnJ4fTp02zbto1atWpVKICEh6/w8fPzw9PTk549e+Lq6opGo+H333/n3Llz7Nu3TwlihRBCCCGetKf6W9jmKvpb2AkJCc+4RkIIIYQQfz1Ffwv7qb5IXAghhBBC/PFJACmEEEIIIcwiAaQQQgghhDDLcz0HUgghhBBCPHsyB1IIIYQQQjwWCSCFEEIIIYRZJIAUQgghhBBmkQBSCCGEEEKYRQJIIYQQQghhFgkghRBCCCGEWZ7ab2GXpFmb/ljbVOdSzH/Iv5/1rKsjhBBCCCHK8ExHILsOWkLXQYvp/MZbNGvT77Hzc3JyIiwsDHt7e5ydndm3bx/W1taVUFMhhBBCCFHomQWQXQctoVmbflyK+Q8AmipaZZ1d/WZMXHKaZm36m5VnUlISERERbNmyhWXLlvHhhx+Sn59f7u379evHq6++alaZQgghhBB/Nc8kgHw0eDy8e0Gx9XduXuJ2yiW6DlpM4xdfMyvvzZs34+HhwahRo9i/f79Z2/bq1Yv09HSztqmopUuXMnDgwKdSlhBCCCFEZXoqcyBr1HakXdeJ1KjdAI2NFjuHZiaDxxq1HencZzbf717Avs3/wGtyGK8NWsL2oD7lmh/ZqFEjAgICeOmll1CpVJw9e5bVq1eTkpJS5rYqlQpHR0cuXLgAgJubGwEBAbRo0YKCggJOnDhBUFAQd+/erVgjmOlZly+EEEIIUZKnMgLZdeBimrXtD1iQdz+LM8e3mxx5BGj84mv0G7eJ/PtZHP/mPaxtavDCi6+Xq5ygoCD0ej0zZsxgzpw52NnZMWXKFGV9eHg4AwYMIDg4mE8++YSPP/6YVq1aPSy3cWPOnz+PXq9Ho9Gwdu1aYmJi8PDwYOTIkdjZ2bFo0SKjvDw9Pfn444/x8fExWR+NRsO0adPYs2cPkZGRBAUF4ejoqKyvVasWCxYs4MCBA+zfv5/Bgwcr21VG+UIIIYQQT8JTGYFs8EJ7zhzfzo/h75WaLutuMse/ee9/H6rpz6WYr8m7l0WjF1/jUszXpW5raWnJrl27OHToELdu3QIgKiqKrl27GqVzdHQkMDAQvV5Phw4dWL16NSNGjCAuLo63334bgLy8PCZOnEhSUhIA9+/fZ+3atWzZsoVGjRqRkJAAQPv27QkMDCQry/To6KJFi9Dr9bz55pvk5OTQt29f3NzcSE5OBqBnz57861//YsmSJXTp0oXly5ezb9++SitfCCGEEOJJeGpzIHV55Qtyzv64XQka4eF8SMcX2pe53YMHD9i7dy+tW7dm0qRJrFixgrFjxxZLt3//fvR6PQC//PILp06dokePHsXSFQZvhX777TcKCgpwdnZWlm3evLnE4M3Z2ZmOHTuydOlSfv/9d3Q6HXv27OHw4cNKmrCwMC5dugTAsWPHKCgowNbWtlLKF0IIIYR4Up75eyBNuXPzEhqbGgBk/X6DBuUIIKtVq8YHH3xAbm4u33//PTExMZw9e5bXXy/99ndKSgr29vZGy3r06GF0u/hRKpXpmDs0NBRXV1fg4cjnDz/8wM2bN8nNzS2z7oUKCgqwsLCoUPlCCCGEEE/LcxlA2tVvxo34aABq1GpA3r2yR9natWtHgwYN8PDw4P79+wBKQFcaV1dXfvrpJ6NlN27cQK/X07NnT+7duwdAzZo1CQ8P5/r16ybzmTRpktHfzs7O1K9fn6pVq5oVRFa0fCGEEEKIp+WpDWdZaWqUK93fXhmBpkoNEmK/B4yDydJkZ2dTpUoVOnfujJ2dHd27d2f48OHUqFHD6GXi48ePx87ODisrK7y8vHjppZeIjIw0yis2NpaEhAT8/f2xsbGhevXqTJs2jZMnTxIfH1+u/UhMTOTEiRMsWLAAW1tbNBoN3t7evPZa2a8lqozyhRBCCCGelKcSQN64Fk3LziPwHPcxnuM+pvMbb5lMV6O2I53feIvbKZe4FPM1jV98zSiYLM2pU6fYsmULM2fO5NNPP6Vz587MnDkTa2tr5s+fr6Q7duwYq1atIiIigjfeeIPAwEDS0tKM8iooKGD27NnUq1eP3bt3s3fvXmxsbPjXv/5l1n4vWrSImzdvsnnzZr755hs6deqkzHksTWWVL4QQQgjxJFg4Ojoa4GHQotfrlYc4KlON2o60e82PGrUaYG1TgzoOzbh06msO73kHgIlLTnPy+w+4FPMfXukzW3nFj5f/TqxttOxYU773QJYlPDwcPz8/5SlmIYQQQghRtvT0dNRqtfIsxlOZA5l1N9novY9dBy353/dCogSRhekO7pgOwGD/MGrUduTbHdMrJXgUQgghhBCV45k8RFMYTBYGkUXZ1W9GHYdmHN79DvHluH0thBBCCCGenmf2FHbRIDLvXqay7s7NS3y4oFWll9mnT59Kz1MIIYQQ4q/mmb7G5/DuBaRci8bapjqXYv7zLKsihBBCCCHK6Zm/B7KsnygUQgghhBDPF/lZEyGEEEIIYRYJIIUQQgghhFkkgBRCCCGEEGaRAFIIIYQQQphFAkghhBBCCGEWCSCFEEIIIYRZJIAUQgghhBBmkQBSCCGEEEKYRQJIIYQQQghhFgkghRBCCCGEWSSAFEIIIYQQZpEAUgghhBBCmEUCSCGEEEIIYRYJIIUQQgghhFkkgBRCCCGEEGaRAFIIIYQQQpjlqQSQarWa48ePs2DBAlasWMGhQ4c4cOAAPj4+Rml8fX3Zu3cvR44cYfv27XTv3l1Z7+vry/Hjx43y3b59OytWrDBa7+XlRVhYGN9//z2hoaHY29s/jV0UQgghhPjLeKojkO7u7nz//ff4+/sTFxfH1KlTqVmzJgD+/v6MHj2aw4cPs3z5cm7cuMHixYt55ZVXzCqjdevWLFy4kPfee4+//e1vDBs27EnsihBCCCHEX9ZTDSB37drFt99+y8WLF9m3bx8qlQp7e3s0Gg1Dhgzhm2++Ye3atURERPDPf/6TxMRExowZY1YZCxYsIDY2lvDwcJKTk3FwcHhCeyOEEEII8df0VANIg8Gg/Fun0yn/dnBwQK1Wc/HiRWWZXq/n4sWLODs7V7iMBw8ePEZthRBCCCGEKc/FQzQpKSno9XqaN2+uLFOr1TRv3pzExETg/wJDS0vLZ1JHIYQQQgjx0HMRjeXl5REWFoaPjw85OTlcunSJbt264ezszLp16wC4ffs2AEOHDuX48eP06NGDxo0bKwGmEEIIIYR4Op6LABIgNDSU/Px8PDw8GDBgAPHx8fzzn/9UnryOiIjA3d2df/zjHwwcOJCIiAiSkpKeca2FEEIIIf56LBwdHQ0ABQUF6PV6bG1tn3WdhBBCCCHEcyQ9PR21Wo1K9XD243MxB1IIIYQQQvxxSAAphBBCCCHMIgGkEEIIIYQwiwSQQgghhBDCLBJACiGEEEIIs0gAKYQQQgghzCIBpBBCCCGEMIsEkEIIIYQQwiwSQAohhBBCCLNIACmEEEIIIcwiAaQQQgghhDCLBJBCCCGEEMIsEkAKIYQQQgizSAAphBBCCCHMIgGkEEIIIYQwiwSQQgghhBDCLM9NAKlWq2ndujWtWrWqlPyCg4M5fvw4bm5ulZLfs7R8+XIGDx78rKtRYV5eXixZsuRZV6NUj1vHP8I+PmtLly5l4MCBAPj4+PDuu+8q6w4dOoSDg8OzqpoQQggzPRcBpFqtpmXLllhZWVVKfo0bN6ZNmzZER0fj5eVVKXk+S1988QXHjx9/1tUQotIcPXqUsLCwZ10NIYQQFWT5rCsAUK9ePTIyMsjLy6NOnTqPnZ+3tzf//e9/2b59O+vXr2fjxo1kZGQo68PDw9m0aRMdO3akTp062NjYsGzZMs6dO2cyPycnJ6ZNm0aLFi3Iz8/nhx9+IDQ0lPv37yv5ffjhh7z++utotVoePHhASEgIp0+fVvLw8fHBy8sLGxsbbt26RUhICDExMcDDkZmUlBTs7Oxo0KABderU4dNPP+Xrr78GYMiQIURHR7Nnzx68vLzo1KkTiYmJuLq64ujoSHR0NCtWrMBgMGBlZYWfnx89evRApVIRGRlJnTp1OHfuHDt37iy13WxsbJgzZw4vv/wyBoOBy5cvExwcTFpaGkuXLlXqUOjw4cMMGTKEtLQ0AAYOHIi3tzf29vYkJycTEhJCdHQ0ACqVinHjxuHh4YFWq+Xw4cMsX76cgoKCYvVo1aoVfn5+ODs7AxAREcGGDRswGAyl1tGcfEwpq44dOnTAz88PJycn0tPT2bVrF3v27DGZn5OTE4GBgTRt2hSDwcDhw4cJCQlBp9OVegwA7OzsmD17Nm3atCEzM5OtW7cyYcIEZs2axZUrV7C3t2fq1Km0bt0aS0tLTp8+zcqVK7l79y4uLi6EhISwadMmunXrRu3atUlOTmbVqlUm26ioqlWr4u/vj7u7O5aWlpw/f561a9eSkpICPDxX4+PjcXNz4/79+7zzzjtG25f3+Lzyyiu0atWKGzdusGPHDmxsbNi2bRs7duxg8+bNZdZTCCHEs/VcjEDeuHGDuLi4SsmrevXq9OnTh927d3P+/Hni4+Pp379/sXSNGzdm3rx5jBs3jgMHDjBx4kST+VWrVo2NGzcSExPDgAEDGDt2LPXq1WPBggVG6RwdHQkMDGTs2LF8+OGHrF69Gnt7ewAGDRpE9+7d8fX1xdPTk1WrVrFw4UJlPUDLli0JDg5m4sSJzJ8/n8DAQCwtTcf3L774It9++y0BAQGMGjWKLl26KLf+fX19ad26tVLWL7/8Qrt27crVdsOGDUOtVuPj44OPjw8RERFGdSxNYYD89ttv07NnT4KDg2nZsqWyvkOHDiQkJODl5cXo0aNxd3enbdu2JvMaPnw4mzZtom/fvvj6+tKzZ0+6detmdh1Ly8eU0urYokULli5dykcffUSfPn2YO3cuQ4YMMTm1QKPRsGbNGiIjI/H09GTw4MHY2NgwZcqUMtvRwsKCFStWkJmZycCBAxk+fDharRZbW1slTf/+/Tl37hwDBgxg0KBBVKlShQkTJijrtVot6enpTJ48meHDh3Pp0iXee+89VKqyu/vixYupWbMmo0aNYtCgQVy4cIENGzZgY2OjpHF3d2f9+vXFgkcw/xy6ffs2PXv25P79+4waNUqCRyGE+IN4LgLIytS3b19SU1OVka/du3czaNAg1Gq1Ubpdu3bx4MEDAM6ePUu9evVM5tejRw+Sk5PZsWMHOp2OjIwMli5dSpcuXXB0dFTS7d+/H71eD8Avv/zCqVOn6NGjBwBjxozh/fff5+7duwDExsayf/9+BgwYoGwfHh5utF6lUlG7dm2TdTp16hQXL14EIDc3l7i4OKX+np6eBAcHc/PmTQwGA8ePH+fEiRPlarucnBwaNmxI27ZtUavVHD16tMRR2aJGjhzJmjVruHbtGgUFBZw8edIoGDhx4gRRUVEYDAZSUlK4ePFiiYHF3LlzleN348YNjh49SuPGjc2uY2n5mFJaHYcOHcquXbs4ceIEBQUFxMfHs27dOkaOHFksn549e5KUlERERAQAOp2OoKAgPD090Wg0pbaji4sLL7zwAkFBQeTm5qLT6dixYwfp6elKmk2bNrFz5070ej337t1j3759RvuVmZnJ4cOHlb+3bNlC/fr1adasWallF7br8uXLycrKIj8/n61bt5Kenk737t2VdHv37uX69esm83icc0gIIcQfx3NxC7uyqFQqBg8ebDS36uDBg0ydOpWuXbsSFRVlcrvCwM8UR0dHrl69arQsKyuL27dv4+DgQHJyssntUlJSsLe3x9ramrp16xIQEGBUTpUqVbhw4UKJ5RYUFGBhYVHi+qL1t7CwQKPRoNVqS/xwL8uuXbvIysrizTffxNXVlVOnThEUFMSdO3dK3c7a2ho7OzuzRpEL62xKr169GDBgALm5uVy7dg1LS0tl9MycOpaWj7l1bNCgAUeOHDFaHxcXh729fbGRYmdnZ1xdXdmwYYPR8tu3b1O3bl2SkpJKLNPe3p60tDTy8vJKTNO8eXMmTJiAtbU1qampXL16tdT90uv1pKWlUa9ePWJjY0tM5+joyM2bN8nNzS22nw0aNChxu0dV9BwSQgjxx/KnCiALRwUnTJjAuHHjlOVVqlTB29u7xACyNMnJyfTq1ctomVarpW7dusq8MFNcXV356aefyM/P586dO4SGhhrNiXwS8vLyyMrKomHDhspopjkMBgPh4eGEh4dTvXp1/Pz8CAgIYOHChQAlBnyF++jq6qqM+FWUq6srM2fOZPz48cTHx6PValmxYgW3b98uVx3Lm4+5bty4gYuLi9E51KRJE9LS0pSR7ELJyckkJCQQEBBgdjm3bt3C3t4ejUZjMoi0sLBg1apVhISEEBERgVqtLvPWuI2NDY6OjqSmppaaLjk5GQcHB6pVq0ZOTo6y3NXVlTNnzpSr/uU9PkIIIf7Ynutb2I6OjlhbW5c7vbe3N0eOHGHkyJGMGTNG+S8wMJCWLVuWeQvPlMjISBwdHRk5ciQajYbatWszf/58jh49ajT6OH78eOzs7LCyssLLy4uXXnqJyMhIAD777DNmzJihjOJUq1aNsWPHlnk7syL2799PQECAcuu1U6dOdOjQQVlfo0YNBg4cWOyWPjycW9elSxcsLCzIzs4mIyNDGTVNS0vjxRdfVNJ6enoaPTVfuI9ubm6o1Wo6dOhgNC+vvKysrMjNzVXaNjMzk5s3b5arjubkY67PP/8cb29vXnnlFdRqNa6urgQEBPDZZ58VSxsZGYmzszM+Pj7KyGDbtm3p2rUrUPoxuHr1KgkJCcyYMQMbGxusrKzw8fFRpjOoVCqsra25fPky8HB0segIuVarVc6v6tWr89Zbb5GYmMilS5cA6Nevn8npEdevXyc6Opp58+ZRq1YtNBoN48aNw9bWlu+++65c7VTe41NUfn4+Dg4OVK1aFXg4p7YyHqgTQgjxZDy3I5AqlQonJyfu3btnNP+rJI0bN6Z9+/b4+voWe+IzLS2NkydP4u3tbfTuufLIycnB39+f6dOnM2LECPLy8jhy5AihoaFG6Y4dO8aqVato1KgRCQkJBAYGKvUICwsjLy+PVatWUa1aNXQ6HQcOHCg2clUZPvzwQyZNmsSmTZsoKChg//79nDx5UlnftGlTAgMDiYuLKzYievHiRSZNmsTs2bPJz88nPj6elStXAg9fJfTuu++yfft2UlNTiYyMNHqiOCwsDJ1Ox6JFi3BwcOD69euEhISYXf+LFy8SFhZGUFAQ165dIzs7G1tbWyX4K62O5uRjrtjYWN5++238/PxYvHgxd+7cISwsjN27dxdLm5ubi7+/P1OmTGHo0KFYWlry22+/sXHjRqD0Y2AwGPjnP//JzJkz2bt3LxkZGYSGhiojynq9nnfeeYdZs2aRkJBARkYGWq3WKI/MzEzS0tLYvn07Wq2W06dP89Zbb1FQUEDVqlWZPHkydnZ2bNmypVjdFy5ciL+/P1u3bsXKyoqzZ8/i7++vvHGgLOU9PkX95z//YfXq1Rw5coSVK1cybNgwrl+/XuERYyGEEE+WhaOjowEezrnT6/VGT3uK8gkPD8fPz4+EhIRnXRWT1q9fz549mopWDgAAIABJREFUe4iKikKlUrFq1SrefffdCt3mFo/P3GNgaWlJVFQUAwYMKDN94Wt8PDw8SkwzYcIEYmNjOXr0qNl1F0II8deUnp6OWq1W7qw917ewhfkGDRpEv379lNuj3bt3p0mTJvz666/Aw2kBe/fuleDxGSrrGMyaNUt5LZOVlRWTJ0/mypUrlXLMrKysyMjIkOBRCCHEY3lub2GLiomOjmbatGlMnDgRvV7P9evXmTVrlvIUbGJiIomJic+4ln9tZR2DY8eOMX36dOrWrcuDBw84ffo0c+fOrZSydTqd/AKMEEKIxya3sIUQQgghRKnkFrYQQgghhHgsEkAKIYQQQgizSAAphBBCCCHMIgGkEEIIIYQwiwSQQgghhBDCLBJACiGEEEIIs0gAKYQQQgghzCIBpBBCCCGEMIsEkEIIIYQQwiwSQAohhBBCCLNIACmEEEIIIcwiAaQQQgghhDCLBJBCCCGEEMIsEkAKIYQQQgizSAAphBBCCCHMIgGkEEIIIYQwy3MTQGq1Wl5++WU6d+5M586dadmyJTVq1KhwfsHBwRw/fhw3N7dKrGXlCg8Pp1GjRgAsXbqUgQMHPvEyHRwcOHToEABWVlZ89dVXNG/e/LHzXb16NR4eHuVK6+LiwoEDB0pN82jb/NH4+Pjw7rvvPpG8W7RowZdffomlpeUTyf9pGj58OPPnz1f+rqx28/LyYsmSJSbXVVYZzZs3Z/fu3Y+dz9NkTh99Uv7I/fqvqGgfLUtpfe/PomibPO4+Pw/9sqKei08htVpNs2bNSE5O5sqVKxgMBho0aEDLli35+eef0el0ZuXXuHFj2rRpQ3R0NF5eXixfvvwJ1fyPTafTERISQnx8/LOuyp/K0aNHiY2NfSJ5X7t2jeDgYB48ePBE8n+WnmS7Pc0yhBDir+C5CCD1ej3R0dEYDAZlWXx8PA0aNKB69ercvXvXrPy8vb3573//y/bt21m/fj0bN24kIyPDZFoXFxdCQkKMvgGMGjUKZ2dnli1bho2NDXPmzOHll1/GYDBw+fJlgoODSUtLw8vLi1atWrFgwQJl2/fff59vv/2WiIgI7O3tmTp1Kq1bt8bS0pLTp0+zcuXKUvenXbt2LFiwgMGDB6PX6wGwsLAgLCyMkJAQfvjhB6P0ZZXx4osvMmPGDBo1akRKSgrbt2832n7OnDn4+fmRkJDA0qVLiY6OZs+ePcr6w4cPM2TIENLS0nB3d2fixIloNBru379PWFgY+/fv55NPPsHV1ZV27drRq1cvAgICyrXvHh4ejBkzhlq1anHq1ClWrVrFnTt3TLaLj48PXl5e2NjYcOvWLUJCQoiJiTGZtmrVqvj7++Pu7o6lpSXnz59n7dq1pKSkAA9HexMTE3F2dqZ+/fpoNBq++uoro/3u2LEj/v7+2NrakpeXx+eff66MOBWeM1u2bKFLly44ODhw+/ZtFixYwN27d3nllVdo1aoVZ86cKTMtwEsvvURgYCANGzbkxo0bfPHFF8yYMYOePXsW2zcHBwfmzJmjnAfh4eFs2rSJjh07UqdOHWxsbFi2bBnnzp0z2TZ9+/Zl+PDh1KxZk5ycHDZv3kxERITSLikpKdjZ2dGgQQPq1KnDp59+ytdff13p7RwYGEi/fv1Qq9X8/e9/x8PDw6jdAOrXr8/06dN5+eWXUavVHDp0iODgYPLy8mjVqhV+fn44OzsDEBERwYYNG4yuIaaYc2xK6vt/+9vfmDdvHjY2Nhw8eJB58+bRuHFj2rVrR2pqKl26dMHb27vM/rR06VLS0tKoW7cuzs7OWFlZsXLlSvr06YOLiwu2trYsX76ckydPAmBjY8PUqVP5f//v/6FSqYiNjWX16tWkpqaWeS6Y6qOlKamvF5ZTeM2Ah+fvwoULGTJkCAAajQY/Pz+6du1K9erVOXPmDGvWrCE5ORkANzc3Zs2aRbNmzbh79y7Lli3j9OnTJutR2vlaWh3Nyaeo0upf2nXNxcWF4OBgPv/8c/7nf/6HF154gYiICM6fP4+npycNGzbk4sWLLFy4kIKCAqD064yXl1exc8rcz5QOHTrg5+eHk5MT6enp7Nq1iz179mAwGJTz/6OPPlJG5i9cuKBsa6qP6nS6UutclJOTE4GBgTRt2hSDwcDhw4cJCQlRBoXGjBmjfPbeuXOH0NDQcvV/Jycnpk2bRosWLcjPz+eHH34gNDSU+/fvAw/P0Q8//JDXX38drVbLgwcPCAkJMTrPzPlMKa1NAFQqFePGjcPDwwOtVsvhw4dZvnw5BQUFWFtbM2HCBLp160aVKlVITk4mKCiI2NhYs/vl8+a5uYVd9MJvY2ODWq3m3r17ZuVTvXp1+vTpw+7duzl//jzx8fH079+/wvUaNmwYarUaHx8ffHx8lMCwPPr378+5c+cYMGAAgwYNokqVKkyYMKHUbU6ePMn9+/fp1KmTsqxdu3ZYW1tz7Ngxs8qoXbs269at47vvvsPDw4Pp06fTuXNnM/b+/1hZWbFkyRLeeecdhgwZwuTJk9FqtQCMHTuWEydOsHr1aqUDlLXvWq2WmjVrMnLkSPr3709GRgbvvfceFhYWxcoeNGgQ3bt3x9fXF09PT1atWsXChQtLPA6LFy+mZs2ajBo1ikGDBnHhwgU2bNiAjY2NkqZFixasXLmSf/zjH8yaNYsxY8bw6quvAtCkSRPmz5/P8uXL6devHxMnTsTDw4OuXbsa1T83N5fAwECGDRvGvXv3SpyCUFra2rVrs3btWvbt28cbb7xBYGAgHTt2NOPIPBxxnzdvHuPGjePAgQNMnDjRZLrq1avzxhtv8NZbb+Hh4cH777/P3LlzqVu3rpKmZcuWBAcHM3HiRObPn09gYGCJt8sfp53ff/99/v3vf3Pw4EF69uxZ7C5D1apV+eCDDzh37hyDBg3C29ube/fuKcd8+PDhbNq0ib59++Lr60vPnj3p1q2bWe0GpR+bkvp+VFQUkydPJjU1lZ49exIdHQ1A27ZtOXHiBN7e3uUuv3nz5qxYsYIxY8Zw9epV5s+fz7Zt2/D19WXXrl2MHj1aSfv2228DD/uDp6cnR44c4b333kOl+r/LeEnngqk+WpLS+np5LFq0CHt7e958803eeOMNjh49ajSVqEePHixcuJDevXvzww8/4OfnZzKf0s5Xc+pYnvO+vPUv67pWs2ZNUlJSCAgIYOrUqYwYMQIXFxdmzZrFyJEjadu2LS+99BJQvutM0XPKnM+UFi1asHTpUj766CP69OnD3LlzGTJkCIMHDzaqb/Xq1Rk1apRR8AiY7KPlqXMhjUbDmjVriIyMxNPTk8GDB2NjY8OUKVMAaNWqFR4eHrz55psMGTKElStX0qBBA6D0/l+tWjU2btxITEwMAwYMYOzYsdSrV89oIAfA0dGRwMBAxo4dy4cffsjq1auV64e5nymltQk8DNQTEhLw8vJi9OjRuLu707ZtW+DhNdXOzo7Ro0fj4eHBzz//zMKFCwHz+uXz6LkJIB+lUqlo3rw5KSkpyjeK8urbty+pqanKRX337t0MGjQItVpdobrk5OTQsGFD2rZti1qt5ujRoyWO7hS1adMmdu7ciV6v5969e+zbt4/GjRuXud3evXuNgt5+/frxn//8RxmRLG8Z3bt35+rVq+zcuROdTsfdu3f58MMPy1X3ogoKCsjJyaFr167Y29uTlZXFjh07Skxf1r5nZmayY8cO8vPzuXfvHqtXr8bJyYlmzZoVy2vMmDG8//77yrfs2NhY9u/fz4ABA4qlLTxWy5cvJysri/z8fLZu3Up6ejrdu3dX0n3//fdkZmYCcPPmTT7//HP69esHwIgRIwgLC+PSpUsApKens3HjRoYOHWpU/2+++QZ4+OXn/Pnz1KtXz2RblJa2e/fuxMbG8vXXX/PgwQPu3r3L5s2bS2xXU3bt2qXc0j579myJ9cjOzmbKlCkkJSUB8OOPP5KSkkLDhg2VNOHh4UbtrFKpqF27drG8KqOdS9OjRw9u3LjBZ599Rn5+PtnZ2axfv57ExEQA5s6dq/TxGzducPTo0XL1raJKOzbm9v2ff/6ZH3/80azyDx48SHZ2NgBxcXHExMQoI3VXr16lVq1awMORnE6dOrF27VoePHiAwWBg//795OTkKB9UUP5zoTTm9vVHOTs707FjR5YuXcrvv/+OTqdjz549HD58WEmzceNG0tPTKSgo4PDhwyV+aJd2vppTx/Kc9+Wtf3mua4VzzOPj49Hr9ezfvx+DwUBeXh6JiYlKfyrPdaboOWXOZ8rQoUPZtWsXJ06coKCggPj4eNatW8fIkSOVNBkZGWzfvt3kZ4sp5alzoZ49e5KUlKSM9Op0OoKCgvD09ESj0ZCbm4tWq8Xd3Z1q1aoRHx+vpC2t//fo0YPk5GR27NiBTqcjIyODpUuX0qVLFxwdHZXy9+/fr+zXL7/8wqlTp+jRowdg3mdKeZw4cYKoqCgMBgMpKSlcvHhROa+jo6N59913yc7OpqCggC+//BJnZ2ejL35/VM/FLexHWVlZ8fLLL3P//n2uXr1q1rYqlYrBgwcTFhamLDt48CBTp06la9euREVFmV2fXbt2kZWVxZtvvomrqyunTp0iKCioxFutj2revDkTJkzA2tqa1NRUrl69Wq6TJjw8HF9fX+rWrUteXh7u7u6EhISYXYa9vb3ZbVgSvV7P+PHjGT16NB988AE6nY5t27aVeMvI3H3X6XSkpKRQv359Ll68qCy3trambt26BAQEGF3kqlSpUuwbMzz81nnz5k1yc3ONlsfFxSnfbk25efOm0uGdnZ1p2rQpr7zyirJerVaj0WhK3F6v15scPS0rrb29PdevXy/XduXNuyRqtRpfX1/at2/PrVu3iImJQafTlVrvgoICk+sro51L4+TkRFxcXInre/XqxYABA8jNzeXatWtYWlpWygX50WPzOH2/sjk5OaFWq1m7dq3R8po1a1KnTh2T25Q3KDC1nTl9vWg9TZ0XpZVV0vlX2vlqTh3NOe/Lqn9Fr+mmVOQ6Y075DRo04MiRI0bL4uLisLe3r/BDeObU2dnZGVdXVzZs2GC0/Pbt29StW5crV67w1ltvMWzYMAICAkhKSmL9+vWcPXu21P7v6OhY7HMtKyuL27dv4+DgoHwBKyolJQV7e3uzP1Mq4tHz2s7OjsmTJ9OwYUNSU1M5dOgQFhYW5f68eJ49VwFkjRo1aNGiBbdu3eLatWtlzmcqqvAbyIQJExg3bpyyvEqVKnh7e5sMIMsqw2AwEB4eTnh4ONWrV8fPz4+AgAAWLlyIwWAo8SSwsLBg1apVhISEEBERgVqtVobuy5KRkcGRI0fo27cvubm5/Pzzz9y6dcvsMtLS0sy+HVraSX3z5k3ee+894OHtkaCgIM6cOVMsAKrIvltZWeHg4KDM5yqUn5+vzI0paZ7Uo5KTk3FwcKBatWrk5OQoy11dXZW5Naa4urqSlpam5BEfH8+WLVvKLO9x3bp1C3d39ydeDsDAgQPp2LEjU6dOJTs7m8aNGzNq1KgK5VUZ7VyapKQkevfuXWIeM2fOZPz48cTHx6PValmxYgW3b982f0dKUVrfL6/K+pBITk7GYDAQGBhIfn5+peRZmtL6emnXvaSkJOrXr0/VqlXLHUSWpKzztbzXI3PO+9Lq/zjXdFPMvc6YW/6NGzdwcXEx+txr0qQJaWlpFX4Iz5w6Jycnk5CQUOqt2TNnznDmzBnUajW9e/dm2bJleHp6ltr/k5OT6dWrl9EyrVZL3bp1lfnXpri6uvLTTz+Z/ZnyuGbMmEFmZiYTJ05Er9ebvN3/R/XcjKE6OTnRsmVLEhISSEhIQKVSoVarlQtVtWrVyhy58Pb25siRI4wcOZIxY8Yo/wUGBtKyZUuTt0fv3LmDVqtVhr5r165tdID79+9Ply5dsLCwIDs7m4yMDOVby61bt3Bzc8PKygp4eBErfCWOSqXC2tqay5cvAw+/kZgzGrh37148PT3p168fe/fuNZmmrDKioqJo1aqVEkSq1epSXxeQlpbGiy++qPzt6emp7FuNGjUICAhQbr/cvHmTgoICZTJ4fn6+cuEtz75rtVpGjBiBRqOhWrVqzJo1i5s3byq3Rh712WefMWPGDGVkq1q1aowdO9bkt97r168THR3NvHnzqFWrFhqNhnHjxmFra8t3332npBswYABNmzZFpVLRvn17hg4dqjws8vnnn+Pj46PcGlSr1fTr169Ct0jL8t1339GiRQtlYrZWq2XMmDGVXg48HM29ceOGcss0OTm5wh/yldHOOp0Oe3t7NBqNcp4VioyMpH79+owdOxYbGxtq1qzJtGnTaNiwIVZWVuTm5iojDZmZmdy8ebNC+1Ga0vq+TqejZs2aVK1alapVq5rcvrT+ZK7ExER++eUX5s6dq5Tn6Oho8tZhSR7to/DwgSJTr/Aqq6/funVLmcdnaWlpNCUhMTGREydOsGDBAmxtbdFoNHh7e/Paa6+Zvc+lna9l1bG8+RRVWv0f95pelLnXGXPL//zzz/H29uaVV15BrVbj6upKQEAAn332WbnrWLSPmlPnyMhInJ2d8fHxUUZJ27Ztq3y+tmjRguHDh2NtbY1eryc1NVXpX6X1/8jISBwdHRk5ciQajYbatWszf/58jh49ajT6OH78eOzs7LCyssLLy4uXXnqJyMhIoOzPlJL6hqk2KYtGo+Hq1avKvl25csVofdF++UfyXIxA1qhRAxcXFwCaNm1K06ZNlXWXLl0iNTUVW1tb7OzsShy9aNy4Me3bt8fX17dYmrS0NE6ePIm3t3exd8BlZmYSGhpKSEgIqampJCYmcv78eeVBgIsXLzJp0iRmz55Nfn4+8fHxrFy5EoBjx47RvXt3duzYQUpKCmfPnlWG3fV6Pe+88w6zZs0iISGBjIwMsyainz59mvv376PRaDhx4oTJNGWVkZ6ezsyZM5k2bRqTJ08mOzu72FPcj/riiy9499132b59O6mpqURGRiqThHNzc8nOzlbmUD548IAPPvhAmVf07bff8vbbb9OjRw9GjRpV5r5nZmYq82+0Wi1nzpxhzpw5Jj8AwsLCyMvLY9WqVVSrVg2dTseBAwdK/Ba9cOFC/P392bp1K1ZWVpw9exZ/f3+j+bRHjhxh3LhxtG/fnvT0dD744AOlbS5evMjcuXPx8/OjXr16WFhY8NNPPxW7HVQZ0tPTCQwMZPr06UyePJnExEQ+/fRT5YGeyvTVV1/RpEkTVq5cSXJyMpmZmY912/dx2/nHH3/Ex8eHvXv3Mn36dKO8c3Nz8ff3Z9q0aezevRuVSkVUVBSpqank5eURFhZGUFAQ165dIzs7G1tb20oPIkvr+/Hx8Vy4cIF9+/YVu0VXqLT+VBH/+te/8PX15ZNPPsHGxob09HQ++eSTcm9ftI8OGzYMoNgIUVl9PSQkhNmzZzNo0CDS0tL49ddfadOmjbL9okWLmDhxIps3b6ZGjRr8+uuvBAUFmb2/pZ2vZdWxvPmYUlL9H/eaXpS51xlzy4+NjeXtt9/Gz8+PxYsXc+fOHcLCwsx6f2nRPmpOnQv78JQpUxg6dCiWlpb89ttvbNy4EXh4S3nQoEGEhYWRn59PZmYm77zzjtG2JfV/f39/pk+fzogRI8jLy+PIkSOEhoYalX/s2DFWrVpFo0aNSEhIIDAwUIkNyvpMKalvmGqTsqxdu5ZZs2bRokUL0tPT+f33343WF+2Xj3ONeNosHB0dDfBwrpNer8fW1vZZ10n8r+XLl3PhwgW2bdv2xMoIDw9n4sSJlToP73ln6vUqz5M2bdowe/Zshg8f/qyr8lie93b+q2vfvj2dO3cmODj4WVdFiEpV9FVT5pK+YVp6ejpqtVr5Avbc3MIW/0elUuHm5kb79u3LNXHdXBqNBq1Wi4ODA1WrVn0mDwWIhzQaDUuWLMHBwQF4OIViwoQJHD169BnXTPzZNWrUqMJvZRDiz0z6Rvk8F7ewhbEVK1Yok8LNfYl6eTRu3JglS5ZQtWpVQkNDjR6CEE9Xfn4+sbGxBAcHo9FoyM/PJyoqio8//vhZV038yX311VfPugpCPJekb5SP3MIWQgghhBClklvYQgghhBDisUgAKYQQQgghzCIBpBBCCCGEMIsEkEIIIYQQwiwSQAohhBBCCLP8qQJILy8vlixZAjz8maQvv/yyQj8aX3Tb1atXl/oTgCVp3ry50Vv/XVxcOHDggNn5/FlUtB0LvfDCC2zbto19+/YV+w3YR9vWysqKr776qsSfoirq0fPGlKLH8XnwOOd3eRQ9VuHh4TRq1OiJlFVRS5cuZeDAgX+4vJ93hw4dUt5L+jwxt18LIZ6sP+17IK9du0ZwcHCFfjT+cbYVT86AAQOIjo5m3bp1qNXqEtPpdDpCQkKIj49/epV7yuQcFX81f4V+LcQfyZ82gHRwcGDOnDnK7+6Gh4fz6aef0r59exo2bEhiYiKbNm1ixIgRODo68uDBA+bMmcPt27eNtv3kk09wdXWlXbt29OrVi4CAAMaMGaOMzty5c4fQ0FDOnDljVH63bt2YN28eNjY2HDx4kHnz5pGenq6sGz16NE5OTly+fJm3335bWefk5ERgYCBNmzbFYDBw+PBhQkJCTP4+prW1NRMmTKBbt25UqVKF5ORkgoKCiI2NBR6OoqSlpVG3bl2cnZ2xsrJi5cqV9OnTBxcXF2xtbVm+fDknT55Uyp42bRotWrQgPz+fH374gdDQUOW3jYv+PNRLL73EwoULGTJkiLJ+06ZNdOzYkTp16mBjY8OyZcs4d+6cyXYsqrTy16xZQ7t27SgoKKB9+/aMGjWq1OM/Z84cpa5WVlb4+fnRo0cPVCoVkZGR1KlTh3PnzrFz507g4a//jBs3Dg8PD7RaLYcPH2b58uW89tprxY5jdHS0UVleXl506NCBlJQUmjVrRq1atThx4gQbN24kPz8fgL59+zJ8+HBq1qxJTk4OmzdvJiIiAgB3d3cmTpyIRqPh/v37hIWFKb9AVNK5Zur8LqntAezs7Jg9ezZt2rQhMzOTrVu3MmHCBGbNmsWVK1eM9qekY+Xm5sasWbNo1qwZd+/eZdmyZZw+fVopf+PGjfTv35/IyEh27tz52OdTeepcq1YtFixYQKdOnTAYDGzZsqXElwC3atUKPz8/nJ2dAYiIiGDDhg0YDIZSzyWAjh074u/vj62tLXl5eXz++efKqLSXlxedOnUiMTERV1dXHB0diY6OZsWKFRgMBho1asRbb71F3bp1KSgo4L///S8ff/wxeXl5xcqpWrUq/v7+uLu7Y2lpyfnz51m7di0pKSnAwz4dHx+Pm5sb9+/fV347+FGltbuLiwshISFs2bKFLl264ODgwO3bt1mwYAFqtZodO3ZgY2PDtm3b2LFjB5s3by6zTo/TzuZeox7t16baoqLnYdFthBBl+1Pdwi6Lvb298hvDLi4ujBs3jkWLFjFmzBhu3bpl8vbq2LFjOXHiBKtXryYgIIBWrVrh4eHBm2++yZAhQ1i5ciUNGjQotl1UVBSTJ08mNTWVnj17KkGHVqvFxcUFX19f+vbtS0FBAYMHDwYe/qzdmjVriIyMxNPTk8GDB2NjY1Psdm2hli1bYmdnx+jRo/Hw8ODnn39m4cKFRmmaN2/OihUrGDNmDFevXmX+/Pls27YNX19fdu3axejRowGoVq0aGzduJCYmhgEDBjB27Fjq1avHggULzGrjxo0bM2/ePMaNG8eBAweYOHGiyXYsqqzyZ8yYwbfffsvmzZvLDB6L8vX1pXXr1vj6+uLp6ckvv/xCu3btjNJ06NCBhIQEvLy8GD16NO7u7rRt27bE41hUs2bN+Prrr5k0aRJjx46lUaNG+Pv7A1C9enXeeOMN3nrrLTw8PHj//feZO3cudevWxcrKiiVLlvDOO+8wZMgQJk+ejFarBSj3uVZW21tYWLBixQoyMzMZOHAgw4cPR6vVlvijASUdqx49erBw4UJ69+7NDz/8gJ+fn9F27du3JzAwkJ07dz72+VTeOvfs2ZOwsDA8PDxYvnw506ZNw9ra2mSew4cPZ9OmTfTt2xdfX1969uxJt27dyqxLkyZNmD9/PsuXL6dfv35MnDgRDw8PunbtqqR58cUX+fbbbwkICGDUqFF06dKFVq1aATBz5kyioqIYMmQII0aM4Pbt22g0GpNlLV68mJo1azJq1CgGDRrEhQsX2LBhAzY2Nkoad3d31q9fbzJ4LE+7a7VacnNzCQwMZNiwYdy7d4+BAwdy+/Ztevbsyf379xk1ahSbN28ud50ep53Le40yxVRbVOQ8fHQbIUT5/KUCyL1791JQUIBOp+P69etERkYqowBxcXHUqlWrzDxyc3PRarW4u7tTrVo14uPjlZGk8sjMzOTf//43eXl53Lt3j59++gl7e3vg4YdhUlKSkp9OpyMoKAhPT0+THzjR0dG8++67ZGdnU1BQwJdffomzs7PylniAgwcPkp2drexjTEwMycnJAFy9elXZ5x49epCcnMyOHTvQ6XRkZGSwdOlSunTpgqOjY7n3b9euXcpt1bNnz1KvXr1ybVdZ5Zvi6elJcHAwN2/exGAwcPz4cU6cOGGU5sSJE0RFRWEwGEhJSeHixYvKcSmPs2fPcu3aNQDy8vIIDQ2lX79+AGRnZzNlyhSSkpIA+PHHH0lJSaFhw4YUFBSQk5ND165dsbe3Jysrix07dgDmn2sltb2LiwsvvPACQUFB5ObmotPp2LFjhzLqXV4bN24kPT2dgoICDh8+XKx9Nm/eTFZWFvD4x7O8dQ4LC+PSpUsAHDt2jIKCghID47lz5ypfAG7cuMHRo0dp3LhxmXUZMWKEUTnp6els3LiRoUOHKmlOnTrFxYsXgYfHLS4uTmn/nJwc2rRpg5ubG3q9np07d5KZmVmsnIYNG9K2bVuWL19OVlYW+fn5bN26lfT0dLp3766k27t3L9clD4eBAAAgAElEQVSvXzdZ1/K0e2ZmJt988w0ABoOB8+fPl9hPy1unR5nbzuW9Rpliqi0qch4+uo0Qonz+tLewn5QrV67w1ltvMWzYMAICAkhKSmL9+vWcPXu2Qvnp9XosLCwAcHZ2xtXVlQ0bNhiluX37NnXr1lUCkEJ2dnZMnjyZhg0bkpqayqFDh7CwsFDyM4ejoyNXr141WpaVlaXc0i+8oJtDr9c/0/Lh4aiuVqst8QO3JI8el4pISUnBxsYGrVZLTk4Ovr6+tG/fnlu3bhETE4NOp8PCwgK9Xs/48eMZPXo0H3zwATqdjm3btrF///7HOtcebXt7e3vS0tJM3jKtqLLa53GPZ0XrXFBQUGK9evXqxYABA8jNzeXatWtYWloafdkqibOzM02bNuWVV15RlqnV6hJHEcG4fRYvXsywYcOYP38+derUISIigtDQ0GLzVx0dHbl58ya5ublGy+Pi4kodeS6aR2ntbupLQ2nHsiJ1qmg7PwlP6roihJAA8v+3d+fxUdX3/sdfZ9bsyUzInrBkZRGQgMii1l6t9lahgmgEi1qvVYxKRXCHi2vFBbEiiNZC9VYRbrVSseDCLSqL2iAYyr5kgSyQZLIns2Tm/P7Ib04TMklmWELAz/Px4CHMnPM933O+55x5z/f7PeNJyc/PJz8/H71ez89//nN+97vfMWHChFMut6SkhKKiIp9DvL488MAD1NXVcdddd+F2u9sNqZ3Mtq+++up2r0VERBATE6PNdVJV9ZRC1alu/2Q4HA7q6+vp27cv1dXVp1pNv6WlpWG326mrq2PKlCmMHj2a++67j4aGBvr3799uGL68vJwXXngBaH26euHCheTn51NcXHxazrWKigpiY2Mxm82nNUR25VTPp9Nd57S0NGbPns0dd9xBYWEhERERLFiwgMrKSr/2pbCwkBUrVpzUtpubm1m+fDnLly8nPj6ep556imuuuYY1a9Z02E5CQgKhoaE0Nja2q/uJc6y7qmtXx72r0NtZeYHU6VSO85lwpu4rQogf2RD2yXI6ncTHxxMSEsLgwYOZNm0aJpMJt9vNsWPHOu1pc7lcREZGEhISQkhISLfb+fzzz0lJSSEnJ0f7xp6dnd1pMDSbzRw6dEjb/okPQwTi888/JykpiV/96leYzWYsFgtz585l06ZN2rf0iooKhgwZAoDBYNCGaP3V9jiezPZP1tq1a5k5c6Y25DpmzBguuugiv9f3px0vuugiLr/8cnQ6nfYglDcgmEwmSktLtWG6kpISrUcnPDycmTNnYrFYgNYw6fF48Hg8AZ1rXTl06BBFRUU88MADBAUFYTQaycnJ0bbpS1dt5Y9TPZ9Ops5dMRqNNDU1aduuq6ujvLzcr3VXrlxJTk4O2dnZQGvv48SJE/0a/ga4++67SU1NBVofhLLb7T7bsbi4mLy8PB577DGioqIwm83cfvvtWK1WvvjiC7+2dTquI6fTSUJCAiEhIQHX6VSO85kQ6PHIyMjoEDiFEL5JD6QfPv30Ux5//HF+9rOfcd9995Gamsrq1atxOp3U1dX5nMwOUFhYyO7du/n4449ZsmQJO3bs6HI7TU1N5Obmcu+993LTTTdhMBg4ePAgS5cu9bn8K6+8wpw5cxg8eDA2m42ampqT3sfGxkZyc3O5//77ufnmm3E4HHz55Ze8/vrr2jKLFy/mwQcfZPLkyRw/fpwdO3YwYsQIv7fR9jhOnz693ZPl/mz/ZL3xxhvcfffd/PGPf8Tj8bB27VrtqU5/nNiOvn4Tctu2bQwbNoyHHnoIVVX54osvWLZsGQAffPAB6enpPP/885SUlFBXV6d9QWhqaqKhoYE33ngDgJaWFpYtW8bRo0exWCxMnjzZr3OtK6qq8sgjjzB79mw++ugjamtref3117vskT2xrQJ1qufTydS5K3v37mX16tUsXLiQgoICGhoasFqtfoWbvXv38uijjzJjxgzi4uJQFIVvvvmGL7/80q9t79+/n/nz5xMWFobb7WbLli2sW7fO57Lz588nNzeXt99+G6PRyM6dO8nNzdWeGO7O6biO/va3v/HSSy/x5Zdf8uSTTwZUp1M5zmdCoMdj9OjRXHLJJXz66ac9XFMhzj1KUlKSCq1zh9xud6cT0IU4n7z22mv89a9/ZcOGDadc1pQpUxg+fHjAT6yfTQaDgQ0bNnDdddf16ND+qTgX6yyEEOcLm82GXq/XOkBkCFuc9yZPnszEiRO1Hx+/8sorSU9P77ZH+HwyZ84c7WdljEYj99xzDwcOHOjVQexcrLMQQvxYyBC2OO/l5eXx29/+VnvYqLi4mDlz5lBVVXW2q9ZjNm/ezP33309MTAwtLS388MMPPProo2e7Wl06F+sshBA/FjKELYQQQgghuiRD2EIIIYQQ4pRIgBRCCCGEEAGRACmEEEIIIQIiAVIIIYQQQgREAqQQQgghhAiIBEghhBBCCBEQCZBCCCGEECIgEiCFEEIIIURAJEAKIYQQQoiASIAUQgghhBABkQAphBBCCCECIgFSCCGEEEIERAKkEEIIIYQIiARIIYQQQggREAmQQgghhBAiIBIghRBCCCFEQHpNgExMTCQ7O5tLLrmEcePGMWzYMCIiIvxe32QysWXLlk7/ZGdnk5qayieffHIG9wKuueYaXnrpJQAGDx7MX/7yFwwGwxndpi8DBw7kww8/7PHt5ubmsm7dOlatWkViYmKPbHPdunX069evR7bV2+Tk5PDMM8+c7WoAEBQUxMKFC/nkk0947bXXuPnmm5k7d+7ZrtZ56cMPP2TgwIFnuxp+O/Hc0Ov1Z7U+zz77LJMmTTqrdRDiXNfzycaHkJAQwsLCOHjwIHa7HZ1OR2JiIhdccAFbt25FVdVuy3A6nVxxxRXavzds2MDdd9/N/v37tfd7OmQUFBTw6quv0tLS0qPbPVsiIiKYOnUqEyZMoL6+HrfbfbardN7btGkTe/bsOdvVAGDMmDFYrVYmTpwItIZbIaDjuSH3BiHOfb0iQDY1NWlBD0BRFOx2e8DBq7m5ud2/HQ5Hh9cArrjiCm655RaSk5PZv38/jz/+ODabDYDk5GRmzZpFZmYmqqqyceNGFi9ejMvl8rnNX/ziF9x6661YLBby8/PZuXOn9l5CQgIPP/wwX331FQDDhw9nxowZpKSkALB+/XqWLFmCqqqkpqby6quvsnLlSi6++GIGDBjA+vXr2bVrFxMmTKBv377s3buX+fPn4/F4gNYP6ClTphAUFERFRQWLFy9m+/btXHHFFTz22GMEBQXx2Wef8dhjj5GXl9flvqWmprJ48WLefPNNrVdr9+7d7fZVURRuvPFGJk2ahMVi4ciRIyxdupTvv/+eESNG8MILL6DX61m9ejUvvfQSn332Wbv1L7nkEu666y7MZjN2u53Vq1ezdu1aoLUXccaMGRQVFQEwZMgQ5s+fz4033giA2WxmxowZXH755YSFhZGfn8/LL79MSUkJABkZGcyZM4esrCyqq6v53e9+xw8//OCzza699lqmTZtGZGQkjY2NLF++nPXr1wOtPRNlZWVER0eTmJhInz59eOedd1izZo3PskJCQsjNzeWSSy7BYDCwa9cuXnnlFcrKyrTyjhw5QkpKCvHx8ZjNZj744AP++te/amWMHj2a3NxcrFYrDoeDlStXar3HU6ZMYcyYMRw5coS0tDSSkpLIy8tjwYIFqKrK2LFjGT58OPn5+VobrlixgvHjx5OQkEBlZSXz5s2jurpaO66zZs2ib9++lJaW8v777/PAAw9w1VVX+dw/f/f1tttu49Zbb8VgMLBu3Tq+/PJLrrzySvR6PZdddhnXXHMNLpfrlPbVl86ugcTERN58801mz57Nvn37tLY4fvw4v//977ttlylTpjBy5EiOHTvG+PHjueGGG7rcHkC/fv146KGHiImJwePx8PXXX/PWW2/hcDi6PPe7u+dYrVbmzJnDyJEjqa+v55133umynbq6z3RVx0DKCaStTjw3pk+fzrFjx9ot0925O2XKFIYPH868efO0dRYtWsSnn37K+vXrmTJlCmPHjqWsrIz09HTi4+N57bXXSElJYcSIEfTt25f333+f999/X1vfYrGwYMECsrOzqa6u5n/+53+0NoHur0tf54cQPya9IkB6RUdHk5WVhV6vp6amhu+//96v3sdAREREkJqayp133olOp+Oll17i+uuv5w9/+ANms5mXX36Z5cuXM3v2bIxGIw8++CD33nsvixYt6lDWxRdfzP33389jjz3Gtm3bSEtL4/HHH6eqqsrntqdNm8Yf//hH8vLySExMZNmyZezdu5cvvvgCgMjISMrKypg5cyb9+/fnvffe46233mLOnDmYTCY+/PBDhgwZws6dO5k8eTJXXnkld955J9XV1QwaNIjnnnuOO++8kw0bNlBSUsLvfvc7Jk+eDODXvkVGRhIWFsb06dN99hBMmzaNX/ziFzz00EMcPXqUMWPGsGDBAu655x62b9/OzTffzOrVq32GEaPRyNNPP83tt99OQUEB4eHhTJgwwe92e/LJJ3G73fz617+msbGRa6+9loyMDC1A/uxnP2P+/PnU1NRw9913M2PGDO6+++4O5YSFhbXbh7Fjx7JgwQK2bdtGRUUFAMOGDePhhx/Wjuvrr7/OJ5984vMLzVNPPUVzczPTp0/H4XAwdepUlixZwrRp07Db7UDrVIa5c+dSV1dHfHw8y5Ytw2az8eWXX5Kens7cuXN58MEH2bdvH1arlRdffBGbzcbGjRsBGDRoEG+99RZ79+4lJCSE1atXM3z4cHbs2NGhPhERETQ1NTFr1iwUReGFF15g0qRJLF++HIvFwiuvvMJrr73GJ598Qnh4OPfdd5/fbdDVvv7pT3+ivLycq6++mlmzZgGtPfCpqanaEPvp3teuroHS0lJeeuklnnrqKW677Tauvvpq4uPjeeKJJ7T1u2oXgOzsbJ544gleeeWVbrd3/PhxZs+ezYYNG/jwww/R6/VMmTIFs9mMx+Pp9Nzv7rpUFIXnnnuO8vJyJk+ejMvl4sYbbyQmJqbTdurqPtNZHX0FyO7uV/62la9zw5euzl1/ZGZm8tprr1FQUMDkyZN5/PHHeeyxx1ixYgWZmZm88cYbrF69WvsCfskll/Dss89y6NAhhg0bxoIFC6iurmbz5s1+nasnnh9C/Nj0mjmQADU1NWzbto0ffvgBVVVJS0s77duoq6vjD3/4g9Y7+c033xAbGwvAVVddxdGjR7XeKJfLxcKFC5kwYQJms7lDWb/85S/53//9X/Ly8lBVlYMHD/KXv/yl020/+uij5OXlAVBaWsqmTZvo379/u7r93//9HwCFhYW43W7Wrl2Lqqo4HA6OHDmCxWIB4NZbb2XRokVaz9KePXtYu3Yt1113nc9t+7NvtbW1vPvuu50OL02dOpVFixZRXFyMx+Nhy5YtrFmzhqlTp3a6z14ej4fGxkYuv/xyYmNjqa+v57333ut2PYCUlBRGjx7Ns88+S01NDS6Xi7/+9a/ajRxg6dKl2Gw2PB4PGzdu1Nr0RA0NDdx7770cPXoUgK1bt1JWVkbfvn21ZdatW9fuuOp0Ou24t9W3b1+ys7N57rnnqK+vx+l08vbbb2Oz2bjyyiu15f7xj39QV1cHQHl5OStXrtSG8ryh29tLZrPZWLp0KTfddJO2/vfff8/evXuB1t76w4cPExcX53P/6urq+Pvf/w6Aqqrs2rVLW/bKK69kz549rFmzhpaWFqqrq/3+cPZ3X7tyuve1u2tg48aN/POf/+SZZ57hjjvuYP78+e1GErpqF4DvvvuOrVu3+r29xsZGRowYQUZGBm63m1WrVlFXV9flud/ddZmamkpmZibPP/88jY2NOJ1O/vznP2tfdnzp6j7TWR0DLSfQtvJHV+euP3bs2EFBQQEAhw4doqKiQmu/Q4cOYTabCQkJ0Zb/+OOPOXToEAD5+fm8++672rxIf87VE88PIX5selUPpNvtxu1243A42Lt3L+PGjaOoqEjryTlT21QUBWgNKmlpaSxZsqTdMpWVlcTExGihwysuLk77Nu6Pq6++muuuu46mpiYKCgowGAzodIFneJPJRExMDDNnzmwX9oKDgzsMO3t1t2/dMZvNWK1W7YbrdfjwYYYOHdrt+m63mzvuuINbbrmFZcuW4XK5OgwZdSY5OZny8nKampq6Xda7LW+bnkiv13PnnXcyatQoKioq2L59Oy6Xq9PloTX8+no/KSnJZ70OHz7c5QNE5eXlWsBNSUkhMzOTsWPHtqujry8s/uxfV8vGxsZSXFzs13onOtl9bet07qu/18A777zDBx98wNq1aztcvydq2y4ns72nnnqKqVOnMnfuXPr06cP69et5/fXXaWlp6fTc7+66jI2NpayszO9zH7q+z3RVx0DK8cXf83LcuHHteoJvu+22UyrvdCkuLubnP/85cHLnqhA/Nr0iQOp0OkwmU7ug6B267skbSElJCUVFRcycOdOv5Y8dO+b3N+S0tDRmz57NHXfcQWFhIRERESxYsIDKysqA6+l0OqmqquL111/vdJ7fibrbt9TU1C7Xdzgc2Gw20tLStF4JaB2WLC0t9asO5eXlvPDCC0Dr8OHChQvJz8+nuLgYVVU7beujR48SHx9PSEhIQB+kvkyaNInRo0dz33330dDQQP/+/Zk+ffpJlVVSUkJCQgKhoaE0NjZqr6elpZGfn9/pemlpaRw/flwro7CwkBUrVpxUHQJRUVHBJZdcclLrnuy+nljG6dpXf64BRVF45JFHWLVqFVdccQXDhw/v8npp2y4ns73m5maWL1/O8uXLiY+P56mnnuKaa65hzZo1nZ773V2XZrOZPn36oNfr/XrwpLv7TFd1DKScU7Fly5YO01y6u/90dX84Xfr27XtWrkshzlW9Ygg7OjqaCy+8kJiYGEwmEyEhIWRlZVFfX689BJOUlITJZDqj9fj8889JSUkhJydH+6adnZ3N5Zdf7nP5tWvXkpOTQ0JCAtA6v+4//uM/fC5rNBppamrS5uzV1dVRXl5+0nX985//zAMPPKD1/oSGhnLbbbdp35BdLheRkZGEhIQQEhIS8L758u677/LAAw8wYMAA9Ho9l156KRMnTmTlypXdrhseHs7MmTO1oeDy8nI8Ho82H6miooIhQ4YAYDAY2g0lHjlyhG+//ZZ58+ZhtVoxm83ccMMN/PSnP/W77l4mk4nS0lIaGhqA1g+Kkw2lxcXF5OXl8dhjjxEVFYXZbOb222/HarW265m+7rrryMzMRKfTMWrUKG666SbtA3vlypXk5OSQnZ0NtPZyTJw4sd1Q4enyxRdfMHjwYCZOnIheryciIoJbb7213TITJ070OVzv77625XK5iI2NxWw2YzQaT/u+dncN3HzzzRgMBpYuXcqzzz7LE088QVRUlLZ+V+1yMtu7++67tSBUVVWF3W7H7XZ3ee53d10ePnyYI0eOcPvtt2v1GDduHNHR0T7r2N19prM6BlpOT6uoqCAjIwOj0Qi0hvBT/RmjCRMmkJ6ejqIoDB8+nJtvvpmPP/4YCPy6zMnJoU+fPqdUHyHONb2iB7KiogJFUUhOTiYzMxO3201NTQ27du0CWnsok5OTaW5u1p6WPhOamprIzc3l3nvv5aabbsJgMHDw4EGWLl3qc/ktW7awfPlyXnzxRRwOB9XV1Rw+fJgBAwZ0WHbv3r2sXr2ahQsXUlBQQENDA1ar9aRvyqtXr8bhcPDiiy8SGhqKy+Vq96BHYWEhu3fv5uOPP2bJkiV8+OGHAe2bL++//z4ej4cFCxZgsVgoLi7m4Ycf5sCBA92u29TURENDA2+88QYALS0tLFu2TBtWXLx4MQ8++CCTJ0/m+PHj7NixgxEjRmjrP/nkk9x1110sX76c8PBwduzYwcKFCwM5ZAB88MEHpKen8/zzz1NSUkJdXd1JTSPwmj9/Prm5ubz99tsYjUZ27txJbm5uu970L7/8kttvv51Ro0Zhs9lYtmyZ9mT+3r17efTRR5kxYwZxcXEoisI333yjPchxOtlsNmbNmsX999/PPffcw5EjR3jnnXf4yU9+ArQ+ZX3PPfcQHR3ts+fFn31ta+vWreTk5PDRRx9x//33n/Z97eoauOCCC8jJyeHXv/41Ho+HvLw81q9fz7x585gzZw7QdbsEuj2A/fv3M3/+fMLCwnC73WzZsoV169YBdHnud3VdqqrKI488wuzZs3n33Xepq6vju+++6/Q+2N19pqs6BlJOT9u8eTNXXnkl7733HmVlZezcuZPDhw+fUpmbNm3iN7/5DSNHjqS6upo//vGP2rzqQM7VoKAgpk6dSnFx8WnpoRXiXKEkJSWp0DrPy+12Y7Vaz3adhDhvPPvss+Tl5bX72Z7eZMSIETz44INMmzYNgN/85jfs2bOHTZs2neWanVm9vV2EEKK3sdls6PV6rdOlVwxhCyHOPLPZzNNPP61NubBYLPzmN7/RwqLRaKS2tva8D49CCCFOXa8YwhZCnHlOp5M9e/bw6quvYjabcTqdbNiwgbfeegtonbO4evXqs1xLIYQQ5wIZwhZCCCGEEF2SIWwhhBBCCHFKJEAKIYQQQoiASIAUQgghhBABkQAphBBCCCECIgFSCCGEEEIERAKkEEIIIYQIiARIIYQQQggREAmQQgghhBAiIBIghRBCCCFEQCRACiGEEEKIgEiAFEIIIYQQAZEAKYQQQgghAiIBUgghhBBCBEQCpBBCCCGECIgESCGEEEIIERAJkEIIIYQQIiASIIUQQgghREAkQAohhBBCiIBIgBRCCCGEEAGRACmEEEIIIQIiAVIIIYQQQgREAqQQQgghhAiI4WxXQJxfoqKiMBqNKIpCZWUlHo/nbFdJCCGEEKeZPiIi4gkAVVVRVZXg4ODTvpHU1FQGDhxIcnIyAwYMICkpiZSUFDweD0FBQcTHx1NdXX3K28nKymLQoEGUlpae0eCSmZmJoig0NTWdsW1kZ2dTV1eHy+XSXgsKCmLEiBGUlpYGVFbb+sbExOB2u3G73ae7ylitVgwGA3q9HrfbTVRUFPX19e2WiY6OZuTIkdo5kJCQgMFgoK6uTltm5MiRXYZPk8lEnz59aGxs9Gv53sJgMDB06FASEhJwOp00Nzdr7yUnJ2vHICYm5pSuCb1ez6WXXkpiYiIpKSnaH5vN1u58CkRGRgYAzc3N3R7vtst2xdc5fj664IILyMjIIDk5uUNbtL0eTSYTw4cPp6ysrMvy0tLSGDx4cLvyQkNDqaqq6rBsYmIiVquV2tradu3W9nzrifuZEOLc19zcjE6nQ1EUoId6IA8fPszhw4cxGo2MGjWKrVu3au/FxMSclm3o9XosFgsVFRXExsYGHLICUVhYSEtLyxkr/3RrW9+YmBicTicOh+O0b0ev1+Nyuaivryc6Opra2lpCQ0O1oOdls9nYvXs3AGazmfT0dAYOHMiePXsA2LVrV5ehwmg0EhcXx7Fjx/xavreIjIykubmZ/fv3d3gvJSWFo0ePnrZttbS0tLvOTqdz5Xj3Jnv27MFms3V4/WSvx8LCQkpKSgJap227tT3fzrX7mRCid+gVQ9hGo5GsrCzCwsJQVZV//etfOJ1OFEVhwIABhIaGotPpqK+vp6CgAFVVO5QRHx9PRUUF5eXlZGVltQuQo0aNoqKiguDgYMLCwigqKsJisRAcHExDQwOHDh0CIDw8nH79+qHT6VBVlYKCAhoaGoiJiSE6OhpoDT+RkZFUVVVhs9kwm81kZGRgNpsBKCoqorKykj59+pCcnIyiKHg8Hvbt24fdbicjIwOPx4NerycoKAiHw8G+fftO6rjFx8cTGxsLgMvl4uDBg7hcLjIyMmhpaSEkJITCwkISExOpqqoiPDycqKgo7fWamhpSU1MJDg7GaDRy7Ngxjhw5ArR+sPXr1w+Px0NVVRXx8fF8++23XR4nr7i4OBwOh9ar3RWHw8GePXsYOXIkERER1NXVccEFF7B9+3bcbjeJiYkkJCSgKAqNjY0UFhYyaNAgzGYzQ4cOZefOne2Wj4yMJDU1FZ1OR0tLCwcPHqSxsZGYmBjtw9pkMmEymbQP1JCQEFJTUzEYDOh0OgoKCqiurm7X7rW1tfTt25e8vDyt9zYjI4P6+nrKy8vb7ZO3zgCNjY0cPHiQ0NBQbRsZGRkcOHBAW37IkCEYDAays7PZtWsX0Pk1YTKZSEtLw2g0otPpKC0t5fjx436fMyaTiWHDhlFZWUlwcDAhISEcPHiQ2tpaDAYDWVlZBAcH43Q6aWxspKWlhaKionZleI93cHAwaWlpWjsXFhZqPc5hYWEkJiYSHBxMfX09e/fu9at+iqKQkpKCxWJBr9fT1NTEvn37UFW1y2uns/PVZDJxwQUX8P333wNo7bBz585O2x1aR02io6NxuVzYbDaioqLIz88HOr/uAtWvX79212NdXR2KotCvXz8sFgtGo5F9+/a1653vjsFgIDMzk5CQEJxOJ01NTVrdvO02cODAdudb3759O9zPTCYTiqJQWFio9WyOGjWK8vJyQkNDCQ0Npby8/Ix+URdC9G69IkCGhISwc+dOWlpaSE9PJzo6mrKyMvr160d9fT2HDx8GWm+4CQkJPm9a8fHx7Nmzh6amJjweD+Hh4e2GT2tqaigqKiIpKYm4uDjtg/riiy/m8OHDGAwG+vfvz65du/B4PJhMJoYMGcKOHTuA1uHj/Px8PB4PkZGRWrmDBw/myJEjVFZWYjAYCA8PB8DtdmvLx8fHk5KSooUGt9uthdbs7GxCQkJ8Dh8NGzasw2venoKoqCjCwsK0D7XIyEjS09O1XjxFUbR99CoqKiI0NJSSkhJqa2sxmUyUl5dTV1eHTqdj1KhRHDt2DJ1OR2pqKjt27MDhcBAREUFKSgrQGmw6O04tLS0YjUZKS0uJiooiKirKr14Sj8dDdXU1UVFR7T4sre9JlkQAABbiSURBVFYrMTEx7NixA7fbjdVqxel0smfPHtLS0ti5c2e7ckwmE1lZWezcuZPm5mYiIyMZPHgw27ZtA1o/XPfs2YOqqqSmphITE0NpaSl6vZ4DBw7gcDgIDg5myJAh5OXldWj30NBQYmJiKC8vx2AwYLVatXbsrM4pKSmkp6ezd+9eCgsLCQ8P185nr127djF27Fgt5EDn10RmZiaHDh2iubkZRVEYMmQIjY2NHXp5DQYDF198cbvXvOUbDAZKS0txOp1ER0eTmJhIbW0tqampNDU1sWvXLnQ6HYMGDWr3xeBEycnJFBUVUVNTg8FgwGD49+3EG9Ch63Pcl8bGRoqLiwEYOHAgffr0oaKiAvB97Xg8nk7P16501u6xsbGEhYWxbds2PB5Pu7K6u+4606dPH/r3749er6eyspLCwkKf16PJZKKyspKioiJiYmJISkryGSD79etHcnKy9u9jx45RWFjIgAEDsNvt7N69W2vDE8Otr/PNa/DgwRQXF1NVVaUNqTc3N2tt19DQwNGjR9Hr9Vx00UUSIIX4EesVAbK2tlYLRk1NTdoHUUxMDMHBwfTp0wcAnU7nc15VZGQkLpdLu8mVlJSQkJDQLkB6PwhbWlpoamrSesbcbjc6nQ6LxYLZbCYrK6td2d6exbq6ug5zvkwmk/aB4C3b24Oh1+sZPHiw1gtgNBq19dp+INjtdvR6vc/jkp+f3y4YBAUFMXToUABiY2MJDg5m0KBB2vttt1FTU+OzzLa84TYpKYnm5mYcDgdGo5GwsDAqKyu1YbW289S6Ok7eEBgVFYWiKN3O5WpLURRtXoVXnz59KC0t1Xr8fA0BthUVFYXNZtPOkdraWux2O2FhYUDrOeBtd4fDoR13j8dDWloabreb2tradu3Rtt1LS0vJysqivLyc2NhYjh8/3uGcOLHOR48eZcyYMX4fBy9f14TJZCIiIoL+/ftry+l0OkJCQjoEyJaWFq3HuC2TyYTT6cTpdAKt55/3eouKitJChTfUtz2nTlRVVUVaWhpVVVVUVVW1u95sNpt2rJubmzs9x0+kqiphYWHEx8fjcDi0LyVevq6d8PDwTs/XrnTW7lFRUe3mUVdVVWGxWIDurztfvD3EBw4cQK/XM2jQIBITE31+uXI4HFpbtr0XnqioqMjn+lFRUdqXXn/asC2z2Yxer9d6HJ1OJ+Xl5VitVu3e6m1jt9vd4XoVQvy49IoA2RlFUSgqKuq25yI+Pp7Q0NB2PS4Gg4FDhw4F9LBIY2Ojz54Eb6+ir/r5YjAYSEtL4/vvv8flcmnDmafb8ePHAwppJ+rbty92u53i4mIMBoPf81E7O07gX3A9kaIoWCwWn3MDe0JWVhYHDx6krq5Omy7hS1NTE263m/DwcBISEvjXv/7Vo/X0ToforrfrVLfhr4qKCqqrq7FYLAwYMIDq6mptCsTJslqtREREaMd24MCBp1ReV/xt9xMFet21nWLQ0tLCsWPHiI6ODngOoz8URel22ogQQpwOvfp3ICsqKujXr5/2oRYdHd3hG7nBYCA6OprvvvuOb7/9VvtTWVlJXFyc39uqrq4mMjJS663yltsVbw+Jt4fUYDBgsVhQFAW32631gnT3NOrJqKysJCkpSetdCAkJ0ereFVVVtQ/Ktj26LS0tWn1ra2vp06eP1vsaGRmpbedkjlNXTCYTgwYNorGxsUP4rKysJDExUesZslqt6PX6dvvQVk1NDVarlaCgIAAiIiIICgrqchgWWo+D3W4HWtuqqw/g0tJSMjMzsdvtPh988LaLt37Jycl+PU3d2T615XA4cDgcJCYmaq955+KdDjU1NdqwqE6nIyoqqsvlo6KiUFWViooKCgoK2k3tOFl6vV5rA1VV/bp2ujpfvT2Y3ntI2y+DnbV7TU0NiYmJWnu0Pb+7uu68PXgnSktL03rl9Xo9sbGxWk+qP+0eiJqamnb3vdDQUJ/L+dqu937m3V/vw2rd9fwbjUZCQkJOseZCiHNNr+6BLCoqYsCAAYwYMQK3201zczO1tbXtlomLi6O6urpDT2NFRQUDBgzwe46Oy+XS5tZ5P2y887C6smfPHjIyMrSgW1BQgMvl4tixY2RlZdHc3Oz3EFIgvBPehw4dqv0MyInz8TpbLzMzk9LSUo4ePUp6ejqhoaF4PB4tnNvtdg4fPqyVXVFRoYXLkz1ObVmtVi6++GJ0Oh1ut5tjx475LMNmsxEUFMSFF16oPUTjHZb2ztn0DtdB65Dbvn37GDhwIHq9npaWFnbv3t3tz/scOnSI9PR0Ghsbu+2xrqqqIiMjo9Nj7a3ziBEjgH8/RNMdm83GRRdd1O0DVbt37yY9PZ3Y2FhUVfX50y3gew6kd05lZwoKCsjMzGTUqFHY7XZtPnFnvD9L5PF4UBSlw9xOfwwdOlQLbi6Xi+3btxMdHU1aWhpOp5OwsLBuA0xX56vH46GiooJhw4Zht9vbDW131u7Hjx8nLCyMUaNG4XA42v1kUVfX3YABA3A4HBQUFLSrn/de5J2vefz4ce2+1PZ69P6qgD9OnANZXV3N/v37KSgoICMjA4vFgsvl6vTLUGfn24n3s8LCwm5HgKKjo4mMjDzphwGFEOcmJSkpSYXWG633QQUh2v78TlhYGOnp6e3C2o9VSEgIgwYN0h7MOZ+YzWbcbjctLS0oisLgwYMpLS09Lb/ReqadzvNVp9MRFBSkBaekpCRMJlOHYHgi7whJIEFQCCHOFTabDb1er41e9OoeSHF2KIpCYmIiISEh2lDi2Zqf2Jv07duX2NhYv3oUz0VBQUEMGDBAG9602WznRHg83eerwWDQft5HVVUcDke7n13qjMvl6rRHWAghzjfSAymEEEIIIbp0Yg9kr36IRgghhBBC9D4SIIUQQgghREAkQAohhBBCiIBIgBRCCCGEEAGRACmEEEIIIQIiAVIIIYQQQgREAqQQQgghhAhIj/yQuKKAqsItI5uZNMxOlNnDrgoTi/4RzCFbaxUyolv47U8aGRLTQq1Tx4c/mHnn+xBtXSGEEEII0Tv0SIBUVZg9vpE7Lm8GuwpuiM9wMDzORc6fI1GAFTm1RIer4FCJD/Xw6H+6iQlWWbg5tCeqKIQQQggh/NQjAXJ0kpM7RjXhrgY8oNNBS7NKn3APC/6jAVVViQ4BV42KQQ8eD2BXuWNUE18VGPlnqaknqimEEEIIIfzQIwFy6sBmVBfgUNHrFFQ3GAFPtYeL4p0AeKpVjDoF1dM6MdPjUlFRmDrILgFSCCGEEKIX6ZGHaAZHtECziuJUUR2tw9SqQ0XnAk+jiqex9e/e9xRH67I0qwyJcHVb/ty5c9myZQuXXXZZh/f69+/P5s2beeutt87Erp2UadOmMXfuXJ/v/fKXv2Tt2rUoiqK9FhYWxldffcXIkSPbLfvKK6/w0EMPnbZ6zZ07l2nTpvm1bE5ODs888wwAqampfPLJJ6etHkIIIYTo3XokQEaiojQrKA4FHP/+Lw4Fxdn6hzbvqf//v0qzQiT+PUHjcDjIycnp8PpNN92E0+k83bt0xmzatAmLxUJWVpb22ujRowEYN26c9prZbGb48OFs2rSpx+sIrfVcvXr1Wdm2EEIIIc6uHhnCrm+ACFRUj4q3Y83bv6a0Wa7t31VVBR3U1bd9tXP/+Mc/+OlPf0pGRgYHDhwAICoqiquvvppPP/2U9PR0bdnk5GR++9vfMnjwYJxOJ1999RWvv/46drsdgHXr1rF06VJ++ctf8vnnn7Nq1SqSk5OZNWsWmZmZqKrKxo0bWbx4MS6X7x7Sa6+9lmnTphEZGUljYyPLly9n/fr1zJo1i4kTJ6LX67nsssu45ppr2pVRVVXF3r17GTt2LHv37gVag+Nf/vIXxo0bx+LFiwHIzs5GVVXy8vJQFIUbb7yRSZMmYbFYOHLkCEuXLuX7778HYMqUKYwcOZJjx44xfvx4brjhBoxGI3fddRdXXXUVer2eL774AoPh36dDamoqixcvZsWKFYwfP56EhAQqKyuZN28e1dXVjB07luHDh5Ofn99h3y0WC0uWLOHjjz9m5cqVfrWfEEIIIc4dPdID+VWJGaUF1GZQ7CqqXW19GtvHH9Wuti7TDEoLfF1q9msbtbW1rF+/vl0v5KRJk9i5cycHDx7UXgsNDWXp0qVs376d6667jttuu424uDjmzZvXrrxRo0Yxa9YsVq1ahdls5uWXX+bzzz9nwoQJXH/99QQFBXHvvff6rEtYWBi/+MUveOihh7jmmmtYtGgRjz76KDExMSxatIg//OEPfPbZZ1x11VU+A+imTZsYM2YMAIqiMHbsWN59913MZjNJSUkAXHzxxXz33Xc4nU6mTZvGxIkTeeihh/jP//xPli9fzoIFC8jIyNDKzM7O5ttvv+WGG24A4I477mD06NHk5uZy7bXXsm3bNq2n0ysiIoKmpiZmzZrF1KlTaW5uZtKkSV22g8Vi4bXXXuOzzz6T8CiEEEKcp3okQL5dEEJjrQIu8DSDYldQ7Qqc8Ee1Kyh2BU8z4IKmWoV3Dgf7vZ1Vq1ZxxRVXYLFYMBqNXH/99bz//vvtlvnZz35GSUkJ7733Hi6Xi9raWp599lnGjx+vhTOA5cuXU19fD8BVV13F0aNHWb9+PQAul4uFCxcyYcIEzOaOAbehoYF7772Xo0ePArB161bKysro27evX/vx9ddfM3jwYMLDwxk0aBDHjh2jqqqKrVu3asPYY8eO1Yavp06dyqJFiyguLsbj8bBlyxbWrFnD1KlTtTK/++47tm7dqv174sSJvPrqqxw9ehRVVfnqq6/YsmVLu3rU1dXx97//HWjtEd61axdxcXGd1jsyMpLf//73bNy4kT/96U9+7asQQgghzj09MoRd3Kzn9QPBzMlqosWuoiit8xpV/j1srbb5r1sFY7DCm4dCKLL7X8XCwkK2b9/O5MmTKSsro7Gxka1bt3L99ddryyQlJXHo0KF269XX11NZWUlCQgIlJSUdyk1JSSEtLY0lS5a0e72yspKYmBgtKHrp9XruvPNORo0aRUVFBdu3b8flcrV7MKYrBw8epKKigtGjR5OamqoFuy1btnDDDTewadMmkpKS2Lx5M2azGavV2mGfDh8+zNChQ32WbzabiYyM7LBOd9xud6f7YDQa+f3vf09KSgobNmwIqFwhhBBCnFt6JEDqgBVlYVwc4uTSaBcuh4pRaQ2LbR+RUYAWFYwmhW+OGnirNLT1J30C2Nb777/P/PnzsdlsrFq1qnUuZRslJSVcffXV7V6LiIggJiaGsrIyn2WWlJRQVFTEzJkz/arDpEmTGD16NPfddx8NDQ3079+f6dOnB7AX/x7GTk9P58UXXwQgLy+P+fPn89Of/pTdu3dTXV0NgM1mIy0tjby8PG399PR0SktLfZbtcDioq6sjLi5OK+NUhYaG8re//Q2DwcCCBQv4r//6L60HVwghhBDnlx4Zwvb8/z+zCyLZV6XH6FFosYPioM3T19BiB4Nb4bBNz+zCKNwqfj6D/W/fffcdNTU1xMbG+vxpmc8//5ykpCR+9atfYTabsVgszJ07l02bNvnsffSuk5KSQk5ODjpd6yHLzs7m8ssv97m8yWSitLSUhoYGoDWANjU1ae+7XC5iY2Mxm80YjUafZXz99ddcdtllxMbGag/TOBwOdu3axS233MLXX3+tLfvuu+/ywAMPMGDAAPR6PZdeeikTJ07scg7i2rVrmTFjhjYEn5KSwoUXXtjp8t2pqanhww8/ZPXq1ezcuZOnn34avV5/0uUJIYQQovfqkQDp3VC9R8+MIguHag0YtBDZ+ruPLQ4weBSK6/XcVRiFrUWHjsADJLT2Qq5ZswaHw9HhvcbGRnJzc7nwwgv56KOPWLFiBWVlZTz99NOdltfU1ERubi7Dhg3jgw8+4OOPP2b69OmdBs4PPvgAh8PB888/z8yZM7n55pu14AmtcyITExP56KOPSE1N9VnG9u3b0el0fPPNN3g8/+6D3bJlCxEREe0CpHd/FyxYwLp167j11lt5+OGHtafRfXnzzTcpKChgxYoVvPHGG9x6663tHjY6Fc8//zyRkZHk5uaelvKEEEII0bsoSUlJKoDH48HtdmO1Ws/YxrzD0TE6N8viahgc7MLtUlEBg1HhgN3AjGNRlLoNAQ9dCyGEEEKIM8Nms6HX67UOsR7rgYTWQKgDKjx6biu38H/VJvQeBYNH4esaE7eUWSU8CiGEEEL0cj3yEE1b3hBZr+q4t9rKky21GFCZVxeJW1EkPAohhBBC9HI9HiDh3wFRBf67PrL1H0r794QQQgghRO/Uo0PYQgghhBDi3CcBUgghhBBCBEQCpBBCCCGECIgESCGEEEIIERAJkEIIIYQQIiASIIUQQgghREAkQAohhBBCiIBIgBRCCCGEEAGRACmEEEIIIQIiAVIIIYQQQgREAqQQQgghhAiIBEghhBBCCBEQCZBCCCGEECIgEiCFEEIIIURAJEAKIYQQQoiASIAUQgghhBABkQAphBBCCCECIgFSCCGEEEIERAKkEEIIIYQIiARIIYQQQggREAmQQgghhBAiIAZfL4aGhvZ0PYQQQgghRC/U2NjY4TXpgRRCCCGEEAGRACmEEEIIIQIiAVIIIYQQQgREAqQQQgghhAiIBEghhBBCCBEQCZBCCCGEECIgEiCFEEIIIURAJEAKIYQQQoiASIAUQgghhBABkQAphBBCCCECIgFSCCGEEEIERAKkEOJH74YbbiA2Nrbb5RISEpg2bVoP1EgIIXo3fURExBMAqqqiqirBwcGYTKazXC0hhOgZM2bMYPr06YwfP57NmzfT2Njoc7mkpCQWLlzI+PHjiYiI4J///GcP11QIIc4Ol8tFc3MzOp0ORVEA6YEUQvzI2Ww2AOLj41m4cCFxcXEdlklKSuKll16iT58+qKrKkSNHerqaQgjRq0gPpBDiR23Xrl3U1dVx0UUXER4ezrhx49i6dSsNDQ0AJCcn8/LLLxMdHY3H4+Hll1/m73//+1mutRBC9BxfPZASIIUQP3r79u3j+PHjjBkzhvDwcMaPH8+WLVuwWq0sXLgQq9VKS0sLzz33HBs2bDjb1RVCiB7lK0AqSUlJKoDH48HtdmO1WgkNDT2rFRVCiLPh8ssv55FHHkGv13P8+HFMJhNRUVE4nU6eeeYZtm7derarKIQQPa6xsRGbzYZer0ena539aDjLdRJCiF5j48aNuFwuHn/8ce2pbIfDwbx589i+fftZrp0QQvQe8hCNEEK0sXnzZv77v/8bp9NJU1MTjzzyiIRHIYQ4gQxhCyGED8OGDcNut7N///6zXRUhhDirZAhbCCH8lJ+ff7arIIQQvZYMYQshhBBCiIBIgBRCCCGEEAHReX/PRwghhBBCiO4oitK+B1LCpBBCCCGEONGJGbHDELaqqj1WGSGEEEII0bv5yoYSIIUQQgghRKe6DJCKoqAoCna7vUcrJYQQQgghei+73a7lRK8OcyAlQAohhBBCCC9vgGxLB7RLlTqdjoaGhp6vnRBCCCGE6FUaGhq0//tMu7zYdiHvGzU1NRIihRBCCCF+xBoaGqipqekwfA2gJCcnazMjVVXV/ng8HjweD0FBQQQHB/tcWQghhBBCnB+8GbC5uRm73Y5Op0On02kZsG0O7PD/wm47lK0oCg6HQ5sXKU9oCyGEEEKcn7wZUFEU9Hq9z+DoZThxRVVV2y2o1+u1ROolQVIIIYQQ4vzQNve1DYwn/r2tTnsgvX/3BkoJjUIIIYQQ57cTA2Nn0xc7BMgTC+js30IIIYQQ4vzUXe7rNEB2VYD0RgohhBBCnB9OppPw/wE4ojBzR6/QYwAAAABJRU5ErkJggg=="
    }
   },
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Polyfill\n",
    "\n",
    "To convert a polygon to a set of DGGS cells, we \"fill\" it, the operation is called \"polyfilling\". It's conceptually similiar to rasterising a polygon.\n",
    "\n",
    "Just as we did to get the H3 cell of a point, we need to be explicit about our resolution. Let's try a higher resolution this time.\n",
    "\n",
    "Each additional resolution adds 7 times as many cells. 7 is therefore the H3 DGGS' \"aperture\".\n",
    "\n",
    "![Screenshot%20from%202022-04-28%2010-12-26.png](attachment:Screenshot%20from%202022-04-28%2010-12-26.png)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "resolution = 13\n",
    "chaletPolygonH3 = h3.polyfill_geojson(\n",
    "    chaletPolygonGeoJSON['geometry'], resolution\n",
    ")\n",
    "chaletPolygonH3"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Notice how much more terse this representation is: it only requires eight cell IDs. \n",
    "\n",
    "As text, compression would be extremely efficient (and lossless), since they all share the same prefix `8dbb2b66e37`. This makes a DGGS an excellent format for use with a web API (possibly avoiding the need for large `POST` payloads in favour of URL parameters.)\n",
    "\n",
    "Also, no funny characters, or flipping coordinates."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Now, let's `map` these H3 cells into Shapely polygons so we can look at them with GeoPandas.\n",
    "\n",
    "Since this is a nice opportunity to write a generic function that accepts a set of H3 cells to render them, we'll do that too."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import itertools\n",
    "from typing import Set\n",
    "\n",
    "from shapely.geometry import Polygon, Point\n",
    "\n",
    "def h3set_as_gdf(label: str, h3set: Set[str], asPolygon: bool = True) -> gpd.GeoDataFrame:\n",
    "    if asPolygon:\n",
    "        geomFunc = lambda cell: Polygon(h3.h3_to_geo_boundary(cell, geo_json=True))\n",
    "    else:\n",
    "        geomFunc = lambda cell: Point(h3.h3_to_geo(cell)[::-1])\n",
    "    gdf = gpd.GeoDataFrame({\n",
    "        'thing': itertools.repeat(label, len(h3set)),\n",
    "        'cellId': list(h3set),\n",
    "        'geometry': map(geomFunc, h3set)\n",
    "    }, crs='epsg:4326')\n",
    "    return gdf\n",
    "\n",
    "h3set_as_gdf('The Chalet', chaletPolygonH3, asPolygon=True).head()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "h3set_as_gdf('The Chalet', chaletPolygonH3).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "scrolled": true
   },
   "source": [
    "## Large things\n",
    "\n",
    "Wouldn't representing a large object require a lot of cells? That could be _more information_ than recording the outer ring as a series of coordinate pairs."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "path = gpd.datasets.get_path('naturalearth_lowres')\n",
    "world = gpd.read_file(path)\n",
    "oceania = world[(world.continent == \"Oceania\")]\n",
    "oceania.explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "How do we polyfill a GeoDataFrame?\n",
    "\n",
    "We'll lean on another dependency."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "pip install h3pandas"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "scrolled": true
   },
   "outputs": [],
   "source": [
    "import h3pandas\n",
    "\n",
    "resolution = 5\n",
    "oceania = oceania.h3.polyfill(resolution, explode=True)\n",
    "\n",
    "oceania.head(5)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "scrolled": true
   },
   "outputs": [],
   "source": [
    "oceania['geometry_h3'] = oceania.apply(\n",
    "    lambda row: Polygon(\n",
    "        h3.h3_to_geo_boundary(row.h3_polyfill, geo_json=True)\n",
    "    ),\n",
    "    axis=1\n",
    ")\n",
    "\n",
    "oceania.head(5)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "oceania = oceania.set_geometry('geometry_h3')\n",
    "oceania.explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "This is **only resolution 5**. Polyfill will result in a lot of cells at higher resolutions.\n",
    "\n",
    "But remember that this is a **hierarchical DGGS**, and we can use that to compress our representation of polygons."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "resolution = 5\n",
    "oceania = world[(world.continent == \"Oceania\")]\n",
    "oceania = oceania.h3.polyfill(resolution, explode=False)\n",
    "oceania"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "This added the `h3_polyfill` column:  a set of H3 cell ids that approximate the original polygon.\n",
    "\n",
    "Because our input was a MultiPolygon, this is in fact a list of lists, one list for each Polygon part of the original MultiPolygon.\n",
    "\n",
    "Let's \"compact\" them.\n",
    "\n",
    "**Compaction**: when all 7 of a cell's higher resolution \"children\" are present in a set, we can omit the 7 child IDs, and record just the parent cell ID. We can do this recursively until we have the smallest possible set of IDs without losing information.\n",
    "\n",
    "(Note: since we did `explode=False`, we're somewhat fighting against Pandas design for _panel data_, and it'd probably be better to use normalise the data.)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "import pandas as pd\n",
    "\n",
    "flattened = list(itertools.chain(*oceania.h3_polyfill))\n",
    "compacted = h3.compact(flattened)\n",
    "\n",
    "diff = len(flattened) - len(compacted)\n",
    "perc = diff / len(flattened) * 100.\n",
    "print('Set reduced by {0:,} cells ({1:.1f}%)'.format(diff, perc))\n",
    "\n",
    "h3set_as_gdf('Oceania', compacted).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Anywhere all of the \"children\" of a large \"parent\" cell are *all* present in the complete set, we can **store a reference to the parent instead of all of its children**.\n",
    "\n",
    "No information has been lost (except, possibly: the original higher resolution)."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## \"Doing GIS\"\n",
    "\n",
    "There are some foundational geospatial operations that we can implement with a DGGS.\n",
    "\n",
    "For two spatial objects, do/are they:\n",
    "- Equal\n",
    "- Disjoint (no point in common)\n",
    "- Touching (meet, but do not overlap)\n",
    "- Contained\n",
    "- Cover\n",
    "\n",
    "Because objects in DGGSs are often expressed in terms of sets, we can typically just use operations on sets rather than getting out our \"geometry crayons\". Working with sets lends itself well to functional programming and set theory. Terms like _intersection_, _union_, and _difference_ are familiar in both GIS and in sets (mathematics). Working with sets, it is often the case that complex ideas can be expressed in remarkably terse code — which makes for quite robust software.\n",
    "\n",
    "We'll use sample data from http://geojson.xyz/"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "antarctica = gpd.read_file('https://d2ad6b4ur7yvpq.cloudfront.net/naturalearth-3.3.0/ne_10m_admin_0_antarctic_claims.geojson')\n",
    "antarctica.explore()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "antarctic_nz = antarctica[(antarctica.sov_a3 == \"NZ1\")]\n",
    "antarctic_au = antarctica[(antarctica.sov_a3 == \"AU1\")]\n",
    "antarctic_gb = antarctica[(antarctica.sov_a3 == \"GB1\")]\n",
    "antarctic_chl = antarctica[(antarctica.sov_a3 == \"CHL\")]\n",
    "\n",
    "resolution = 3\n",
    "\n",
    "from typing import Union, Set, Any\n",
    "from shapely.geometry import Polygon, MultiPolygon, mapping\n",
    "\n",
    "def h3set(geom: Union[Polygon, MultiPolygon]) -> Set:\n",
    "    '''\n",
    "    Returns a Set of H3 cells representing a Shapely (Multi)Polygon\n",
    "    The result is a flat set (multiple geometry distinction is not retained)\n",
    "    '''\n",
    "    collection = geom.geoms if geom.geom_type == 'MultiPolygon' else [geom]\n",
    "    h3set = map(lambda geom: h3.polyfill_geojson(mapping(geom), resolution), collection)\n",
    "    h3set = itertools.chain(*h3set) # Flatten\n",
    "    return set(h3set)\n",
    "\n",
    "antarctic_nz_h3, antarctic_au_h3, antarctic_gb_h3, antarctic_chl_h3 = map(\n",
    "    lambda gdf: h3set(gdf.geometry.values[0]),\n",
    "    [antarctic_nz, antarctic_au, antarctic_gb, antarctic_chl]\n",
    ")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "h3set_as_gdf('British Antarctic Claim', antarctic_gb_h3).explore()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "scrolled": false
   },
   "outputs": [],
   "source": [
    "h3set_as_gdf('Chilean Antarctic Claim', antarctic_chl_h3).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We can get the set intesection of these two areas using Python's built-in `Set.intersection()` method.\n",
    "\n",
    "Example:\n",
    "\n",
    "```python\n",
    "x = {\"apple\", \"banana\", \"cherry\"}\n",
    "y = {\"google\", \"microsoft\", \"apple\"}\n",
    "\n",
    "z = x.intersection(y)\n",
    "\n",
    "print(z)\n",
    "\n",
    "{'apple'}\n",
    "```\n",
    "\n",
    "Exactly the same principle applies to H3 cell IDs, which are also (hexadecimal) strings (or 64-bit integers)."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "scrolled": true
   },
   "outputs": [],
   "source": [
    "disputed = antarctic_chl_h3.intersection(antarctic_gb_h3)\n",
    "\n",
    "h3set_as_gdf('Chilean/British Disputed Antarctic Claims', disputed).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Which parts of Antarctica are Chilean, and not disputed by the UK?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "undisputed = antarctic_chl_h3.difference(antarctic_gb_h3)\n",
    "h3set_as_gdf('Chilean/British Undisputed Antarctic Claims', undisputed).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Are the British claims a subset of the Chilean claims?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "antarctic_gb_h3.issubset(antarctic_chl_h3)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Let's explore both claims together."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "both_claims = antarctic_gb_h3.union(antarctic_chl_h3)\n",
    "h3set_as_gdf('Chilean/British Antarctic Claims', both_claims).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Set methods like `union` and `intersection` are built in to Python. Once you have DGGS cells, **it is possible to do some spatial analysis tasks using native Python without any dependencies.** These kinds of operations are extremely efficient, and a lot easier than using GIS libraries."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Do NZ and Australian claims intersect?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "not antarctic_nz_h3.isdisjoint(antarctic_au_h3)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Do NZ and Australian claims touch?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "# Touching?\n",
    "touches = lambda ab: h3.h3_indexes_are_neighbors(ab[0], ab[1])\n",
    "\n",
    "# Cartesian product of two sets\n",
    "product = itertools.product(antarctic_nz_h3, antarctic_au_h3)\n",
    "any(map(touches, product))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Do NZ and Chilean claims touch?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "product = itertools.product(antarctic_nz_h3, antarctic_chl_h3)\n",
    "any(map(touches, product))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Where do NZ and Australian claims touch?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "scrolled": true
   },
   "outputs": [],
   "source": [
    "# All combinations (Cartesian product)\n",
    "product = list(itertools.product(antarctic_nz_h3, antarctic_au_h3))\n",
    "\n",
    "boundary = set(\n",
    "    itertools.chain(*set(\n",
    "        itertools.compress(\n",
    "            product, \n",
    "            map(touches, product)\n",
    "        ) # All combinations where a.touches(b) is True\n",
    "    ))\n",
    ") # Working back from a pairwise data structure to a simple set\n",
    "\n",
    "h3set_as_gdf('NZ/Aus Antarctic border', boundary).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "This last one required us to calculate a Cartesian product, which is inefficient. We can re-work this using another useful property of a DGGS like H3: getting a cell's k-nearest neighbours.\n",
    "\n",
    "- k = 1 → returns a cell's 1st degree neighbours\n",
    "- k = 2 → returns a cell's 2nd degree neighbours\n",
    "- k = n → returns a cell's nth degree neigbours\n",
    "\n",
    "Another way to think of it is **buffering**."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "cell, k = '83ed1dfffffffff', 3\n",
    "h3set_as_gdf(f'{k} ring of {cell}', h3.k_ring(cell, k)).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "So if we take the k=1 neighbours of the NZ claims, and then check for intersection with the Australian claim, we can infer that they touch."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "k = 1\n",
    "kring = map(lambda cell: h3.k_ring(cell, k), antarctic_nz_h3)\n",
    "kring = set(itertools.chain(*kring)) # Flatten\n",
    "\n",
    "kring_exterior = kring.difference(antarctic_nz_h3) # Just get \"buffered\" cells, excluding any in the input set\n",
    "\n",
    "aus_border_cells = kring_exterior.intersection(antarctic_au_h3)\n",
    "\n",
    "h3set_as_gdf(f'{k} ring of {cell}', aus_border_cells).explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Lines?\n",
    "\n",
    "Representing lines in a DGGS seems odd at first. but remember: any line you've ever used in a GIS has some level of positional uncertainty or inaccuracy. It is not known to an infinite degree of precision, so representing a line as a set of DGGS cells (each with an explicit area) is not actually very different to what you're already doing.\n",
    "\n",
    "You may have converted a vector line to a raster; that is similar but involves a loss of even more information than converting it to an _ordered set_ of DGGS cells.\n",
    "- Order is retained\n",
    "- Lines can self-intersect (cells can be repeated)\n",
    "- In a hexagonal DGGS, there are six shared-edge directions, rather than four wth a shared-edge (and another four of a different type).\n",
    "\n",
    "Unfortunately, `h3-pandas` doesn't ([yet](https://github.com/DahnJ/H3-Pandas/issues/11)) have a function for encoding linestrings as H3 cells, like `polyfill` for polygons.\n",
    "\n",
    "Let's make one!"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "coastlines = gpd.read_file('https://d2ad6b4ur7yvpq.cloudfront.net/naturalearth-3.3.0/ne_50m_coastline.geojson')\n",
    "coastlines.explore()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "scrolled": true
   },
   "outputs": [],
   "source": [
    "from shapely.geometry.linestring import LineString\n",
    "from shapely.geometry.multilinestring import MultiLineString\n",
    "from typing import Iterator, Union\n",
    "\n",
    "def sequential_deduplication(func: Iterator[str]) -> Iterator[str]:\n",
    "    '''\n",
    "    Decorator that doesn't permit two consecutive items to be the same\n",
    "    '''\n",
    "    def inner(*args):\n",
    "        iterable = func(*args)\n",
    "        last = None\n",
    "        while (cell := next(iterable, None)) is not None:\n",
    "            if cell != last:\n",
    "                yield cell\n",
    "            last = cell\n",
    "    return inner\n",
    "\n",
    "@sequential_deduplication\n",
    "def h3polyline(line: Union[LineString, MultiLineString], resolution: int) -> Iterator[str]:\n",
    "    '''\n",
    "    Iterator yeilding H3 cells representing a line,\n",
    "    retaining order and self-intersections\n",
    "    '''\n",
    "    if line.geom_type == 'MultiLineString':\n",
    "        # Recurse after getting component linestrings from the multiline\n",
    "        for l in map(lambda geom: h3polyline(geom, resolution), line.geoms):\n",
    "            yield from l\n",
    "    else:\n",
    "        coords = zip(line.coords, line.coords[1:])\n",
    "        while (vertex_pair := next(coords, None)) is not None:\n",
    "            i, j = vertex_pair\n",
    "            a = h3.geo_to_h3(*i[::-1], resolution)\n",
    "            b = h3.geo_to_h3(*j[::-1], resolution)\n",
    "            yield from h3.h3_line(a, b) # inclusive of a and b\n",
    "\n",
    "resolution = 3\n",
    "coastlines_h3 = list(map(lambda geom: h3polyline(geom, resolution), coastlines.geometry))#[:2]\n",
    "coastlines_h3 = list(itertools.chain(*coastlines_h3)) # flatten\n",
    "\n",
    "coastlines_h3_gdf = h3set_as_gdf('World Coastlines H3', coastlines_h3, asPolygon=False)\n",
    "\n",
    "coastlines_h3_gdf.explore()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "What parts of the coastline are subject to Antarctic claims, and who claims them?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "# Polyfill \"official\" Antarctic claims\n",
    "antarctica_h3 = antarctica[(antarctica['type'] == 'Official')].h3.polyfill(resolution, explode=True)\n",
    "\n",
    "# Join (merge) our coastlines H3 set with the Antarctic claims\n",
    "merged = coastlines_h3_gdf.merge(antarctica_h3, left_on='cellId', right_on='h3_polyfill', suffixes=[None, '_'])\n",
    "\n",
    "# Render it\n",
    "merged.explore(column='name', cmap='Set1')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Can we work **across different resolutions**? What if we H3-indexed our coastlines coarsely, but our Antarctic claims at a higher resolution?\n",
    "\n",
    "Some bindings, notably [`h3-pg`](https://github.com/bytesandbrains/h3-pg/blob/master/docs/api.md#r-tree-operators) (H3 bindings for PostgreSQL/PostGIS), have special operators to efficiently handle operations that work across resolutions.\n",
    "\n",
    "> ## R-tree Operators\n",
    "> \n",
    "> Operator: `h3index && h3index`\n",
    "> \n",
    "> Returns `true` if the two H3 indexes intersect\n",
    ">\n",
    "> ---\n",
    "> \n",
    "> Operator: `h3index @> h3index`\n",
    "> \n",
    "> Returns `true` if A contains B\n",
    "> \n",
    "> ---\n",
    "> \n",
    "> Operator: `h3index <@ h3index`\n",
    "> \n",
    "> Returns `true` if A is contained by B\n",
    "> \n",
    "> ---\n",
    "> \n",
    "> Operator: `h3index <-> h3index`\n",
    "> \n",
    "> Returns the distance in grid cells between the two indices\n",
    "\n",
    "In Python we will just take a cell and use the API to calculate its parent cell at a specific resolution, to do a table join.\n",
    "\n",
    "The alternative would be to perform a polyfill on both inputs at the same, higher resolution. This can be expensive if one or both datasets is very large or detailed. Also, it may not be sensible to represent a dataset at a particularly high H3 resolution if it isn't actually recorded with high precision. You may have also received a dataset with location encoded as H3 cells at a lower resolution than the rest of your analysis."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "scrolled": true
   },
   "outputs": [],
   "source": [
    "lower_res = 2\n",
    "higher_res = 4\n",
    "antarctica_h3 = antarctica[(antarctica['type'] == 'Official')].h3.polyfill(higher_res, explode=True)\n",
    "\n",
    "coastlines_h3 = list(map(lambda geom: h3polyline(geom, lower_res), coastlines.geometry))#[:2]\n",
    "coastlines_h3 = list(itertools.chain(*coastlines_h3)) # flatten\n",
    "\n",
    "coastlines_h3_gdf = h3set_as_gdf('World Coastlines H3', coastlines_h3, asPolygon=False)\n",
    "\n",
    "# Pandas doesn't do merge/join with functions, so we create an extra column containing the higher resolution\n",
    "#   cell's parent (lower-resolution) cell ID\n",
    "lowResColName = f'cellId_res_{lower_res}'\n",
    "antarctica_h3[lowResColName] = [h3.h3_to_parent(cell, lower_res) for cell in antarctica_h3['h3_polyfill']]\n",
    "\n",
    "merged = coastlines_h3_gdf.merge(\n",
    "    antarctica_h3,\n",
    "    left_on='cellId',\n",
    "    right_on=lowResColName,\n",
    "    # how='left', # Include this if you want to keep unmatched parts of the world coastline\n",
    "    suffixes=[None, '_']\n",
    ")\n",
    "\n",
    "merged.explore(column='name', cmap='Set1')\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Other things\n",
    "\n",
    "- Very few people want to consume DGGS output. Converting from a DGGS to a raster or vector is not easy. But using a DGGS internally can make analysis a lot simpler, and it involves explicit accounting of positional accuracy.\n",
    "- What's the best way to represent a raster in a DGGS? What's an efficient way to index it?\n",
    "- High resolution polyfilling can be extremely resource intensive and take a long time. In Pandas there are ways to perform indexing on rows in parallel. I've done most of my H3 work in PostgreSQL. Polyfilling is by far the most expensive part of any pipeline with H3—but once it is done, doing analysis and extracting results tends to be very fast.\n",
    "    - Running analysis pipelines at a low resolution is an effective way of validating a method or process quickly; and once satisfied, a longer run can be kicked off at a higher resolution."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "![I wrote 20 short programs in Python yesterday. It was wonderful. Perl, I'm leaving you.](https://imgs.xkcd.com/comics/python.png)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "# import antigravity"
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.9.12"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}

Any questions, feel free to leave a comment

Best usage example: after installing Jupyter Notebook, download this file and run jupyter notebook in a conda environment, in the same directory. The Python version must be at least 3.8 in order to have GeoPandas >= 0.10.

This is ideal for making use of the frequent use of explore on GeoDataFrames in this notebook.