4. Statistical Data Modeling.ipynb

{
 "metadata": {
  "name": "4. Statistical Data Modeling"
 },
 "nbformat": 3,
 "nbformat_minor": 0,
 "worksheets": [
  {
   "cells": [
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "# Statistical Data Modeling\n",
      "\n",
      "Some or most of you have probably taken some undergraduate- or graduate-level statistics courses. Unfortunately, the curricula for most introductory statisics courses are mostly focused on conducting **statistical hypothesis tests** as the primary means for interest: t-tests, chi-squared tests, analysis of variance, etc. Such tests seek to esimate whether groups or effects are \"statistically significant\", a concept that is poorly understood, and hence often misused, by most practioners. Even when interpreted correctly, statistical significance is a questionable goal for statistical inference, as it is of limited utility.\n",
      "\n",
      "A far more powerful approach to statistical analysis involves building flexible **models** with the overarching aim of *estimating* quantities of interest. This section of the tutorial illustrates how to use Python to build statistical models of low to moderate difficulty from scratch, and use them to extract estimates and associated measures of uncertainty."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "import numpy as np\n",
      "import pandas as pd\n",
      "\n",
      "# Set some Pandas options\n",
      "pd.set_option('display.notebook_repr_html', False)\n",
      "pd.set_option('display.max_columns', 20)\n",
      "pd.set_option('display.max_rows', 25)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 1
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Estimation\n",
      "==========\n",
      "\n",
      "An recurring statistical problem is finding estimates of the relevant parameters that correspond to the distribution that best represents our data.\n",
      "\n",
      "In **parametric** inference, we specify *a priori* a suitable distribution, then choose the parameters that best fit the data.\n",
      "\n",
      "* e.g. $\\mu$ and $\\sigma^2$ in the case of the normal distribution"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "x = array([ 1.00201077,  1.58251956,  0.94515919,  6.48778002,  1.47764604,\n",
      "        5.18847071,  4.21988095,  2.85971522,  3.40044437,  3.74907745,\n",
      "        1.18065796,  3.74748775,  3.27328568,  3.19374927,  8.0726155 ,\n",
      "        0.90326139,  2.34460034,  2.14199217,  3.27446744,  3.58872357,\n",
      "        1.20611533,  2.16594393,  5.56610242,  4.66479977,  2.3573932 ])\n",
      "_ = hist(x, bins=8)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAWoAAAECCAYAAADXf53UAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEENJREFUeJzt3G9IlffDx/GPfzpa2fmdLMxtIlnZstZ/K8QiswhKuRkb\nFFhgRLGZ0qJ2l2wPasWy4Wxu61QMG+vJYOxBsI2xcbex6LbGNj0NmWVZQUkrl5WezKPHc677gc1f\n7TbP6WfnXN+29+uZeKEfDN9cfs+5irEsyxIAwFixdg8AAAyOUAOA4Qg1ABiOUAOA4Qg1ABiOUAOA\n4eJDXXDt2jVVV1f3f3zjxg2tXr1aK1eujOgwAECfmMd5H3UwGNSrr76qvXv3auzYsZHcBQC477GO\nPhoaGjRu3DgiDQBR9Fihrq2t1cKFCyO1BQAwgLBD3dvbq7q6OuXk5ERyDwDgL0K+mPgnj8ejCRMm\nyOl0Dvj5H3/8UZ2dnU9sGAD8E7hcLs2dO3fQa8IOdW1trXJzcx/5+c7OTs2ZMyf8dRHywf9e0Vfn\n2mzd8P5/TVZWykhbNwB4OtTX14e8JqyjD5/Pp4aGBi1YsGDIowAAjyesO+rExEQdOXIk0lsAAAPg\nyUQAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoA\nMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMFx8qAt8Pp9qamp0\n5coV+f1+lZSUaPLkydHYBgBQGKGuqanR1KlTVVZWpkAgoO7u7mjsAgDcN+jRx71793Tu3Dnl5+dL\nkuLi4jRixIioDAMA9Bn0jrq1tVVOp1Nut1uXLl1SZmam1q9fL4fDEa19APCPN2ioA4GALl68qJde\nekkbN27URx99pNOnT2vx4sXR2och+L2jW613e2zdkJLk0DPOBFs3AE+7QUM9ZswYJSUlKTs7W5KU\nm5urEydOEOqnROvdHv331822bqhcOYlQA0M06Bm1y+VSamqqLly4oGAwqPr6es2YMSNa2wAACuNd\nH6WlpXK73ero6FB6errWrFkTjV0AgPtChvrZZ5/V22+/HY0tAIAB8GQiABiOUAOA4Qg1ABiOUAOA\n4Qg1ABiOUAOA4Qg1ABiOUAOA4Qg1ABiOUAOA4Qg1ABiOUAOA4Qg1ABiOUAOA4Qg1ABiOUAOA4Qg1\nABiOUAOA4Qg1ABiOUAOA4Qg1ABiOUAOA4Qg1ABguPpyLSktLNXz4cMXGxiouLk4VFRWR3gUAuC+s\nUEvSrl27lJSUFMktAIABhH30YVlWJHcAAB4hrDvqmJgY7d69WzExMVq+fLmWLVsW6V0AgPvCCvWe\nPXs0evRotbS0qKKiQs8995yysrIivQ0AoDCPPkaPHi1JSktL0/z589Xc3BzRUQCAfwsZ6u7ubnV1\ndUmSOjo65PF4lJ6eHvFhAIA+IY8+2tvbVVlZKUkaNWqUCgoKNHPmzIgPAwD0CRnqlJSU/lADAKKP\nJxMBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gB\nwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHBhhToYDGr79u3a\nt29fpPcAAP4irFB//fXXSktLU0xMTKT3AAD+ImSo29ra5PF4lJ+fL8uyorEJAPCAkKE+evSo1q5d\nq9hYjrMBwA7xg32yrq5OTqdTGRkZ+u2336K16alnWZZ+vea1e4Z6AkG7JwB4AgYNdVNTk+rq6uTx\neOT3+9XV1aUDBw6orKwsWvueSu2+Xu38n8t2z9DOZRl2TwDwBAwa6qKiIhUVFUmSGhsb9cUXXxBp\nAIiyxzp45l0fABB9g95RP2jq1KmaOnVqJLcAAAbAWzkAwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAM\nR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gBwHCEGgAMR6gB\nwHCEGgAMR6gBwHCEGgAMR6gBwHDxoS7o6enRrl275Pf75XA4lJOTo8LCwmhsAwAojFA7HA7t3LlT\nCQkJ8vv9Ki8vV3Z2tlJTU6OxDwD+8cI6+khISJAk+Xw+BQIBxceH7DsA4AkJq7jBYFA7duzQ1atX\ntW7dOo0dOzbSuwAA94UV6tjYWFVWVqq1tVUVFRV6/vnnlZGREelt+BuIi5V+vea1dUNKkkPPOBNs\n3QAMxWOdYaSkpGj27NlqbGwk1AhLuy+gt45ftnVD5cpJhBpPtZBn1B0dHers7JQkeb1enTlzRunp\n6REfBgDoE/KO+s6dO3K73QoGg3K5XCosLNT06dOjsQ0AoDBCnZ6ernfeeScaWwAAA+DJRAAwHKEG\nAMMRagAwHKEGAMMRagAwHKEGAMMRagAwHKEGAMMRagAwHKEGAMMRagAwHKEGAMMRagAwHKEGAMMR\nagAwHKEGAMMRagAwHKEGAMMRagAwHKEGAMMRagAwHKEGAMMRagAwXHyoC27evCm326329nY5nU7l\n5eUpLy8vCtMAAFIYoY6Pj1dxcbHGjx+vjo4Obdu2TZMmTVJaWlo09gHAP17Iow+Xy6Xx48dLkpxO\npyZOnKjbt29HehcA4L7HOqO+fv26WlpalJmZGak9AIC/CHn08Sefz6fq6moVFxcrMTExkpuAJyou\nVvr1mtfuGUpJcugZZ4LdM/AUCivUvb29qqqq0qJFizRv3rxIbwKeqHZfQG8dv2z3DFWunESo8R8J\nefRhWZYOHz6stLQ0FRQURGMTAOABIe+om5qadPLkSaWnp2v79u2SpKKiIs2aNSvi4wAAYYR6ypQp\n+uyzz6KxBQAwAJ5MBADDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByh\nBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDDEWoAMByhBgDD\nxYe64ODBg/J4PHI6naqqqorGJgDAA0LeUS9ZskRvvPFGNLYAAAYQMtRZWVkaOXJkNLYAAAbAGTUA\nGC7kGTWAJyMuVvr1mtfWDUmOON3tCfzjN0hSSpJDzzgT7J4RFkINREm7L6C3jl+2dcPOZRlsuK9y\n5aSnJtQcfQCA4ULeUVdXV+vs2bPyer0qKSnRqlWrtGTJkmhsAwAojFBv2bIlGjsAAI/A0QcAGI5Q\nA4DhCDUAGI5QA4DhCDUAGI5QA4DhCDUAGI5QA4DhCDUAGI5QA4DhCDUAGI5QA4DhCDUAGI5QA4Dh\nCDUAGI5QA4DhCDUAGI5QA4DhCDUAGI5QA4DhCDUAGI5QA4Dh4kNd0NjYqKNHjyoQCGjp0qVasWJF\nNHYBAO4b9I46GAzq0KFD2rZtm/bt26fvv/9eLS0t0doGAFCIUDc3Nys1NVUpKSmKj49Xbm6ufvnl\nl2htAwAoRKhv3bqlMWPG9H+cnJysW7duRXwUAODfQp5RP20WTRit5/6VaOuGuJgYW78/gL+XGMuy\nrEd98vz58/r888/15ptvSpKOHTummJgYvfjii//v2rq6Ot25cydySwHgb8jlcmnu3LmDXjPoHfXE\niRN1/fp1tba2Kjk5WadOndJrr7024LWhvhEA4D8z6B211Pf2vE8++aT/7XkrV66M1jYAgMIINQDA\nXjyZCACGI9QAYLgn8vY8Ex8zP3jwoDwej5xOp6qqquyeI0m6efOm3G632tvb5XQ6lZeXp7y8PFs3\n9fT0aNeuXfL7/XI4HMrJyVFhYaGtm/4UDAZVXl6u5ORklZeX2z1HpaWlGj58uGJjYxUXF6eKigq7\nJ8nn86mmpkZXrlyR3+9XSUmJJk+ebOuma9euqbq6uv/jGzduaPXq1ba/vnX8+HH98MMP8vv9ysrK\n0rp162zdI0nffPONvvrqKzkcDhUUFGjp0qUDX2gNUSAQsMrKyqwbN25Yfr/fev31162rV68O9csO\nWWNjo3Xp0iVr69atdk/pd/v2bevy5cuWZVlWe3u7tWHDBiN+Vj6fz7Isy+rp6bG2bt1q/f777zYv\n6vPll19a77//vrVv3z67p1iWZVmbNm2yvF6v3TMe8uGHH1rfffedZVmW1dvba3V2dtq86GGBQMDa\nuHGj9ccff9i6w+v1Wps2bbK6urqsQCBg7d271/J4PLZu6uzstDZv3mx5vV6rq6vLKi8vf+Tv3pCP\nPkx9zDwrK0sjR460e8ZDXC6Xxo8fL0lyOp2aOHGibt++be8oSQkJCZL67s4CgYDi4+1/DqqtrU0e\nj0f5+fmyDHq926Qt9+7d07lz55Sfny9JiouL04gRI2xe9bCGhgaNGzdOY8eOtXWHw+GQ1Pcz6+np\nUXd3t5KSkmzd1NTUpIyMDCUlJSkxMVHTpk3TTz/9NOC1Q/6NHOgx8+bm5qF+2b+969evq6WlRZmZ\nmXZPUTAY1I4dO3T16lWtW7fO9l8qSTp69KjWrl2rrq4uu6f0i4mJ0e7duxUTE6Ply5dr2bJltu5p\nbW2V0+mU2+3WpUuXlJmZqfXr1/dHyQS1tbVauHCh3TPkcDi0YcMGlZaWatiwYVqxYoUmTZpk66as\nrCx9/PHHam1t1bBhw+TxePTCCy8MeC0vJtrA5/OpurpaxcXFSky093F3SYqNjVVlZaU++OADffvt\nt7p8+bKte+rq6uR0OpWRkWHUHeyePXtUWVmpzZs369ixYzp79qytewKBgC5evKgFCxaooqJCvb29\nOn36tK2bHtTb26u6ujrl5OTYPUUdHR2qqanRe++9J7fbrfPnz6u+vt7WTYmJiSouLtaRI0e0f/9+\nZWVlKeYR//3EkO+ok5OT1dbW1v9xW1ubkpOTh/pl/7Z6e3tVVVWlRYsWad68eXbPeUhKSopmz56t\nxsZGZWRk2LajqalJdXV18ng88vv96urq0oEDB1RWVmbbJkkaPXq0JCktLU3z589Xc3OzsrKybNsz\nZswYJSUlKTs7W5KUm5urEydOaPHixbZtepDH49GECRPkdDrtnqLm5mZlZmYqNTVVkpSTk6PGxkbN\nmTPH1l3Z2dn9/36ffvrpI/+aHfId9YOPmff29urUqVP93xgPsyxLhw8fVlpamgoKCuyeI6nvTqOz\ns1OS5PV6debMGaWnp9u6qaioSIcOHZLb7daWLVs0bdo02yPd3d3dfwzT0dEhj8dj+8/J5XIpNTVV\nFy5cUDAYVH19vWbMmGHrpgfV1tYqNzfX7hmSpClTpujixYu6e/eu/H6/PB6PZs6cafcstbe3S+p7\nR9jPP//8yGOiId9Rx8XFqaSkRO+++27/2/PS0tKG+mWHrLq6WmfPnpXX61VJSYlWrVqlJUuW2Lqp\nqalJJ0+eVHp6urZv3y6pL0qzZs2ybdOdO3fkdrsVDAblcrlUWFio6dOn27ZnII/6czCa2tvbVVlZ\nKUkaNWqUCgoKjPhFLy0tldvtVkdHh9LT07VmzRq7J0nqO95raGjQK6+8YvcUSdKIESP08ssvq7Ky\nUj09PZo5c6amTZtm9yzt379fnZ2dSkxMVGlp6SNfDOYRcgAwHC8mAoDhCDUAGI5QA4DhCDUAGI5Q\nA4DhCDUAGI5QA4DhCDUAGO7/AJwLUlXIi0vUAAAAAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11335a110>"
       ]
      }
     ],
     "prompt_number": 2
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Fitting data to probability distributions\n",
      "\n",
      "We start with the problem of finding values for the parameters that provide the best fit between the model and the data, called point estimates. First, we need to define what we mean by \u2018best fit\u2019. There are two commonly used criteria:\n",
      "\n",
      "* **Method of moments** chooses the parameters so that the sample moments (typically the sample mean and variance) match the theoretical moments of our chosen distribution.\n",
      "* **Maximum likelihood** chooses the parameters to maximize the likelihood, which measures how likely it is to observe our given sample."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Discrete Random Variables\n",
      "\n",
      "$$X = \\{0,1\\}$$\n",
      "\n",
      "$$Y = \\{\\ldots,-2,-1,0,1,2,\\ldots\\}$$\n",
      "\n",
      "**Probability Mass Function**: \n",
      "\n",
      "For discrete $X$,\n",
      "\n",
      "$$Pr(X=x) = f(x|\\theta)$$\n",
      "\n",
      "![Discrete variable](http://upload.wikimedia.org/wikipedia/commons/1/16/Poisson_pmf.svg)"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "***e.g. Poisson distribution***\n",
      "\n",
      "The Poisson distribution models unbounded counts:\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$$Pr(X=x)=\\frac{e^{-\\lambda}\\lambda^x}{x!}$$\n",
      "\n",
      "* $X=\\{0,1,2,\\ldots\\}$\n",
      "* $\\lambda > 0$\n",
      "\n",
      "$$E(X) = \\text{Var}(X) = \\lambda$$"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Continuous Random Variables\n",
      "\n",
      "$$X \\in [0,1]$$\n",
      "\n",
      "$$Y \\in (-\\infty, \\infty)$$\n",
      "\n",
      "**Probability Density Function**: \n",
      "\n",
      "For continuous $X$,\n",
      "\n",
      "$$Pr(x \\le X \\le x + dx) = f(x|\\theta)dx \\, \\text{ as } \\, dx \\rightarrow 0$$\n",
      "\n",
      "![Continuous variable](http://upload.wikimedia.org/wikipedia/commons/e/ec/Exponential_pdf.svg)"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "***e.g. normal distribution***\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$$f(x) = \\frac{1}{\\sqrt{2\\pi\\sigma^2}}\\exp\\left[-\\frac{(x-\\mu)^2}{2\\sigma^2}\\right]$$\n",
      "\n",
      "* $X \\in \\mathbf{R}$\n",
      "* $\\mu \\in \\mathbf{R}$\n",
      "* $\\sigma>0$\n",
      "\n",
      "$$\\begin{align}E(X) &= \\mu \\cr\n",
      "\\text{Var}(X) &= \\sigma^2 \\end{align}$$"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Example: Nashville Precipitation\n",
      "\n",
      "The dataset `nashville_precip.txt` contains [NOAA precipitation data for Nashville measured since 1871](http://bit.ly/nasvhville_precip_data). The gamma distribution is often a good fit to aggregated rainfall data, and will be our candidate distribution in this case."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "precip = pd.read_table(\"data/nashville_precip.txt\", index_col=0, na_values='NA', delim_whitespace=True)\n",
      "precip.head()"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 3,
       "text": [
        "       Jan   Feb   Mar    Apr   May   Jun   Jul   Aug   Sep   Oct   Nov   Dec\n",
        "Year                                                                         \n",
        "1871  2.76  4.58  5.01   4.13  3.30  2.98  1.58  2.36  0.95  1.31  2.13  1.65\n",
        "1872  2.32  2.11  3.14   5.91  3.09  5.17  6.10  1.65  4.50  1.58  2.25  2.38\n",
        "1873  2.96  7.14  4.11   3.59  6.31  4.20  4.63  2.36  1.81  4.28  4.36  5.94\n",
        "1874  5.22  9.23  5.36  11.84  1.49  2.87  2.65  3.52  3.12  2.63  6.12  4.19\n",
        "1875  6.15  3.06  8.14   4.22  1.73  5.63  8.12  1.60  3.79  1.25  5.46  4.30"
       ]
      }
     ],
     "prompt_number": 3
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "_ = precip.hist(sharex=True, sharey=True, grid=False)\n",
      "tight_layout()"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEZCAYAAADCJLEQAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlcVPX+P/DXsCPbMBJoIoICapYLLmWWK3pvZt1c8ndF\nEzJTSfymZYG7pYbL1VQ0LS0VvPUt7801l3Kva3aVxQrEK5oLKaKsA7EMM5/fH36Zy8DADMMMM8y8\nno8Hj4dzzpnhfXh75n2Wz3kfiRBCgIiIyMLYmTsAIiIibVigiIjIIrFAERGRRWKBIiIii8QCRURE\nFokFioiILBILFBGRlVm6dClCQkLMHUaT2USB+v333+Hg4IB27dpBqVSaOxybx3xYjqioKNjZ2cHO\nzg6tWrVCaGgohg8fjh07djA3ZlYzNzV/vvrqK3OH1mxsokB9+umn6Ny5M8rKynDw4MEmf15lZaUR\norJdxs4HNc3AgQORk5ODrKwsJCYm4rnnnkNsbCzCwsJQVlZm7vBsWnVuav785S9/MXdYzcbqC5RK\npcJnn32GWbNmYeLEifjkk0805gcGBmLZsmWYM2cO2rdvj8DAQMTHx2tdJjY2FiEhIRg0aFBzroJV\n0ScfK1as0Jg2depUDBkyRP1aoVBgzpw5aNeuHTp27IgFCxZgyZIlVnFKwxwcHR3h6+uLRx99FE89\n9RTeeust/PTTT8jKykJcXJx6ucTERISFhcHDwwOhoaH44IMPNI6yVCoVPvzwQ3Tv3h1ubm7w9/fH\n//zP/5hjlayGk5MTfH19NX6cnZ1x5coVvPjii2jTpg18fX0xduxY3Lp1q877Dx8+jN69e0Mmk+Gl\nl15Cbm6uGdbCcFZfoI4cOYL8/HxMmjQJ06ZNw7fffoubN29qLLN+/Xp4enri5MmTWL58OVasWIGN\nGzfWWcbNzQ1HjhzBjh07mnMVrIqufEgkEkgkkjrvqzlt7ty5+OKLL/Dxxx/j6NGjUKlU2Lx5s9b3\nkWGCgoIwadIk7Nu3DwCwbt06xMbG4rXXXsP58+cxd+5cJCQk4L333lO/580338TKlSsRGxuLX3/9\nFfv27UNwcLC5VsEqaOtEd+vWLfTu3RsdOnTA119/jc8//xylpaUYPnw4Kioq1MvdvXsXa9aswbZt\n2/Dtt9/i7t27GDlyZHOG33TCyr344oti+vTp6tcDBgwQCxcuVL/u0KGDCAwM1HjPxIkTRfv27TWW\n6dSpk+mDtQG68hEYGChWrFih8Z7XXntNDB48WAghRElJiXBychKLFy/WWKZt27YiJCTEhJFbp8jI\nSBEeHq513tq1a4VEIhFyuVy4u7uLbdu2acxfvny5kEqlQgghbt68Kezt7cU///lPk8dsKyIjI4WD\ng4Nwd3dX/3Tu3FlMnz5dDBgwQGPZmzdvCgcHB7Fv3z4hhBBLliwREolEnD59Wr3Md999JyQSiThx\n4kSzrkdTWPUR1O+//47Dhw9jxowZ6mnTpk3DZ599BpVKBeDhnnl4eLjG+4YPH47s7GyUlJSol/nz\nn//cfIFbKX3yoUtWVhYUCgWGDx+uMT08PFzr3iYZTggBiUSCW7duobS0FLNnz4aHh4f6Z8WKFSgu\nLkZeXh5+/vlnqFQqjBgxwtxhW5WnnnoKly5dUv8cO3YMKSkpuHjxokYuunXrBiEEsrKy1O91dXXF\n008/rX79zDPPwNXVFRkZGeZYFYM4mDsAU/r000+hVCrRt29fjekqlQoHDhzASy+9BCGEXl9sjz76\nqKnCtBn65MPOzq7O6DG5XM7Td2Zw+fJltG/fXr3z8I9//AOhoaF1lvP29m7u0GyGi4sLOnbsqDFN\npVJh8uTJGtcHq8lksuYKrVlY7RGUSqXCp59+igULFmjsgaSlpeGvf/2rxsX5EydOaLz3u+++g7+/\nP9zd3Zs7bKulbz58fX2RkpKifl9lZSW+/fZb9evg4GA4OTnhu+++0/j848ePs4gZSNvf7fr16/j8\n888xZswYdO7cGW5ubrh27Ro6duxY58fOzg7du3eHnZ0djh07ZoY1sF7achMWFoZLly5pzYVUKlUv\nV1ZWhnPnzqlf//DDDygrK8Njjz3WLLEbg9UeQR05cgTZ2dmYPn06/P39NeZFRUXhueeeU1+cl8vl\nWLp0KSIiInDx4kXs379fYyQZTx01nb75CA8Px8aNG7Fjxw6EhIQgISEB9vb26hy4ublhxowZ+OST\nT9CvXz+EhIRg586dUCgULFAGqqiowL1796BQKHD79m38+OOPWLlypXqknqOjIz744APMnz8fEokE\nw4YNQ1VVFX755RekpaVh5cqVCAgIwPTp0/HGG2+gvLwcTz31FPLz8/Hjjz9yJF8TaPvuWbx4MZ54\n4glMmjQJb775Jnx8fHDjxg3s378fb775JoKCggAArVq1wnvvvYc1a9ZACIGFCxeiV69eGDp0aHOv\nhsGstkBt27YNTz31VJ0vQwAYMmQIZDIZtm/fDolEgjfffBMPHjzA0KFD4eDggLi4OI2Nil98TadP\nPj799FPExsbi5s2bmDt3Lnx8fPDGG2/A09MT165dUy+/Zs0a2NnZYdq0aXB0dMSECRPw6quv4syZ\nM825SlZBIpHg+++/R9u2beHs7Ax/f38EBgZi1apViIyMhJ3dw5Mss2bNQtu2bbF27VrMnz8fdnZ2\n6Ny5M6KiotSflZCQgMDAQKxcuRLXrl1D69at8fLLL5tpzVq++ka0+vv7IyUlBfPmzcPYsWPx4MED\ntGvXDsOGDVOfbpVIJHj00Ufx1ltv4bXXXsPNmzcxcODAOrd1WDqJ0OPwQKVSIS4uDjKZDHFxcfjq\nq69w8uRJeHp6AgAiIiLQs2dPkwdrCkFBQXj99dcxf/58c4dCTTB06FA8+uij2L17t7lDISIj0esI\n6vDhw/D391ffVS6RSDBq1CiMGjXKpME1B56+a3l+/fVXJCcno3///rhx4waSkpJw5swZ/PDDD+YO\njYiMSOcgiby8PKSmpmLo0KHqL3N9R761BDx91/JIJBJs3boV/fr1w7hx4/Cf//wHe/fuRf/+/c0d\nGhEZkc4jqF27dmHSpEkaPbkkEgmOHj2KkydPIjQ0FJMnT4abm5tJAzWV3377zdwhUCN169YNP/74\no7nDICITa7BAJScnw9PTE0FBQUhPT1dPHzFiBMaNG4eysjIkJSUhMTER0dHR9X7O+fPnUVpaaryo\nbZRUKkXv3r2N8lnMifEwL5bJWHlhToynsTlpsEBduXIFycnJSE1NhUKhQFlZGTZt2oSYmBgAD4cx\n/ulPf0JCQkKDv6S0tBRhYWF6B0Xa1bw/qKmYE+NhXiyTsfLCnBhPY3PSYIGKiIhAREQEACAjIwMH\nDhxATEwMCgoK4O3tDaVSiR9++AEBAQGGR0xERKSFXqP4VCoVtmzZgvLycgAPr0ulpqZCqVTC29sb\nCxcuNGmQRERke/RqdXT48GGEhISoW+f7+PhgzJgx2L17N4YNG4bjx4+bNEgiIrI9Bg0zv3jxovqh\nfYMHD8aFCxdMGyUREdkcnQWqeph5dcsTACgqKlI3JfTy8kJRUZHpIiQiIpvUYIGqOcy8vhtzeaMr\nERGZQqOHmSckJMDLywuFhYWQSqUoKCiAl5dXc8VLREQ2Qucw83HjxmHp0qWQy+VQKBQICgqCt7c3\nNm7ciDt37kClUkGlUiEtLc2oDWPvFlcgt6RSY5qvuxPaejob7XcQEZHl0jnM3MnJCUuWLMG1a9dw\n4MABnDp1CjExMbh48SJUKhVCQkIwa9YsuLi4GDWw3JJKvHM4S2PampHBLFBE0L4DB3AnjqyLXvdB\nOTs747HHHkP79u2xaNEieHh4YMCAAXBxccELL7xg6hiJqBZtO3AAd+LIuuh9o25sbCxu376NqKgo\n+Pj4AIDVNIwlIiLLo1eBsrOzw5o1a5Cbm4v4+Hh07ty50Q1jqeWqfTqJp5GINPGauWk06pHvvr6+\n6NWrFzIyMvD8888D0L9hLLVctU8n8TQSkSZeMzeNBgtUZWUlFi1ahKqqKri4uKBXr15IS0tDREQE\nVqxYgYKCAvj6+sLPz48NY4mIyKgaLFBOTk54/fXXsW3bNlRUVODAgQN46aWXkJmZieLiYgDA9evX\nUVBQgNjYWJMHa28HXLoj15jGw2giskT8vmo6naf4goODsWrVKsjlcixevBgDBw7E8uXLsXTpUkil\nUhQWFqr/bWpF5Uq8d1zzCbg8jCYiS8Tvq6bTWaC0jeBjLz7rVvuCb6VSZcZoiMhW6SxQ2kbw1cRe\nfNan9gXfJeFBZoyGiGyVXs+DAjRH8FX34gPAXnxERGQSDRao4uJilJaWAgDkcjnS0tIQEBCAPn36\n4PTp0wCAM2fOoG/fviYPlIh0q74wX/vnbnGFuUMjarQGT/EVFhZiw4YNyM3NBQDIZDLk5eVh7Nix\nmDdvHr788ks4OzvDx8cH3bp1M2qzWCJqPG0X5gFenKeWqcECFRAQgEWLFqGwsBCBgYEoLi7G22+/\njeDgYAwYMACurq4YNWpUc8VKREQ2ROcgCalUqh6x5+npiU6dOiE/Px8A6n2IIREZx7W8P6CqtZm5\nOOh96ZioRWtUq6OcnBxkZ2cjNDQUV65cYbNYIhPbcv53/Hy3RGPaxF5+6NnWw0wRETUfvQtUeXk5\n1q9fj8jISLi4uLBZLBFRI2nrLgGww0R99CpQVVVVWLt2LZ599ln1iL3qoeVsFktk+dh2xzJwEEvj\n6CxQ9+/fx/z586FUKqFQKODm5obBgwfj7t27SEpKwr1796BQKBAYGNgM4RKRIdh2h1oinQXqxo0b\nKC4uRkBAAORyObZu3QqFQoEjR46gpKQEMpkMrVq14s26RERkVDoLVN++ffHll1+qX69cuRJ+fn5Q\nqVRYvXq1RsNYQ2h70BfA/m9ERLbO4FF8xmoYq+1BXwD7vxER2Tq9b6ioPYqvJjaMJSIiY9OrQNU3\nio8NY4mIyFR0FighBLZu3Qp/f388//zz6ulsGGu7ajckZSNSIjIFndeg4uPjkZaWBkdHR6SnpwMA\n/P39kZ6ejvLycuzZswdBQUFYuHChyYMly1B7yDKHKxORKegsUKNHj8aECROwadMmrF69GgCwZ88e\ndOzYkY1ircDvRRU4da1A/TqsnbsZoyGybFcf/IGfbhVrTOvfwdNM0Vg/nQWqa9eu6sdt1MRGsdah\nvEqJxJS76tdO9o+i8yOtzBgRNRe23Wm8a3l/aGwvABAoc4GHk72ZIrJujRpmXhMbxRK1bGy7Q5bO\noL79I0aMwKZNm7BixQrY2dkhMTHR2HEREZGNM+gIypIaxbIJpvkxB0RkCjoL1EcffYTk5GSUl5er\np1lSo1g2wTQ/5oCITEFngXrw4AEAQKFQIDo6Gi+//DIOHTrERrFERGRSOgvU4sWLkZubi1WrVmHt\n2rUAgAMHDhjUKFZeUQVlredXq0wwGpCnnIiIWj6DrkEZ2ij22//kY2+65pD1WU+3NySEhuPjKSci\nohbP4GHm1RrTKLaksgq5JYqm/koiIrIBBo/iKywshFQqZaNYIqImasxlCW3P0LPWSxgGFajqRrEv\nvfQSG8USETVRYy5LaHuGnrVewtBZoNavX4/Lly9DLpcjOjoa48ePx9ixY5GQkIAJEybAyckJjzzy\nCH799VfEx8c3R8zUAtTeI7TWPTwiMh2dBWr27Nlap7/77ruYOXMmVq1aBXd3NhglTbX3CNeNCtY4\nLcGCRUS6NHmQREtpGsvGmObFR3QQNU5931mVSpUZojGPJhUoiUSC999/HxKJBCNGjEB4eLix4jI6\nNsYkopakvu+sJeFBZojGPJpUoJYtWwZvb29kZ2cjPj4e7dq1Q9euXY0VG9mQ2iOTeGRLRE0qUN7e\n3gAePmG3X79+yMrKYoEivdQ+fVGpVGHBsevq1zyyJdKftXbPMbhAVVRUICMjA//7v/+LyspKlJSU\nICYmxpixNQtrTaylq336wpZOW1i6xl6v1XZfTkPLk/FZa/ccgwtUQUEB1qxZAz8/P0ilUpSVlaF1\n69bGjK1Z6JtYW7o5jmxbY6/Xarsvp6HluS01D2sYGGZwgSouLka3bt2wYMECAMC+fftw8eJF+Pv7\nGy04S2JLN8cRmRK3peZhDQPDDC5Q+fn5GkdMMpkMWVl196JqauPhjO5tec+UJbGTSDRy4uvuZMZo\n/os3+j7USeZaZ1obD/P8HTjsGZC1cqzzHebuZG+maAzTki5rSISBNzKdP38eaWlpmDFjBgDg7Nmz\nyMrKwpQpU+osm5ycjMLCwqZFSpBKpejdu7dRPos5MR7mxTIZKy/MifE0NicGH0HJZDLk5eWpX+fl\n5UEmk2ld1lgbLxkPc2KZmBfLw5yYj52hb+zUqRNycnKQm5uLqqoqnDt3Dn369DFmbEREZMMMPsUH\nABkZGdi5cyeUSiWGDRuGkSNHGjM2IiKyYU0qUERERKZi8Ck+IiIiU2KBIiIii8QCRUREFokFioiI\nLBILFBERWSQWKCIiskgsUEREZJFYoIiIyCKxQBERkUVigSIiIovEAkVERBaJBYpanJ07d8LR0dHc\nYRCRidlEgYqKisLw4cPNHQbVg/mxHMyFZYiKioKdnR3Gjh1bZ97+/fthZ2dnEztpNlGgJBIJJBKJ\nucOgejA/loO5sAwSiQQBAQH45ptvkJubqzHv448/RocOHZqUJ4VC0dQQm4VNFCghBKqfKpKSkoLn\nnnsOfn5+8PDwQL9+/XDs2DGN5QMDA7F8+XIsWLAAQUFBaNOmDd566y0olUpzhG/1aj7xRdse/O7d\nu2FnZxP/Vc2usblYunQpQkJCcOrUKTz55JPw8vLCkCFDkJWV1WwxW6uQkBA8+eST2Llzp3rarVu3\ncPz4cbz66qvqXBUUFGDSpEno0KEDWrVqhS5dumDdunUan1Wdy927dyMsLAxubm6oqKhoztUxiM1s\n9dV7G3K5HBMmTMDp06dx4sQJhIWF4cUXX8TVq1c1ll+/fj2KioqwZ88exMXFYcOGDdi1a5c5Qrc5\n3IO3HPrkIicnB0uXLkVcXBy++uor3L9/H1OmTGmG6KxXdfGZNm0atm/frp6+fft2hIeHo0OHDupp\nlZWVeOKJJ7B//36kpKRg2rRpiIuL0yhsAHDx4kXs27cPu3btQmpqaos4Rehg7gCaS3XCBw0apDE9\nLCwM33zzDfbs2YP58+erp7dt2xabNm0CAPTp0wc7d+7E8ePHueE1Az5D03Lok4vS0lKsW7cOvXv3\nBgBcvnwZb7/9NiorK+Hk5GTqEK2WRCLBuHHj8Oabb+LMmTN45plnsGPHDiQkJKCwsFC9nJ+fH2Jj\nY9Wvu3Tpgp9++gmff/45oqKi1NOLioqwfv16+Pv7N+dqNInNHEFVu3//Pt544w107doV3t7e8Pb2\nRk5ODm7duqVeRiKRYNSoURrvCwsLw71795o7XJvEIyjLoU8ufH191cUJAHr16gUhRJ1rJ9R4zs7O\neOWVV/DJJ5/gm2++QVVVFV544QWNZVQqFVauXImePXvikUcegYeHB/bv36/xnQYAjz32WIsqToAN\nHUFVb2hRUVH45Zdf8NFHHyEoKAguLi548cUXUVlZqbG8h4eHxms7OzuoVKpmi9dW2dnZoaqqSmOa\nXC43UzS2Td9c1N5W7O3tAYDbSxPVPM0XFhaG27dvY8qUKeq/b7W1a9di4cKF2Lp1K/r27QsPDw8s\nX74cp06d0lju0UcfbbbYjcXmjqDOnj2LGTNmYNSoUejWrRscHR2RmZlp7rDo//j6+uLSpUsap5YO\nHjzIoyozYC4sQ9euXdG3b1+cO3cOU6dOrTP/7NmzGDp0KKZOnYoePXqgY8eOOHv2bJ08tcRT5zZX\noLp06YI9e/bghx9+QFpaGmJiYuDl5aWRvJaYSGsxfPhwFBQUYOHChUhJScH8+fORlpbGnJgBc2E5\njh07hgcPHiAoKKjOvC5duuDHH3/Evn37cOXKFSxYsACFhYVWkSebKFAqlQoODg/PZiYmJqJHjx4Y\nPXo0pkyZgoiICPTu3Vtjb0PbHiLvDzGdmvkZNmwYli9fjl27dmHkyJHIy8vD8uXL6/ztmQvTaGwu\n6tsumJ+mqf13dXV1hVQqrbMMACxatAgzZszAnDlz8PzzzwMAZs+erVeeLJ1E6FFmVSoV4uLiIJPJ\n1ENJT548CU9PTwBAREQEevbsafJgDTVixAi0b98en376qblDIS2YH8vBXJAl0WuQxOHDh+Hv74+y\nsjIA/x3lVnukm6XJzc3FP/7xD5w9e7bOPQFkfsyP5WAuyBLpLFB5eXlITU3F6NGjcejQIQCanRks\n2f/7f/8PWVlZePvttzF+/Hhzh0O1MD+Wg7kgS6SzQO3atQuTJk1SHz0BD4+gjh49ipMnTyI0NBST\nJ0+Gm5ubSQM1RO1hlmRZmB/LwVyQJWqwQCUnJ8PT0xNBQUFIT09XTx8xYgTGjRuHsrIyJCUlITEx\nEdHR0fV+zvnz51FaWmq8qG2UVCrVuCGyKZgT42FeLJOx8sKcGE9jc9Jggbpy5QqSk5ORmpoKhUKB\nsrIybNq0CTExMQCAVq1a4U9/+hMSEhIa/CWlpaUICwvTOyjSLiUlxWifxZwYD/NimYyVF+bEeBqb\nkwYLVEREBCIiIgAAGRkZOHDgAGJiYlBQUABvb28olUr88MMPCAgIMDxiIiIiLfQaxadSqbBlyxaU\nl5cDgLobrlKphLe3NxYuXGjSIImIyPbodaPu4cOHERISguDgYACAj48PxowZg927d2PYsGE4fvy4\nSYMkIiLbo7NAVQ8zHzp0qHpo+cWLF9WPrRg8eDAuXLhg2iiJiMjm6CxQ1cPMaz5Fs6ioSN12w8vL\nC0VFRaaLkIiIbJJBw8xrMmV/p7vFFcgtqdQ6z9fdCW09nU32u4mIyLwaPcw8ISEBXl5eKCwshFQq\nRUFBAby8vEwSXG5JJd45nKV13pqRwSxQRERWTOcw83HjxmHp0qWQy+VQKBQICgqCt7c3Nm7ciDt3\n7kClUkGlUiEtLc2iG8YSEVHLovMalJOTE5YsWYLo6Gh07twZp06dwoABA5Cfnw+VSoWQkBBs2rSJ\nxYmIiIxKr/ugnJ2d8dhjj6F9+/ZYtGgRPDw8MGDAALi4uOCFF14wdYxERGSD9L5RNzY2Frdv30ZU\nVBR8fHwAoEU0jCUiopZJrxt17ezssGbNGmzcuBHHjh3Db7/9hhEjRmDTpk1YsWIF7OzskJiYaOpY\niYjIhuh1BFXN19cXvXr1QkZGhvrRwvo2jCUiw9V3y4W7kz1KKpUa03gLBlmLBgtUZWUlFi1ahKqq\nKri4uKBXr15IS0tDREQEVqxYgYKCAvj6+sLPz48NY4lMqL5bLpaEB+G9479pTOMtGGQtGjzF5+Tk\nhNdffx0ODg6oqKjAgQMH8MwzzyAzMxPFxcUAgOvXryMzMxORkZHNEjAREdkGnaf4goODsWrVKsjl\ncixevBgDBw7E8uXLsXTpUkilUhQWFqr/TURE/6Xt1CxPy+pPZ4HSNoLPmL34GmpnVKlUGfy5RETm\npu3ULE/L6k9ngaoewZebm4v4+Hh07txZY35Te/E11M5oSXhQkz6biIhaLr2GmQOaI/iqe/EBMGkv\nPiIisl0NFqji4mKUlpYCAORyOdLS0hAQEIA+ffrg9OnTAIAzZ86gb9++Jg+UiIhsS4On+AoLC7Fh\nwwbk5uYCAGQyGfLy8jB27FjMmzcPX375JZydneHj44Nu3bqxH5+NqH3dkBd4icgUGixQAQEBWLRo\nEQoLCxEYGIji4mK8/fbbCA4OxoABA+Dq6opRo0Y1V6xkIWpfN+QFXiIyBZ2DJKRSqXrEnqenJzp1\n6oT8/HwAUD8CnoiIyNj0HiQBADk5OcjOzkZoaCiAh81i58yZgy1btqivVRERERmD3gWqvLwc69ev\nR2RkJFxcXNgsloiITEqvAlVVVYW1a9fi2WefVY/Y8/LygkQiUTeLzcrSfi8TtTx3iytw6Y5c/XO3\nuMLcIRGRDdJ5Der+/fuYP38+lEolFAoF3NzcMHjwYNy9exdJSUm4d+8eFAoFAgMDmyFcag4cBNGy\n2dsBl+7INaZxpKXpaeuKw244TaOzQN24cQPFxcUICAiAXC7H1q1boVAocOTIEZSUlEAmk6FVq1a8\nWZfIQhSVK9lKxwzqa2tEhtNZoPr27Ysvv/xS/XrlypXw8/ODSqXC6tWrNRrGNidte4kA9xSJiKxF\nox5YWHMUnzEbxhpC214iwD1FU6i9M8DTFkTUHPQuULVH8dXU1IaxZNlq7wzUPm1Ru4DxKJaIjEGv\nAlXfKL7CwkJIpVI2jLVxtQsYj2KJyBh0DjMXQmDr1q3w9/fH888/r57OhrFERGRKOo+g4uPjkZaW\nBkdHR6SnpwMA/P39kZ6ejvLycuzZswdBQUFYuHChyYPVR32DJwCeeiIiy8RBX9rpLFCjR4/GhAkT\nsGnTJqxevRoAsGfPHnTs2NEiG8XWN3gC4KknIrJMHPSlnc5TfF27doWbm1ud6WwUS0REptSoYeY1\nHT16FCdPnkRoaCgmT56stYjVdC3vD63Tq1QsdEREVJdBBWrEiBEYN24cysrKkJSUhMTERERHRzf4\nnui9V7ROXzaioyEhEFEj8BoHtUQGFajqIeXVjWITEhKMGhS1bLwvyvLwGge1RDoL1EcffYTk5GSU\nl5erp7FRLDWE90URkTHoLFAPHjwAACgUCkRHR+Pll1/GoUOH2CiW9MYjqsa5dEeOmldmJRJAyWu1\nZIN0FqjFixcjNzcXq1atwtq1awEABw4cMGujWGpZeETVOAuOXUOl8r8FycPZHvOGBJotHiJzMega\nlLkbxRIR2Sptz52y1rMSBg8zr8ZGsUQtFx9u2PJoe+6UtZ6VMHgUHxvFWodbBWW4UfDfATBBMlcz\nRkPNTdvovnWjguvsoQMsXJbMWm8jMKhAVTeK/e6771BZWQkhBObNm4f4+Hhjx0cmdkdeieUnb6hf\nr3wuGPY8KLZpHJLesLvFFfhDodSY5uHc5JNRTWKtOdP5V12/fj0uX74MuVyO6OhojB8/HmPHjkVC\nQgLy8/O6QWp/AAAd30lEQVTRvXt3zJkzp84zooiIrNEvOSX429lbGtPi/9wJDnbcszM2nQVq9uzZ\nWqe/++67mDlzJmJiYliciIjI6Jp0XCqRSPD+++9DIpFgxIgRCA8PN1ZcZMVqny93d7JHSeV/T5m0\n9PPmRMai7dpSpVJlpmiaX5MK1LJly+Dt7Y3s7GzEx8ejXbt26Nq1q7FiM7qGnhVV+0uyGr8sjU/b\nI+R5nxRRXdquLS0JDzJTNM2vSQXK29sbwMMHGPbr1w9ZWVkWXaAaelZU7S/JavyyJCIyD53Pg6pP\nRUUFysrKAADFxcVITU1FQECA0QIjIiLbZvARVFFREZYtW4aCggJIJBKEhYWhR48exoytRdN2t3c1\nnjYkItLN4ALl4+MDAFi3bh1kMhnmzZuH7Oxs+Pv7Gy24lkzb3d7VeNqQrFl9O2fcMaPGMrhAZWVl\noU2bNvD19QUADBgwABcvXmSBIrJx9e2ccceMGsvgApWfn4/WrVurX8tkMmRlaT9iAIAXurbWOt3S\nW/kZMvIPaDlDQWWuDhq58XC2xx/1rFNzsfX+cM93aY2qGo/XcHEw+FKxUWnLi7ZtoKX83zdUe6lL\nne8zTxcHs2832uibM0vdviRCCIMeNHP+/HmkpaVhxowZAICzZ88iKysLU6ZMqbNscnIyCgsLmxYp\nQSqVonfv3kb5LObEeJgXy2SsvDAnxtPYnBh8BCWTyZCXl6d+nZeXB5lMpnVZY228ZDzMiWViXiwP\nc2I+Bp876NSpE3JycpCbm4uqqiqcO3cOffr0MWZsRERkwww+xQcAGRkZ2LlzJ5RKJYYNG4aRI0ca\nMzYiIrJhTSpQREREpmIZw4OIiIhqYYEiIiKLxAJFREQWiQWKiIgsEgsUERFZJBYoIiKySCxQRERk\nkVigiIjIIrFAERGRRWKBIiIii8QCRUREFokFioiILJLVFaioqCjY2dlh7Nixdebt378fdnZ2cHR0\nNENkVJ2b2NhYjenZ2dmws7PD2bNnzRQZAUBpaSliY2PRu3dveHh4oHPnzpg0aRJu3ryp92dMnToV\nQ4YMMWGUtqGsrAyLFi1CSEgIWrVqhdatW6Nfv35ISEgwd2jNyuoKlEQiQUBAAL755hvk5uZqzPv4\n44/RoUMHSCz9OfNWSiKRwMXFBRs3bsStW7fMHQ7VcP/+fTzxxBM4ePAgFi1ahLS0NGzduhXFxcV4\n/PHHufPQzKKjo7FlyxbExsYiOTkZp0+fxsyZM1FUVGTu0JqXsDJRUVEiPDxcDBw4UKxatUo9/ebN\nm8LR0VG89957wsHBQQghRH5+vpg4caIICAgQrq6uonPnzmLt2rXq95w6dUrY29uL27dva/yOXbt2\nCS8vL/HHH380z0pZiaioKDFs2DDx5JNPiokTJ6qn3759W0gkEnHmzBkhhBC3bt0SY8aMEX5+fsLP\nz0+8/PLL4s6dO0IIIYqKioSrq6v4/PPPNT77999/F/b29uLEiRPNt0JW5JVXXhFt27YVcrm8zrzn\nnntOhIaGioqKCiGEED/99JMYNmyY8PHxEV5eXmLQoEHi2rVrYsmSJUIikWj87Nq1q7lXxSp4eXmJ\n9957T+dy33zzjejfv7/w8vISgYGB4q233hKlpaXq+YMGDRJTp04VH3zwgQgODhZt27YVc+bMEQqF\nwpThG43VHUGJ/3u81bRp07B9+3b19O3btyM8PBwdOnRQT6usrMQTTzyB/fv3IyUlBdOmTUNcXBx2\n7twJABg8eDBCQkLw2WefafyObdu2YeLEiXB1dTX9ClkRIQQkEgn+9re/4YsvvkBycnKdZcrKyvDM\nM8+guLgYR44cweHDh3H//n0MHDgQCoUCnp6eGD16NJKSkjTet3v3brRr1w5Dhw5trtWxGpWVlfji\niy8QExMDd3f3OvPnz5+Pq1ev4ty5c/j3v/+Np59+Gt27d8fJkyfx73//G6+++iqqqqrwzjvvICIi\nAk8//TRycnKQk5OD8ePHm2GNWr5HH30UJ06cQEFBQb3LfP311xg/fjzGjBmD77//HsuXL8ehQ4cw\nY8aMOsvduHEDhw4dwieffIK///3vePfdd029CsZh7gppbJGRkWL48OGivLxctG7dWpw+fVpUVVUJ\nf39/sXfvXrFjxw71EZQ248ePF8OHD1e/XrdunejQoYNQqVRCCCEuX74sJBKJSEtLM/m6WJvq3Agh\nxOjRo8XgwYOFEJpHUNu3bxcSiURkZmaq3/fzzz8LiUQiEhMThRBCHD16VDg4OIicnBz1Mo8//riY\nP39+M66N9fj111+FRCIR+/bt0zo/Ly9PSCQSsXnzZjFs2DDxwgsv1PtZr732mjqvZLh//etfokOH\nDsLe3l50795dTJs2rU5+QkNDxYIFCzSm7d69W0gkElFYWCiEeHgE5erqKsrLy9XLLFiwQLi4uLSI\nM0BWdwRVzdnZGa+88go++eQTfPPNN6iqqsILL7ygsYxKpcLKlSvRs2dPPPLII/Dw8MD+/fs1ro9E\nRkYiNzcXx44dA/DwSKxPnz7o0aNHs66PtRD/d4S7atUq/Otf/8LBgwc15qWnpyMwMBCdO3dWT3/i\niSfQrl07ZGRkAADCw8Ph6+uLzz//HACQkpKC9PR0TJ48uRnXxDZdunQJI0aMMHcYVu/pp5/GtWvX\n8P333yMyMhKXL1/G6NGj8eKLLwJ4OKDl6tWr+PDDD+Hh4aH+mT59OiQSCbKystSfNWDAADg7O6tf\nDx8+HBUVFbh27Vqzr1djWWWBEjVO83399df429/+hilTpsDe3l5jubVr12LhwoWIiYnB8ePHcenS\nJURERKCiokK9jEwmw7hx47Bt2zYoFAokJiZi2rRpzbo+1igkJATTp09HbGwslEqlxrzq/NXH3t4e\nEydORGJiIgAgMTER/fr10yhqpL+QkBDY29vjl19+0To/PT0dAPDYY481Z1g2z97eHv3798dbb72F\ns2fPYt26dTh06BC+//57qFQqAMDGjRtx6dIl9c/PP/+Mq1ev4vHHH1d/jq7tyZJZZYGq1rVrV/Tt\n2xfnzp3D1KlT68w/e/Yshg4diqlTp6JHjx7o2LEjzp49W2eU3/Tp03Hw4EFs3boV5eXlmDBhQnOt\ngtWp+bddsmQJ7ty5g48//lg97/HHH8fNmzeRmZmpXu7nn3/G77//rrHRTZ48GZcuXUJaWhq++OIL\nHj01gZOTE/76179i06ZNkMvldebHx8cjNDQU/fv3R8+ePdVnE+r7rNo7HGQcISEhAICSkhJ4eHgg\nODgYmZmZ6NixY52fmkdM586d09jp/u677+Di4oJOnTo1+zo0mllPMJpAZGSkCA8PV7/+448/REFB\ngfp1zWtQc+fOFe7u7mLv3r0iMzNTzJ8/X7Ru3VoEBgbW+dzHH39cODs7i2nTppl+JaxU7dwIIUR8\nfLxwdXVVX4MqKysTHTp0EMOGDRMpKSni4sWLYvDgwSIkJKTOyKOwsDDRs2dP4eLiIvLz85tzVaxO\nbm6uCAwMFF26dBFff/21uHr1qjh58qQYNWqU8PDwEGfPnhVCCHH+/Hlhb28vZs+eLS5duiQyMzPF\njh07xJUrV4QQQqxZs0Y88sgj4ty5c+L+/fvqkX/UOAMHDhRbt24VFy5cEFeuXBFJSUniscceE+3a\ntVNfXzpw4IBwcnISK1asEL/88ovIzMwUe/fuFdOnT1d/zqBBg4RMJhPTp08Xly9fFocOHRJ+fn5i\nzpw55lq1RrG6AhUVFaUxyKG2HTt2CEdHRyHEwyHLc+fOFYGBgaJTp05i/vz5YtmyZSIoKKjO+9av\nXy8kEom4ePGiyWK3dtpyU15eLgICAoSdnZ16mPnt27fF2LFjha+vr/Dz8xPjx49XDzOvacOGDUIi\nkYgxY8Y0S/zWTi6Xi7lz54pevXoJd3d3ERISIiZNmiRu3Lihsdy5c+fEkCFDhEwmE15eXmLo0KHi\nt99+E0I8vHVj5MiRwsvLi8PMm2DlypXi2WefFb6+vsLFxUUEBASIV155Rb0jUO3UqVNiyJAhwsfH\nR3h6eoqePXuKZcuWqecPHjxYvP7662L58uUiKChItGnTRsyePbvFDDOXCKH7BKVKpUJcXBxkMhni\n4uLw1Vdf4eTJk/D09AQAREREoGfPniY/2jOnd999FydOnNA6NJqIyBINGTIEISEh+OSTT8wdikEc\n9Fno8OHD8Pf3R1lZGYCH1wpGjRqFUaNGmTQ4S1BUVIRLly5h27ZtNtdmhIhaNvHwLJm5wzCYzkES\neXl5SE1NxdChQ9Ur2tJXujH+8pe/YOzYsZg8eTImTpxo7nCIiPQmkUhadGs3nUdQu3btwqRJk9RH\nT8DDlT569ChOnjyJ0NBQTJ48GW5ubiYN1FxOnz5t7hCIiAxy6tQpc4fQJA0WqOTkZHh6eiIoKEh9\nLwQAjBgxAuPGjUNZWRmSkpKQmJiI6Ojoej/n/PnzKC0tNV7UNkoqlaJ3795G+SzmxHiYF8tkrLww\nJ8bT2Jw0WKCuXLmC5ORkpKamQqFQoKysDJs2bUJMTAwAoFWrVvjTn/6k89pMaWkpwsLC9A6KtEtJ\nSTHaZzEnxsO8WCZj5YU5MZ7G5qTBAhUREYGIiAioVCrMnj0bKpUKMTExuHv3LpKSknDv3j0oFAoE\nBgY2JWYiIqI69OokcfjwYfj4+Kgvtq1ZswZZWVlwdHSEl5cXvLy8TBokERHZHp2DJKpH8Y0ZMwaH\nDh0C8PC+qNWrV0MqlaKwsBBLly41dZxERGRjDBrFV1RUBKlUCgDw8vIy6lMe7xZXILekUus8X3cn\ntPV01jqPiIisi0Gj+Goy9hj73JJKvHM4S+u8NSODWaCIiGxEo0fxJSQkwMvLC4WFhZBKpSgoKOA1\nKCIiMjq9RvEBQEZGBg4cOIBZs2Zh9+7dOH36NF566SWcOXMGffv2bZZg7e2AS3fqPg4A4Ok/IiJr\no/MaVGVlJZYuXQq5XI6SkhIcOnQIY8eOxbx58/Dll1/C2dkZPj4+6Natm8kbxhaVK/He8d+0zuPp\nPyIi66KzQDk5OWHJkiVwdnaGQqFAXFwcevfujQEDBsDV1dUmGsYSEVHz0+s+qOqnM5aXl0OpVMLR\n0RFAy36UMBERWTa9HrehUqkQGxuL27dvIyoqCj4+PgBgMw1jiYhq03ZLDK+FG5deBcrOzg5r1qxB\nbm4u4uPj0blz50Y3jCUisibabonhtXDj0usUXzVfX1/06tULGRkZ8PLygkQiUTeMzcrSfu8SERGR\nIRo8gqqsrMSiRYtQVVUFFxcX9OrVC2lpaYiIiMCKFStQUFAAX19f+Pn5ISAgoLliJiIiG9DgEZST\nkxNef/11ODg4oKKiAgcOHMAzzzyDzMxMFBcXAwCuX7+OzMxMREZGNkvARERkG3RegwoODsaqVasg\nl8uxePFiDBw4EMuXL8fSpUs1msVW9+YjIiIyBp0FStsIPlM2iyWi+tUcOcYRY2TtdBYobSP4ajJ2\ns1giql/NkWMcMUbWTu9RfLVH8BUWFgIAm8USEZFJNHgEVVxcDHt7e7i5uUEulyMtLQ2vvvoq+vTp\nY5ZmsUS2pvbNoJVKlRmjIUPxpl7DNFigCgsLsWHDBuTm5gIAZDIZ8vLyzNYslsjW1L4ZdEl4kBmj\nIUPxpl7DNFigAgICsGjRIhQWFiIwMBDFxcV4++23ERwczGaxRERkUjoHSUilUvWIPU9PT3Tq1An5\n+fkA2CyWiIhMR69efNVycnKQnZ2N0NBQXLlyxaBmsQVlCsgrlFrnudhzRCARET2kd4EqLy/H+vXr\nERkZCRcXF4Obxd6TV+J/DvxH67y5AwPg5+6kf/RERGS19CpQVVVVWLt2LZ599ln1iL3qoeXVzWIT\nEhJMFyWZFW8OtUz2dsClO3L1a+bG/GrnpBpHXxpGZ4G6f/8+5s+fD6VSCYVCATc3NwwePBh3795F\nUlIS7t27B4VCgcDAwGYIl8yh5gikdaOCNYbL8kvRfIrKlXjv+G/q1xwVZn61c1KNoy8No7NA3bhx\nA8XFxQgICIBcLsfWrVuhUChw5MgRlJSUQCaToVWrVrxZ10bwS5GImovOAtW3b198+eWX6tcrV66E\nn58fVCoVVq9erdEw1pzqO7QGuJdPRNQSGTyKz9IaxtZ3aA1wL7+x2L2AiCyBwaP4amLDWOvC7gVE\nmvb8fE9jp83dyR6Pt3E3Y0S2oUmj+AoLCyGVStkwlois2qlrBcjKK1O/bt3KkQWqGejsZi6EwNat\nW+Hv74/nn39ePb26YSwANowlMqJbBeW4VVBep7koka3ReQQVHx+PtLQ0ODo6Ij09HQDg7++P9PR0\nlJeXY8+ePQgKCsLChQtNHiyRLZj6z8sAgHcGBcDXjTeuk+3SWaBGjx6NCRMmYNOmTVi9ejUAYM+e\nPejYsSMbxRJvFiUik9FZoLp27ap+3EZNbBRrHfL/UCA5uxjV2ezyiO5+ijXpui+q9ohAFjAi0lej\nhpnXZEijWLI8CqUKH/5wG1WqhyVq/pBAeLsa/N+ijtojAjnkn4j0ZdA3kaGNYomI6CFtzQV4hkGT\nQQWKjWKJiJpGW3MBnmHQpLNAffTRR0hOTkZ5ebl6GhvFElme2nvk7k72KKn877PXuHdOLY3OAvXg\nwQMAgEKhQHR0NF5++WUcOnSIjWJJq9pfkmyT1Hxq75EvCQ9iY19q0XQWqMWLFyM3NxerVq3C2rVr\nAQAHDhywqEaxZDm0fUkSERnCoGtQltYolojIGnDghKYmjydmo1giIuPgwAlNOnvxaVPdKBYAG8US\nEZFJGHQEVd0o9rvvvkNlZSWEEJg3bx7i4+ONHR8REdkonQVq/fr1uHz5MuRyOaKjozF+/HiMHTsW\nCQkJyM/PR/fu3TFnzpw6z4iyJHzaLhFRy6OzQM2ePVvr9HfffRczZ85ETEyMRRcngE/bJSJqiZo0\nSEIikeD999+HRCLBiBEjEB4ebqy4yEqx+zkR6atJBWrZsmXw9vZGdnY24uPj0a5dO3Tt2tVYsZEV\n0tX9nIiomkGj+Kp5e3sDePgAw379+iErK0vHO4iIiPRj8BFURUUFVCoVXF1dUVxcjNTUVLz66qvG\njI1sAE/5NR/26rNNtZ/JBrScXBtcoIqKirBs2TIUFBRAIpEgLCwMPXr0MGZszaKhEX5Ay0lkS8VT\nfs1HV6++daOC1V9k/H9vPWo/kw1oOduZwQXKx8cHALBu3TrIZDLMmzcP2dnZ8Pf3N1pwzaGhEX6A\n5kZbGzdi4+MRlfnU3BZayhcYWTeDC1RWVhbatGkDX19fAMCAAQNw8eLFFlegdOEQ9ebFIyoiqmZw\ngcrPz0fr1q3Vr2UymV6DJNyd7TH9yXZa54X4tEJxeZWhIbUY2s4JV2vuIwYHOzu83u9R/N8T39HB\n28UmcmDJqreP4Nbm2x54JKtp7BO+KCz7by5cHZs0vqxRtF2GqH39sJq15UkihBCGvPH8+fNIS0vD\njBkzAABnz55FVlYWpkyZUmfZ5ORkde8+MpxUKkXv3r2N8lnMifEwL5bJWHlhToynsTkx+AhKJpMh\nLy9P/TovLw8ymUzrssbaeMl4mBPLxLxYHubEfAw+Tu3UqRNycnKQm5uLqqoqnDt3Dn369DFmbERE\nZMMMPsUHABkZGdi5cyeUSiWGDRuGkSNHGjM2IiKyYU0qUERERKbSfENRiIiIGoEFioiILFKTupnr\nkpGRgV27dqmvUT333HN1lnnw4AE2b96MoqIieHp6YvDgwRg8eHCd5VQqFeLi4iCTyRAXF6f195WX\nl2P79u24desWFAoFoqOjERoaqrHM8ePHcfr0aSgUCnTt2hVRUVH46KOPkJqaCk9PT6xduxYAUFZW\nhoSEBOTm5sLPzw+zZs3CZ599Vme5pKQkpKSkwMnJCV27doVcLsfPP/+ssUy1gwcPYvfu3RgwYAB+\n+eWXOsucOnUKx44dg0KhAAAUFxdrLJOdnY3du3cjLy8PrVu3xqRJkwy6MVpXXvTNCaA7L/rkBDA8\nLy4uLnX+3qbKSa9evdR9J42dF2NuK4Bx8sJthdtKTWbZVoSJKJVKERMTI+7duycUCoWYO3euuH37\ndp3lCgoKxG+//SaEEKKoqEhMnTpV63IHDx4UGzZsECtXrqz3dyYkJIgTJ04IIYSoqqoSpaWlGvPl\ncrl44403RFlZmVAqleKDDz4QqampIiMjQ1y/fl289dZb6mWTkpLEvn37hBBC7N27V+zevVvrcpcu\nXRJKpVIolUqxZcsWsWHDhjrLCCHE/fv3xfLly8Ubb7whkpOT6yzzyy+/iPfff18oFAohhBAXLlyo\ns8yHH34o/vWvfwkhhPj+++/Fhx9+WO/foj765EXfnAihOy+6ciJE0/Ki7e9tqpwUFRVpjampeTH2\ntiJE0/PCbYXbSk3m2lZMdoqvZiskBwcHdSuk2qRSKQIDAwEAnp6e6NSpEwoKCjSWycvLQ2pqKoYO\nHQpRz5iOP/74A5mZmRg6dCgAwN7eHq1atdJYxsnJSb1sZWUlKioq4O7ujq5du8LNzU1j2YsXL2LQ\noEEAgMGDB+PChQtal+vevTvs7OxgZ2eHnj17AkCdZQAgMTERkyZNAgCEhobWWebbb7/F6NGj4eDw\n8KC2T58+dZZp1aoVSkpKoFKpUFJSAnd3d61/i4bokxd9cgLozos+OQGalpfr1683W048PT21xtTU\nvBhzWwGMkxduK9xWajLXtmKyU3yGtELKyclBdnY2QkJCNKbv2rULkyZNQllZWb3vzc3NhaenJzZv\n3ozr168jJCQEU6ZMUScUeJjcqVOnYubMmXB0dMRzzz2H4OBgrZ9XVFQEqVQKAPDy8kJRUZHOdT5x\n4oT6P1hNFy5cgEwmQ4cOHep9b05ODjIyMpCUlAQXFxdERkbWSd6kSZMwf/58/P3vf4dMJsMHH3yg\nM6baGpuX+nIC6M6LPjkBTJsXY+ekY8eOdZZral6Mua0AxskLtxVuK9XMua1YzCCJ8vJyrF+/HpGR\nkXBxcVFPT05OhqenJ4KCguo9egIApVKJa9eu4cknn0R8fDyqqqrw448/aixTXFyM7du348MPP8Tm\nzZvxn//8BykpKTpjk0gkOpf5+uuv4eLigv79+2tMr6iowN69ezF+/Hj1NG3roVQqkZubi2XLluGF\nF15AUlJSnWW2bNmCP//5z/jss88wfPhwbNmyRWdcTVFfTgD98qJPTgDT5aU5cgJYZ164rTQOtxXT\nbCsmK1CNaYVUVVWFtWvX4tlnn0Xfvn015l25cgXJycmYOXMmNmzYgPT0dGzatKnOZ7Ru3Rru7u7o\n06cPnJycMGDAAKSmpmosk5WVhZCQELRp0wYeHh7o378/MjIytMbk5eWl7r9VUFAALy+vetf19OnT\nSE1NxaxZs+rMu3fvHu7fv4933nkHM2fORH5+PuLi4iCXazZ/bN26NZ5++mk4OTmhT58+uHPnjvoC\ncLXqUwD29vYYOnQoLl++XG9M9dE3Lw3lBNAvL/rkBDBNXkyVk8rKuk1+m5oXY20rgPHywm2F2wpg\n/m3FZAVK31ZIQghs3boV/v7+eP755+vMj4iIwJYtW7B582bMnj0b3bp1Q0xMTJ3lpFIp2rRpg6tX\nr0KlUiElJQXdu3fXWKZLly64du0aSkpKoFAokJqaWu9DFvv06YPTp08DAM6cOaP1Px4ApKWl4cCB\nA3j33XfrHI4DQEBAALZt24bNmzdj8+bNkMlkWLVqFTw8PDSW69u3L1JTUyGEwNWrV+Hn5wdHR0eN\nZbp166Y+B37hwoU666cPffKiKyeAfnnRJyeA8fNiypxo+7ym5sVY2wpgvLxwW+G2Aph/WzFpJwl9\nWiFlZmZiyZIlCAgIUB+GRkREqC/Y1f68gwcPIjY2Vuvvu3PnDjZv3ozi4mIEBARg1qxZdQ63T58+\njVOnTqGyshI9evTA+PHjsXHjRly+fBlyuRxeXl4YP348nnrqqTpDZ7du3YrLly+juLgYUqkUL7/8\nMvbt24eqqir1OfDy8nJUVFRofNaQIUPUvz8mJgaBgYG4evWqxjKDBg3C9u3bkZ6eDgcHB0ilUmRn\nZ6t/1/jx4xEcHIx//vOf+P3339G+fXuMHTsW7dppf3RJU/LSmJzoyos+OWlKXuzt7XHlypVmycnr\nr7+Oo0ePavwfMFZejL2tGCMv3Fa4rZh7W2GrIyIiskgWM0iCiIioJhYoIiKySCxQRERkkVigiIjI\nIrFAERGRRWKBIiIii8QCRUREFun/A0YTXjj9DG0yAAAAAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x113377a90>"
       ]
      }
     ],
     "prompt_number": 4
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "The first step is recognixing what sort of distribution to fit our data to. A couple of observations:\n",
      "\n",
      "1. The data are skewed, with a longer tail to the right than to the left\n",
      "2. The data are positive-valued, since they are measuring rainfall\n",
      "3. The data are continuous\n",
      "\n",
      "There are a few possible choices, but one suitable alternative is the **gamma distribution**:\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$$x \\sim \\text{Gamma}(\\alpha, \\beta) = \\frac{\\beta^{\\alpha}x^{\\alpha-1}e^{-\\beta x}}{\\Gamma(\\alpha)}$$\n",
      "</div>\n",
      "\n",
      "![gamma](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e6/Gamma_distribution_pdf.svg/500px-Gamma_distribution_pdf.svg.png)"
     ]
    },
    {
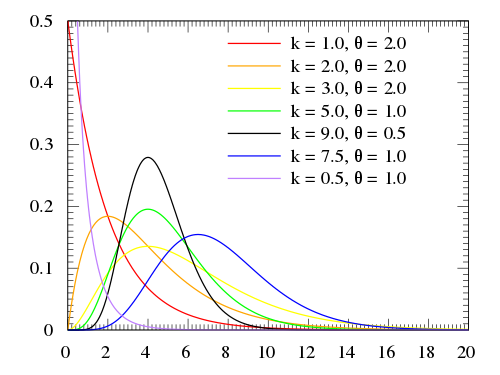     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "The ***method of moments*** simply assigns the empirical mean and variance to their theoretical counterparts, so that we can solve for the parameters.\n",
      "\n",
      "So, for the gamma distribution, the mean and variance are:\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$$ \\hat{\\mu} = \\bar{X} = \\alpha \\beta $$\n",
      "$$ \\hat{\\sigma}^2 = S^2 = \\alpha \\beta^2 $$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "So, if we solve for these parameters, we can use a gamma distribution to describe our data:\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$$ \\alpha = \\frac{\\bar{X}^2}{S^2}, \\, \\beta = \\frac{S^2}{\\bar{X}} $$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Let's deal with the missing value in the October data. Given what we are trying to do, it is most sensible to fill in the missing value with the average of the available values."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "precip.fillna(value={'Oct': precip.Oct.mean()}, inplace=True)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 5,
       "text": [
        "<class 'pandas.core.frame.DataFrame'>\n",
        "Int64Index: 141 entries, 1871 to 2011\n",
        "Data columns (total 12 columns):\n",
        "Jan    141  non-null values\n",
        "Feb    141  non-null values\n",
        "Mar    141  non-null values\n",
        "Apr    141  non-null values\n",
        "May    141  non-null values\n",
        "Jun    141  non-null values\n",
        "Jul    141  non-null values\n",
        "Aug    141  non-null values\n",
        "Sep    141  non-null values\n",
        "Oct    141  non-null values\n",
        "Nov    141  non-null values\n",
        "Dec    141  non-null values\n",
        "dtypes: float64(12)"
       ]
      }
     ],
     "prompt_number": 5
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Now, let's calculate the sample moments of interest, the means and variances by month:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "precip_mean = precip.mean()\n",
      "precip_mean"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 6,
       "text": [
        "Jan    4.523688\n",
        "Feb    4.097801\n",
        "Mar    4.977589\n",
        "Apr    4.204468\n",
        "May    4.325674\n",
        "Jun    3.873475\n",
        "Jul    3.895461\n",
        "Aug    3.367305\n",
        "Sep    3.377660\n",
        "Oct    2.610500\n",
        "Nov    3.685887\n",
        "Dec    4.176241\n",
        "dtype: float64"
       ]
      }
     ],
     "prompt_number": 6
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "precip_var = precip.var()\n",
      "precip_var"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 7,
       "text": [
        "Jan    6.928862\n",
        "Feb    5.516660\n",
        "Mar    5.365444\n",
        "Apr    4.117096\n",
        "May    5.306409\n",
        "Jun    5.033206\n",
        "Jul    3.777012\n",
        "Aug    3.779876\n",
        "Sep    4.940099\n",
        "Oct    2.741659\n",
        "Nov    3.679274\n",
        "Dec    5.418022\n",
        "dtype: float64"
       ]
      }
     ],
     "prompt_number": 7
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We then use these moments to estimate $\\alpha$ and $\\beta$ for each month:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "alpha_mom = precip_mean ** 2 / precip_var\n",
      "beta_mom = precip_var / precip_mean"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 8
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "alpha_mom, beta_mom"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 9,
       "text": [
        "(Jan    2.953407\n",
        "Feb    3.043866\n",
        "Mar    4.617770\n",
        "Apr    4.293694\n",
        "May    3.526199\n",
        "Jun    2.980965\n",
        "Jul    4.017624\n",
        "Aug    2.999766\n",
        "Sep    2.309383\n",
        "Oct    2.485616\n",
        "Nov    3.692511\n",
        "Dec    3.219070\n",
        "dtype: float64,\n",
        " Jan    1.531684\n",
        "Feb    1.346249\n",
        "Mar    1.077920\n",
        "Apr    0.979219\n",
        "May    1.226724\n",
        "Jun    1.299403\n",
        "Jul    0.969593\n",
        "Aug    1.122522\n",
        "Sep    1.462581\n",
        "Oct    1.050243\n",
        "Nov    0.998206\n",
        "Dec    1.297344\n",
        "dtype: float64)"
       ]
      }
     ],
     "prompt_number": 9
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We can use the `gamma.pdf` function in `scipy.stats.distributions` to plot the ditribtuions implied by the calculated alphas and betas. For example, here is January:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "from scipy.stats.distributions import gamma\n",
      "\n",
      "hist(precip.Jan, normed=True, bins=20)\n",
      "plot(linspace(0, 10), gamma.pdf(linspace(0, 10), alpha_mom[0], beta_mom[0]))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 10,
       "text": [
        "[<matplotlib.lines.Line2D at 0x113540450>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAECCAYAAAASDQdFAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtUW9edL/DvkYQQIAlxsEEGGdtgY4NjY2Pi2GEyTkK4\nHcc3d5p7b7I6TWY1zaRrFdtZzpo0TrxmZfJqB0+MV9rp2EzzWC110zWrzW0yyUymiZ+tW/IwhviF\nbSy/sQ0yEpIACT3P/YNYMTEIAZKOHt/PXwjtI/3Esr9s9t5nb0GSJAlERJQWFHIXQERE8cPQJyJK\nIwx9IqI0wtAnIkojDH0iojTC0CciSiOqiRp0dnaipaUFgUAAdXV1WLt27ajnDx06hN/85jcAAFEU\n8dBDD2H+/PkRXUtERHEmhREIBKSNGzdKvb29ks/nk37wgx9Ily9fHtXG7XaHvj5x4oT0j//4jxFf\nS0RE8RV2eMdsNsNoNKKgoAAqlQq1tbVoa2sb1Uaj0YS+drlcyMjIiPhaIiKKr7DDOzabDfn5+aHH\noijCbDbf0u7zzz9HS0sLhoeHsXXr1kldS0RE8ROVidyVK1dix44d+Lu/+zts27YtGi9JREQxELan\nL4oirFZr6LHVaoUoiuO2v/POO/HWW2/B5XJN+tpPP/0UQ0NDk6mdiCjtGQwGrFixIuL2YUO/rKwM\nPT09sFgsEEURra2t2LRp06g2PT09KCwshCAIaG9vh1qtRnZ2dkTX3mxoaAjV1dURF05EREB7e/uk\n2ocNfaVSiYaGBjQ1NYWWXZpMJuzevRsAUF9fj88++wx//OMfoVQqMXfuXGzevDnstUREJB9BkhJj\na+W9e/eyp09ENEnt7e2oq6uLuD3vyCUiSiMMfSKiNMLQJyJKIwx9IqI0wtAnIkojDH0iojTC0Cci\nSiMMfSKiNMLQJyJKIwx9IqI0wtAnIkojDH0iojTC0CciSiMMfSKiNMLQTxKOfjc8wz65yyCiJBf2\nEBWSn88bQOs+M44d6oYkSViwuBBVK2fDaMqFIAhyl0dESYahn8DOd13Hnv/oxKzZufjuU38BADje\nfgX/+e9HkKlR4a5vlGNe+UyZqySiZMLQT0BSUMLvf3cMl8/3477/VYnShV8F+x1rSrHyrnk413Ud\nH/7mKP7vd2tQWJwrY7VElEw4pp+ATh/rQV/vIB7bVDsq8G8QFALKFhXgvr9ejPfe7sDQoEeGKoko\nGTH0E0zAH8Sfdp/Bmr9aCLU6/B9iC5cYsXh5Md5/+wsE/ME4VUhEyYyhn2COtnXDkJ+FkrL8iNrX\n1s2HJjsDez/oRIKccU9ECYyhn0C8Hj8+3X8Wd31jYcTXCAoB9z+0FFcu2vHFZ5djWB0RpQKGfgI5\n/OeLmD0vD4VF+kldl6lR4Zt/uxx/3n0GA47hGFVHRKmAq3cShGvIi7Y/X0DN/1mCI1cHJn19gVaN\npbeb0LrXjG/879tiUCERpQKGfoL47A/nMHN+Pl5ovTKl67fdPx8r15Tire1/RM1fzEV+gTbKFRJR\nKuDwTgIYcAzjxOErKK2ZPa3X0WRlYOWaUhz8uCtKlRFRqmHoJ4DTx65hweJCZOaop/1ay1eVoPeK\nE1cu9kehMiJKNQz9BGA+acH8yoKovJYqQ4na++bjj7/v4hJOIrrFhGP6nZ2daGlpQSAQQF1dHdau\nXTvq+YMHD+L9998HAJhMJjz44IMoKSkBAGzYsAFZWVlQKBRQKpVobGyMwUdIbm6XF5arAygpy0fn\ndVdUXrNyeTEOHbyAc6euo6wiOr9MiCg1hA39YDCI5uZmPP/88xBFEVu2bMGSJUtgMplCbQoLC/HS\nSy8hOzsbBw4cwM9+9jP86Ec/Cj3/4osvQqvlpOJ4znf1YXapiIwMZdReU6EQ8Jd/VY4//r4L8xbO\nhELB3TiJaETY4R2z2Qyj0YiCggKoVCrU1taira1tVJvy8nJkZ2cDAKqrq2G1Wkc9zyGG8M6etGB+\nDHrjpQtnQp2pxNmTlqi/NhElr7Chb7PZkJ//1XYAoijCZrON237Pnj2oqakJPRYEAS+//DI2b96M\nPXv2RKHc1BLwB3HhTN+Ym6pNlyAIWHHnXBxuvRD11yai5BW1dfrHjx/HwYMH8cMf/jD0vVdeeQV5\neXno7u5GY2MjiouLUVFREa23THrdF2wQZ+YgR5cZk9dfcFshDvz3KViuOlEwybt8iSg1he3pi6I4\narjGarVCFMVb2l28eBGvv/46nn32WeTk5IS+n5eXB2BkgnflypUwm83RqjslmE9aYjrRqlQqsOyO\nErR/cjFm70FEySVs6JeVlaGnpwcWiwV+vx+tra2jhm8AoK+vD9u3b8eTTz4Jo9EY+r7H44Hb7QYA\nOJ1OdHR0hFb10Mhcx9mTFpQtiu3qmqW3z8aZE71wDXpj+j5ElBzCDu8olUo0NDSgqakptGTTZDJh\n9+7dAID6+nq88847GBwcxBtvvBG6prGxEXa7HU1NTQAAnU6HdevWoaqqKsYfJ3n09QxCEATMKIzt\nyqZsrRoLFhfi6KHLWHVPWUzfi4gSnyAlyPKavXv3orq6Wu4y4ubT/WfhGvTi3ge+muM4cnUAz3w4\ntSGwbffPR1WRbsznrl8bwP9racP3nlkDpZL34xGlkvb2dtTV1UXcngkgk1iP599s5iwd8vJzcOZ4\nb1zej4gSF0NfBoPOYfT3DcE0Ly9u71ldO4fLN4mIoS+Hc6evY175jLgOtZQtKsDQoBfXLtvj9p5E\nlHgY+jLoPt8f8Rm40aJQCKhaORtHD3XH9X2JKLEw9GXQ0+2A0ZQb9/ddvLwIZ070wuv1x/29iSgx\nMPTjzDPsw4BzGDNkONlKq9egeI4BXZzQJUpbDP04673ixEyjDgqZlk7eVmPC8TYO8RClK4Z+nF2T\naWjnhtKFM2HrG0J/35BsNRCRfHgwepRdc3pgCbPlwWmzFQWlIo5cHbjlOW8gGMvSAIzsx1O5rAjH\n26/grv9RHvP3I6LEwtCPMsugN+xdtXdd6sfvPIDrrPOW5164b14sSwu5bUUx3vl5G2rr5ss2zERE\n8uD/+DhSB4JQBSW4onhK1lTMKNRBl6vBBbN14sZElFIY+nGk9/jgzMwABPmPL7xthQnHOKFLlHYY\n+nGUO+yDIzMxRtQWLTXi0lkrt1wmSjMM/TgK9fQTQKYmA2WLCtD5xVW5SyGiOGLox4skIdfjgyNB\nQh8YmdBl6BOlF4Z+nGj8QUiCAE8CrZYxzRPhGvSgr/fW5aNElJoSJ4FS3EgvX5UQk7g3KBQCKqqK\ncPKLa3KXQkRxwtCPk0Qaz79ZxbJZOHnkKqRgQhygRkQxxtCPk0Qbz79hplEHdaYKVy72y10KEcUB\nQz8eJAk6jz8he/qCIKBiWREndInSBEM/DrJ9AfiUCvgSaBL3ZhVVs9B1vBd+f+z3/iEieSVmCqWY\nXI8PzgS5KWssekMWZhi1ON91Xe5SiCjGGPpxoE/Q8fybVS4rQmcHh3iIUh1DPw70CTqef7Py24y4\naLZi2O2TuxQiiiGGfqxJErQ+PwbViTu8AwCarAzMmZ+PMyd4lCJRKmPox5g6EIQEJOwk7s0qlxXh\nRMcVucsgohhK/CRKcjm+AIYyEruXf8O8hTPR1zOIAcew3KUQUYww9GMsx+fHUIIP7dygUikwv7IA\np45yWwaiVMXQj7EcbwBDMp+UNRkVVUUMfaIUNmEXtLOzEy0tLQgEAqirq8PatWtHPX/w4EG8//77\nAACTyYQHH3wQJSUlEV2bDnJ8flizs+UuI2KzS0UMOj3o7xtC3owcucshoigL29MPBoNobm7G008/\nja1bt2Lfvn3o7h59xF5hYSFeeuklbNu2DVVVVfjZz34W8bXpIMfnT6qevkIhYOFtRpw8wt4+USoK\nG/pmsxlGoxEFBQVQqVSora1FW1vbqDbl5eXI/rInW11dDavVGvG1qU4ZlKAOBOFWJU/oA8Ciqlk4\ndeQaJIk7bxKlmrChb7PZkJ+fH3osiiJsNtu47ffs2YOampopXZuKsn1+uDISaw/9SMyanYtAIAjL\nNR6uQpRqojaRe/z4cRw8eBB/8zd/E62XTHrJNrRzgyAIod4+EaWWsKEvimJouAYArFYrRFG8pd3F\nixfx+uuv49lnn0VOTs6krk1lIyt3kmO55tctWjoLp45e4+EqRCkmbOiXlZWhp6cHFosFfr8fra2t\noeGbG/r6+rB9+3Y8+eSTMBqNk7o21Y2s0U++nj4wcrhKpoaHqxClmrDdUKVSiYaGBjQ1NYWWXZpM\nJuzevRsAUF9fj3feeQeDg4N44403Qtc0NjaOe206yfEGMGRIzp4+MLLP/smj12Cal15/oRGlsgkT\nqbKyEq+++uqo79XX14e+/v73v4/vf//7EV+bNiQJ2f4vJ3KT1MKls/B286e4939WQJkEewcR0cT4\nPzlGsvwBeJUKBBTJtXLnZgYxGwYxCxfN1okbE1FSYOjHSDJttBYOt2UgSi0M/RjJ8fpTIvQXLjHi\n7EkLfL6A3KUQURQw9GMkmVfu3CxHlwmjKRfnTvH8XKJUwNCPkWReo/91vFGLKHUw9GMkWe/GHcuC\nykJcPMvzc4lSAUM/BjICQQgAvCmyzFGTlYGSMhFnOnl+LlGyS41USjChSdwk22gtnIqqIg7xEKUA\nhn4MpNLQzg2li2aip9uBoQGP3KUQ0TQw9GMgxxdImnNxI5WRoUTZogKcPtYjdylENA0M/RgYGd5J\nrZ4+MLKK5+SRq3KXQUTTwNCPgVS5G/fr5szPh93qgt3mkrsUIpoihn6UBfwBZAYCcKdgT1+pVKB8\niZHbMhAlMYZ+lLmdHgyrlJBSaOXOzSqqitDZcZXn5xIlKYZ+lLmdw0l3EPpkFJcY4Pfz/FyiZMXQ\njzK305PSoS8ohJHDVb7ghC5RMmLoR5nbOZyS4/k3u7HdcpDn5xIlHYZ+lKX68A4AzCjUIlubicvn\nbHKXQkSTxNCPMrfTA1eK9/QBoHIZ1+wTJSOGfhRJkoThNOjpA8CipbNw5kQvD1chSjIM/Si6sfWw\nP4nPxY2UVq/h4SpESYihH0UOmxtZek1K7a4ZDlfxECUfhn4UOfrdyNJnyl1G3CxYbMSlcza4XV65\nSyGiCDH0o8huc4309NNEpkaFeeUz0MWdN4mSBkM/ipz97rQKfQCoXFaETg7xECUNhn4UOfpd0KTR\n8A4AzC2fgf4+F/qtQ3KXQkQRYOhHkd3mRnZuevX0lUoFFlXNwol29vaJkgFDP0qCQQkDjmFodOkV\n+gCwuLoYnR1XIHFbBqKEN+FJH52dnWhpaUEgEEBdXR3Wrl076vkrV65g586duHDhAr71rW/hgQce\nCD23YcMGZGVlQaFQQKlUorGxMfqfIEEMOoeRlZ0BpSr9fo8WzNIhU5OByxdsKCnNl7scIgojbOgH\ng0E0Nzfj+eefhyiK2LJlC5YsWQKTyRRqo9Pp8Pjjj+PQoUNjvsaLL74IrVYb3aoTkMPmRm5eltxl\nyEIQBCyuLsKJ9qsMfaIEF7ZbajabYTQaUVBQAJVKhdraWrS1tY1qo9frUVZWBqVy7K0H0uWwDUe/\nC7l52XKXIZuKqiKYO3vh9fjlLoWIwggb+jabDfn5X/XcRFGEzRb5zoqCIODll1/G5s2bsWfPnqlX\nmQTsNjdyxfTs6QNAji4TxXPycOZEr9ylEFEYMT29+5VXXkFeXh66u7vR2NiI4uJiVFRUxPItZePs\nd6OkTEQ6bz+2uLoYRz67hMXVxXKXQkTjCNvTF0URVqs19NhqtUIUxYhfPC8vDwBgMpmwcuVKmM3m\nKZaZ+Bz9LuSK6Tu8AwBli2bCcm0Ajn633KUQ0TjChn5ZWRl6enpgsVjg9/vR2tqKmpqaMdt+feze\n4/HA7R75z+90OtHR0YGSkpIolZ147Gk8kXuDKkOJhUuN6Ozgmn2iRBV2eEepVKKhoQFNTU2hJZsm\nkwm7d+8GANTX18Nut2PLli1wuVxQKBT48MMP8dprr8HhcKCpqQnAyAqfdevWoaqqKvafSAY+XwDD\nbh+0eg3gGpS7HFndVl2M//rNUay6pxRCmuw2SpRMJhzTr6ysxKuvvjrqe/X19aGvDQYDmpubb7lO\no9Fg27ZtUSgx8Tn73dDnaqBIg330J2I05UKpVKD7Qj9mz4t8KJCI4iP97iSKAUd/eq/cuZkgCFhS\nY8Kxtm65SyGiMTD0o8BhS+81+l9XubwIZ09aQieJEVHiYOhHgZ09/VGyc9SYu2AGT9UiSkAM/Shw\n2tzs6X/N0ttNONrWnTZ3ZBMlC4Z+FIys0WdP/2YlpfnwDvvRe8UpdylEdJOY3pErl2tODyyDUz+3\ntUCrxqwID0ORJIlr9McgKL6a0DWacuUuh4i+lJKhbxn04pkPp37377b750cc+jcmKzVZGVN+v1S1\nuLoYLf/yZ6xZuxDqzJT8p0aUdDi8M00OmxsGMYs3Io1Bl6tB8RwDTh/nwelEiYKhP02Ofk7ihrPk\n9tk4dohr9okSBUN/mpx2N/R56XdEYqRKy2fA0e9GX++A3KUQERj60+a0u6HL5STueBRKBZbUmPDF\nZ5flLoWIwNCftgH7MPQG9vTDqVo5G6eOXINnmKdqEcmNoT9NTrsbegN7+uHocjUoKRPR2XFF7lKI\n0h7X0U2T0z6cEKGvVABHrk593Hwy9yZMxbJVJdjzH51YtqqEK52IZMTQnwavxw+/P4CsHPnX6DuG\nA3hpz/kpXz+ZexOmYvY8EYIg4PI5G0rK8ie+gIhigsM70+C0D0OfyzX6kRAEActXlaDj00tyl0KU\n1hj60zDgcEPHSdyIVS4vwuVzNgw4huUuhShtMfSnwdnPSdzJUGeqUFE1C0c+5/JNIrkw9KfB6eBy\nzclatqoERw9dht8flLsUorTE0J8Gp90NHXv6k5JfoMWMQh26uB8PkSy4emcaUunGrOks+Zzscs/q\n1SX4ZP9ZVFTN4iQ4UZwx9KfBkUI3Zk1nyedkl3uWLSrAH/77NLov9GP2PHFK70lEU8PhnSkKBoIY\nGvBAp0+Nnn48CQoBNX8xF20Hp35fARFNDUN/igYHPMjOUUOp4o9wKiqri3HtsgNWy6DcpRClFSbW\nFCXK9gvJKiNDiao7ZuPwny/IXQpRWmHoT9HIlsoc2pmOZatKcPpYD4YGPHKXQpQ2GPpTNGB3Q8/D\n0KclR5uJRUtncWsGojhi6E/RyL477OlP14raOTjy+WX4vAG5SyFKCxMu2ezs7ERLSwsCgQDq6uqw\ndu3aUc9fuXIFO3fuxIULF/Ctb30LDzzwQMTXJjOn3Y3ShTPlLiPpiTO1KC4x4ET7FSxbVSJ3OUQp\nL2xPPxgMorm5GU8//TS2bt2Kffv2obt79CHXOp0Ojz/++Kiwj/TaZMaJ3OipuWseDv3pPIIBbs1A\nFGthQ99sNsNoNKKgoAAqlQq1tbVoa2sb1Uav16OsrAxKpXLS1yYrSZK+3IKBwzvRYJqbB51eg5NH\nr8ldClHKCxv6NpsN+flfHXghiiJsNltELzydaxPdsNsHQRCgyZL/8JRUsfre+fh0/1kEg5LcpRCl\nNE7kTkEq7bmTKErKRGRlq3H6GHv7RLEUNvRFUYTVag09tlqtEMXI9kqZzrWJjoehR58gCFh9bxk+\n2XcWEnv7RDETdvVOWVkZenp6YLFYIIoiWltbsWnTpjHbSpI05WuTjdM+zPH8m0Rrh865C2ZAnalC\n14leLFxijGaJRPSlsKGvVCrR0NCApqam0LJLk8mE3bt3AwDq6+tht9uxZcsWuFwuKBQKfPjhh3jt\ntdeg0WjGvDYVsKc/WrR26LzR2z/4cRfKFxdCUHDbZaJom3CdfmVlJV599dVR36uvrw99bTAY0Nzc\nHPG1qcBpH0ZhsV7uMlJS6cKZaN1jhvmkBQsWF8pdDlHK4UTuFLCnHzuhsf39Z28ZMiSi6WPoT8GA\ngzdmxVJZRQEA4MyJXpkrIUo9DP1J8vuDcLu8yNFFflIUTY4gCPjLb5Tj4MddCPAuXaKoYuhP0oDD\nDa1eAwUnGWNqzvx86HKzcLwtdbbuIEoEDP1JGuDumnFxo7ffuu8svF6/3OUQpQwejD5JDu6jH1Vh\n1/grFNAadfiv33ehtGb2LU9r1UoMTmNL5pvvESBKFwz9SWJPP7omWuOf5ZNwx+eX8eY1N3zK0X+Y\nvnDfvCnfHwCMvkeAKF1weGeSRnbXZE8/XtwZKvRoNSjtH5K7FKKUwNCfJEe/G7kc3omrc4YczBp0\nI8vH07WIpouhP0lOhn7ceVVKXMrNRrltavv7ENFXGPqTEAxKGHQOc3hHBhdyc6Dz+CG6PHKXQpTU\nGPqTMOgcRlaOGioVf2zxFlQIOJ2vQ4V1AAK3ZyCaMqbXJDj7ueeOnK5nq+FSKTHH4ZK7FKKkxdCf\nBAc3WpOXIOD0DB3m2oeQ6eekLtFUMPQngZO48nNlqNCtz0a5bVDuUoiSEkN/Ehz9vBs3EZw35MAw\n7IXjqlPuUoiSDkN/EtjTTwyBLyd1z//pHBQ8T5doUhj6k8B9dxKHJUeDrLxslNo5zEM0GQz9CAWD\nEgYd3HcnkcyrnYvigWHoPT65SyFKGtxwbQxj7fw4POiBMlOFE9fDLxf08tCPuFFnq3Fa1GKxxYlP\nTSIkgWccEE2EoT+GsXZ+NAx7UR4AnvnQHPbaF+6bF8vS6Gt6tBoYh4ZR2j+Es6JW7nKIEh6HdyKU\n5QvArVLKXQZ9nSDg5Aw9Zjtd0HGYh2hCDP0IafwBuDP440pEHpUSXfk6LL7u5BYNRBNgikUoy8+e\nfiK7qtXArVKi3MrVPEThMPQjlOUPYpihn7gEASdm6lHgGsbMoWG5qyFKWAz9CHFMP/H5lQocLchF\nZd8A9+YhGgdDPxKSBI0/wJ5+EnBo1Likz8ZSi4Pj+0RjYOhHIDMQhE+pQFDBdeDJ4LwhG0FB4Lm6\nRGOYcJ1+Z2cnWlpaEAgEUFdXh7Vr197S5te//jXa29uRmZmJ9evXo7i4GACwYcMGZGVlQaFQQKlU\norGxMfqfIA44iZtkBAHHZuqx6ooNdk0GrNmZcldElDDChn4wGERzczOef/55iKKILVu2YMmSJTCZ\nTKE27e3tuHjxIpqamnDmzBns3LkTP/rRj0LPv/jii9Bqk/umGY0vADdPy0oqXpUSRwtzsazHjs+L\nRLjUvA+RCJhgeMdsNsNoNKKgoAAqlQq1tbVoa2sb1aatrQ1r1qwBACxYsABDQ0Ow2+2h56UUGFfN\n8gfgzmBPP9nYNWqcEXVY3muHittjEAGYIPRtNhvy8/NDj0VRhM1mC9smPz8/1EYQBLz88svYvHkz\n9uzZE82644rLNZPXFX0W+rIyObFL9KWo/M07Xm/+lVdeQV5eHrq7u9HY2Iji4mJUVFRE4y3jKssf\nQG8Ox4WTVVe+Fst77Ci3DuL0DJ3c5RDJKmxPXxRFWK3W0GOr1QpRFCNuk5eXBwAwmUxYuXIlzObw\nm5UlKg3X6Cc1SRBwtCAXM9wemJw8VJ3SW9iefllZGXp6emCxWCCKIlpbW7Fp06ZRbWpqavDRRx+h\ntrYWXV1dyMnJgcFggMfjQTAYRFZWFpxOJzo6OvDd7343ph8mJiQJmgDX6Cc7v1KBdqMBt1/th0+h\nQK9WM+YW2pEq0KoxSz+1v/6uOT2wDHrj/r5EwAShr1Qq0dDQgKamptCSTZPJhN27dwMA6uvrUV1d\njZMnT+Lpp5+GRqNBQ0MDAMBut6OpqQkAoNPpsG7dOlRVVcX440RfZiAIv4Jr9FOBO0OFdqMBK3rs\n8CuEMbfQjtS2++dPOXwtg94Jt+iOxfsSARGM6VdWVuLVV18d9b36+vpRjx955BE88sgjo75XWFiI\nbdu2RaFEeWm4Rj+lDGZm4MiXSzkHeqfWyydKZlx8PoGRG7P4Y0oldo0axwtycfrjLmi93IOf0gvT\nbAJZPi7XTEV92ZmYu3oOqq/ZoeXhK5RGGPoT4I1ZqWvG/Bk4na/Dih479MMMfkoPDP0JcEw/tfVq\nNeicoUd1Tz8M7qmtqCFKJgz9CXAf/dR3PScTRwtysazXDtHlkbscophi6IehCI6s0efwTuqzZWfi\nC6MBSy0OzBpwy10OUcww9MPQ+vxwZaggCVyjnw7sGjUOFYko6x/CfNsgwL16KAUx9MPQev0Y4Ja8\naWVIrcJnxSLy3F5UWRxQBBn8lFoY+mFovX4MMvTTjk+pQFtRHgKCgNuv2XjeLqUUhn4YOoZ+2pIE\nAcdn6tGbo8GqKzbMGOIEL6UGJloYHN5Jc4KAC4Yc2DUZWNLrQO+wBmdELed4KKmxpz8OdSAIhSTB\no+SPKN3ZNWp8aspHts+PlVdtyPL55S6JaMqYaOPQen0jvXz26ggj4/xfFBpwTavBHVdsuPjFVQQ5\nyUtJiKE/Dq2H4/n0NYKAS7k5+LxIhOWcFf/++mewWgblropoUhj64+AkLo3HpVah5sHbULmsCP/+\n+mf4ZJ8ZPh9X+FByYOiPQ+vjJC6NTxAELFtVgr/deCcs1wbw89cO4tTRa+OeF02UKJhqY5CCEtfo\nU0T0hiz89SPLcfmcDfs/PIX21ou4Z90izJptkLs0ojEx1cYw7ByGV6lAQME/hCgys0tFPLp+NU50\nXMF/vN0BY3EuVtfNR2GRXu7SiEZh6I/BZXNxaIcmTaEQsGSFCYuWzsLRzy/j3V8eRmFxLlbfWwZj\nca7c5dEUpOIh9ky2MbhsLgyqM+Qug5JURoYSK2rnYunK2Th2qBvv7WpHfoEW1XfOQWn5TLnLo0lI\nxUPsGfpjYE+foiEjQ4nqO+dg6crZOH3sGlr3mrH/P0+hcHEhlMEghw9JFky2Mbhsbgzqc+Qug1KE\nSqXA4uXFqFxWhKuX7Ni314y/vGTD9exMXNVlwabJ4E2AFDfsanyNMijBO+SFiwenUJQJgoDiOXlY\n+leL8KfZM+DMzEC5dQB3Xe7DfNvgyAHtXPJJMcae/tfkeP3QGDTcVItiyqdU4FJuNi7lZkPn8WHW\n4DCW99oRhABLTiZ6czRwZnIbEIo+hv7X6Lx+ZIvZAG+wpDgZyMzAQGYGukQtdF4/CoeGseS6A6qg\nBGuWGn2SN3knAAAI7UlEQVTZmbBmqeHj5n8UBQkb+pfsbgx6ppa83kBwyu+r9fqRLRqA69w/neJM\nEEK/AMyiDlk+P/LdXhgHh1Fx3Ql3hhKnDyqRvaQQprl5yMpWy10xJaGEDf0/X3Dg523XpnTtS/Xz\npvy+2hs9fYY+ycydoUJ3hgrd+mwIkgS9x4fqrAwc+fwy/vu3x6DVZ2LW7FwYTQbMMuViplEHpWr8\nvwams+YcmN66c7nWu0/3M0+nA5moEjb0ZSFJ0Hl9I6GPfrmrIQqRBAEOjRrzakyoKtIhGAjieu8g\nerod6Ol24Mjnl+Aa8KJhyz0QFGPPA0xnzTkwvXXncq13n+5nfuG+qXcgE9WEod/Z2YmWlhYEAgHU\n1dVh7dq1t7T59a9/jfb2dmRmZmL9+vUoLi6O+NpEov3ycAx1Nm/MosSmUCpQWKRHYZEeVStnAwD8\n/uC4gU90Q9iZoWAwiObmZjz99NPYunUr9u3bh+7u7lFt2tvbcfHiRTQ1NeGxxx7Dzp07I742keg8\nPqy4ZkdXvg4CV0xQElKFGdohuiHsvxKz2Qyj0YiCggKoVCrU1taira1tVJu2tjasWbMGALBgwQIM\nDQ3BbrdHdG2iMLi9WHGtHydn6HBVlyV3OUREMRM29G02G/Lz80OPRVGEzWYL2yY/Px82my2iaxPB\nDJcHy3rtOFqQC0uORu5yiIhiKioTudE6OOJ3vzwc+trnCeCvPVM7gPrk709j+fWhiRtKgN7rR4fR\nAIeGy9+IKPUJUpjE7urqwm9/+1v8wz/8AwDg3XffhSAI+OY3vxlq8/rrr2Px4sWora0FADz11FN4\n8cUXYbFYJrz2ZocPH4bdbo/aByMiSgcGgwErVqyIuH3Ynn5ZWRl6enpgsVggiiJaW1uxadOmUW1q\namrw0Ucfoba2Fl1dXcjJyYHBYIBOp5vw2ptNpmgiIpqasD19YGTZ5S9+8YvQssv7778fu3fvBgDU\n19cDAN5++220t7dDo9GgoaEBJpNp3GuJiEg+E4Y+ERGlDi7sJSJKIwx9IqI0khB77yTDdg19fX3Y\nsWMHHA4H9Ho97r77btx9991ylzWmYDCI5557DqIo4rnnnpO7nDENDw/jzTffxKVLl+Dz+dDQ0IDy\n8nK5y7rFnj17cODAAfh8PlRUVOCxxx6TuyQAwM6dO9HR0QG9Xo/t27cDANxuN37605/CYrGgsLAQ\nTz75JDQaee89GavOXbt2ob29HWq1GhUVFXj44YeRnZ2dcHXe8MEHH+BXv/oV3nrrLWi1WpkqHDFe\nnfv378dHH30En8+H5cuX49FHHx3/RSSZBQIBaePGjVJvb6/k8/mkH/zgB9Lly5flLusW/f390vnz\n5yVJkiSHwyE98cQTCVmnJEnSBx98IP3kJz+Rtm7dKncp4/rpT38q7d27V5IkSfL7/dLQ0JDMFd1q\nYGBAWr9+veR2u6VAICD90z/9k9TR0SF3WZIkSVJnZ6d07tw56e///u9D39u1a5f03nvvSZIkSe++\n+670q1/9Sq7yQsaq88iRI1IgEJACgYDU3NycsHVKkiRdv35d+uEPfyitX79eGhgYkKm6r4xV57Fj\nx6SXX35Z8vl8kiSN5FM4sg/vJMt2DQaDAXPnzgUA6PV6lJWVob8/8XbitFqt6OjowL333hu1m+ai\nzeVy4dSpU7j33nsBAEqlUvae3ljU6pEb9lwuF7xeLzwej+w9vRsqKiqQkzP6HOebt0S5++67cejQ\nITlKG2WsOpcuXQqFQgGFQoFly5bBarXKVN1XxqoTAH75y1+G7zXH2Vh1fvzxx3jwwQehUo0M3Oj1\n+rCvIfvwzljbNZjNU98KNR56enrQ3d2NBQsWyF3KLVpaWvDoo4/C7XbLXcq4LBYL9Ho9duzYgXPn\nzmHBggV4/PHHQyGbKNRqNZ544gls2LABGRkZWLt2LebPny93WeNyOBwwGAwAgNzcXDgcDpkrmtje\nvXtDv/wTzaFDhyCKIubMmSN3KWH19PSgs7MTu3btgkajwXe+8x2UlpaO2172nn6yGR4exo9//GN8\n5zvfkX289OsOHz4MvV6PefPmJWwvHwACgQDOnj2LO+64A42NjfD7/fjkk0/kLusWTqcTb775Jl57\n7TXs2LEDXV1daG9vl7usiCTDTrG/+93voNFosHr1arlLuYXH48G7776Lhx9+OPS9RP0/FQgEYLFY\n8Morr+CBBx7Arl27wraXPfRFURz1553VaoUoijJWND6/34/t27fjrrvuwu233y53Obc4ffo0Dh8+\njA0bNuAnP/kJTpw4gX/913+Vu6xb5OfnQ6vVoqamBmq1GrW1tejo6JC7rFuYzWYsWLAARqMROp0O\nq1evRmdnp9xljSs3Nze0lUl/fz9yc3Nlrmh8Bw4cQEdHB5588km5SxlTb28vrl+/jmeeeQYbNmyA\nzWbDc889l5B/PeXn5+POO++EWq1GTU0Nrl69Cq93/NPCZA/9m7d68Pv9aG1tRU1Njdxl3UKSJPzb\nv/0bTCYT1q1bJ3c5Y/r2t7+N5uZm7NixA0899RQWL16MjRs3yl3WLQwGA4xGI86cOYNgMIj29nYs\nXbpU7rJusWjRIpw9exaDg4Pw+Xzo6OhAVVWV3GWNq6amBgcOHAAA/OEPf0jIjgkAfPHFF3j//fex\nefPmhBvSu6GkpARvvPEGduzYgR07dkAURfzzP/9zQv4ivf3229HR0QFJknDmzBkUFhaG/bkmxB25\nybBdw6lTp/DCCy+gpKQk9Kfzt7/9bSxbtkzmysbW2dmJDz74AM8++6zcpYzp6tWr2LFjB5xOJ0pK\nShJieeFYDhw4gP3798Pr9aKqqgoPP/wwFArZ+0r48Y9/jJMnT2JgYAC5ubl4+OGHsWrVqoRbsnmj\nTqfTCYPBgIceegjvvfce/H5/aFK8vLwcTzzxRELUefPP85577gk9v3HjRmzdulX2ifyx6lyzZg3e\nfPNNnDhxAiqVCt/73vewaNGicV8jIUKfiIjiQ/4uCxERxQ1Dn4gojTD0iYjSCEOfiCiNMPSJiNII\nQ5+IKI0w9ImI0ghDn4gojfx/x/DcAaaZhjIAAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x1135404d0>"
       ]
      }
     ],
     "prompt_number": 10
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Looping over all months, we can create a grid of plots for the distribution of rainfall, using the gamma distribution:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "axs = precip.hist(normed=True, figsize=(12, 8), sharex=True, sharey=True, bins=15, grid=False)\n",
      "\n",
      "for ax in axs.ravel():\n",
      "    \n",
      "    # Get month\n",
      "    m = ax.get_title()\n",
      "    \n",
      "    # Plot fitted distribution\n",
      "    x = linspace(*ax.get_xlim())\n",
      "    ax.plot(x, gamma.pdf(x, alpha_mom[m], beta_mom[m]))\n",
      "    \n",
      "    # Annotate with parameter estimates\n",
      "    label = 'alpha = {0:.2f}\\nbeta = {1:.2f}'.format(alpha_mom[m], beta_mom[m])\n",
      "    ax.annotate(label, xy=(10, 0.2))\n",
      "    \n",
      "tight_layout()"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAI5CAYAAAC8QJvjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4U1X+P/D3zdImabqlJd3S0n2DslPAAgVKWVXc+KkD\njM7oKOgA35lBERUFlMGhZZwZHJnBUQEddVxAZQSFInsBKWURyxaWlu60pW3aZs/9/VGbaWiabklu\nkn5ez5PnIbnbJ5rTc88953wOw7IsC0IIIYQQQgghfcbjOgBCCCGEEEII8RTUwCKEEEIIIYQQO6EG\nFiGEEEIIIYTYCTWwCCGEEEIIIcROqIFFCCGEEEIIIXZCDSxCCCGEEEIIsRNqYBFCCCGEEOJmVq1a\nhYSEBK7DIFZQA8uDlZWVQSAQICIiAkajketwCHELVG4I6ZnHH38cPB4PPB4PEokEiYmJyM7Oxvvv\nv09liJAutC8/7V+ffvop16GRPqAGlgd79913kZSUBLVajZ07d/b5fDqdzg5REeLa7F1uCOkPJk6c\niMrKSiiVSmzbtg0zZ87E8uXLMWLECKjVaq7DI8SltZWf9q85c+ZwHRbpA2pgeSiTyYT33nsPixcv\nxrx587B582aL7dHR0Xjttdfwu9/9DpGRkYiOjsa6deus7rN8+XIkJCQgMzPTmV+BEKfrTrlZu3at\nxWdPPvkkJk+ebH6v1+vxu9/9DhEREYiNjcVLL72EV199lYZxEI8mFAohl8sRHh6OsWPH4ve//z1O\nnDgBpVKJF154wbzftm3bMGLECPj6+iIxMRF//OMfLXq5TCYT3nzzTQwZMgQ+Pj5QKBRYsmQJF1+J\nEKfx8vKCXC63eHl7e+PSpUu49957ERoaCrlcjgcffBAlJSUdjt+1axdGjhwJmUyG++67D9XV1Rx8\nC9IeNbA81O7du1FXV4f58+fjqaeewp49e1BcXGyxz1/+8hf4+fnh+++/x+uvv461a9fib3/7W4d9\nfHx8sHv3brz//vvO/AqEOF1X5YZhGDAM0+G49p8tW7YMH3/8Mf75z3/i22+/hclkwt///nerxxHi\nyWJiYjB//nx8+eWXAIA///nPWL58OZ544gkcP34cy5Ytw8aNG7F69WrzMUuXLsUbb7yB5cuX4/z5\n8/jyyy8RHx/P1VcgxClYlu3wWUlJCUaOHImBAwdi+/bt+Oijj9Dc3Izs7GxotVrzfhUVFcjJycE7\n77yDPXv2oKKiArNmzXJm+MQalnike++9l3366afN7zMyMtiXX37Z/H7gwIFsdHS0xTHz5s1jIyMj\nLfaJi4tzfLCEuIiuyk10dDS7du1ai2OeeOIJdtKkSSzLsmxTUxPr5eXFvvLKKxb7hIWFsQkJCQ6M\nnBDuPPbYY+zUqVOtbtuwYQPLMAyrUqlYqVTKvvPOOxbbX3/9dTYgIIBlWZYtLi5m+Xw++8UXXzg8\nZkJcxWOPPcYKBAJWKpWaX0lJSezTTz/NZmRkWOxbXFzMCgQC9ssvv2RZlmVfffVVlmEY9sCBA+Z9\n9u7dyzIMw+7bt8+p34NYoh4sD1RWVoZdu3Zh4cKF5s+eeuopvPfeezCZTABan7hPnTrV4rjs7GyU\nlpaiqanJvM+MGTOcFzghHOpOuemKUqmEXq9Hdna2xedTp061+oSSEE/HsiwYhkFJSQmam5vxf//3\nf/D19TW/1q5di8bGRtTW1uLcuXMwmUyYNm0a12ET4lRjx47F2bNnza/vvvsOhYWFKCgosCgvgwYN\nAsuyUCqV5mPFYjHuuusu8/vx48dDLBajqKiIi69CfibgOgBif++++y6MRiNGjx5t8bnJZMLXX3+N\n++67DyzLduuGLzw83FFhEuJSulNueDxeh6xoKpWKhv8R0okLFy4gMjLS/JDi888/R2JiYof9AgMD\nnR0aIS5DJBIhNjbW4jOTyYRf/vKXFnMY28hkMmeFRnqJerA8jMlkwrvvvouXXnrJ4mnImTNn8Mgj\nj1hM2t+3b5/FsXv37oVCoYBUKnV22IRwqrvlRi6Xo7Cw0HycTqfDnj17zO/j4+Ph5eWFvXv3Wpw/\nLy+PGmHEo1n7fV+7dg0fffQRHnjgASQlJcHHxwdXr15FbGxshxePx8OQIUPA4/Hw3XffcfANCOGO\ntfIzYsQInD171mp5CQgIMO+nVquRn59vfn/kyBGo1WqkpqY6JXZiHfVgeZjdu3ejtLQUTz/9NBQK\nhcW2xx9/HDNnzjRP2lepVFi1ahV+8YtfoKCgAF999ZVFhjQa0kT6i+6Wm6lTp+Jvf/sb3n//fSQk\nJGDjxo3g8/nmsuLj44OFCxdi8+bNSE9PR0JCArZs2QK9Xk8NLOLRtFotqqqqoNfrcfPmTRw7dgxv\nvPGGOVOgUCjEH//4R7z44otgGAZZWVkwGAz48ccfcebMGbzxxhuIiorC008/jWeeeQYajQZjx45F\nXV0djh07RpkEiUezdr/1yiuvIC0tDfPnz8fSpUsRHByMGzdu4KuvvsLSpUsRExMDAJBIJFi9ejVy\ncnLAsixefvllDB8+HFOmTHH21yDtUAPLw7zzzjsYO3Zsh5tEAJg8eTJkMhn+9a9/gWEYLF26FDU1\nNZgyZQoEAgFeeOEFi0qMbghJf9GdcvPuu+9i+fLlKC4uxrJlyxAcHIxnnnkGfn5+uHr1qnn/nJwc\n8Hg8PPXUUxAKhXj00Ufxq1/9CgcPHnTmVyLEaRiGweHDhxEWFgZvb28oFApER0fjT3/6Ex577DHw\neK2DZRYvXoywsDBs2LABL774Ing8HpKSkvD444+bz7Vx40ZER0fjjTfewNWrVxEUFIS5c+dy9M0I\ncbzOstMqFAoUFhZixYoVePDBB1FTU4OIiAhkZWWZh9QyDIPw8HD8/ve/xxNPPIHi4mJMnDixwxIj\nxPkYtotuiqKiImzduhVGoxFZWVmYOXOmxfaTJ0+aV5uWyWSYO3euOaXqs88+C7FYDB6PBz6f32Gd\nJcKdmJgY/OY3v8GLL77IdSiEeLwpU6YgPDwcH374IdehEEIIIcTBbPZgmUwmbNq0CStXroRMJsOK\nFSuQlpZm8ZQ3LS3NPCm8qKgIH3zwgcWaFqtWraI5PS6Ihv8R4hjnz5/HqVOnMG7cONy4cQMffPAB\nDh48iCNHjnAdGiGEEEKcwGaSC6VSaV49WiAQICMjAwUFBRb7iEQi879bWlogFAotttONvGui4X+E\nOAbDMPjHP/6B9PR0PPTQQ7h8+TJ27NiBcePGcR0aIYQQQpzAZg9WXV0dgoKCzO9lMplF7v02P/zw\nA7Zu3QqNRmMxDJBhGKxZswYMw2DatGkd1l0i3Ll+/TrXIRDikQYNGoRjx45xHQYhhBBCOGKXJBfp\n6elIT09Hfn4+cnNzsX79egDAa6+9hsDAQJSWlmLdunWIiIhASkqK1XMcP34czc3N9giHELcQEBCA\nkSNH9vk8VHZIf2OvsgNQ+SH9C5UdQnqnp2XHZgNLJpOhtrbW/L62ttbm4mZ33XUX3n33XbS0tEAi\nkZiznCgUCqSnp0OpVHbawGpubsaIESO6HTgh7q79ekp9QWWH9Df2KjsAlR/Sv1DZIaR3elp2bM7B\niouLQ2VlJaqrq2EwGJCfn49Ro0ZZ7FNZWWmeZ1VYWAgvLy9IJBJotVqo1WoAQGNjI06fPo2oqKge\nBUcIIYQQQggh7sRmDxafz8eiRYuQm5trTtOuUCiwd+9eAEB2djZOnDiBQ4cOgc/nIzo6Gs8//zwA\noL6+Hrm5uQAAX19fzJ49G0OHDnXw1yGEEEIIIYQQ7nQ5Bys1NdU8p6pNdna2+d9z5szBnDlzOhwX\nEhKCnJwcO4RICCGEEEIIIe7BLkkuPFVFoxbVTbpOt8ulXgjz83ZiRIQQQgghhBBXRg0sG6qbdHhu\nV8e09G1yZsVTA4sQQgghhBBiZjPJBSGEEEIIIYSQ7qMGFiGEEEIIIYTYCTWwCCGEEEIIIcROqIFF\nCCGEEEIIIXZCDSxCCCGEEEIIsRNqYBFCCCGEEEKInVADixBCCCGEEELshBpYhBBCCCGEEGIn1MAi\nhBBCCCGEEDuhBhYhhBBCCCGE2Ak1sAghhBBCCCHETgRd7VBUVIStW7fCaDQiKysLM2fOtNh+8uRJ\nfPrppwAAmUyGuXPnIj4+vlvHEkIIIYQQQognsdnAMplM2LRpE1auXAmZTIYVK1YgLS0NCoXCvE9a\nWhpGjx4NoLVB9cEHH2D16tXdOpYQQgghhBBCPInNIYJKpRKhoaGQy+UQCATIyMhAQUGBxT4ikcj8\n75aWFgiFwm4fSwghhBBCCCGexGYPVl1dHYKCgszvZTIZlEplh/1++OEHbN26FRqNBm+88UaPjiWE\nEEIIIYQQT2GXJBfp6en4+9//jieeeAI5OTn2OCUhhBBCCCGEuB2bDSyZTIba2lrz+9raWshksk73\nv+uuu1BbW4uWlpYeH0sIIYQQQggh7s5mAysuLg6VlZWorq6GwWBAfn4+Ro0aZbFPZWUlWJYFABQW\nFsLLywsSiaRbxxJCCCGEEEKIJ7E5B4vP52PRokXIzc01p1pXKBTYu3cvACA7OxsnTpzAoUOHwOfz\nER0djeeff97msYQQQgghhBDiqbpcBys1NRXr16+3+Cw7O9v87zlz5mDOnDndPpYQQgghhBBCPJVd\nklwQQgghhBBCCKEGFiGEEEIIIYTYDTWwCCGEEEIIIcROqIFFCCGEEEIIIXbSZZILQgipaNSiuknX\n4XO51Athft4cREQIIYQQ4pqogUUI6VJ1kw7P7VJ2+DxnVjw1sAghhBBC2qEhgoQQQgghhBBiJ9TA\nIoQQQgghhBA7oSGChJBeERpNKD1fCeONWhgMJhj0JiSlhSJILuU6NEIIIf0Ea2LB8BiuwyDEAvVg\nEUJ6Jb6uCZVXbuF2bQvUzXqoGjT47ydnYTKauA6NEEJIP1B0phxvvb4P+fuU0Kj1XIdDiBk1sAgh\nPcY3mRDarMHg7ERk3ZOKzJlJmHb/IIjEQpz94SbX4RFCCPFwWo0BB3dfQvacQWi4rca7Gw7hyN4r\n1NAiLoEaWISQHgtr0qBO5AWR9H8ZBBmGwZR7UpC/T4kWKyndCSGEEHvJ/16JmMRgJA8Nw8yH0jDv\nmXGor23B1x+d4To0QqiBRQjpIZaFolGNUj9xh00DQn2ROjwch/dc5iAwQggh/UFNVROKCsswYXqi\n+bMAmQQz56ahoa4FN6/XcRgdId1IclFUVIStW7fCaDQiKysLM2fOtNh++PBhfP311wAAhUKB+++/\nH1FRUQCAZ599FmKxGDweD3w+H+vWrXPAVyCEOJOf1gCBiUWt2Mvq9ruy4vHem0dQcbMeYZEBTo6O\nEPem1ehRV9OCoAE+8PKmPFSE3IllWXz/3wsYNyUOPlLLdRj5fB7GTYlDfp4SD/8mnaMICemigWUy\nmbBp0yasXLkSMpkMK1asQFpaGhQKhXmfkJAQrF69GhKJBAcOHMA///lPrF271rx91apVkEopqxgh\nnkKhakGZrxhgrGdt8hYJMWF6IvbtvIB5C8dSdidCulBechuHv7uCuppm6LQG+Ph6w9dPhLlPjAaP\nyg8hFq78VIWWJi2GjYmyuj11WDiOH7iGkqu1iIoLcnJ0hLSyOURQqVQiNDQUcrkcAoEAGRkZKCgo\nsNgnMTEREokEADBixAjU1tZabGdZ1s4hE0K4IjCZENKsRZmvyOZ+g4aFAwAu/1TljLAIcWuHvr2M\nmKRgzFs0FktemYpf/24CWLA4eega16ER4lIMBhP277qIKfekgMe3fgvL+7kX62ieku5BCWdsNrDq\n6uoQFPS/1r9MJkNdXefjWvPy8jBq1Cjze4ZhsGbNGjz//PPIy8uzQ7iEEC6FqTSoFXtBJ+Db3I/h\nMRg2Ngo/nS5zUmSEuKeqsgY03FZjZEY0/ALEYHgMeDwGs+YOwamjxai4Wc91iIS4jMrSBkh8vBAV\na7tnKmVIGNTNOhQra23uR4ij2C3Jxfnz53H48GE8+uij5s9ee+015OTkYMmSJdixYwcuXLhgr8sR\nQpyNZaFQqVHq2zG5hTWJg0JQduM2mpu0Dg6MEPd16mgxho+LAv+Op/F+AWJMnZOK//7nLLQaA0fR\nEeJaykvqER7V9dxeHp+HcVlxyN9HvViEGzYbWDKZzGLIX21tLWQyWYf9iouLsXnzZixfvhw+Pj7m\nzwMDAwG0Jr9IT0+HUqm0V9yEECfz1RnAN7Go6yS5xZ28vAWIS5Hj4tkKB0dGiHtqatTg2qVbGDI6\n0ur2xMGhGBgXhLyvf3JyZIS4popuNrAAICktDBq1Hjeu1Dg4KkI6stnAiouLQ2VlJaqrq2EwGJCf\nn28xBBAAampqsGHDBixevBihoaHmz7VaLdRqNQCgsbERp0+fNmcXJIS4nopGLc6Wq6y+dEYT/LV6\n1ImFnSa3sGbQ8HD8dLrcgVET4r7OHC9B8tAwiMTCTveZPDsFVaWNuHbplhMjI8T1sCyL8pvdb2Dx\neAxGZkTjx4JSB0dGSEc2swjy+XwsWrQIubm55jTtCoUCe/fuBQBkZ2fj888/R1NTE9555x3zMevW\nrUN9fT1yc3MBAL6+vpg9ezaGDh3q4K9DCOmt6iYdnttlvZf51akx8NUZ0OTV+Y2gNZGxQWhp0uJW\npQoDQn3tESYhHkGvN+LsyVL84ukxNvcTevExZnIsCvNvIDZpgJOiI8T1NNa3PrT3C+jeMHUASBwc\ngoO7L0Gr0cNb1LP6i5C+6HIOVmpqKtavX48NGzZg1qxZAFobVtnZ2QCAhQsX4r333sP69euxfv16\n81pXISEhyMnJQU5ODl555RXz/sQzDR06FLdv3+7zPvb21ltvISgoyOp1S0tLce+992LcuHG45557\n8NFHH5m3XbhwAVOmTMGoUaPwxBNPmHtj+zOp1gCVV8/W5eHxGKQOD0cR9WJ1ytXKztq1azFhwgRM\nnDgRCxcu7DSxUX5+PiZNmoTx48dj8+bN5s9VKhXmz5+P8ePHY8GCBWhqanJK3O6m6HQ5wiL9ERjs\n0+W+SWlhqK5Qoe4W/bdszx3Ljq1655VXXsGYMWMwadIkrFixAo2NjU6J212Ul9QjPDIATA9GUYgl\nXoiKleEKZbS14I5lB+i83mlj657P2eyW5IL0b935g8cwjFMnm5aWluLAgQOIjLQ+v0EoFGLt2rU4\nduwYtmzZgjVr1uDy5csAgD//+c9YsmQJCgoKkJaWhjfffNNpcbsilmXhq+t5AwsAUodFoOhMOUwm\nmmhsjauVnSVLluDw4cM4dOgQYmNj8Y9//KPDPkajEYsXL8a2bduwf/9+fPjhh7h06RIAIDc3F+np\n6Thy5AhGjRqFDRs2OCVud8KyLE4dvYFRGdHd2l8g4GHIKAVOHy9xbGBuxh3Ljq16Z/LkyTh27Bi+\n//57tLS09Pt6507lJfUI6+bwwPaSh4bhAs0FtuCOZcdWvQN0fc/nbNTAIj2yYMECTJ48GXPmzMGX\nX37ZYXtJSQnGjh2LxYsXY9iwYXj88ceh0WjM27dt24bx48fjkUceQXFxMQDg1KlTmD59OjIzM/HM\nM8/g+vXrdon15ZdfxurVqzvdHhISgrS0NABAUFAQhg8fjoqK1j/CR48exYwZMwAAM2bMwM6dO+0S\nk7vSqrQw8BgYOll3xJbgECmkft4oVvbvicbuUnZ8fVuHchoMBrS0tEAk6rjm2alTpxATE4OoqCgI\nhUI88MAD2L17NwDg22+/xSOPPAIAeOSRR7Br164+x+Rpym7cBo/HIDK2Y9KozgxJj8SFMxXQaftf\nRkFPKju26p3JkyeDx+OBx+NhypQpKC+nnv/2uptB8E5xKXJUljagWdX/Mtp6UtmxVe8AXd/zORs1\nsEiPbNy4Efv378cHH3yAV155BfX1HddouXLlCqZPn44TJ07AZDJhz5495m1qtRpHjhzB6NGj8Z//\n/AdA62LVu3btwsGDB5GdnY1Vq1Z1OKdKpUJmZmaH16RJk8xP/9rbtWsXwsPDMWjQoG59r2vXruHi\nxYvmJC6TJk3Cxx9/DK1Wi08++QRlZf17PaeWuhaovHvee9Vm0PCIfj9M0F3KDgC8/vrrSE5OxvHj\nx/Hb3/62w/aKigpERESY34eHh5tvEqurqyGXywEAcrkc1dXV3f+P1E+UldRjYHxQj4Y6+QWIERkr\n65dJYzyp7LR3Z73T3rZt2zBz5kybx/cner0RtdXNCInw6/GxQiG/NaPtuf7Xi+VJZcdWvdPTez5n\n6P0dE+mXtm/fjq+//hq3bt1CY2Mjrl69ipEjR1rs4+fnh7vvvhsA8OCDD2Lfvn249957AcD8ZHvC\nhAnIyckBAGg0GqxduxZHjx4Fy7LQ6/Udruvr64uDBw92K8aWlhb8+c9/xvbt282f2ermbmpqwpNP\nPom1a9ealxl44YUX8NZbb2HatGmYPXs2vLy6l5rcUzXXtvRqeGCb5KFhOLL3CrQaA7xF/fPPjjuU\nnTYvv/wyfv/73+P111/HqlWr8Mc//tFi+50NA5ZlrTYWGIbpUSOiv6gsbUDioJAeHzd8XBTyvirC\nsDGR/eq/qyeVnTbW6p02GzZsgFQqxX333deja3uyqtIGBIdIIRTaXuS+M6nDwnFk7xWM7OawXE/h\nSWWns795arW6R/d8ztI/73RIr9y4cQPvvfcedu7cicDAQGRmZkKr7brLvX2hCAho7d4XCoXmY999\n910EBgbi+++/x8WLF7FgwYIO51CpVJg9e7bVArZ582YkJSVZxHnz5k1MnDgRAFBeXo7JkycjLy8P\nAwZYZuHS6/V47LHHMHfuXHMSFwCIiorC+vXrAQBKpdLiiU5/1FLbAlUPMwi2J/HxQsTAAFy/fAvJ\nQ8LsGJl7cJey055EIsH8+fOxcOHCDtvCwsIsenXLy8sRFtb6/1Uul6OqqgohISGorKzsUOZIawNr\n4ozEHh8XGSMDj8fg5rU6RMUFOSAy1+NpZQfovN4BgI8++gh79+61OpyrPyvr5fDANlGxMjTWq3G7\nprlbiWU8gaeVnTvrnbKyMoSHh+P69evdvudzJmpgkW6rrKxEcHAwAgMDcfz4cZw/f97qfo2Njfjm\nm28wdepUbN++HQ899JDN81ZUVGDcuHEAWodFWOPr64tDhw51K87U1FSLiY/Dhg3D/v37zQtft2FZ\nFkuWLEFycjIWLVpksa2mpgbBwcEwmUzYsGEDfv3rX3fr2p6qpa4FTX59q5TiU+RQFlX3ywaWu5Qd\nALh69Sri4uJgMBjwxRdfIDU1tcM+w4cPx7Vr11BSUoLQ0FDs2LHDvFTHjBkz8Mknn2Dp0qX45JNP\nOtxA9ndNjRrodUYEyCQ9PpZhGAwfG4XTx0r6TQPL08qOrXonLy8PGzduxDfffGN1Dkp/VlFSj+Sh\nva87eHwektNak13clRVvx8hcl6eVnc7qnaSkpG7d8zkbzcEi3TZ27FgoFAqMGTMG//jHP5CZmWl1\nv4SEBOzevRtjxowBwzCYNm0aAMunIu2HDj311FPYsmULpkyZgoiICLsPfWl/voqKCjz88MMAgBMn\nTuDTTz/F4cOHzeOD8/LyAABffPEF0tPTMWXKFCQkJOAXv/iFXWNyJ3yTCboWHVp6OTSjTVyKHNcv\n34LRYLJTZO7DncrOmjVrkJGRgRkzZsBgMOD1118HYFl2BAIBNm7caJ5APW/ePPMTyWXLluHkyZMY\nP348Tp06hT/84Q99jskd2Fqou+1V0ahFZVkjQhX+vf5/lTIsHDev10HVoOl6Zw/gaWXHVr3zwgsv\noLm5Gffffz8yMzOxbNmyPsfkCViW7XWCi/ZShoXhwtlylxg+5gyeVnZs1TvtucrwaYZ1kV/avn37\nMGLECK7DsHC2XNXpwqsAkDMrHkPDafHU9kpKSvDoo4/i6NGjXIfi8goLC5GVldXn89ir7HT2e/fX\n6DBFp8MOP2mHbT0tA//edAwZUxMQnRDcp1g9EZWd7rNX2QEcX37ay5kVD9VPlQCA8dkJvb7Wd9vP\nQzbAB6MnxPT6HJ6Eyk73uWLZ6Up9XQs+2XwCTy+f1KebZ5Zl8e6Gw7j70aEIjfC3Y4Tui8pO9/W0\n7FAPFrE7V3l6QOzDV2eAJKjnw5msiU8NgbKIssp1hsqO56ssrUeYom83d8lDQvtlRjRbqOx4rvKS\neoT1cIFhaxiGQeLgEFp0+A5UdhyDGljErqKionDkyBGuwyB25KszwKcX80WsiU+RQ3mhCiwtOtwB\nlR3Px7IsKktbhwj2RWRsEFQNGtyuabZTZO6Nyo5ns8fwwDb0kM8SlR3HoQZWL/BNLKRaPaqUNbh8\nvrLfjOctKSlBRkZGj475+OOPUVlZ6aCIWuXn52PSpEkYP348Nm/ebHUflUqF+fPnY8SIEZg2bZrF\nwnhbt27F9OnTMXnyZKxYscKhsbojqdZ+PVhBcim8vASoLG+0y/nchauWnd/+9rdISkqyGdvly5cx\nbdo0hIWF4a233jJ/XlpainvvvRfjxo3DPffcg48++sihsXoCdYMGQi8+fHy9+3QeHo9BUlr/6MVy\n57Kza9cuTJgwARMnTsTDDz+MwsJC87bu1FukVYUdG1hhCn9o1Pp+8XDCU8vO0KFDMX78eGRmZmLq\n1KkOjbUvqIHVA2K9ARklNZhUXI0h1Q2ouHQL+d8r8d9PzkKnNXAdnktydGE1Go1YvHgxtm3bhv37\n9+PDDz+0yCbT5osvvoBCoUBhYSFef/118yJ2t2/fxptvvont27dj3759uHr1Kvbt2+eweN0Oy7YO\nEZTZL61tfKocV4toiEZXnFHRzZs3D5999pnNfWQyGf70pz91WPhRKBRi7dq1OHbsGLZs2YI1a9ZY\nLXvkfxqqmvrce9UmeUhrRrT+8oCvJ1yl7GRmZuLw4cM4dOgQlixZgpUrVwLofr1FAJOJRU11E+Th\nPV9g2BqGxyAueQCUF6gXyxpXLztA65DGnTt34uDBg+YEMa6IGljdxDexGFbVgJv+EuyLliM/MhjD\nZqdg3qJx8PIW4MO3j6G2uonrMB3OZDJh8eLFGDZsGB5//HFoNK2ZrM6cOYPs7GyMGTMGDzzwAGpr\na/HVV19rhuvzAAAgAElEQVThzJkzePrppzFp0iRoNBqsX78eU6dORVZWFnJzc/scz6lTpxATE4Oo\nqCgIhUI88MAD2L17d4f9Dh8+jOzsbABAeno6rl69ipqaGohEIrAsi8bGRqjVaqjVavO6D56qs2xn\nOmPH7H5igwkGHgNhJ4sD83noNFtaZ+JT5bjSD4douFrZAYBx48Z1+XsPDg7G8OHDIRBY/gZCQkKQ\nlpYGAAgKCsLw4cMdXjG7u8ZqFcIi7dPACo8KgEFvxK1KlV3O58rctey0X0C4sbER3t6tPZfdrbcI\noGrQQOLj1esFhq1pHSbYPx7yeVrZaeMOD5a6bGAVFRVh+fLlWLZsWac3rs899xyee+45/PWvf0VJ\nSUm3j3UbLIvUmkaovAQo8RMD7SYECoV8TH9gMEZPiMEnm0/giocX2suXL2P69Ok4ceIETCYT9uzZ\nA71ej9/+9rfYsmULTpw4gdmzZ+PDDz/EnDlzMGzYMGzevBkHDhyASCTCU089hby8POzZsweFhYX4\n7rvvOlzj888/N6evbf/61a9+1WHfiooKREREmN+Hh4ejoqLjsJkpU6Zg+/btUKvV2L17N27duoXy\n8nKIxWLk5uZi2LBhSElJwZgxYzqscu5pqpt0eG6XssNLZ+z4B0uq00Pl1flyeQ0ao9VzVTfpOj0m\nTBEAdYsOt2s9f4hGe65Wduzp2rVruHjxIkaNGuXQ67g7e/ZgMQyD5CFhuHjW84cJunPZ+e9//4uh\nQ4di8eLF+Otf/wqg+/UWARrqWuAfKLbrOaPiglBT1YTmpq4X3XV3nlJ2/vKXv5g/ZxgGc+bMQWZm\nJrZu3dqnaziSzYWGTSYTNm3ahJUrV0Imk2HFihVIS0uDQqEw7xMSEoLVq1dDIpHgwIED+Oc//4m1\na9d261h3EdWoho/OgB/CZRaNq/bSRikwINQXX2wpQHCIFIFBnrlSuJ+fH+6++24AwIMPPoh9+/Yh\nISEBN2/eNK8VZTQaERUVZT6m/ZOG06dP4/3338eVK1fQ2NiIixcvYvr06RbXeOihh7pc6K5Nd7Pf\n3H///SgvL8c999yD+Ph4DB8+HHw+HzU1NVi2bBmOHTuGgIAA/OpXv8KePXvM60D0d746A1Te9l2P\nnOEx5kWH+1OaaVcrO/bS1NSEJ598EmvXrrV46kgsMSwLVU2zXdNDJw8Jw5cfFmLC9ESPzgTmzmXn\n7rvvxt13343t27dj/vz5OHjwoN2v4cnq61oQYKc5wG0EAh6iE4Jx7eItpI1yv3vSnvCUsrNgwQJz\n2dm9ezdCQ0Nx6dIlPPzww0hMTDQvfOxKbN45KZVKhIaGQi6XAwAyMjJQUFBg0UhKTEw0/3vEiBH4\n5JNPun2sOwhU6xBT34wfwmUw8WxXYKEKf4ydHIfdn/2IR36TDh6/f4zAZFkWgYGBnVYcbRU/y7J4\n4YUX8P777yM1NRUvvviiubu6vc8++8xiMn2bmJgYbNmyxeKzsLAwlJWVmd+XlZUhPDy8w7ESicTc\n0wq0rvQ9cOBA5OfnY9SoUYiNjQUAzJkzB/n5+dTA+pmv1oAqqcju541PDcGJA9f6VQPLGi7Ljj3o\n9Xo89thjmDt3LmbNmmX383sSqc4AsZ83vOz4wGJAmC8EQj4qbtYjPCrQbud1B+5Wdh544AEsX74c\njY2NCA8P71a9RX5uYNkpi2178SlyXDhX4fENLGvcuez4+fkhNDQUAJCUlITZs2fj1KlTLtnAstkC\nqKurQ1BQkPm9TCZDXV1dp/vn5eWZh4j09FhXZDKxGHyrAecH+EHdzfG/I8YNhEDIx8nD17ve2Q01\nNjbim2++gVarxfbt2zF16lQkJLQumPn111+DZVno9XpcvHgRACCVSnHr1i0AgFarRVNTE6KiolBe\nXo7du3dbfeo6d+5cHDx4sMPLWkEdPnw4rl27hpKSEuh0OuzYsQMzZsywGrdO1zpsbevWrcjIyIBU\nKsXYsWNx5swZ3L59G1qtFnl5eZg8ebK9/nO5PanOYHOIYG9Fxcpwq1KFFhtDCT2Nq5WdnrpzzDvL\nsliyZAmSk5OxaNGiPp/f0/lp9fCX23dh+rZhghc8fJigu5ad69evm8vN3r17IRKJ4Ofn1+16iwD1\ntWr4y+w7RBAAYpIGoPR6nccnKPO0stPS0gKVqnXeaU1NDfLy8pCamtrr6ziS3bpYzp8/j8OHD+PR\nRx+11yk5V1NcBy2fj1pJ91PqMjwGMx4cjIKjxaj2sFTUDMMgISEBu3fvxpgxY8AwDKZNmwahUIgP\nP/wQb7/9NtLT05GZmYmTJ08CABYsWID169dj0qRJAIClS5di6tSpeOKJJ8xJJ/pCIBBg48aNWLBg\nASZPnox58+YhKSkJALBlyxZzAb948aI5refx48eRk5MDoLX7/A9/+AMWLFiAWbNmYdCgQZgwYUKf\n4/IEfBMLkdGIFjtOLm4jEPIxMD4I1y7fsvu5XZErlh0AePLJJzFjxgxcvXoVgwcPxr///W8AlmWn\nqqoKgwcPxqZNm7BhwwakpaWhqakJJ06cwKefforDhw+bx9y7ckYnrvlr9fALkdr9vMlDw3Dpx0qY\nPHRtOXcuOzt37kRGRgYyMzPx1VdfmfexVW8RSw23HdODJRILERYZgBtXaux+blfhiWWnuroas2fP\nxsSJE/Hkk09i0aJFmDJlil3isjeGtZGK4/Lly/jss8/w0ksvAQB27NgBhmFw3333WexXXFyMDRs2\n4MUXXzR33XX32Db79u3DiBEj7PKluquiUWtzMv6pnT/hUIsJ5b7Wn57kzIrH0HDrTySLTpfjxMFr\nWPDsOAgccINK3F9hYSGysrL6fJ6elp2z5So8t0vZ4fNXp8Zgdd7/el6lOgOGVNUjPzK4w7bOjmlj\nq2y0OX+qFFcv3sKcecO7HTshgP3KDmC/uqezctVmXGktsuakYuJw+w8F27rxKKbMTkFkrMzu5yae\nxRXLji0b1+ThiT9MhMTHy+7nPn2sGBWlDZg1d4jdz008T0/Ljs2xP3FxcaisrER1dTVkMhny8/Ox\ndOlSi31qamqwYcMGLF682Ny46u6xXGvLpmaNyGDElKomVIb1rsJKGRaGK0VVOH7gGsZnJ/QlTEI4\nITIYoRE47uFATNIA7P/mIgwGEwSC/jFfkfRPfBMLid4A32DHJAFJHBSKyz9VUgOLeBR1iw4sC4gl\nQoecPy5FjqN5ShiNJvD7yZx54jw2G1h8Ph+LFi1Cbm4ujEYjsrKyoFAosHfvXgBAdnY2Pv/8czQ1\nNeGdd94xH7Nu3bpOj3UXEY1qBMcHwaTu3fEMw2Dy7GRs25iP4WOj4OPb/WGGhLgCkcEItQMbWD5S\nbwTJpSi9XofohGCHXYcQrkn0BrQIBd1KfNTVyAoAkEu9EOb3vzolcXAIPnvvJKbMTgHTRTImQtxF\nQ50aAUESh2XI9AsQw18mRtmN24iKC+r6AEJ6oMvZ66mpqVi/fr3FZ+3HYS5cuBALFy7s9rHugGFZ\nRKjUkKfEAYW9X9fKL0CMQSPCcWz/VUy91zUn4RHSGbHesT1YABCXPABXL1RTA4t4NIneiJZuliVb\nIyva5MyKt2hgBcml8BYJUX6zHhED+1c2QeJ+uvsQwRFrYN0pPkUO5YVqamARu7N/ejAX0lUh1hlN\nVj8PatFBI+DDxw4TK8dkxuH9vxzGqPHRDpmoSYijiAwm1Egc+yciNlmOHdtOYco9KR69jg/p38QG\nxySLaS9xcAgun6+kBhZxed19iKB2wBpYd4pPCcGODwsxeXYy1UHErjy6gdVVIX51qvU1eBSqFpT6\n2eepiUTqheHjBiI/T4lZ/48mUhL34eghggAQHCIFGAY1VU0YEGrfFNaEuAqJ3oAGb8fMI2mTODgU\n27edwqRZdKNIPENDnRqhEX4OvUZwaGtmT6qDiL15dAOrN7wNRgRq9PhRHmC3c44aH41/bTiEW5Uq\nKsDEbYgdnOQCaJ2rGJc8AFcvVlPZIB5LojeiUioGn9eabdCWzkZWdCU4RAqBgIfKskaEKfx7dQ5C\nXEl9bQuSh4R2vWMfMAyD+GQ5lEVUBxH7ogbWHSJUalRIRTDacaKwl7cAYzJjcWTPZdz/y5F2Oy8h\njsKwLLyMJmidkN0vLlmOo3lXMHZSnMOvRQgXJPrWIYINGqPVZQ3a62xkRVcYhkHi4FBcPl9JDSzi\n9vg84FZNMyoMLOqtPJSQevHRpDN2evydiWBsiU+V4+C3lzBuCtVBxH6ogXWH0CYNfhpg/y7poemR\nKDh6A2XFt2mMPHF53gYTtHweWCcMNYqMkaHuVjOam7TwkVK2TeJZeCYWQpMJGiekgU4cHIqvPzqN\nidMTaZggcWu3m/VoUWnx6uGbVuuhztZgbHNnIhhbIqID0VCnhqpBA19/Ua9jJqQ9SvzfjrfBCG+j\nySFj5QVCPsZmxuLEgWt2Pzch9uaM4YFt+AIeBsYH4dqlW065HiHOJGmby+iEBo88rHWI060K28MQ\nCXF1WpUWGgHfKQ/5+HweYhKDcfVitcOvRfoPamC1I1PrUCf2clhFOGhEBKrKG6nyIy5PZDBC4+Cs\nZ+3FJctx9QJVbsTziPUGqJ1UlhiGaV10+HylU65HiKNoGjUOz7zZXtzP6doJsRcaIthOkFqHGrGX\nw84vEPIxMmMgfjh8DbP/31CHXYeQvmrNIOi85y+xyQOwb+cF6PVGCJ1YqRLiaK1rYDmvqk0cHIJd\nn51DRnYCDRMkbkvTqO1TFtuuEsrcOYfL4CfCzeu3cerGbQi8BD2aw0WINdTAasOyCFLrcDVQ6tDL\nDE2Pwr9yD6K+roXWxSIuS2wwodHbeX8exBIvhIT7oVhZi/gUudOuS4ijSfRGNHk5ryyFKvxhNJhQ\nU9mEAWGUFY24J62qbz1YXSWUsTaHa4SAj798eRFVUlGP5nARYg0NEfyZVGeAkWEcPpTDWyTAkNGR\nKDh8w6HXIaQvRE6cg9UmPlUOZVGVU69JiKNJnLDIcHsMwyAxLRSXfqxw2jUJsTdNo9ZpQ2vb3JJ4\nY0CL1qnXJJ6LGlg/C1LrUOvA4YHtjbhrIC6eq0CzigoycU3OWGT4TvGpIbh6oRqmXq4DRIgrkugN\nTm1gAUBSWhguna8Ey7JOvS4h9qJp1KDFyXVQtY83glu0YKjcEDugBtbPgtQ61Eqc08Dy8fVG8pAw\nFB4rdsr1COkRlv05i6Bz/zz4B4rhGyBGWXG9U69LiKMwLAtvg8npvcGhEX4wGlncqqSESsQNsSy0\nKuf3YGkFfKiFfASqdU69LvFM1MBC6zolARo96kTOaWABwKgJ0Tj3w01oNQanXZOQ7hCaWJgYBkae\n8/88xKfIobxAwwSJZxDrW3uCnZFquj2GYZA0OBSXfqRsgsT9eBlN4Al4nNRBVT4ihDTT6CLSd13O\nvC0qKsLWrVthNBqRlZWFmTNnWmwvKyvD22+/jRs3buCRRx7BPffcY9727LPPQiwWg8fjgc/nY926\ndfb/BnYQoNWhyUsAgxMWgjRfUybBwPhgnDt5E6MnxDjtuoR0hYvhgW0SBoVgxweFmDQrmTKgEbcn\n0Rud/hS+TVJaKL75z1mMp2yCxM1IDEaI/LhZ8LfKxxvp5bfBmmiYIOkbmw0sk8mETZs2YeXKlZDJ\nZFixYgXS0tKgUCjM+/j6+uLXv/41Tp48afUcq1atglTq2Mx8fRXU4rz5V+2NmhCNrz48jRF3DQTf\niY07Qmxx5iLDdwoOkYJhWhdKlYf7cRIDIfYiMTh//lWbkAg/mEwslSXidsR6I0T+3gAH03HVQgG0\nfB7qKxoBBZUb0ns27+qVSiVCQ0Mhl8shEAiQkZGBgoICi338/PwQFxcHPt96JeIOk2ydOf+qvdAI\nfwQESWgYB3EpIoPJ6fOv2jAMg/jUEFyhbILEA0j0RrQIuVkN5X/ZBKl+Ie5FojfCm6MeLKA12UXV\n1VrOrk88g827qLq6OgQFBZnfy2Qy1NXVdfvkDMNgzZo1eP7555GXl9f7KB1IaDRBrDeiwVvIyfVH\nT4hBweHrbtEQJf0Dl0MEASAhNQTKC9WcXZ8Qe2ltYHFXlpJ+bmBR/ULcidhghMiXuzWoqnxEqL5W\nS8MESZ849DH1a6+9hpycHCxZsgQ7duzAhQsXHHm5XglSa3FbLHT6JOQ2MYnBMBpZlFztfsOVEEfi\ncoggAIRHBaC5UYv6uhbOYiDEHiR6o9NTTbcXEu4HFiyqKyibIHEfYj13c7AAoNlLAIGQj4rSBs5i\nIO7PZgNLJpOhtvZ/3aS1tbWQyWTdPnlgYCAAQKFQID09HUqlspdhOo5MrUedmLsnJQzDYNSEaJw8\n0vmK44Q4ExeLDLfH4zGIS5FDWUS9WMR9MSzb2hvMYQ+WOZvgOVp0mLgPkcEIL6nzp220J48LwuWf\naHgt6T2bDay4uDhUVlaiuroaBoMB+fn5GDVqlNV97xyCoNVqoVarAQCNjY04ffo0oqKi7BS2/fhr\n9agXcTM8sE3K0HDcqlDRmiXEJYgMJqg5moPVJmFQCC6fp8qNuC+RwQitgMfZ6Ig2yUPDcPFcBQ13\nIu6BZeFtNMGLg3nx7YXEBeHK+SoaXkt6zebsWz6fj0WLFiE3N9ecpl2hUGDv3r0AgOzsbNTX12PF\nihVoaWkBj8fDrl278Oabb6KhoQG5ubkAWjMNzp49G0OHDnX8N+oBo84Isd4IlRc3k5DbCAQ8jBgX\nhYIjNzDzoTROYyH9G8/EQmAyQcdxVsuBcUHY/dk5NNar4Rcg5jQWQnqDywQX7Q0I9YWXtwClxbcR\nGdP9ESiEcMHbaIKezwOP4zpIGuwDMEB1hQohlIWT9EKXf/1TU1Oxfv16i8+ys7PN/w4ICMCmTZs6\nHCcSiZCTk2OHEB2n6VYTVF4Czp8wAsDQMVH4V+4hqBo08PXnbuwx6d9EBiO0fD7QxzLB5wFny633\nyEq9+GjSGTt8Lpd6IcyvdbguX8BDwqAQXDxXifSJtE4ccT9cz79qwzAMUoaF48KZcmpgEZfnbTBB\n4wLL1jAMg8RBobhyvpIaWKRXuH+8xiFVdRMaOB4e2EYkFmLQiHAU5hcjc2YS1+GQfspeGQQbNEas\nzrM+r/DVqTFWt+XMijc3sAAgeUgYDu6+RA0s4pa4ziDYXsrQMGzbmI8pd6dA4CIxEWKNyGiE1gUe\nTABA4uAQ7PrsHDJosW7SC9w/JuBQU1UTZ+nZrRmZEY0fC0qhUeu5DoX0U2IO18C6kyJGhiaVFnU1\nzVyHQkiPcbnI8J38AsQYEOaLa5ducR0KITZ5u1AdFKrwB8sCVWWNXIdC3JBr/Iq5wLJQVas4T3DR\nnl+AGLFJA3D2h5tch0L6Ka4zCLbH4zFIHBxCGdCIW3LkHKy2IbidvSoatR2OSR0ejqLT5Q6JhxB7\ncaU6iGEYpA6jckN6p98OERQbjODxeX3qirY1zwSwnFPSXaMnxuDz9wsw8q6BNJSDOJ3IYMRtEbfZ\nm9pLHhKG77afx9jJcTREg7iPthTtDrpRtDUEF+g43BYAEgeFYP9/L0LdooOY4wxthHRGZDShiePE\nY+2lDAvDx/84gcxZSeC7wNww4j5c51fsZP5aPaRyaZ/O0ZtKrisDQn0hD/NF0ZlyDBkd2af4COkp\nscGIChcZngG0Ljps0BtRU9WEAaG+XIdDSLd4G00w8Hgw8VznoYC3SIiYxGBcOleJYWNdb8kUQgDA\n24V6sAAgMMgH/jIxipW1iE0awHU4xI24zp2Uk/lr9PDtYwPLUUZPjMHJw9dp3RLidCKDCRoX6jll\nGAZJQ1rX8SHEXbQOc3K96jV1eDiKztBwJ+K6RAYTtC5WdlJ/zsJJSE+41q/YiQK0ekhDXLOBFRkj\ng7dICOWFaq5DIf0Iy7LwNhqh4btOAwtoHSZ48VwFLfhI3IbYYHLY8MC+iE4Ixu3aFtTXtXAdCiEd\nuWgdlJQWhmuXbkGnNXAdCnEj/bKBxTOxkOoM8Al2zQYWwzBInxiDHw5do5tK4jQGjQFGhnGpYU0A\nIA/zBY/HoLK0getQCOkWV5qo3x6fz0NyWih+KizjOhRCOhCaWJesgyRSL0REB+JKURXXoRA30i8b\nWH46PZq8BOC7WDd0e/GpIdBqDCi5Wst1KKSf0DXrXGb9kfYYhkHykDAa2kTchljvuAQXfZU2WoHz\np8pgMpq4DoUQCyKD66yBdScaJkh6ynVbGA7kr9G71PpX1vB4DMZOikP+vqvUi0WcQtesg8ZFsyQN\nHhmBi2crYNAbuQ6F9ENXalrwU1VTp6/rdWqL/V21BwsA5GF+kPp54/rlGq5DIcSCyGBy2TooLlmO\nipsNaGrUcB0KcRP9Mougv1aPaknPsvtxIXlIKPK/V+Lm9TpExQZxHQ7xcK7agwUA/oESyMP9cOWn\nKqQMC+c6HNLPbDtVgRM3O19s9J6UIEyMCTS/FxuMUHM4QqKrJURkiQOQf+QGmvzFNs/Tm6VGCOkt\nb6PrPpgQevERnxqCi+cqMGp8DNfhEDfQLxtYARo9rshcc/5Vezw+D2MnxeL491epgUUcTtuig9ZF\nnx4CwJDRkThzooQaWMS1sSzEBiOn2Ti7WkKEZ2Ixo6IRK7+6ZDPO3iw1QkhvuWIGwfYGDQ/Hvp0X\nMDIjmtZlJF1y3V+yg3gbjOCxrMuOj79TyrBwNNxWo/TGba5DIR5O16xzydTSbeJS5KipasLt2mau\nQyGkU0ITCxPDwMBz3bJk4jEITgiGQqXuemdCnMTV1sC6U2SsDKyJRRndj5Fu6LIGKCoqwvLly7Fs\n2TLs3r27w/aysjK89NJLmDdvHnbu3NmjY7ngr9GjQSQE3OTpA5/Pw5hJsTi+X8l1KMTDufIQQQAQ\nCHhIHR6OHwtKuQ6FkE6JDK6b4KK9kBQ5wlVqMDTHl7gIkdF152ABrQmXho6JxJkTN7kOhbgBm79k\nk8mETZs24Q9/+APeeOMNfP/99ygttby58fX1xa9//Wvcc889PT6WC/5a109wcadBwyNQe6sZFTfr\nuQ6FuAmV1oCyBo3VV2dcOclFmyGjFPipsBxGyoBGXJRY79pP4dtIAiVQC/kY0KLlOhRCALh2FsE2\ng0ZE4PrlW2huonJDbLM5B0upVCI0NBRyuRwAkJGRgYKCAigUCvM+fn5+8PPzQ2FhYY+P5YK/Vo/r\nAT6cxtBTfAEPYybG4ug+JR56fBTX4RA3cFttwJOfX+jweYpcgl+Nsj6HSdesg9bPtecmBsmlCJCJ\ncf3SLcSnhnAdDiEdcJ3goidu+omhaFSj2kfEdSikv2NZeBtMLj1MHQBEYiESBoXg/KkyjMmM5Toc\n4sJs/pLr6uoQFPS/5AoymQx1dXXdOnFfjnUYloWv1oBGN+vBAoDBoxS4fasZN69x/N+QeCSeiYXJ\naILexRZ4tCZtlALnaJggcVGunKL9TlU+Ivhp9RDrDVyHQvo5gal1qKrRhecuthk2Jgpnf7gJk4mG\n15LO9assgj56I/R8HvQuPgzKGoGAh4zsBBz67hJ+sXAsZbAhdiUyGuEl8XKLuYmJaaE4sOsSVA0a\n+PrTk3fiWsQGE26LvbgOo1tYhkGpnxhRDS24FOzHdTjEQ1yvU6OwrPNlAiL9O2amFBldv/eqTajC\nH2KJEDeu1CA2aQDX4RAXZbOBJZPJUFtba35fW1sLmUzWrRP35VhHaZ1/5b5typQhYTh5+Dqu/FSF\nxMGhXIdDPIi3wQQvH/e4KfTyEiB5SBjOnijB+GmJXIdDiAV3SXLRpsRPgozSWlwLlLrlw0fieq7U\ntOCfJ8o63b46u+M6Uq6eQfBOw8ZE4cyJEmpgkU7Z/GsaFxeHyspKVFdXw2AwID8/H6NGWZ8DxN6R\niagnxzqLn1bvlsMD2zA8BhOnJ+LInisw0SR/Ykcig9FtGlgAMHL8QJz94SZ0WhraRFyL2M1uFHUC\nPqp8RIhqaOE6FNKPiQxGl16H8U7JQ8JQXlyPhttUboh1Nrtz+Hw+Fi1ahNzcXBiNRmRlZUGhUGDv\n3r0AgOzsbNTX12PFihVoaWkBj8fDrl278Oabb0IkElk9lkv+Wj0qpc4bUsTnAWfLO+8ml0u9eryI\nY3RCMHx8vXG+sAxDRkf2NURCAADexp97sJrco+EeGOQDRYwM50+VYsRd0VyHQwgAQGAygceybjGX\nsb0b/hKkl9fhRoAPjG4WO/EM3kaTWz2YEHrxMWhEOM4cv4nMmUlch0NcUJfj5VJTU7F+/XqLz7Kz\ns83/DggIwKZNm7p9LFcYloVUZ4DKy3k9WA0aI1bnXe90e86s+B43sBiGwcQZifjq36eRMjQcQi/3\n+YNEXJe3wQhvHy+gqfM07q4mfWIMdn58BsPGRIHnRk8+iecS6X8eHugGcxnba/ES4LbYCxEqNUr8\nJVyHQ/ohkcHkdlM4RmZEY9vGfKRnxkAscZ8RIMQ5+s1dia/OgBahwCOezoVFBiAsMgCn8m9wHQrx\nECI3moPVJiwyAH4BYlw6X8l1KIQAaE1w4U7zr9q77u+DgQ3NtPAw4YQ7rIF1J78AMeJT5Th9rITr\nUIgL6jcNLH+Neye4uFPmjCScOnIDjfVqrkMhHsDbaGrNIuhmRk+IwcnDNzrMASWEC+6Uov1OjSIh\nWgQChLpRLzbxHN4Gk8svdG/NmMxYnD5WTPOBSQfu92vuJXdMcFHRqMXZcpXVV7HWiPjhEdj/zUWu\nwyQeQGQwwkvqfg2s2KQBMOiNKLlK68MR7okNRqiF7tnAAoAbARLE1DcD9MCCOJnI6J4PJwKDfTAw\nPghnTlAvFrHkOV06XfDX6t1ubHl1kw7P7VJ2uv2NaTE49elZXL98CzGJlCqU9BLLwstoglDiXg8g\ngNbMmq29WNcxMP5/C5tXNGpR3aTrsH9vEssQ0l0ig9HtHuS1Vyv2golhENKsRZUTE0KR/o3/c3IY\ng5tO4RgzKQ6fv1+A4eMGQujGD1iIffWLBhbfZILYYESTl2d9Xb6Ajyl3p+D7nRfw2NIgCNxkkT7i\nWh851QwAACAASURBVLyNJuj5PPB47vn7SRkWjqN5V1BV1oCQCH8AnT+c6E1iGUK6S2wwQu3Of4cZ\nBpdlUqTUqFDtQ+WEOEfr8ED3Sw7TZkCoL8IU/vjxZClG3DWQ63CIi3DjmqD7/LSt2QNZNy28tsQl\nyyGTS1FwpPNshYTY4m0wudX6I3cSCHgYOykOB7+9THOxCKdEBvdKNW1NncQbaiEfikaa30ucQ2Q0\nQuvODyYAjJkch5OHr8NocI+lTojjufcvupv8tZ6V4OJOU+5OxqkjN2jBO9Ir3kYjNG5euaWNVkDV\noMaNKzVch0L6KaPeCIHJvR9WtLkskyK2vhl6mrhPnMATHkyEKfwRJJfiXEEp16EQF+H+NUE3uGOC\ni57wD5Rg1PhofLf9J7AmeoJPekZkMLldetw78fk8TJyehEPfXoaJygDhgKZJ69bDnNpr8haiRuyF\n4sIyrkMh/YC3wf0f8gHAxBmJOLZPCY1ab5fz2Up0drZchYpGrV2uQxzDc7t12vHX6qEMlHIdhkON\nnhAD5YVqnD5eQmOASY94G40ukR6XzwPOlqs6fN7dxBTxqXKcPHwdRWfKgVA/R4RISKfUjVpoPGiC\nu1ImRfT5SqimxsPXnxJeEMcRGUweMUdeHuaHhEEhyN+nxJS7U/p8vq4SndGcYtfG/V2VgwmNJghM\nLFo8qOKzhsfnYdbcITj2vRK11U1ch0PciKv0YDVojHhul7LDy1o2QGsYhkHmzCQc3XsFRoPRwdES\nYkmj0rp3gos7aAV8RAwKwdG8K1yHQjycuy9v0F7G1ARcOFNO92HE/XuwOkvHDAA6owkBmp+HB7rg\nsI3Onti30Rl7NlkyMNgHGVMTsOuzc/jFwrHgu0CvBHF97rrAozURAwMRqvBHydkKrkMh/YxapXX7\neSR3ih6pwMlPzqC8pB7hUQFch0M8lERvRIuHlB2J1AtjJsVh/zcX8eDjI8G44L0ncQ63b2DZ6kJ9\ndWoMAjQ63Ba55vyrBo0Rq/M6z/736tSYHp9z6JhIKC9W48SBa7grK74v4ZF+ojWDk2dUbgAwYXoi\nPnj7GLzkAdB50Pcirk2j0kDtYb83obcAk2cn49svfsQvf3sXBB7Sy0BcB8Oy8Da6Xg9WVw/Agc6H\nrw8fG4VzP9zEtUu3EJcsd1SIxMW5fQOrK4EaPa7IPHv+VXsMw2DGA4OxbWM+BsYHIWJgINchEVfG\nsq1p2j1oaJMs2AeKwaFILbqFMyH+Ltl7TTyPulELjcDzqtSktFBcOleJY/uvYsK0RK7DIR5GZDBC\nx+e53DI6XT0ABzqfA8UX8DBpdjL2//cCouODwfeg+pV0X5e1QVFREbZu3Qqj0YisrCzMnDmzwz4f\nffQRCgsL4e3tjWeeeQYREREAgGeffRZisRg8Hg98Ph/r1q2z/zewwag3QqozoMGDMwhaI/UTYfqD\ng7Hz4zOY/8w4SP1ogjKxTvDzulEGF6vc+ip2dCTOna1EaJMGlb5irsMhHo5lWTTfVqM51PMeaDEM\ng6lzUrH1b0eRMCgEoT8v5k2IPUj0RrQIPe/BRGzSAJz94Sbyv1fSg4l+yuav2mQyYdOmTVi5ciVk\nMhlWrFiBtLQ0KBQK8z6FhYUoLi5Gbm4urly5grfffhtr1641b1+1ahWk0t71IFU0alFQ2tjp9iFh\nts+rqmqCylsAE8+zbh67Iy5Zjup0Fb7692k8/JsxENATFGKFuffKwxpYPD4PP8n9MLyyHnViLxoq\nSBxLawTDADoPrWt8fL2ROSsJ331xHvOfGUdP5IndeNL8qztNu28Qtr2Vj5iEYChiZFyHQ5zMZgNL\nqVQiNDQUcnnrGNKMjAwUFBRYNLAKCgqQmZkJAEhISEBzczPq6+sRENA6IZZle78mjVpvwsb8zhdt\ne2NmHPg2bgwbKxtxW+TV6+u7u7GTYlFd0Yh9Xxdh2v2DaLIl6cDbYGxdu8cDNXoLUeYrRmqNioYK\nEodim7TwkUk8+jeWOiwcl85V4sRBmt9L7EdsMHpslmcfX29Mu28Qdn3+Ix5bfBe8XTQfAHEMm4+h\n6urqEBQUZH4vk8lQV1dnc5+goCDzPgzDYM2aNXj++eeRl5dnz7i7RVXR6LIJLpyB4TGY+VAaykvq\ncfaHm1yHQ1yQyOhZ86/udDXQBxK9AaHNGq5DIR6MbdLi/7N35/FRlufi/z/PzGRmMtkn+0IChCWE\nJRD2zYAQFFBxX6qe41YrWvR864otVqoe/QG29thq3SpYalulLrhQDYggsggkIAgIYYuQhOx7Mvvv\nj5AhIWQjk8xk5nq/XjHMzLPcg3Nxz71dd0CYd09FVRSFzKuHs2dHHnlHS91dHOElDBarxyW4cKXk\nYVH0HxTOhk8Oursoope55JtVW6NUzzzzDMuXL+fBBx/kww8/5ODB3vuAKQ4HNcW1VPhwAwtAq9Nw\n9e1j2Lo+l+OHi91dHOFhdFYbDV7cwHIoCvsjQxhaWoO/xeru4ggvZa82EWg0uLsYPS4oRM/8G0fx\n2XvfU1le7+7iCC/QuAbLextYADPmp1CQV8GP+wrdXRTRi9qdImg0GiktPddTVVpaitFo7PQxYWGN\nC34TEhKYMGECubm5DBvW/d2tOyPEZME/1B+bynu/PHaURrQphWhYeAALbhvDR6tzuOpno+knc4HF\nWXqrnRqtZy8wbu9z3laa3Oaq9H4cDQtgTGEFVnPbjay29tTrzD2Eb3NOETxd5+6i9LikQRGMm9af\ntX/P4eZfTMTPy78cix7kcDRuMuyF2Teb02o1zLtxFB++k01UXBBh4QHuLpLoBe1+qpOTkyksLKSo\nqAij0cjWrVt56KGHWhwzbtw4vvjiC6ZOncrhw4cJCAggNDQUk8mE3W7H39+fqqoqcnJyuPPOO3v0\nzTQXVm8hOCEIai9+DZin6yiNaPMUovFJYVxxUxpr393Dtf89ltgEyQQlQGezUaLx7HWK7X3O20qT\ne75TwQaCTFb2fXmY9HsmoFwgGUFbe+p19h7CdzlqfGMEq8m4af0pyq8i68MfmHvDSFnfKy6KzmbH\nolJh89LkMC067dRqksb34903dzLh+lFo/f2k887LtdvAUqvVLFy4kBUrVjjTtCckJJCVlQVAZmYm\n6enpHDx4kIcffhi9Xs/ChQsBqKioYMWKFQAEBQUxf/580tLSevjtnBPWYCY4NhhyK3vtnp4uaVA4\nl187gg/f2c0Nd40nMibI3UUSbmaw2Gjw0gxO5zsUEcRIUwNb1h+RtLnCZfxsdrA70Bp8Zzq6oijM\nuWYE/3htO7u2nGD89AHuLpLogwwWz9tg2JUu1Gk3GBX5q3PYHRvG/3fFYGlgebEOx2VTU1NZtmxZ\ni+cyMzNbPL711lu59dZbWzwXHR3N8uXLXVDErlMcDkIbLATFBEkD6zzJw6K41DKMNW/v4tr/Sida\n9jTxWWq7HX+rzeOnCLqKQ1FIm5tCzgf7iIwOIiUt1t1FEl4g0GxFCdL53CiOn1bNgtvS+ecbO9Dq\nNKRN6OfuIok+xmCxem2K9rYcMQYyqqiS4cWV3cqyLTyfVy5QCjJbadCo8PPxBBdtSRkVy+yrUlmz\ncrckvvBhQSYrNVoNDh/6Yqj19+Oa29L56tODHN4vC45F9wVYrCiBvtkLHRLmz013T2D7xqPs29X2\nlipCXIi3bjLcrrOJl/RWO7nbTkojy4t55Sc7rN5Mub9nrytxt8HDozEEavn47zlMnzOEkeMSOj5J\neJUQk4VKne91QkTGBnHdneP498pd2O0OUkbJSJa4eIFmK0qk76y/Ol9ouIEb7x7Pe2/tRFFgxFip\nS0TnGKw2CgN8rw6yqxT2xITS72Q577+/jyFT+19wBNxss7uhdMJVvLOB1WChMFDv7mJ4vPikMG6+\ndyL/XrmLyrI6pswejMpLF5uK1oJNFkoNfbvnva0Mgx1VTNFxwdxw53jWrNyF3eYgdUxcTxVReLkA\nsw1VUN+Oo+4KiwjghrvG8d5bO7HbHYwaL9MFRcf8fSBFe1ssahXDrkgl65972ZZbxoHI4FazSX47\nW9Y29mXeN0XQ4SC0wezTGwx3hTEigJ/9YhKnT1bw/ls7qa6UDVl9RbDJ2udHsCobbDz6eW6rH7Ot\n42kXkbFB3HDXODZ/8SN7d+T1QmmFNwr04SmCzRkjA7nxngns3Hycrz49iF1630V7HI7GJBc+tgar\nOY1Ow+7YMHQ2O2lnKlHZZbqgN/G6BlZogwWzWoXJh4O2qwKCdNxw93gSk8P525+3knuwyN1FEj1M\nY7Ojs9mp9dHewyYR0UHceM8Edm89yQ8bjkgFJ7pEY7OjtjtA75WTQbrMGBHArfdPpqy4ljVv76K+\nrvW+ckIAaG127ApY1V73NbRLbCqFnJhQbAqMLShHZ7W5u0jCRbzuk51QXc/pIH93F6PPUakUJl+a\nzIJbx/DVJwfI+ugHGuot7i6W6CHBJgvVOg34UIKLthgjArjt/snYLDYm5Jfhb5EKTnROoKUxUYyv\nZRBsj97fj2v/eyzR8SGs/vM2Ck9JJl/RmsHa9xNcNE1Rb+uns2uoHIrCvqgQigN0TDpdRmStzCTy\nBn37030ejd1OZJ2Jw+Gyv9PFik8K478WTeWbLw/z1z98w/Q5QxiRHn/BjVlF3xXiBdMDXUmr0zDy\nsqFs+uf3TMgv41B4EGcCdNIAFe0KMFt9fhS4xWaqzYSmxZFo8OO9t3cxaFQsmfOG4tfNv6u27tVE\nNm7tOwxesP6qssHG0vXH23y9S2uoFIUToQGU6/0YVVRJeL0Zu1Wm2fZlXtXAiqlpoNRfi9nHh5y7\nS+/vR+aC4Ywal8D6tQf4fudPzJyfQlximLuLJlwk2GThjCSCaUFRFPJCAqjU+ZFaXE18dT0HI6Sz\nRrQt0Ow7+8i15UKbqTanjQwhrKyOVf/3LXOuGU7iwPAeu9fyeYOkgdVH+Pv4+qu2VOq1bIsPJ7Wk\nir3//p4Ifz0lfTwZla/yqpZIfJVMD3Sl6PgQfvaLSaRN6Men/9zLe2/tJO9Yqezb4AWCTRYqdb79\nxbAtlXot2xOMlPprmXi6jKPf5WExy7RB0VqAxUqtjzewOmLWqBl12VBmzEth3fv7WPtuDiVnWmf+\nFL7FG0aweopVreL76FD6T05iaGk16QXlBJit7i6W6CKvqRmCTBa0Njulsv+VU1sprAECtWpq2vnS\n2DTVQlEpjBibwLDRcRzck0/Whz9gCNQydmp/klOiUGsu3EaXqRyey1RnRuNwSO9hOxyKwsnQAAoD\n9fQrq+ON5ZtIn5rE6ImJ6P1laqVoFGi2UtPH15H0lkHDokhMNrJ3x0+89+ZOEpONTL50EOFRge4u\nmnADg9VKnZ90iLcnLDGMrQnh9KusY3x+GUUBOk6GBEinTh/hNf+X4qvryQ/ylzUTzbQ3P/i3swe0\nO3f4/KkWarWKEWMTSB0Tz+H9heRsy2P9xwdITY9j5NiEVpWkTOXwXNVFNVTp/CRWOsGkUTPq8kHE\nqxW+23yMN1dsZtT4BEZN6Eeo0Xc3lxWNa341dgcNbXQyeYP2OumadGUzVK1Ww/jpA0ib0I+c7Xn8\n8/UdRCeEkDa+HwNTIlF7yPT+jjoIQToJu6txBMtrvoL2GIeikBcaQEGQP/2q6hhXUE6VVsPJ0ACZ\nTeThvOLTrbI7iKlpYHv8xc/tFp2jUimkjIolZVQs5SW17Nt1ivfe2okhQMug1CgGp0YTGSvrVjxZ\n5ZkamR7YRRHRgcy7YRQVZXVkf3uSv7+yjfCoQIanxzNkRAw6SdPtcwLMVmq1aq/uqOhoET9c3Gao\nWp2GiRkDSZ+SxOH9hezacoL1aw8wfEwcg0fEEBMf7NbMjB11EIJ0EnaHpcEKDrBI8qxOs6hVHAsL\n5ERIALE19aSUVPHt37KpSY8jJS2WiGj53uVpvOJbQVRdA1U6PxpkPm+vCosI4JLLhzJtzhDyT5Zz\n5GARH/89B4fDQWBsMLHVDZT7a2mQqWgexTmC5YPa65Fvqyf+/HPCxyYwZXQcNacrydmTz/pPDhIS\nE0REUigRSWEYQv2JDtLJly8vF2i2USs98N3i56dm+Jh4ho+Jp+RMDT/knObz9/ZiMdtIHhZFckoU\n8Ulh0oHhZRqqGqj38+7OiZ5iVymcDjZwOsifJeNjsRZUsubtXegNfgwcEknSoAjik0LRyPdht+vw\nX60DBw6watUqbDYbs2bNYu7cua2Oeffdd8nOzkan03H//fcTHx/f6XO7y2F30K+qnrxgma7jLiqV\nQsIAIwkDjMyYO5TSohq25xQQmVfJ0NJqbCqFKp0fVVo/qnQaqrUaGdp2F4eDqqIaKiND3F0St+ho\n2mxXzvnt7AGs3l+KOt5IeL2ZiL1niNiWh0OB/gOMDBscQVxiCFGxwVLZeaFgk8XnMwh2VmemGkYF\nasm4fCgZlzfWIbkHi/hu8zHOnK4iLCKAhKQwLEE6AsxW6vzUOOTLeZ/VUNUgCS66S1EIiwnEFhXI\npFFxVBZWU5xXzo+fH6KmtJaQ6CBCooOIig9GazSgD7xwh19H6/E7u15ftNZu7WC323n11VdZsmQJ\nRqORxYsXM3LkSBISEpzHZGdnc/LkSVasWMGRI0d45ZVXeO655zp1bneZas0cyDqCHYWiAPkf7AkU\nRSEiOoh+o+D7U7XgcGCw2Ag2Wwg2WRlQUUug2crXb+7gh6hAwiICCAs3EBzmT3Bo409gkK7N5Bmi\ne9RmGyhg8pC1Dt7AplJRFKCnKEDv/LyPSwqjorSOg3vyKS2qIShET3hUIOFRgYRFGAgJa/zMBwXr\nUMn/iz5FcTgYWlqNsd5MdqhsXdEZnZlq2HzKXVOsTMwYiNVqpyi/klMnyjl0uJQxhRXobDZq/DTU\najXU+akbfzQaTHVmHHaH7NvowQJNFk7l5Ms+jC5wwbgyGNDo9YTWWwg5Ws7YohqKTlfiUBRq/dTU\nNoubBo2a/5k9kGc357V5j66u1xfntNvAys3NJSYmhqioKACmTp3Krl27WjSSdu3aRUZGBgCDBw+m\ntraWiooKioqKOjy3O4z1Jna+t5eE4THs1sqGoB5LUajTaqjTaihslgfjuZlJxKoVyoprqCir4/iP\nJVRV1FNVUU9djRmdXkNAkI6AIB3+Bj/0Bm3jb38/dHoNOn3jb61Og59Wfe7HT41ao3Lr/H1Ppq01\nERwZKPHSU85+3uNSokiLa5wTb7PZKS+po7SohtKiGvKOllFZfvrsZ92EIVCHIVDb+HkP1OEf4Ie/\nQYve3w+9wQ+dToP27Gddq1Xjp9Xg56eShpkb6Kw2Rp2pxKJW2BFvxCr/D3qcRqMiLjGMuMQwdIMi\nWf15Lmq7nUCzlQCzDYPVSlStCYOljm3v5vCtxUZAkI7AYP25eArQ4m/QovPXoNc31SEa/JrHlFaN\nShpmPUZxOBhQUUtiZR1xlwzgo5M17i6S17KqVJQE6CgJ0HHb7AG8l3UMnc1OgKUxZgIsViLqTOit\nNnat3s1MuwOTWoVJrcasVp39URqvk1tCeJ0Jq0rBplJhVRSsKgW7omCXcGlXuw2ssrIywsPPJY4w\nGo3k5ua2e0x4eDhlZWWdOvd8364/0uJxRb2VKZazmXwcZ//jAJXFhq68jrQrhhEaHwIdLEYVnkfr\n70dCXBAJ/Vv3ANvtDurrzNRVm6mpbqC+zkJDnYX6OjMVpXWYTFbMDVZMDVbMJisWsw2zufG31WLD\nZnegUavQnG1sqdXK2d+NPyq1gkrV9Lv5jwpF1TgKpyiNzzV/rCiNf0YBhcbHzj83/56lKCg0vtb4\nq+mcptcbfwVGuu7v8/zYqWpoFjvNBFWaCU42Qkn7GbKE66jVKiKiA4mIbp2O2ma1U1tjora68aem\n2kRDnYWaahMlZ2poqLdgPvs5b/rcWyyNn3NFpTg7FNQaFZqzv9VqFSqVcvazrmrxGVeafnf0+T77\nGT73+GyBm322lXMf8Naf92aPm7Sqi9tp5HfU/vc3tv96V50fP+eLPlPNFLMF/6Iq6mJCMCWEktqs\nkPEhsml3b7KpVFTqtVSe99e+fN4ghkcaqKk2UVPZQF2tmfpaM3W1Fqoq6jEVWjDVW2loOBtXZltj\n/WFqjCuVSkGjUYFKxXSLDbui4ICzXyYVHArOxzmfHOCYwe9cbClK6/qjnTrDGVeK0qJuUJpVFq1i\nrdlxzX51qcPM4OJcYBeKncoqU6v6R1dWh91PRUV6ItFDoyGv1rUFEW1TFEwaNSaNmrLzMuM/Nas/\nz395DJ3VhtZmR2ezo7XZ8bPb0ZutlJ0oJ6myDo3dgcZuR+1woLE7UDkcqByw4S8lbNGeq4fU6sa6\nSKVu/O7l/K7VrC5qjA9QmuKmK/Fy9v20iI3z4qXxV/frofNf7mq9ozjaWQyzfft29uzZw3333QfA\n5s2byc3N5a677nIe88ILL3D11VeTkpICwDPPPMOtt95KUVFRh+c2t3v3bioqKrpWeiH6sNDQUMaO\nHdvt60jsCF/jqtgBiR/hWyR2hLg4XY2ddkewjEYjpaWlzselpaUYjcZOHWO1Wjs8tzlXBbwQvkZi\nR4iLJ/EjxMWR2BGibe1OIE9OTqawsJCioiKsVitbt25l3LhxLY4ZN24cmzdvBuDw4cMEBAQQGhra\nqXOFEEIIIYQQwpu0O0UQGlOtr1y50plqfd68eWRlZQGQmZkJwN///neys7PR6/UsXLjQmcjiQucK\nIYQQQgghhLfqsIElhBBCCCGEEKJzJMesEEIIIYQQQriINLCEEEIIIYQQwkWkgSWEEEIIIYQQLiIN\nLCGEEEIIIYRwEWlgCSGEEEIIIYSLSANLCCGEEEIIIVxEGlhCCCGEEEII4SLSwBJCCCGEEEIIF5EG\nlhBCCCGEEEK4iDSwhBBCCCGEEMJFpIElhBBCCCGEEC4iDSwhhHChlStX4ufn5+5iCCGEEMJNpIHl\n5e644w4yMzPdXQwh+iyJISG6RmJGiM654447UKlUXHfdda1e+/jjj1GpVNJh10dJA8vLKYqCoiju\nLoYQfZbEkBBdIzEjROcoikJiYiKfffYZRUVFLV577bXXSEpK6lYsWSyW7hZRXCRpYHk5h8OBw+EA\nIDs7m7lz5xIdHU1QUBATJkzgiy++aHF8//79efbZZ/n1r3/NgAEDiImJ4Ve/+hU2m80dxRfC7Zri\nBy7cM7969WpUKvmnVIgmXY2Zp59+msGDB7Nx40YmTpxISEgIM2fOJDc3t9fKLIS7DB48mIkTJ7Jy\n5Urnc3l5eaxfv54777zTGU/l5eXcdtttJCUlYTAYSElJ4fe//32LazXF2+rVq0lPTycgIACTydSb\nb0ecJd8KfEBT70d1dTW33HILX3/9NRs2bCA9PZ2rrrqKI0eOtDj+pZdeorKykvfff58nnniCP/7x\nj6xatcodRRfC40jPvBBd05mYKSws5Omnn+aJJ57gvffeo7i4mLvuuqsXSieE+zQ1nu69917efPNN\n5/Nvvvkms2fPJikpyfmc2Wxm5MiRfPzxx2RnZ3PvvffyxBNPtGiYAezatYuPPvqIVatWkZOTI1MM\n3UTj7gKIntcUwBkZGS2eT09P57PPPuP999/nySefdD4fGxvLn/70JwDGjRvHypUrWb9+vVR2QtCy\nd14I0bHOxExtbS2///3vGTt2LAAHDx7k4Ycfxmw2o9Vqe7qIQriNoihcf/31PPTQQ2zatIlp06bx\n9ttv8/LLL1NRUeE8Ljo6mscff9z5OCUlhR07dvDuu+9yxx13OJ+vrKzkpZdeIiEhoTffhjiPjGD5\nkOLiYu6//36GDRtGWFgYYWFhFBYWkpeX5zxGURSuuOKKFuelp6dz5syZ3i6uEB5JRrCE6JrOxExU\nVJSzcQUwZswYHA5Hq3UpQngjnU7H7bffzuuvv85nn32G1WrlyiuvbHGM3W7nhRdeYPTo0URGRhIU\nFMTHH3/c4jscQGpqqjSuPICMYPmApsrtjjvuYN++fbzyyisMGDAAvV7PVVddhdlsbnF8UFBQi8cq\nlQq73d5r5RXCU6lUKqxWa4vnqqur3VQaITxfZ2Pm/HpHrVYDSN0jvF7zaYLp6en89NNP3HXXXc4Y\naPLiiy/ym9/8hr/85S+MHz+eoKAgnn32WTZu3NjiuLi4uF4ru2ibjGD5kM2bN3PfffdxxRVXMHz4\ncPz8/Dh06JC7iyVEnxEVFcXevXtbTHn65JNPZFRLiDZIzAjROcOGDWP8+PFs3bqVe+65p9Xrmzdv\n5tJLL+Wee+4hLS2NgQMHsnnz5laxJNPYPYM0sHxISkoK77//Plu2bGHPnj388pe/JCQkpEUwSmAK\n0bbMzEzKy8v5zW9+Q3Z2Nk8++SR79uyRuBGiDRIzQnTeF198QUlJCQMGDGj1WkpKCtu2beOjjz7i\nxx9/5Ne//jUVFRUSSx5KGlhezm63o9E0zgR95513SEtL45prruGuu+7iZz/7GWPHjm3R+3GhXkXZ\n00T4suYxNGvWLJ599llWrVrFvHnzKC0t5dlnn20VHxIvwpd1NWbaqmMkjoS3O/+z7+/vT2hoaKtj\nAJYsWcJ9993H//t//4/58+cD8D//8z+diiXR+xRHB03fAwcOsGrVKmw2G7NmzWLu3LktXt+5cyfv\nvfceAEajkRtuuIFBgwYB8MADD+Dv749KpUKtVvP888/30NsQbZkzZw79+vXjrbfecndRhOiTJIaE\n6BqJGSGEr2s3yYXdbufVV19lyZIlGI1GFi9ezMiRI1tkJxk5ciTjx48HGhtjf/vb31i6dKnz9aef\nfprAwMAeKr5oS1FREWvWrGHz5s2t9kgQQnRMYkiIrpGYEUKIRu02sHJzc4mJiSEqKgqAqVOnsmvX\nrhYNLL1e7/xzXV1dqw3NZG6oe9x0003k5uby8MMPc+ONN7q7OEL0ORJDQnSNxIwQQjRqt4FVVlZG\neHi487HRaCQ3N7fVcd999x2rVq2ioaGhxTRARVH43e9+h6IozJkzh9mzZ7uw6KI956ftFEJ0NIWw\newAAIABJREFUjcSQEF0jMSOEEI1csg/WhAkTmDBhAlu3bmXFihUsW7YMgGeeeYawsDBOnTrF888/\nT3x8PMOGDbvgNbZv305tba0riiNEnxAaGtpiY82LJbEjfI2rYgckfoRvkdgR4uJ0NXbabWAZjUZK\nS0udj0tLSzEajW0eP2XKFN566y3q6uowGAyEhYUBkJCQwIQJE8jNzW2zgVVbW0t6enqnCy5EX5ed\nne2S60jsCF/jqtgBiR/hWyR2hLg4XY2ddtO0JycnU1hYSFFREVarla1btzJu3LgWxxQWFjrXWWVn\nZ6PVajEYDJhMJurr6wGoqqoiJyeHxMTELhVOCCGEEEIIIfqSdkew1Go1CxcuZMWKFc407QkJCWRl\nZQGNGwju2LGDzZs3o1ar6d+/P4899hgAFRUVrFixAoCgoCDmz59PWlpaD78dIYQQQgghhHCfDtdg\npaamOtdUNcnMzHT+ecGCBSxYsKDVedHR0SxfvtwFRRRCCCGEEEKIvqHdKYJCCCGEEEIIITpPGlhC\nCCGEEEII4SLSwBJCCCGEEEIIF5EGlhBCCCGEEEK4iDSwhBBCCCGEEMJFpIElhBBCCCGEEC4iDSwh\nhBBCCCGEcBFpYAkhhBBCCCGEi0gDSwghhBBCCCFcRBpYQgghhBBCCOEi0sASQgghhBBCCBeRBpYQ\nQgghhBBCuIg0sIQQQgghhBDCRTQdHXDgwAFWrVqFzWZj1qxZzJ07t8XrO3fu5L333gPAaDRyww03\nMGjQoE6dK4QQQgghhBDepN0Glt1u59VXX2XJkiUYjUYWL17MyJEjSUhIcB4zcuRIxo8fDzQ2qP72\nt7+xdOnSTp0rhBBCCCGEEN6k3SmCubm5xMTEEBUVhUajYerUqezatavFMXq93vnnuro6/Pz8On2u\nEEIIIYQQQniTdkewysrKCA8Pdz42Go3k5ua2Ou67775j1apVNDQ08MILL3TpXCGEEEIIIYTwFi5J\ncjFhwgT+/Oc/c/fdd7N8+XJXXFIIIYQQQggh+px2G1hGo5HS0lLn49LSUoxGY5vHT5kyhdLSUurq\n6rp8rhBCCCGEEEL0de02sJKTkyksLKSoqAir1crWrVsZN25ci2MKCwtxOBwAZGdno9VqMRgMnTpX\nCCGEEEIIIbxJu2uw1Go1CxcuZMWKFc5U6wkJCWRlZQGQmZnJjh072Lx5M2q1mv79+/PYY4+1e64Q\nQgghhBBCeKsO98FKTU1l2bJlLZ7LzMx0/nnBggUsWLCg0+cKIYQQQgghhLdySZILIYQQQgghhBDS\nwBJCCCGEEEIIl5EGlhBCCCGEEEK4iDSwhBBCCCGEEMJFpIElhBBCCCGEEC4iDSwhhBBCCCGEcBFp\nYAkhhBBu5HA4cNgd7i6GEEIIF+lwHyxf8+36Ixz7sRgcjZWeWqNi/k1phBoN7i6aEEIIL2O3O/jP\nmn1UlNVx/Z3j0OqkWhZCiL5ORrCaqa0xkb31JJdeMYzMq4dz2bUjSOhvZNO6H91dNCGEEF7Gbnfw\nn3/vo6baRHhUIB+8sxuL2ebuYgkhhOgmaWA1cyAnn0GpUcQnhRGTEEJ0fAhTZg/izOlKfjpW5u7i\nCSGE8BIOu4MvPthPdUUD19yeTubVwwkK0bP23RxsVru7iyeEEKIbpIF1lsPhYN/OU4wc16/F835+\nai65fCgbPzuIXebICyGE6CaH3cGXH/1AZVkd1/x3On5aNSqVwtzrRqLRqPn0X3ux26SRJYQQfZU0\nsM46faIcFIhPCm312tCRMfhp1fyQfdoNJRNCCOFNjh0upuBUBdf+91i02nNrrlRqFfNvTsNssrLz\nm+NuLKEQQojukAbWWd/vOsXIcQkoitLqNUVRmDl/GFuyjmBqsLqhdEIIIbzFiSMlDEuLu2BCC41G\nxYy5KeRsz8Mmo1hCCNEndZiu6MCBA6xatQqbzcasWbOYO3dui9e/+eYb1q5dC0BCQgLXXHMNiYmJ\nADzwwAP4+/ujUqlQq9U8//zzPfAWuq+h3sLRg0XMmJvS5jExCSH0HxzOjk1HueSyob1YOiGEEN4k\n72gZc68f2ebrkbFBhBoN5B4oYujImF4smRBCCFdot4Flt9t59dVXWbJkCUajkcWLFzNy5EgSEhKc\nx0RHR7N06VIMBgNff/01r732Gs8995zz9aeffprAwMCeewcucHBvAUmDIjAEats9bvqcIbz90hYm\nXDIQvb9fL5VOCCGEt6ipaqC22kRUXHC7x42elMie7XnSwBJCiD6o3SmCubm5xMTEEBUVhUajYerU\nqezatavFMUOGDMFgaNwjKj09ndLS0havOxyenxhi365TjBqf0OFxgcF6kgaFc3h/YS+USgghhLfJ\nO1pGvwFGVKrW09GbGzw8mvLSWooLq3upZEIIIVyl3QZWWVkZ4eHhzsdGo5GysrbTla9fv55x48Y5\nHyuKwu9+9zsee+wx1q9f74Liul7h6Uoa6i0kJYd3fDAwbHQcB/bk93CphBBCeKOTR0tJHNRxfaNW\nqxg1vh97tuf1QqmEEEK4ksuSXOzfv59vvvmGW265xfncM888w/Lly3nwwQf58MMPOXjwoKtu5zKH\n9hYwfEwcSge9iU0GDImk9EwNVRX1PVwyIYQQ3sThcJB3tJSkZGOnjh81PoFD3xfQUG/p4ZIJIYRw\npXYbWEajscWUv9LSUozG1hXDyZMnef3113n88ccJCAhwPh8WFgY0Jr+YMGECubm5riq3yxQVVBOX\n2Do1e1s0GhWDh0dzcG9BD5ZKCCGEt6korcPhcBAWEdDxwTROSx8wJEK2CBFCiD6m3QZWcnIyhYWF\nFBUVYbVa2bp1a4spgAAlJSW8+OKLLFq0iJiYc4txTSYT9fWNozxVVVXk5OQ4swt6kpLCaiKig7p0\nTuroOA7k5PeJ9WVCCCE8w8ncUpIGhV9wO5C2jJmcxJ7teThko3shhOgz2m1gqdVqFi5cyIoVK3j8\n8ceZOXMmCQkJZGVlkZWVBcCaNWuoqanhjTfe4LHHHmPx4sUAVFRU8NRTT/Hoo4/y0ksvMX/+fNLS\n0nr+HXVBbY0Ju91BYLCuS+fFJ4VhNltl8XEzaWlplJeXd/sYV3nqqaeYOHEiM2bMYPHixVRVVV3w\nuDfeeIMxY8YwefJk3nnnHefzL7zwAsOHDycjI4OMjAyPXUMo+j5Pi50mf/rTnwgPD2/zvlu3bmXG\njBlMmzaN119/3fl8Z2PPF508WkpiJ9f7NolLDEWjVZN3rO31z77K02Knu/XOoUOHuPnmm7nkkku4\n5ZZb+PHHH3ul3ML3eFrsNOmo3qmtreX+++8nIyODSZMmORPveWK90+EarNTUVJYtW8aLL77IvHnz\nAMjMzCQzMxOA++67j7/+9a8sW7aMZcuWOfe6io6OZvny5SxfvpynnnrKebwnKSmsISI6sEu9iQCK\nSiE1LY6De2SaYJPO/B0qitJro34zZ85k27ZtfPXVV9TV1fGHP/yh1TFVVVW88cYbbNy4kaysLN55\n5x2OHz/uLOv999/Ppk2b2LRpE7Nnz+6Vcgvf42mxA3Dq1Cm+/vpr+vXrd8HXbTYbixYt4p133mHj\nxo2sXr3a+WWwM7Hni+x2Bz8dK+t0QqUmiqIwLC1WstdegKfFTnfrneXLl3PTTTexefNmrr/+epYv\nX94r5Ra+x9NiBzqudwAeffRRpkyZwqZNm9iyZQtDhgwBPLPecVmSi76o5Ew1ETFdmx7YZNjoWA7u\nzcfuY9M2br/9dmbOnMmCBQv46KOPWr2el5fHpEmTWLRoEaNHj+aOO+6goaHB+fo777zDtGnTuPnm\nmzl58iQAu3fv5rLLLiMjI4P777/fWdl0x8yZM1GpVKhUKi699FLy81tnftyxYwejRo0iNDSUwMBA\npk2bxieffOJ8XaaAClfqK7ED8Jvf/IalS5e2+fru3bsZMGAAiYmJ+Pn5ce2117Ju3Tqgc7Hni4oK\nqjAEagkM1nf53CHDYzhy4IzP1TdN+krsdLfeCQ4Opry8HLvdTllZGaGhnV8fLsSF9JXYgY7rnaqq\nKrZt28Ztt90GgEajITi4cT9BT6x3fLqBVVxYTWT0xW2CHBEdhCFAy6njvjVt4+WXX2bjxo387W9/\n46mnnqKioqLVMUeOHOGyyy5jx44d2O12vvzyS+dr9fX1bNmyhfHjx/Ovf/0LaNxL7fPPP2fTpk1k\nZmby9NNPt7pmdXW1c7pe858ZM2Zw+PDhdsv8zjvvMHfu3FbPT5kyhezsbE6ePElhYSFZWVktgvKN\nN95w/sNTWVnZ2b8iIS6or8TO559/TlxcHMOHD2/zvRQUFBAfH+98HBcXR0FB6xH9tmLPGxVUmdib\nX93mT873hQTEBLf5ekGVqc1rh4YbCAjScfpk707X8RR9JXaau5h6Z+nSpbz22msMGDCAN998k9/+\n9rdd+WsSopW+EjudqXdOnjxJeHg4DzzwAFOmTOGhhx5y5npozlPqHY27C+BOJWdqGDnu3AbDBVUm\nimrMHZ4XFaglNljn3BOrq3Pq+7IPPviAtWvXUlxcTFVVFUePHmXs2LEtjgkODuaKK64A4LrrrmPD\nhg1cddVVANx8880ATJ8+3Tn9oaGhgeeee45vv/0Wh8OBxdI6JXFQUBCbNm3qcnlffPFFAgMDufrq\nq1u9FhAQwP/+7//y6KOPUlVVxeTJk1GpGvsc7rrrLh577DGqq6t56qmn+M1vfsPLL7/c5fsL0aQv\nxE5dXR2///3v+eCDD5zPXWgktzPTS9qLPW9UVGPm0c/bzpR7g7mBry3wVhvHLJ83iNh21gMPGR7N\n4f2F9BvQuRTv3qQvxE5zXa131Go1AIsWLeLnP/85d9xxB2+++SYPPvggb7/9dpfvL0STvhA7na13\nrFYrOTk5PPLII6xYsYJf/epXfPzxx84ygmfVOz7bwHLYHZQW1bTIINhRBdmkqSJMGRXLqv/7FvvV\ndlRq7x8MPHHiBH/961/55JNPCAsLIyMjA5Op7V7XJs2/jDVNefDz83Oe+9ZbbxEWFsZXX33FoUOH\nuP3221tdo7q6mvnz51/wi93rr7/O0KFDWz3/7rvvkpWVdcFh8SaXX345l19+OdC4b1tCQmODOzIy\nEmj8h+eee+7hF7/4RYfvU4i29JXYOXHiBD/99BOXXHIJAPn5+cycOZP169c7YwIgNjaW06fPpQ4/\nffo0cXFxzsediT1fojgcVJ+ppjzu4jvjBg+PYc3bO7l0/rBO79voDfpK7DTpTr2zY8cO/vKXv6DR\naLjtttt46aWXOnyfQrSlr8ROZ+uduLg4jEajM3auvfZa/vWvfzkbWJ5W7/hsA6uivA69wQ+d/uL/\nCoJC9IQY/Tl9soJ+A72/V7GwsJCIiAjCwsLYvn07+/fvv+BxVVVVfPbZZ8yePZsPPviA66+/vt3r\nFhQUMHnyZIAWGZWaCwoKYvPmzZ0u6/r163n55Zf57LPP0OvbXvNQXFxMZGQkp06d4tNPP3Vmxyws\nLCQmJgar1cqaNWtITU3t9L2FOF9fiZ3U1NQWmctGjx7Nxo0bnXsaNhkzZgzHjh0jLy+PmJgYPvzw\nQ9544w2g87HnSwIsVnQBOqzd6IiLiA5Eq9NQcKqyS3s39nV9JXag+/XOtGnTWLdunXNN44wZMzp9\nbyHO11dip7P1TnR0NAMGDGDXrl2kp6eTlZVFRkYG4Jn1jvcPu7Sh5EwNkV3c/+pCklOiyD1U5IIS\neb5JkyaRkJDAxIkT+ctf/uL8YJ9v8ODBrFu3jokTJ6IoCnPmzAFa9oooiuJ8fO+997Jy5UouvfRS\n4uPju5zV8UKeeOIJamtrueaaa8jIyOCRRx4BGv9huOmmm5zH3XHHHUybNo27776bV155xblgcunS\npUybNo05c+ZgsVh47rnnul0m4bv6Uuw01/x6zWNHo9Hw8ssvOxdQ33rrrc4eybZiz5cZLDb0Id2v\n9IcMj+bwD76VTbAvxU53652HH36Yzz//nOnTp5OVlcWvfvWrbpdJ+K6+FDvNtVXvALzyyissXryY\n8ePHU1BQwLXXXgt4Zr2jODwkVdqGDRtIT0/vtftt+yoXi8XGJZedG6bcm1/d6SmCaXGNjbOi/CrW\nvruHux+e7vIPWV+Ul5fHLbfcwrfffuvuoni87OxsZs2a1e3r9HbsNGlrzWLTGsUmDruDY4eL+fH7\nQkaMjfepNYtdIbHTea6KHXBd/LRXf/SvqCUjPohVtfY2z29er7SlKL+Kj/+ewz2PXCL1TTMSO53n\nibEj3Edip/O6Gjs+O0WwuLCGwalR3b5OZGwQNpudsuJawqMuLiOht5GK3ze0tWaxaY2i2WRl/+7T\n5Gw7iVanYcjIGNat2cfAoZFkzB2KVuez//y0SWLHOzlHsGrrunWdyNggUKCooJrouGAXlc47SOyI\ni9FRcrPzOwy9kcROz/DZbzglZ6qZfGlyt6+jKErjNMGDRdLAAhITE9myZYu7iyHczG538M/XdxBi\nNHD59SOJSwxFURTSJvTj688PsfL/vuWya0aQNEhGs5pI7Hgvg8WKf4ge8rvXwFIUpXFPrP2F0sBq\nRmJHXKyOkpt1lN2zr5PY6Tk+uQbLarFRVV6PMSLAJddLHhbJ0YO+sQ5LiM7Yv/sUWp2Gq342mvik\nMGcPmd7fj8uvG0nmglQ++9deCn5qvSeHEN7GVWuwAIaMiObwD2dcci0hhBA9wycbWKXFtYSGG1Br\nXPP2+w0Mp7SohtqajtNf9mV5eXlMnTq1S+f84x//oLCwZxdl//KXv2To0KHtlm3Lli0kJSU5N7tb\nsWIF0Lifw+zZs7nkkkvIzMzklVde6dGy+gKr2cq363OZMT+lzakHA4ZEMuuqVNat2YfFYuvlEvY+\nT42drVu3MmPGDKZNm8brr79+wWOqq6u57bbbSE9PZ86cORw/fhxo3Jyy+QaSSUlJvPbaaz1a3r5I\nbXfgZ7ejDdC65Hox8SGYTVZKi2pccj1P56mx05l6pylhxSWXXMJNN91Edna287XOxJ4Q3dGXYwfg\nd7/7HdOmTSMzM7PF5sSrVq3isssuY+bMmSxevLhHy9odPtnAKimsbrH/VXdpNCqSBoVz7Mdil13T\nW/RGsN566628//77HR43depUNm3axKZNm5wZZvR6PWvXrmXz5s18+umnrF69mmPHjvVoeT1VQZWJ\nvfnVrX4KqrrWcXBi92mSBoUTEx/S7nFDR8YQGRPElqwj3Sm21+rp2LHZbCxatIh33nmHjRs3snr1\n6hapcpv8+9//JiEhgezsbJ599ll++ctfAo2Zp5riaePGjRgMBubPn99j5e2r/C1W6jVql61zUFSN\n09KP+kj22ovhKfVORkYG33zzDZs3b+bBBx9kyZIlQOdjT4je5imxk5WVxf79+9myZQvPP/88Dzzw\nAADl5eX84Q9/4IMPPmDDhg0cPXqUDRs29Gh5L5ZPNrCKz1QTEePa9VLJw6J8Ypqg3W5n0aJFjB49\nmjvuuIOGhgYA9uzZQ2ZmJhMnTuTaa6+ltLSUjz/+mD179vCLX/yCGTNm0NDQwLJly5g9ezazZs1y\njiJ11+TJk52b4bWnrYSZBoMBgNraWmw2G1qta3qa+5qmuejn/7S3APh8eouNU/sLmT5nSKeOn70g\nlR+/L+Cn42UXW+w+w9NiZ/fu3QwYMIDExET8/Pyce++c75tvviEzMxOACRMmcPToUUpKSloc8/XX\nX9O/f3/nhqniHIPFRp2fa5c7Jw+L4tgh3+nQ87TYgc7VOwEB55YhVFVVodM1ruXpbOwJ0V19NXbW\nrVvn3EB43LhxVFVVUVRUhF6vx+FwUFVVRX19PfX19Z36/ucOHTawDhw4wOOPP84jjzzSZuX76KOP\n8uijj/LHP/6RvLy8Tp/rLiWFrtkDq7mBQyPJO1qG1cunOx0+fJjLLruMHTt2YLfb+fLLL7FYLPzy\nl79k5cqV7Nixg/nz57N69WoWLFjA6NGjef311/n666/R6/Xce++9rF+/ni+//JLs7Gy++OKLVvdY\ns2ZNi6lHTT933nnnRZdbURS+++47Jk+ezI033sihQ4ecr9ntdqZPn87QoUO555575EtiNwwuq6Hf\nqFiCOrnexN+gJXPBcP6zZh9mk7WHS+denhY7BQUFxMfHOx/HxcVRUFDQ6rhLL72UDz74gPr6etat\nW0dxcTH5+fktjunM5pS+ymC1Ueenduk1EwcaKSqoor6u850ffZmnxU5XfPrpp6SlpbFo0SL++Mc/\nAp2PPSG6q6/GTlsx4u/vz4oVKxg9ejTDhg1j4sSJjB079qLv05Pa7Vaz2+28+uqrLFmyBKPRyOLF\nixk5cmSLL6DR0dEsXboUg8HA119/zWuvvcZzzz3XqXPdpaQHRrD8DVqiYoPIO1bGwKGRLr22JwkO\nDuaKK64A4LrrrmPDhg0MHjyYn376iZ/97GdA4/SHxMRE5znNR45ycnJ4++23OXLkCFVVVRw6dIjL\nLrusxT2uv/56l39ZGzVqFPv27cPPz49//OMf3HrrrezevRsAlUrFN998Q15eHjfeeCMTJ05k1KhR\nLr2/LwhpMBPWYKZ/enzHBzeTPCyKwz+cYdN/fiRzwfAeKp37eVrsdHbK2jXXXEN+fj5XXnklgwYN\nYsyYMajV5xoMZrOZL774gqeffrpT1/M1BouVSp2fS6+p8VPTb2A4xw+XkDo6zqXX9kSeFjtdccUV\nV3DFFVfwwQcfcNttt7Fp0yaX30N0XX2dmZ+OlXHkUDFBJgvVLo5RT9GXY+dCs45KSkp45JFH2LZt\nG6Ghodx55518+eWXzs2RPUm7Dazc3FxiYmKIimrcL2rq1Kns2rWrRSNpyJBzU4HS09P55z//2elz\n3aG+zozZZCU41N/l104eFkXugTNe3cC6EIfDQVhYWJsVR9MXOYfDwRNPPMHbb79NamoqTz75pHO4\nurn333+fP/3pT62eHzBgACtXrryoMgYFnRuxvP3221m6dCnl5eWEhYU5n09MTCQzM5Nvv/1WGlgX\nIamyjuOhAagvord+5vwU3npxM2On9ndZds++wJ2xExsby+nTp52PT58+TVxc6y/rBoPBOUsBYPTo\n0SQlJTlfX79+PWlpaURERHT8hn1QgMVGQWAP1DcpjdlrfaGBdSF9od5p7tprr+Xxxx+nqqqKuLi4\nTsWe6FhX97HK2XaS/btPU15aS3xSGATqSC+soNigIzcsALPGtaPNnqgvxM759VN+fj6xsbFkZ2cz\nbtw4Bg4cCMCCBQvYunVr32tglZWVER5+bp8ao9FIbm7b+wWsX7+ecePGXdS5vaXkTA0R0UE9srFa\nckok7711AofD4bUbt1VVVfHZZ58xe/Zs57SgwYMHA7B27VquvPJKrFYrR48eJSUlhcDAQIqLG9cK\nmEwmampqSExMJD8/n3Xr1nHLLbe0uscNN9zADTfc4NJyFxUVERkZiaIo/Oc//0Gv1xMWFkZpaSka\njYaQkBDKyspYv349L7zwgkvv7QsUh4PwejOHwi9u6q3e34/0Kf3ZvvEo827wzsatp8XOmDFjOHbs\nGHl5ecTExPDhhx/yxhtvXLDcer0erVbLqlWrmDp1KoGB52YA/Pvf/+a66667mL8Sn9C4Bsv1X9oG\nDo1k07ofsdnsqNXevZza02Kns44fP07//v1RFIWsrCz0ej3BwcGdjj3Rsa7sY3VobwE7t5xg3vUj\nie0XilqjYm9+NX8tNTOwopYpp0o5HhrAyRADeMl3uL4aO3PnzuWNN97guuuuY+fOnQQHBxMVFcWk\nSZNYvHgx5eXlGAwG1q9fzy9+8QuX3ttVXPav8v79+/nmm28u+JfvSUqLanpsQ+CwiAA0fmqKC6p7\n5PrupigKgwcPZt26dUycOBFFUZgzZw5+fn6sXr2aV155hQkTJpCRkcHOnTuBxtGiZcuWMWPGDAAe\neughZs+ezd133+1cON9d99xzD5dffjlHjx5lxIgR/P3vfwdg5cqVzt6TtWvXMnXqVC655BLWrl3r\nPObMmTMsWLCA6dOn8/Of/5z777+fjIwMl5TLlxjrzdT4abrV+5c+JZHjPxZTVlLrwpJ5Bk+MHY1G\nw8svv8ztt9/OzJkzufXWWxk6dCjQMnYOHTrEtGnTyMjIYPv27Sxfvtx5jdraWjZt2uScgiJaUtvt\naOx2TD3QAAoM1hMabuD0iXKXX9uTeGLsQOfqnU8++YSpU6eSkZHBxx9/7DymvdgTPaOooIoNnxzg\n6tvGkDDA2GKbHqtaxeHwIL6LMxJX00BSZfc2BPcUfTl2MjMzGT58OFOnTuXJJ590jpAFBwfz8MMP\nc/vttzNv3jyGDx/O9OnTXVIuV1McbaVWo3Fx3Pvvv8+vf/1rAD788EMUReHqq69ucdzJkyd58cUX\nefLJJ4mJienSuU02bNhAenq6S95Uc+cPHx/ZdhK1RsXA8f1aHWu22fn1Fx2n6F4+bxBpcRfuqd/4\n2UH0/lomX5p88YUWPiE7O5tZs2Z1+zquip29+dUX7Als6/Pe/PhhxVXU+6k5ERrQbnx0ZNtXRykv\nrfXaUSzhGq6KHejZ+AkyWRhRVMW2fuH8dvYAlq4/3ub5FxM3WzfkYmqwMHP+sIsqs/A9nhg73dFW\nvdVk+bxBDAnVsfrP25g+ZwgpabHtnq+32JiQX8aByGBKDLpu1WfCu3Q1dtqdIpicnExhYSFFRUUY\njUa2bt3KQw891OKYkpISXnzxRRYtWuRsXHX23N5w/vDxiKJKSv21FBS33tvnt7MHdPt+A4dGsiXr\niDSwhO9wOIisM7ErNqzjYzuQPiWRN1dspqyk1qfWYgnv1FPTA5skD4vik3/sYca8tjf1FsKX2e0O\nPv3nXgaPiG7VuLqQBj81e6NDGFNYwc44Yy+UUHirdhtYarWahQsXsmLFCmw2G7NmzSIhIYGsrCyg\ncQhvzZo11NTUOOcPq9Vqnn/++TbPdTe91UZDDy5iTOhvpKy4ltoaEwGBuo5PEKKPCzalax2jAAAg\nAElEQVRZsaoU6rTd3+tHp/f+tVjCd/R0AysqNgirxUZ5SS3GyJ6Z+i5EX3Zi9ykALunk3owAlXot\nh8ODGFNYgbne0lNFE16uw29EqampLFu2rMVzzedh3nfffdx3332dPtfd9FY7DZqeWxCs1qhITG5M\nnzuii+mqheiLouoaKApwXWeCjGIJb2GwWKnQ91z6Z0VRSE6J4uihYmlgCXEeld1B3vcF/NfCSai6\nuA4yP8ifQLOV/V8eZtx9E2WEWHSZd6ceOp/Dgd5qw6Tu2TScA1MiOXaoqEfvIYSniKo1UWzo3MbC\nndE0irXj66Muu6YQ7tC4yXD3R3bbM/BsunYhREuxNQ2ERAUSdpEddUeMgZjrLRzcK5tAi67zqQaW\n1mbHolZhV/VsT8TAIZGczC3FZrX36H2EcDeDxYrG7qBS59ovkaMn9SP3QBE1Va333BCir+jpKYIA\nicnhFBVUUV/X9l5AQvgch4PEqjoSO7Huqs1LKAopGQPZtO5HTA0yVVB0jU81sPRWOw29sF9IQJCO\nsIgATp/07vS5QkTWmig26Fy+Z4i/QUtKWix7dvzk0usK0Vt6MkV7c35+avoNbJyWLoRoFNZgQXE4\nMPYL7dZ1QmODGTg0km+z3L+Pq+hbfKyB1bMJLpobODSSozJNUHi5qDoTxS5cf9Vc+uQkvv/uJ6wW\nW49cX4ie1Dh6pemVDUsHDYuSaYJCNJNYWUdeiMEla6emXzaEg98XUJRf5YKSCV/hgw2s3nnLySmR\nHPuxuFfuJYQ7mOvMBJqtlPpre+T64VGBRMcHy/x30ScZLDbqerFD78SREpmWLgTgb7ER1mCmINDf\nJdczBGiZPmcw69cewGFvc+tYIVro2dW3HkZvs/faCFZUXDBmk00yoYk+T61q3IzxfIXHyyj11+I4\nr4ewreMBArVqasytR6SiArXEBrceCRs7tT9ff36IEWPjJYuT6FMMFmuPr79qEhCkwxgZwE/Hy+g/\nOKJX7imEp+pXVUd+kD82F663Hzk2gX27TrE/+zQjx7l/yyHh+XyrgWW1UanruZS5zSmKwsChkRw7\nVIxxmjSwRN9V2WBj6frjrZ6/TeugXN969Kqt46FxM+8LvbZ83qALNrCSBoXjcEDe0TKSBoVfROmF\ncA+DxUbFBeKjpwwaFsXRQ0XSwBI+TW23E1ddz/Z419YXikrh0itT+Xh1NimjYvHT9k7niei7fGqK\noH8vThEESJZ58cKLVZ+p7tE9fqCxo2Ls1CR2bz3Ro/cRwtV6I4NgcwNTGusbh0OmMAnfFVPTQLle\nS0MPxF5sQgix/ULJ2Z7n8msL7+NTDSydtfemCEJj7/uZfEmfK7yP2m7HVG2iRtvzg+DDRsdR8FMl\nZSW1PX4vIVylcQ+s3qtvIqIDURSFksKaXrunEJ4mqtZEYaDr9mU839TZg9n5zXFJ2y465DMNLMXh\nQGvr+ZS5zfn5qUlMNnLskCS7EN4lpMFCQERAq/VXPcHPT82o8Qlkbz3Z4/cSwhVUdgd+vVzfKIpC\n8rAocmXWhPBRaruDsAYLpYaem5obER3IwKER7NpyosfuIbyDzzSwdFY7Jo2qV1LmNjdIKjzhhUJM\nFoKiAnvtfmkT+nFobwFmk7XX7inExdLZbG6rb2R7EOGrjPUmKvV+WFXnvto2JV1q68ds63rmzcmX\nDiJnWx51NTI7SbTNZ5Jc+FttNKh7f1HiwJQovvr0EBaLDb9enC4iRE8KbbAQGB0ENZW9cr/gUH/6\nDTTyQ04+YyYl9so9hbhYOqvdLfVNfP8wKkrrqKlqIDC456ZJCeGJopo2vm+mvaRL0Jh4qatCjQZS\n0mLZsfkYM+eldPl84Rt8aASrdxNcNDEEaImKDSLvaGmv31uIHuFwNI5gRffeCBbAmEmJ5Gw7KYv4\nhcfT287OmOhlarWK/oPDZQ9G4XscDiLqzRT34PTA5ibNGMgPu09TXdnQK/cTfU+HI1gHDhxg1apV\n2Gw2Zs2axdy5c1u8fvr0aV555RVOnDjBzTffzJVXXul87YEHHsDf3x+VSoVareb55593/TvopN7c\nA+t8g1KjyD1QRHJKlFvuL4QrGSw2bCoFbS9VZE36DTSiKAo/HSsjMVlStgvPpbPaMLlhBAsas9ce\n3FPAqPH93HJ/IdwhxGTBolKo9+udiVmBwXpGjk9g+9dHyVwwvFfuKfqWdj+JdrudV199lSVLlmA0\nGlm8eDEjR44kIeHcJmtBQUHcdddd7Ny584LXePrppwkM7N2e7gvxt9qo6aXAO9+gYdF8t3k7DrsD\nxYUb3wnhDiEmCxW9tJ9cc4qinB3FypMGlvBoeqvdLTMmAAYOjSTrox8wNVjR6X1mFYDwcZF1JooC\nWu+l2JPGTxvAX//wDZNmJBMUIlNyRUvt1gC5ubnExMQQFRWFRqNh6tSp7Nq1q8UxwcHBJCcno26j\nt85TpvPo3TRFECA03IC/QUvBqQq33F8IVwptsFDZw/tftSV1TBw/HS+jqqLeLfcXojMak1y4fgSr\noMrU7oL9gioTOr0f8f2NHPtRkl0I3xFZa261/qqnGQK1jBgXz3ebjvXqfUXf0G73VllZGeHh53qK\njUYjubm5nb64oij87ne/Q1EU5syZw+zZsy++pN3U23tgnW9QahRHDhQRlxjmtjII4QohJgv5Qf5u\nubdWpyF1dBx7d/zE9MuGuKUMQnSkMcmF6zv0imrMPPp523Xw8nmDiA3WMWRENIf3n2FYWpzLyyCE\np/G32NDa7VS6YWbF+GkDePulLUycMVASy4gWenRI55lnnmH58uU8+OCDfPjhhxw8eLAnb9cuf6vN\nzQ2saI4ekB5F0bep7XYCLFaqdO6bejR6Uj/27TqF1WJzWxmEaI++h0awOmvQsChO5pZiNsu2BsL7\nRdaZKPHX9vq2CAABQTqGp8fx3ea2MxUK39RuA8toNFJaei77XWlpKUajsdMXDwtrHK1JSEhgwoQJ\nXRr9ciW13YHK4cDixvVPMXHBmM1Wyopr3FYGIbor2GSlWuvXKxsMt8UYGUhUXBCH9hW6rQxCtMnh\nODtjwn1Jev0NWuISQzj+Y4nbyiBEb3HH+qvmxk8fwIGcfGqqJKOgOKfdGiA5OZnCwkKKioqwWq1s\n3bqVcePGXfDY89damUwm6usb10lUVVWRk5NDYqJ79q/RNY1eufFLoaJSGDQsmsM/nHFbGYTortAG\nCxVuWn/V3JjJSZKyXXgkrc2OVaW4tRMCYMiIGA7vl04I4d0sJishDRbK/N3XwAoM1pM6Oo6dW064\nrQzC87Q7z0etVrNw4UJWrFjhTNOekJBAVlYWAJmZmVRUVLB48WLq6upQqVR8/vnn/OEPf6CyspIV\nK1YAjZkG58+fT1paWs+/owvQu3l6YJOhI2P46tODTJqR7O6iCHFRQkwWCgLdP8984JBINn56iPy8\nCuKTZF2j8Bw6N24J0tygYdFsWvejbHIvvFrZqUoq9H7Y3JyhefwlA1j1f98yYfoAAoLc19gTnqPD\nhRSpqaksW7asxXOZmZnOP4eGhvLqq6+2Ok+v17N8+XIXFLH7/HtowXFXxfcPo77OTGlRDeFR7k9d\nL0SXOByENpg5GBHk7pKgqBTGTE4ke+tJaWAJj6K32tyyyfD5DIFaouKCOXGkhMGp0e4ujhA9ovx0\nJWX+vbsn44UEhehJGRXLri0nyJg71N3FER7A/bVAL/CUESyVSmHIiBh+lLUjog/yt9qwKwomD+is\nABgxNp6TuaVUV8q8d+E5dDY7DW7aZPh8Mk1QeLvy05WU693fwAKYkDGAfbtOUVdjdndRhAfwjG9K\nPUxnc98eWOdLGRXDoe8LZO2I6HOCTVaqdH5uXcvYnE7v9/+zd+fxUdXn4sc/Z2YyW2aSyYSELEMg\nJGyRsEgAAREQgiK11NparbW21aqobW/tT621Wq1aewVtr23F/QpubW+ruFdBhLBD2HcI+5IQSMg6\nmf38/ggZE8gKSWbJ8369osmcc4ZnYL4583yX58uQ4alsWXsk1KEIEWT0BcJiBAtgQE4yB3afwucL\nhDoUITpdndNDXZU7pFVtG4uzmRiUm8KGlYdCHYoIA+FxF+hiphDvgdVYah8bPq+f0yVSTVBEFqvH\nGzY3sgYjx2Wwdb2UbBfhw+Dzh80IliXOSFKKlcNFUk1QRJ9jh85gS7WGvKBMY2Mm9WfLuqPUOWUU\nq6frEQlWuEwRhPrNlwflprJ7W3GoQxGiQ6xuH9X68Eqw7EkWktPj2L1V2pMID0Z/+IxgAQwc2lum\npYuodPRAOQlp8aEOo4n4BBMDLunNhpWHQx2KCLHwuQt0EVVVzyZY4fNSBw1LYc/WEpkmKCKK1eOj\n2tC9JdqLq9xsOVF93ldxlTt4zqXj+rJx9RFpTyIsGMKoQw9gUG4q+3eVyqbDIiK1dA/YcqKafXtP\nY0kNfdGlc42d3J8ta4/gqvOGOhQRQuHVHd0FvC4fAUXBrwmfBKt3WhwocPJ4FSmO8Op9EaI5ep8f\nrap2ezXO0hoP9396/gblc67JJjWuvhRu5oBefPXJLo4dPEOf/u3fCF2IrmD0BS6oEIxWA1tOVLd6\njsff8bVUsVYDaX0TKNpRSs7ItA5fL0QotXQP0PkDXFHmxJBoDkFUrbPZzWQNSWbDykNMmDYg1OGI\nEIn6BMtd4w6r3kSonyY4ODeF3duKJcESEcHqOTs9MIzmujdQNAp5E/qxfsVBSbBESGkDARRUfBew\nJ0+ly8/jiw+2es7vpmVeUFyXjExjW+ExSbBE1EhweagwxqAJo87zxi6bnMXb81YzakI/jKbunfkh\nwkN4vjM7kavWExZ7YJ1r0LBU9myTaYIiMlg9ZysIhqmcS9MpOVbJ6ZNSPEaEjqGhoFKYdURkDUnm\n5PEq2dJARI0El5czxvC9J9kSzfQfnCwVBXuw8Ms8Opm7xoM7zEawAJJSrOj1Oo4frgh1KEK0KRwL\nXDQWE6Nl5GUZFK5ofQRAiK5k9PnDZp+4xmJitAy4pDe7tpwIdShCNNHaGqstJ6pbnBZrr/NwJgw2\nGG7NuCuz2LzmiFQU7KHC9xNTJ3HXesLyhgf1G6VuKzyGo19CqEMRolVWj5eDtvCb697YiMsyeO3Z\n5dTku7DEGUMdjogyxVVuSlvZQNTjD2D0h3ZLkNbWcRkybGwpOMDoiZkoYTbCJnqultZYNWhuWqzO\nH8Ds9VMZxrMqoH4t1sChKawrOMikqweFOhzRzSI2wWrrZtfAWeMOq5K5jeWMTOP155bjdg3BYIzY\nfwoR5fw+Pyafn9owHsECMJn1DBmRysZVh7lCbmaik7Xng2D9FMHQ3W9aXcelqszy+Dl5ooqUdFn7\nKyKXzeWl0hgTVvtfteSyKVnMf34leRP6EWs1hDoc0Y3C+xNTK9q62TW4wesJm00fzxVrMZCRlcju\nrcUMH9Mn1OEI0SxnuZPaGF1E3MxGTejHW39bzdjJWdJpIbqd0e+nJiZM33eKQuqgZHZuPCEJloho\ndpcnrNdfNWaNN3LJpWmsXXqAK68dEupwRDcKz6GdTuRxesJ2BAsgN8/BtsJjoQ5DiBY5TzvDev1V\nYza7mb7ZiWxdfzTUoYgeyOALr02Gz5U6OIldW4vxX0C5dyHCRYLLwxlj96y/aph229JX4z0ZWzLm\niv7s3HyCqoq6bohYhIs2PzXt3LmT+fPn4/f7mTp1KjNmzGhy/Pjx47zwwgscOnSIG2+8kWuvvbbd\n13YHT60Hd2znrh1pz34lABa9lhqPv9Vz1FgDVZUuThVXkxSGG+YJUVtW2+0bDF+M0Vdk8sFbm7h0\nXF+0YfxhV0Qfg88ftjMmAMzxJuy9zBzce5rsIcmhDkeIDtMGAsR6um/9VVvbJzTek7ElsVYDw0Y7\nWPPVfqZfN7SzQxRhqtUEKxAIMG/ePB555BHsdjsPPfQQubm5OByO4DlWq5Wf/OQnrF+/vsPXdjVF\nVfF7/Hg6uchFe/Yrgfo5+e05787BSWwrPCbDx6LLtbZ2saVqTbVlTqr1kZNgpaTHk5hsYfuGYwwf\nmxHqcEQPYvSH9wgWwNBRDrauOyoJlohINpeXKoOOwAXsNRdKo6/I5PXnlpM3MRN7r9hQhyO6Qat3\ngqKiIlJSUkhOTkan0zFhwgQKCwubnBMXF0dWVhbac3rt2nNtVzP4AsSYYsJuT5JzpQ+pL5/r87Y+\n2iXExWpYu9jcl8ffzJ5sqoqz3Em1ITKmCDYYPzWbNUsP4PPJVCjRPQKBADH+QNhWrW0weFgqxUcr\nqChzhjoUITrM5vJS0U3TAzuTyawnb2Imy/+zN9ShiG7S6p2gvLycxMTE4M92u53y8vJ2PfHFXNtZ\nDH4/+tjwb4imOCPJaXHs23ky1KEI0YTZ6yfGFINPE94fGs+VlmGjV28L22V9o+gmXqe3frZEmHfo\nxei1DB3lYNOaw6EORYgOS4igAhfnunR8X0pOVHLsYPd+FhahEVmfmjrI4AugN0dGQ6wvdnE81GEI\n0YTV4yM2MTKnM4yfms3aZQdkZFh0C0+tJ6R7YHXEiMv6sGPjCTxuX6hDEaLdFFUlzu2jMkITrJgY\nLROnD2TpZ3tQA83MGBFRpdUEy263U1ZWFvy5rKwMu93erie+mGs7i9EfIMYc/iNYANk5vTldUk1Z\naU2oQxEiyOrxEtsrvDcYbklqHxtJKVa2yiiW6AaeMN7U/lzxCWYc/RLYuflEqEMRot3i3D7qYrQR\nN6OisSHDUlFVlT3bSkIdiuhirb5Ls7KyKCkpobS0FJ/Px6pVq8jLy2v2XFVVL/jarmLw+TFEwBRB\nAJ1Ow/Cxfdiw8lCoQxEiKM7tw9wNI1gtlcJtqfBGa6VzG5fNHT81m3UyiiW6Qf0IVuR88Bs5ri+b\nVh85794tRLiyRfD0wAaKRmHSjEEUfLFX7ktRrtWV61qtltmzZzN37txgqXWHw8GiRYsAyM/Pp6Ki\ngoceegin04lGo+HTTz/lT3/6E0ajsdlru5PBHyAmVg9lzVdNCzcjL+vL639azoRpA2THbxEW6qcI\nmmFfRZf+OS1V5vzdtMwOnQ9Ny+amOOLpnRbH1vVHuXR8v06LV4hzuWs9uCNkiiBARlb9jJKjB8rJ\nyEps42whQs/m8nLSEvmfjTL6J5KUYmXTmiOMntj8PU5EvjZLg+Xk5PDMM880eSw/Pz/4vc1mY968\nee2+tjvVr8GKjBEsALNFz6BhKWxafZjLpw8MdTiih9P7/CiqGhGFYlozfmo27y3YyNBRDvQRVg1R\nRA5PrQdXhEwRBFAUhZGXZbBx9WFJsET4U1USXB5294qO/UInXT2Qd19ay5DhqVjijKEOR3SByLkb\nXACj348+NrKGk/Mm9GPLuqOy+FiEXJzHR7UhBiXMq6K1pXd6PBlZdtYtOxDqUEQU80TYCBZAzsg0\njh08Q+WZulCHIkSrzF4/fo0ScW2sJfYkC7mjHSz9dE+oQxFdJKoTrEgbwQJI6BWLI9PO9g1SUVCE\nltXtpUofHSM+E6cPZPPao/JBUnQZT407otZgAegNOnLzHKxf3vx0WyHCRUKE7n/VmnFTsjlx5AyH\ni06HOhTRBSLrbtAB2kAABRWtPvJ6O0ZPzKRw5SECLSzwF6I7xLnrR7CiQZzNxMhxGSz/XHoLRRdQ\nVTxOb8SUaW8sb2I/dm8ppqpCOh9E+IqGAhfnitFrmXptDos/3InPd2Gf94qr3C0WfDq36JPoXtHR\nPd0Mgy+AS6uNyOlNaRk2rHFG9u44yeBhqaEOR/RQVo+PfVEyggUw+opMXn9uOccPnyG9b0KowxFR\nxOAPoDPqUCPwfhNrMZA72sHaZQcYOiWb0pqWi0IlW/TBAjJCdCeby8thW2RuGdKarCHJbCs8xvqC\nA4y7MrvD15fWeLj/06IWjzcu+iS6V/R8ejqHwR/AHSHTNRpKTjfW65LeLPuyCFdibDBJtOi11Hja\nLuspN0FxsXT+AHp/AGdM5PXIt0Sv1zFx+kC++mQ3N991GYom8j4Mi/Bk9PkxRHB1s9ET6zsfrIN7\n8+jyoy2eJx/WRCjofX70gQA1MdH5kfXKa4fw5l9XMXh4KgndsC2K6B7R+W6l/obn1kbGh8NmS06r\nKpdVunn2/3Zw0lJfYeZ30zJbLE3dmNwExcWqL3ChgwjskW9Nzog0Nq4+zK6txeSMSAt1OCJKmHx+\nDJbIXR9ijtUzbIyDg4UtJ1dChIrN5aXCEBN196MGcTYTo6/IZNHCnXz3x3nS+RclojbBiqQRrGYp\nCnsTreScqqI01hCRU09E5IqmAheNKRqFK78xhI/e3Uz/QUkYTdE1p1+EhtEXQG8xQE3krpsdPTGT\nTXMKMCbbcEXRyLWIfOFc4KK5GUiNtTWjqLjKTWmNh5j+vajYdIKPv9hHRqOlITIjKXJF3yeoswy+\nAHWRnGAB5SY9zhgtjqo6jsZH39xj0XWOV7pwNbNo1htQ23V9nMdHmSk8b2gXK71vAtk5vfnqk93M\n+E5uqMMRUSA4RbAmcgtFmMx6HENT6L+3jJ1JcaEOR4ggm9vDHnt47n/V2qb30PaMosZrqMwxBsas\nOMhrBypxnu3glBlJkSt6Eyy/n4ooqDiz125hVEkFxVbZiE6031f7K1iwsfi8xx/Pb9+u8Va3l4NR\nnNRfcdVA3vifFRzce4rMgUmhDkdEuK+nCEZuggXQd2QaezYd55DNjDNK17uIyOLz+Ij1+KmKkoq2\nrXHqdexPsJB7qpJ1aXaZuRThInuIpxUGX4RPETyrxhDDaZOefhXOUIcieghtIIDJ56c2CqcINtAb\ndEy/bihfLNyB2yWbeouLY/QFIrrIRYMYYwyHbLEMPl0NavtGu4XoSlXF1VQaYgj0kHVJR+NMeDUa\n+p+pDXUo4iJFfgbSAqPfj1sbHS+vyG7BUeXEXSP7GYiuZ/H4qNFHZsnpjug3oBd9sxIpkL2xxEUy\n+vz1a7CiwOF4M0afn+Raud+I0Ks6Xkl5T1orqyjsSIrDUV1HnMsb6mjERYjOLmpVrR/BipAqgm1x\n67QcizNxtPAoEB2vSYSvOLePKn3PuKFNvmYwb/zPCgblppDRPzHU4YgQOV7p4sU1x1s8fllGPI74\n5hMoXSCAooLOEB2/m1VFYVevOHJLKykz6/Frvu6obGtBP8iifNG5Kk9UUW7qWe8nt07LrkQrw0sr\n8NRJkhWpojLBigmo+DRKVA0pH7TFMvhEJYkWM2XmnvXLRnSvOLeXyihYv9geRlMM068bymf/t41b\n7hmPOYJLbYsLpwJrj1a1eDzFqm8xwTL6/Lh0mojc1L4lZ0x6yk16ss7Usjfx6+ICbS3oB1mULzqP\n3h/AXeOmKt4S6lC6XanFSLzby7bP9zDqzrFoomRGVk/SZoK1c+dO5s+fj9/vZ+rUqcyYMeO8c955\n5x02btyIwWDg7rvvJj09HYB77rkHk8mERqNBq9Xy9NNPd/4raIYhgvbAai+/RkPWFf2p/GIvqx2J\n+DTS2ETXsHp8HI2L3AIXLfWyt7RRd3JqHENGpPLJP7dw/Y/y0ERRx4zoekZfAJcuuu43UF9gafyx\nMk5YTdRE8XpMEb7sdR7iUuKifrp6S/bZLYzyeVj+xT4mzRgU6nBEB7X6WzMQCDBv3jweeeQR7HY7\nDz30ELm5uTgcjuA5Gzdu5PDhw8ydO5d9+/bxwgsv8NRTTwWPP/bYY1gs3dv7YIz0PbBaYHPYKDMZ\nGFhWI2V0RZdQVJVYry+iP1C11Mve0kbdc67J5vJpA/jn6+tZvaSICdMGdEeYIkoYfX7qojDB8ui0\nFNktDDldxfrUhKjd5FWEL3udh/isZDjpCnUooaEo5E4fyKb3ttE7PY7BjfbHEuGv1SykqKiIlJQU\nkpOT0el0TJgwgcLCwibnFBYWMmnSJAAGDBhAbW0tFRUVweNqCCoR1Y9gRV+CBbAn0UJinZtEpyxA\nFp3P4vHhjNFF1fTa9tBoNVx74wi2FR7j4N5ToQ5HRJCGKYLR6JjVBCr0q5QqtqL72es8xKXHhzqM\nkNKbYvjWzSP58sOdlJ5oeRqzCD+t3hXKy8tJTPx64bfdbqe8vLzVcxITE4PnKIrC73//ex544AEW\nL17cmXG3yuAP4I7CHkWonyq4s1ccOaer0AXO30hWiIsR5/ZSHcGjVxcj1mpg5veG89m/tlF5JrL3\nMxLdx+SNzimCACgKW3vH07fSic3lCXU0ogcxev1oVRVzginUoYRccloc02ZdwnsLNlBRJp0dkaJT\nut1aGqV64oknmDNnDj//+c95//332bVrV2f8cW0y+AJR26MIUGY2UGYyyF4lotPFuX09YkPHlvTJ\ntDPmiv68N38DdU75QCnaVj+CFaUJFvUVzXYkxZF7shKvlI0W3SSxzkO5MSaqisdcjEG5KVw2JYv/\ne309NVU9dMpkhGk1C7Hb7ZSVlQV/Lisrw263t/uchIQEABwOB2PGjKGoqKjTAm9NNO2B1ZLdiVYs\nHh99ZeqG6ERWj4+qHjqC1SDv8n5kDurF+ws24vHIJsSiddG6Bqux02YDJy1Gir7aL516olvY6zyU\nm6Sqa2MjxmaQO9rB/71eKB2AEaDVLCQrK4uSkhJKS0vx+XysWrWKvLy8Jufk5eVRUFAAwN69e4mN\njcVms+F2u6mrq59mU1VVxaZNm8jIyOiil9GUwRe9UwQbBDQKm1Js9K100kvWY4lO4PcFsHh8VBt6\ndoIFMOmqQdgSzXz0zmb8fpmKK5qnqOrZKenR3aEH9RXNfG6frMcSXU9VsbskwWrO2En9yRzYi/fm\nb8Djlg7AcNbqJymtVsvs2bOZO3dusEy7w+Fg0aJFAOTn53PppZeya9cufvWrX2E0Gpk9ezYAFRUV\nzJ07FwCr1crMmTMZPnx4F7+cegZ/IOpHsKB+6saW3vGMLKlgfZqd2h4+8iAuTnVJFdV6XZONRXsq\nRaNw1beH8sFbm/j839uZ8Z1clB5W+EO0zeAL4NFqekQZaVVRGDh1AKf/uYU6nXyCQr8AACAASURB\nVJaTFmOoQxJRKtbrJ6BAXYx8pjmXoihMmjGIxR/s5J+vrWfQVVK+PVy1+e7NycnhmWeeafJYfn5+\nk59vvvlmbr755iaP9e7dmzlz5nRCiB2jqCox/vqbXk9QadSzN9HKiJIK1qbb8fWQ1y06X+WxSukx\nbESr1XDtTSP41/8W8p/3tjH9uqFopX2JRnrC9MDGDFYDm1JsjCo+g1ejUC6b3osukFjnoUzuRS1S\nFIVps3JYsWgf6/+9DaM1FldMz/k9FCmi7tOCyevHresZPYoNTlhNlMYaGFVyBp1MZxIXqOJ4JWVm\nuak1FqPXcv2PR+Gs8fDBW5vwNrNRsei5orlEe0uqDTFsTrExrLSSeKksKFpRVuvlQFldi1+lNc2/\nf2T9VdsURWHi9IH0yU1hzIlyYmW9cNiJuvFXm8tLhaHnNcx9dgsDy2vIKz6Dp679lZ6Kq9wt/pJr\nLNmiJzVOeiujld7nx13tpjKuezcFDwdaDWw5Ud3sMYteS43HT/+pA9i5pIg3XlzDyG8MIb1XrLQH\ngckXxSXaW1Fh1LM9OZ4RJyvZkGqjRt9zK4+Klp2scfNfH+1r8fiTV2Vh0DbtDNf5AyTUediRFNfV\n4XWL1u4vAJ6L7BTPGJ7G/+0pI6/4DNuT4iiTUeWwEX0JlttDhbEH/rJXFPbaLWSfqaXw/e3k3DmW\nWGvbDa20xsP9n7Zd3XHONdnygTKK2V0e4lLjetTIb4NKl5/HFx9s9tjvpmV+fUxVGFjn5/j8DVz1\nveGk5iR3Y5QiHBl9fmp66NrX02YDexItjCquYEvveCqMPa9jU3S+3rUuyk16vFEyHbu1+wvU32Mu\nVonFhEurZVhpJcetJvYnxEIPvJeHm+h4BzeS4PL2zAQLQFEosltIGdCLv7+ylsozUu1JtE+i04PN\nER/qMMKborA30crRODPr/r2N3VuLQx2RCLGetgbrXCUWE9uT4hhRUkFKjWzOLS5eWo2LE1YpoNJR\nFSY9a9Lt2FxeRhVXoPfJdPZQi6oEK8YfQO8LUN1DexQb9B/dh5GXZfD2C2s4sOdUqMMR4U5VSazz\nEJ8uCVZ7HI03c+m1Oaz4Yh+LPtiBzys3sp7K1APXYJ2rzGygMDWBAeU1ZJ6pQZV9ssQFMnl9xHp8\nnJZpbhfEo9OyIdVGhTGGy46Xk1zjkvYYQlGVidhcHiqNMTI0Clw6vh/JqXF8/I8tDB3lYPzUbDRS\nZlo0I9brR1XAGC+9hu0Vl2zhlnvH8fl7O3j7xTVMv24oqTIC2LOoKsYIW4PVVetBagwxrE2zM7Kk\ngm2f72HQjcMxScEc0UFp1S6KLcYeOVW9JR1us4rCfruFMrOenFNVbPl0N/2/m0uczdTFkYpzRVmC\n1YOnBzbDkWnnlnvG8/Hft/DvNwq56ttDpZGJ89SXxDWgyE2tQwzGGK69aTg7N59g4Zsbyc5JZuL0\ngRhN8juoJ9AFVFSIqK0xunI9iEenZX2andxYHfOfX0n+ty4ha7CsUxTtpKqk1rjY2ls6qhq70DZb\nYdSz2pHIsCQDb/51FWMnZzHisgx0PXzEvTuFXYJ1oKyO/eVtz+W2Gc/vNbS5vOy3x3ZFWBEr1mrg\nuz/JY+2yA7z511XkTcwkb0I/tFHWyNpbDRGkIuK5EuvcnLBI4n0hFEXhkpHpZA1OZsUX+/jfP6/g\n8vwBXDIyDU0EffAWHVdfoj1yRq+6Q0CjMGhiJvYxDv7z723s3X6SKTMHS6eDaJPN7SWgQFUPX+LR\nmVRFIWtMBpPG92XpZ3vYsOoQ46/MlvtTNwm7d3LhsSpeXX+izfOemN6/yc+agEqcx0ulQX6Rn0uj\n1TDuymyGjEhjyUe72LHhOFO/OYS+2b1CHVqnaW81RJCKiI0pqoqtzsv2JOk1vBhGUwzTZuUwdFQ6\nSz/bzZql+7lschY5I9KirjND1Ksv0S7/ts3pk2nn1p9NoODzvbz2bAF5EzO5dFxfYvSSkIrmpVW7\nOGE1yRKPLpCYbOH6W0dx/PAZVnyxj3XLDjB2ShaDh6XKiFYXCrsE60LFebzUxOjwa+TN0hKb3cx1\nP7yU/btPseiDncRa9CTlpoKqyi+1Hsrm8uLUa6OmJG6opTjiufGnYzl2sJzVX+1n9ZIi8i7vR87I\ndOnFjzIygtW8xmtGkvL6YM5KZO/aI6xbcYjMPAcjRvfBYe+6EfP2zGaQWQzhRRNQ6V3rYpUjMdSh\nRLX0vgnccPtojuwvY/3ygxR8tofc0Q5GjM3AKmuwO13UJFiy/qp9FEUhe0gy/QclsXd7CcsWFzGu\nys3heDMnY434pRBGj2Kv81BmksXonc2Raee7mXZOHKlg46pDrFxcRNbgZHLzHDgyE2S9WxQw+vzU\nxUiCda7m14zosNosHFt3jP3rjjJitIPhY/pgs5s7/c9vz2wGmcUQXpKcbioNMbilw6LLKYpC3+xe\n9M3uRVlpDZvXHmH+8ytJ62tj8LBUsockozdETWoQUlHzt2hzeSiWdSTtptEoDB6Wiisxlv/+904y\nKp0MKqvmlNnACYuRcpNeRrWinCagklLrYkevuFCHErXSMmykZYzAWeth1+YTLP5wJx6PjwFDepOd\nk4yjX4LMhY9A2oBKcq2bXb2soQ4lYlQbYtiUmsCs8el4DpXz9gur6e2IZ/CwVLIGJ0nVwR7K5/GT\ndaaG/QmWUIfS4yQmW5h6bQ4Tpw+kaGcpu7cWs/iDnfTNTiR7SDJ9sxOxxMnI1oWKjgRLVbG5vOyS\nD4odpigKZWYDZWYDep+flFoXA8trMPr8nDYbKDPpZYQjSg0uq6bSECMjvxegpdK5LU09MsfqGTWh\nH5eO70tZaQ1FO0tZ9p89VJbXkZFlp0+mHUemnV7JFhQZRQ57A8qrqTTGUC779XRYrM3E+GsGMyF/\nAPt2nGTf9pMs+WgXKelxZOf0pk9/aQc9haqq7PhyHxXGGE7GSlsKFb1BR87INHJGpuGq87Jvx0n2\n7y7lq092Y4k30C+7F+n9EkjrYyPWKv9O7dVmgrVz507mz5+P3+9n6tSpzJgx47xz3nnnHTZu3IjB\nYODuu+8mPT293dd2BrPXj1+jyPDyRfLotByJj+VIfCxGr5/EOjfJtW4Gl1Wz6p2NFGfaSXXEk9rH\nRmKyRRbvR7DeNS4SXB7WpNtlpPICtFQ6t62pR4qi0Ku3lV69rVw2JYvqShdH9pdx9GA5hSsP4XH5\n6O2Ip3dqHMlpcSSnWYlPMMsedmHEfvb3oqwXuTBNOieSrfS70kqfiZmUHa1g9/4y1q44iMflw5YW\nhy0lDmtSLNZesejPrmGU9VPR4+im47hq3OxOjJP7UBdpax+tc9uT0RRDbp6D3DwHAX+AHXtPs2/P\nKQ4WHKTyZA06vZb4FCvWxFgsiWb69okn2xEvHSLNaDXBCgQCzJs3j0ceeQS73c5DDz1Ebm4uDocj\neM7GjRs5fPgwc+fOZd++fbzwwgs89dRT7bq2syS4PJwxyihLg7YaVGMtbSzpitFyPMbM8Tgziqry\n6NhUzhRXs33PaVYVHKSuyoUpzkhsgonYBDOmeCNGqwFHipWs9Lg2k6/2llWXm2nnM3l9DDldxYbU\nBCkKE2LWeCOXXJrOJZfWd0pVV7o4eaKKk8cr2bn5BEs/raKu1kO83Yw9KZaERDNxNhNxCSas8Uas\n8UYMRp2s6eomukCAS05VsSMpLqL2vwonre/ro/C7G0bwx/8UkVDjJX77SaweH1aPD7+iUKPXMSLb\nzoAMG7azbUHaQGTq5XRzYvsZxn53GP8qOBrqcKJWW/totdYpqNFqCMSbePG0B3QGSNNj9vqJr/Bg\nLXVi8fhI10DA68dmN2Ozm4lPNBGfYK6/P8UZsMQbMZv1PTIBazXBKioqIiUlheTk+s0CJ0yYQGFh\nYZMkqbCwkEmTJgEwYMAAamtrqaiooLS0tM1rO4sUuGiqrQbVWHs2llQVBeJMPL+uBFAgIQ7FZiXW\n6yO2xo+l/AxGnx+Tz09ajAaP04PBoCPWasBsMRBr0WM0x2A0ff11otbLa5tK8Gk0+DUKfkUhoFHw\nK+BXlGBvlixG7lwBf4BhpZUcSLBQLVsahJ2GpCl7yNcbtHo8PipOOyk/XcuZ005Ki6so2l1K1Zk6\naqpc+P0qZoueWIsBU6weU0M7M8dgMOrQG3UYDDr0Bh0xem39V4wWXYwWXYwGnU6LVqeRUbJ2GHS6\nmtOm+inVouu4dVpKLFpKLGfXf6gqRl8Ai9fHBJuJijInB/eepqqijpoqN4FAAEuckViLHo9WQ86p\nOjxaBZ9Gg1dT/3+fRsGvUfApCs6KOmosMWfbgBatVpEErZtoAwHiXV4uOVXFkGtzMFqkLUUMRcGp\n1+HU6yg++9BN12Qz2G6kosxJRXkdFeVOThVXcXDPKaqrXNRUunC7fJhi9Zhj9Zgt+uDnQINRh8EU\nU39/Mtbfo/Rn71G6mK/vVVqdBp1Og1aniah22mqCVV5eTmLi19Mg7HY7RUVFrZ6TmJhIeXl5u649\n1xfvb8dX6+Vqr7vNwPct20/OqbOlYJ31VfBE91EVhRp9DDX6GE42enzONdnkplioc3pw1niorXbj\nrPHgqvNQ5/RSUe7EXefjVKWLzAonOjWANqCiVdXg/zUqqICqwFevlLFKr0WjUdBqNWi0Sv2Xpv4D\noaLUF+xwegOMKnehnm17KoACKso5P8PW/+zmiCnmbA5Xf1xR6r9V6v8TdH5bVlp4nA43/KR+HTq9\nVV+8v71pLDWN2pGqgl8Ff4BtC3fg1mo4EicFYSKFXq87O12w+TWmXq8fZ42b2moPdU4PLqcXV503\n2N48bj8etw+3y4fP68frOfvl9eP3BfB5/fh8ATTa+jam1WqCCZdGq6DVaFA0Sv2HUI1S/7im/gOp\notQ/piic/f/Z7xUFhbNt4myzaHi84XtQgu3u7E8N3wR93aSatrvktvuFOqTwP3tave9Y9pWybe9J\nElxeVjvsnfuHi7YpCq4YLa4YLRnD0xie1rS4iMfto7rSVV9M5lgVy6qOE+MPoPcHMHtVdIEAuoCK\n7uw9ZuOHO9nkD+DzBfD7/PgDKrqG9722/sNcw/tfozl73zn3vR/8nq/bgvL1e77h5+D7nFbe9+e9\n55veS9q6tXTk3tOZ9x04/97TWJXb/3W78voJVLnA7UOxGtHmptI3M4E6b/OzaETkMBhj6J0eT+/0\n5vfT9PsCwc+Eztqv71Eul5c6p4fKhvuUx4fH7cPnDQTvUT6PH39DW/UH0GoUNM3cp+rb5tm22qR9\nKiia+jbS0F5RWr5XtdZmUwd07O9FUVVVbengmjVr2Lx5M3fddRcABQUFFBUV8ZOf/CR4zh//+Ee+\n9a1vMXjwYACeeOIJbr75ZkpLS9u8trENGzZQUVHRseiFiGA2m41Ro0Zd9PNI2xE9TWe1HZD2I3oW\naTtCXJiOtp1WR7DsdjtlZWXBn8vKyrDb7e06x+fztXltY53V4IXoaaTtCHHhpP0IcWGk7QjRslZX\n6WZlZVFSUkJpaSk+n49Vq1aRl5fX5Jy8vDwKCgoA2Lt3L7GxsdhstnZdK4QQQgghhBDRpNUpglBf\nav2NN94Illq/5pprWLRoEQD5+fkAvP3222zcuBGj0cjs2bODhSyau1YIIYQQQggholWbCZYQQggh\nhBBCiPaRjTyEEEIIIYQQopNIgiWEEEIIIYQQnUQSLCGEEEIIIYToJJJgCSGEEEIIIUQnkQRLCCGE\nEEIIITqJJFhCCCGEEEII0UkkwRJCCCGEEEKITiIJlhBCCCGEEEJ0EkmwhBBCCCGEEKKTSIIlhBBC\nCCGEEJ1EEiwhhBBCCCGE6CSSYAkhhBBCCCFEJ5EEK0r86Ec/QqPRcP3115937IMPPkCj0RATExOC\nyIQIfw3t58EHH2zy+LFjx9BoNBQUFIQoMiEiS21tLQ8++CCjRo3CarUyaNAgfvCDH3D48OF2P8ft\nt9/OlClTujBKIcJDXV0djzzyCAMGDMBsNpOYmMiYMWP4y1/+EurQxEWSBCtKKIpCRkYGn3zyCaWl\npU2OvfTSS/Tt2xdFUUIUnRDhTVEUjEYjzz//PEeOHAl1OEJEpFOnTpGbm8tHH33EI488wubNm3nx\nxRepqqpi6NCh0lEhxDlmz57NvHnzePDBB9mwYQNLly7lnnvuobKyMtShiYskCVYUGTBgAGPHjuWN\nN94IPnbkyBEWL17Mj3/8Y1RVBeDMmTP84Ac/oG/fvpjNZgYPHsxzzz0XvGbp0qXodDqOHTvW5PkX\nLFiAzWajrq6uW16PEN1p/PjxDB8+nN/85jctnnP06FGuv/56UlJSSElJ4YYbbqC4uBiAqqoqzGYz\n7777bpNrTpw4gU6nY8mSJV0avxCh9qtf/QqXy8W6dev41re+RVZWFlOmTOHDDz9k4sSJ/PSnP8Xj\n8QCwbt06pk2bRlJSEjabjcmTJ3PgwAEee+wxXn/9dZYtW4ZGo0Gj0bBgwYIQvzIhusbChQv5+c9/\nzu23386QIUPIzc3l1ltv5be//W2T8z799FPGjx+PzWYjMzOTX/3qVzidzuDxyZMn89Of/pSnn36a\nAQMGkJaWxn333YfP5+vulyTOkgQrSjQkT3fccQevvvpq8PFXX32VadOm0bdv3+BjHo+H3NxcPvjg\nAzZu3Mgdd9zBr3/962BiNnnyZAYMGMDrr7/e5M945ZVXuPnmmzGZTF3/goToRqqqoigKc+fO5d13\n32XDhg3nnVNXV8fll19OVVUVn332GZ9++imnTp3iiiuuwOv1EhcXx3XXXcebb77Z5Lq33nqL9PR0\nrrzyyu56OUJ0O4/Hw7vvvsu9996LxWI57/hvfvMb9u3bx6pVq1i3bh3jx49n2LBhLFmyhHXr1vHj\nH/8Yn8/H/fffz/e//33Gjx9PSUkJJSUl3HDDDSF4RUJ0vbS0NL788kvOnDnT4jnvvfceN9xwA9/+\n9rdZvnw5Tz75JB9//DF33XXXeecdOnSIjz/+mJdffpm3336bBx54oKtfgmiJKqLCrbfequbn56su\nl0tNTExUly5dqvp8PtXhcKjvv/+++r//+7+qTqdr8fobbrhBzc/PD/783HPPqX379lUDgYCqqqq6\na9cuVVEUdfPmzV3+WoTobg3tR1VV9brrrlMnT56sqqqqHj16VFUURV22bJn66quvqoqiqLt37w5e\nt3XrVlVRFHXBggWqqqrqf/7zH1Wn06klJSXBc4YOHar+5je/6cZXI0T32759u6ooirpw4cJmj5eV\nlamKoqh/+9vf1KlTp6rXXntti8912223BdugENFs5cqVat++fVWtVqsOGzZMveOOO85rQwMHDlQf\nfvjhJo+99dZbqqIoakVFhaqqqjpp0iTVZDKpLpcreM7DDz+sGo1G1el0dv0LEeeREawoYzAYuOWW\nW3j55Zf55JNP8Pl8XHvttU3OCQQC/PGPf2TEiBEkJSVhtVr54IMPmqw9ufXWWyktLeXzzz8H6kfC\n8vLyGD58eLe+HiG6i3p2FPi///u/WblyJR999FGTYzt27KBfv34MGjQo+Hhubi7p6ens3LkTgGnT\nppGcnMw777wDwMaNG9mxYwc//OEPu/GVCBHetmzZwvTp00MdhhAhN378ePbv38/y5cu59dZb2bVr\nF9dddx3f/OY3gfqiMfv27eNPf/oTVqs1+HXnnXeiKApFRUXB55owYQIGgyH4c35+Pm63m/3793f7\n6xIyRTCqqI2mCb733nvMnTuXn/zkJ2i12ibnPfvss/z2t7/l3nvvZfHixWzZsoXvf//7uN3u4Dl2\nu53vfOc7vPLKK3i9XhYsWMAdd9zRra9HiFAYMGAAd955Jw8++CB+v7/JsYY21hKtVsvNN98cXDOy\nYMECxowZ0yQpEyIaDRgwAK1Wy7Zt25o9vmPHDgBycnK6Mywhwp5Wq2XcuHHcd999FBQU8Nxzz/Hx\nxx+zfPlyAoEAAM8//zxbtmwJfm3dupV9+/YxdOjQ4PO0dX8S3UsSrCg0ZMgQRo8ezapVq7j99tvP\nO15QUMCVV17J7bffzvDhw+nfvz8FBQXnVRm88847+eijj3jxxRdxuVzcdNNN3fUShOh2jd//v/vd\n7zhx4gQvvfRS8NjQoUM5fPgwu3fvDp63detWjh8/3uQm98Mf/pAtW7awefNm3n33XRm9Ej2CXq/n\nxhtv5K9//SvV1dXnHX/66acZOHAg48aNY8SIEcHZES0917mdG0L0FAMGDACgpqYGq9VKdnY2u3fv\npn///ud9NR6xWrVqVZOO8kWLFmE0GsnKyur21yAkwYpan3/+OadPnyYzM/O8Y4MHD2b16tUsXLiQ\nPXv28PDDD1NRUXFe78eECRMYNGgQ999/PzfddBOxsbHdFb4Q3a7x+79Xr178+te/5s9//nPwse9/\n//tkZGRw7733smnTJjZs2MAvfvELsrOz+d73vhc8b+jQoYwcOZIf//jHVFVVSceE6DGee+45TCYT\nY8aM4f3336eoqIivvvqKa6+9lhUrVvDKK69gMBh48skn+eyzz/jlL3/J1q1b2bNnD2+88QZ79+4F\noH///uzevZvVq1dz+vTpYOVBIaLNpEmTeOmllygsLGTv3r289dZbPPDAA6SlpTF+/HigftbR888/\nzx/+8Ae2b9/Onj17WLhw4XlFLkwmE7/4xS/YvXs3n3zyCa+++ip33XWXFCYLEUmwooSiKE164E0m\nEzab7bxzAB555BHuuusufvnLXzJz5kwA/uu//qvZfbJuv/12PB6PTA8UUe3c9gPwy1/+kqSkpODj\nRqORFStWYLPZuPrqq5k5cybJycksW7YMnU7X5Npbb72VLVu2cM0115CQkNBtr0OIUEpKSmLbtm18\n4xvf4IknnmDkyJHceeed2Gw2tm3bxsSJEwEYO3Ysy5cvZ8uWLUyZMoWxY8fy5ptvotfrAbjtttsY\nPXo0M2bMIDk5mb///e+hfFlCdJlrrrmGt99+m5kzZzJ8+HAefvhhRo0axZIlS4iPjwfg2muv5fPP\nP2fx4sVMmTKFMWPG8Pjjj+NwOILPoygK119/PX369OGaa67h9ttv56abbuKZZ54J1Uvr8RS1jUmb\nO3fuZP78+fj9fqZOncqMGTOaHF+/fj3//Oc/gfp1O9/97nfJzs4G4J577sFkMqHRaNBqtTz99NNd\n9DJEV3nggQf48ssvmy1bLYQQQgghQmvKlCkMGDCAl19+OdShiLN0rR0MBALMmzePRx55BLvdzkMP\nPURubm6TrDk3N5fRo0cD9cnYm2++yeOPPx48/thjjzW7J4YIb5WVlWzZsoVXXnmFv/zlL6EORwgh\nhBBCNENVVSlyEWZaTbCKiopISUkhOTkZqF+TU1hY2CTBMhqNwe+dTicxMTFNnkP+wSPTrFmzguWl\nb7755lCHI4QQQgghmtHcNHcRWq0mWOXl5SQmJgZ/ttvtTWruN1i3bh3z58/H5XI1mQaoKAq///3v\nURSF6dOnM23atE4MXXSlpUuXhjoEIYQQQgjRhq+++irUIYhztJpgtdeYMWMYM2YMq1atYu7cucFF\ndU888QQJCQkcO3aMp59+mvT0dIYMGdLsc6xZs4ba2trOCEeIiGCz2Rg1atRFP4+0HdHTdFbbAWk/\nomeRtiPEhelo22k1wbLb7ZSVlQV/Lisrw263t3j++PHjee2113A6nZjN5mD1LIfDwZgxYygqKmox\nwaqtreXSSy9td+BCRLqNGzd2yvNI2xE9TWe1HZD2I3oWaTtCXJiOtp1Wy7RnZWVRUlJCaWkpPp+P\nVatWkZeX1+SckpKS4DqrjRs3otfrMZvNuN1u6urqAKiqqmLTpk1kZGR0KDghhBBCCCGEiCStjmBp\ntVpmz57N3Llzg2XaHQ4HixYtAiA/P5+1a9dSUFCAVqulX79+PPDAAwBUVFQwd+5cAKxWa7DGvxBC\nCCGEEEJEqzbXYOXk5Jy3UVl+fn7w+1mzZjFr1qzzruvduzdz5szphBCFEEIIIYQQIjK0OkVQCCGE\nEEIIIUT7SYIlhBBCCCGEEJ1EEiwhhBBCCCGE6CSSYAkhhBBCCCFEJ5EESwghhBBCCCE6iSRYQggh\nhBAi7Pl8Aaoq6kIdhhBtarNMuxBCCCGEEKFwpqyW/btOcajoNCcOn0FV4a5fT8FglI+wInzJCJYQ\nQgghhAg7AX+At/62mvJTNQzLc3DHA5Ppm5XI3h0loQ5NiFZJgiWEEEIIIcJO+Wknplg9068bysCh\nKRhNMeSMTGPnxhOhDk2IVkmCJYQQQgghws6pkiqSUqxNHus/OJnTJ6upPCNrsUT4kgRLCCGEEEKE\nndLiapJT45o8ptNpGJibwq7NMoolwpckWEIIIYQQIuycKq4mOdV63uOXjExnx6bjqKoagqiEaJsk\nWEIIIUQXqq12s/jDnfj9gVCHIkREOVVSTVIzCVZqn3hQoeRYZQiiEqJtbda43LlzJ/Pnz8fv9zN1\n6lRmzJjR5Pj69ev55z//CYDdbue73/0u2dnZ7bpWCCGEiGaqqrLogx0c2V9OnM3EmCsyQx2SEBGh\ntsaNz+vHGm8875iiKOSMTGfHxhOk9rGFIDohWtfqCFYgEGDevHn86le/4o9//CNLlizh2LFjTc7J\nzc1lzpw5zJkzh1mzZvHmm2+2+1ohhBAimu3eUsyZ006+f9dlrC84QEW5M9QhCRERThXXj14pitLs\n8ZyRqezZVozfJyPDIvy0mmAVFRWRkpJCcnIyOp2OCRMmUFhY2OQco/HrngWn00lMTEy7rxVCCCGi\nVW21m68+2c2M7+TSq7eFvMv7sfjDnbJuRIh2OFVSTXJKXIvH4xPMJPa2cGDvqW6MSoj2aTXBKi8v\nJzExMfiz3W6nvLz8vPPWrVvHPffcw7x587jzzjs7dK0QQggRbVRVZdHCHeTmOUhxxAOQNzGTmkoX\ne7bKJqlCtKW0uIqktPPXXzV2ych0dm6SaoIi/HRKkYsxY8bwt7/9jdtuOe7IbQAAIABJREFUu405\nc+Z0xlMKIYQQEWv3lmLOlDkZNzU7+JhWq2H6dZfw1ae7cdV5QxidEOHvVHE1ySmtJ1j9ByVx9EA5\nakBGhUV4aTXBstvtlJWVBX8uKyvDbre3eP748eMpKyvD6XR2+FohhBAiGqiqylef7ubq64ei0zW9\nzaZlJJCdk8yKL/aFKDohwp/PF6CizElisqXV82KtBkzmGE6X1nRTZEK0T6sJVlZWFiUlJZSWluLz\n+Vi1ahV5eXlNzikpKQnOJ9+4cSN6vR6z2dyua4UQQohoU1vtRg2oLVY3Gzcli11bTsjifCFaUFZa\nQ7zdjC5G2+a56f0SOHZQlqCI8NJqmXatVsvs2bOZO3dusNS6w+Fg0aJFAOTn57N27VoKCgrQarX0\n69ePBx54oNVrhRBCiGhSXOWmtMYT/LnsaAUGm4niKjepcYbzzrfEGUnoFcuxQ2fom5143nEherpT\nxVXNbjDcHEe/BA7uPc3IcX27OCoh2q/NfbBycnJ45plnmjyWn58f/H7WrFnMmjWr3dcKIYQQ0aS0\nxsP9nxYFf+5T6cTi8TG6xtNsggWQNTiZ/btLJcESohktbTDcHEemnRWL9qGqaosl3YXobp1S5EII\nIYQQ9SxeH7X61vsvs4YksX93qZRsF6IZpSeqSU5tuUR7Y/EJJgAqy+u6MiQhOkQSLCGEEKITxXp8\n1LSxdiQpxUrAr1JWWttNUQkRGVRVrR/BaqOCYANFUXD0S+DYIVmHJcKHJFhCCCFEJ4r1+tscwVIU\nJThNUAjxtepKFxqtQqy1+em1zUnvZ+fYoTNdGJUQHdPmGiwhhBBCnF/MooHH/3U1QJ0/gDag4ta2\n3X+ZNSSJ1Uv2M3ZS/06NU4hIdqqkut0FLho4+iWwYeWhrglIiAsgCZYQQgjRDucWs2jwu2mZwe/r\n119poR2L7fv0T+Tjv2/BWePBbNF3aqxCRKpTxdUkpbRv/VWDXskWXE4vtdXuDo18CdFVZIqgEEII\n0Unq11+1r+9Sp9OQkZXIgb2nujgqISJHaXH7Kwg2UDQK6X1tMk1QhA1JsIQQQohO0p71V41lDU5i\n/y5ZhyVEg4qyWuxJsR2+Lr2fXTYcFmFDEiwhhBCik1g8PmrbqCDYWOagJI7sL8PnC7R9shA9QJ3T\nizm241Nm+2QmcOywjGCJ8CAJlhBCCNFJYr0+ajowghVrMZCYbJGedyGoL9FeV+vBZO54gpWcFkdF\nmRNXnbcLIhOiYyTBEkIIITqBNqCi9weo07V/BAvOThOUcu1C4PX6QYEYfcfaEIBWqyG1j43jMool\nwoAkWEIIIUQnMHt9OGN07aog2FhGViJHD8gIlhB1td4LGr1q4OiXwHEpdCHCgCRYQgghRCeweHzU\ndGD9VYPeaXFUVdThrD1/jy0hepI6pwfTBay/apCWYePEkYpOjEiICyMJlhBCCNEJOlpBsIFGqyEt\nQ3rehahffxVzwdenOOI5eaKKgF+KxojQavNOsHPnTubPn4/f72fq1KnMmDGjyfHly5fz4YcfAuBw\nOLjuuuvIyMgA4J577sFkMqHRaNBqtTz99NNd8BKEEEKI0Iv1+CixGC/o2j6ZCRw9WM6AS3p3clRC\nRI46p/eiEiyjKQZrvJHTJ2tITuvYZsVCdKZWE6xAIMC8efN45JFHsNvtPPTQQ+Tm5uJwOILn9O7d\nm8cffxyz2czSpUt56aWXeOqpp4LHH3vsMSwWS9e9AiGEECIMWLy+CxrBAnBk2vnyo12dHJEQkcXl\nvLAKgo2l9rFRfLRCEiwRUq1OESwqKiIlJYXk5GR0Oh0TJkygsLCwyTkDBw7EbDYDcOmll1JWVtbk\nuKqqnRyyEEIIEV4UVcXo83doD6zGUtLjOXO6VkpMix7NWeu9qDVYAKl94jlxtLKTIhLiwrSaYJWX\nl5OYmBj82W63U17ecqWjxYsXk5eXF/xZURR+//vf88ADD7B48eJOCFcIIYQIP2avH5dOi9rBCoIN\ntDopMS1EnfPi1mABpJ0dwRIilC5sLkMztm/fzvLly3nyySeDjz3xxBMkJCRw7Ngxnn76adLT0xky\nZEhn/ZFCCCFEWIj1+KiNubhbasM6rKzByZ0UlRCRpa4TRrB69bZQXenCVefFaLq4ZE2IC9XqCJbd\nbm8y5a+srAy73X7eeYcPH+bll1/mwQcfJDY2Nvh4QkICUF/8YsyYMRQVFXVW3EIIIUTYsHh91FzA\n5qiNOTLtHDsoI1ii56rrhDVYGq2G3mlxlByTaYIidFpNsLKysigpKaG0tBSfz8eqVauaTAEEOH36\nNM8++yw/+9nPSElJCT7udrupq6sDoKqqik2bNgWrC0aSstIaPG5fqMMQQggRxmI9/osewUp1xMs9\nR/Ro9ftgXfyoU32hC0mwROi0mmBptVpmz57N3LlzefDBB5kyZQoOh4NFixaxaNEiAP71r39RU1PD\nK6+8wgMPPMBDDz0EQEVFBY8++ij3338/f/7zn5k5cybDhw/v+lfUiQ7sOcU7L67hpf9eyn/+vY1j\nh85I0Y4WDB8+nDNnWu95bc85neWpp55i4sSJXHHFFdx1110trh0cPnw4l19+OZMmTWLatGkdvl6I\nixWpbae2tpa7776bSZMmcdlll7F+/XoAdu3axZVXXkleXh633XZbsKMt2pl9PpwXWOCigS5GS+/0\nOFmH1U7h1nYeffRRxo4dy+TJk3nooYeoqqpq8Vy/38+kSZO46aabgo/11LbTWF2t96JHsKC+0IWs\nw2pZJLYdl8vFtGnTuOKKK8jPz+eFF14IHlu4cCHjxo2jV69ebNmypVtibkubGw3n5OTwzDPP8Oyz\nz3LNNdcAkJ+fT35+PgB33XUXr7/+Os888wzPPPNMcK+r3r17M2fOHObMmcOjjz4aPD9SnCqp5rN/\nbeP6H43iJ7+cSGKyhS/e386Cv6ySKk/NUNqxsFtRlG5LUH/+85+zfPlyCgoK6N+/Py+++GKLMX30\n0UcsW7asSSGW9l4vxMWK1LZz//33M378eJYtW8aKFSsYNGgQAM899xw///nPKSwsJDc3lz/96U/d\nEneo6f0BPNqLS7AAHP3sHD0oHTrtEW5tZ8qUKaxevZolS5bgdDpbfe+/+OKLDBo0qMlr6Kltp4Gq\nqtQ5PRgvssgFfF2qXTrFmxeJbcdoNPLhhx9SUFDAxx9/zFtvvcWBAweA+lzlzTffZPz48d0Sb3u0\nmWD1RLXVbt5fsIErvzGYtIwEYq0GRk/M5Mf/dTlpGTaWfbYn1CGGzC233MKUKVOYNWsWCxcuPO/4\nkSNHuOyyy/jZz37GiBEj+NGPfoTL5QoeX7BgAZdffjk33ngjhw8fBmDDhg1cddVVTJo0ibvvvpuD\nBw9edJxWqxUAn8+H0+nEaGx588/mfoF05HrRvIpyJ26XTHVqEE1tp6qqitWrV/ODH/wAAJ1OR1xc\n/Z4zK1eu5Oqrrwbg6quv5qOPPrromCJBfYJ1YRUEG+sj67DOEyltZ8qUKWg0GjQaDVdeeSUnTpxo\n9rzjx4+zePFibrnllib3n57adhp4PX60Wg0xFzkSDGCNN6LVaag80/NGARuLtrbTsC1UbW0tfr8f\nvb5+tHPgwIFkZ2dfdBydSRKsc3i9fha+tZFLLk1nyPC0JscURWHSjEEcKjrNoX2nQxRhaP3lL3/h\nq6++4s033+TRRx+louL8Ifh9+/Zx1VVXsXbtWgKBAF988UXwWF1dHStWrGD06NH84x//AOobxqef\nfsqyZcvIz8/nscceO+85q6urmTRp0nlfkydPZu/evc3G+uSTTzJ48GDWrFnDvffe2+w5iqIwa9Ys\nJk2axPz58zt8vWjelrVHePOvq3jtuQI2rzlCwB8IdUghF01t5/DhwyQmJnLPPfcwfvx4fvGLXwSn\nM02ePJl3330Xt9vN3//+d44fP34hf10Rxe/11///Aku0N5aWYaO0uBqPRzonGkRS22mwYMECZsyY\n0eyxhx9+mMcffxyNpulHsJ7Ydhpz1l58ifbGUvvYKD7Ss6cJRlvbCQQCTJw4kUGDBnH77bfjcDg6\n8LfRvTqtTHu0WPrpbuITTIyf2nwmrDfomP6tS/ji/e386BeXozf0rL/C9957jw8//JBTp05RVVXF\n/v37GTVqVJNz4uLi+MY3vgHA9ddfz5dffsk3v/lNAG688UYAJk6cyJw5c4D6ebVPPfUUK1euRFVV\nvN7zp2BarVaWLVvWoVh/+9vfct999/Hkk0/y2GOP8Yc//OG8cz777DNSUlLYs2cP3/ve9xg4cCDj\nxo1r9/WiKb8vwJKPd3H0YDk33z0Or8fPsk93s3H1YSZfM5j+g5JCHWLIRFPb8fl8bNq0if/3//4f\nc+fO5b777uODDz7gxhtv5Ne//jV//etfmT59OjNnzgz2MEYzr8uLR6uBTkiwYvRaklOtFB+poG92\nr06ILvJFUtsBePbZZ7FYLHzrW98679jnn39OUlISw4YNY8WKFU2O9cS201id8+JLtDfWUOhiyIi0\ntk+OUtHUdgA0Gg3Lly/nyJEj3HDDDYwdO5Zhw4Z1+M/pDj0rO2iDz+tn95ZifnLfxFbnp2YOTCIj\nK5GCz/cy7Zs53RhhaB06dIjXX3+djz76iISEBCZNmoTb7W7zusZ/lzabDYCYmJjgta+99hoJCQks\nWbKE3bt3c8stt5z3HNXV1cycObPZf5eXX345uP7jXGazmR/84AfcddddzR5vqHw5aNAgZs6cyYYN\nG4IJVnuuF1+rrXbz4TubMJr13Dx7HAZj/a+X7942mgN7TrFo4Q6mzBzMwKEpbTxT9Im2tpOWlobd\nbg9OZ/r2t7/NP/7xD2688UYyMjJ45plnACgqKmrSGxqtvHU+PJrOmxDSJ9PO0YNnJMEi8trOO++8\nw6JFi5qdjgWwbt06PvvsMxYtWoTb7aa6uprZs2czb968Htl2GqurvfgS7Y2l9oln2faSTnu+SBNt\nbaexjIwM8vPzWblypSRYkeBQURlJqVZiLYY2z518zWDe+J8VDM5NwZF5/t5g0aikpIRevXqRkJDA\nmjVr2L59e7PnVVVV8cknnzBt2jTee+89vvOd77T6vMXFxcGkZsGCBc2eY7VaKSgoaHes+/fvJysr\nC5/Px7///W9ycs5PhJ1OJ36/H6vVyunTp1m8eHGwSEt7rhdNLf5wJymOeCbPGIyi+fqXqqIoZA1O\nxmDQ8fE/tpCRldjjNn+MtrbTu3dvMjMzKSws5NL/396dh0dV34sff5/ZMskkk8lkIRuBEBL2RQib\nqCCLBam11Wpttb+2lvYW0dt7b2uveh9v9+pVfGwfFXprF1Hsom3d9Sq4geJCIKxhCztZIfs+M+ec\n3x9DYgLZM/t8Xs8zD2Ryzvd8A/PJOd/t8501i82bN7No0SLAu3VHSkoKmqbxyCOPcPvttw/62uHK\n0zmC5SNZY5PYsXXk6xoiQTjFzpYtW3jsscd47bXX+ly3e//993P//fcD3jVXjz/+OBs2bACiM3a6\n81WK9k6jsuycr2rG49EwmaJvRUykxU5NTQ0mk4nExERqa2vZsmULDz744CXHhUpik+j7xPXj6IFK\nCqYMrnfdGmtm6Rcm89aLB9C10PjP9Lf58+eTnZ3NvHnz+O1vf9v1QHWx/Px83njjDebNm4eiKFxz\nzTVAz14RRVG6vv7ud7/LU089xZIlS8jKyhpUdpuB/OxnP2PhwoWsWLECj8fDL37xC8D7i+ErX/kK\nANXV1axatYqrrrqK1atXs2bNGpYsWdLv+aJ3zY3tnD5Ww8Jl+T0aV91l5zoZP2kU771+KMC1C75I\nix2A9evXc++99zJnzhwqKiq44YYbAPjHP/7B3LlzWbJkCfn5+Xzta18bcZ1CnbvNjduXDawxDirL\nGlA9snYxnGLnnnvuoaWlhS996UssWrSIH/7wh8ClsdNd9+tGY+x056sU7Z0sFhPOlDiqy/tOlx/J\nIi12Kisruf7667nyyiv5zne+07VNCMCrr77K1KlTKSoq4pZbbuGmm24acZ1GStFDpKn39ttvM2vW\nrKBdX1U1NvzqXb7xrwtJSBxcxjhd19n0xEdcvmw8eRPT/FzD8HD69Gm++tWv8uGHHwa7KiFv165d\nLF26dMTlBDt2AD565xhNDW1c86Wp/R7X0e7hqd98wIobpzFmfHKAahceJHYGz1exA0OLnz3lTdz9\neukl769OiWHr4fMcSU7o8f7D145nRmbCJccPxtOPfcjSL0wma0zSsM6PJhI7gxes2BmMbW8dwWQy\nsGCJ77LBbX7xAM5UG7MXjvVZmZFEYmfwhho7MoJ1wZnjtSSlxA26cQXeFv3shWPZ+eEpP9Ys/Pii\nN0OED03T2Vt0hhnzcgY8NsZqYtn1k3nrhf2SJa0XEjvhye3jKYLgnSZ49qSkax8siZ3w5+s1WAAZ\nOQ7KozyT4EAkdvxDGlgXHNlfSf4gpwd2N2FaOrXnmqmuiM4h6Ivl5ORckhlJRLYTR85hi49hVKZ9\nUMfnTUwjM8fBh1suHQmIZhI74cvT5vsGVvZYJ2XSwBoUiZ3I4OssguDd9qD8jDSw+iKx4z/SwMLb\nA19aUk3B1FFDPtdoMnDZ/BwZxRJRa++nZ5gxd/SQzrl61SRKdpVRX9vqp1oJETju9qFlEaxo7GBP\nedMlr4rGzzJ8ZY9NouxUXdSs8RWirdW3+2ABJCXH4XGpNDW0D3ywED4kDSyg7GQd8fYYHM64YZ0/\nfe5oSkuqaG6M7AA+ffo0CxcuHNI5f/nLX6is9G+a1DvvvJMJEyb0W7fnn3+eK6+8smtxZElJCeDd\nz2HZsmVcddVVLF++nPXr1/u1rpGmsb6NslP1TJg+tNHfuHgL0wqz2fnhSf9ULMSEc+yAN/HFFVdc\nwfLly3tsErl9+3YWL17MFVdcwe9+9zu/1jWUDXWKYHWzi7tfL73kVd3s6jrGlhBDnM3C+apmf1Q5\nbERq7MyYMYMrrriCRYsWsWzZMr/WNZR172yoa+jgdIu7z06H4VAUJWqnCYZ77IB33VNqaiqvvPJK\n13stLS1dCS7mz5/Pjh07/FndYZMGFnDkwPCmB3aKjbMwcUYGuz8548NaRYZABOutt97K888/3+8x\nY8aM4bXXXmPbtm0sWbKE73//+wBYrVZefvlltm7dyquvvsqmTZs4fvy4X+sbKSoaO9jy7nFSxydz\n8HzbkG+Isy4fw8HdFbS1ugY+OAqFSuxs3ryZ/fv388EHH/DAAw+wdu1aAFRV5a677uLpp5/m3Xff\nZdOmTRw+fNiv9Q1Vvs4i2Mm7DqvW5+VGulCPHfA++L/yyiu8//77bNmyxa91DWXdOxtqG9p5cPvZ\nPjsdhkumCQ5eqMQOeO8xP/3pT1m6dGmP1Ot33303l19+Oe+//z4ffPBBn3s5BlvUN7B0TefogapB\nTw/sa2qHbXwqOz8+za7T9T7pdQlVmqZx1113MXPmTL75zW/S3u4dtdu9ezfLly9n3rx53HDDDdTU\n1PDSSy+xe/du/uVf/oXFixfT3t7OQw89xLJly1i6dCnr1q3zSZ0WLFjQtRleX+bOnYvd7l0jdM01\n11BeXt71vbg478hlS0sLqqpisfh2DnikqmzsoGRXGX+rcw3rhhhvtzJ+chq7Pz7t55qGhnCNnTfe\neINbbrkFgMLCQhobG6mqqmLnzp3k5uaSk5OD2Wzmhhtu4I033vBJvcKNp82Dy+j7heLZkugCiKzY\nqa6u7vp+iCRxDg26jlnV/NJRkTnaQUUUjmBB+MYOeDck/sIXvkBy8mcZhxsbG/noo4+47bbbADCZ\nTF3PdqFmwE9ySUkJ//mf/8kPf/jDXm+e27Zt4+677+buu+/mN7/5DadPnx70uaGgsqwBS4yJ5LT4\nQR3f19SOn3xURpmi8NjfD/is1yUUHTlyhM997nN88sknaJrGW2+9hdvt5s477+Spp57ik08+YdWq\nVWzatInrr7+emTNn8rvf/Y733nsPq9XKd7/7XbZs2cJbb73Frl27ePPNNy+5xt///ncWLVp0yetb\n3/qWT36GjRs3cu2113Z9rWkaV155JRMmTGD16tVkZ2f75DqR7vypWtpMRpotw58zP+fKXIo/Oo3b\nrfqwZqEpXGOnoqKCrKysrq8zMzOpqKigsrKy1/ejjfHCGinVD5m4ssc6veuwovxBPNJiB7wjWNdf\nfz2LFi1i48aNw75GpDBpOqqioPshjtKzE6muaMIThfvKhWvslJeX88Ybb3Rttt2Z6fDUqVMkJyez\ndu1aLr/8cr7//e/T1tY27Ov4k6m/b2qaxoYNG7j//vtxOp3ce++9TJs2rccD6KhRo/jpT39KXFwc\n7733Hv/7v//LL3/5y0GdGwpKS6rJnzL05Ba9OW2Po6C2mTL78NZyhQO73c7nP/95AG688Ubefvtt\n8vPzOXPmTNemiKqqkpPzWcru7g8HxcXF/OlPf+Lo0aM0NjZy6NAhPve5z/W4xpe//OUBdxIfrm3b\ntvHcc8/1+CVhMBjYtm0bp0+f5uabb2bevHlMnz7dL9ePJLWn66m2xYyojOS0eDJGJ3JgVxkzB5Hm\nPZyFc+xE+wN+fyyqhinWBH54MEx0xqLr0FDbhiM5cu8rA4nE2HnjjTdIT0/n8OHDfOUrX6GgoIAF\nCxb4/Prhwqz5Z/QKwBLz2YbDmTkDj5xEknCNnfvuu4///u//7mpYddbJ4/FQXFzMD3/4Q9atW8d/\n/Md/8NJLL3WNFIeSfhtYpaWlpKenk5bm3UR34cKFFBUV9WgkFRQUdP191qxZ/PWvfx30uaGg4kw9\nhVfm+qSs2lgLZk0jocPtk/LCha7rJCUl8f777/f6/e4Bcs899/CnP/2JyZMnc99993UNV3f3/PPP\n8/jjj1/yfm5uLk899dSw63ngwAH+/d//neeee47ExMRLvp+Tk8Py5cv58MMPpYE1CHUVTdRbRz6d\ncs6VufzfP/czfc5oDIbo2o8jHGInIyODsrKyrq/Ly8vJzMzE7Xb3eL+srIzMzMxhXSOcmVUNs7X3\nUVyjwbs58cVc6uB60hVFuTBNsDaqG1i9CdfYycjIACA93bvue8KECaxatYqdO3dGdQPLomq4/TDN\ntlNnootoa2D1JhxiZ8+ePaxevRqA2tpatmzZgtlsZtasWTidTlasWAHADTfcwN/+9rfwa2DV1tb2\nmPvodDopLe1775otW7ZQWFg4rHODQdd1qsobB71/z4AUhfL4WDKbQnO40hcaGxt57bXXWLZsGf/8\n5z/58pe/TH5+PgAvv/wy1113HR6Ph2PHjjFx4kTi4+M5d+4cAB0dHTQ3N5OTk9M1/PvVr371kmvc\ndNNN3HTTTT6t99mzZ/nGN77Bb3/7W8aNG9f1fk1NDSaTicTExK4gfvDBB3167UjU0e6mraGNxmzb\niMvKGptEbJyZ0pIqCqYOP9lMqAvX2Fm5ciVPPvkkN954Izt27MBut5OWlobT6eT48eOcPn2a9PR0\nXnjhBZ588kmfXjscWDQNc2zvDayGdpWfbjlxyfs/Xjb4Tr3ODYenzg6tzslAirTYaW1tRVVVEhIS\nOH/+PFu2bOGBBx7w6bXDjVnVh7TVwVBl5jg4dvCc38oPVeEaO8XFxV1/X7t2LStWrGDlypWAt+FW\nVFTErFmz2Lx5M4sWLfLptX3FZ5/m/fv3s23btl7/8UNVQ10bZosRW8LIpjl1V54QS0ZzO9ogeyjD\niaIo5Ofn88YbbzBv3jwUReGaa67BbDazadMm1q9fz9y5c1m0aFFX2syvf/3rPPTQQyxevBiA73//\n+yxbtoxvf/vbLF++3Cf1Wr16NStWrODYsWNMnTqVZ599FoCnnnqqq/fkoYceoq6ujh/84Ac90uJW\nVlZy/fXXd6Vv70z9GckGswfPQMpO1WNPi/fJfHlFUZhzZS47tl36IBopwjl2li9fzpQpU1i4cCH3\n3XdfV0+lyWTiscce4+tf/zpXX301t956a8hmc/Ini6phtvbbVzkio6N8w+FIjJ3q6mpWrVrFVVdd\nxerVq1mzZg1LlizxSb3ClcWPUwTB28CqiLJMguEcO/1Zv3499957L3PmzKGiooIbbrjBJ/XyNUXv\nZ3L9kSNHeP755/mv//ovAF544QUUReGLX/xij+NOnTrFI488wn333dc17D3Yczu9/fbbzJo1yyc/\n1GAd3ldJye5yvvT1wV93T3kTd7/e/0hcYXktixeP45qrfDP1UESmXbt2sXTp0hGXM9TY6esz/PC1\n45mRmTCoMra9dYTqZhf/W3vpdNihlNNJUzWeXLeVG/7fbFIzhnauiD6+ih0YWvz0Fjtj61tYlJ3A\nxuZLO9V+vCy3zxGs3t7vLXZ0TefxX7zN7f9+pU87A0V0Clbs9KUzpsbUtxCjahxJ7vn5H879pDe6\nrrP+V+/y9bULsDtiR1yeiD5DjZ1+uwvy8vKorKykuroaj8fD9u3bu6YAdjp//jyPPPIId911V1fj\narDnBltVeYPvpgd2U5YQS9nB6oEPFCJMlZ2sI8mHsWMwGpg6O4u9O2QvORFeLP2swfIFxaB0TRMU\nIlKZNQ23H6cIKori3Q8rStO1i8Drd16D0WhkzZo1rFu3DlVVWbp0KdnZ2WzevBnwDn///e9/p7m5\nuWvuvdFo5IEHHujz3FBSVdbIrMvH+L5cm5WGihqaGtpJSLT6vHwhgsnj0agqbyT/mgLYX+OzcqcV\nZvP0Y9u5asUEzBajz8oVwp8sqoY51gT4b+/D0blOTh+vYcK0yF2jKKKbRdVpiPFvkqPOaYITp2f4\n9TpCwAANLIDJkyfz0EMP9Xiv+zzM733ve3zve98b9LmhQtd1qsq8CS4qGjsGvW/VYLI/aQaFUXkp\nlOwuZ96icQMeL0Q4qSprICnFhsni23UndkcsmTkODu+vZOqsrIFPECIE9JdF0FdyxjnZV3TWr9cQ\nIpj8tclwd5mjHWx987BfryFEJ/+tzA1xjfXtGE0G4u1Wjg1iXVVx9dAyAAAgAElEQVSnwWZ/ypyU\nxv73jzH3qtyulJdChKOLOyBO7qskJsXWZ2dDX6mp4y1Gml2XbiicFm8hw+5dWzJ97mg+ff+4NLBE\n2PDug+XfBlZqhp3WZhfNje3E22VWhAgfA3Vgd95HLMOcIthf+d3vLQCjsu2cq2zG41YxmWWWhPCv\nqG1gVZX5Z/1Vp8T0BBQUyk/XkzUmyW/XEcLfqptdPTogZlbWUREfy/fU3vPj9Jeauq+F/Z03wXEF\nKWx56QDnKptITZdkFyL0WTT/ZhEEMBi8+2GdOVHLpBnRt9eYCF8X3z8u1tlpbVY1XMMYweqv/O73\nFgCLxURyqo2q8kZ5LhN+59/x2BBWXd7IqCz/NbAURWHK7CwO7Cob+GAhwoWu42h3U+enKVHeZBfZ\n7Nsh06FEGND1C2uw/DuCBTB6nJMzx2v9fh0hgsGiargDsNG8JIwRgRK1DaxKX24w3IfJMzM5sr8K\nj/vSaVFChCObW8VjMOAy+W96xbTCLA7uKcctcSNCnPHCLicGk/9vpTnjkjktDSwRiXQdk6b7fQ0W\neBPGnDkhcST8LyobWF0JLrIS/XqdhEQraRkJHDsUfbuHi8iU1O7y2+hVp8SkOEZlJ3J0f5VfryPE\nSFlUHZfREJB1timj4uloc9PU0O73awkRSCZNRzUoPtm4fiBZY5MoP1WPNoiEZUKMRFQ2sJobO1CA\neLv/N22cfFkmJbvL/X4dIQLB0e6m3s8NLIDphdmyJ5YIeWZVw+XHvXu6UwwK2RfStQsRSSwBjKM4\nmwW7w0pVeWNArieiV1Q2sKrKGkjLsgek17FgajpnT9TS2jK4NPBCBEtn9r+LX92zBXpHsCx+r0ve\nxDRqz7VQd77F79cSYrgsw1yYP1w5sg5LRCCz5v8U7d15pwnKOizhX1GZRbCqvJF0P6+/6mSJMZFb\nkMrhvRVctsD3mxoL4Sv9Zf8DiPGoGDWd1gCktzWaDEy6LJP9u8q48poCv19PiOGwBPrBcFwyRR+c\nDNj1hAgEi6rhNgZuO5vsXCcHdpUx96rBbbsjxHBE6QhWI2kBamCBTBMUkSGxw02D1QwB2tdt2oUs\nnJrWezp4IYIt0CNYyWk23C6Vhrq2gF1TCH8zq3rApggCZOcmUXaqTu4twq+is4FV7v8EF92NHZ9M\nQ10btTLdSYSxeJeHJkvgBr1TRiWQkGjl5NHzAbumiE61re4er5ZeNsTuTaAbWIqiXEjXLuuwROQI\n9EiwLT4GW0IM5ypkHZbwn6hrYDU3tqOpGnaHNWDXNBgNTJqRQUmxjGKJ8BXv8tAcwAYWwNTZ2ezf\nKXtiCf9a88KhHq/SmtZBnRfoBhZ498OSdO0ikgx3k+GRkHTtwt+iroFVVe6dHhiIBBfdTb4si5Ld\n5egyJC3CVEIQGlgTp6dzqrSmK0lMRWNHr4k4Kho7AlovEVnq2jw9XtogMzgHMvtZp85EF7ou9xIR\nGcxaYDYZ7m70OEl0Ifwr6pJcnK9qJjU9IeDXTctIwGw2UnaqjuxcZ8CvL8RIGDQdq0elxRzYXxkx\nVjN5k9I4uLuc2QvHUt3s4u7XSy857uFrx5MRgG0XhOguGD3vSSk2dF2nvqaVpBRbQK8thD+YNR1P\ngDsqRuc62fJSCbqmowS4cSeiw4BPSyUlJWzcuBFVVVm6dCkrV67s8f2ysjLWr1/PyZMnueWWW7ju\nuuu6vrd27VpiY2MxGAwYjUYeeOAB3/8EQ1R7rpmsMUkBv66iKEyZlcmB4nJpYImwY3N7aDWZArIR\n5MWmzs7inVcPMutyycIpQkug146A914yNj+FE0fOSwNLRASjpuPxQyOnc+uRvphjTZyraiItI3BJ\nz0T06LeBpWkaGzZs4P7778fpdHLvvfcybdo0srOzu45JSEjg9ttvZ8eOHb2W8ZOf/IT4+Hjf1noE\nas+1MG129sAH+sHkmZk89ZsPWfL5SZgt/k91LYSveNdfBeczO3qsE7dLpaqsEQLcyylEn3T9whqs\nwHc65Baksn/nWel0EBHB5KcGVl9bj3T6VrqdsydqpYEl/KLfp5XS0lLS09NJS0vDZDKxcOFCioqK\nehxjt9vJy8vDaOz94SuU5onruk7d+VaSUoPT6xdvt5I+OpHSkqqgXF+I4fKuvzIH5dqKQWHqrGz2\nFUmyCxE4va33677ptvHCvU0NwqjumPHJlJ2qw+0eXLZDIUKZSdMCPkUQICnLzpnjsg5L+Ee/n+ja\n2lqSk5O7vnY6ndTWDj7riqIo/OxnP+NHP/oRW7ZsGX4tfaStxQ1AnM0StDpMvSyL/bvKgnZ9IYYj\nGBkEu5s6O4vD+ypR5YFSBEjner/uL5f6WYehRdW966+C0MCyxppJvdD7LkS489cI1kCSshI5e7JW\nko8Jv/DrE9PPf/5zkpKSOHv2LA888ABZWVlMmjTJn5fsV+35FpJS4gKeQbC7vMlpbHm5hKaGdhIS\nA5cqXoiRCPQeWBdLSLSSOcZBVansiSVCQzAyCHaXOyGFE4fPk1uQGrQ6COELJk1H7aOBNdA6qu6j\nykNljY8hJtYs67CEX/T7xOR0Oqmp+WxDw5qaGpzOwSdoSEryJpPIzs5m7ty5lJaWBreBda4ZZ5Cm\nB3Yym41MmJZOSXEZ8xbnBbUuQgyGp8ODSdNpNwV3/dP0OaN5d/NRiIsLaj2EgOBkEOwutyCVV/+y\nGwjePVWIkdJ1HaOu4+mj43ugdVQ/XpY7ouvnXkgYIw0s4Wv93h3y8vKorKykuroaj8fD9u3bKSws\n7PXYi9dadXR00NbWBkBjYyPFxcXk5OT4qNrDU3u+BWcIZF2aMiuTA7vKQ2p9mhB9aa1t9U4PDOLI\nL8C4ghTaGtuxuTxBrYcQEJwMgt2lZSTgcqnUD3JTZCFCkepWvesYg3R/yZ2QyonD54JybRHZ+h3B\nMhqNrFmzhnXr1nWlac/Ozmbz5s0ALF++nPr6eu69915aW1sxGAy8/vrrPProozQ0NLBu3TrAm2lw\n1apVzJgxw/8/0QUVjR1UN7t6vHfyTAOZk0ZdMtw8kiHm4cgY7UBHp/JsAxmjHQG9thBD1dXACjKD\n0UDWpFFkH63lcErg97ITojtLkEewOtO1Hz9yjlkLJJugCE+qSw3K+qtOo3OdvPrX3XS0u4mxBieR\nk4hMAz41TZ48mYceeqjHe8uXL+/6u8PhYMOGDZecZ7Vaefjhh31QxeHpbUPShWWNvOQx0HK4Z9aY\nkQ4xD5V3T6ws9u8skwaWCHmtta1BXX/VXebkNDKKyzjqjEeTzSFFEAWqgdVbZyFAWryF3IIUDhSX\nSwNLhC3VHdwGltliJHNMEieP1jBhWnrQ6iEiT2g8NQWAoutYPSqt5tDYf2ryzEyefmw7V6+aiClE\n6iREb1pr20JiBAsgLjGWphgzaa0dVMZLkhgRPBZVo9ns/7jorbMQ4OFrx1MwPpk3/7kfj1uV+4gI\nS6pL7TPBRaCMK0jhxJFz0sASPhUaT00BEOtW6TAa0QM0z3egzDcAcSk2tnxwihmzs8iwxwSkXkIM\nia7TWtdKc8bgk9v429mEWLIb26SBJYLKrGm4g7DJcHexcRZS0xM4c6JWsgmKsOQdwQpuAqXcglQ+\n3XoCXdeDmmVaRJaoaWDZ3B5aAtjDN1DmG4BRHTqjt50gY0KqNLBESIpRNQxGQ1AX81+s2hbDpPON\nxLo9tAVgBEGI3phUPegPhuB9ODxxRNK1i/CkutQ+MwgGSlKKDZPZyLlKSdcufCf4d4cAsblVWkJk\nmlOnaluMt151kgVKhKYEl4c4Z2ilRdcVhfILo1hCBEsojGDBhf2wjkgWNBGegr0Gq1NuQYpkExQ+\nFTUNrLgAj2ANhq4olCVYObu/KthVEaJX8SHYwAI4Y48lq6kNgyZbHYjgMGs67hAYwRqVYcftUqmp\nbg52VYQYsmBnEezUORIshK8E/+4QIDaXSmsITicqS4il4nA1Hrca7KoIcQlvAys22NW4RJvZREOM\nmfTm9mBXRUQjXcekaSHRwFIMCgVT0jm8rzLYVRFiyFS3ihoCcTR6nJPqikba29zBroqIEMH/VAdI\noNdgDVab2YQ9NZ4jB2QUS4SeUB3BAjiTGEdOYyvIht0iwAwXPnJa8DveAZgwPZ0j+6WBJcKPJ0RG\nsMxmI1ljkjhVWhPsqogIEXpDOn5gVjUUnaBuCtmfrKnp7P30DJNnZga7KkJ0UXQdm9tDbFLojWAB\nnI+1MEHTSeyQHkcRWGZN8ya4CJGMY5mjHbS3uampbiY5LT7Y1RFR5Lm9VZyo6X097MysBNLjLf2e\nHypTBKFzmqCkaxe+ERUNrDi3h1aLMWRuhhdLHZvEsQ9OcL6qmZRRcnMUoaFzawOjKfRGfgFQFM4k\nxpLTIMkuRGCZNQ13iDwUwmfTBI/sr2TBkvHBro6IIsVlTews631LGqvZMHADK0SSXIA3Ycwn7x9H\n13SUEKmTCF+hOaTTC1XTqWt1D+rV2OHpca7NrdISguuvOhmMBqbOzmJf0ZlgV0WILvFuDy2WEG1c\nXVAeH0tKWwcdLa5gV0VEEbMaGgkuuiuYls5hmSYowow3TXtoxFJSso1Ym5my0/XBroqIAKHb6rhI\ni8u7r1RV88APUt+Zm0lynLnra5srNNdfdTetMJtn13/EFcsLMIf4Q62IDjaXSnMId0wAeIwGKm1W\nzh6oZG5+crCrI6KEKURStHeXleOgvdVN7blmnKkyE0KEB2+Si9C5z0yclsGhvRVkj00KdlVEmAuN\nboNBqm1zU9M68Kvdo/U4L84dmhkEu3M448jMcVBSXBbsqggBXEgME2J7x/XmTGIsZQeqUFVt4IOF\n8AGzFhqbDHenGBTyp4zi8D5JmCTCRyitwYILCWP2VaLJ/USMUGjdIfzEFgZTnQAKr8hl54en0GVv\nHxECQjXz5sWaLWbiHLEc3ivTo0RgmNXQSNF+sQlTJZugCC+htAYLvNMEExxWzpyoDXZVRJgbsHu6\npKSEjRs3oqoqS5cuZeXKlT2+X1ZWxvr16zl58iS33HIL11133aDPDQRF14n1qLSaQr8nPjs3CbPF\nyPEj58ibmBbs6ohopuvYXKG9drG7sbOy+HTrcSbNzEAJ0WQ2InKYNT3kpggCZI1JorXFJdMERdjw\njmCFVmfFxOkZHNpbyZjxKcGuighj/X6qNU1jw4YN/OAHP+DBBx/knXfe4ezZsz2OSUhI4Pbbb+/R\nsBrsuYEQ61FxGQ1oIdRD0hdFUZh9xViKPjgZ7KqIKBejaqgGBU+Ibm1wseQcBwaDwvHD54JdFREF\nQmWT4Yt5swnKNEERJnQ95KYIAkyYls7RA1WoHpkmKIav3ztEaWkp6enppKWlYTKZWLhwIUVFRT2O\nsdvt5OXlYTQah3xuIMSFUS88eAO77nwLVeWNwa6KiGLxYZAYpjtFUZh71Tg+ff9EsKsiooB3imBo\nPRR2mjAtnUN7K9BlA24R4gw6YAA9SLMOjAbYU950yetEqwerw0rx3oqg1EtEhn5bHrW1tSQnf5aZ\ny+l0UlpaOqiCR3KuL4XLOpJORqOBWZePYeeHJ7n2punBro6IUja3SnMYJLjormDqKLZtPsLZk3WS\nAUr4lVnT/TK62/nA151riIvts8YmoaoaFWcayMxx+LJ6QviUSdMwBvH5rKHdm526N6NdELuvksJZ\nWQGulYgU4fUENQxxYfigOH3OaH6/bitNDe0kJFqDXR0RhWwuT1DjpqKxg+petmTo72HTYDQw58pc\nPt16nOyxs/1ZPRHl/LXRcG8PfD9eljukMhRFYfqc0ezdcUYaWCKkmXQdY4gmIKuyxXDuRC1ut4o5\njDrpRejotwvO6XRSU1PT9XVNTQ1Op3NQBY/kXF8KtxEsAGusmUkzMyj++FSwqyKiVLAzb1Y3u7j7\n9dJLXi61/2lPU2dlUVXWyLnKpn6PE2IkTCG40XB3U2ZlcvRAFR3t7mBXRYg+GTUdU4g+n7lMRuxp\n8ZyQdb1imPq9Q+Tl5VFZWUl1dTUej4ft27dTWFjY67EXz/ceyrn+FOdWaQ2zESyA2ZePZd+Os7S3\nyQ1SBJ7NHV5rFzuZzEZmXT6GHVtlLZbwH7OmhXQCGFt8DGPzUyjZLWtIROgyaaE7ggUwKj+FQ7IO\nSwxTv09QRqORNWvWsG7duq5U69nZ2WzevBmA5cuXU19fz7333ktraysGg4HXX3+dRx99FKvV2uu5\ngWTUNMyaRnsI3wj74kiOY9zENHZ+eJKFy/KDXR0RRUyqhkHT6QjDuAGYOc87xbbufAtJKbZgV0dE\nGl3HpOkhm+Si0/Q5o3nv9UPMnDdati4QIcmkaRhjQrcjb1ReCh99dIqWpg5sCTHBro4IMwN+sidP\nnsxDDz3U473ly5d3/d3hcLBhw4ZBnxtIcW6VVrMJwvTmsmBJHs+u/4hZl48hNs4S7OqIKBHv9tBq\nMYZt3MRYzcxeOJYPNh/luq/ODHZ1RIQx6TqaogQt89lg5Yxz4napVJ5tIGO0rMUSoadrBCtEs6Gb\nrSYKpqazr+gs86/OC3Z1RJgJ3a4DHwjH9VfdOZxx5E8ZxY5tJ7jqcxOCXR0RZnaVNVLf5unx3qj4\ngRvqNpeH5jCbHnhx9jXLuGROfHiS/UfOM7VANosUvmNWQ2OT4d4yDgKkxVvIsMegGBSmzclmz6dn\npIElQlJXA6s92DXp22Xzc3jhmV3MvSoXQ5jO6hDBEV5PUUPUNYIVxuZfncfTj21n9sKx2OJliFoM\n3l92V7GnornHe8vGJ/G5guQ+zvCyuVVawmzdYm/Z17LjrCS8XSoNLOFTobLJcF8pph++djwZdu+9\nYuqsLP746DauXjWRGKs50FUUol9GXfemaW9Xg12VPqVl2rE7rJQerKZganqwqyPCSPDvEn5kc6lh\nPYIFYHfEMnFGhizaFwFjC7NNhvtSlhBLa2M7p4/VDHywEINkVjU8Ib7+qpMtIYYx41M4KMkuRAgK\n9j5Yg3XZ/DEUf3w62NUQYSaiG1hxbk/Yj2ABzF88jv07y2huDOFxdBEx4t2esBvB6o2uKIyfl8PW\nN49ckuVUiOEya6Gdov1iM+eNZuf2k2iaxIAILaGeRbBT/pRR1J5r4XyVbP8hBi987hJDpOv6hVTT\noR+8A4m3W5kyK5NP3jse7KqICGfQdCyqRpsp/OMGvGl2NU3n6IGqYFdFRAiTpuEOo7UYo8c5iY2z\ncGRfZbCrIkQP4dLAMpoMTJ+TLaNYYkjC5y4xRK5WN5pCSO9VMhTzFuVxaF+lbKAq/Mrm9tBqMoV8\nhrTBUhSFK6/JZ9ubR/B4QjRVlQgr5jBI0d6doijMvzqPj949hi6jWCKEmDQ9LKYIAsyYO5rDeytl\n824xaJHR+uhFS31bWG6U2pe4eAuXL8njnVcOynQn4Tc2t4eWAPcodmZD6/5yqb5rDOUWpOJMi2fH\nVhkBFiPnXYMVXrfO3IIUTGYDR0tkJFeEDpOmYQqDESzwziQaMz6ZA7vKut6raOy45N7V/VXR2BHE\nGotgi5wWyEVa69poDZOekcGaMXc0e4vOcnhvJRNnZAS7OiICeRPDBPbXQm/Z0H68LNen11h63SSe\neXw7E6dnyObDYkTMmk6bOXxGsMA7irVgyXi2v11K/pRRsvGwCAnGMBrBApi9cCyv/HU30+fmYDIZ\nqG52cffrpX0e3z2jp4g+4dUNNwSt9W0RsVC/O4PRwLIvTOa9Nw7h6vAMfIIQQxSMEaxAsDtimbto\nHFteLpERYDEi5hBJ0z5UeRNT0XWd44fPBbsqQgDeTbvDYQ1Wp8wcB6npCez9VNZiiYFFVgukm5b6\n8BnB6mvDyN6kJcWRk5fMR+8eY9EK2XxY+Fa8y8MJR2SO8My+fAwlu8s5tLeCSTMyg10dEabMqhZW\na7A6KYrC/MV5fPTOMcZNSJVRLBF04ZLkorsrlufz9z8VMXV2drCrIkJcxDawWuvbaIkPjwfFvjaM\n7M3D145n0YoJPPWbD5g6K4vktHg/105EC03ViPUEfopgoBiMBq754hRe3FRMbkEq1ljZeFUMnUnT\nwyqLYHcFU0ax/e1STh49T25BarCrI6JcqO+D1Xvnt4I9w85rbx4h+7KsoNRLhIeIfJLSNY32pg5a\nk+zBropf2BJiWLAkj7de2M9XVs/FEKY3exFa2uraaDMZ0cKwd36wMkY7GD8pja3/d5hrvjQ12NUR\nYcishV+Si06KQWHhsvG8/8ZhcvKSMcq9QwSJousYdDCYQvcz2Ffnd5xbZ+6nZ0gqSAtCrUS4CN1P\n9gi4ml3E2GIiJtV0by6bPwaj0cAn7w9u5EuIgTSfb6ExJvJHda5aUcCp0hqO7Jd9gcTQmdXwStN+\nsfwpo4i3W9m1/VSwqyKimFHT8RiUsJyq2mo2UWWzUr6nPNhVESFswBGskpISNm7ciKqqLF26lJUr\nV15yzJ///Gd27dpFTEwMd9xxB1lZ3mHTtWvXEhsbi8FgwGg08sADD/j+J+iFq7GdOIc1INcKFsWg\nsPKm6Tzz+HbG5ieTMdoR7CqJMNdyvoXGmIgc1O4hxmrm87fM4IWndzEqK5HEpNhgV0mECU3TMOre\nB8NwpSgKS78wiT9v+JiJ0zNISIzse6UITSYtvOPoeJKN3EPVWEY5cJlCd5qjCJ5+R7A0TWPDhg38\n4Ac/4MEHH+Sdd97h7NmzPY7ZtWsXp06dYt26dXzzm99k/fr1Pb7/k5/8hIceeihgjSsAV0M7cY7I\nf2hKSLSy9AuTee25vZJVUIxYS00LTZbIH8EC71TBwitzee1ve9B8uOeWiGxqh+odvQrDXvfukpJt\nzJyfw7uvHQx2VUSUMukaHiV8J1F1mIykTkiloLY52FURIarfT3dpaSnp6emkpaVhMplYuHAhRUVF\nPY4pKipi0aJFAOTn59PS0kJ9fX3X94ORErmjsR1blPRKT5iWTvbYJN55VW6UYgR0ndaaVpqiYASr\n05wrxmKJMbH97b73MRGiO0+HJ2zXX11s7qJxVJc3ceKIpG0XgRfuI1gAo2dn42h3k9IqGwqLS/V7\np6itrSU5Obnra6fTSW1tbb/HJCcndx2jKAo/+9nP+NGPfsSWLVt8We9+eacIRkcDC2DJ5ydx9kQd\nh/ZUBLsqIkzZ3CrmOHPEPDwOhnea7TT27yrjVOn5YFdHhAFPhwe3MbwfCjuZzUaWXDeJt18+iMet\nBrs6IsqYNB01zBtYRrORA6l2Jp9rxCQzIcRFfPI01dco1c9//nMefvhh/vVf/5UXXniBgwcDM8ri\nauzAFkUNLEuMiS98bSZvv1JC+en6gU8Q4iIJHW7iU8JjWwNfqGjsYE95E6WNLiYsyeelv+zhw/1V\nVDRKT6Tom6fDE5abDPdl3IRU0jIT2PrmkWBXRUQZYwSMYAHUxVqotsUwoWZwe5mK6NHvncLpdFJT\nU9P1dU1NDU6nc9DHJCUlAZCdnc3cuXMpLfX/VByjpqG6VWLiLX6/VihJy7Sz4svTeOnZYuprW4Nd\nHRFm7C4PtuToaWBVN7u4+/VS7n69lAf2nmNnfCzvPLeH05VykxR983SuwYog13xpKscOVnN4n2TV\nFIFjCuPtDi521BlPkkwVFBfp99Odl5dHZWUl1dXVeDwetm/fTmFhYY9jCgsL2bp1KwBHjhzBZrPh\ncDjo6Oigra0NgMbGRoqLi8nJyfHTj/GZxA4P1qTYsEz9OVJ5E9OYtyiXf27cSXubO9jVEWHE3uHG\nFkUjWBerSIjlbEIcu189KAljRJ88HR48EbZ3lDXWzHVfm8mWlw5Qe04W7IvAiIQ1WJ1Ug0GmCopL\n9Lui3Wg0smbNGtatW9eVpj07O5vNmzcDsHz5cmbNmsXBgwf5wQ9+gNVqZc2aNQDU19ezbt06ABIS\nEli1ahUzZszw848Die0uYjPi/X6dUDXr8rHUnW/l5T/v5sZvzpaNJMXAdJ0El8fbwDpcF+zaBM0J\nRxxX2wy8/OdivvT/JHbEpSJtimCn9KxErrimgJee3c2td8zHYomeZDciOEyajhpBHeF1sRaqbFam\nVzdQnO6I6H1YxeAM+Ft08uTJPPTQQz3eW758eY+vb731Vm699dYe740aNYqHH37YB1UcGke7m7jU\n6G1gAVy9aiIv/Xk3r/x5N5//6kxMIbxTugi+WI+GqiiYY6MjRXufFIUJV43j5LulvPqXPay6ZYbE\njuhB7fBE3BTBTtPnZFN2qo4tL5aw8qZpUTkLRASOSdNpj7Dfr0eS45lZWc/E800cTEkIdnVEkEXW\np1vXSexwE5savVOdAAxGA1/46kwUg8KLz+zE7ZIMUaJvCR3uqErP3h+DQeG6r85EMcALT++U6YKi\nB48r9EewjAbYU950yevY+dZe3+9M7KIoCsuvn8K5qibZukD4nVHXImaKYCddUdg7KhFHh5ucBlkL\nH+0i6qkqzq2iGhTMcdGV4KI3RpOB626Zwf/9Yz//eKqIG74xG4s8RIte2F0eGqNkg+HBMJkMfP6W\nmWx+8QDP/3EHN3xjNrHyO0UAnnY15NO0N7Sr/HTLiUve//Gy3F7ff/ja8WTYYwAwW4x8+ZuF/O33\nn2I0Gph/dZ7f6yuik3cNVmh3VgyHajBQnO5gblkt1cdrIFNGsqJVRH26HR1u6mMi+0Gxr97J3l5V\nLW5WfnkayWnxPPeHHbQ0SYYbcamEDjeN0vjuwWBQuOZLU8gak8TfnvyUxvq2YFdJhACPK3I2Gu6L\nLSGGm789hwPFZXzy/vFgV0dEqEhKcnGxdpOR3ekOSt4p5fTxmoFPEBEpop6qHO1uGqyR3dPcV+9k\nbzp7JpddP5kPt5Syaf1HfP6WGWSNSfJzLUU4sbs8NEV4x8RwKIrCopUTsCXEsGn9R6y4cRrjJqQG\nu1oiiDwdHty2yI+VeLuVm789l7/9/lMMBoU5V+YGu0oiwkRyAwugMcbM9BUTeOUve1h+/WQKpqYH\nu0oiwCKqgZXY7uZsQvRsMDxYiqJwxfJ8MkYn8tKmYuYtHriU1KcAABTBSURBVMesy8fIImaBxaOi\n6DrtkjGvV4rifbhMz07ktb/tYeqsLC5fOh6D/HtFJU+HB3dCdPzfJyRaufnbc3j+DztorGtj8bUT\nMUZYUgIRPCZNQ43w0WBntoMvf6uQF57eSWuzi5nz/b9V0WBVNHZQ3ezq8/tp8ZauqcNieCKmgWXS\nNGI9qizW76ZzOmEXeyyzbpxG0RuHKDl8jomL8rBcyBwnwRSdukavpLHdr9G5Tr5+5+W8/txenvvj\nDlbcOA2HMy7Y1RIBFqlp2vtid8Ry6x0LeP35vTz3hx1c99UZxNutwa6WiACRPoLVaVSmnVu+O4+/\n/6mI5qYOFi4djxICP3d1s4u7X+87mU33tZlieCKmNWJv92ZCk70HPtPXdEKDzcb4c82cfqqI0qR4\nyhKsPLwqX4IpCiV0uGmM4D1vLulkuMA1xM0gO3v78q+ZwKndZWx8fDs5MzKZc2Uu2U4ZNY8GBk0H\nHbQIu8X0FiPxFiPN3bLPjluaz/EdZ9j4xEd88WszZZq5GDGjpuOJkuc1hzOOr/7LPF5+tpjnT9Wx\n4svTsDvkvhHpIubJKhoSXPiKZlA4kpxARbyVyecbyWxuo7mmVbLdRCF7h4eq+Mjtke4vo9pQXNzb\nZ011MHFfFRWHq1l1w1TGjE8ZcV1FaDNrGqYYU8SN9vYWI31lHPzRonG8tKmYCdPTuWJ5PjFWueeK\nYdB1THp0jGB1ssXH8JXvzGPH1uM888RHLL52ApNnZspSjQgWMXMdHO1u6uWX/ZA0xZj5JNNJpc1K\n0Qv7eO1ve6ipbg52tUSAmFUNZ7uLWombIWs3e7NEFSzMZfOLJfz1yU84VVqDruvBrprwE7OmextY\nUSx1rJNv/tsVeNwaf3z0A0p2l8tnXgyZUddRFSXiOisGYjAozFucx03fKuTT90/w0rPF1J1vCXa1\nhJ9Ext3iwgbD+2Pswa5J+FEUziTGcceNk/GcrOWvT35Kzjgn8xaPIy1D/j0jWXZjK9VxMbhMxmBX\nJWyl5jpZMn80B/dW8PbLJVjjzMxbNI7cCakYoqh3NhqYVA1TjMRKnM3C526YSvnpera8XMKeT04z\nb3EeuQUp0hsvBiVa1l/1JS3TztfXLqDog5P8+bcfkz9lFPOvzpNpgxEmIhpYNreK22CQB8URMFlM\nzF6cx2ULxlD88Wn+uXEn8XYr0wqzmTg9gxhrRHxUxAWKrpPT2MbODEewqxL2DEYDUy7LYtKMTI7s\nr+Sjd4+x+aUDTJ2dzdTZWZIMI0J0TREUAGTmOLhtzXwO76tk21tH2Pp/h5lzVS4Tp2dglCyboh9G\nTUeN4gYWgMlsZP7VecyYN5od207w9GPbmTgjg5nzRpMySpZrRIKIuFvI9MCR677Q2Zqfyvy8FM6f\nrmPP3kreff0QyWOSSMt1kjwmiaSEmB4LoPsj2QlDU0ZzO00WE80WiRtfMRgUJk7PYOL0DM5VNrGv\n6CzPrv+I5LR48ialMX5SGkkptmBXUwyTWdMxxphhcL/6IlKvSWPSElh4y0xOldbw8fbTvP3qIUaN\nTyG9IIX88clkJkbuGk8xPNE+gtVdbJyFqz43gVkLxrD749P8/U9F2B2xTJ+TTcG0dCwRnIQq0kXE\n/1xih4sGSXAxIn1vYGzCkp5Eal0HaWUnSdp8lOTMBHa0adRZzTTGmPvN3CipPkOPruuMrW/hcLL0\nkvlLanoCSz4/iatWTOBU6XmOHzrHX5/8lBiribH5KWSPTSJrbBK2eImNcGH1qN4RrNboXXPUX9KY\n/zlQAzFWYlNMpJ9tJONQNftjTUyelk5OXjKjc51YZARQ4N1WxxNF2x0MRrzdyhXXFHD50vEcP3yO\nvTvO8s6rB8ka6yRvQirjJqbKFMIwM+Bvu5KSEjZu3IiqqixdupSVK1decsyf//xndu3aRUxMDHfc\ncQdZWVmDPnekDJpOUpubM3aZhuMvLpORMnscZfY4jJrOHQUOYj4+w6Tz7cS5VRpjTDTGmGmymGiy\nmGixSLr8UFZzuh5dUaiJtQS7KhHPZDKQNzGNvIlpLPvCZCrLGzl9rIZ9O8t485/7iYu3kJHtIDUj\ngbSMBFLT7cTFy/9LqElp7SCnoZW0q8fB7upgVyektZlNnEiK54TDxn/PzcBU10rRByd59a97GJVp\nJyPHwahMO+lZiSQ6Y2XdVhQy6dGTor0/fW7264gjb3kBkzSd08dqOHD4HO+/dQRzjInE9AQSMxJw\npNsZOzqR7KS+G139bSY81K1KxND128DSNI0NGzZw//3343Q6uffee5k2bRrZ2dldx+zatYtTp06x\nbt06jh49yvr16/nlL385qHNHyubyML26gcYY74O98D/VoOAc6+RwaQPg7YlKbHeT4PKQ0tpBbn0L\nsR6VdpORVpORQ1uPo+YkkpAYS3yiFXuilTibJSQ22rvYQDubdxfOUx9P7S7jVGJc1GVwCjbFoJCR\nnUhGdiLzFoGm6ZyvaqKqvJFz5U0cO1jNucomFEUhKSWOpGQbjuQ4EhxWEuxWEhK9L7PFKA+lAZTc\n2sHU6gaK05NYJFM8B09RSEiNZ8aMDOYvzsPtUik7VUfFmQYO7ang/TcO4+rw4Ey1kZRiw5ni/bzb\nHbEkJFqxJcRIopgIJVMEvQba7PfHy3J55Gg9YIAMJ/FuD4k17TjKmnB0nCJB00hKtpGcZiM5LZ5E\nZxyJjljsSd57Rn/lD3WrEjF0/bZKSktLSU9PJy0tDYCFCxdSVFTUo5FUVFTEokWLAMjPz6elpYX6\n+nqqq6sHPHfYdJ2spnbya5s46kygLMEqD4tB4jEYqImLoSbus8aGQdOJ9ajEuT0sTIih9lwrp47V\n0tzQTlNDO+1tbqyxZuLiLcTaLMTGmbHGmomxmrHGmrDEmDDHmLBYjJgtRsxmIyaLEZPJiMlswGQy\nYLzwMhkNKAbFJw+cA/2y6y5spz42tdNS20ZFmiS3CDaDQSEtw+7N1jnb+56u67S2uKivaaXufAv1\nNa2cOV5LU0O7N34a2wFvJre4+Bhi4zrj5kLsWM1YYoxYLCYsMd74MZm9L7PZgNFk/Cx+jAaMRsVn\n8ROJnK0dTKtuoDjdQYOs8x0Rs8XI2PwUxuZ/tmdca7OL2vMt1F14Hd5XSdOF+0Rbq8v7ObdZut0r\nLMRYTcRYzcTEmj77nJt7ftZNJgMms9H7OTcoIdmhF60Mmk6sW5UG1lApCs0WM80WM2UXEjw/eE0u\n2WYDNVXN1Jxr4VTpeRrr2mmsb6OlqQNTjIkFqo7LaMBlNOA2KLgNBjwGhepD1Yxqbkc1KHgMCqri\nfWmKgmZQ8Lg8eNwqRpNB7g/D1G8Dq7a2luTk5K6vnU4npaWl/R6TnJxMbW3toM692D+f3tnn91RN\nZ2GrG4+mo7lUNLdK2oqJTEi8dHh0QqqN5g5Pv9cS/qMZFFouTBUcc1kWMy7awFhVNdpaXLS1uGlt\n6aCt1U1Hu4f2NjcdbW6aGjpwuTy4O1RcF4Lc7dYu/KmiejTvS/X+qetgNCoYjAYMBsX7uvB3RfGO\nHBguPER2/undgkOBC38qCrS6NebUeR9gufD75OLVFvqFb+x8cT+HY0w92vWf/V3p8cdF73bJne67\nOei9xc6EVjdjPRq6qqN7VG/cnD1PzpzR6BVtPru28B1FUbDFx2CLjyFrTFKvx7hcHlqbXbS1uGht\ncfWIndaWDhpqVVwdHlwdHtwub8x4PBoel/fPztjxXPgTwNgtZrrHkWJQMCgKioEB46ez/t6/f/Ye\nCihcOPazH/SSPrEe8RPA2AG4vr1nPJT830HcHp3p1Q3sTnfQYJVpm/4QF+9tPGWPvfSzrno0Wpo7\naG357LPe1uKmo91NU0Mb5yq7fcZdHlwuFU/nZ/3C/UJTNVRV7/pcG40X3R/6+nwbPvuMd33Wocff\nuz7XXX+n60Pc732hly8veXwd4IF2JI+7Y6f59mE579R5sj29TzezlVRQXFLBZdUtGDWdOLeKWdNo\nMxk5lhTv03pEI6PJSFpGQq9b6miqRtHxOh586xgxqoZF1bx7+WkaVo9GY2UT6S3tGDUdk6Zj0HWM\nuo5B8/659U81bNV0b/wYFQyGS+OnZwx1i6OL7g39xs8IY+eSL0ModhS9n10CP/74Y3bv3s33vvc9\nALZu3UppaSm333571zEPPvggX/ziF5k4cSIAP//5z7n11luprq4e8Nzudu7cSX19/ZAqL0Q4czgc\nzJ49e8TlSOyIaOOr2AGJHxFdJHaEGJ6hxk6/I1hOp5Oampqur2tqanA6nYM6xuPxDHhud74KeCGi\njcSOEMMn8SPE8EjsCNG3fudZ5OXlUVlZSXV1NR6Ph+3bt1NYWNjjmMLCQrZu3QrAkSNHsNlsOByO\nQZ0rhBBCCCGEEJGk3ymC4E21/tRTT3WlWr/22mvZvHkzAMuXLwfg2WefZdeuXVitVtasWdOVyKK3\nc4UQQgghhBAiUg3YwBJCCCGEEEIIMTiylbYQQgghhBBC+Ig0sIQQQgghhBDCR/rNIhgoJSUlbNy4\nsWut1sqVK0dU3vnz53niiSdoaGjAbrezePFiFi9ePOJ6aprGPffcg9Pp5J577hlxee3t7fz+97/n\n9OnTuN1u1qxZQ0FBwYjK3LJlC++99x5ut5tJkybxzW9+c8hlrF+/nuLiYux2O4888ggAbW1tPPbY\nY1RXVzNq1CjuuusurFbriMp85pln2LVrFxaLhUmTJnHzzTcTFxc3ojI7vfLKK2zatIk//OEPxMcP\nfr+Nvsp89913efPNN3G73Vx22WXcdtttIyrz7NmzbNq0iZqaGpKTk7ntttuGtQl3uMQOSPyEUvxI\n7EjsSOxI7EjsDJ3Ejjy3DTp+9CBTVVW/88479aqqKt3tdus//OEP9TNnzoyozLq6Ov3EiRO6rut6\nQ0ODvnr16hGXqeu6/sorr+i/+c1v9AcffHDEZem6rj/22GP622+/reu6rns8Hr2lpWVE5TU1Nel3\n3HGH3tbWpquqqv/qV7/Si4uLh1xOSUmJfvz4cf0//uM/ut575pln9BdffFHXdV1/4YUX9E2bNo24\nzD179uiqquqqquobNmzwSZm6ruvnzp3Tf/GLX+h33HGH3tTUNOIy9+3bp//sZz/T3W63ruvez9RI\ny3z00Uf1Dz/8UNd1Xd+2bZv+6KOPDqlMXQ+v2NF1iZ9Qih+JHYkdiR2JHYmdoZPYkec2XR9c/AR9\nimBpaSnp6emkpaVhMplYuHAhRUVFIyrT4XAwduxYAOx2O3l5edTV1Y2ozJqaGoqLi1myZAm6D/KC\ntLa2cujQIZYsWQKA0WgcUi9AbywWS1fZLpeLjo6OIfUCdJo0aRI2m63He0VFRSxatAiAxYsXs2PH\njhGXOX36dAwGAwaDgZkzZ/bYN224ZQI8/fTTQ+qpGKjMt956iy996UuYTN4BX7v90l3Th1pmXFwc\nzc3NaJpGc3PzsP6fwiV2QOIn1OJHYkdiR2JHYkdiZ2gkduS5bSjxE/QpgrW1tSQnJ3d97XQ6KS0t\n9Vn5lZWVnD17lvz8/BGVs3HjRm677Tba2tp8Uq/q6mrsdjtPPPEEx48fJz8/n9tvv70r2IbDYrGw\nevVq1q5di9lsZuXKlYwfP94n9W1oaMDhcACQmJhIQ0ODT8rt9Pbbb3f90hqJHTt24HQ6GTNmjA9q\n5VVZWUlJSQnPPPMMVquVb3zjG4wbN25EZd52223cd999PPvsszidTn71q18NuYxwiR2Q+AmH+JHY\nkdgZLokdiR1fkdiJrtiByI2foI9g+VN7ezu//vWv+cY3vjGkeacX27lzJ3a7ndzcXJ/0ggCoqsqx\nY8eYN28eDzzwAB6Ph48++mhEZTY2NvL73/+eRx99lCeeeIIjR46wa9cun9S3O0VRfFreP//5T6xW\nKwsWLBhROR0dHbzwwgvcfPPNXe/54v9LVVWqq6v5+c9/znXXXcczzzwz4jI3bNjAihUr+OMf/8jy\n5cvZsGHDiMv0JV/FDkj8XCwU40dix3ckdiR2JHaGR2InumIHIjt+gt7AcjqdPYYYa2pqcDqdIy7X\n4/HwyCOPcOWVVzJnzpwRlXX48GF27tzJ2rVr+c1vfsOBAwd4/PHHR1RmcnIy8fHxFBYWYrFYWLhw\nIcXFxSMqs7S0lPz8fNLT00lISGDBggWUlJSMqMxOiYmJ1NfXA1BXV0diYqJPyn3vvfcoLi7mrrvu\nGnFZVVVVnDt3jrvvvpu1a9dSW1vLPffcM+Jem+TkZC6//HIsFguFhYWUl5fjcrlGVGbnNAOj0ciS\nJUs4ePDgkMsIh9gBiR8I/fiR2JHYGQmJHYmdkZLYib7YgciOn6A3sPLy8qisrKS6uhqPx8P27dsp\nLCwcUZm6rvPb3/6W7OxsVq1aNeI6fu1rX2PDhg088cQT/Nu//RtTpkzhzjvvHFGZDoeD9PR0jh49\niqZp7Nq1i+nTp4+ozIkTJ3Ls2DGam5txu90UFxczY8aMEZXZqbCwkPfeew+A999/3ye/AHfv3s3L\nL7/Mj370oxENsXfKycnhySef5IknnuCJJ57A6XTyP//zPyP+pTJnzhyKi4vRdZ2jR48yatSoEdd3\nypQpXfPWd+zYMaz/+3CIHZD4gdCPH4kdiZ2RkNiR2BkJiZ3ojB2I7PhRdF+NnY5ASUkJTz31VFfK\nz2uvvXZE5R06dIgf//jH5OTkdA2Lfu1rX2PmzJk+qesrr7zCf/7nf464rPLycp544gkaGxvJyckZ\ncgrN3rz33nu8++67uFwuZsyYwc0334zBMLR29K9//WsOHjxIU1MTiYmJ3HzzzcyfP39E6T47y2xs\nbMThcHDTTTfx4osv4vF4uhYKFhQUsHr16hHV8+qrr+76/p133smDDz44pAWjvZW5aNEifv/733Pg\nwAFMJhPf+c53mDhx4rB/9ptvvpnx48fzj3/8g7KyMkaPHs2NN95IVlbWoMvsFE6xAxI/oRI/EjsS\nOxI7EjsSO0MnsSPPbYONn5BoYAkhhBBCCCFEJAj6FEEhhBBCCCGEiBTSwBJCCCGEEEIIH5EGlhBC\nCCGEEEL4iDSwhBBCCCGEEMJHpIElhBBCCCGEED4iDSwhhBBCCCGE8BFpYAkhhBBCCCGEj/x/ITxq\nbrXsTa0AAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11366a390>"
       ]
      }
     ],
     "prompt_number": 11
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Maximum Likelihood\n",
      "==================\n",
      "\n",
      "**Maximum likelihood** (ML) fitting is usually more work than the method of moments, but it is preferred as the resulting estimator is known to have good theoretical properties. \n",
      "\n",
      "There is a ton of theory regarding ML. We will restrict ourselves to the mechanics here.\n",
      "\n",
      "Say we have some data $y = y_1,y_2,\\ldots,y_n$ that is distributed according to some distribution:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$Pr(Y_i=y_i | \\theta)$$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Here, for example, is a **Poisson distribution** that describes the distribution of some discrete variables, typically *counts*: "
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "y = np.random.poisson(5, size=100)\n",
      "plt.hist(y, bins=12, normed=True)\n",
      "xlabel('y'); ylabel('Pr(y)')"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 12,
       "text": [
        "<matplotlib.text.Text at 0x11367bf10>"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAY8AAAEUCAYAAADTO7pnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGLhJREFUeJzt3X9wVNX9//FXsmEJkJ83NomyXwYawjSUGIsBf2QQxhA6\ngTpTOiOl0hkppR0DMlhpwfzByI/aMCQULSYpaNUM1ZlWBxnsMOMELDVDbEvcYIuRwvoDBLvmwy5J\ngBAgu/v9w3HHFBL2yO7dJDwff+XuPefs+zKOr73nnntvQigUCgkAAAOJ8S4AADD0EB4AAGOEBwDA\nGOEBADBGeAAAjBEeAABjSXZ9UVtbmxoaGhQIBFRaWqry8vI++w8dOqQ///nPkiTLsvTggw9q4sSJ\nEfUFANjLlvAIBoOqr6/X2rVrZVmWKisrVVhYKJfLFW5TWFioadOmSfoiLHbu3Kn169dH1BcAYC9b\npq08Ho9yc3OVnZ2tpKQklZSUqKWlpU+b5OTk8N/d3d0aMWJExH0BAPay5czD7/crKysrvG1Zljwe\nz1Xt/vnPf6qhoUE9PT3atGmTUV8AgH0G1QXz6dOnq7a2Vj/96U9VXV0d73IAAP2w5czDsiz5fL7w\nts/nk2VZ/ba/99579Yc//EHd3d3Gff/+97/rwoUL0SkcAG4SGRkZuvPOOyNub0t45OXlyev1qr29\nXZZlqbm5WStXruzTxuv1KicnRwkJCXK73XI6nRo9enREfb/qwoULmjp1aqwPCQCGFbfbbdTelvBw\nOByqqKhQTU1NeLmty+VSY2OjJKmsrEz/+Mc/9Pbbb8vhcGj8+PFavXr1gH0BAPGTMNweyb5//37O\nPADAkNvtVmlpacTtB9UFcwDA0EB4AACMER4AAGOEBwDAGOEBADBGeAAAjBEeAABjhAcAwBjhAQAw\nRngAAIwRHgAAY4QHAMAY4QEAMGbLI9lx8/lv1yW1n78ck7GzU5y6NW1kTMYGEBnCAzHRfv6yfrU3\nNu+ar547kfAA4oxpKwCAMcIDAGCM8AAAGCM8AADGCA8AgDHCAwBgjPAAABgjPAAAxggPAIAxwgMA\nYIzwAAAYIzwAAMYIDwCAMdueqtvW1qaGhgYFAgGVlpaqvLy8z/6mpibt2bNHkuRyuTR//nyNGzdO\nkrR8+XKNGjVKiYmJcjgcqqqqsqtsAMA12BIewWBQ9fX1Wrt2rSzLUmVlpQoLC+VyucJtcnJytH79\neo0ePVoHDhzQ9u3b9dRTT4X3r1u3TikpKXaUCwC4DlumrTwej3Jzc5Wdna2kpCSVlJSopaWlT5tJ\nkyZp9OjRkqSpU6fK5/P12R8KhewoFQAQAVvOPPx+v7KyssLblmXJ4+n/RUH79u1TcXFxeDshIUEb\nNmxQQkKC5syZo9mzZ8e0XgDAwAbdmwSPHDmipqYm/frXvw5/tnHjRmVmZurUqVOqqqrS2LFjVVBQ\nEMcqAeDmZsu0lWVZfaahfD6fLMu6qt2JEye0Y8cOrVmzRmPGjAl/npmZKemLC+nTp08f8KwFABB7\ntoRHXl6evF6v2tvb1dvbq+bm5j7TUpJ05swZbdmyRStWrFBubm7480uXLunixYuSpK6uLrW2toZX\nYQEA4sOWaSuHw6GKigrV1NSEl+q6XC41NjZKksrKyvTaa6/p/Pnzeu6558J9qqqq1NHRoZqaGklS\namqq5s2bp6KiIjvKBgD0IyE0zJYx7d+/X1OnTo13GTe99z47p1/tjc30YvXciSq6LTUmYwM3K7fb\nrdLS0ojbc4c5AMAY4QEAMEZ4AACMER4AAGOEBwDAGOEBADBGeAAAjBEeAABjhAcAwBjhAQAwRngA\nAIwRHgAAY4QHAMAY4QEAMEZ4AACMER4AAGOEBwDAGOEBADBGeAAAjBEeAABjhAcAwFhSvAsAbib/\n7bqk9vOXYzJ2dopTt6aNjMnYwP8iPAAbtZ+/rF/t9cRk7Oq5EwkP2IZpKwCAMcIDAGCM8AAAGCM8\nAADGCA8AgDHCAwBgzLalum1tbWpoaFAgEFBpaanKy8v77G9qatKePXskSS6XS/Pnz9e4ceMi6gsA\nsJctZx7BYFD19fVatWqVNm3apLfeekunTp3q0yYnJ0fr169XdXW1ioqKtH379oj7AgDsZUt4eDwe\n5ebmKjs7W0lJSSopKVFLS0ufNpMmTdLo0aMlSVOnTpXP54u4LwDAXraEh9/vV1ZWVnjbsiz5/f5+\n2+/bt0/FxcVfqy8AIPYG3QXzI0eOqKmpST/60Y/iXQoAoB+2hIdlWeFpKEny+XyyLOuqdidOnNCO\nHTu0Zs0ajRkzxqgvAMA+toRHXl6evF6v2tvb1dvbq+bm5vC01JfOnDmjLVu2aMWKFcrNzTXqCwCw\nly1LdR0OhyoqKlRTUxNebutyudTY2ChJKisr02uvvabz58/rueeeC/epqqrqty8AIH5su89j8uTJ\n2rx5c5/PysrKwn8/8sgjeuSRRyLuCwCIn0F3wRwAMPgRHgAAY4QHAMAY4QEAMEZ4AACMER4AAGOE\nBwDAGOEBADBGeAAAjBEeAABjhAcAwBjhAQAwRngAAIwRHgAAY4QHAMAY4QEAMEZ4AACMER4AAGOE\nBwDAGOEBADBGeAAAjEUcHh0dHTp+/Lg6OjpiWQ8AYAhIGminx+PR7t279f777+vixYtKTU3VuXPn\nlJycrClTpuj73/++Jk6caFetAIBBot/wWL9+vXp6evTd735XCxcuVE5OjkaMGKErV67o888/l8fj\n0Ysvviin06knn3zSzpoBAHHWb3gsWrTommcVI0aMkMvlksvl0qxZs+TxeGJaIABg8On3msdXg+Pc\nuXP9DsC0FQDcfAa85vGlZcuWqbCwUPfdd5+Ki4uVlBRRNwDAMBXRaqtnn31WU6ZM0e7du/Wzn/1M\n27dv19GjR2NdGwBgkIroFCI9PV1z587V3Llzdfr0ab399tvatm2bEhISNGPGDN1///36xje+MeAY\nbW1tamhoUCAQUGlpqcrLy/vsP336tOrq6vTJJ59o4cKFeuCBB8L7li9frlGjRikxMVEOh0NVVVVf\n41ABANFiPP/U0dGhzs5OdXd365vf/KZ8Pp8ef/xx/fCHP9T3vve9a/YJBoOqr6/X2rVrZVmWKisr\nVVhYKJfLFW6TmpqqJUuW6NChQ9ccY926dUpJSTEtFwAQAxGFx8mTJ9XU1KSDBw/K6XRq5syZqq6u\n1i233CJJ+sEPfqC1a9f2Gx4ej0e5ubnKzs6WJJWUlKilpaVPeKSlpSktLU1ut/uaY4RCIaMDAwDE\nTkThsW7dOt177736xS9+ofz8/Kv25+bmqrS0tN/+fr9fWVlZ4W3LsoyW+CYkJGjDhg1KSEjQnDlz\nNHv27Ij7AgCiL6Lw2LFjx3VXWC1cuDAqBV3Lxo0blZmZqVOnTqmqqkpjx45VQUFBzL4PADCwfldb\nHTx4UMFgUJL6DY5AIKCDBw9e90ssy5LP5wtv+3w+WZYVcZGZmZmSJJfLpenTp3NjIgDEWb/h8a9/\n/UsrVqzQq6++qsOHD8vr9erSpUvyer06fPiwXn31Va1cuVL//ve/r/sleXl58nq9am9vV29vr5qb\nm1VcXHzNtv97bePSpUu6ePGiJKmrq0utra0aN26cyTECAKKs37moiooK+Xw+/eUvf9HLL78sr9er\ny5cvy+l06rbbbtOUKVO0YcOGiM4gHA6HKioqVFNTE16q63K51NjYKEkqKytTR0eHKisr1d3drcTE\nRO3du1dbt25VZ2enampqJH2xImvevHkqKiqK0uEDAL6OAS9kZGVl6eGHH5b0xXLbc+fOKS0tTQkJ\nCcZfNHnyZG3evLnPZ2VlZeG/MzIyVF9ff1W/5ORkVVdXG38fACB2rnvBPBAI6LHHHtNvf/tbpaen\n21ETMCBHovTeZ/0/b+1GZKc4dWvayJiMDQwn1w0Ph8OhUaNG6fTp0xo/frwNJQED6+wJaP2+j2My\ndvXciYQHEIGIlurOmzdPL774okpLSzVx4kQ5HI7wvpycnJgVBwAYnCIKj7q6Okm65sMQ//SnP0W3\nIgDAoDdgePT09GjXrl36zne+owkTJmj+/PlyOp121QYAGKQGfCT7Cy+8oKamJlmWpQMHDmjnzp12\n1QUAGMQGDI/W1latWbNGP//5z7V69ep+H1oIALi5DBgePT094RVWEyZMUHd3tx01AQAGuQGveYRC\nIR05ciT8dyAQCG9/acqUKbGrDgAwKA0YHunp6X3u+k5NTb3qLvDa2trYVAbACDdPwk4DhgfBAAwd\n3DwJOw14zQMAgGshPAAAxggPAIAxwgMAYIzwAAAYIzwAAMYIDwCAsYgeyY7h6b9dl9R+/nJMxr4c\nCMZkXACDA+FxE2s/f1m/2uuJydhPzp4Qk3EBDA5MWwEAjBEeAABjhAcAwBjhAQAwRngAAIwRHgAA\nYyzVHcRieR+GxL0YAL4+wmMQi+V9GBL3YgD4+mwLj7a2NjU0NCgQCKi0tFTl5eV99p8+fVp1dXX6\n5JNPtHDhQj3wwAMR9wUA2MuW8AgGg6qvr9fatWtlWZYqKytVWFgol8sVbpOamqolS5bo0KFDxn0B\nAPay5YK5x+NRbm6usrOzlZSUpJKSErW0tPRpk5aWpry8PDkcDuO+AAB72RIefr9fWVlZ4W3LsuT3\n+2PeFwAQGyzVBQAYsyU8LMuSz+cLb/t8PlmWFfO+AIDYsCU88vLy5PV61d7ert7eXjU3N6u4uPia\nbUOh0NfuCwCwhy2rrRwOhyoqKlRTUxNebutyudTY2ChJKisrU0dHhyorK9Xd3a3ExETt3btXW7du\nVXJy8jX7ArCPI1F677NzMRk7O8WpW9NGxmRsxI5t93lMnjxZmzdv7vNZWVlZ+O+MjAzV19dH3BeA\nfTp7Alq/7+OYjF09dyLhMQRxwRwAYIzwAAAYIzwAAMYIDwCAMcIDAGCM8AAAGCM8AADGCA8AgDHC\nAwBgjPAAABgjPAAAxggPAIAxwgMAYIzwAAAYIzwAAMYIDwCAMcIDAGCM8AAAGCM8AADGCA8AgDHC\nAwBgjPAAABgjPAAAxggPAIAxwgMAYIzwAAAYIzwAAMYIDwCAsSS7vqitrU0NDQ0KBAIqLS1VeXn5\nVW1eeeUVud1ujRw5UsuWLdPYsWMlScuXL9eoUaOUmJgoh8Ohqqoqu8oGAFyDLeERDAZVX1+vtWvX\nyrIsVVZWqrCwUC6XK9zG7XbrxIkTqqmp0fHjx1VXV6ennnoqvH/dunVKSUmxo1wAwHXYMm3l8XiU\nm5ur7OxsJSUlqaSkRC0tLX3atLS0aObMmZKk/Px8XbhwQR0dHeH9oVDIjlIBABGw5czD7/crKysr\nvG1Zljwez4BtsrKy5Pf7lZGRoYSEBG3YsEEJCQmaM2eOZs+ebUfZAIB+2HbNIxL9nV1s3LhRmZmZ\nOnXqlKqqqjR27FgVFBTYXB0A4Eu2TFtZliWfzxfe9vl8siwr4jaZmZmSJJfLpenTp1911gIAsJct\nZx55eXnyer1qb2+XZVlqbm7WypUr+7QpLi7Wm2++qZKSEh07dkxjxoxRRkaGLl26pGAwqFGjRqmr\nq0utra36yU9+YkfZAGzgSJTe++xczMbPTnHq1rSRMRv/ZmVLeDgcDlVUVKimpia8VNflcqmxsVGS\nVFZWpqlTp+qDDz7QqlWrlJycrIqKCklSR0eHampqJEmpqamaN2+eioqK7CgbgA06ewJav+/jmI1f\nPXci4REDtl3zmDx5sjZv3tzns7Kysj7bixYt0qJFi/p8lpOTo+rq6pjXBwCIHHeYAwCMER4AAGOE\nBwDAGOEBADBGeAAAjBEeAABjg+rxJAAQbbG8CfFmvgGR8AAwrMXyJsSb+QZEpq0AAMYIDwCAMcID\nAGCM8AAAGCM8AADGCA8AgDHCAwBgjPAAABgjPAAAxggPAIAxwgMAYIzwAAAYIzwAAMYIDwCAMcID\nAGCM93ncoK6eXgVDoZiMHatxAeBGER436PX329V43B+TsVfc+/9iMi6A6LiZ31JIeNygrp5etZ+/\nEu8yAMTBzfyWQq55AACMER4AAGO2TVu1tbWpoaFBgUBApaWlKi8vv6rNK6+8IrfbrZEjR2rZsmUa\nO3ZsxH0BAPax5cwjGAyqvr5eq1at0qZNm/TWW2/p1KlTfdq43W6dOHFCNTU1Wrx4serq6iLuCwCw\nly3h4fF4lJubq+zsbCUlJamkpEQtLS192rS0tGjmzJmSpPz8fF24cEEdHR0R9QUA2MuW8PD7/crK\nygpvW5Ylv98/YJusrCz5/f6I+gIA7DWoluqGhuBNcTMmZOq2tOSYjJ2YEJNhAeCG2RIelmXJ5/OF\nt30+nyzLiqhNb2/vdft+VUZGhtxudxSrv74JsRr4/6RNU2M1uCT/R7Ebf4iOHfAel9sbm7G/NBT/\nXYbs2LEef4j/t/hVGRkZRu1tCY+8vDx5vV61t7fLsiw1Nzdr5cqVfdoUFxfrzTffVElJiY4dO6Yx\nY8YoIyNDqamp1+37VXfeeWesDwcAbnoJIZvmitra2vTSSy+Fl9vOnTtXjY2NkqSysjJJ0ssvvyy3\n263k5GRVVFTI5XL12xcAED+2hQcAYPjgDnMAgDHCAwBgbFAt1b1Rw/kxJmfOnFFtba06OzuVlpam\nWbNmadasWfEuK6qCwaCeeOIJWZalJ554It7lRFVPT4+ef/55nTx5UleuXFFFRYUmTZoU77KiZt++\nfTpw4ICuXLmigoICLV68ON4l3ZC6ujq1trYqLS1NW7ZskSRdvHhR27ZtU3t7u3JycrRixQolJ8dm\nmX6sXev4du7cKbfbLafTqYKCAi1YsECjR4/uf5DQMBEIBEKPPvpo6PPPPw9duXIl9Mtf/jL06aef\nxrusqDl79mzo448/DoVCoVBnZ2do6dKlw+r4QqFQ6I033gg988wzoU2bNsW7lKjbtm1baP/+/aFQ\nKBTq7e0NXbhwIc4VRc+5c+dCy5YtC128eDEUCARCv/nNb0Ktra3xLuuGtLW1hT766KPQ448/Hv5s\n586dod27d4dCoVDo9ddfD/3xj3+MV3k37FrH995774UCgUAoEAiE6uvrr3t8w2baarg/xiQjI0Pj\nx4+XJKWlpSkvL09nz56Nb1FR5PP51Nraqvvvv39I3iw6kO7ubh09elT333+/JMnhcAz8i26IcTqd\nkr44zsuXL+vSpUtKSUmJc1U3pqCgQGPGjOnz2VcfoTRr1iwdOnQoHqVFxbWO7/bbb1diYqISExN1\nxx139Lm/7lqGzbTVtR5j4vF44lhR7Hi9Xp06dUr5+fnxLiVqGhoa9OMf/1gXL16MdylR197errS0\nNNXW1uqjjz5Sfn6+lixZEv6f7lDndDq1dOlSLV++XCNGjFB5ebkmTpwY77KirrOzM3wjXXp6ujo7\nO+NcUezs378//GOnP8PmzONm0dPTo6effloPP/zwkJ1v/V/vvvuu0tLSNGHChGF31iFJgUBAH374\noe666y5VVVWpt7dX77zzTrzLipquri49//zz2rp1q2pra3Xs2DHbn/Jgt4SE4fvsoF27dik5OVn3\n3HPPgO2GTXhE8giUoa63t1dbtmzRjBkzNG3atHiXEzX/+c9/9O6772r58uV65pln9P777+vZZ5+N\nd1lRk5WVpZSUFBUXF8vpdKqkpEStra3xLitqPB6P8vPzlZubq9TUVN1zzz1qa2uLd1lRl56ero6O\nDknS2bNnlZ6eHueKou/AgQNqbW3VihUrrtt22ITHVx+B0tvbq+bmZhUXF8e7rKgJhUL6/e9/L5fL\npXnz5sW7nKh66KGHVF9fr9raWj322GP69re/rUcffTTeZUVNRkaGcnNzdfz4cQWDQbndbt1+++3x\nLitqvvWtb+nDDz/U+fPndeXKFbW2tqqoqCjeZUVdcXGxDhw4IEn629/+Nqx+wEnS4cOHtWfPHq1e\nvTqiKdVhdYf5cH6MydGjR/Xkk09q3Lhx4VPmhx56SHfccUecK4uutrY2vfHGG1qzZk28S4mqzz77\nTLW1terq6tK4ceOG9DLPazlw4ID++te/6vLlyyoqKtKCBQuUmDh0f5s+/fTT+uCDD3Tu3Dmlp6dr\nwYIFuvvuu4fNUt0vj6+rq0sZGRl68MEHtXv3bvX29oYXO0yaNElLly7td4xhFR4AAHsM3Z8GAIC4\nITwAAMYIDwCAMcIDAGCM8AAAGCM8AADGCA8AgDHCAwBgjPAAABgjPIAY2rNnT/hNbV964YUX9NJL\nL8WnICBKCA8ghu677z4dPnxY3d3dkr54PPs777wTfqkQMFQRHkAMZWRkqKCgIPz+jsOHD4ffXQIM\nZYQHEGMzZ85UU1OTJKmpqUkzZsyIc0XAjSM8gBibNm2aTpw4oZMnT8rtdhMeGBYIDyDGnE6n7rrr\nLv3ud79Tfn6+srKy4l0ScMMID8AGs2bN0qeffspZB4YNwgOwwS233CKn06m777473qUAUUF4ADEW\nDAa1a9culZSUDNnXlgL/i/AAYqinp0eLFy/W6dOntWDBgniXA0QN7zAHABjjzAMAYIzwAAAYIzwA\nAMYIDwCAMcIDAGCM8AAAGPv/upraxx831S0AAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11371f390>"
       ]
      }
     ],
     "prompt_number": 12
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "The product $\\prod_{i=1}^n Pr(y_i | \\theta)$ gives us a measure of how **likely** it is to observe values $y_1,\\ldots,y_n$ given the parameters $\\theta$. Maximum likelihood fitting consists of choosing the appropriate function $l= Pr(Y|\\theta)$ to maximize for a given set of observations. We call this function the *likelihood function*, because it is a measure of how likely the observations are if the model is true.\n",
      "\n",
      "> Given these data, how likely is this model?"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "In the above model, the data were drawn from a Poisson distribution with parameter $\\lambda =5$.\n",
      "\n",
      "$$L(y|\\lambda=5) = \\frac{e^{-5} 5^y}{y!}$$\n",
      "\n",
      "So, for any given value of $y$, we can calculate its likelihood:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "poisson_like = lambda x, lam: np.exp(-lam) * (lam**x) / (np.arange(x)+1).prod()\n",
      "\n",
      "lam = 6\n",
      "value = 10\n",
      "poisson_like(value, lam)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 13,
       "text": [
        "0.041303093412337726"
       ]
      }
     ],
     "prompt_number": 13
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "np.sum(poisson_like(yi, lam) for yi in y)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 14,
       "text": [
        "11.968386407200342"
       ]
      }
     ],
     "prompt_number": 14
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "lam = 8\n",
      "np.sum(poisson_like(yi, lam) for yi in y)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 15,
       "text": [
        "8.5185194171986929"
       ]
      }
     ],
     "prompt_number": 15
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We can plot the likelihood function for any value of the parameter(s):"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "lambdas = np.linspace(0,15)\n",
      "x = 5\n",
      "plt.plot(lambdas, [poisson_like(x, l) for l in lambdas])\n",
      "xlabel('$\\lambda$')\n",
      "ylabel('L($\\lambda$|x={0})'.format(x))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 16,
       "text": [
        "<matplotlib.text.Text at 0x113c7ebd0>"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAZMAAAEUCAYAAADuqdsBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xlck1e+P/BPFiBsIT5BiBIRjSBoRUSsC/XKSLEXrZ3p\ntLVe6716vXZmUGfaKdbqTL2zdFqdEWs7LeL8xlmYWud2ua3XTp3pINStaCsmrgERFJAlRBMCJCzZ\nnt8fVFoKapDAyfJ9v16+JOQ8ySeC+eY85zznCHie50EIIYQMgZB1AEIIId6PigkhhJAho2JCCCFk\nyKiYEEIIGTIqJoQQQoaMigkhhJAhE7N6Yq1Wi8LCQjgcDmRmZiI7O7vP/Q0NDdi9ezdqamqwfPly\nLF26tPe+w4cP48iRI7DZbEhKSsLq1atHOD0hhJCvY9IzcTqdKCgoQG5uLrZv346SkhLU19f3aRMe\nHo41a9b0KSIAYDab8eGHH+LFF1/Etm3b0NTUhLNnz45kfEIIId/ApJhUVVVBoVAgKioKYrEY6enp\nKCsr69NGKpVCpVJBJBL1+X5gYCAAoKOjA1arFd3d3QgLCxux7IQQQvpjcprLaDRCLpf33uY4DlVV\nVS4dGxgYiLVr12L9+vUICAhAdnY2Jk2aNFxRCSGEuMDrBuDb2tqwd+9e7Nq1C/n5+aisrIRarWYd\nixBC/BqTngnHcTAYDL23DQYDOI5z6diqqirEx8dDoVAAAObOnQutVovU1NQB2586dQoWi2XooQkh\nxI/IZDLMnDnT5fZMiolKpYJOp4NerwfHcSgtLcUzzzwzYNtvrkOZmJiIP/3pTzCbzQgKCoJGo8Hi\nxYtv+1wWi+W2hYYQQsjABnvGh0kxEYlEyMnJQV5eXu/UYKVSiaKiIgBAVlYWTCYTtmzZgo6ODgiF\nQhw6dAi7du1CSEgIHnvsMezYsQNWqxXTp0/H1KlTWbwMQgghXxL4+hL0xcXF1DMhhJBBUqvVyMzM\ndLm91w3AE9/gcPJw+vbnGEL8CrMr4Il/cjh5fFJpwF/ONKGt24FRwWLIQwJ6/oT2/D15dAhSY6Ss\noxJCBoGKCRkxp6+34fdfNCAsSIRfLJqICVwwjB02GDpsMHbYYfjy699+dh1TokKxbq4SYUH0K0qI\nN6D/qWTYXTN24v993gBduxVr7x+LeeMjIBAIAACK8CAowoP6tF+REo0/nG7E9z6owHPzY5GmpF4K\nIZ6OigkZNla7E/kn63GythUrZijwcFIkxELBXY8LDhBhw7xxmDc+Aq8er8P9ygg8PXssggNEdz2W\nEMIGDcCTYfNmaT1MnXb88YkkfGfqaJcKydelxkjxu+8mwepw4gcfVOB8k3mYkhJChoqKCRkWhypu\nolxvwQsZ44c07hEaKMLGBePxgzlKvFxyDcevmdyYkhDiLnSai7hdhd6CP5U14dWH4xES6J5TU3PH\nRyAyVIWf/KMakaEBSIoKdcvjEkLcg3omxK1aOm14qfgann1gHMbJJG597PjIEDw3Pxa/OHwVuvZu\ntz42IWRoqJgQt3E4ebxSUoPMSRzS42TD8hxzx0fgyeRobP3kKszd9mF5DkLI4FExIW7zh9ONEAkF\nWDVzzLA+z6P3RSFlbDheKq6B3UlX0RPiCaiYELc4drUFx6+Z8JNvxUE0yFlb9+IHc2IQKBLgtyeu\n91tZmhAy8qiYkCGrbenEG6X1+O8HJ0AqGZk5HSKhAD9ZGIcrhg68e14/Is9JCLk9KiZkyApONeCp\nGQrER4aM6PMGB4jw0qKJ+D/tDZyooSnDhLBExYQMyaVmMxpau7EkUc7k+SNDA7E1cwLe+Ow6TJ02\nJhkIIVRMyBDtU+uwPCUaASJ2v0pJUaFYqBqFglMNzDIQ4u+YXbSo1WpRWFjYu9NidnZ2n/sbGhqw\ne/du1NTUYPny5Vi6dGnvfV1dXdi7dy/q6upgs9mQk5ODhISEkX4Jfu9SsxnXW7uwKJ5jHQX/MXMM\nfvBBBT6va8Xs2AjWcQjxO0yKidPpREFBAbZu3QqO47BlyxZMmzYNSqWyt014eDjWrFmD06dP9zt+\n7969mDJlCjZs2ACHw4HubrqAjYV9ah3+LUXBtFdyS3CACM88MA6vHq/DNEWY2668J4S4hsm7QFVV\nFRQKBaKioiAWi5Geno6ysrI+baRSKVQqFUSivm8KHR0dqKiowMKFCwH07CcfEjKyA78E0DZbPKZX\ncktqjBQzxobjj2WNrKMQ4neYFBOj0Qi5/KsBW47jYDQaXTpWr9dDKpUiPz8fubm52LNnD6xW63BF\nJbexT9PkMb2Sr/ve7Bh8VtOKizpaYZiQkeRZ7wQucDgcqK6uxuzZs7Ft2zbY7XacPHmSdSy/om22\noM7kWb2SW8KDxFg3V4lXj9fBaneyjkOI32BSTDiOg8Fg6L1tMBjAca69McnlcoSFhSEtLQ2BgYFI\nT0+HRqMZrqhkAPs0TVg+3fN6JbfMnyDDeJkEb5/VsY5CiN9g8m6gUqmg0+mg1+tht9tRWlqKtLS0\nAdt+c6kMmUwGhUKBK1euwOl0Qq1WIzk5eSRiEwDl+p5eyUMJntcr+boN6eNwqMKAq4ZO1lEI8QtM\nZnOJRCLk5OQgLy+vd2qwUqlEUVERACArKwsmkwlbtmxBR0cHhEIhDh06hF27dkEikWD9+vXIz89H\nW1sbYmNj8dRTT7F4GX7pLbVn90pukYcEYM2ssXj1eB1+++0ECAXDv14YIf5MwPv4KnnFxcVITU1l\nHcMnlOsteLnkGv70xBSPLyZAT6/22Y8qsTRpNB70wPEdQjyZWq1GZmamy+09/x2BeIx9ap1X9Epu\nEQgEWHt/DArPNNFgPCHDzDveFQhzTW3dqLzZgUUePlbyTdMUYZjIBeOg9gbrKIT4NComxCWHq4zI\nmChDoJf0Sr7uv2aNxTvn9WinnRkJGTbe985ARhzP8zh8xei14w6xoySYNz4C/3O2mXUUQnwWFRNy\nV5eaLQgQCZEwwvuVuNN/pI7BPyoN0JtptQRChgMVE3JXRVeMyIrnIPDi6bXy0AAsTYrEn880sY5C\niE+iYkLuqNvuxIkaEzInjWIdZcieSI7Gmfo2VBs6WEchxOdQMSF3VFrbivjIEESGBrKOMmShgSKs\nSFHgD6dpVWFC3I2KCbmjoisGZHnpwPtAFifK0dhmhbqhjXUUQnwKFRNyWwaLDRX6DqTHyVhHcZsA\nkRBr0sZg7xeNcPr24g+EjCgqJuS2iquNSI+LgETsW78m8yfIIBIKcPRqC+sohPgM33qXIG7D83zv\nLC5fIxAIsGrmGLytaabeCSFuQsWEDKjK0IkumxP3KcJYRxkWM2PCERIgxPFrJtZRCPEJVEzIgG71\nSnx16XaBQICVqQq8rdFR74QQN6BiQvqxO3l8Wt2CzEm+d4rr62YppQgUCVFa08o6CiFej4oJ6ef0\n9TYoI4IQExHEOsqwEggEeGqGAvs0un47ehJCBodZMdFqtXjhhRewceNG/P3vf+93f0NDA37605/i\nqaeewkcffdTvfqfTiU2bNmH79u0jEdev+Nq1JXcyJ1YKgQA4WUe9E0KGgkkxcTqdKCgoQG5uLrZv\n346SkhLU19f3aRMeHo41a9Zg6dKlAz7GoUOHoFQqvXq9KE/U1mWHuqEd/zLBd64tuZPe3omaeieE\nDAWTYlJVVQWFQoGoqCiIxWKkp6ejrKysTxupVAqVSgWRSNTveIPBAI1Gg4ULF9IbgJt9VmPCTKUU\nYUFi1lFGzLzxEXDyPL64TlfFE3KvmBQTo9EIuVzee5vjOBiNRpePLywsxMqVKyEU0pCPu52qa8O8\n8RGsY4wooUCAFTR2QsiQeN278ZkzZyCVSjFhwgT6j+9m3XYnzjW1Y5ZSyjrKiHsgToYumxNl9e2s\noxDilZicy+A4DgaDofe2wWAAx7k24Hv58mWcOXMGGo0GNpsNnZ2dePPNN7Fhw4bhius3NI3tUMlD\nIJX4zymuW77qnTQhTRlOY3GEDBKTdw2VSgWdTge9Xg+O41BaWopnnnlmwLbf7H2sWLECK1asANAz\nI+zgwYNUSNzkVF0r5sT6X6/kln+ZIMM+dRPUDe2Y6Ye9M0KGgkkxEYlEyMnJQV5eHhwOBzIzM6FU\nKlFUVAQAyMrKgslkwpYtW9DR0QGhUIhDhw5h165dkEgkfR6LPkG6h5Pn8XldG3YsmcQ6CjMiYU/v\n5O2zOiomhAySgPfxgYfi4mKkpqayjuHxKm90YPuRGvzxiSmsozDlcPL4z/e0eGHBeEz10XXJCHGF\nWq1GZmamy+29bgCeDI+eU1z+NYtrICKhAI9Pi8I755tZRyHEq1AxIQBovOTrHkqQ4/KNDtS0dLKO\nQojXoGJCcMNiRbPZiqnRdFoHAILEQnxn6mi8e17POgohXoOKCcGp2lbMUkohEtJkhluWJkXi87pW\nNLdbWUchxCtQMSE4VddG4yXfEBYkxkMJcvzvReqdEOIKKiZ+rtPmwMVmM2aNo/GSb3rsvigcvmJE\na5eddRRCPB4VEz+nbmhH4ugQhAb2X1DT38lDAzB/ggz/d+kG6yiEeDwqJn6OpgTf2RPJUfio/CY6\nbQ7WUQjxaFRM/Nitq96pmNyeMkKCaYow/P2y4e6NCfFjVEz82OUbHYiQiDFG6tvb8w7Vk9Oj8P4F\nPWwOJ+sohHgsKiZ+7FRtK+b42d4l92Ly6FCMiwjCp9UtrKMQ4rGomPixk3TVu8uenB6Nd8/r4fTt\npewIuWdUTPyUrr0bLZ12JI4OZR3FK8wYG45AkQCn6lpZRyHEI1Ex8VOn6tpw/zi66t1VAoEAy5Kj\n8R4tsULIgKiY+KnP61oxm05xDcr8CTLctNhwqdnMOgohHoeKiR+y2p3Q6i2YMTacdRSvcmt5euqd\nENIf082+tVotCgsLe3dbzM7O7nN/Q0MDdu/ejZqaGixfvhxLly4FANy8eRP5+flobW2FVCpFRkYG\nMjIyGLwC76TVWxArkyA8yP/2eh+qRQkc9ml0uG7qwjiZ5O4HEOInmL2bOJ1OFBQUYOvWreA4Dlu2\nbMG0adOgVCp724SHh2PNmjU4ffp0n2PFYjFWrVqFuLg4tLW1ITc3F5MmTepzLLk9TUM7UqlXck+C\nA0RYmhSJ9y/o8eP5sazjEOIxmJ3mqqqqgkKhQFRUFMRiMdLT01FWVtanjVQqhUqlgkjUd90omUyG\nuLi4Pm1aWugaAFdpGtsxI4aKyb16ZEokjl8zwdhhYx2FEI/BrJgYjUbI5fLe2xzHwWg0DvpxdDod\n6uvrER8f7854PsvcbUetqQtTomhK8L2SBQcgQzWKFoAk5Gu8egC+q6sLr732GlatWgWJhM5fu+Jc\nkxlTokIRKPbqHz1zj90XhY8rbqLDSgtAEgIwLCYcx8Fg+GrxPIPBAI7jXD7ebrdj586dmD9/PmbN\nmjUcEX2SprGdZnG5QUxEEFLGhtMCkIR8iVkxUalU0Ol00Ov1sNvtKC0tRVpa2oBt+W8sYcHzPPbs\n2QOlUoklS5aMRFyfoW6g8RJ3eSI5Ch9c1MPupCVWCGE2m0skEiEnJwd5eXm9U4OVSiWKiooAAFlZ\nWTCZTNiyZQs6OjogFApx6NAh7Nq1CzU1NTh+/DhiY2OxadMmAMCKFSuQkpLC6uV4hRsWK9q67FDJ\ng1lH8QmTR4dirDQIR6pb8GC8671qQnyRgP/mx34fU1xcjNTUVNYxPMI/Kw344nobXsycwDqKz/ji\neiv+eLoRBY8mQiCgpWmI71Cr1cjMzHS5PY3C+hGaEux+s5RSOHngTEM76yiEMEXFxE/wPE8XKw4D\ngUCAJ5Kj8M65ZtZRCGGKiomfqDV1IUAkpF0Vh0HGxFFoaOtG5Y0O1lEIYYaKiZ/QNLQjlU5xDYsA\nkRCP3ReFd89T74T4LyomfoKuLxle2ZPlONvYjobWbtZRCGGCiokfsDt5nG8yI2VsGOsoPiskUIQl\nSZH43wu0PD3xT1RM/MDlGxaMkQZBFhzAOopP+87U0ThytQUttAAk8UNUTPyApoFOcY2EUcEByJg4\nCgdoAUjih1y+Ar6trQ2XL19GfX09bty4gaioKMTExGDy5MmQSmn7V0+mbmzHv01XsI7hFx6bFoVn\nDl7Gk9OjERIouvsBhPiIuxaT5uZmHDx4EKdOnYJCoUB0dDTkcjnq6upw+vRp6HQ6zJ07F4888gii\noqJGIjMZhE6bA1U3O3GfgpacHwm3FoA8dNmAx6fR/wfiP+5aTPLy8vDggw9i5cqVCA7uv6ZTV1cX\njh49ih07dmDHjh3DEpLcuws6MxIiQxAcQJ+SR8qy6dH4edFVfHtKJAJEdCaZ+Ie7FpO7FQiJRIKH\nHnoIDz30kNtCEffR0CrBIy4hMgTjIoLwaXULFiXI734AIT6APjb5OE0jXazIwhPJ0Xjvgh5O315H\nlZBe97QEfXNzMzQaDQAgJSUFCgUN7nqilk4bms02JESGsI7id2bGhEMsFOCL622YExvBOg4hw86l\nnsmPf/zj3q+1Wi02btyIw4cP4/Dhw9i4cSMuXLgwbAHJvbvQZMZ90aEQCWlp9JEmEAiwLDkK79IC\nkMRPuNQz+fr2un/961/x2GOP4Tvf+Q4A4ODBg3jnnXcwbdq0QT2xVqtFYWFh78ZY2dnZfe5vaGjA\n7t27UVNTg+XLl2Pp0qUuH0t6nGsyI3kMXfXOyr9MGIU/lTXhos6M+xT0cyC+bdBjJo2NjVi4cGHv\n7YyMDNTX1w/qMZxOJwoKCpCbm4vt27ejpKSk32OEh4djzZo1fYqIq8eSHud1ZkwfQ+MlrIiEAixL\njsZfz1LvhPg+l4qJw+FASUkJSkpKIBAIEBgY2HufRCLpt0f73VRVVUGhUCAqKgpisRjp6ekoKyvr\n00YqlUKlUkEkEg36WAKYOm24abHRFr2MLUrgcNXYiaqbtDw98W0uFZP4+HgcP34cx48fx7hx4/r0\nBLRaLcaOHTuoJzUajZDLv5oyyXEcjEbjsB/rTy7oLJhK4yXMBYqEeGxaFP6Hxk6Ij3NpzOTnP//5\nbe9LSEjAli1b3JWHuMn5pnYaL/EQSxLleOdcM66bujBOJmEdh5BhMeTrTEJCQga9NhfHcX0G9Q0G\nAziOG/Zj/cm5JjOmUzHxCMEBInx7SiRt7Ut82qCLya9//ever7dt23ZPT6pSqaDT6aDX62G321Fa\nWoq0tLQB235zPGYwx/qr1i479GYrJsnp+hJP8e2po3GyrhXN7VbWUQgZFoO+aLGioqL36/Ly8nt6\nUpFIhJycHOTl5fVO71UqlSgqKgIAZGVlwWQyYcuWLejo6IBQKMShQ4ewa9cuSCSSAY8lX7nQZMbU\n6DAaL/Eg4UFiZE+W4/0LzVg/bxzrOIS43T1dAe8OU6ZMwW9+85s+38vKyur9WiaToaCgwOVjyVfo\nFJdn+u59UXj6f8uxIkWBUSG0URnxLbQ2lw+6oGvHNComHocL6dk864OLtLUv8T1UTHxMW5cdunYr\n4mk9Lo+0LDkahy4b0N5tZx2FELeiYuJjzuvMmBIdCjGNl3ik6PBAzImNwEHtTdZRCHErKiY+5gKt\nx+XxnkyOxoFLN9Bpc7COQojbDLqYTJ48uffrxMREt4YhQ9cz+E7rcXmy2FESJI8Jw8fl1DshvmPQ\nxWTz5s29X//kJz9xaxgyND3jJd00XuIFnkpR4P0LenTZnayjEOIWgyomWq12wO+fOHHCLWHI0Fxs\nNiMpisZLvMFEeTCmRIfhb9obrKMQ4haDKiY7d+7Evn37YLf3zEQxm83YtWsX3n333WEJRwaH9i/x\nLitnKPDeBT2NnRCfMKhismPHDtTW1mLLli0oKSnBxo0bERoaShcQeojzNF7iVSbKg3GfgsZOiG8Y\nVDHhOA7PP/88nE4nfve732HGjBn43ve+B4mEVkJlrb3bjqa2biSMpvESb0K9E+IrBlVMrl27hs2b\nNyM6OhrPP/88Ll68iNdeew0Wi2W48hEXXdRZkEjjJV5nAtfTO/kb9U6IlxtUMXnppZewZMkSbNq0\nCWlpadixYweCgoKwcePG4cpHXHSuqZ3W4/JSK2f0zOyi3gnxZoMqJq+88goyMzN7b99awXfNmjVu\nD0YG53yTGckKKibeaAIXjGnUOyFeblDFRKFQDPj9WbNmuSUMuTfmbjsaaLzEqz1FvRPi5e66BP17\n7703qAcUCAR4/PHH7zkQGbyLzRYkjg5FgIhWx/FWE7hgJCvC8FH5TSxLjmYdh5BBu+u7zzd3OnR3\nezJ05+n6Ep+wYoYC/0u9E+Kl7tozWbZs2bA8sVarRWFhYe9uidnZ2f3a7N+/H2q1GkFBQVi3bh1i\nYmIAAIcPH8aRI0dgs9mQlJSE1atXD0tGb3GuqR05c2i3SW9HvRPizYZ8XsRqtaKkpGRQxzidThQU\nFCA3Nxfbt29HSUkJ6uvr+7RRq9Wora1FXl4eVq9ejd27dwPouer+ww8/xIsvvoht27ahqakJZ8+e\nHerL8FrmbjvqW2m8xFesTFXg/fN6WKzUOyHe5Z6LSVVVFX7/+9/jRz/6Ub9C4MqxCoUCUVFREIvF\nSE9PR1lZWZ82ZWVlWLBgAQAgPj4eFosFJpMJgYGBAICOjg5YrVZ0d3cjLMx/T/H0jJeEIJDGS3zC\n+FHBuH+cFO+db2YdhZBBGdQe8CaTCceOHcPRo0fR3d2N7373u1i5ciWCg4MH9aRGoxFyubz3Nsdx\nqKqqumMbuVwOo9EImUyGtWvXYv369QgICEB2djYmTZo0qOf3JT3jJbSEii/599QxWHegAo9MGQ2O\n9oonXsLlj7P79+/H1q1b0dnZiU2bNuGZZ55Bd3f3oAvJYAw0mN/W1oa9e/di165dyM/PR2VlJdRq\n9bBl8HQ0+O57osMDkRXP4W2NjnUUQlzmcjGRyWT47W9/iyeffBLR0dGIj4/HmDFjsG/fvkE/Kcdx\nMBgMvbcNBgM4jnOpTVVVFeLj46FQKBAeHo65c+fedml8X2exOnC9tQuTabzE5/xbigJHr7agobWb\ndRRCXOJyMVm8eDEEgr7rPqWkpCAuLq53cNxVKpUKOp0Oer0edrsdpaWlSEtL69MmLS0Nx44dAwBU\nVlYiNDQUMpkMiYmJqK6uhtlshs1mg0ajwfTp0wf1/L7ios6MyTRe4pMiJGI8el8UCs80so5CiEsG\nNWYykAceeABRUVGDOkYkEiEnJwd5eXm9U4OVSiWKiooAAFlZWUhNTUV5eTlyc3N7l20BgJCQEDz2\n2GPYsWMHrFYrpk+fjqlTpw71ZXilczRe4tO+e99o/Od7Wly52UG7ZxKPJ+B9/CrD4uJipKamso4x\nLDYcuIzvz4nBNFqTy2cd1N7AydpWbMv230kmhA21Wt1nLca7uev5kQMHDsBsNt+xjdlsxoEDB1x+\nUjJ0NF7iH7Iny9HY1g1NYzvrKITc0V1Pc9ntdjz//POYNm0a4uPjER0dDY7jYDQaodPpUFVVhYsX\nL+LBBx8cibzkS5eazUiIpPESXxcgEmJ12hj88XQjfvtIQr9xS0I8xV2LyeOPP46HH34YJSUl0Gg0\naGxshMFgQGRkJGJiYnDfffdh7dq1vRcTkpFxrtFM+5f4iQUTR+G983qcqGnF/Aky1nEIGZBLA/AS\niQSLFy/G4sWL+93ncDjw/vvv48knn3R7OHJ753VmPH1/DOsYZAQIBQKsmTUWu0/WY974CIhoN03i\ngYZ8jsThcOCDDz5wRxbiIovVgdqWLiTSeInfmBkTjtGhAfi4gjbQIp6JTrh7oUvNX15fIqYfn78Q\nCAT4/mwl3lLr0NZlZx2HkH7o3cgL0RIq/mmiPBjzJ8jwlpqWWSGex6UxkwsXLtx2FondTp+SRtq5\nJjOevn8s6xiEgVUzx2Dt++VYkiRH3KjhWxePkMFyqZjs2bPnjvdHRka6JQy5u6/GS0JZRyEMREjE\nWJESjT2nGrDtX1U0VZh4DJeKSX5+/nDnIC6i8RKydMpofFxhwKm6NswdH8E6DiEAaMzE69B4CREL\nBfjBnBj87vMGWB1O1nEIAUDFxOucazIjmdbi8ntpSinGRQThwKUbrKMQAoCKiVfp+HK8JCmKxksI\n8P05MXj3XDNaOmysoxBCxcSbXGq29KzHReMlBIAyQoJFCXL8qayJdRRCqJh4k/NN7TReQvp4aoYC\nX1xvReXNDtZRiJ+jYuJFzjXR4o6kr9BAEValjcWbn12Hw+nTWxMRDzfknRbvlVarRWFhYe9Oi9nZ\n2f3a7N+/H2q1GkFBQVi3bh1iYnoWNuzq6sLevXtRV1cHm82GnJwcJCQkjPRLGFEWqwO1pi4k0ngJ\n+YaHEjgUXTHg44qbeGTKaNZxiJ9iUkycTicKCgqwdetWcByHLVu2YNq0aVAqlb1t1Go1amtrkZeX\nhytXrmD37t14+eWXAQB79+7FlClTsGHDBjgcDnR3d7N4GSPqXFM7EkeHIojGS8g3CAUCPJsei9yP\nr2Du+AiMDqXtIMjIY/LOVFVVBYVCgaioKIjFYqSnp6OsrKxPm7KyMixYsAAAEB8fD4vFApPJhI6O\nDlRUVGDhwoUAevaTDwnx/dVz1Q3tmBlD+72TgcWOkmBpUiTyS+tZRyF+ikkxMRqNkMvlvbdv7dx4\npzZyuRxGoxF6vR5SqRT5+fnIzc3Fnj17YLVaRyw7K+qGdsygYkLuYHlKNOpMXThRY2Idhfghjz5n\nwvP9BxQdDgeqq6sxe/ZsbNu2DXa7HSdPnmSQbuTozVa0dzugktPCfuT2AkVCPPvAOOw+WQ+L1cE6\nDvEzTIoJx3EwGAy9tw0GAziOc6mNXC5HWFgY0tLSEBgYiPT0dGg0mhHLzoK6oR0pY8MgpEX9yF0k\njwnHLKUUfy5rZB2F+BkmxUSlUkGn00Gv18Nut6O0tBRpaWl92qSlpeHYsWMAgMrKSoSGhkImk0Em\nk0GhUODKlStwOp1Qq9VITk5m8TJGjLqhDakxUtYxiJdYe/9YHK8xoVxvYR2F+BEms7lEIhFycnKQ\nl5fXOzVYqVSiqKgIAJCVlYXU1FSUl5cjNzcXEokEOTk5vcevX78e+fn5aGtrQ2xsLJ566ikWL2NE\nOHkemkZK5/XsAAAXQ0lEQVQz/msW7fdOXBMeJMb3Zyux63gddj+aCDHtGU9GgIAfaGDChxQXFyM1\nNZV1jHtWbejAr4pr8KdlU1hHIV6E53n89JNqJI8Jw/LpCtZxiBdSq9XIzMx0ub1HD8AT4ExDO1Jp\nFhcZJIFAgB+lj8P75/Woa+liHYf4ASomHk5NxYTcI0V4EFanjcX2IzWw0b4nZJhRMfFgVrsT5XoL\nrcdF7tmSRDnkIQHYp9GxjkJ8HBUTD3ap2YK4URKEBTFbQo14OYFAgB/Pj8U/LhtwqdnMOg7xYVRM\nPBhNCSbuwIUE4Efp4/CbI7XooIsZyTChYuLBaPCduEt6nAzJY8Lwu88bWEchPoqKiYdq7bKjsa0b\niaN9fxFLMjJy5iihaWzHydpW1lGID6Ji4qHONrZjmiIMASL6ERH3CAkU4YUF4/H6iTraN564Hb1T\neSiaEkyGw1RFGBYlyPHq8boBF1Il5F5RMfFAPM9TMSHD5t9TFTB02PBR+U3WUYgPoWLigRrbrLA7\necTKJKyjEB8UIBLipwvj8JZahwpaDJK4CRUTD6RuaMOMmHAIaMl5MkxiIiR49oFx+FXJNbR22VnH\nIT6AiokHUje0I3UsneIiwys9ToZvTRyFV0pq4HDS+AkZGiomHsbh5HGuyUzjJWRErE4bCyfP4y/q\nJtZRiJejYuJhKm92IDI0AFxIAOsoxA+IhAL8ZGEciq4Y6foTMiRUTDzM53WtmKWkJVTIyBkVHIAX\nF07Aq8fr0NDazToO8VLMVhDUarUoLCzs3WkxOzu7X5v9+/dDrVYjKCgI69atQ0zMV7sNOp1ObN68\nGRzHYfPmzSMZfVh9VtuKHz8QyzoG8TNTokOxcoYCLxVfxWuPTIZETJ8zyeAw+Y1xOp0oKChAbm4u\ntm/fjpKSEtTX1/dpo1arUVtbi7y8PKxevRq7d+/uc/+hQ4egVCp9asZTQ2sX2rvsSIyiJVTIyHtk\nSiTGjwrG6yfogkYyeEyKSVVVFRQKBaKioiAWi5Geno6ysrI+bcrKyrBgwQIAQHx8PCwWC0wmEwDA\nYDBAo9Fg4cKFPvVL/1ltK+aOj4DQhwok8R4CgQDPPjAOdaYuvE37n5BBYlJMjEYj5HJ5722O42A0\nGu/YRi6X97YpLCzEypUrIRT6Vle8tKYV88bLWMcgfiw4QISXFqnwSaUR/6w0sI5DvIhHvxsP1Os4\nc+YMpFIpJkyY4FO9EmOHDXWmLqSMpV0VCVtcSABefkiFvV80QtPQzjoO8RJMignHcTAYvvrUYzAY\nwHGcS20uX76MM2fOYP369Xj99ddx6dIlvPnmmyOWfbicrGvFrHFSWiWYeITYURK8mBmHVz6twTVj\nJ+s4xAsweedSqVTQ6XTQ6/Ww2+0oLS1FWlpanzZpaWk4duwYAKCyshKhoaGQyWRYsWIFCgoKkJ+f\nj2effRZTp07Fhg0bWLwMt/qsxoR54yNYxyCkV/KYcOTMicGLn1TjpsXKOg7xcEymBotEIuTk5CAv\nL693arBSqURRUREAICsrC6mpqSgvL0dubi4kEglycnIGfCxfmM1lsTqgbbbgxYUTWEchpI+Fkzg0\nm6148ZOr2PlwPEIDRawjEQ8l4H1p4GEAxcXFSE1NZR3jjj6tbkFxlRG/ekjFOgoh/fA8j9c/uw69\n2YpfLlJBLPT+D3Dk7tRqNTIzM11uTyfoPUBpjQnpdIqLeCiBQIAfzhsHkUCAbZ/WwE6LQpIBUDFh\nzOpwoqyhHXNiqZgQzyUSCrA1cwI6bQ78+lNaZZj0R8WEsbON7ZgwSoJRtLAj8XCBYiF+/uBEmK0O\n/OZoLRUU0gcVE8Y+q2mlWVzEawSKhfh51kS0dtmxgwoK+RoqJgw5nDxO1rZiXhxd9U68R9CXBaWl\n04adx6igkB5UTBiq0FswKliMsdIg1lEIGRSJWIhfLFLhhsWGXcfr4PTtSaHEBVRMGPqsthXp1Csh\nXkoiFuKXiyZC125F3tFamuXl56iYMMLzPEprTUiPo/ES4r2CA0R46aGJaO92YOsn1eiwOlhHIoxQ\nMWGkpqULDicwkQtmHYWQIQkOEOHnWROhCA/Exo+vwNBhYx2JMEDFhJHPakyYFxfhE8vBECISCvCj\n9HF4IE6GZw9Woq6li3UkMsKomDDA8zyOXjXhARovIT5EIBBgxQwF/j1VgY0fX8FFnZl1JDKCqJgw\ncEFnAQ/gvuhQ1lEIcbtFCXJsyhiPXxy+huPXTKzjkBFCxYSBv5XfwJJEOZ3iIj4rTSnFtn9VoeBU\nPf5ypomuRfEDVExGWEuHDWX17ciK5+7emBAvNikyBG9+ezIu6Mx48ZNqtHbZWUciw4iKyQj7R6UB\n6XERCAtispUMISOKCwnA9uxJmCQPxvoDFSjXW1hHIsOEiskIcjh5HKowYGnSaNZRCBkxIqEA/3V/\nDNbPHYf//udV/N+lG/DxbZT8EtOPx1qtFoWFhb27LWZnZ/drs3//fqjVagQFBWHdunWIiYnBzZs3\nkZ+fj9bWVkilUmRkZCAjI2PkX8AgldW3IUIiRsLoENZRCBlxc8dH4PVRCfjl4Wu41GzGj+fHIjiA\ndm70Fcx6Jk6nEwUFBcjNzcX27dtRUlKC+vr6Pm3UajVqa2uRl5eH1atXY/fu3QAAsViMVatW4dVX\nX8Vzzz2Ht99+u9+xnuhv5TfxcFIk6xiEMDNWGoTXH0mARCzCDz6owPmmdtaRiJswKyZVVVVQKBSI\nioqCWCxGeno6ysrK+rQpKyvDggULAADx8fGwWCwwmUyQyWSIi4sDAEilUqhUKrS0tIz0SxgUXXs3\ntHoLMlSjWEchhKkgsRDP/UssfjBHie2f1iK/9Do6bbQMi7djVkyMRiPkcnnvbY7jYDQa79hGLpf3\na6PT6VBfX4/4+PjhDTxEhyoMeHASB4mYhqkIAXpOe/3usURYrA7qpfgAj39nu9NAXVdXF1577TWs\nWrUKEolkBFMNjs3hxCeVBiyhU1yE9BEeJMamjDj8YI4S2z6tRX5pPfVSvBSzYsJxHAwGQ+9tg8EA\njuNcbmO327Fz507Mnz8fs2bNGpnQ9+izmlbEyiSIlXluwSOEpbnjI/C77ybCbLXj+x9U4ESNiWZ8\neRlmxUSlUkGn00Gv18Nut6O0tBRpaWl92qSlpeHYsWMAgMrKSoSGhkImk4HneezZswdKpRJLlixh\nEX9Q/lZ+E0upV0LIHUklYryQEYcfPxCLv5xpwqZDVbhq6GQdi7iI2dRgkUiEnJwc5OXl9U4NViqV\nKCoqAgBkZWUhNTUV5eXlyM3NhUQiQU5ODgDg8uXLOH78OGJjY7Fp0yYAwIoVK5CSksLq5dxWbUsn\n6lu7MJf2eSfEJTNiwlHwaCI+rriJzX+vQnpcBFbNHANZcADraOQOBLyP9yWLi4uRmprK7PnzS+sR\nEijEf6aNZZaBEG/V3m3HPrUOJdUtWD49GkunRCJQ5PFDvT5BrVYjMzPT5fb0UxlGnTYHSqqNWJJI\np7gIuRfhQWLkzFVi55J4nG1sx3++q8VB7Q1Y7U7W0cg30AJRw+htjQ73j5MiKiyQdRRCvFrsKAle\nekiFyzcseFujw1/PNmNZchQWJ0YiiKbbewT6KQyTa8ZOfFJpxPfuj2EdhRCfMXl0KH65SIVfLpqI\n801mrHrnEt4/30zTiT0A9UyGgZPn8cZn1/EfqQqMCqFBQ0LcLT4yBD/Lmoirhk68fVaH/zl3CYsS\n5Hg4KRJjpUGs4/klKibDoOiKETYnj8U0VkLIsJooD8bWzAloau/G37Q38czBSkweHYJHpkQiTSmF\nkDagGzF0msvN2rrs+MMXjfhR+jiIhPSLTMhIGBMehKdnx2Df8qmYP0GGP5c1Yc17Wrx/vhktHTbW\n8fwC9UzcbO8XjVgwcRTiI2mZeUJGWpBYiIcS5FgUz6HiRgc+Kr+Jt98vR1JUCBaqOMwbH4GQQFr2\nfjhQMXGjSzozTte3Ye/jSayjEOLXBAIBkqJCkRQVik6bA6fqWlFS1YI3S6/j/nFSZE7iMFMphZjO\nHrgNFRM3sTt5vP7ZdXx/dgxC6ZMPIR4jOECEb6k4fEvFwdRpw7FrJvz1bDN+faQWM2PCMWd8BGYp\npZBK6O1wKOhfz00+vKgHFxKABRNlrKMQQm5DFhyAR6aMxiNTRsPQYcMXda04erUFb3x2HSp5CObE\nSjE7NgLjIoIgoMH7QaFi4gZ6sxXvnGvG648k0C8gIV5CHhKA7MRIZCdGotvuhKaxHafqWrH571Xg\neSB5TBhSxoRh+thwjAkPpP/bd0HFZIhaOmz4xeGrePS+KMRE0BLzhHijILEQc2IjMCc2AjzPo7HN\ninNN7TjbZEahuglioQDJY8IxNToUiaNDEDcqmGZrfgMVkyGob+3CT/9RjQfjOaxIiWYdhxDiBgKB\nADERQYiJCMLixEjwPI/61m6cazJD22zBBxf0uNlhg0oejMTRoZg8OgQJo0MQHRbo19e1UDG5R9pm\nC35x+CpWp41F9mT53Q8ghHglgUCAcTIJxskkePjLfYksVgcu37CgQt+BkqoW7DnVgE6bA3GjgjGB\nk2ACF4yJXDDiRkkQFuQfb7P+8Srd7LMaE147cR3PL4jF/eNonxJC/E1ooAipMVKkxkh7v9fWZUdN\nSyeuGrtQbejE4StG1Jq6IBELERMRBKVUAuWXPR5lRBAU4UE+tUgls2Ki1WpRWFjYuzFWdnZ2vzb7\n9++HWq1GUFAQ1q1bh5iYGJePHS4HtTew/6wOLz+kQsJoujCRENJDKhEjeUw4kseE936P53kYOmyo\nb+1GfWs3Glq7cEFnRn1rN/QWK8ICRYgOC+z5Ex6IqC+/jgwNABcSgAiJ2GtOnTEpJk6nEwUFBdi6\ndSs4jsOWLVswbdo0KJXK3jZqtRq1tbXIy8vDlStXsHv3brz88ssuHTscTJ02vHOuGZ9fb8OuhxMw\nhhaTI4TchUAgQGRoICJDA5EyNrzPfU6eh7HDhmazFc3tVjSbrbhq7MSpulYYLDYYOmzotDkxKkQM\neUgA5CEBGBXcU2BkwWLIvvw7QiIGFxKAcMan05g8e1VVFRQKBaKiogAA6enpKCsr61MQysrKsGDB\nAgBAfHw8LBYLTCYT9Hr9XY91F3O3HaW1rfi0ugUVNzowJ1aKXUsTEEEXNxFChkj4tUIz9Tbzd6x2\nJ4ydPYXFYLHB1GWHqdOOmpYumDrtMHXZYOq0Y/LoELyQETei+b+Jybui0WiEXP7VoDXHcaiqqrpj\nG7lcDqPR6NKx98LJ87BYHWjrcuDKzQ4cudqCs43tSBkbjocS5PjvBycgOICubCeEjJxAsRCK8J7x\nFU/n0R+x3bU9/YufVOPWQ/Hgv3xsoMPWUzzau+0wWx0IDhBBGiRCTEQQMiaOwvMLxtPSKIQQ4gIm\nxYTjOBgMht7bBoMBHMe51MZut9/12K+TyWT4LkwuJrN/+acbMLfh8sVaF48jhBDfIpMNbmkoJsVE\npVJBp9NBr9eD4ziUlpbimWee6dMmLS0Nn3zyCdLT01FZWYnQ0FDIZDKEh4ff9divmzlz5nC/HEII\n8XsC3l3nkgZJq9Xiz3/+c+/03sWLF6OoqAgAkJWVBQB4++23oVarIZFIkJOT0zvIPtCxhBBC2GFW\nTAghhPgO37n8khBCCDNUTAghhAyZR08NHiqWy6646ubNm8jPz0drayukUikyMjKQkZHBOtaAnE4n\nNm/eDI7jsHnzZtZxBtTV1YW9e/eirq4ONpsNOTk5SEhIYB2rn8OHD+PIkSOw2WxISkrC6tWrWUcC\nAOzevRsajQZSqRQ7d+4EAHR2duKNN96AXq9HdHQ0fvjDH0IiYbvdwkA533rrLajVagQGBiIpKQnL\nli1DSAjbJY8GynnLRx99hH379uEPf/gDwsLCGCXscbucn376KT755BPYbDbMmDEDK1euvP2D8D7K\n4XDwGzZs4Jubm3mbzcZv3LiRv379OutY/bS0tPDXrl3jeZ7nW1tb+bVr13pkTp7n+Y8++oh//fXX\n+e3bt7OOcltvvPEGX1xczPM8z9vtdt5isTBO1F97ezu/bt06vrOzk3c4HPwrr7zCazQa1rF4nud5\nrVbLX716lX/uued6v/fWW2/xBw4c4Hme5z/88EN+3759rOL1GijnuXPneIfDwTscDr6goMBjc/I8\nz9+4cYP/1a9+xa9bt45vb29nlO4rA+W8cOEC/8tf/pK32Ww8z/e8P92Jz57m+vqSLWKxuHfZFU8j\nk8kQFxcHAJBKpVCpVGhpaWEbagAGgwEajQYLFy5028Wk7tbR0YGKigosXLgQACASiZh/Mh1IYGAg\ngJ68VqsV3d3dzD+Z3pKUlITQ0NA+3/v60kYZGRk4ffo0i2h9DJQzOTkZQqEQQqEQKSkpfa5HY2Wg\nnADwl7/85c6f8kfYQDn/+c9/4tFHH4VY3HMCSyqVDnRoL589zTVcy64MJ51Oh/r6esTHx7OO0k9h\nYSFWrlyJzs5O1lFuS6/XQyqVIj8/H1evXkV8fDzWrFnT++btKQIDA7F27VqsX78eAQEByM7OxqRJ\nk1jHuq3W1tbeC9giIiLQ2trKONHdFRcX936o8DSnT58Gx3EYP3486yh3pNPpoNVq8dZbb0EikWDV\nqlWYOHHibdv7bM/E23R1deG1117DqlWrmJ+P/qYzZ85AKpViwoQJHtsrAQCHw4Hq6mrMnj0b27Zt\ng91ux8mTJ1nH6qetrQ179+7Frl27kJ+fj8rKSqjVataxXOIN+6B/8MEHkEgkmDt3Luso/XR3d+PD\nDz/EsmXLer/nqf+nHA4H9Ho9XnrpJSxduhRvvfXWHdv7bDFxZckWT2G327Fz507Mnz8fs2bNYh2n\nn8uXL+PMmTNYv349Xn/9dVy6dAlvvvkm61j9yOVyhIWFIS0tDYGBgUhPT4dGo2Edq5+qqirEx8dD\noVAgPDwcc+fOhVarZR3rtiIiImAy9SxJ1NLSgogIz90Q7siRI9BoNPjhD3/IOsqAmpubcePGDTz/\n/PNYv349jEYjNm/e7JG9Pblcjnnz5iEwMBBpaWlobGyE1Wq9bXufLSZfX7LFbrejtLQUaWlprGP1\nw/M89uzZA6VSiSVLlrCOM6AVK1agoKAA+fn5ePbZZzF16lRs2LCBdax+ZDIZFAoFrly5AqfTCbVa\njeTkZNax+klMTER1dTXMZjNsNhs0Gg2mT5/OOtZtpaWl4ciRIwCAo0ePeuQHHgA4e/YsDh48iE2b\nNnncqc1bYmNj8fvf/x75+fnIz88Hx3H49a9/7ZEFetasWdBoNOB5HleuXEF0dPQd/119+gp4b1h2\npaKiAj/72c8QGxvbewphxYoVSElJYZxsYFqtFh999BFeeOEF1lEG1NjYiPz8fLS1tSE2NtYjprEO\n5MiRI/j0009htVoxffp0LFu2DEIh+892r732GsrLy9He3o6IiAgsW7YMc+bM8bipwbdytrW1QSaT\n4YknnsCBAwdgt9t7JzMkJCRg7dq1HpHz6/+e3/rWt3rv37BhA7Zv3858AsZAORcsWIC9e/fi0qVL\nEIvFePrpp5GYmHjbx/DpYkIIIWRksP8oRAghxOtRMSGEEDJkVEwIIYQMGRUTQgghQ0bFhBBCyJBR\nMSGEEDJkVEwIIYQMGRUTQgghQ0bFhBAGDh06hP3797OOQYjbUDEhhIHs7GycPHmydwFFQrwdFRNC\nGBAIBHjggQdw7Ngx1lEIcQsqJoQwkpGRgaNHj7KOQYhbUDEhhJG2tjZ0d3d7/A6ghLiCVg0mhIGz\nZ8+iqakJQUFBqK6uxtNPP806EiFDQj0TQkbYiRMncPHiRWRnZ2Pu3Lk4c+bMHXewI8QbUDEhZARV\nVlbi/PnzWLlyJQAgODgY8+bNw4kTJxgnI2Ro6DQXIYSQIaOeCSGEkCGjYkIIIWTIqJgQQggZMiom\nhBBChoyKCSGEkCGjYkIIIWTIqJgQQggZMiomhBBChoyKCSGEkCH7///NT2O0qvwtAAAAAElFTkSu\nQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x113ca5c10>"
       ]
      }
     ],
     "prompt_number": 16
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "How is the likelihood function different than the probability distribution function (PDF)? The likelihood is a function of the parameter(s) *given the data*, whereas the PDF returns the probability of data given a particular parameter value. Here is the PDF of the Poisson for $\\lambda=5$."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "lam = 5\n",
      "xvals = arange(15)\n",
      "plt.bar(xvals, [poisson_like(x, lam) for x in xvals])\n",
      "xlabel('x')\n",
      "ylabel('Pr(X|$\\lambda$=5)')"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 17,
       "text": [
        "<matplotlib.text.Text at 0x113d83890>"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAZMAAAEUCAYAAADuqdsBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X9w0/X9B/Bnm9JG2ob4ya5EyRgsDUKxwGoYg8iXWs25\n4tjpdBzX9gbX4XYpeDgq2G6yedsYWALFaRo36rTi8Jw74fCud6wICF5x1zRxUwOUgIAFQjSh1Lb0\nR5rP9w/0M0MLpHzaftLyfPyVz+fzfn8+r/Sgz34+n/fn804QRVEEERGRDIlKF0BERCMfw4SIiGRj\nmBARkWwMEyIiko1hQkREsjFMiIhItiSlDuz1elFTU4Pe3l7cf//9yM/Pj9p+9uxZVFVV4dSpU1iy\nZAkWLVokbdu7dy8OHDiAnp4eTJs2DcuWLRvm6omI6JsUOTOJRCJwOp0oLS3Fxo0bsW/fPjQ3N0e1\nSU9PR3FxcVSIAEBbWxt27tyJZ555Bhs2bMD58+fx4YcfDmf5RER0FUXCxOfzQa/XIyMjA0lJSbBY\nLHC5XFFtNBoNjEYjVCpV1Prk5GQAQEdHB7q7u9HV1YW0tLRhq52IiPpS5DJXKBSCTqeTlgVBgM/n\ni6lvcnIyli9fjhUrVmDMmDHIz89HZmbmUJVKREQxGHE34FtbW1FdXY3Kyko4HA40NTXB7XYrXRYR\n0S1NkTMTQRAQDAal5WAwCEEQYurr8/lgMpmg1+sBAHPnzoXX60VOTk6/7T/44AO0t7fLL5qI6Bai\n1Wpxzz33xNxekTAxGo3w+/0IBAIQBAH19fVYtWpVv22vfg/l1KlT8corr6CtrQ0pKSnweDxYuHDh\nNY/V3t5+zaAhIqL+DfSKjyJholKpYLPZYLfbpaHBBoMBdXV1AACr1YqWlhaUl5ejo6MDiYmJqK2t\nRWVlJcaOHYtHH30UmzZtQnd3N2bOnInp06cr8TWIiOgrCaP9FfTvvvsuz0yIiAbI7Xbj/vvvj7n9\niLsBT0RE8UexJ+BpZDrf2oVAW7esfWSkJeMOTcqQ7pOIhhfDhAYk0NaNNbWxPRN0LZsWZkb94h+K\nfRLR8OJlLiIiko1hQkREsjFMiIhINoYJERHJxjAhIiLZGCZERCQbw4SIiGRjmBARkWwMEyIiko1h\nQkREsjFMiIhINoYJERHJxjAhIiLZFHtrsNfrRU1NjTTTYn5+ftT2s2fPoqqqCqdOncKSJUuwaNEi\naVtnZyeqq6tx5swZ9PT0wGazYcqUKcP9FYiI6CuKhEkkEoHT6cS6desgCALKy8uRnZ0Ng8EgtUlP\nT0dxcTEaGhr69K+urkZWVhZWrlyJ3t5edHV1DWf5RER0FUUuc/l8Puj1emRkZCApKQkWiwUulyuq\njUajgdFohEqlilrf0dGBo0ePIi8vD8CV+eTHjh07bLUTEVFfipyZhEIh6HQ6aVkQBPh8sU2OFAgE\noNFo4HA4cPLkSZhMJhQXFyM5OXmoyiUiohsYcTfge3t7ceLECcyZMwcbNmxAOBzG4cOHlS6LiOiW\npkiYCIKAYDAoLQeDQQiCEFNfnU6HtLQ0mM1mJCcnw2KxwOPxDFWpREQUA0XCxGg0wu/3IxAIIBwO\no76+Hmazud+2oihGLWu1Wuj1ehw/fhyRSARutxszZswYjrKJiOgaFLlnolKpYLPZYLfbpaHBBoMB\ndXV1AACr1YqWlhaUl5ejo6MDiYmJqK2tRWVlJdRqNVasWAGHw4HW1lZMnDgRhYWFSnwNIiL6imLP\nmWRlZaGioiJqndVqlT5rtVo4nc5++955551Yv379kNZHRESxG3E34ImIKP4wTIiISDaGCRERycYw\nISIi2RgmREQkG8OEiIhkY5gQEZFsDBMiIpKNYUJERLIxTIiISDaGCRERycYwISIi2RR70SPRUDrf\n2oVAW7esfWSkJeMOTcogVUQ0ujFMaFQKtHVjTW1sU0Ffy6aFmQwTohjxMhcREcnGMCEiItkUu8zl\n9XpRU1MjzbSYn58ftf3s2bOoqqrCqVOnsGTJEixatChqeyQSQVlZGQRBQFlZ2XCWTkREV1EkTCKR\nCJxOJ9atWwdBEFBeXo7s7GwYDAapTXp6OoqLi9HQ0NDvPmpra2EwGHD58uXhKpuIiK5BkctcPp8P\ner0eGRkZSEpKgsVigcvlimqj0WhgNBqhUqn69A8Gg/B4PMjLy4MoisNVNhERXYMiYRIKhaDT6aRl\nQRAQCoVi7l9TU4OioiIkJvKWDxFRPBhxQ4MbGxuh0WgwefJkfPLJJ0qXE9f4rAURDRdFwkQQBASD\nQWk5GAxCEISY+h47dgyNjY3weDzo6enB5cuX8eKLL2LlypVDVe6IxWctiGi4KBImRqMRfr8fgUAA\ngiCgvr4eq1at6rft1fdECgoKUFBQAODKiLDdu3czSIiIFKZImKhUKthsNtjtdmlosMFgQF1dHQDA\narWipaUF5eXl6OjoQGJiImpra1FZWQm1Wh21r4SEBCW+AhERfYNi90yysrJQUVERtc5qtUqftVot\nnE7nDfeRlZU1JPUREVHsOByKiIhkY5gQEZFsDBMiIpKNYUJERLIxTIiISDaGCRERycYwISIi2Rgm\nREQkG8OEiIhkY5gQEZFsDBMiIpKNYUJERLIxTIiISDaGCRERycYwISIi2RgmREQkm2KTYwFXpt2t\nqamRZlvMz8+P2n727FlUVVXh1KlTWLJkCRYtWgQA+OKLL+BwOHDp0iVoNBrk5uYiNzdXgW9ARESA\ngmESiUTgdDqxbt06CIKA8vJyZGdnw2AwSG3S09NRXFyMhoaGqL5JSUlYunQpJk2ahNbWVpSWliIz\nMzOqLxERDR/FLnP5fD7o9XpkZGQgKSkJFosFLpcrqo1Go4HRaIRKpYpar9VqMWnSpKg2Fy9eHK7S\niYjoKoqFSSgUgk6nk5YFQUAoFBrwfvx+P5qbm2EymQazPCIiGoARfQO+s7MTW7duxdKlS6FWq5Uu\nh4jolqVYmAiCgGAwKC0Hg0EIghBz/3A4jM2bN2P+/PmYPXv2UJRIREQxUixMjEYj/H4/AoEAwuEw\n6uvrYTab+20rimKf5ZdeegkGgwEPPfTQcJRLRETXodhoLpVKBZvNBrvdLg0NNhgMqKurAwBYrVa0\ntLSgvLwcHR0dSExMRG1tLSorK3Hq1CkcOnQIEydOxNq1awEABQUFmDVrllJfh4jolqbocyZZWVmo\nqKiIWme1WqXPWq0WTqezT7+pU6fizTffHPL6iIgoNiP6BjwREcUHhgkREcnGMCEiItkYJkREJBvD\nhIiIZGOYEBGRbDEPDW5tbcWxY8fQ3NyMzz//HBkZGZgwYQLuuusuaDSaoayRiIji3A3D5MKFC9i9\nezc++OAD6PV6jB8/HjqdDmfOnEFDQwP8fj/mzp2LH//4x8jIyBiOmomIKM7cMEzsdjseeOABFBUV\n4bbbbuuzvbOzE++99x42bdqETZs2DUmRREQU324YJjcKCLVajQcffBAPPvjgoBVFREQjy029TuXC\nhQvweDwAgFmzZkGv1w9qUURENLLENJrrV7/6lfTZ6/Xiqaeewt69e7F371489dRT+Oijj4asQCIi\nin8xnZl8c96RN954A48++igefvhhAMDu3bvx5ptvIjs7e2gqJCKiuDfg50zOnTuHvLw8aTk3NxfN\nzc2DWhQREY0sMZ2Z9Pb2Yt++fQCAhIQEJCcnS9vUanWfyauIRqPzrV0ItHXL2kdGWjLu0KQMUkVE\n8SOmMDGZTDh06BAA4Nvf/jaam5uRmZkJ4Mo9lDvvvHPAB/Z6vaipqZEmxsrPz4/afvbsWVRVVeHU\nqVNYsmQJFi1aFHNfoqEQaOvGmlqfrH1sWpjJMKFRKaYwefbZZ6+5bcqUKSgvLx/QQSORCJxOJ9at\nWwdBEFBeXo7s7GwYDAapTXp6OoqLi9HQ0DDgvkRENLxkv5tr7NixA36dis/ng16vR0ZGBpKSkmCx\nWOByuaLaaDQaGI1GqFSqAfclIqLhNeAwee6556TPGzZsuKmDhkIh6HQ6aVkQBIRCoSHvS0REQ2PA\nYXL06FHp85EjRwa1GCIiGpkUeQW9IAhRz64Eg0EIgjDkfYmIaGgoEiZGoxF+vx+BQADhcBj19fUw\nm839tr162PFA+hIR0fC4qXdzyaVSqWCz2WC326XhvQaDAXV1dQAAq9WKlpYWlJeXo6OjA4mJiait\nrUVlZSXUanW/fYmISDmKhAkAZGVloaKiImqd1WqVPmu1Wjidzpj7EhGRcjhtLxERyTbgMLnrrruk\nz1OnTh3UYoiIaGQacJiUlZVJn3/9618PajFERDQyyb7M1d3dLb0EkoiIbk03fQPe5/Nh//79aGxs\nxLx58wazJiIiGmEGFCYtLS04ePAg3nvvPXR1deEnP/kJioqKcNtttw1VfURENALEHCY7duzA4cOH\nce+992Lt2rVobW2Fz+djkBARUexhotVq8ec//xkJCQkAgPHjx6O9vR2vv/46ioqKhqxAIiKKfzHf\ngF+4cKEUJF+bNWsWJk2ahKqqqkEvjIiIRg7ZT8Dfe++9yMjIGIxaiIhohBqUJ+CnTJkyGLshIqIR\n6oZnJm+99daAdpiQkIDHHnvspgsiIqKR54ZnJle/An6w2xMR0ch3wzOTxYsXD0cdREQ0gvGtwURE\nJFtMo7n+/e9/Y86cOf1uC4fD+Oc//4klS5YMamG3mvOtXQi0dcvaR0ZaMu7QpAxSRUREsYspTF59\n9VW8//77WL58OcaNGyetP3r0KP7yl7/g9ttvH/CBvV4vampqpNkS8/Pz+7TZsWMH3G43UlJSUFJS\nggkTJgAA9u7diwMHDqCnpwfTpk3DsmXLBnz8eBNo68aaWp+sfWxamMkwISJFxHSZa8uWLdBoNFi9\nejUOHDiAjo4ObNu2DRUVFVi0aBF++9vfDuigkUgETqcTpaWl2LhxI/bt24fm5uaoNm63G6dPn4bd\nbseyZcukByPb2tqwc+dOPPPMM9iwYQPOnz+PDz/8cEDHJyKiwRXTmcltt92Gxx9/HPPmzcOWLVvw\n8ssvIzs7G1u2bIFWqx3wQX0+H/R6vfSwo8VigcvliprL3eVyYcGCBQAAk8mE9vZ2tLS0YOzYsQCA\njo4OAEBXVxfS0tIGXAMREQ2emJ+Ab21txd69e6FSqTBlyhQ0Nzfj3LlzNxUmoVAIOp1OWhYEAT6f\n77ptdDodQqEQtFotli9fjhUrVmDMmDHIz89HZmbmgGsgIqLBE1OYvP/++3j11VeRk5ODyspKpKam\n4uDBg9iyZQu+//3vo6ioSDpjGEz9PbPS2tqK6upqqY4tW7bA7XYjJydn0I9PRESxiemeyRtvvIEn\nnngCJSUlSE1NBQD83//9HzZv3oy2tjasXr16QAcVBAHBYFBaDgaDEAQhpjY+nw8mkwl6vR7p6emY\nO3cuvF7vgI5PRESDK6Yw2bx5M2bOnNln/bhx47B69WoUFxcP6KBGoxF+vx+BQADhcBj19fUwm81R\nbcxmMw4ePAgAaGpqQmpqKrRaLaZOnYoTJ06gra0NPT098Hg8/dZGRETD54aXuXbt2oUHHnjgum2y\nsrKwa9cuPPzwwzEdVKVSwWazwW63S0ODDQYD6urqAABWqxU5OTk4cuQISktLoVarYbPZAABjx47F\no48+ik2bNqG7uxszZ87E9OnTYzouERENjRuGSTgcxpo1a5CdnQ2TyYTx48dDEASEQiH4/X74fD58\n/PHHNwycq2VlZaGioiJqndVqjVouLCxEYWFhn765ubnIzc0d0PGIiGjo3DBMHnvsMfzoRz/Cvn37\n4PF4cO7cOQSDQXzrW9/ChAkTcPfdd2P58uVITk4ejnqJiCgOxTSaS61WY+HChfjhD3+IxES+zouI\niKLFnAy9vb1YunQpenp6hrIeIiIagWIOE5VKhe985zt9Hi4kIiIa0Bzw8+fPx7Zt2zBv3jyYTCao\nVCpp29133z3oxRER0cgwoDDZvXs3AGD//v3Yv39/1DaHwzF4VRER0YgyoDBhYBARUX9iCpPOzk68\n/fbb+OyzzzB58mQ88sgjGDNmzFDXRkREI0RMN+D/9re/4dChQ7j99tuxf/9+vPbaa0NdFxERjSAx\nhYnH48HTTz+NX/ziF1i7di3cbvdQ10VERCNITGHS2dmJSZMmAQAmT54sTUxFREQExHjPRBRFfPzx\nx9Ln3t5eaflrHBpMRHTriilMxo0bB6fTKS2np6dHLQMc6UVEdCuLKUwYFEREdD0Des6EiAbX+dYu\nBNq6b7p/Rloy7tCkDGJFRDeHYUKkoEBbN9bU3vz77jYtzGSYUFxQLEy8Xi9qamqkmRbz8/P7tNmx\nYwfcbjdSUlJQUlKCCRMmALgyuqy6uhpnzpxBT08PbDYbpkyZMtxfgYiIvqJImEQiETidTqxbtw6C\nIKC8vBzZ2dkwGAxSG7fbjdOnT8Nut+P48eOoqqrC+vXrAQDV1dXIysrCypUr0dvbi66uLiW+BhER\nfUWRma58Ph/0ej0yMjKQlJQEi8UCl8sV1cblcmHBggUAAJPJhPb2drS0tKCjowNHjx5FXl4egCuv\nxh87duywfwciIvofRc5MQqEQdDqdtCwIQp95Uq5uo9PpEAqFkJiYCI1GA4fDgZMnT8JkMqG4uJjT\nBhMRKSiu5+AVRbHPut7eXpw4cQJz5szBhg0bEA6HcfjwYQWqIyKirykSJoIgIBgMSsvBYBCCIMTU\nRqfTIS0tDWazGcnJybBYLPB4PMNWOxER9aVImBiNRvj9fgQCAYTDYdTX18NsNke1MZvNOHjwIACg\nqakJqamp0Gq10Gq10Ov1OH78OCKRCNxuN2bMmKHE1yAioq8ocs9EpVLBZrPBbrdLQ4MNBgPq6uoA\nAFarFTk5OThy5AhKS0uhVqths9mk/itWrIDD4UBraysmTpyIwsJCJb4GERF9RbHnTLKyslBRURG1\nzmq1Ri0XFhb2GxR33nmnNEyYiIiUF9c34ImIaGRgmBARkWwMEyIiko1hQkREsjFMiIhINoYJERHJ\nxjAhIiLZGCZERCQbw4SIiGRjmBARkWwMEyIiko1hQkREsjFMiIhINoYJERHJxjAhIiLZGCZERCSb\nYpNjeb1e1NTUSDMt5ufn92mzY8cOuN1upKSkoKSkBBMmTJC2RSIRlJWVQRAElJWVDWfpRER0FUXO\nTCKRCJxOJ0pLS7Fx40bs27cPzc3NUW3cbjdOnz4Nu92OZcuWoaqqKmp7bW0tDAYDEhIShrN0IiLq\nhyJh4vP5oNfrkZGRgaSkJFgsFrhcrqg2LpcLCxYsAACYTCa0t7ejpaUFABAMBuHxeJCXlwdRFIe9\nfiIiiqZImIRCIeh0OmlZEASEQqHrttHpdFKbmpoaFBUVITGRt3yIiOJBXP827u+so7GxERqNBpMn\nT+ZZCRFRnFDkBrwgCAgGg9JyMBiEIAgxtfnggw/Q2NgIj8eDnp4eXL58GS+++CJWrlw5bPUTEVE0\nRcLEaDTC7/cjEAhAEATU19dj1apVUW3MZjP27NkDi8WCpqYmpKamQqvVoqCgAAUFBQCujAjbvXs3\ng4SISGGKhIlKpYLNZoPdbpeGBhsMBtTV1QEArFYrcnJycOTIEZSWlkKtVsNms/W7L47mIiJSnmLP\nmWRlZaGioiJqndVqjVouLCxEYWHhdfeRlZU1JPUREVHsFAsTIhoa51u7EGjrvun+GWnJuEOTMogV\n0a2AYUI0ygTaurGm1nfT/TctzGSY0IDF9dBgIiIaGXhmchPkXkYAeCmBiEYXhslNkHsZAeClBCIa\nXXiZi4iIZGOYEBGRbAwTIiKSjWFCRESyMUyIiEg2hgkREcnGMCEiItkYJkREJBvDhIiIZGOYEBGR\nbAwTIiKSTdF3c3m9XtTU1EizLebn5/dps2PHDrjdbqSkpKCkpAQTJkzAF198AYfDgUuXLkGj0SA3\nNxe5ubnD/wWIiAiAgmESiUTgdDqxbt06CIKA8vJyZGdnw2AwSG3cbjdOnz4Nu92O48ePo6qqCuvX\nr0dSUhKWLl2KSZMmobW1FaWlpcjMzIzqS0REw0exy1w+nw96vR4ZGRlISkqCxWKBy+WKauNyubBg\nwQIAgMlkQnt7O1paWqDVajFp0iQAgEajgdFoxMWLF4f7KxAR0VcUC5NQKASdTictC4KAUCh03TY6\nna5PG7/fj+bmZphMpqEtmIiIrinub8CLonjNbZ2dndi6dSuWLl0KtVo9jFUREdE3KRYmgiAgGAxK\ny8FgEIIgxNwmHA5j8+bNmD9/PmbPnj08RRMRUb8UuwFvNBrh9/sRCAQgCALq6+uxatWqqDZmsxl7\n9uyBxWJBU1MTUlNTodVqIYoiXnrpJRgMBjz00EMKfQOiW4fcqao5TfXop1iYqFQq2Gw22O12aWiw\nwWBAXV0dAMBqtSInJwdHjhxBaWkp1Go1bDYbAODYsWM4dOgQJk6ciLVr1wIACgoKMGvWLKW+DtGo\nJneqak5TPfop+pxJVlYWKioqotZZrdao5cLCQhQWFkatmzp1Kt58880hr4+IiGIT9zfgiYgo/jFM\niIhINoYJERHJxjAhIiLZGCZERCQbw4SIiGRjmBARkWwMEyIiko1hQkREsjFMiIhINkVfp0JEty6+\nPHJ0uSXC5D/nvpTVn/9oiQYfXx45utwSYSLnHyzAf7RERDfCeyZERCQbw4SIiGRT7DKX1+tFTU2N\nNDFWfn5+nzY7duyA2+1GSkoKSkpKMGHChJj7EhHR8FEkTCKRCJxOJ9atWwdBEFBeXo7s7GwYDAap\njdvtxunTp2G323H8+HFUVVVh/fr1MfUloluP3NFhAAfbyKFImPh8Puj1emRkZAAALBYLXC5XVCC4\nXC4sWLAAAGAymdDe3o6WlhYEAoEb9iWiW4/c0WEAB9vIoUiYhEIh6HQ6aVkQBPh8vuu20el0CIVC\nMfUlIhoMPNuJXVwPDRZFUekSiOgWNhRnO6M1oBJEBX5jNzU14a233sJvfvMbAMDOnTuRkJCAhx9+\nWGrz17/+FdOnT4fFYgEAPPnkk3j22WcRCARu2PebGhsb0dLSMsTfiIhodNFqtbjnnntibq/ImYnR\naITf70cgEIAgCKivr8eqVaui2pjNZuzZswcWiwVNTU1ITU2FVqtFenr6Dft+00B+GEREdHMUOTMB\nrgzvffXVV6XhvQsXLkRdXR0AwGq1AgD+/ve/w+12Q61Ww2azSTfZ++tLRETKUSxMiIho9OAT8ERE\nJBvDhIiIZIvrocFyjYTXrnzxxRdwOBy4dOkSNBoNcnNzkZubq3RZ/YpEIigrK4MgCCgrK1O6nH51\ndnaiuroaZ86cQU9PD2w2G6ZMmaJ0WX3s3bsXBw4cQE9PD6ZNm4Zly5YpXRIAoKqqCh6PBxqNBps3\nbwYAXL58GS+88AICgQDGjx+PJ554Amq1Ou7q3L59O9xuN5KTkzFt2jQsXrwYY8eOjbs6v/bOO+/g\n9ddfx8svv4y0tDSFKrziWnXu378fe/bsQU9PD773ve+hqKjo2jsRR6ne3l5x5cqV4oULF8Senh7x\nqaeeEj/77DOly+rj4sWL4qeffiqKoiheunRJXL58eVzWKYqi+M4774jPP/+8uHHjRqVLuaYXXnhB\nfPfdd0VRFMVwOCy2t7crXFFfX375pVhSUiJevnxZ7O3tFf/0pz+JHo9H6bJEURRFr9crnjx5Uly9\nerW0bvv27eKuXbtEURTFnTt3iq+//rpS5Un6q/M///mP2NvbK/b29opOpzNu6xRFUfz888/FP/7x\nj2JJSYn45ZdfKlTd//RX50cffST+/ve/F3t6ekRRvPL76XpG7WWub76yJSkpSXrtSrzRarWYNGkS\nAECj0cBoNOLixYvKFtWPYDAIj8eDvLy8uH2YtKOjA0ePHkVeXh4AQKVSKf6XaX+Sk5MBXKm3u7sb\nXV1div9l+rVp06YhNTU1at03X22Um5uLhoYGJUqL0l+dM2bMQGJiIhITEzFr1iwEg0GFqvuf/uoE\ngNdee+36f+UPs/7q/Ne//oVHHnkESUlXLmBpNJrr7mPUXuYaia9d8fv9aG5uhslkUrqUPmpqalBU\nVITLly8rXco1BQIBaDQaOBwOnDx5EiaTCcXFxdIv73iRnJyM5cuXY8WKFRgzZgzy8/ORmZmpdFnX\ndOnSJWi1WgDAuHHjcOnSJYUrurF3331X+qMi3jQ0NEAQBHznO99RupTr8vv98Hq92L59O9RqNZYu\nXYrvfve712w/as9MRprOzk5s3boVS5cuVfx69NUaGxuh0WgwefLkuD0rAYDe3l6cOHECc+bMwYYN\nGxAOh3H48GGly+qjtbUV1dXVqKyshMPhQFNTE9xut9JlxSQhIUHpEm7o7bffhlqtxty5c5UupY+u\nri7s3LkTixcvltbF6/+p3t5eBAIB/OEPf8CiRYuwffv267YftWEiCELUaW4wGIQgCApWdG3hcBib\nN2/G/PnzMXv2bKXL6ePYsWNobGzEihUr8Pzzz+OTTz7Biy++qHRZfeh0OqSlpcFsNiM5ORkWiwUe\nj0fpsvrw+XwwmUzQ6/VIT0/H3Llz4fV6lS7rmsaNGye9kujixYsYN26cwhVd24EDB+DxePDEE08o\nXUq/Lly4gM8//xxr1qzBihUrEAqFUFZWFpdnezqdDvPmzUNycjLMZjPOnTuH7u5rv1Ns1IbJN1/Z\nEg6HUV9fD7PZrHRZfYiiiJdeegkGgwEPPfSQ0uX0q6CgAE6nEw6HA08++SSmT5+OlStXKl1WH1qt\nFnq9HsePH0ckEoHb7caMGTOULquPqVOn4sSJE2hra0NPTw88Hg9mzpypdFnXZDabceDAAQDAe++9\nF5d/8ADAhx9+iN27d2Pt2rVxd2nzaxMnTsS2bdvgcDjgcDggCAKee+65uAzo2bNnw+PxQBRFHD9+\nHOPHj7/uz3VUPwE/El67cvToUfzud7/DxIkTpUsIBQUFmDVrlsKV9c/r9eKdd97B008/rXQp/Tp3\n7hwcDgdaW1sxceLEuBjG2p8DBw5g//796O7uxsyZM7F48WIkJir/t93WrVtx5MgRfPnllxg3bhwW\nL16MH/zpt/jUAAABlElEQVTgB3E3NPjrOltbW6HVavHTn/4Uu3btQjgclgYzTJkyBcuXL4+LOr/5\n87zvvvuk7StXrsTGjRsVH4DRX50LFixAdXU1PvnkEyQlJeHxxx/H1KlTr7mPUR0mREQ0PJT/U4iI\niEY8hgkREcnGMCEiItkYJkREJBvDhIiIZGOYEBGRbAwTIiKSjWFCRESyMUyIiEg2hgnRMPP7/Sgu\nLsann34K4Mp0CT//+c/j+mWPRDfCMCEaZnq9HoWFhXjhhRfQ3d0Np9OJ++67D1lZWUqXRnTT+G4u\nIoVUVFTgwoULSExMxIYNG6QZ7YhGIp6ZECkkLy8Pzc3NyM/PZ5DQiMcwIVJAZ2cnampqkJeXh3/8\n4x9oa2tTuiQiWRgmRAp45ZVXYDQa8ctf/hI5OTnYtm2b0iURycIwIRpmDQ0N+O9//4vHH38cAPCz\nn/0Mn376Kd5//32FKyO6ebwBT0REsvHMhIiIZGOYEBGRbAwTIiKSjWFCRESyMUyIiEg2hgkREcnG\nMCEiItkYJkREJBvDhIiIZPt/5cwSS3FXK2gAAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x113c8e390>"
       ]
      }
     ],
     "prompt_number": 17
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Why are we interested in the likelihood function? \n",
      "\n",
      "A reasonable estimate of the true, unknown value for the parameter is one which **maximizes the likelihood function**. So, inference is reduced to an optimization problem."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Going back to the rainfall data, if we are using a gamma distribution we need to maximize:\n",
      "\n",
      "$$\\begin{align}l(\\alpha,\\beta) &= \\sum_{i=1}^n \\log[\\beta^{\\alpha} x^{\\alpha-1} e^{-x/\\beta}\\Gamma(\\alpha)^{-1}] \\cr \n",
      "&= n[(\\alpha-1)\\overline{\\log(x)} - \\bar{x}\\beta + \\alpha\\log(\\beta) - \\log\\Gamma(\\alpha)]\\end{align}$$\n",
      "\n",
      "(*Its usually easier to work in the log scale*)\n",
      "\n",
      "where $n = 2012 \u2212 1871 = 141$ and the bar indicates an average over all *i*. We choose $\\alpha$ and $\\beta$ to maximize $l(\\alpha,\\beta)$.\n",
      "\n",
      "Notice $l$ is infinite if any $x$ is zero. We do not have any zeros, but we do have an NA value for one of the October data, which we dealt with above."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Finding the MLE\n",
      "\n",
      "To find the maximum of any function, we typically take the *derivative* with respect to the variable to be maximized, set it to zero and solve for that variable. \n",
      "\n",
      "$$\\frac{\\partial l(\\alpha,\\beta)}{\\partial \\beta} = n\\left(\\frac{\\alpha}{\\beta} - \\bar{x}\\right) = 0$$\n",
      "\n",
      "Which can be solved as $\\beta = \\alpha/\\bar{x}$. However, plugging this into the derivative with respect to $\\alpha$ yields:\n",
      "\n",
      "$$\\frac{\\partial l(\\alpha,\\beta)}{\\partial \\alpha} = \\log(\\alpha) + \\overline{\\log(x)} - \\log(\\bar{x}) - \\frac{\\Gamma(\\alpha)'}{\\Gamma(\\alpha)} = 0$$\n",
      "\n",
      "This has no closed form solution. We must use ***numerical optimization***!"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Numerical optimization alogarithms take an initial \"guess\" at the solution, and iteratively improve the guess until it gets \"close enough\" to the answer.\n",
      "\n",
      "Here, we will use Newton-Raphson algorithm:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$x_{n+1} = x_n - \\frac{f(x_n)}{f'(x_n)}$$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Which is available to us via SciPy:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "from scipy.optimize import newton"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 18
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Here is a graphical example of how Newtone-Raphson converges on a solution, using an arbitrary function:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "# some function\n",
      "func = lambda x: 3./(1 + 400*np.exp(-2*x)) - 1\n",
      "xvals = np.linspace(0, 6)\n",
      "plot(xvals, func(xvals))\n",
      "text(5.3, 2.1, '$f(x)$', fontsize=16)\n",
      "# zero line\n",
      "plot([0,6], [0,0], 'k-')\n",
      "# value at step n\n",
      "plot([4,4], [0,func(4)], 'k:')\n",
      "plt.text(4, -.2, '$x_n$', fontsize=16)\n",
      "# tangent line\n",
      "tanline = lambda x: -0.858 + 0.626*x\n",
      "plot(xvals, tanline(xvals), 'r--')\n",
      "# point at step n+1\n",
      "xprime = 0.858/0.626\n",
      "plot([xprime, xprime], [tanline(xprime), func(xprime)], 'k:')\n",
      "plt.text(xprime+.1, -.2, '$x_{n+1}$', fontsize=16)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 19,
       "text": [
        "<matplotlib.text.Text at 0x113f4ec10>"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAECCAYAAAD9z2x7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VOXZ8PHfLJnJZJIhmUCCJJKEEFkUUQggIjtREdQC\nta+KFbSv7RNRHwRlsUWoqOzIIotFi3v7aKW29a1SFtkMVELiowKyb2ELZJJMMsns5/0jmorsmZmc\nycz1/XzymZwz95z7Ckyu3HOd+9xHoyiKghBCiIinVTsAIYQQjUMSvhBCRAlJ+EIIESUk4QshRJSQ\nhC+EEFFCEr4QQkQJfSAvdrvdTJs2DY/Hg8FgoGfPngwdOvS8du+//z5FRUUYjUYef/xx0tLSAulW\nCCFEA2gCnYfvcrkwGo14PB4mTZrEs88+S8uWLeufLyoqYvXq1UyePJl9+/bx5ptv8tJLLwUcuBBC\niKsTcEnHaDQC4HQ68fl86PXnfmgoLCykb9++AOTk5OBwOKioqAi0WyGEEFcpoJIOgN/vZ+LEiRw7\ndozRo0fTvHnzc5632WwkJyfXbycnJ2Oz2UhMTAy0ayGEEFch4BG+Vqtlzpw5LFq0iNWrV3Po0KHz\n2sjqDUIIob6AR/g/SElJ4eabb2bXrl1kZWXV77darZSVldVvl5WVYbVaL3qcbdu24XA4ghWWEEJE\nhcTERLp27XrJNgElfLvdjk6nw2w2U1VVxVdffcUjjzxyTpvc3FxWr15Nr1692Lt3L2az+ZLlHIfD\nQZcuXQIJSwghok5RUdFl2wSU8CsqKliyZAl+v5/ExESGDh1Kp06dWLNmDQB5eXl06dKF3bt3M378\neGJjY8nPzw+kSyGEEA0U8LTMYFu3bp2M8IUQ4ioVFRUxcODAS7aRK22FECJKSMIXQogoIQlfCCGi\nhCR8IYRoQnQ7d6I5c6ZBr5WEL4QQTYHDgWnqVOKHDUP33XcNOoQkfCGECHP6NWuw9OqF5uRJ7Fu2\n4O3du2HHCXJcQgghgsXvx/yb36DbsYOa+fPxDhgQ0OEk4QshRLjSanH//Od4Fi0Ckyngw0nCF0KI\nMOa5446gHUtq+EIIEQ683pB3IQlfCCFUpl+3DkuPHmj37AltPyE9uhBCiIvSnD5N3O9+h66wkJo5\nc/C3axfS/mSEL4QQjc3vx/Dmm1h698Z37bXYv/gC76BBIe9WRvhCCNHYqquJWbuWqo8/xt+xY6N1\nKwlfCCEam8WC4913G71bKekIIUSUkIQvhBAhojlzhtgXXgCPR+1QAEn4QggRfH4/hrffrlv/xucD\nn0/tiACp4QshRFBpv/uOuHHj0LjdVK9ahe+GG9QOqV5ACf/s2bMsWbKEyspKLBYL/fr1o1+/fue0\n2blzJ7NnzyY1NRWAHj16MGLEiEC6FUKIsKT79lvihw3DOXEirkceAZ1O7ZDOEVDC1+v1jBo1iszM\nTOx2O+PHj6dt27akp6ef065jx45MnDgxoECFECLc+a6/HntBAUqLFmqHckEB1fATExPJzMwEwGKx\nkJ2dTXl5+XntFEUJpBshhGgaNJqwTfYQxJO2p06doqSkhJycnHP2azQa9u7dy7hx45gxYwYlJSXB\n6lIIIdShKCFf9yYUgpLwnU4nCxYsYNSoUcTGxp7zXFZWFsuWLWP27Nl0796dWbNmBaNLIYRQhXbv\nXuLvvpu4CROgiVUvAk74Xq+XefPm0bt3b7p163be8yaTCaPRiF6vZ8CAATgcDqqrqwPtVgghGpfT\nSeyMGSTcdReee+6hetUq0GjUjuqqBHTSVlEUli9fTnp6OkOGDLlgm4qKCpo1a4ZGo2HHjh0YDAbi\n4+MD6VYIIRqVbscOzPn5+Nq3x75xI0pamtohNUhACX/Pnj1s3ryZ1q1bM2HCBAAeeOABzp49C0Be\nXh7btm1jzZo1aLVaMjIy6tsJIURToZjN1E6bhueuu9QOJSAaJcym0Kxbt44uXbqoHYYQQjQpRUVF\nDBw48JJtZGkFIYT4sfAaAweVJHwhhABwuYidNYu4cePUjiRkJOELIaKe/osvsPTpg+6bb6gdP17t\ncEJGFk8TQkQtjc2G6fnnidmwgZpZs/BcZLZhpJCEL4SIWsY//AElIYHKrVshIUHtcEJOEr4QImo5\nJ05schdPBUJq+EKI6BXCZL9jxw7OnDlzxe3dbjcbNmwIWTwgI3whRBTQFxSgaLX4brkl6Md2u91M\nnjyZpKQkNBoNv/3tbykqKqKgoICuXbte8XEMBgM2m41///vf9OjRI+hxgozwhRARTFNeTtxTT2F+\n7DE0DkdI+li4cCGKomA2mzl79iwul4sFCxbw5JNPXvWxhg8fzjvvvMOJEydCEKkkfCFEJFIUDB98\ngKVnT5S4OCq3bsV7matQG+qzzz4jNzeXp59+mldeeYXly5czbNiwBh/v0Ucf5Y033ghihP8hCV8I\nEXHixozBuGQJ1e+9R+3MmWCxhKQfl8vFzp07z1kO5oMPPuDuu+9u8DG7dOnC559/jtvtDkaI55Aa\nvhAi4jjHjcOfmQn60KW4d999l3/961/ExMTw9ttvc80113DHHXeQlJSE/gL91tbW8sYbb6DT6Th4\n8CD3338/W7ZsoaioiMmTJ9O+ffv6tu3atWPz5s2XXRvnaknCF0JEHH/btiHv46GHHsLn81FWVsbL\nL78MwEcffUTbi/S9YsUKHnvsMUwmEw8++CCvv/46ixcvpkOHDufdGjYzM5MjR44EPWZJ+EKIJktT\nUYESFwcGgyr9f/3119x4443122fOnKFZs2bntVMUhe7du2MymQA4cOAAL774Inq9nn379p3X3mq1\ncvTo0aDHKzV8IUTToyjE/OUvWHr2RL9pk2phfPPNN3Tu3Ll+2+12Y7jAHx+NRsMt308JPXHiBIcP\nH+bWW2+96HENBkNI7gwoCV8I0aRoDx0i/uc/J3bhQqrfeQfvoEGqxOHz+di9e/c5I/zmzZufV575\nwQ+3Htm0aROdO3fGbDYDsG3btvPalpeX06JFi6DHLAlfCNE0+HzEvvIKCXl5ePr2pWr9eny5uaqF\ns2fPHnw+3zknWzMyMigtLT2v7erVq+nUqRMAq1atIicnBwC73c533313XvvS0lKysrKCHrMkfCFE\n06DVgstF1fr1uJ56CmJiVA2nuLiY3NxctNr/pNFu3bqxa9eu89parVa6devGwoULmTRpElqtlkWL\nFrFw4UIefPDB89pv376dfv36BT1mOWkrhGgaNBqckyapHQUOhwOz2UxRURF5eXnnPGcwGLj55pv5\n9ttvueGGG+r3d+vWjZUrV9ZvX+o2rmVlZRiNRlJSUoIee0AJ/+zZsyxZsoTKykosFgv9+vW74F+l\n999/n6KiIoxGI48//jhpTfSO70KI6OZ0OuncuTMrVqzg66+/5vnnnz+vzaRJk1i4cCGLFi1qUB/L\nly9nUoj+sAVU0tHr9YwaNYr58+czbtw43nvvPUpKSs5pU1RUxJEjR5g7dy6jR49m6dKlAQUshIhs\n2iNHMD/8MNpjx9QO5TyxsbHcc889FBcXM2HChAtOwczOzqZNmzZs3779qo9/6NAh7HY7t912WzDC\nPU9AI/zExEQSExMBsFgsZGdnU15eTnp6en2bwsJC+vbtC0BOTg4Oh4OKior61wkhBAAeD8alS4ld\nvBjnk0/ib9lS7YguaP78+ZdtM3bsWJYuXUpmZuYVz7Zxu938+c9/ZsaMGYGGeFFBq+GfOnWKkpKS\n+rPPP7DZbCQnJ9dvJycnY7PZJOELIerpvvySuHHjUFq2pGrt2rplEZq4xx9//KraGwwGJk+eHKJo\n6gQl4TudThYsWMCoUaOIjY097/kf5p8KIcRPac6exfyb31A7ZQqeYcMi4g5UiqLg8Su4vX7cPgWX\nz4/b68flU/B8v8/j//7Rp+Dx+fH4Fby+utd5/X68fvD6/Pj8Ct7vv3x+6h4VBZ//+y+lbv+9zS8f\nV8AJ3+v1Mm/ePHr37k23bt3Oe95qtVJWVla/XVZWhtVqDbRbIUSEUJo3x759e0gXOrviWBQFp9dP\nlcuH3emlyuWjyuXF4fFT4/bhcPuo8fiocftxeHzUuH04vX6cXj+1Hj9Orw+np25bAxj1Wgw67feP\nmvrtGJ3m+y8tBu1/vtd//71eq0Gn1RCjrXtNzPfb+h89ajU/3geUVVz25wvoX1hRFJYvX056ejpD\nLnK399zcXFavXk2vXr3Yu3cvZrNZyjlCiHOFMNkrikKF08sZhwdbjYfyWi8VtXWP5bUeKmq9VNR6\nsbvqErxeqyHBqCPBqP/+UYfZoCPOoMMco6N5XAzmxLptU4wWU4yOWL2WWL0WU0zdY2yMDr22cT+p\nFJVdvk1A/8p79uxh8+bNtG7dmgkTJgDwwAMPcPbsWQDy8vLo0qULu3fvZvz48cTGxpKfnx9Il0KI\npsrjIeazz/AEsFb8hSiKgq3Wy/FKF8ftLk5VuTjj8HCm2l336HATq9fSwmwgOS6GJJOeJJOe1HgD\n7VvEkWSKIdGkxxJbl+ANusi9HlWjhFmBfd26dZe8KEEI0fToCguJe/pplBYtqH73XYiLu+pjeP0K\nxyqcHLLVcqTcyXF7XYI/YXdh0GlJsxhJa2akZYKBFmYDKfExtDAbaG6OwRSjC8FPFV6Kioouu36+\n+kUzIUTkstsxvfgihn/8g5rp0/GMGHFFJ2Udbh97zjg4aHNy0FbLIVstJRVOWsQbaGM1kZkUS6/M\nZqRZYklrZsRsiPyEHgyS8IUQIaHbuZP4X/wCz6BB2AsKUJKSLthOURROVrnZebqaXacd7Drt4GSV\nm7bNTWRb4+iUaubejs3JSDIRq4/ccktjkIQvhAgJX5s2VP/xj/h69DjvudNVbraX2NlRYmfnaQd6\nrYbrU810TDVzZ7tkspPjGv2kZzSQhC+ECA2TqT7Zu31+vj1VzfZjdraXVFHp9JKbnkCvzETye6bT\nwhyDJgLm34c7SfhCiMDV1Jx3Itbp9bPtSCUbDpbz1YkqMpJi6ZZu4dm+rclpHodWEnyjk4QvhGg4\nux3Tyy+j/+orqj79FJ8CxSeqWL/fxrajdtq1iKN/dhLjerfGEivpRm3yPyCEuHqKQswnnxA3aRKe\ngQP5evEb/HPrcTYdKicl3sCA7CT+b/c0rHHq3qREnEsSvhDiqmhKSoibOBHt/v0UvDCf1w1ZnNlR\nzh3XJTN/aA5pzc5fT0uEB0n4Qoir4v7fb9h3TVtevHM8VkM8w25oQa+MRHQyqybsScIXQlyRE3YX\nH31TyudlafQY+gjPXZ/CdS2u/opZoR5J+EKIS7LVeHiv+BQbD5YzpENzVozoQLJZavNNkSR8IcQF\n+f7+Cd/8exfT299JXo6VN+7rSDOZadOkyf+eEOIc3qMlOJ54Gu3efRx4cgrLhrUnJd6gdlgiCGRh\nCiEEAIrXS8nLr2C4rTe7WmZj27CBEWNGSLKPIDLCF0JQ5vBwNH88LfbuZO//fEzPnp3VDkmEgCR8\nIaKYoih8tqeMPxaeZNhjT3F9zywMellqOFJJwhciSh2vdLFgy1FqPX5mDW5Lm2ST2iGJEJOEL0SU\nUY4f59NdpfzxlI77O6cy7IYUuWgqSshJWyGihc+Hf+lrxNzaG8f6TSy6tx0/vzG1PtnPnDlT5QBF\nqAU8wl+6dCnFxcVYLBbmzZt33vM7d+5k9uzZpKamAtCjRw9GjBgRaLdCiKug++YbNE88xeFa2D7v\nLYYPv01G9VEo4ITfv39/Bg8ezKuvvnrRNh07dmTixImBdiWEaIDYl16CN1ayZPD/pcMzv2ZYlvWC\n7SZNmtTIkYnGFnDC79ChA6WlpZdsoyhKoN0IIRqg1uPj45h0Cp5/m7HDu9LKYlQ7JKGikNfwNRoN\ne/fuZdy4ccyYMYOSkpJQdymEAI5WOHnqb3s5cEs/pj90y2WTvdTwI1/IZ+lkZWWxbNkydDodGzdu\nZNasWSxevDjU3QoRffx+0GhAo6H4RBUvrz/Mo91aMbhdstqRiTAR8hG+yWTCaDSi1+sZMGAADoeD\n6urqUHcrRFTRffstCXfcgX7DBjYeLGfG+sNMGZh1VcleaviRL+QJv6Kior6Gv2PHDgwGA/Hx8aHu\nVojo4HBgmjqV+OHDcf3yl6xq0ZHXth1n5uC23HiN/J6JcwVc0lmwYAG7d+/GbreTn5/Pfffdh8/n\nAyAvL49t27axZs0atFotGRkZTJgwIeCghRCgX7OGuGefxdu9O5WbN/PmMR8bd5Ux7+4crkm4+pOz\nM2fOlFF+hAs44Y8dO/aSz995553ceeedgXYjhPgxj4fYFSuomT8fV7/+LPriGAfKannl7hwSTXJz\nEnFhsrSCEE1RTAzVH3yA2+vn5XWHcHn9zBnSFlNMwxc+k9F95JOlFYRoopxeP79dfQCjXssLt7cJ\nKNmL6CAJX4hwVlND7Lx58JOZbW6fn9+vOUiLeAMT+2UQowv8V1nm4Uc+SfhChCn92rVYevVC9913\naNzu+v1ev8JL6w9jNugY37s1Wo2siSOujNTwhQgzmtOnifvtb9EVFVEzdy7egQPrn/P5FeZsPILf\nrzBxQGZQF0CTGn7kkxG+EGFEc+oUlt698bVujX3LlnOSvV9RWLjlGOW1Hn43MCsoZRwRXeQdI0QY\nUVq2xL5+Pc7nn4e4uP/sVxSWbzvO0Qonv89rg1Ef/F9dqeFHPinpCBFmlPT08/a9WXiSb09VM/uu\nwKZeiugmI3whVKI9fPiK2n3wv6cpOFLJjMFtiTeGbowmNfzIJwlfiEamKS0l7te/Jv6++8DlumTb\nTYfK+duuM8wYnE2zWPlALgIjCV+IxuL3Y3j7bSy33YbSqhX2DRvAePE1b/accbD4ixJ+n9eG5mZD\nyMOTGn7kkyGDEI1Ae+gQcWPGoHG7qV61Ct8NN1yyfWm1m9+vOcTY266lbfO4S7YV4kpJwheiESgG\nA54RI3CNHg26S590rfX4mLrmID+7oQW9MhMbJ0Ckhh8NJOEL0QiUtDRcv/rVZdv5FYWZG47QNtnE\nfZ1SGiEyEU2khi9EGPnj9hNUu3w81etaNI28ZILU8COfJHwhgkVRMLz7LuYrGMlfyGd7ythyuJKp\ng+QqWhEaUtIRIgi0e/YQN348GqeTmvnzr/r1X5+s5o/bTzB3aA4WlaZfSg0/8skwQohAOJ3Evvwy\nCUOH4rn3XqpWr8Z3441XdYiyGg8zPj/MhH4ZtE6MDVGgQkjCFyIghj/9Cd2ePdg3bsT12GOXnYHz\nUz6/wsvrD3NX+2Ry0y0hivLKSA0/8gX82XHp0qUUFxdjsViYN2/eBdu8//77FBUVYTQaefzxx0lL\nSwu0WyHCgnv0aNyPPNLg17+54yQGnYYHb2oZxKiEuLCAR/j9+/fnueeeu+jzRUVFHDlyhLlz5zJ6\n9GiWLl0aaJdChI8AZtJsO1rJ+v02JvbLCOq69g0lNfzIF3DC79ChA2az+aLPFxYW0rdvXwBycnJw\nOBxUVFQE2q0QjUq7dy/6jRuDdryTVS7mbzrKcwMySTTFBO24QlxKyGv4NpuN5OTk+u3k5GRsNluo\nuxUiOJxOYmfOJOGuu9CWlATlkG6fn5fWHeb/dE7l+tT4oBwzGKSGH/kaZf6XoiiN0Y0QQaXfvJm4\n8ePxtW+PfeNGlCCde3pt23FS4mMYfkOLoBxPiCsV8oRvtVopKyur3y4rK8NqtYa6WyECEjtrFsZ3\n36Vm1iw8d90VtOOu329jx/EqlvysXaNfSXs5UsOPfCEv6eTm5rJp0yYA9u7di9lsJjGx8RaEEqIh\n3MOHU1lQENRkf7TCybJtx5kyMBOzQe5aJRpfwCP8BQsWsHv3bux2O/n5+dx33334fD4A8vLy6NKl\nC7t372b8+PHExsaSn58fcNBChJo/Jyeox3P7/Mz4/DCjul5DdnJ4Lnc8c+ZMGeVHuIAT/tixYy/b\nZuTIkYwcOTLQroQIPpcLvF64xEyzYHir8CQpZgND2idfvrEQISJX2oqopS8owNKnD4YPPwxpP8Un\nqlh/oJynezf+CphXQ0b3kU8WTxNRR2OzYZo6lZjPP6dm5kw8Q4aErC+708ucjUcY36e1zLcXqpMR\nvogqhg8+wHLrrShmc91J2aFDA7pa9lIURWHhF8fonZmo+jo5V0Lm4Uc+GeGLqKI9coTq99/H16VL\nyPtas8/GsQonE/tmhLwvIa6EJHwRVZzPPtso/RyvdLHiyxPMvqstBn3T+CAtNfzI1zTeiUI0IV6/\nwqwNh3nwplSyrCa1wxGiniR8EXE05eXEPf00um++UaX/94pPEW/Uce/1TWvpBKnhRz5J+CJyKAox\nf/lL3UlZgwFfRuPXzneddvDP784yvk8G2jCegimik9TwRUTQHjpUd0/Zs2epfvddfF27NnoMTq+f\nORuPMObWdJLjmt4UTKnhRz4Z4Yumz+Ui/r778PTvT9X69aoke4A/bj/BdS3i6JOVpEr/QlyOJHzR\n9BmN2L/4AteTT4JenQ+tX52oYvOhCsb0TFel/2CQGn7kk4QvIoPRqFrXNW4f8zYdZext12KJlSqp\nCF+S8EXToSjo164Fv1/tSM7xhy+Pc1OreHq0bqZ2KAGRGn7kk+GIaBK0hw8T98wzaE6dorpTJ5TU\nVLVDAmD7MTs7SqpYPry92qEIcVkywhfhzePBuGABCYMG4enTh6rPPw+bZF/l8vLKlqOM6906Im5o\nIjX8yCcjfBG2NCdOkHDfffhbtaJq3Tr8Ksyrv5RlW0u4NaMZN6clqB2KEFdEEr4IW0pqKjVTp+LN\nywvZipYN9cXhCnaVOlg2LHJKOVLDj3xS0hHhS6fDe/vtYZfsK51eFhcc49k+GZhimn4pR0QPSfgi\nPLjdakdwxV4tOMaAbCvXt4xXO5Sgkhp+5Au4pLNr1y7eeustfD4fAwcOZPDgwec8v3PnTmbPnk3q\n9yfaevTowYgRIwLtVkQKjwfjsmUY33sP+5YtEBPeSxJsPlTBgbJanukTXucThLgSASV8v9/PsmXL\nmDJlClarlcmTJ9OpUyfS08+92rBjx45MnDgxoEBF5NFt307cuHEoKSlU//nPYZ/sK2o9LCk4xpRB\nWRibyBr3V0Nq+JEvoIS/f/9+WrZsSUpKCgC9evWisLDwvISvKEog3YhIY7djmj4dwyefUPPii3iG\nDw+7Ov2FLCkoYUBbK9enRlYpR0SPgIYpNpuN5OTk+m2r1YrNZjunjUajYe/evYwbN44ZM2ZQUlIS\nSJciAuj27kXjdmPfuhXPiBFNItlvOlTOAVsto7peo3YoISM1/MgX8mmZWVlZLFu2DJ1Ox8aNG5k1\naxaLFy8OdbcijPlyc6nJzVU7jCtWUethaUEJzw9qE5GlHBE9Anr3Wq1WysrK6rfLysqwWq3ntDGZ\nTBiNRvR6PQMGDMDhcFBdXR1It0I0qh9KOR1TzWqHElJSw498ASX87OxsTp06RWlpKV6vl4KCAnJ/\nMnKrqKior+Hv2LEDg8FAfLzUQKOBrqgI46JFaocRkGgo5YjoEVBJR6fTkZ+fz9y5c+unZaanp7Nm\nzRoA8vLy2LZtG2vWrEGr1ZKRkcGECROCErgIY3Y7ppdfxvC3v1H7wgtqR9NgP5RypuZFRyln5syZ\nMsqPcAHX8Dt27Mjs2bPP2ZeXl1f//Z133smdd94ZaDeiKVAUYj75hLhJk/AMHIi9oAAlqene/enV\nghIGtrXSISWySzkieshaOiJojK+/jvH113GsWIH31lvVDicgGw6Uc8hWy7N9o+cCKxndRz5J+CJo\nXPffj+vhh1W9+1Qw2Go8LN1awgu3R0cpR0QPeTeL4ElIaPLJXlEUFm45xuD2ybSPslKOzMOPfJLw\nxdWrqkJ7+LDaUYTEmn02Tle7eOjmlmqHIkTQScIXVyXmn/+k2a23Yli1Su1Qgu6Mw82KL0/wbN8M\nYnTR96shNfzIJzV8cUU0JSXETZ6Mbu9eHMuW4b3tNrVDCipFUZi/6Sg/u74F2clxaocjREhE3zBG\nXDXD229j6dcP3w03YN+0KeKSPcA/95RR5fJxf+fwuF+uGqSGH/lkhC8uy3/NNVR9+in+nBy1QwmJ\nk1Uu3iw8ydwhbdFpw38hNyEaShK+uCzvjy6kizR+RWHexqPcd2MKGUkmtcNRldTwI5+UdMS5ouze\nBX/beQavX2HEDSlqhyJEyEnCFwBoTpzA/PDDGP70J7VDaTSHy2t5/6vTPNs3Q0o5SA0/GkjCj3Y+\nH8Y//AFL3774OnTAPXy42hE1CrfPz8zPD/Not1akNWvaF4sJcaWkhh/FdN98Q9zTT6PExlL1//4f\n/uuuUzukRvNm4UlaJhi58zrr5RtHCanhRz5J+NFKUYidORPX6NG4R45sErcZDJbi41V8fqCc5cPb\no4min1sIKelEK40Gx3vv4X7ooahK9nanlzmbjjC+T2uaxcp458ekhh/5JOGLqKEoCgu/OEbvzERy\n0y1qhyNEo5OEH+l8PgwrV6I5c0btSFS3Zp+NYxVOftWtldqhhCWp4Uc+SfgRTPfttyTccQeGDz9E\nU1OjdjiqOmF3seLLE0zql4lB1rgXUUre+ZHI4cA0dSrxw4fjevhhqj/5BH9G9Ny56ad8foXZG45w\nf+dU2iRH99W0lyI1/MgX8FmrXbt28dZbb9XfxHzw4MHntXn//fcpKirCaDTy+OOPk5aWFmi34mJq\narD06YO3a1fsW7agpMgVpO8Wn8Ko1zLshhZqhyKEqgIa4fv9fpYtW8b48eOZOXMm69evp6Sk5Jw2\nRUVFHDlyhLlz5zJ69GiWLl0aUMDiMuLiqP6f/6HmD3+QZA8Ultj5bE8ZE/tloI2i2UgNITX8yBdQ\nwt+/fz8tW7YkJSUFvV5Pr169KCwsPKdNYWEhffv2BSAnJweHw0FFRUUg3YrL8Ldtq3YIYeGMw82c\njUeY2C8Da1yM2uEIobqAEr7NZiM5Obl+22q1YrPZLtkmOTn5vDaiYTQnT6odQtjy+hVeXn+Yezu2\n4KZWCWqH0yRIDT/yNcqVJ8pVrsBotcrl7pdiAp4HHgGygFp1wwlrbwFPqB1EEzJ79my1QxANtHbt\n2su2CSgaTFGFAAASQklEQVThW61WysrK6rfLysrOS9ZX0uan5BPAxenXriXu2Wfx5eZS8+KLPLly\npdRef2LrkUpeLTjG0mHt5WpaETWKioou2yagkk52djanTp2itLQUr9dLQUEBubm557TJzc1l06ZN\nAOzduxez2UxiYmIg3UYlTVkZ5l/9irgJE6iZOxfHihUoqamS7H/iZJWL+ZuP8tsBWZLshfiJgH4j\ndDod+fn5zJ07t35aZnp6OmvWrAEgLy+PLl26sHv3bsaPH09sbCz5+flBCTzq6HT4rrsOx+LFECc3\n2b4Qt8/PS+sOc3/nVDqmmtUOR4iwo1GutsAeYuvWraNLly5qh9FkzJw585Kj/NraWt544w10Oh0H\nDx7k/vvvZ8uWLRQVFTF58mTat2/fiNGG1qsFxzjr8DB1UJasghmAaHrPRJKioiIGDhx4yTbymTfC\nrVixgsceewyTycSDDz7I66+/zuLFi+nQoQPl5eVqhxc06/bb2H7MzpKftZNkH6Boec9EI1laIczo\n16/H/Mtfgs93Re0vNbpXFIXu3btjMtUtJ3DgwAGGDx+OXq9n37599OzZMygxq23XaQfLtx1nWl4b\n4o0yhglEtLxnopUk/DChKS0l7te/Jm7cOFwPPww6XeDH1Gi45ZZbADhx4gSHDx/m1ltvDfi4l7Jo\n0SIKCgpC2sePna5y88K6g4zv05osq6yTEyg13jOi8UjCV5vfj+Gtt7DcdhtKq1bYv/gCb17eFb/8\nchfL/HCKZtOmTXTu3Bmzue5k5rZt2xoU7q5duy643+l08tprr/H3v/+9QcdtiFqPj6lrDvDzTqnc\n0rpZo/Ub6YL9nhHhQxK+ymLWrMH4zjtUr1pF7bRpYA7e7JLVq1fTqVMnAFatWkVOTg4Adrud7777\nrkHH/Mc//nHB/bGxsfzmN7+hXbt2V32hXUP4FYWZnx/huuZmRsiiaEETiveMCB9S8FSZ5/bb8Qwa\n1OASzqVq+FarlW7durFw4UImTZrEypUrWbRoEZWVlUycOBGAf//736xdu5bMzExatGjBV199Rd++\nfenRo0eD4mksK7efwOH28buBmXKSNogi+T0jJOGrT6MJSr3+Qrp168bKlSvrty803bW2tpZrrrmG\nM2fOMHLkSFwuF1999VVY//L+a28Zmw9XsOiedsTo5ENqMEXqe0bUkd+WRqI5exb9unVBP26gC171\n69ePLVu2cO+99wKwZcsWunfvXv/8kSNHWL58ef1XYWFh/fevvfYaHo/nvGOGcsT97alqVnx5ghfy\nsrHIlbSquNx7RoQv+Y0JNUXB8N57mKZPx/XII3gvc2GEGg4dOkRWVhZ+v5/i4mLGjRvHnj17aNeu\nHRkZGfzXf/1XfdvKyspzti8kVDX845VOXlx3iIn9MmidFBuSPsSVudR7RoQvSfghpN2zh7jx49E4\nnVT/5S/4vj8ZFkyBrqVTUlJyzsf29u3bs23btvrR29VYvnw527dvx+1243a76d+/f0Cx/VhptZtJ\nnx5gVG4rctMtQTuuuHrBfM+IxiVLK4SI4U9/wvT88zgnTMD16KMhq9M3tgULFjB27NhG7bO8xsO4\nT/Zxd8fmDL9B7uIlxIVcydIKUsMPEe8tt2DfuBHXY4+FNNk39k0rGjvZ251eJn26n4FtkyTZCxEg\nKemEiD8rS+0Qmrwat4/frT5A13QLI29uqXY4QjR5MsIPlKKAw6Fa95G6Hr7L62fqmoNkWU081r2V\nzLUXIggk4QdAu28f8ffcQ+z8+WqHElG8foUX1x3CGhfDU72ulWQvRJBIwm8Ip5PYmTNJGDwYz9Ch\nOJ97TrVQIu3G0z6/wqwNh9Fo4Nm+Gei0kuyFCBap4V8l/ZYtxI0bh699e+wbN6KkpakdUsRwef28\nuO4QfgWmDspCL8leiKCShH+VdEVF1E6bhueuu9QOBYicGn61y8vz/zpISryBZ/pmSLIXIgQk4V8l\n11NPqR1CxCmr8fDbz/bT+ZoEfnNLGlqp2QsREg1O+LW1tSxevJjS0lJSU1N58skniY09/3L3MWPG\nYDKZ0Gq16HQ6ZsyYEVDA4lyXu6dtuDthdzH50/3ccV0yD9yUKidohQihBif8jz76iHbt2jFhwgQ+\n/vhjPvroI0aOHHnBttOmTSM+Pr7BQTY6l4vYRYvw9uiBt08ftaOJWAfKavjt6gM8dPM1DO3QXO1w\nhIh4DZ6lU1hYSN++fYG61fO2b99+0bZhtnrDJekLCrD06YOuuBhfmzZqh3NZTXV0//XJKiZ9eoDH\ne6ZLsheikTR4hF9ZWUliYiIAzZo1o7Ky8oLtNBoNL7zwAhqNhttvv51BgwY1tMuQ0thsmKZOJebz\nz6mZORPP0KFqhxSRFEXhk91nebvoFM/1z+TmtAS1QxIialwy4U+fPp2Kiorz9j/wwAPnbF+q7jp9\n+nSSkpIoKSlhxowZpKWl0aFDhwaGGyKKQvx99+Ht1o3KggKwNJ3VGJtSDd/p9bPoi2McOFvDgrtz\nSGsmSxwL0ZgumfCnTJly0eeaNWtGRUUFiYmJlJeX06zZhW8inZSUBEB6ejrdu3dn//794ZfwNRqq\n/vY3aErnGZqYE3YXL6w9SGaSiQX3XIcpJjJWDxWiKWlwDT83N5cNGzYAsHHjRrp163ZeG5fLRW1t\nLVB3E+Ti4mJat27d0C5Dq4km+6Ywut92tJL//vte7mrfnIn9MiTZC6GSBtfwR4wYweLFi3nmmWfq\np2UC2Gw2XnvtNSZPnkxFRQVz584FICEhgSFDhtC5c+fgRN5Auu3b8XXuDAaDqnFEA59f4d3iU6ze\nW8a0vCyuT22af1SFiBRRcwMUTXk5pmnTiFm7lqqPPsLfvn3Q+1BDuNbwT1a5eGXzUfx+eG5AJta4\nGLVDEiKiyQ1QoO6esh9+iOXWW1FiY6ncujVikn048isKf/22lCc/3kNumoVZd7WVZC9EmIjspRWq\nqogfNQrNmTNUv/MOvtxctSMKunAa3R+rcDJ/81EAXrn7Oq5NlFk4QoSTyE748fG4HnoIz913Q4yM\nMkPF51f4yzelfPj1aX7Z5Rru7thc1sMRIgxFdklHo8EzfHhEJ3u118Pfd7aGp/6+h6LjVbz6s3bc\ne30LSfZChKnIGeH7fCG9Wbg418kqF28WnuR/T1QxOrcVd1xnlYXPhAhzTX+EryjEfPQRlh490Fxk\neYdI1tg1/IpaD8u2lvDkx3u4tpmRlb/oyJ3tkiXZC9EENOkRvvbwYeKeeQbNqVM4li5FucjVviJw\ntR4ff/32DKu+LaV/dhIrft6BJFPklsqEiERNc4Tv8WBcsICEQYPw9OlD1eef4+veXe2oVBHqGr7D\n7eMv35Ty6Ie7OWSrZeE97Rhz67WS7IVogprkCF979Cj67dupWrcOf0aG2uFEpJNVLj7eeYa1+2x0\nTUvg97e34brmcWqHJYQIQNRcaSsuT1EUdp128NG3Z/j6ZBV3XJfMvde3ICVelqEQItxdyZW2TXKE\nL4LL7vSy+XAFn+0po8rlZdj1KTzbt7UsciZEhAnrhK89cgTDqlU4n35a7VDCVkPX0nF7/fz7mJ11\n+218daKK3HQLI29uSbd0CzqtzLgRIhKFZ8L3eDAuW0bsokU4n3gC/H7QNs3zy+HE51f45lQ1nx8o\nZ8vhCrKTTQzItvJs3wzMBhnNCxHpwjLhJwwYgJKSQtWaNfizstQOJ6xdbnRfXuNhe4md7cfsFJ2o\nIjXeQL/sJJYPb08Ls9TmhYgmYZnwnWPH1i2JIBfzXDWPz8++s7UUltj58pid43YXN7dKoPu1Fv7r\nlnSSzTKdUohoFZYJ3zNihNohNBkvvPQyd/xyDDtPO9h52sG+szW0shjpmpbAY91b0THVTIxOymFC\niDBN+OLCql1eDtqcHLTVcrCslt1nHGz/9gyOb0u5PjWeB25KpUOKWerxQogLkoQfhmo9Po5Xujhu\nd3Gk3MmB7xN8pdNLljWWNlYTOc1NDO3YnOxh82VWjRDiijQ44W/dupUPP/yQ48ePM2PGDNq0aXPB\ndrt27eKtt97C5/MxcOBABg8e3OBgI4VfUSiv9VJa7eZMtZtT1e66BF/posTuxOHy0cpiJK2ZkWsT\nYxmYncRj3VtxTYJRkrsQosEanPBbt27NM888w4oVKy7axu/3s2zZMqZMmYLVamXy5Ml06tSJ9PT0\nhnYb1nx+BbvLS0WtF1uNh/JaLxW1Hmy1XsprPZRWezjjcFPm8BBv1JESb6CFOYbUeAM5zePo1yaJ\ntGZGmptjZE15IUTQNTjhp6WlXbbN/v37admyJSkpKQD06tWLwsLCsE34Pr+C0+vH6fVT6/HhcNd9\n1bj9ODw/fO+jyuWjyuXF/sOjs+6x2u0j3qAjyRRDUpy+7tFU95iZFEtKvIGUeAPNzTEY5ESqEKKR\nhbSGb7PZSE5Ort+2Wq3s37//sq8rqXTi9Sv4/Ao+P/gUBa9fqd/n8X3/6P/Po8fnx+NT8Pi/f/TV\n7XP7FNw+Py6vH5dPwe314/L5cXsVXD9K7k6vH69fwajXEqvXEhejI86gxWzQERejq3+MM2hpEW8g\nO9lEglGPxagjIVZPglFHglGPXkouQogwdcmEP336dCoqKs7b/8ADD5AbwhuCT1l9EJ1Wg14LWo0G\nvVbz/fb5Xzqthhidhhittu5RpyFGV5e0E4w6YnRajHotRp0Gg16LUafFqNdg+H6/KaaubWyMDqNO\nIzfyEEJErEsm/ClTpgR0cKvVSllZWf12WVkZVqv1kq9JTEzkybbn/5G5agrg/f7Lde5TP+yuAcoD\n70kIIVSXmJh42TYhLelkZ2dz6tQpSktLsVqtFBQU8N///d+XfE3Xrl1DGZIQQkStBq+H/+WXX7Jy\n5UrsdjtxcXFkZWXx3HPPYbPZeO2115g8eTJQNy3zzTffrJ+WeddddwX1BxBCCHFlwu4GKEIIIUJD\n5gYKIUSUkIQvhBBRImzW0onkJRiWLl1KcXExFouFefPmqR1O0J09e5YlS5ZQWVmJxWKhX79+9OvX\nT+2wgsbtdjNt2jQ8Hg8Gg4GePXsydOhQtcMKKr/fz6RJk7BarQ26g1o4GzNmDCaTCa1Wi06nY8aM\nGWqHFFROp5PXX3+do0eP4vF4yM/P57rrrrtg27BI+JG+BEP//v0ZPHgwr776qtqhhIRer2fUqFFk\nZmZit9sZP348bdu2jZj/P4PBwNSpUzEajXg8HiZNmkRubi4tW7ZUO7Sg+ec//0l6ejq1tbVqhxIS\n06ZNIz4+Xu0wQuL111+nY8eOPPHEE/h8Plwu10XbhkVJ58dLMOj1+volGCJFhw4dMJvNaocRMomJ\niWRmZgJgsVjIzs6mvDyyrnAwGo1A3WjK5/Oh14fFWCkoysrKKC4uZsCAAUTqHI5I/blqamr47rvv\nGDBgAAA6nY64uLiLtg+Ld21Dl2AQ4efUqVOUlJSQk5OjdihB5ff7mThxIseOHWP06NE0b95c7ZCC\n5q233uKhhx6K2NG9RqPhhRdeQKPRcPvttzNo0CC1Qwqa0tJSLBYLS5Ys4eDBg+Tk5PDoo49iMFz4\n9qVhMcIXkcHpdLJgwQJGjRpFbGys2uEElVarZc6cOSxatIjVq1dz6NAhtUMKih07dmCxWMjKyorY\nUfD06dOZM2cOTz31FH/961/ZvXu32iEFjc/n48CBA/To0YMZM2bg9XrZunXrRduHRcJvyBIMIrx4\nvV7mzZtH79696datm9rhhExKSgo333wzu3btUjuUoNizZw87duxgzJgxLFy4kJ07d0bcuaakpCQA\n0tPT6d69e0RVD5KTk4mPjyc3NxeDwUCvXr0oLi6+aPuwSPg/XoLB6/VSUFAQ0sXZRHApisLy5ctJ\nT09nyJAhaocTdHa7HYfDAUBVVRVfffUVrVu3Vjmq4HjwwQdZtmwZS5YsYezYsVx//fU88cQTaocV\nNC6Xq75UZbfbKS4ujpj/O6g7f9ayZUv27duH3++nqKiIG2+88aLtw6KGr9PpyM/PZ+7cufXTMiNl\nhgfAggUL2L17N1VVVeTn5/OLX/yC/v37qx1W0OzZs4fNmzfTunVrJkyYANQlkptuuknlyIKjoqKC\nJUuW4Pf7SUxMZOjQoXTq1EntsEIi0laLraysZM6cOQAkJCQwZMgQOnfurHJUwTVmzBiWLFmC3W6n\ndevWjBw58qJtZWkFIYSIEmFR0hFCCBF6kvCFECJKSMIXQogoIQlfCCGihCR8IYSIEpLwhRAiSkjC\nF0KIKCEJXwghosT/ByIk0e9o3HtaAAAAAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x113daf350>"
       ]
      }
     ],
     "prompt_number": 19
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "To apply the Newton-Raphson algorithm, we need a function that returns a vector containing the **first and second derivatives** of the function with respect to the variable of interest. In our case, this is:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "from scipy.special import psi, polygamma\n",
      "\n",
      "dlgamma = lambda m, log_mean, mean_log: np.log(m) - psi(m) - log_mean + mean_log\n",
      "dl2gamma = lambda m, *args: 1./m - polygamma(1, m)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 20
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "where `log_mean` and `mean_log` are $\\log{\\bar{x}}$ and $\\overline{\\log(x)}$, respectively. `psi` and `polygamma` are complex functions of the Gamma function that result when you take first and second derivatives of that function."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "# Calculate statistics\n",
      "log_mean = precip.mean().apply(log)\n",
      "mean_log = precip.apply(log).mean()"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 21
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Time to optimize!"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "# Alpha MLE for December\n",
      "alpha_mle = newton(dlgamma, 2, dl2gamma, args=(log_mean[-1], mean_log[-1]))\n",
      "alpha_mle"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 22,
       "text": [
        "3.5189679152399647"
       ]
      }
     ],
     "prompt_number": 22
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "And now plug this back into the solution for beta:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$ \\beta  = \\frac{\\alpha}{\\bar{X}} $$"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "beta_mle = alpha_mle/precip.mean()[-1]\n",
      "beta_mle"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 23,
       "text": [
        "0.84261607548413797"
       ]
      }
     ],
     "prompt_number": 23
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We can compare the fit of the estimates derived from MLE to those from the method of moments:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "dec = precip.Dec\n",
      "dec.hist(normed=True, bins=10, grid=False)\n",
      "x = linspace(0, dec.max())\n",
      "plot(x, gamma.pdf(x, alpha_mom[-1], beta_mom[-1]), 'm-')\n",
      "plot(x, gamma.pdf(x, alpha_mle, beta_mle), 'r--')"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 24,
       "text": [
        "[<matplotlib.lines.Line2D at 0x113ed5f90>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAECCAYAAAASDQdFAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VNXdx/HPnTuZ7NskmSyECIawFlBAKqJ1idEirT5a\npQpoFe2CgFqxIG2xiiJUgtYFoqh9yqN1qxWrldYCSl2iAiZaISAJIBCyT/Y9c+c+f0RH0oRJIJO5\nM5nf+/XiJXPuuTO/IHxzc+655yi6rusIIYQICCajCxBCCOE9EvpCCBFAJPSFECKASOgLIUQAkdAX\nQogAIqEvhBABxNxbh4KCAjZu3IimaWRmZjJjxowux3fu3Mkrr7wCgNVq5ZprrmHEiBF9OlcIIYSX\n6W5omqYvXLhQLy8v1zs6OvS77rpLP3r0aJc+LS0trt/v2bNHv+eee/p8rhBCCO9yO7xTVFREUlIS\nNpsNs9nM9OnT2bVrV5c+ISEhrt83NzcTFBTU53OFEEJ4l9vhnerqauLi4lyvrVYrRUVF3frt2LGD\njRs30trayurVq0/qXCGEEN7jkRu5U6dOZd26ddx8882sWbPGE28phBBiALi90rdardjtdtdru92O\n1Wo9Yf9zzjmHZ599lubm5pM+9+OPP6apqelkahdCiIAXExPD5MmT+9zfbeinp6dTVlZGRUUFVquV\n3Nxcbr/99i59ysrKSExMRFEU8vLysFgshIWF9enc4zU1NTFp0qQ+Fy6EEALy8vJOqr/b0FdVlfnz\n55Odne2adpmamsqWLVsAyMrK4pNPPuG9995DVVWGDRvGkiVL3J4rhBDCOIqu+8bSytu2bZMrfSGE\nOEl5eXlkZmb2ub88kSuEEAFEQl8IIQKIhL4QQgQQCX0hhAggEvpCCBFAJPSFECKASOgLIUQAkdAX\nQogAIqEvhBABREJfCCECiIS+EEIEEAl9IYQIIBL6QggRQCT0hRAigEjoCyFEAJHQF0KIACKhL4QQ\nAURCXwghAoiEvhBCBBAJfSGECCAS+kIIEUAk9IUQIoBI6AshRACR0BdCiAAioS+EEAFEQl8IIQKI\nhP4gptVptOxuQdd0o0sRQvgIs9EFiP7TmjSacptoK2qjrbCN1sJW2grbcDY5UWNUgkcEk7YhjaCE\nIKNLFUIYrNfQLygoYOPGjWiaRmZmJjNmzOhy/P333+eNN94AIDU1lSuvvJK0tDQAFixYQGhoKCaT\nCVVVWbVq1QB8CYFNd+gcuvYQertO6BmhhIwNIfqKaIJHBBOUEgQalK0uo/DCQtKeTiNiWoTRJQsh\nDOQ29J1OJzk5OSxfvhyr1cqyZcsYP348qamprj6JiYncd999hIWFsX37dp566ilWrlzpOn7vvfcS\nESFBM1DKVpehmBXSX09HUZXuHcyQ/Ntkwr8bzuEbD5OwIIGEhQkoph76CiEGPbdj+kVFRSQlJWGz\n2TCbzUyfPp1du3Z16TNy5EjCwsIAmDRpEna7vctxXZfx5IFSv6WempdqSNuQ1nPgHycqK4qMbRnU\nvVnHV3O/wlHj8FKVQghf4jb0q6uriYuLc722Wq1UV1efsP/WrVuZMmWK67WiKKxYsYIlS5awdetW\nD5QrvtFe3M7RhUdJe6bvY/WWVAvpb6VjGWah8MJCmvOaB7hKIYSv8diN3N27d/P+++/zwAMPuNru\nv/9+YmNjKS4uZtWqVQwZMoQxY8Z46iMDlrPdyeGbOodqIs4+uaEzk8XEkAeHEH52OAd/fJCR74zE\nMtQyQJUKIXyN2yt9q9XaZbjGbrdjtVq79Tt8+DAbNmxg6dKlhIeHu9pjY2OBzhu8U6dOpaioyFN1\nB7TSe0sxJ5hJWJhwyu8Rc3kMtkU2jsw/IlM6hQggbkM/PT2dsrIyKioqcDgc5Obmdhm+AaiqqmLt\n2rUsWrSIpKQkV3tbWxstLS0A1NfXk5+f75rVI05d7Ru11G+uZ+j6of2+GZuwoPObRuW6Sk+UJoTw\nA26Hd1RVZf78+WRnZ7umbKamprJlyxYAsrKyePXVV2lsbOTpp592nbNq1Spqa2vJzs4GIDIykpkz\nZzJx4sQB/nIGt7aDbRy76xjDXxqOOab/I3OKqpCWk0ZhZiGRF0YSOj7UA1UKIXyZovvI9Jpt27Yx\nadIko8vwWc52J4VZhcRdH0f8LfEefe/ql6upfLSSjHcyMIXIQ9pC+JO8vDwyMzP73F/+hfuJ+n/U\no0aoxN0cd8I+psOH4RS+h8fOiiV4VDClK0r7U6IQwg9I6PuJ6hersd5gRVFOMI6vaUT8+MdETZ5M\n6D33oO7cCU5nn95bURRSH06l7o06GrY3eLBqIYSvkdD3Ax1lHTR/0kz0D6JB11GOHeveSVWp/+gj\nmjZuRA8OJnzRIqLHjyf0178GR+8PYpljzQx9fChHFx6VB7eEGMQk9P1AzV9qiJoZRfDO94m8+GLC\nli3ruaOioI0fT+tvfkP9xx/T8NprdFx6KZj7dtM38sJIon8QTfHiYnmSWohBSkLfx+m6Ts1LNQwZ\nvpPwhQtpXbiQpj/9qU/nOkeNwnH++Sf1ecm/S6Z1byu1r9WeQrVCCF8noe/jWj5vQWmsxfrscpqe\nfpqOK68E08D9bzOFmkh9JJXSFaU42/p2T0AI4T8k9H1c9YvVjLQ+S/vMmTimTfPMm/YydBNxdgQh\nY0Kw/8nutp8Qwv9I6PswZ5uT2tdqcS77OS3Ll3vkPZWSEiKzslDKytz2S16eTMUjFWgNmkc+Vwjh\nGyT0fVj9v+oJGROC6ZLJEBXlkffUU1LouOwyIi+/HKWk5IT9QseFEnlBJJXrZYkGIQYTCX0fVvNi\nDdbrui9w11+td95J25w5RF51FTSfeHnlxGWJVD1dhaNKpnAKMVhI6PuojooOmj5qIvqH0QPy/m23\n3472ne8Qev/9J+wTfFowsVfHUr62fEBqEEJ4n4S+L9J1av9SS9RlUagR6oB9TPOaNQT9619ux/dt\nd9qoeaWG9iPtA1aHEMJ7JPR9UMjq1QSt2zAgQzvH02Njqc/NRT9uSez/FmQLIv7meMp+7/7GrxDC\nP0jo+xh1zx4sG57FbjqP8HPCez+hv4KDe+2SsDCBhq0NtBS0DHw9QogBJaHvY0LvvpuyCYsInzOy\n35ukeIoapWK73UbZSrnaF8LfSej7EFNREWphIYcKLiD22lijy+kibl4cLV+00PRJk9GlCCH6QULf\nh1hefJGGKVcQPCqc4OG9D7sMBHXHjh7bTSEmku5OonRFqSzGJoQfk9D3IXpsLMcaLzHuKr+tjfCF\nCwn62996PBz741gcVQ4a/93o5cKEEJ4ioe9DWn+xgKp8G9EzBmZufq+Cg2lat46wpUtRKiq6HVZU\nBdvtNioe7X5MCOEfJPR9SMvuFixDLJjj+r/p+anSzjqL9muvJfSee3o8HnN1DG2FbTR/duIneYUQ\nvktC34c0fdjknWmavWhZvJig995Dzc/vdsxkMZGwIEGu9oXwUxL6PqTxo0bCpxkf+kRG0rJ0KcFP\nPdXjYev1Vho/aKTtQJuXCxNC9JeEvo/QnTpNHzURcU6E0aUA0D53Ls2PPdbjMTVCJX5ePBVPyNW+\nEP5GQt9gpv37ibjmGlr3taLGqgQlBxldUidVBYvlhIfjfxZP3d/q6Cjr8GJRQoj+ktA3WPCLL6KN\nHUtTbhMR03zjKr8vzHFmYmfFUvmkrLcvhD+R0DeSpmF55RXarr2WxtxGn7iJezISFiRQ/Vw1Wr3s\nriWEv5DQN5D53XdxJiejjR7deaU/3Yev9LXuwW4ZaiEqK4qqP1YZUJAQ4lRI6Bso+MUXab/uOtoP\ntKMEKQQN9ZHx/P+maUReeCGmgwe7HUq4LYGqp6pwtjoNKEwIcbKMewpokCutb6Oi0c3GI5rGpKJD\n/Oeue3FsroIzgvlPqWeWN7BFWEiO8uDaPapKxxVXEHrffTRt3NjlUOjYUEInhlLzUg1xN8Z57jOF\nEAOi19AvKChg48aNaJpGZmYmM2bM6HL8/fff54033gAgNTWVK6+8krS0tD6dO5hVNLbzq81F7jtd\nvxY+rOLaNxQODtfZsbneI5+95rIRng19oHX+fKK/+13Ujz9GO/vsLsdsd9g4uuAo1uutKKpvLAct\nhOiZ2+Edp9NJTk4OixcvZvXq1bzzzjsUFxd36ZOYmMh9993HmjVrmDhxIk99/UBPX84VnU4/CIeG\nG11FL8LCaPntbwn77W/B2XUoJ+LsCMw2M3Vv1BlUnBCir9yGflFREUlJSdhsNsxmM9OnT2fXrl1d\n+owcOZKwsDAAJk2ahN1u7/O5AmJqwOyAygSjK+ld+zXXgMNB0N//3u2Y7XYbFY9VyLLLQvg4t6Ff\nXV1NXNy347RWq5Xq6uoT9t+6dStTpkw5pXMDVfpBODgc8IdREZOJllWr0BO6f4eKuiQKZ7OTplzZ\nZEUIX+ax2Tu7d+/m/fff57rrrvPUWwaE4QcVDp7uP1fHjmnTcEyb1q1dMSnE/yKeyhx5WEsIX+Y2\n9K1Wq2u4BsBut2O1Wrv1O3z4MBs2bGDp0qWEh4ef1LmBJqy1mZu2/dn1+vRDcOh0AwvyIOuPrTR9\n0kTbQVmITQhf5Tb009PTKSsro6KiAofDQW5urmv45htVVVWsXbuWRYsWkZSUdFLnBqJJBz/nrKI8\nACLrIbwJyhINLspDTGEm4n4SR+VTcrUvhK9yO2VTVVXmz59Pdna2a9plamoqW7ZsASArK4tXX32V\nxsZGnn76adc5q1atOuG5gW5qUR47MiYB387a0QfRI3LxN8fz5TlfkrQsCXOMPAYihK9RdB+ZbrFt\n2zYmTZpkdBke83lJQ4/z9F9aezMrrvkVBWmjuXKTgt2q8975nv3sNZeNYGJKpGfftAdKbS2mI0fQ\nJkzo0n5k/hFCxoRgu8024DUIEejy8vLIzMzsc/9BdI3p++Lq7STUV7EvNQOA4YfgoB+P56u7dxN+\n003gcHRpj58fT9WGKvQOn7ieEEIcR0Lfi6YW5fFp+hk4TSphTRBTCyUpRld16hznnoszNRXLyy93\naQ+bEIZluIXaN2oNqkwIcSIS+l6UP3wCG7JuADqv8o+kgVM1uKh+ar37bkKys6Gj62YqCbcmULm+\nUh7WEsLHSOh7UVlsIkXJ6QCcfsi/5uefiGPaNJzDh2N54YUu7VGXRqHVaTR9Ig9rCeFLJPQNcvpB\n/x7PP17L3XcTsnZtl7F9xaSQ8IsEqtbLWvtC+BIJfQOEtEBCJRwdJDNYtalTafzrX8HcdYpm7LWx\nNOY20vaVPKwlhK+Q0DfAaYc7A18bRNPYnRkZ3drUCBXr9VaqnpKrfSF8hYS+N+h656+vnXZE4fAw\nw6rxqvhb4ql5uUb20RXCR0joe8G4o/t44pklrtcpJXAsxf9v4vaFZYiFyIsjsW+0995ZCDHgJPS9\nYGphHkVJ3+6SklwKpckGFuRlCfMTqHq6Ct0RGN/ohPBlEvpeMLXwU3aMmAxAaDOENYF9sG4n295O\nyAMPdJnJE3ZmGJahFurelJ21hDCahP4AC25vZWzxl+Sf3rk+TXIplCUPrkXWurBYMH/8MZa//rVL\nc8L8zoe1hBDGGqzR4zPO+Go3+4Zk0BIcCkBKqX8vvdAXrXfdRcjDD4P27c3bqBlROOwOmnbIw1pC\nGElCf4ANrzjMJyO/3UcgpUShJHlwj207zj8fPSaGoL/9zdWmqArxP4+Xq30hDCahP8BeOvdH/PGi\nOa7XySWD/0ofRaHlrrsIzc4Gp9PVbJ1tpfH9RtqPtBtYnBCBTULfG5TOXc9VB9gqoSypl/6DgOPi\ni9EjI1E//9zVpkaqWOdYZWctIQwkoe9FtkqojYEOi9GVeIGi0PDWW2hnntmlOf5n8dS8JA9rCWEU\nCX0vCoihneOZu68zYUm1EHF+BNV/rjagICGEhL4XpZQolATIk7juJNyaQNVTVeia/FkI4W0S+gPE\nXFvDpAOfd2lLKYWSAHoS90TCp4RjTjRT95Y8rCWEt0noD5DYjz/kug9e/bZB71xzJ6CGd9z4Zmct\nIYR3SegPkKgv8tkzdMy3r+tBV6Ah0sCiDBS6fDnm7dtdr6NnRtNR2kHTLnlYSwhvktAfIJFffM6e\noaNdr11X+YpxNRlJmzCBkIceci0xrZgVEn6eQFWOrLUvhDdJ6A+Ejg4i9+6hYOgoV1OgD+20X3kl\npspKzB984GqzzrXSsL2B9qPysJYQ3jKI9m7yHerevbSmDKEpJNzVllKqsGesd2arqCb4vKTBK591\nPFuEheSo4J4Pms203nknIWvW0HjeeQCoUSrW2VYqcyoZ8uAQL1YqROCS0B8AutlM8dx5XdpSSmDL\nxd75/LpWjfu2HvLOhx1nzWUjThz6QPs11xCyZg3m3Fwc55wDQPwv4tl/3n4SlyRijpG/jkIMNBne\nGQDOsWMpvWa267WlDaLroDLBwKJ8gdlM67JlmA4edDVZhliI+n4U9j/KzlpCeINcWnlBchmU28Cp\nGl2J8dqvuaZbW8LCBA7+6CAJtyZgCpHrECEGUq+hX1BQwMaNG9E0jczMTGbMmNHl+LFjx1i/fj1f\nffUV1157LT/84Q9dxxYsWEBoaCgmkwlVVVm1apXnvwI/EHDLL5yk0LGhhI4PpeblGuJ+Mli3FBPC\nN7gNfafTSU5ODsuXL8dqtbJs2TLGjx9Pamqqq09kZCTz5s1j586dPb7HvffeS0REhGer9jMpJQql\nsvyCW7bbbBTfWYz1eiuKKUDntQrhBW5/li4qKiIpKQmbzYbZbGb69Ons2rWrS5+oqCjS09NR1Z7H\nLnRdwi4Qdsvqr/Dp4ZgiTdT/o97oUoQY1NyGfnV1NXFx3/64bbVaqa7u++qIiqKwYsUKlixZwtat\nW0+9Sj8S/MQTmIqKXK8VJySVQWkArKF/0nQdmjqfyFUUBdtCGxWPVxhclBCD24DeNbv//vtZs2YN\nt912G5s2bWLv3r0D+XHG03VCnngCLN8umB9fBY0R0BpqYF0+KmjTJsJ/9jPX6+gfRuOocND0sSzN\nIMRAcRv6VqsVu/3bqXR2ux2r1drnN4+NjQUgNTWVqVOnUnTcFfBgpBw7BrqOc+hQV1tyKZTKypo9\n6rjsMsyffebaXUsxKyTcmkDFE3K1L8RAcRv66enplJWVUVFRgcPhIDc3lylTpvTY97/H7tva2mhp\naQGgvr6e/Px80tLSPFS2bzLv2oVj8mTX9ogga+i7FRJC6x13EHLcrC7rbCvNO5pp3d9qYGFCDF5u\nZ++oqsr8+fPJzs52TdlMTU1ly5YtAGRlZVFbW8uyZctobm7GZDKxefNmHnnkEerq6sjOzgY6Z/jM\nnDmTiRMnDvxX9F9aO7y3LV/Qzl20nXEmrR0a38R8Sil88l2vleB32m64gZDHHkPduRPtrLMwhZmI\nmxdH5bpKhj46tPc3EEKclF7n6Y8dO5aHHnqoS1tWVpbr9zExMeTk5HQ7LyQkhDVr1nigxFPXrjl5\n7MNivqpp8crn3bP1Q167fB67/17IDZM7x3RSSmTjFLeCg2lZvJjQVatofO01AOJviWff1H0k/TqJ\noMQggwsUYnAZ9E/kHq1rpcjundB/9MLrKYhJp8XeAjqEN4KlHWpivfLxfqt9zhwUTQOnE0wmzPFm\nYn4UQ9WGKpKXy3dMITxJnnn3oE9HnElL8LfTdFzbI8qzRu4FBdF2881g+vavY8KCBOwb7Wh13hue\nEyIQSOgPoEBfQ78/gocFE3VJFFUbZJMVITxJQn8AJZfKzJ3+sP3SRuWGSrQGudoXwlMk9AdQSonM\n0e+PkIwQIs+PlGWXhfAgCf2B0q4TZ4fyRKML8TNOJ0Fvv+3aS9d2p43KnEq0JrnaF8ITJPQ94MyD\n/+GeV7pOa1W+6qAmFhwy4/CkhTz4IEGbNwOdyy6HTw2nemPf13wSQpzYoJ+y6Q0TDu+hPrTr8tGm\ng+2UBdhVvqf25o37+R0MX7GSzyee2zmj5ycR1C0oo2SGBYJ7vk5xuz+vEMJFQt8Dxh3Zy5aJF3Zp\nUw50UBFgoe+xvXn10/jfVnj7939k68QLALgpTuHL+w+Se07Pp/S2P68QopMM7/SXrvOdI/vYkza6\nS7PpYAflNpm5c0oUhZxLb+IXb/8vquYAYGumzgXbFVSHwbUJ4eck9Pspsa4S1alREtt1wXzlUIfc\nxO2HHRmTKY+xccln7wJwNA0qbDD5U4MLE8LPSej30+ji/Z1X+cetrKk6QClxUJlgYGH+TlH47exf\n868zLnI1bc3UuehdBZNM5BHilMmYfj/9e9x0Phk5uUtbfBXoySqaWdKpP2oiui5a9NVwqImBM/Ph\n055X+BZC9EKu9PtLUWi1dN0WK7EC9NMtJzhB9MfWi3UuekdBcRpdiRD+SUJ/ACSWg/N0maA/EA6k\nQ3M4TPzc6EqE8E8S+gPAVq6gS+gPDAX+eanOpf+SsX0hToWE/gBIrJArfU8beayQpa/9AYADI6Da\nClN3GFyUEH5IQr8fYhprUbWul5sm7esbuadJ6HvSYVsa5+39mPGH9wDwj+/rXLxNIajd4MKE8DMS\n+v3wwIsrOXv/zi5tcXaoiwZC5I/Wk9qCgnny0hu57a0NoOsUD4WvhsH0D42uTAj/Isl0qnSdUccK\n2Zc6sktzYjmU2wyqaZDbPCmL8NYmvleQC8Dbl+ic/55CaLPBhQnhRyT0T1FSbQUdqgV7pLVLe2IF\nlCed4CTRL06TyhOX/ZSF/3gGVdOotMHucXDBv2U/SiH6SkL/FI0+Vsi+ISO6tSeWK7LmzgDKHTWV\nj0dOwdrYudTy1ot1vvsJUCGL8gjRFxL6p2j0sUK+HJLRrT2xXDZOGVCKwsOXL6AyunONi7oY2DkF\neLLG2LqE8BMS+qfIrDn4z7BxXdoUZ+fMnQoZ0/eqdy/U4V9NtB1sM7oUIXyehP4peuKyn/LRqKld\n2qzV0BgBHbICg1c1hwPXR1O2qszoUoTweRL6HiRDOwa6PprGDxpp+aLF6EqE8GkS+h6UWCHTNb0t\nuqmO7xwugDATiYsTKb2/1OiShPBpEvoelFiuUJ4oM3e8aWjVMX7/3L2ojQ1Yb7DSdqCNhnf6v0+v\nEINVr6FfUFDA0qVLueuuu/jHP/7R7fixY8f4zW9+w5w5c3jzzTdP6tzBRoZ3vG/3aWPZkTGZ0558\nDJPFRMrKFI4tO4beId98heiJ29B3Op3k5OSwePFiVq9ezTvvvENxcXGXPpGRkcybN48f/vCHJ32u\nv/reng+7rbmjOMFWITN3jPDEZT8l+fW/YNq/n6hLo7CkWajaUGV0WUL4JLehX1RURFJSEjabDbPZ\nzPTp09m1a1eXPlFRUaSnp6Oq6kmf649iGmu59+Xfo5m6/tHF1EJTOLSFGFRYALNHWjn80wWELVuG\nAqQ8mEL5I+V0lHcYXZoQPsdt6FdXVxMXF+d6bbVaqa6u7tMb9+dcXzaqpIh9QzK67IkLnUM7cpVv\nnGOzb8RUWor6xReEZIRgnW2Vm7pC9EBu5J4keRLXN+lBQdRv24Y2YQIAiXcl0vBuA82fympsQhzP\nbehbrVbsdrvrtd1ux2q1ujnDM+f6stHF+zuv9P9LYoWsuWO40G/3KlajVJKXJ3Ns6TF0p/x/EeIb\nbkM/PT2dsrIyKioqcDgc5ObmMmXKlB776rp+yuf6k86F1uRK3x/EzooFE9S8KOvyCPENs7uDqqoy\nf/58srOz0TSNzMxMUlNT2bJlCwBZWVnU1taybNkympubMZlMbN68mUceeYSQkJAez/VnitPJB2PO\n5mj8kK4HdJm544sUk8KQ3w/h0OxDRP8wGjVK7f0kIQY5t6EPMHbsWB566KEubVlZWa7fx8TEkJOT\n0+dz/ZluMrH2ioXd2mNqoc0CLWEGFCVOSCktJezMZKIuiaL8oXJSHkgxuiQhDCc3cj0gsQIqZGjH\ntzQ0EHXhhZgKCkj6bRLVL1fT+mWr0VUJYTgJfQ9ILIcyCX3fEhlJy69/TfhttxEUq5C4OJFjS451\nu/ckRKCR0PcAW7lChay543Par78ePSKC4Jwc4m+JR2vSqN7o/8+KCNEfvY7pi94lVsCn/j8xya+p\nJvi8pPtCayHLVjL5usv54qwLaLknheKbSigeb4Jkz/zVt0VYSI4K9sh7CeENEvp9dHrZV3znSAFv\nTL2s6wH96+maMnPHUHWtGvdtPdTjsevOvZYzlvyWpTfcS+ZUGLbwMM/O08ED+6mvuWyEhL7wKzK8\n00dTDuQzpnh/t/aoenCYv969Sfikl8+9kgd/9EsA3r0AIhtg8qfG1iSEUST0+2hM8f6el1+QjVN8\nntOkUhce3fl7FV6ZpfODtxSi6gwuTAgDSOj30agTPIlrK5fpmv6mJAU+Ohuu2qSA3H8XAUZCvw+C\nO9oYai/hQNKwbseSZLcsv7QtUyfODmd8ZnQlQniXhH4fpJce4nDCUDrMlm7H5Cau/1E1jaH2w7w8\nS+fyNxXCG42uSAjvkdDvg/KYBB6d+fPuB3RIKoPSZO/XJE5dRukBnnxqMa1RVeyaAle+7oFpPEL4\nCQn9PrBHxbEzY1K39phaaLfIzB1/sy91JK9Ou5wVL61ia6aD5FKYKMM8IkBI6PdDcimUJRldhTgV\nf8ycg+p0MvvDl3nhOp3/+ZtCnL3384TwdxL6/ZAsQzt+y2lSuee6ZVz7wV+J1QrYcrHO3OcVVIfR\nlQkxsCT0+yG5VKE0WWbu+KvyGBurr/olV+zYTO45UBMLP3hLxvfF4Cah3w9JZVAqwzt+bft3zmXl\n1YtBgVeu0RmzF8Z/YXRVQgwcCf1eLP7bE0z4ak+3dnMHxNllt6xBQem8um8Nhefn6Fz1moJVxvfF\nICWh34sLd3+APTK2W7utAuxxoMmSdYNK8dDOB7fmvCDj+2JwktB3I76uiuCONo5Zu9+tlZu4g9cH\n06E+CmZulvF9MfhI6Lsx7ug+9gwd7frx/3hyE3dwUjUHD/55Bdu+X8W4PTBut9EVCeFZEvpuuEK/\nB8mlchN3MNJUMweShrPiL7/j5R+38aPXFBIqjK5KCM+R0Hdj3NEvTxj6svzC4PVs5lzKYmzcsONh\nNn/fybxBLsPdAAAUQklEQVT/lfV5xOAhoe/G3XPvYdeIM7u1hzeC2QF10QYUJQaeorBi1q8YUXaI\nUS1/4fMJcONGBXOH0YUJ0X8S+m40hEXSHtR9Zc2ksq+XX5D7fINWqyWUxT9Zwez3X6Vk9G5qo2HW\nKwqK0+jKhOgfCf1TkFwqQzuBoDw2kXkLn+CL08bw8o91rDVwyRb5Ti/8m4T+KUguVShLkpk7gaA8\nxoZuMuEIgv+9UefMfJi8y+iqhDh1EvqnQOboB6amCPjjTTozNyucfsDoaoQ4NRL6PVA1jeD21h6P\nKc7O3bLKZF/cgFSRCH+erTP3zzKVU/inXhcRKCgoYOPGjWiaRmZmJjNmzOjW54UXXiAvL4/g4GBu\nvfVWhgwZAsCCBQsIDQ3FZDKhqiqrVq3y/FcwAEYf28/STY9yw+1PdjsWXwUNkdAWYkBhwnBBjnYW\nvHcv//ze7fz0mSS4uANSjK5KiL5zG/pOp5OcnByWL1+O1Wpl2bJljB8/ntTUVFefvLw8Dh8+THZ2\nNoWFhaxfv56VK1e6jt97771EREQM3FcwAMYd3cfe1JE9HpP5+YGtw2xhx8jJ/Cz3Vzx99h+4+OYg\n2t+KwJLWfZaXEL7I7fBOUVERSUlJ2Gw2zGYz06dPZ9eurnexdu3axfnnnw9ARkYGTU1N1NbWuo7r\nuv/d8HT/JK4iT+IGuJfO/RH/PPNi5uUtxnJlKweuOED70XajyxKiT9yGfnV1NXFxca7XVquV6upq\nt33i4uJcfRRFYcWKFSxZsoStW7d6su4BNe7IPvakjenxWHIZlMmaOwHvmawbeGvyJZy56SaSr27i\nwOUHaC+W4Be+zyMLA5/oav7+++8nNjaW4uJiVq1axZAhQxgzpucw9RWRzQ3ENVRzyJbW4/HkUtjc\n/baGCED/d+F1XPLdEaQ1b6Xjpzdz4PIDpL+RjiVVhnqE73Ib+larFbv9290k7HY7Vqu1z31iYzvX\noU9NTWXq1KkUFRX5fOgn15bz0aizcJrUbseCWyGyAariDShM+KTSq6/DlhJJAqA7dQ5c8XXwD5Hg\nF77J7fBOeno6ZWVlVFRU4HA4yM3NZcqUKV36TJkyhffeew+A/fv3Ex4eTkxMDG1tbbS0tABQX19P\nfn4+aWk9Xz37kv0pI/j13Ht6PJZUDuU20GWiq+iBbaGNuJ/EdY7xy1CP8FFur/RVVWX+/PlkZ2e7\npmympqayZcsWALKyspg0aRJ79+5l8eLFhISEMH/+fABqa2vJzs4GIDIykpkzZzJx4sQB/nIGVpIs\nvyB6YbvNhqIqFF1axLAXhxE2IczokoTootcx/bFjx/LQQw91acvKyuryes6cOcyZM6dLW2JiImvW\nrPFAib4juUyWXxC9s13txPrlVvZedSFpOacRlRVldElCuMhAxUmQhdZEn3R0EPPFJiZPeJhjiwqp\nerbK6IqEcJHQ7ytdHswSfaOnptKweTOqLZizYu6g4Yn/ULK8BN0pPyUK40noH2fskX3E1dt7PBZd\nB5raueiWEL0KDaU5J4eOn8zmjKb5mN/ZzuEbD+NslgX5hbEk9I9z2+YNjCg71OMxGdoRJ01RaJs/\nn6ZnnyF1lh0lRJGHuIThPPJw1mCgahqjjhVSkDqqx+OynLI4VY7zzoPzziNN16l8vJLCzEJSH04l\neqbstym8T670vzbh8B6OxaXQEBbZ4/HONXdkTFacOkVRsN1mY9jzwyj5TQnFS4txtspwj/AuCf2v\nfa8gl3+PPeeEx+UmrvCU8LPCGfnvkZj376Mo6wvaitqMLkkEEAl9AF3ne3tyeW/stB4Pq47OdfQr\nbF6uSwxaarTK8JFbOKPqFkqz3qT65ereTxLCAyT0AbPm4K0pl/DlkIwej9sqoNoKjiAvFyYGtZbV\nq+l44G4mKMuw/GYVh28uoqOyw+iyxCAnoQ84zEH8MXMuKEqPx1NKZGhHDABFoeNHP6Lhg3+TOP4g\no96/npKpm7BvtMucfjFgZPZOH4z+UqFwhPwjFANDT0mh6bVXCdq0idTmGA5urKb6pWpS16YSOjbU\n6PLEICNX+r1QHTByP+wda3QlYlBTFDquugp17kWMeHsEsbNiOXDFAUpXlMoDXcKjJPR7cfpBqEzo\n3AxdCG9QTArxN8Uz6v1RtB9u58tz9lD7eo0M+QiPkNDvxbgChT1j5R+b8L6gpCBOe/Y0xpz/T+IX\n/g8VU5+nfmudX+47LXxHQId+SHsLG9bfjqppPXfQYWwB7Bnn3bqE6OLhO1EeWcTprY9jveEHVJ37\nHE0fNRpdlfBTAR36UwvzcJiD0NTuWyNC56wdhyrz84XBVJWOa66m6fOPUB77JcNq1xF95fc5dHUB\nzf9pNro64WcCevbO+W4eyAIYt0ehYCzQ80xOIbxLVem4+io6rvofTB98TMS+BA5de4iQUSEk3JpA\nZGYkikn+sgr3AvZK3+TUOHfvx7znZumFzqEdGT8VPsZkwvm9c0j4WQJj8scQe20sZSvL+HLal1Q9\nU4HWdILhSiEI4ND/zpG92CNjKbH2/NRVTA3E1sLh07xcmBAnwRRswvpjKxnvZpD6SCrR6+9FOf1y\n6m96hfbDrUaXJ3xQwIb+pIP/4b1x0094fOxe2DsGnD0P9wvhUxRFIeKcCII+yMa87GpsHz5K9OQz\naZ1wB42//xCtzmF0icJHBOyY/p8uvA6zduJ/COP2KHx0tgztCPdUE3xe0uD1z7VFWEiOCu5+ICwM\n5x030Xr7jSif7Sb04RcIefxW8tbnEHbpEGJnxRJ5QSSK+dTH/kvr26ho9P5GMCf8msVJCdjQR1Fw\nmHteQS2kBdKOwMYbvFyT8Dt1rRr3be15t7WBtOayEe4DUFHQzxwPz62iRX+QjGqN2k21lK8u5+ii\no0TPjCbqkggivheJKeTkfpytaGznV5uL+vkVnLxev2bRJwE7vOPOqC/h0HBol79fYjBQFMxxZuJv\niSdjawbpb6RjSbPQ8rs3CR/yHRxn/pzW3/wVR3G90ZUKL5DQ74E8hSsGs5CMEGy32UjMnUvzW69i\nOvN0Il5+ktgJY1GGz6Rh3os0vNeAs0XW/BmMAnd45wRMWueV/t9nGl2JEANMUVDOHody9jgcLKW+\nvAbt2X+hFUdSubKM1oJWQieGEjE9gojzIgibFIopTGY2+LuAC/2MkgM0B4dyLC6lx+OnH4SqeKiX\nPatFgFESYzH/+sfEADGA1qjRvKOZxg8aKb2vlGGf/ZqQoMOMShrL4pjh7Bo9kk/Gnk5riMXo0gfc\nYLp5HVChH97axG9fXcuL5151wtAfW6DIA1lCAGqESuRFkURe1LnErLN2I02bP6PhzY8YuyufS3f/\nnShHMf9IepgvThtDWZJOeSKUJUFThMHFe9hgunkdMKEf01jLY8/eze60Mbx9xkU9d9JhXAH88Sbv\n1iaEPzDFhGGafQ4lF4x3BWBkQxtJpSoJlTpJ5QoTP4ekctBUGKffR2NYMMXWFL5KTKFwaAp7hqdQ\nExl1wl3qxMDrNfQLCgrYuHEjmqaRmZnJjBkzuvV54YUXyMvLIzg4mFtvvZUhQ4b0+VxvSKwp54ln\nlrJtwvk8ecmNJ/wLl1wKugLlid6tTwh/1RAZTEMkFI4E+PonZB2i6uHcL65mzOGvGFpVyiUluVz7\nYQmRWglvRz9HaUI01bFQF6NTGwO1MZDQ8iVfJVspi7PiNMm9g4HiNvSdTic5OTksX74cq9XKsmXL\nGD9+PKmpqa4+eXl5HD58mOzsbAoLC1m/fj0rV67s07neENLSxIYnf8lL06/ixe9d7bbvuALYIwus\nCT9g1ENhAO1aL7N6lM57YpvPHcvmc7tuOWfSILZGJ96uE1sD0bUKpx+EmBqdK488QYSjnCDqaDNF\n0xQUS0OwlecmrqQ+ygRaAw0jQbWqmK1mglrKYEgcSnj4AH61g4/b0C8qKiIpKQmbrXNt4enTp7Nr\n164uwb1r1y7OP/98ADIyMmhqaqK2tpaKiopez/WG1tBw7rxpJQeShrvtpzhh7B6Fv/9AxvOF7zPq\noTCA313s/t+SO04V7PEK9vhvWr799/YUj4MO0fUdDC2vJaWqhsTqGuojTETWK/BBCxX/bMFR7cBp\nb2FyySyCqENHwWGORrNE4wi1cihrA2qU2vkrWsUUZUIN1YnY/Q+IjUSJi4K4SJT4KBRbFKQloQTQ\ncJPb0K+uriYuLs712mq1UlRU5LZPXFwc1dXVfTrXW3oK/LCmzqdu044opB2FoUehOha+Gub9+oQQ\nX1OgLjqIuugEdo9MOO6AzvmX2UhP+Xbf0mb242zWcByrhyN29JJq9KoGIhIj0Oo1tDqN9mPtaAUa\nem0T0Z/+HVNbE6aOZkwdTahaM7oOO3geU6gJU5gJJVTBFGrCHNzCuAO/wKkGowcFM95k4YUOlWZL\nFG+MvAtNBYcZNLOOQwWUdqYfeZ12cxAdqpl2sxmH2UxLUAg70s9DM3Xe53B+/V/QGF5VSIeq4jCr\ntJtVNFWlLSiIsthEnKbOvrR6/lkJj9zI9dT2baZRV3RrKx61mLbwod3aU/dmE9xS7La/U9e5oRk6\ntNDjigXLEQemOidto4NoHRNEa6aF8tFBaHEqP/XIVwImeexNiAFnClOxZMRCRqyrLeSEvV9GB7Sv\nf3V83TrBqeNsceJsdqK36DibnTgb2qnf9yg0tkJTCxVl9Xy0rwyzQ6faqmPWwOwAVVMIboOQNifJ\n9mqCHO2ouoZZc6A6HegEEVzyPVQNTE5c/w12tJJZ9RgmNEy6A0V3YkLDQSgfhG5A0Tv7kV8Ff/Ts\n/HG3oW+1WrHb7a7Xdrsdq9Xapz4Oh6PXc48XExPDrhd/d4KjNT203Oym8m/7q1//6kkwDoJpwfVH\n2nGCjqeiElZP8uD7nYzqg8Z8tlGfa+RnB9rnGvjZWlkheWVe+jAVGGcBLEAUkMgIMgAYxvEXud/8\nPphGft7jW42gp6v1MD5jXY/9Q4/rr1FHXl6e21JjYmLcHv9vbkM/PT2dsrIyKioqsFqt5Obmcvvt\nt3fpM2XKFN5++22mT5/O/v37CQ8PJyYmhsjIyF7PPd7kyZNPqnAhhBAnT9F7GZspKCjgT3/6k2va\n5WWXXcaWLVsAyMrKAuDPf/4zeXl5hISEMH/+fNfN2p7OFUIIYZxeQ18IIcTgIbcbhRAigEjoCyFE\nAPGJtXd8ZbmGU1FVVcW6deuoq6sjKiqKCy64gAsuuMDosk6K0+nk7rvvxmq1cvfddxtdzklpbW3l\nmWee4ciRI3R0dDB//nxGjhxpdFl9tnXrVrZv305HRwdjxozhxhtvNLokt9avX09+fj5RUVGsXbsW\ngJaWFh5//HEqKipITExk0aJFhISceOKkkXqq/7nnniMvLw+LxcKYMWOYNWsWYWFhBlfas57q/8ab\nb77J888/z7PPPktEhJsV73SDaZqmL1y4UC8vL9c7Ojr0u+66Sz969KjRZfVZTU2NfujQIV3Xdb2u\nrk6/5ZZb/Kp+Xdf1N998U3/00Uf11atXG13KSXv88cf1bdu26bqu6w6HQ29qajK4or5raGjQb731\nVr2lpUXXNE1/8MEH9fz8fKPLcqugoEA/ePCgfuedd7rannvuOf3111/XdV3XN23apD///PNGlder\nnur//PPPdU3TdE3T9JycHL+rX9d1vbKyUn/ggQf0W2+9VW9oaHD7HoYP7xy/1IPZbHYt1+AvYmJi\nGDZsGABRUVGkp6dTU9P9uQJfZbfbyc/P56KLLvLYQ3be0tzczL59+7joos5VU1VV9dkrtJ5YLJ3r\n0Dc3N9Pe3k5bW5v7KzQfMGbMGML/a62b45diueCCC9i5c6cRpfVJT/VPmDABk8mEyWTijDPO6PJ8\nka/pqX6A//u//2Pu3Ll9eg/Dh3d8abmG/iorK6O4uJiMjAyjS+mzjRs3MnfuXFpaWowu5aRVVFQQ\nFRXFunXrOHjwIBkZGcybN88Vpr7OYrFwyy23sGDBAoKCgpgxYwYjRowwuqyTVldX53pAKDo6mrq6\nOoMrOnXbtm1zXUT4i507d2K1WjnttNP61N/wK/3BorW1lT/84Q/85Cc/8dnxzP/26aefEhUVxfDh\nw/3uKh9A0zQOHDjAd7/7XVatWoXD4eCjjz4yuqw+q6+v55lnnuGRRx5h3bp17N+/v9enL32dPy9c\n9tprrxESEsK0adOMLqXP2tra2LRpE7NmzXK19fZv2fDQ78tSD77O4XCwdu1azjvvPM466yyjy+mz\nL7/8kk8//ZQFCxbw6KOPsmfPHp544gmjy+qzuLg4IiIimDJlChaLhenTp5Ofn290WX1WVFRERkYG\nSUlJREZGMm3aNAoKCowu66RFR0dTW1sLQE1NDdHR/rfX6Pbt28nPz2fRokVGl3JSysvLqays5Fe/\n+hULFiygurqau+++2+1PW4aH/vFLPTgcDnJzc5kyZYrRZfWZrus8+eSTpKamMnOmf+2mPnv2bHJy\ncli3bh133HEH48aNY+HChUaX1WcxMTEkJSVRWFiI0+kkLy+PCRMmGF1Wn40ePZoDBw7Q2NhIR0cH\n+fn5TJw40eiyTtqUKVPYvn07AP/+97/96sIH4LPPPuONN95gyZIlfjM0+I20tDSefvpp1q1bx7p1\n67Barfz+9793+43XJ57I9eflGvbt28fvfvc70tLSXD/azp49mzPOOMPgyk5OQUEBb775JkuXLjW6\nlJNSUlLCunXrqK+vJy0tzaenC/Zk+/btvPvuu7S3tzNx4kRmzZqFyYeXaP3DH/7A3r17aWhoIDo6\nmlmzZnH22Wf7zZTNb+qvr68nJiaGa665htdffx2Hw+G6iT5y5EhuueUWgyvtWU9//hdeeKHr+MKF\nC1m9erXbCQE+EfpCCCG8w3cvKYQQQnichL4QQgQQCX0hhAggEvpCCBFAJPSFECKASOgLIUQAkdAX\nQogAIqEvhBAB5P8BUL5B+4nuU50AAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x113ed5f10>"
       ]
      }
     ],
     "prompt_number": 24
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "For some common distributions, SciPy includes methods for fitting via MLE:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "from scipy.stats import gamma\n",
      "\n",
      "gamma.fit(precip.Dec)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 25,
       "text": [
        "(2.2427517865962434, 0.65494603858755807, 1.5700739281147422)"
       ]
      }
     ],
     "prompt_number": 25
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "This fit is not directly comparable to our estimates, however, because SciPy's `gamma.fit` method fits an odd 3-parameter version of the gamma distribution."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Example: truncated distribution\n",
      "\n",
      "Suppose that we observe $Y$ truncated below at $a$ (where $a$ is known). If $X$ is the distribution of our observation, then:\n",
      "\n",
      "$$ P(X \\le x) = P(Y \\le x|Y \\gt a) = \\frac{P(a \\lt Y \\le x)}{P(Y \\gt a)}$$\n",
      "\n",
      "(so, $Y$ is the original variable and $X$ is the truncated variable) \n",
      "\n",
      "Then X has the density:\n",
      "\n",
      "$$f_X(x) = \\frac{f_Y (x)}{1\u2212F_Y (a)} \\, \\text{for} \\, x \\gt a$$ \n",
      "\n",
      "Suppose $Y \\sim N(\\mu, \\sigma^2)$ and $x_1,\\ldots,x_n$ are independent observations of $X$. We can use maximum likelihood to find $\\mu$ and $\\sigma$. "
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "First, we can simulate a truncated distribution using a `while` statement to eliminate samples that are outside the support of the truncated distribution."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "x = np.random.normal(size=10000)\n",
      "a = -1\n",
      "x_small = x < a\n",
      "while x_small.sum():\n",
      "    x[x_small] = np.random.normal(size=x_small.sum())\n",
      "    x_small = x < a\n",
      "    \n",
      "_ = hist(x, bins=100)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAECCAYAAAAFL5eMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFfBJREFUeJzt3V9M2+e9x/GPsZvQ0NquqQhn9UFkMQEuqi0r7ChCUSCt\nUoUgrVK3SkmmUa6OwhatUwhkrapkQxORMiYQIY20i63dxVFboUWrxOmklRC1dNMgJb0YWSafrVpZ\nw/GJDTbN+A/nIovrELAJNv7hx++XNKnYv5/99bZ+/Pj5fX/PY1taWloSAMAoOVYXAABIPcIdAAxE\nuAOAgQh3ADAQ4Q4ABiLcAcBAjnhPzs7O6syZM5qbm9OWLVu0Z88e1dXVaWpqSl1dXQoEAtq+fbuO\nHz+u3NxcSVJvb6/6+vpkt9vV0NCgsrKytHwQAMAXbIn63GdmZrR161bNzc3p1KlTampq0nvvvadH\nH31U3/jGN3Tp0iXdvn1bR48e1ejoqDo7O9XW1qZQKKTW1lZ1dnYqJ4cfCACQTglTd+vWrZKk6elp\nLS4u6qGHHtLQ0JD27dsnSaqurtbg4KAkaXBwUFVVVXI4HCooKFBhYaH8fv8Glg8AWEncaRlJWlxc\nVEtLiz799FO9+OKLevzxxxUOh+V2uyVJLpdL4XBYkjQ+Pq6SkpLoufn5+QqFQhtUOgBgNQnDPScn\nR+fOnVMgEFBbW5tKS0vved5ms8U9P9HzAIDUSxjudxUUFGj37t0aGRmRy+XSxMSE3G63xsfH5XK5\nJEkej0fBYDB6TjAYlMfjWfU1//CHP+j27dtJlA8A2cftduupp56Ke0zccI9EIrLb7crLy9Pk5KSu\nXbumhoYGVVRUqL+/X88995yuXLmiyspKSVJFRYU6OztVV1enUCiksbEx+Xy+VV//9u3b+trXvraO\njwYA2eujjz5KeEzccJ+YmFB3d7cWFxfldrtVV1enJ598Uj6fT11dXWpqaoq2QkqS1+tVTU2NWlpa\nZLfb1djYyLQMAFggYSvkRnrvvfcYuQPAA/roo4/09NNPxz2GBnQAMBDhDgAGItwBwECEOwAYiHAH\nAAMR7gBgIMIdAAxEuAOAgQh3ADAQ4Q4ABiLcAcBAhDsAGIhwBwADEe4AYCDCHQAMRLgDgIEIdwAw\nEOEOAAYi3AHAQIQ7ABiIcAcAAxHuAGAgwh0ADES4A4CBCHcAMBDhDgAGItwBwECEOwAYyBHvyVu3\nbqm7u1vhcFhOp1PV1dWqrq7WW2+9pb6+PjmdTknS4cOHtXv3bklSb2+v+vr6ZLfb1dDQoLKyso3/\nFACAe8QNd4fDofr6ehUXFysSiejEiRPy+Xyy2Wyqq6tTXV3dPcePjo7q8uXLOnv2rEKhkFpbW9XZ\n2amcHH4gAEA6xU1dt9ut4uJiSZLT6dTOnTsVCoUkSUtLS/cdPzg4qKqqKjkcDhUUFKiwsFB+vz/1\nVQMA4lrzkHpsbEyjo6PatWuXJOndd9/VD37wA7322mu6ffu2JGl8fFz5+fnRc/Lz86NfBli/m5EZ\nffzZpD7+bFI3IzNWlwMgA6wp3Kenp9XR0aH6+nrl5ubqwIEDOn/+vH7yk58oJydHb7zxxqrn2my2\nlBWbrQKfz+pkr18ne/0KfD5rdTkAMkDCcJ+fn1d7e7v27t2ryspKSZLL5ZLNZtO2bdv07LPPRqde\nPB6PgsFg9NxgMCiPx7NBpQMAVhM33JeWlnTx4kV5vV4dOnQo+vj4+LgkaWFhQR988IGKiookSRUV\nFRoYGND8/LwCgYDGxsbk8/k2sHwAwEridsvcuHFD77//voqKitTc3CzpTtvjwMCAPvnkEzkcDpWX\nl6u+vl6S5PV6VVNTo5aWFtntdjU2NjItAwAWiBvuZWVlevPNN+97/G5P+0pqa2tVW1ubfGUAgHWL\nG+5IvZuRmehF0YJHtujfnFstrgiAibi7KM3ofAGQDozcN4nYEb3EqB5Acgj3TeLuiP6uc7U+wh3A\nujEtAwAGItwBwEBMy2xS9hzp488mJUmzC4sWVwMg0xDum1R4ekE/+t3fJEmnn9lhcTUAMg3TMgBg\nIMIdAAxEuAOAgQh3ADAQF1STwDoxADYrwj0JsXeVrueOUtodAWwUwv1frBiFb2S7I78qgOxGuP9L\nKkfhkvWBmuznAZDZCPcUiR2FSwQqAGtlRbhn+xRF7K+KbPz8QDbKilbIbN8gIzy9kNWfH8hGWTFy\nNwmjcABrQbivIN7F0dgpHivaF2Pn9pnXB7Aawn0F8S6OxnahsFojgM0qK+bcASDbMHLfIMyNA7AS\n4b5BrJgbt/p6AIDNg3A3SLLXA7L9fgDAJIR7Blve1ZPsaJ0lCwBzEO4ZbHlXD907AO6iWwYADBR3\n5H7r1i11d3crHA7L6XSqurpa1dXVmpqaUldXlwKBgLZv367jx48rNzdXktTb26u+vj7Z7XY1NDSo\nrKwsLR9kM2PddgDpFjfcHQ6H6uvrVVxcrEgkohMnTsjn86m/v1+lpaVqbm7WpUuX1NPTo6NHj2p0\ndFSXL1/W2bNnFQqF1Nraqs7OTuXkZPYPhGTDeSPXbQeAlcRNXbfbreLiYkmS0+nUzp07FQqFNDQ0\npH379kmSqqurNTg4KEkaHBxUVVWVHA6HCgoKVFhYKL/fv7GfIA1iF96aXViyuhwASGjNF1THxsY0\nOjqqXbt2KRwOy+12S5JcLpfC4bAkaXx8XCUlJdFz8vPzFQqFUlxy6tAXvja0SAKZZ03hPj09rY6O\nDtXX10fn1u+y2Wxxz030vJVYJ2ZtaJEEMk/CyfD5+Xm1t7dr7969qqyslHRntD4xMSHpzmjd5XJJ\nkjwej4LBYPTcYDAoj8ezEXUDAOKIG+5LS0u6ePGivF6vDh06FH28oqJC/f39kqQrV65EQ7+iokID\nAwOan59XIBDQ2NiYfD7fhhV/MzKjjz+b1MefTepmZGbD3gcAMk3caZkbN27o/fffV1FRkZqbmyVJ\nR44c0fPPP6+uri41NTVFWyElyev1qqamRi0tLbLb7WpsbNzQaRmmCx4cC5oB2SFuuJeVlenNN99c\n8bm7Yb9cbW2tamtrk68MG4LNPoDskNkN6ACAFRHuAGAgIxcOi+3LluhhB5B9jAz32AutEj3sq0n1\nksEANg8jwx1rw5LBgLmyLtxZoRFANjAm3Nca2qzQCCAbGBPuhLY1WFQM2JxohURS7l68Ptnrv6dD\nCYC1CHcAMBDhDgAGMmbOHelBbzyQGQh3PBB644HMwLQMABiIcAcAAxHuAGAgwh0ADES4A4CBCHcA\nMBDhDgAGItwBwEDcxISUib17lRUiAWsxckfKhKcXWCES2CQIdwAwEOEOAAYi3AHAQBlxQZWt3NKP\njcSBzLYpwz02zKU74fLKb/8qSTpX6yPc0yBde9LyxQ1sjIThfuHCBQ0PD8vpdKq9vV2S9NZbb6mv\nr09Op1OSdPjwYe3evVuS1Nvbq76+PtntdjU0NKisrOyBi7q7L+ddrBlurtj/rfniBlInYbjX1NTo\n4MGDOn/+fPQxm82muro61dXV3XPs6OioLl++rLNnzyoUCqm1tVWdnZ3KyVl9av+dkf+TM9eh//h3\np3IfsifxUQAAdyW8oFpeXq68vLz7Hl9aWrrvscHBQVVVVcnhcKigoECFhYXy+/33HRer68NR/de1\n/9X9rwYAWK91z7m/++676uvr065du/Sd73xHeXl5Gh8fV0lJSfSY/Px8hUKhNb3erdtzCv3zn5K4\ngGeyla6nAEi9dYX7gQMH9M1vflNTU1P61a9+pTfeeEPHjh1b8Vibzbam17x1e1Yt//0/kphjNxnX\nU4D0WFefu8vlks1m07Zt2/Tss89Gp148Ho+CwWD0uGAwKI/Hk5pKAQBrtq5wHx8flyQtLCzogw8+\nUFFRkSSpoqJCAwMDmp+fVyAQ0NjYmHw+X+qqBQCsScJpmY6ODl2/fl2RSETHjh3Tt771LY2MjOiT\nTz6Rw+FQeXm56uvrJUler1c1NTVqaWmR3W5XY2PjmqdlAACpkzDcX3rppfse279//6rH19bWqra2\nNrmqAABJ2ZR3qCLzrWdt99hzHtli1+ezCw90PoAvEO7YELHLF6z1ztPlSx486PkAvsCqkABgoIwb\nubNaIQAklnHhnq7VCgEgk2VcuCP7xP5ak7jACqwF4Y5NL/bXmsQFVmAtuKAKAAYi3AHAQIQ7ABiI\nOXdknPXc/QpkG0buyDjh6QWd7PXrZK//no0/AHyBcAcAAzEtgw3HXcVA+hHu2HDcVQykH9MyAGAg\nwh0ADMS0DDIabZHAyhi5I6PRFgmsjHAHAAMR7gBgIMIdAAxEuAOAgQh3ADAQ4Q4ABiLcAcBAhDsA\nGIhwBwADJVx+4MKFCxoeHpbT6VR7e7skaWpqSl1dXQoEAtq+fbuOHz+u3NxcSVJvb6/6+vpkt9vV\n0NCgsrKyjf0EAID7JBy519TU6OWXX77nsZ6eHpWWluqnP/2pSkpK1NPTI0kaHR3V5cuXdfbsWZ04\ncULd3d1aXGT9bgBIt4ThXl5erry8vHseGxoa0r59+yRJ1dXVGhwclCQNDg6qqqpKDodDBQUFKiws\nlN/v34CyAQDxrGvOPRwOy+12S5JcLpfC4bAkaXx8XPn5+dHj8vPzFQqFUlAmAOBBJH1B1WazJfU8\nACD11hXuLpdLExMTku6M1l0ulyTJ4/EoGAxGjwsGg/J4PCkoEwDwINYV7hUVFerv75ckXblyRZWV\nldHHBwYGND8/r0AgoLGxMfl8vpQVC6zHzciMPv5sMvqfm5EZq0sCNlzCVsiOjg5dv35dk5OTOnbs\nmF544QU9//zz6urqUlNTU7QVUpK8Xq9qamrU0tIiu92uxsZGpmVgiZuRmejmHbMLi3rlt3+NPvez\nOl/0OXZvgqkShvtLL7204uPNzc0rPl5bW6va2trkqgLWIXbLvdhAP/3MjnuOC08v6Ee/+5sk6Vyt\nj3CHkdhDFcaIDe3lgQ5kG5YfAAADEe4AYCDCHQAMRLgDgIEIdwAwEOEOAAaiFRJIIPaGKIkbn5AZ\nCHcggcDnszrZ+8XS1dz4hEzAtAwAGIhwBwADEe4AYCDm3JHVYhcb40IpTEK4I6vFLjbGUsAwCdMy\nwL+Epxd0stevk73+e1ofgUxEuAOAgQh3ADAQ4Q4ABuKCKrCC5Vv2AZmGcAdWwJZ9yHRMywCAgQh3\nADAQ4Q4ABiLcAcBAhDsAGIhwBwADEe4AYCD63IEUid1rlVUlYbWkwv273/2uHn74YeXk5Mhut6ut\nrU1TU1Pq6upSIBDQ9u3bdfz4ceXm5qaqXmDTit1rlX1WYbWkR+5nzpzRI488Ev27p6dHpaWlam5u\n1qVLl9TT06OjR48m+zYAgAeQ9Jz70tLSPX8PDQ1p3759kqTq6moNDg4m+xbApnJ33ZmPP5vUzciM\n1eUAK0pq5G6z2fTjH/9YNptNBw4c0DPPPKNwOCy32y1JcrlcCofDKSkU2Cxi151h+gWbVVLh3tra\nqscee0yjo6Nqa2vTE088cc/zNpstqeIAAOuTVLg/9thjkiSv16uvf/3r8vv9crlcmpiYkNvt1vj4\nuFwuV0oKBTJJ7JLBEt0zSL91z7nPzMxoampKkhSJRDQ8PKyioiJVVFSov79fknTlyhVVVlampFAg\nk8Tux8qerLDCukfu4XBY586dkyQ9+uijOnTokL7yla9o165d6urqUlNTU7QVEgCQXusO94KCgmi4\nx3r44YfV3NycVFEAgOSw/AAAGIhwBwADsbYMkAQ20sZmRbgDSWAjbWxWTMsAgIEIdwAwEOEOAAZi\nzh1Ig9gLryxFgHQg3IE0iL3w+rM6X3Q5gke22PX57IKk+KHPLk94UIQ7kGbLO2xWCv3lAc4uT3hQ\nhDuwSaw2upfooceDI9yBTSg26CV66PHg6JYBAAMR7gBgIMIdAAzEnDuQwWiRxGoYuQMZ7G6LJFv5\nYTlG7oChGNVnN8IdMNRabnziC8BchDuQYVbbICT28eXPrYY7X81FuAMZZrUNQrjxCbG4oAoABmLk\nDmQBlhzOPoQ7kAVip2xWm1tfPmfPl0BmI9yBLLPaBdnlc/ZcYM1shDuQZVa7ILvcWqZyYlsp4x2H\n9CPcAaxoLVM5sa2U8Y5D+tEtAwAG2pCR+8jIiF5//XUtLCzo6aef1sGDBzfibQBsMnTlbB4pD/fF\nxUW99tprevXVV+XxePTDH/5QTz75pLxeb6rfCsAms5apHJY8SI+Uh7vf71dhYaEKCgokSVVVVRoa\nGiLcgQwWOyJ/ZItdn88uSFrf3q4seZAeKQ/3UCik/Pz86N8ej0d+vz/OGQA2u+UdNqnqtlneWx/7\nxbGWf4732tn+C8Hybpn//I8n5Mq1vAwAKRb7hfCzOl80aOP11i//4kj0z8tfe/mvild++9e4xyz/\nO11fAun44rEtLS0tpfIF//KXv+jtt9/WK6+8Ikn69a9/LZvNpueee+6+Y69evaqJiYlUvj0AGM/t\nduupp56Ke0zKh8w7d+7U2NiYAoGAPB6PPvzwQ33/+99f8dhExQEA1iflI3fpTivkL3/5y2grZG1t\nbarfAgAQx4aEOwDAWtyhCgAGItwBwECW9iD+/ve/19tvv61//OMfamtr05e//GUry7EESzV84cKF\nCxoeHpbT6VR7e7vV5Vjm1q1b6u7uVjgcltPpVHV1taqrq60uyxKzs7M6c+aM5ubmtGXLFu3Zs0d1\ndXVWl2WpxcVFnTp1Sh6PR6dOnVr1OEvDvaioSE1NTfr5z39uZRmWYamGe9XU1OjgwYM6f/681aVY\nyuFwqL6+XsXFxYpEIjpx4oR8Pl9W/v9iy5YtOn36tLZu3aq5uTmdOnVKFRUVKiwstLo0y/T29srr\n9WpqairucZZOyzzxxBP60pe+ZGUJlopdqsHhcESXashW5eXlysvLs7oMy7ndbhUXF0uSnE6ndu7c\nqfHxcWuLstDWrXdu8JmentbCwoIcjuy96TEYDGp4eFj79+9Xol6Y7P1vaRNgqQYkMjY2ptHRUZWU\nlFhdimUWFxfV0tKiTz/9VC+++KIef/xxq0uyzOuvv65vf/vbCUftUhrCvbW1dcW7UA8fPqyKioqN\nfnsgY01PT6ujo0P19fXKzc21uhzL5OTk6Ny5cwoEAmpra1Npaal27Fh9TRtTXb16VU6nUzt27NCf\n/vSnhMdveLi/+uqrG/0WGcvj8SgYDEb/DgaD8ng8FlaEzWJ+fl7t7e3au3evKisrrS5nUygoKNDu\n3bs1MjKSleF+48YNXb16VcPDw5qbm9PU1JTOnz+v733veysez7SMhR5kqQZkj6WlJV28eFFer1eH\nDh2yuhxLRSIR2e125eXlaXJyUteuXVNDQ4PVZVniyJEjOnLkiKQ7XXa/+c1vVg12yeI7VP/4xz/q\nF7/4hSKRiLZt26YdO3bo5ZdftqocS7BUwxc6Ojp0/fp1TU5OyuVy6YUXXlBNTY3VZaXdn//8Z50+\nfVpFRUWy2WyS7vyL/dWvftXiytLv73//u7q7u7W4uCi32609e/Zo//79VpdluZGREb3zzjtqaWlZ\n9RiWHwAAA3GHKgAYiHAHAAMR7gBgIMIdAAxEuAOAgQh3ADAQ4Q4ABiLcAcBA/w9OXYm5ZIu9UQAA\nAABJRU5ErkJggg==\n",
       "text": [
        "<matplotlib.figure.Figure at 0x113ffb610>"
       ]
      }
     ],
     "prompt_number": 26
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We can construct a log likelihood for this function using the conditional form:\n",
      "\n",
      "$$f_X(x) = \\frac{f_Y (x)}{1\u2212F_Y (a)} \\, \\text{for} \\, x \\gt a$$ "
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "from scipy.stats.distributions import norm\n",
      "\n",
      "trunc_norm = lambda theta, a, x: -(np.log(norm.pdf(x, theta[0], theta[1])) - \n",
      "                                      np.log(1 - norm.cdf(a, theta[0], theta[1]))).sum()"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 27
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "For this example, we will use another optimization algorithm, the **Nelder-Mead simplex algorithm**. It has a couple of advantages: \n",
      "\n",
      "- it does not require derivatives\n",
      "- it can optimize (minimize) a vector of parameters\n",
      "\n",
      "SciPy implements this algorithm in its `fmin` function:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "from scipy.optimize import fmin\n",
      "\n",
      "fmin(trunc_norm, np.array([1,2]), args=(-1, x))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 10930.807932\n",
        "         Iterations: 47\n",
        "         Function evaluations: 89\n"
       ]
      },
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 28,
       "text": [
        "array([-0.01353635,  0.9928185 ])"
       ]
      }
     ],
     "prompt_number": 28
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "In general, simulating data is a terrific way of testing your model before using it with real data."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Kernel density estimates\n",
      "\n",
      "In some instances, we may not be interested in the parameters of a particular distribution of data, but just a smoothed representation of the data at hand. In this case, we can estimate the disribution *non-parametrically* (i.e. making no assumptions about the form of the underlying distribution) using kernel density estimation."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "# Some random data\n",
      "y = np.random.random(15) * 10\n",
      "y"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 29,
       "text": [
        "array([ 4.74511593,  7.90840801,  0.4757153 ,  2.20288601,  1.84984043,\n",
        "        7.10173654,  2.44884627,  1.34956892,  6.86027822,  3.71783498,\n",
        "        7.42356175,  4.07499025,  1.42352956,  3.6932789 ,  9.22449069])"
       ]
      }
     ],
     "prompt_number": 29
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "x = np.linspace(0, 10, 100)\n",
      "# Smoothing parameter\n",
      "s = 0.4\n",
      "# Calculate the kernels\n",
      "kernels = np.transpose([norm.pdf(x, yi, s) for yi in y])\n",
      "plot(x, kernels, 'k:')\n",
      "plot(x, kernels.sum(1))\n",
      "plot(y, np.zeros(len(y)), 'ro', ms=10)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 30,
       "text": [
        "[<matplotlib.lines.Line2D at 0x11400ae50>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAECCAYAAAAFL5eMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdgU9fZxp8ryZJlybIlG+89wDYQloEEwoYySwYJGbSB\ntE1T6JcFZCeFpCUEQnaA7GY0SUNLA6FJSBwMGEgMAQMBDBi895IlWbJlrfv9oUj10LiSr6bP7y+k\ne3Tvwbp67nve8w6KpmkaBAKBQAgqOL6eAIFAIBDYh4g7gUAgBCFE3AkEAiEIIeJOIBAIQQgRdwKB\nQAhCiLgTCARCEMJzdFCn02Hjxo3Q6/Xg8/m47rrrsGTJkj5jLly4gK1btyI2NhYAMHnyZCxbtsxz\nMyYQCASCUxyKO5/Px4YNGyAQCKDX6/HYY48hPz8fcXFxfcbl5eXh0Ucf9ehECQQCgcAcp24ZgUAA\nANBqtTAajeDxBj4PSB4UgUAg+BcOLXcAMJlMePTRR1FbW4tVq1YhOjq6z3GKolBWVoa1a9di2LBh\n+O1vf4ukpCSPTZhAIBAIzqGYlh9oaWnB5s2bcf/99yM9Pd36fnd3NzgcDrhcLg4fPow9e/bg9ddf\n99iECQQCgeAcp5a7hZiYGIwbNw6lpaV9xF0oFFr/PXv2bHzyySdQq9UQi8U2z1NcXAyNRjOIKRMI\nBMLQIzIyEhMmTGA83qG4q1QqcLlciEQidHZ24syZM7j77rv7jFEoFIiIiABFUTh16hT4fL5dYQcA\njUaD8ePHM54ggUAgEICSkhKXxjsUd4VCge3bt8NkMiEyMhJLlizB6NGjUVBQAACYN28eiouLUVBQ\nAA6Hg9TUVDzyyCPuz55AIBAIrMDY584WBw4cIJY7gUAguEhJSQnmzJnDeDzJUCUQCIQghIg7gUAg\nBCFE3AkEAiEIIeJOIBAIQQgRdwKBQAhCiLgTCARCEELEnUAgEIIQIu4EAoEQhBBxJxAIhCCEiDuB\nQCAEIUTcCQQCIQgh4k4gEAhBCBF3AoFACEKIuBMIBEIQQsSdQCAQghAi7gQCgRCEEHEnEAiEIISI\nO4FAIAQhRNwJBAIhCCHiTiAQCEEIEXcCgUAIQoi4EwgEQhBCxJ1AIBCCEJ6jgzqdDhs3boRerwef\nz8d1112HJUuWDBj36aefoqSkBAKBAGvWrEFiYqLHJkwgEAgE5zgUdz6fjw0bNkAgEECv1+Oxxx5D\nfn4+4uLirGNKSkpQXV2Nbdu24cqVK9ixYwc2bdrk8Yn7MzqDCSFcChRF+XoqBAJhiOJQ3AFAIBAA\nALRaLYxGI3i8vh85efIkZsyYAQDIzs6GRqOBQqFAZGSkB6br33R06fHW8XocrugADUDE5yJcwMWv\nsqNw8+gYhPKIF4xAIHgHp+JuMpnw6KOPora2FqtWrUJ0dHSf43K5HFFRUdbXUVFRkMvlQ0rcjSYa\nX19qw0clTVgwXIb/3HUNQrgcaHRGtGl0+PRMM373r1LcnR+POVkycIhFTyAQPIxTcedwOHjhhRfQ\n0tKCzZs3Y8SIEUhPT+8zhqZpj00wEHjxSA0alD3YuigL6TKh9f2IUB4iQnl4ek46LjSr8fbxehws\n78DGeRngc4kVTyAQPAdjhYmJicG4ceNQWlra532ZTIb29nbr6/b2dshkMvZm6OecqFXiQpMamxdm\n9hH2/oyMFeOlJcMRFsLF3w5UQm80eXGWBAJhqOFQ3FUqFTQaDQCgs7MTZ86cQUpKSp8x+fn5KCoq\nAgCUlZVBJBINGZdMl86I147V4oHrkyEM4Todz+VQeGxWGgDg+UPVMJqG9oqHQCB4DoduGYVCge3b\nt8NkMiEyMhJLlizB6NGjUVBQAACYN28exo8fj4sXL2LdunUIDQ3F6tWrvTJxf+DvJxsxNj4c4xMl\njD/D41B4anY6NhRU4MWiajw8I5VE1RAIBNahaC87zA8cOIDx48d785IeobRZg2e/r8Dby3IhCXW6\ndTEArcGE+/dexm/Gx2F6utQDMyQQCMFESUkJ5syZw3g82dVzAxNN45WjNVh9XZJbwg4AoTwO/m9K\nMt4srke33sjyDAkEwlCHiLsbnGtUAwCmpw9ub+GaeDHGxIvx6ekmNqZFIBAIVoi4u0HBFTnmZctY\n8ZXfMykR+8vkqOnQsjAzAoFAMEPE3UW69UYcq1ZidhY74Z6ysBDcOTYW23+sHfL5AgQCgT2IuLvI\nsSol8mJEiAoLYe2cS/OGQdFtQHGNirVzEgiEoQ0RdxcpuNKOXw1nN0mLy6Fw6zWx2HexldXzEgiE\noQsRdxdoUetwtb0b16VEsH7uaemRKGvtQlNnD+vnJhAIQw8i7i5w4Koc09MjwfdAdUcBj4PZWTLs\nv9zufHCA0q03oqiyg+wtEAhegIg7Q2ia/iVKJsr5YDdZOCIK35bJg7IsAU3TePlIDbYdrsH2H+tg\nIgJPIHgUIu4MudTaBZoGcmPCPHaNdJkQsWI+TtQG38bqvottqFX24MPleaiUa7H5YBUpnkYgeBAi\n7gw5UavC9emRHq8DsygnCl9favPoNbzNpRYNPi5pwtNz0iENC8HmBZnQG2k8/V0FegxE4AkET0DE\nnSGn6zsxLkHs8etMS49EaYsGLWqdx6/lDVRaAzYVVuHB65ORIDF39eLzOHh6TjpoGjhY3uHjGRII\nwQkRdwZodEZUyLsxMtbz4i4M4WJmhjRoNlY/LmnCtSkRmJrWt1QDl0NhaV40vr8i99HMCK5iMNGk\nDlIAQcSdAeea1BgxLAwCL/VAnZctw+GKwLdoaZrG8VolFuXY3oSelCxBVUc3Cf8MAPRGE9buK8Mt\n/ziH/9tzGTt/rMPZhk5fT4vgACLuDDjd0InxieFeu97wYWFQ9RjR3BnYrpkGVQ8MRhpp0lCbx0O4\nHMzIkOLA1cB/kAU775xogFQYgv/89hr86dpESMN4+FthFSrl3b6eGsEORNwZcKa+E2MTvCfuHIrC\n+MRwnKwP7KiZE7Uq5CdJHG5Cz82W4fsrchL77scUVXSguEaJ9TNSIOBxMCpOjNvHxOHu/HhsKyId\nxfwVIu5O6OjSo1Wjx/Boz4VA2mJikgQnAzwk8mRdJ/KTHT8Uc4aFgaLMoaYE/6NeqcXrP9Thqdnp\nCBf07V2wcEQUxHwe/n2uxUezIziCiLsTzjR2YnScGFyOd1vhTUgMx5lGNQwBahX1GEy40KzGeCcr\nHoqiMDdLhgKysep30DSNTYVV+O34OAwfNtC4oSgKD01Lxr9+bkaNgpSs9jeIuDvhdL0aY70QAtkf\naVgI4sP5KG3WeP3abHCuSY0MmRBigfNOVXOyZCiq6ICOJDX5FZdbu6A1mPDr3Gi7Y+LCBbhrQjxe\nJO4Zv4OIuxO8vZnam4lJEpysC0zXzE91Zn87E2LD+UiXCYMyMzeQOVzRgRkZUqeJe0tyo0HTwLFq\nhZdmRmACEXcHNKp6oDeZkBJpO9rD0+QnB664n6xVIT+ZmbgDwKxMKYqCIPwzWDDRNIoqFYxaSXIo\nCjeOHIavLgZHbkawQMTdAacbOjE2PtzjJQfskRsjQmOnDh1dep9c312aOnvQ2WNEVpSQ8WcmJEpw\npkFNomb8hEstXQgL4SJdxuw7vD49EhXybtQrSc6Cv0DE3QGnGzoxzkcuGQDgcSiMSxDjVH1gJYuc\nrOtEflI4OC48FGPD+RCGcFBNNub8gsMVHZiewbwBPJ/LwbxsWdDVRQpkHO52tbW1Yfv27VAqlZBI\nJJg5cyZmzpzZZ8yFCxewdetWxMbGAgAmT56MZcuWeWzC3qS0WYNVE+J9Oof8JAl+qlNhbja73Z88\nyU91KsxgsJzvz9iEcJyu70SalLnFT2Afi0tmy8Islz63OCcKD+27gpX58eBzid3oaxyKO4/Hw8qV\nK5GWlgaVSoV169YhKysLSUlJfcbl5eXh0Ucf9ehEvU17lx5ag8la7MpX5CdJ8PeTjTCaaK+HY7qD\niaZxtqETD16f7PJnxyaIcahCgZtGxXhgZgSmlDZrIBFwkWIns9geiRGhSJeF4liVErMypR6aHYEp\nDh+vkZGRSEtLAwBIJBJkZmaio2Pgplcw+kkvtWgwYliYz/ztFmLEfIQLuKjqCIw070aVDmIBF1Kh\n6w3Ex8SH41yjmoTU+RizS8Y9cV6cE42vLhLXjD/AeO3U1NSEuro6ZGdn93mfoiiUlZVh7dq12Lx5\nM+rq6lifpC+41NqFnGEiX08DAJATIwqYDM5yeRcyZe5l88rCQhAVFoLy9sB4kAUjRhONI5UKzHDB\n396b61IjUKfUkqQmP4CRuGu1WrzyyitYuXIlQkP7LtXS09Oxc+dObN26FZMmTcKWLVs8MlFvc6lF\ngxwPdl1yhdxhYbjUEhjJTOXt3ch0IUqmP2MTxDhDqg36jAvNGkQKQ5AU4V74bwiXg18NjwqaktWB\njFNxNxgMePHFFzFt2jRMnDhxwHGhUAiBQAAej4fZs2dDo9FArVZ7ZLLewmiicaXNfyz33BgRLrUE\nhuVe0d6NjEGJezjONBJx9xU/N5ojnQbDrEwpjlQqgtJdG0g4FHeapvHmm28iKSkJixcvtjlGofjf\nl3jq1Cnw+XyIxd5P12eTGoUWkcIQSEKdp857g3SZEM1qHdQ9Bl9PxSnl8m5kMoyNtsU18WKUNmtI\nf1UfUdqiQW7M4IyaNGkouBzgKnGv+RSH6nX58mUcOXIEKSkpeOSRRwAAd9xxB9razBsm8+bNQ3Fx\nMQoKCsDhcJCammodF8iY/e3+4ZIBzF2LsqKFuNzahQkMU/p9gVJrQJfOiNhwvtvnCBfwkBghwOXW\nLoyKC2wjIdAw0TQut3bh4emDE3eKojA1NRLHqhTI9nI1VcL/cCjuOTk5+Pzzzx2eYMGCBViwYAGr\nk/I1Zn+7f7hkLOQMM2+q+rO4W1wyriQv2WJsfDjONHQScfcydcoeiPhcSMNcj3Tqz9S0SLx8pAar\n8hNYmBnBHUimgQ0ut2qQ6yebqRbMfnf/3lQtb3c/UqY3YxPCcbohsPdtApGLLLhkLOTEhKFTZ0At\niZrxGUTc+9GtN6JepUPGIPzGniA3JgyXWrv8epOqQj64SBkLo+JEKGvrQo+B+N29SWkze+LOsbhm\nSKVIn0HEvR9X2rqQIQtFiJ+lT0eL+AjhUGj0476qgw2DtCAM4SJNGoqytsCIEAoWLrZokMeiO3Jq\nWgSOVSlZOx/BNfxLwfyASy3+EwLZnxw/ds3oDCbUq3qQylJ55LxYEc43EdeMt9DojGjq1A0qjLU/\n18SHo0HVgxa1/xokwQwR935cavWf5KX+5MSE4aKfxrtXK7RIkAjA57FzS42KFeNCgHahCkQutWiQ\nFS0Ej8X6RTwOhckpEfihmljvvoCIez/82XLPjRHhUqt/Ch5bLhkLI2NFuNiigcmP9xiCCbZdMhau\nT4vAsSrid/cFRNx70a7RQ2+iETeIOG1Pkh0dhqoOLXR+uNFYMcjkpf7IwkIQLuCiuoNEW3gDNpKX\nbDEhUYKyti50BkACXrBBxL0XZW1dyI4W+rwSpD1CeRwkRwj8MvPPbLmz684aSVwzXsGSvOQJy13A\n42BkrAinSb0gr0PEvRdX2rr8PqMuxw9dMzRNo0I+uJoythgVK8KFZrKp6mnYTF6yRX6SBKfqiLh7\nGyLuvShr68JwPxf37Cih31nuTWodhDwOIliuxTMyVozzTf71IAtG2ExesoWlm5g/52gEI0Tcf4Gm\n6YCw3DOihKjwM3Gv9IDVDgDJkQJ0641o05BQOk/CZvKSLZIjBOBQIDXevQwR919o69KDpoFhIs8s\nTdkiTSpEnVLrV1UTaxRapLAU394biqKI390LXGnrwggPFsqjKOoX6524ZrwJEfdfsFjt/rqZakHA\n4yAuXOBXVlCtogfJHhB3wBwSSVwznsNoolGr0LKWfGaP/EQJTtWpPHoNQl+IuP9CWas5UiYQyJCF\nokLuP66ZWoUWKRGeaSQ+Mo5sqnqSBlUPpGEhCONzPXqdcYnhKG3RQOuHYbzBChH3X7jS1o3hflTD\n3RH+5HenaRq1Ss9Z7tnRYahT9qBLZ/TI+Yc6lR3dSJd63qgR8bnIlAlxrpE8qL0FEXeYBaosADZT\nLWTIhH5juXd0G8DjUB7rWsXncpAVJcRFP62pE+hUybVIk3nWJWMhP0mCk8Q14zWIuANo1ejBoYBo\nD8X5sk2mLAwVcq1fhJbVKrRI9pBLxsKoOLKp6imqvGS5A0TcvQ0Rd8Bqtfv7ZqoFWZjZSpZ3+T6l\n25MuGQuj48Q4RypEeoRKuRbpXrLcs6KFUPUY0ezHZauDCSLuCIzM1N5QFIUMmRDlct9XiPSG5Z4X\nK8Ll1i7o/Cj8MxjQGkxo0+iQGOEdcedQFMYnhuNUPbHevQERd5jF3d8zU/uTGSVEuR9sqtYqtR63\n3EV8LpIjBShr9f3DLJio6dAiMSKU1TK/zhgbL8ZZsqnqFYa8uJszU7sDJgzSgr9sqnoyxr03xDXD\nPpUd3V5zyVgYmxCOsw2dfrFfFOwMeXFvUevBpYCoANlMtZAh8304pNZggqJbj1ix50skE3Fnn0q5\n9zZTLcSF88HjUqhV9Hj1ukORIS/ugZKZ2p/kSAFa1DqfJoXUK83dl7heWNaPihOjtFkDo4lYfGxR\n6cUwSAsURWFsfDjONJJSBJ7GYXByW1sbtm/fDqVSCYlEgpkzZ2LmzJkDxn366acoKSmBQCDAmjVr\nkJiY6Kn5sk4gxbf3JoTLQWJEKKrk3cjxYNEnR9R4ySUDABGhPAwT81HeHjjJZv5OVUc30rxsuQPA\nmAQximtUWJo3zOvXHko4tNx5PB5WrlyJl156CWvXrsUnn3yCurq6PmNKSkpQXV2Nbdu2YdWqVdix\nY4dHJ8w2/twz1RmZUb71u9cqPL+Z2pvRcWL8TFwzrKDo1kNnpH1SKG9MvNnvTlooehaH4h4ZGYm0\ntDQAgEQiQWZmJjo6OvqMOXnyJGbMmAEAyM7OhkajgUIRGD0TTTSNstYujPDTnqnO8PWmqjfCIHtD\n/O7sUdmhRbo01CfuyBgxH2IBD1Vy/yl+F4ww9rk3NTWhrq4O2dnZfd6Xy+WIioqyvo6KioJcLmdv\nhh6kVqFFRCiP9SYT3sLXNWa8EQbZm9FxIpxvUhOLjwWq5N1IY7HnrauMiRcTv7uHYSTuWq0Wr7zy\nClauXInQ0IE/5kANa7rc2uUzfzUbWCx3X/z9jSYa9coeJHnRco8W8UnTbJaolJstd19hDokkqzBP\n4lTcDQYDXnzxRUybNg0TJ04ccFwmk6G9vd36ur29HTKZjN1ZeohLLZ5tUuBpIkJ5COVx0KrRe/3a\nLRodJKE8CEM8Wyq2P8Q1ww7mGHffWu7nmtQk+smDOBR3mqbx5ptvIikpCYsXL7Y5Jj8/H0VFRQCA\nsrIyiEQiREZGsj9TD3CpVYOcAPW3W0iVClHV4X3XjLc3Uy2MjhOTsrGDxETTqFFokeZDy10WFoKo\nsBC/yLIOVhw6my9fvowjR44gJSUFjzzyCADgjjvuQFtbGwBg3rx5GD9+PC5evIh169YhNDQUq1ev\n9vysWaDHYEKtQotMD/T+9CbpslBUybWYlBzh1evWKnqQ7KWaJL0ZmxCOd040wETT4ARYboK/0KzW\nQcTnQizw7V7TmASz352EtnoGh99uTk4OPv/8c6cnWbFiBVasWMHapLzB1fYupEhDIeAFdh5XmlSI\nn32wMVWr1CLDB8v6GLHZ717e3h2Q+Qn+QK2Het66ypj4cHxzuQ3Lr4n19VSCksBWtkFg9rcHtksG\nMFvulT7YYPSV5Q6QuuCDxZffXW9Gx4lwsaWL+N09xJAV98utGuQEwXIwJTIUdQqt138gdUotkiO9\nFynTmwmJ4SipJ2F07lLrw++uN5HCEMiEPFT6QQG8YGQIi3tXwG+mAoAwhAtZWAjqVd4rxNTZY4DW\nYPJZsbVr4sUoa+tCt570VXWHWkWPX7hlAHPNIBL95BmGpLgruvVQ9RiR5AfWCxukybwbMVP3S3y7\nr4qtCUO4GB4dRuqCu0mNjyKdbGEObSUtFD3BkBT3srYuDI8WBk20RZo01Kup3OayA74VhwlJ4ThF\n/O4uo9IaoDeaIBP6R1b26DgxzjepAzYR0p8ZkuJ+qSU4XDIW0r0c616r7EGSjy2//EQJThG/u8tY\nSkb4S4nr2HA+QriUV92KQ4WhKe6tGowI0EqQtkiThaLKixEzdQotUrxYdsAWGVFCqHuMaOokouAK\n3uqc5QqjiGvGIww5cTeaaFxq6UJuEFnuSRGhaFHr0OOlxh21St8LxP+aLRPr3RW8XcmTCaSkhGcY\ncuJeLu+GLCwE0gBrq+cIHodCokSAGoXnrXejiUZjZw8SJL4XCLPfnYi7K3i7kicTLNU+Cewy5MT9\nbEMnxsSLfT0N1vFWxExTZw+iwkL8IrN3fKIEZxo6SRKMC9QqepDiBwlMvUmJDEWXzog2jc7XUwkq\nfP8L9TJnG9UYkxCE4i4NRaUXImZq/CS7ETA3NY8N5+NCM7H6mKAzmtCi0SFe4vmG5q5AURRGEr87\n6wwpcTeaaJxvUmNMfLivp8I6aV6KmKlTav0qP2BqWiSOVSl9PY2AoEHVg1gxHyFc//vZE787+/jf\nt+xBytq6ECvmB2znJUd4K2LGX+qSWLg+LQJHqxQkTpoB/hgpY4H43dlnSIn72cZOjEkIPqsdAGLF\nfGh0RnT2GDx6nVqlf0VbpEaaK3uWtXX5eip+T60fhLDaIysqDC1qHVRaz96/Q4mhJe4N6qDcTAXM\noYGpkZ633uv8IAyyNxRF4fq0SBwlrhmn+GOkjAUuh8KIYWG42EL87mwxZMRdbzThYosG1wSpuANA\nukzo0Qp7Kq0BBhMNqZ+krlu4Pi0SRyuJa8YZ/uyWAYC8WDFKm4m4s8WQEfey1i4kSAQI93H3GU+S\nGSX0aNuyWqXWpwXD7JEdLYTOaEK1F+L8AxWapq3fn78yMlaEC0TcWWPIiPuZxuB1yVjIkAlR4UHL\n3V8tP+KacU5blx6hPI5fGze5MSKUtXXBQPIWWGHIiHswb6ZaSJcJUd3hucYd/pi6bmHqL64Zgm38\noZKnM0R8LuLD+ShvJ5vjbDAkxF1nNOFyaxdGxwW35S7icxEp5KHBQxX26pT+FQbZm5GxIsi79B77\nvwc65lWXfz6Ye5MXKyJ+d5YYEuJ+oUmDlMhQiPhcX0/F43jSNeMv7dlsweVQmPJLzDthIP4cKdOb\nkbFi4ndniSEh7kcqFZiaFuHraXiFDJkQFR7YVDWYaDSrdYj3g4Jh9piZIcXB8g5fT8Mv8bfkM3vk\n/bKpSiKfBk/Qi7vRRONIlQIz0qW+nopX8JTlXqfUIlbMB98PU9ctXBMvhlJrIA2XbVDrZ2Uj7BEf\nzoeJptGi1vt6KgGP063zHTt24PTp05BIJHjxxRcHHL9w4QK2bt2K2NhYAMDkyZOxbNky9mfqJmca\nOhEr5vu1xckmGVGeEfeK9m5kyISsn5dNOBSF2ZlSFJZ34Pd+Pldv0q03olNrQIzIvwqG2YKiKOTF\niHChWY3YcJmvpxPQODXDZs2ahSeeeMLhmLy8PGzduhVbt271K2EHgKJKBWZkRPp6Gl4jLtxchoDt\nNO5KeTfSA0AwZ2fKUHhVDhNZ1lupU5rr73M5/pWfYI+RsSKUkkzVQeNU3HNzcyESOe5a5K/+MYOJ\nxrEqBaYPEZcMYLZe06TsZ6pWyLV+b7kD5pWLmM/FeVI+1kpdgGymWhgZRzZV2WDQDlSKolBWVoa1\na9di8+bNqKurY2NerHC6vhOJEQLEhvv/cpRNPOGaMVvugSEQc7JkOHBV7utp+A21ih6/zkztT2aU\nEPXKHnTpjL6eSkAzaHFPT0/Hzp07sXXrVkyaNAlbtmxhY16scLiiAzMyho7VboHtTVWV1oAuvRGx\n4sB4SM7MlOJolQI6L/WU9XdqFYFlufO5HGRFCXGplVjvg2HQ4i4UCiEQCMDj8TB79mxoNBqo1b6v\ny6wzmvBjjRLT04eOv90C2zVmLP52f6spY48YMR8ZMiFO1Kp8PRW/oNaPk8/skUfqzAyaQYu7QvG/\nanynTp0Cn8+HWOz7TNCS+k6kRoYiOgAiBNgmTRqKWgV7ZQgqAmQztTdzsmT4nrhmYKJp1Pt5wTBb\n5MWKSPnfQeI0FPKVV17BxYsXoVKpsHr1atx6660wGs2+sHnz5qG4uBgFBQXgcDhITU3FI4884vFJ\nM6HgihwzM4eeSwYAhCFcRIn4qFVqkSYdvChXyrUYPiyMhZl5j2npkXjreD1UWgMkQdh5iymtaj3C\nBTyEBVh2dm6MCC8croGJpsEJkBWjv+H0rn/wwQcdHl+wYAEWLFjA2oTYoFahxc+NaqybluLrqfiM\njF9qu7Mi7h3dmD8isGKORXwu8hPDUVSpwJLcaF9Px2cESvJSf6TCEESE8lDdoQ24VaO/4L/phoPg\n87PNuCEvOuCsFTbJiGKnDIHRRKOqg50VgLeZmy3D91eGtmsmEKpB2iOPxLsPiqAT96bOHvxYo8QN\nI4f5eio+JTtKiMss9BVt7OyBVMgLyKJrE5IkaFD1oF45dCtF1ioDKwyyN3kxpELkYAg6cd/1cwsW\n5UT7dVMCb5AbI0JZa9egN1Ur5P5fdsAePA6FWZnSIR3zHmgJTL3JiyGbqoMhqMS9XaPH4YoO3Dxq\naFvtACAJ5SEqLARVHYNzzVQGSGaqPeZkmxOa/DWL2tMESjVIW6RKQyHv0kPJcimNoUJQifu/zzVj\nbpYMUmGIr6fiF7DR+CAQwyB7kx0lBJ/LGZLL+y6dEWqdEcPEgfl74HIo5BDXjNsEjbi3qHX47ooc\nt1wT4+up+A15MYPfkKqUdyMjQMoO2IKiKMzJlqJgCLpm6pQ9SJQIAjqUkI17eKgSFOJO0zRePVqL\nm0fFYNgQTFqyx2Atd43OCEW3AXHhgbkhZ2F2pgxHKodeOYIahf92zmIKabvnPkEh7geudqC9S4fb\nxsT6eip+RXJkKDp7jOjocq/xQZW8G6nS0IApFWuPGDEfmVFCHB9i5QjqlIEbBmkhN0aEK21dMHio\n6XswE/DdXbhyAAAgAElEQVTi3tGtx9vH67F2eip4AS5CbMOhKOTEhLm9rC2XdyM9AOPbbTEzQ4rD\nFUOrBV+tMjCaYjtCxOciPpyP8vbBh/UONQJe3Hf8WIdfDZdheHRgpcd7i7xYsdvL2vNNauTFOq7l\nHyhcnxaJU/Wd6NYPnTKydQotkgLccgeAXOKacYuAFvdjVQpcaevGb8fH+3oqfkteTJhbscI0TeNM\ngxrjEsI9MCvvIwnlIS9GhOIapa+n4hWMJhr1qp6AjXHvDdlUdY+AFXdFtx6v/1CL9dNTIOAF7H/D\n44wYJsLV9m7oja5tJlYrtBCGcIKq0cmMjEgcqlD4ehpeobGzB7KwEIQGwW9jZKwIF5o0QzZXwV0C\n8punaRqvHavD7EwZRsX5vrywPyPic5EgEbhc3/1Mgxpjg8RqtzA1LRJnGzqh7gn+pJiqDi1Sg8Bq\nB4AEiQAGE40WtXuBAUOVgBT3g+UdqFVosWoCcccwwZ1l7ZmGToxNCK4Hp4jPxZiEcPxQHfyumZoO\nLVKlwSHuFEVhVJwI55t93wQokAg4cW/T6LCzuB4Pz0wFPwiWnN7A1Vhho4nGuSY1xsQHl+UOmKNm\nDg2BqJlqhRYpQWK5A8CoODHONxFxd4WAU8dXj9bi17nRJDrGBSziztRnWS7vhkwYAllYYKatO+La\nFAlKmzVBX6+kOkDLNNtjVKwY50nEjEsElLifrFOhVtmDO8aSZCVXiA/ng8uhGDfNPlMffC4ZC8IQ\nLvKTJDhaFbwbq0aTubVeoMe49yYzSohWtQ6qIH8os0nAiLvRROPt4/W4Z1ICQrgBM22/gKIozM6S\n4sBVZu6IM42dGBNkm6m9mZEhRVEQR800dfYgUhgCYUjg1eC3B5dDYcQw0jTbFQJGJb8ta0e4gIcp\nqRG+nkpAMidThsJyudP67nqjCaXNGoyJD07LHQDyk8JxuVWDziCNmqlWBM9mam9GxYlwgWyqMiYg\nxL1LZ8RHpxpx77WJoAK4wp0vSZGGIiosBGcaOh2Ou9zahcQIQVA3OxGGcHFNvBgngrTWTHVHcG2m\nWhgVK8b5JmK5MyUgxP3zs80YnyQhm6iDZG6WDAfKHbtmzjR0YmwQRsn0Z0pqZNCGRJo3U4NP3HNi\nwlAu70bPEKvu6S5+L+5tGh3+e6kNd+eTmPbBMjNDih+rlQ7rq5yq7wy65CVbXJsiwak6VVCWAa4J\nsjBIC8IQLtKkobjcSoqIMcHvxf3L0jbMzpSROu0sIA0LQW5MGH60Y7GerFNB3qXHmCCNlOlNpDAE\nGVFCnHbipgo0jCYatcqeoBR34JdSBMTvzgin4r5jxw7cc889WLdund0xn376KdavX48nn3wS9fX1\nrE1OazDhm8vtuHFkNGvnHOrMzZLZjJrRG03Y8WMd/nRtEvhDJBppahC6ZprVOkSEchHGD55Imd6M\nihPjHElmYoTTX/GsWbPwxBNP2D1eUlKC6upqbNu2DatWrcKOHTtYm1zhVTlyY8KQGARlS/2F61Ij\ncLFFM6CBxxcXWpEgEeDaFImPZuZ9pqRG4MdqpdMIokAiWDdTLYyMFeFiS1dQfWeewqm45+bmQiSy\nX9P75MmTmDFjBgAgOzsbGo0GCsXgY4hpmsYX51tx0yjSE5VNhCFcTM+IxHMHq9Cg6gEAtGv02HW2\nGauHWDRSvEQAWRgPl4KonGy1ojuoMlP7IxWGQCrkoarDtUJ4Q5FBr7/lcjmioqKsr6OioiCXD74Z\ncUl9JzgUMNZP4q29WW5Up9OhqanJY+e/b0oyJiVLcP/ey/j8bDPePlGPhTnRQb1CunTpErRa7YD3\np6RG4lgQuWZq3LTcjcbAaWIyJl6M0w2+dc0YTTQKrrTjfJPab1sAsuJc9YTwfXHBbLVbLEmTyYTZ\ns2dDpfJObLJcLofJZI6kaGtrQ25urvWh5er/t7W1Fb///e8djjEajdbz0jSNW265BXq97RKn9fX1\nuOuuu1yaQ2+4HAq3XhOL128cgTMNnTjXpMadLJZ0MBgMuP7669HTY14ZqFQqXLp0ye54o9GIjRs3\nWv++nZ2d+PDDD1m7rzQaDdauXYuQkIG1cqakRuCHakXQ1Ap3J4GpuroaixYtsvs3aG1txZ///Ge7\nn+/p6cGaNWusr7u6uvDCCy+4NIdjx45ZH75KpRIffPCB3bHjEsNxut53G+HqHgPu21WCLy+0YvuP\ndbjl459x11vfo8zPongGLe4ymQzt7e3W1+3t7ZDJZIM6Z61Ci7LWLszOlFotCg6Hg3fffRdisdmS\nLy0ttWmJscWTTz6JQ4cOAQD4fD7WrVtn/X/t2rULDz/8sMPPHzt2DPv37wcAiEQi/PGPf3Q4/ne/\n+x1KSkoAAAKBAIWFhX3E6KeffkJhYSEA8+po/fr1bv2/ehMfLsBzCzLx/q15rKaq83g85OTkWO+L\nv/71r3jqqafsjudwOMjLy7O6/7q7u6FUKq0PV3cwGAzW1Y9IJMJXX30FLtf8f/zpp59QU1MDwFyz\nRG+kUavocfta/oKJplGjcB4pQ9M07r33Xhw8eBAAkJqaio8++qiPS2737t34z3/+AwAQCoW4/fbb\n7Z6Pz+djzpw5fYwTsVjs0gNz3759qK6uBmB+OHR12RfKsfHhuNCshs7FBjRsUKfU4v4vy9BRU4Z7\nh5uw86YcbJsdi3huFzZ+X+FXtW8GLe75+fkoKioCAJSVlUEkEiEyMnJQ5/zvxTYszIlCfW01fv3r\nX1tvkoyMDHA45im///77+Pnnnwc3eQe8+uqraGtrg16vh0QiwT333GM9tmTJEmzcuNHh58PCwqxi\nFRYWhsmTJwMAFAoFtm7dOuDG37JlC8aOHWt9zeebQz8NBgOef/55aLVa64MuNDQU11xzDQCzVfz4\n44/DYHDvpqIoirVuPcXFxVZBfvfdd5GQkAAAWLduHd566y2Hc1i+fDkEAnOhq5iYGNx///1WMXaH\nAwcO4JVXXulzDQsXL17ElStXrO9PTolAcW3gu2aa1TqEC7gQOYmUoSgKmzdvxtSpU63vxcaaV24a\njQbvvvsucnNzMXr0aACAWCzGtGnTAJjvt927dw8437Jly6x/Y5FIhNWrV7u0f/P8889jxIgRAID4\n+Pg+K4H+SEJ5SIoI9fpeSXl7F9buu4JbRsfgs0fuwKi8PABAVnIctvxhKWZmSLGtqNpvVoFOf9Wv\nvPIKnn76aTQ0NGD16tUoLCxEQUEBCgoKAADjx49HSkoK1q1bhw8//BCrV68e1IQMJhoHyzswf3gU\n0tPT8f7779u8SbZt24ZJkyYN6lr9UavV6OgwhwnqdDqUlJQMuPbevXuxceNGh5vMADBu3DjrD6I3\nIpEIUVFRA6zSuLg4u2IWGxuLcePGYd68eQOOicViTJgwwecboSaTCU8//TR27do14FhcXJx1X6aw\nsNDqolmzZg3OnDnj8LzFxcXW78QV5s+fb/cBfNddd2HOnDnW15OTJThRE/ilCKrkzDNTZTKZ1YDo\nDZ/PR2trK7KyspCdnT3guF6vx/nz50HTND744AMcOXLE4XUKCwvtGmGHDh3CyZMnHX5+165dVq3p\nzbjEcJR40TVjomn89ZtSLEwCFuXYDs2+Oz8eV+ta8OxnB7w2L0c4FfcHH3wQb731Fj777DPs3LkT\ns2fPxrx58/oIzYoVK/Diiy9i06ZNSEpKGtSETtWpkCARIEFituLi4uIcjjeZTG79+G1x7Ngx/O1v\nfwNgFs3nn38ePF7fGiuLFi3C008/DcDsl7/nnnv6+MY/+OADdHbav+lCQkLw+9//HlwuFwaDAc88\n8wzUavubQ1999RWWLVtmdUf1h8Ph4JZbbhmUlcsGHA4HL730EsaNG2d3jMFgwIYNG6y5EA8++CDy\nfrF+7HH06FFUVFS4NafQUMdCZzKZoFab2wlebe8K+EJiV9u7kBVlv0SHTqfD+vXr7d5ver0eTz/9\nNB566CGbwg+YXYIbNmwARVHIzc1FSkqKwzl1d3eju9t2ZIter3e64szIyEB6evqA98cnhns1Aa3g\nihy00YgUY6vdMSFcDu4dI8FZfTTK233vf/e7bJXvr8ohVVViz549jMZ/8cUXeP7551m59vz587Ft\n2zaHN1xISAgkEnMsuFQqxYoVK6wPAIPBgLq6Ors/jP4cP34cycnJCAuz/YOkaRrFxcXW185CTA8f\nPuzwQeEpLA+30aNHW5fWtuDxeHj99dcxa9YsAMDw4cOd/q3Wr1+PCRMmMJ7LoUOH8NlnnzEa+/77\n7+P111+HgMfB6DgxTtYFdrbq1fZuZEXZD4OkKApTpkyxu+o0Go0YN26c9aHoyO8NAElJSUhNTXU4\nZvHixVaXZH/mzZuHa6+91uHn8/PzkZWVNeD9kTEiVHVovdIPV6Mz4u8/NeDJRaMxZ85sh2NnTBiJ\nNVNSsPVQNUw+ds/4lbhrdEacrOvEr8emIjc3l9FnbrzxRtbEHTDf0NOmTXN6Y5eVleGdd97BzJkz\nrS4RHo+Hp556yuo7dsbnn3+O6dOnW/cR+mPxjUokEnR2dmL+/PkON5EPHz5s3Sj0FiqVChMnTkRb\nWxuj8WPHjkVVVRXa29td8k3SNM1ofHJyMjIzMxmd86677sKjjz4KAJicEoHjNYHtd7/a1oVMB5Z7\nSEgIbr75ZrsuvNDQUNx2220AzBErs2bNgk6nGzCupaUFarUav/nNb9DS0sJobgaDwWo09Y4MY0p7\nezvq6uqsr/k8DnJjRDjb6Hlj5qNTjZiULMHwYcwKF87JksJoNGDficsenplj/Ercj1YpMCZejPGj\nchxagL3hcrmD9jcrlUps2rQJNE1DJBJh3759dq1pC5GRkRg2bBgA8417+vRpl64pl8vx2muv2bRK\ngIHhluHh4Thy5IhDV8Nf/vIXp24OtpFIJLj55ptd+v9/9dVXuOWWW6zRP0xYs2aNNbrDEZmZmYz3\nYvh8vvXBOilZgpN1qoDNfFRpDdDojIiX2F4JWSJR7H6+X4hxREQECgsLba6sdu/ejY8++giFhYWI\niWGWZHj//fdbfee7d+92GD1liz179uD777/v8543XDNVHd34prQJ9d++z/gzFEUhXVeH3eeZPfg8\nBXejs7APlqmsrER8vO0Kj28V12N2mhgZ0a4nLn3//fdobGx06gO0RVdXF5RKJUaNGgUAToUdMG+M\nWlYXHR0dWLBgAaZMmWKNEHEETdNYuHAh5s2bZ3Xx9GflypVITU3t87fytV/dHjNmzGBsLQNAdHQ0\nioqK8NhjjzF+ME+cOBEjR460O95oNEKtVjNeNfWmoKAA3aoOlGlFyJQJESMOvCJ1F5rVqFPqsGBE\n1IBjBoMBt9xyC2688UabxgFN01i0aBFmzpzZJ9LNnsts4sSJyM/Pd8momj59OkaOHAnAnPU+YcIE\nCIXMM2nHjx/fJ5oMAARcDnb93IIbRg5jfB5X2VZUg/kjonH7rHyEhzOvlnrdyEzsvqzGuAQxa72I\nGxsbkZGRwXi831juLWodrrZp8NfVd7oVSsTn8wdsfjJFJpNh+fLlKCoqcjm7lqZpREZG4tixYwNu\nPntQFIXCwkIkJSWhtrYWmzZtGjDmueees4Y79qa+vh4ff/yx3XPX19c7jcFnix9++MGtbOTMzEx8\n8cUXLolDbGysXfcVAPz8889YtWqVy3MBzA9NLpeLySkSFAdoAw9H/nYej4cDBw4gIsJ2FzOKorB/\n/36b/vO6ujprvkb/zwDmFYElHt4RvYWRw+FAKpU6/YwzMqKE6OwxokU90HXEBuXtXShv78bSkTF2\nDVJ7hHA5WJoXjf+ct78B62n8RtwLy+WYkSnDt9987ZabZfr06XY3bhzRe/P04MGDLkfePPXUU/jX\nv/6FYcOGuWRZW8ZGR0fb3F9ISkqy+bAKDQ2FRmM/vjc2NhZz5871Sqztnj17sG3bNsbjT5w4gTff\nfNP6Wq/Xu+SaMRqN+Omnn2weGzdunM0wTCbMnj0b+fn5mJwcgRMB6ncvb+9GppPNVEfYs9K1Wi0q\nKysBmA2H/vkKFEUx/s3odDps3LjR7eQ0mqaxadMmazQah6IwNkHsMdfMrp9bME6sAc9Nr+/inGgU\nXmrC5ZpGdifGEL8R9wNXOzAnS+Y0fI1NaJrG3Llzrf7IDRs2uOReAIC7774b+fn5AIBvvvkGP/zw\ng8PxFy5cwKlTp6yvhUIhbr75ZutrlUrlsGxyVFQU/vSnP9k9zuPxMH/+fK/EvT/00ENOox16k5CQ\n0Gd1c+jQIWzbts1apsAZGo0GL7zwgt1oJndXbhZGDAuDvNuA5k7PWIKe5Gqb7TDIEydO9Im46s/5\n8+etmdG2yMrKsuau0DTdp44UAKSkpDgtrWFBLpdj//79DkOFHUFRFDIzM/t8/+MTJTjpgdVWY2cP\nfqpV4ucv3nH7tyQJ5WGURI/CGt8UOfMLca/u6IZc1YU43uDKCeh0OsyePZtxOCBFUdi7d69bfnoL\nNTU1+Ne//gXAHBvvzI/Y1NRkM6KFpmnodDqcOXMGL7/8stvzsWAymezGF7NFfHw8li5dynh8UlJS\nn4dBREQE/vKXvzD2k0skEuzatWuAiBcWFjKO1rGHSqXCr5csRn6iGMcDLFu1W292TaTYSGDSaDQO\nV3qNjY2ora1ldJ2kpCTccsstbs8zLi4OxcXFdt1DTLj99tv7uHSmpEbgZH2nw+5i7rD7XAsW50Tj\nH39/d1CG0oOLJqKwSsP6/JjgF+JeVKlAuLIKajef6Bb4fD7effddp9mjvYmIiEB5eTm2bt3q1jVn\nz56N9evX46effsK0adMcJvEAwJw5c3DTTTcNeP+5557Dhx9+iOnTpzNydaxdu9ZhhMrzzz+PDz/8\n0Pl/wA1+/vlnvPTSSy59xtZSfNKkSS5Z/vYoLi4edEE5iUSCbdu24drUSBwPsGzVCnk3UqVC8DgD\nRWjWrFl9snH7M2/ePNxwww1Or7F+/XqHyWQbNmywmUnqKSxux4hQHnKGhbHa7FzRrcfB8g7cyEK5\n8cQIAXKGheFIBTuJlq7gN+L+8B3zbWaiuUpGRgajJ21nZ6f1Zg0PD7e6Vtyhp6cHL7zwgrX2izv+\n7vvvvx9/+MMfGI//wx/+4DBcdP369bj33ntdngcTYmJisG/fPly8eJHxZ2677Ta7D6O9e/fi8OHD\njM/1zTff4NixY9bXTzzxhEtRBPbIy8tDfpIEF5rVPrG03MWZv50NGhoaUFVVZff4ypUr+9Sq6c/e\nvXutoaz79u1jnKRoi4MHD+L//u//rK9nZEhxyEnjd1fYW9qGTEEXzp045nwwA5JNrXjty6OsnMsV\nfC7uNR1aaHqMyI1hbm07Q6vVOs3mvHTpEl5//XUA5k3I2bMdZ57Z4oMPPkB9fT3EYjF27doFLpcL\njUaDWbNmDSjXa6nEZ8/CDA8Px3/+8x/GbQrz8vIchmzy+XyP+d3j4uKwa9cum7VH7PH2229bQ017\n097ejpdfftml6AmxWMwoXNUdOEYdMqR8nPFxvXBXuNo2MFKmp6cHN998s80kJMB8Pz700EOM3Vlb\ntmzBxIkT7R7PyMhw+J3Ex8cjOjraOnb48OGMrmuLSZMmWcuEAMDUtAicbuiERjf4B3K33oj/XmzD\njFiKtf2/26ePAT82Ha0a7+7l+Fzcvy1tALfpIjgsCtFLL73k1DKYOHEiXn755UFFleh0ugE3tEgk\nwvvvvz+gdrjJZMKyZcscxsrW19e7XEfFkTuiu7vbaWEmV7H8vYYNG+bSBqZUKrVZTz0qKgo7duyw\nViBkgsX9VVFR0edHzgYvvfQS+G0VKA6gqJmr7V3Iiu57H/J4PDzxxBN2o2BomsacOXMYl+dOTk5G\neHi4w81vmqbt3o+TJk2yfscjR44cVLKdSCTqYwyEC3gYHSe22/jdFf57sQ1j48VYPGMyKy5DAJCI\nhLg+TYqDNnoXexKfi3txfRempjBPDmDC448/zjjm+e6773Ya4WKPP/7xj31usn//+98oLy+36SLg\ncrn41a9+5dCaXrhwId577z3G1y8qKuqzPO1PR0cHdu7cyfh8TPjTn/5k3UBmgsFgcPrAysvLc2uV\nIZFIHLoC3OGJJ57Afcvm4Hit0m9KtzpCbzShVqFFuqyv5c7lch26GjkcDpYsWeIwd8CCZRX87bff\nOrzfDhw4gIceeojhzAff5Kex8X8hhjMypDg8SL+2zmDC7vMtuJ3FxjUW5mZL8XVpk1fvKZ+Ke41C\niy4D8Mdl81k9rzOh2LNnj1VwXnvtNYwfP56161rCtDQajbUOjMlkYvSlZmdnO+xA05/rr7/e4fiE\nhASXHhZMuO+++/Duu+8yHl9eXm6touls3IIFCxjf/OXl5Xj44YetRcjYgqIoJEaEIiyEi6vt/t+n\ns0ahRWy4oE9Nfr1e7zCWnOn9CADNzc3WLk2zZs3Cjh077I6dNWsW3nnnnT7v9fT0YPr06QMidpqb\nmzFz5ky3xc5gMODmm2+2rhSuS43AuSb1oCp77i9rR1aUEGt/dwcrfaB7kxcThoaWdpwq917Mu0/F\n/UilAtenRbLqkrGgUqnw7bff2j1muakkEonLvrXLly/bbDu2bNky6ybnAw88YF0RHDhwwGGd+/r6\neocWkT04HA4jy4tNRo0aZTNj0R4jRozAJ5984nTcli1bsGLFCsYWfEpKCivdqGyhUCiQxOkMiEJi\ntjJTv/76azzwwAN2P7N//37cd999jM4fGxuLI0eOgKIo8Pl8m641C1wud8D9KBAI8PHHHw+IYIuN\njcU///lPt/eFeDwefvjhB2v5DhGfi3EJ4ThW5d53ZjDR+NfPLbhzbBw2bdo06IZD/eFxubhjSg5O\ntXmve5RPxf0/J65Ac/lHj5zbaDTaDc266667kJmZ2afKnCskJyc7TCQCzBuIlk3auXPn4rnnnrM7\nNiIiAr/5zW+srz/66CPGiR4mkwlFRUUOLaB33nmnTytEd7HE53tio3bnzp347W9/y3j8c889h/Pn\nz7M+D8D88O8o/RHFARASaWsz9YYbbnAY2rtw4UI8++yzjK/RO/PaZDI57IBmMplw8ODBPvejvbLA\nrqb096f/fTgz033XTOFVOeIlfOTFim1u/LPBnGwZDpZ3eK04nc/EvU6pBU8UgZWLZ3jk/FKp1GG8\nuEqlwu233+5We7qwsDC7G4DHjx/Hs88+28eCoSjK4caVWCzus3mjVCoZx21TFIX33nvP4Xg+nz/o\nhKaOjg7cdtttOHfuHOPPnDhxgrEAWwREqVRaQ0odsW7dOsyfPx8ajWZQvVZtkZKSgpeffAANqh60\nd9luUu4vXGhW24w0c5RM5+x+tFBeXo6rV6/2ec9gMODJJ5+0ez9RFIWPP/4YSqUSWq3WaUJha2vr\noHohl5SUWF2sk5IlKGvrQr3StX64RhONz840Y/moaMbZ0u6QEhkKIXT44gfmv6HB4DNxL6pQYHqG\nFLEMS4ayQU9PD1auXGnti3rkyBGXU9Z7enocWsnZ2dlYtmwZALNf8dtvv3V4w9gSsvvuuw+JiYmM\n5kNRFD788EOHWX8rV64cdIcsqVSKxx9/3FpnhAlNTU1obm5mPL61tRU33ngjLl92XgdbLBYjMjIS\ny5Yts7btYxMeh8KEpHBWk2PYRqMzok7Zg+xedcYvX77sUFDr6+vthkf25/z58wNKF/D5fOzbt8/u\nw4OiKLz//vuIjIxEcXExHnzwQYfXePjhh10yGPpz7tw564pSGMLFTaNi8OGpBpfOcbiiA5JQLnpq\nL2LlypVuz4UJ6RwFjtV5p0uTz8S98EobpmcMvjKcMzZv3myN5aUoCqtWrbL6Dd1xL7z44ot9il/1\nRyaTWUublpeX49VXX8WBA/Z7Kr766qt47bXXXJ6HL1i6dKlL5QaWLl3qMDuyP2VlZVi8eLHTMLne\nD4x9+/Z5pIY9TdNoKjmIYxWDd2d5iostGgyPDgOf+7+f8ccff4yzZ8/a/czOnTvxzTffMDr/DTfc\n0Mdd6CozZ87E22+/7XDM3//+d4fx885YuXIlZs6caX29bNQw/NyoRlkbMwFVaQ14+0Q97pmUiKlT\np+Cjjz5yey5MuO+G6ajShUFr8LzvnaK9HO914MABRKfn4vcfF+PdGzOROoi6Lkz44osvMG3aNGsC\nBWAuU9rU1ORWFUmapqHVap3WkDEYDIxWBQaDAV1dXQPquu/duxdardbaGccZ+/btQ1paml130Zdf\nfonm5mbcc889jM7Xm8rKSrS0tLj192IbmqYxffp07N69m3GjCHf54NPP8YVuBP65YjSEIf5XS//v\nPzWAooBV+c57CLDNN998g5ycHLtZ5f/973+RkJDAWiSaK+wrbcXRKiW2LLLdCKc3Ww5VIVzAw5rr\nBreydYXHvrmKBcOjMDPTNeO2pKTEJWPJJ5b7kSolbszP8riwA8BNN92E6OjoPuFf9fX1bm/GURTl\nVNh1Oh0mTJjgtFUfYN71t9WwIycnh3F9eMB5I4+xY8di7ty5jM/Xm4aGBrzyyiuMs2cBYOPGjX3i\nkF2hurrarmuGoigUFRX1Efb6+nqX3EVMWXXnbciJ8d/equea1Rgd53pjGya89957DguKdXR0OHX/\nMC0FXFFR4bAypTPKysr6rKYX5kSjRa3DqTrHLrXiGiVKmzW4Oz8eV65cQWurd2qvjxTr8fb+4x6/\njk/EvaiiAzO94JLpzd69e61NLKZMmcK4TGlvSktLGfkr+Xw+jh49iq+++goKhQLPPfecTT99ZWWl\n3c3DESNGMG41CACLFi1ymOWZkpLidu2eqVOnYunSpYyzGQFzs+z+5WGZ0NXVhWeeeaZPWeT+9Hen\nHTx40O1ENGdMS4/E0Sp2Y57ZQGcw4WpbN/JizZupNE3jzTffHFD2ojd79uxhvHnJ5XIdlhO48847\nHd5vBoOBcX+DyspKlJaWMhpri4iIiD6RNzwOhbsnxuO9nxrsNqlW9xjw2tFarJ2WAmEIF999953H\n7s/00O0AACAASURBVKH+zM2Ngyp02KBi8pngE3Fv6+xCbix7tWSc8eGHH6KpqQlPPvnkoM7zt7/9\njXFDYD6fj+LiYojFYshkMpsPhccff3xANEJ/2PaauRMdBAB33HGHS23Rli1bZjf13RFCoRBjx461\nWVpWqVTi0KFDA97/zW9+gxUrVrh8LSZUHt2HY+Vt0Bm9F5/MhMttXeboi1/cRRqNBnK53K4r0NIY\nhangrlq1yq2Hs4U///nPfXzhjpgzZ86gfPuxsbEDKltOS4sEl0PhvRMNA767br0Rrx6txXWpERiT\nEG6dL5PqmGwQHy3FpFQpjroZk88Up+JeWlqKRx99FOvXr7e5EXPhwgWsXLkSjzzyCB555BHs3r3b\n6UVD2656JHHJHvPmzcNtt90GqVSKt99+220r4dNPP2UcdSIQCLB27VpoNBr86U9/slmz/J///KdD\n67yiogILFy5kPL+SkhL85S9/sXu8rq4OM2bMcOmB8c477+DChQuMxw8WiqJw//3323wwNDQ09KkG\n6Q1uXDAX6VFhOF3vX66Zc41qjI77n4EkFovxxBNP2A0SCAkJwWuvveYwCclVTpw4gVdffdXu8dOn\nTw/aoHIXiqKwYW466pQ9WP2fSzjfpIbRROObS2343b8ugqKAP0zy/l6FhZmZUhwsd71FpSs4FHeT\nyYSdO3di3bp1eP7551FYWGgz8ScvLw9bt27F1q1brWGAjnjit4vdn7EbmEwma8Gu5ORk1rPP7PH6\n6687rLnujLS0NJd27zMzMx02U0hKSsI333zjUpQQn8936Qd66dIlLF++nPF4e7S2tuKNN97o815u\nbq7dubS0tHgk0iE5ORmzsqP9zjVzvlmNUR7wt8vlctx5J7M+xikpKbjuuuv6vEfTNLZs2QK1Wo3M\nzEzcfvvtjK7b3t7uMNHPGUajEYsXL+6T7xEt4mPjvHSsyk/ApsIqrNx1Ad9f7cDGeel4Yna6ddXz\nzjvvDLofgKtMSpLgdFULLle7FrbpCg7F/erVq4iLi0NMTAx4PB6mTp1qs8qgq64DNsv7MuHll19G\nUVERVCoVFi5ciIQE157YCoUC//jHPxiPP3fuHHbu3Innn3/eujR99tlnrTXLu7q6GBXf4nA4LkWE\nRERE2Gyq3Rtbm7eOWLFiBV544QXG44cPH44XX3zRpWvY4o033kBNTQ3je0sgELjc/5YpU1Mj8WO1\n0muZhc4wmmiUNmus4n7kyBGHNV/Onz8/oPepPUQiEdatW8fIAIiLi8OkSZP6vGcwGBAeHg6RSASJ\nRMK42mdERAQSEhLcdkNyuVy88MILEIv7PvAoisK09Ei8sywHj89Mw7bFWRgx7H/6YzKZ0N7e7pLL\nkQ1CQ7iYmibFeZXnorAcirtcLu/jd5PJZAO63VMUhbKyMqxduxabN29mlNLvTZcMYI5Nz8rKwpIl\nS9z6fGdnp0t9H6VS6YCm18uXL7d2aZLL5SgvL2d8voaGBpeyMB1tqgHm+HumiSw8Hs+luu0cDgfJ\nycmMx9tj+fLlePLJJ60i88UXXzjc8IqIiHBYT2UwtNVcgaqpGj83+keN93J5N4aJ+IgINfvXMzMz\nHZanjYiIYPwdCgQCTJgwwaX59BbkkJAQrFmzps/Dwdn9CJjvs1WrVg2qtEVeXp7dWktiAQ8j48QD\nzs/hcPDYY4+x6q5iypJrknCownMrwkFvqKanp2Pnzp3YunUrJk2ahC1btrAxL9aRSqUQCASMUtv7\nk5yc7LDwV3+SkpKsFnt1dTUKCgqQk5NjtZqTkpLw2GOPMT7fH//4R4ddcHpjMplw7bXXOrRin3nm\nGadleJVKJebOncv4IQCYH1pMfshMGDlyZJ+s2+jo6EH13hwMeXl5WDlngt+4Zs43qTGql7/dWTx5\ncnIyo2Y0Wq3WZctZp9Nh0qRJdvu0GgwGTJ48GUqld4qwWfJGAoFxCeFo6exBaa1nQjAdirtMJutT\ncKq9vX1AOJxQKIRAIACPx8Ps2bOh0WgYN6j2NCaTCZ988gmMRiPCw8Oxfft2xtECbKHRaPo0xHan\ndsW+ffsYt5HjcDg4fPiww85GH330EXJychyex1Ir3ZXs2XfffZf1vq1r1qxBaWkppk2bZs38dcQD\nDzzA+EHIFIqiMCNThmPVCruhdd7EvJlqdj+wGU319ttvu+xS4/P5+OqrryASiVBYWDigIBmPx0NR\nURHjB/ODDz44qE3zp59+Gnv37mU09uTJk/jrX//q9rUGC5dDQdR+BW9/536MvyMcintmZiaamprQ\n0tICg8GAH374YUADAIVCYb3BTp06BT6fP8Dv5Ss6Oztx8eJFcDgcUBSF4cOH4/jx4w67wffn/fff\nx3fffcd4/P33398nXC8vL88aU//111/jpptucqlkLuB6mQQ2/v4UReGZZ55xWhukN4888ohb+QP2\nOHjwIBobG5GWlsb4MytWrOiTjcwWSRGhCDHpcLbBt7VmTDSN87387b///e9RVFRkd/wDDzzAuD/t\nfffdZ7OUtTMs+0ITJ060uYHqyv34wAMPDKocwbPPPos77riD0djMzEy3XbVs8ZffLkKTMMEj+zlO\nyw+Ulpbigw8+gNFoxJw5c7Bo0SJrKd158+Zh//79KCgoAIfDQWpqKhYtWuTQyjxw4IDXU5I1Gg1C\nQkLA5/Px2GOPYeXKlQN84vYoLS1FWFgYY4Fpa2tDaGiozRtap9PhwoULEAgELtdDKSsrQ0dHB+MS\nAE1NTaAoCrGxtrvKXLp0CQ0NDTaX6yqVCqGhoW7FqbOJXq+HwWDArbfeik8++cRnbhkLy59+AyOv\nm40Ni9ivZcOUiy0avFhUg3dvMd+/KpUKfD7fbk+ClpYWCIVCh+0d2aCjowNcLtfuhn1jYyOMRuOg\nC9gFI/ftvYzfjIvD5BTH97er5Qd8UlvG2+L+6aef4sKFC9i0aZNXr2uBpmmsXr0aW7dudTlaxUJR\nUREaGhoYh5Zt27YNWVlZuPHGG20eP3XqFCoqKnDrrbcOOPb3v/8dP/zwA9544w2b8fm22L9/P2bM\nmMF61AFN0ygtLUVaWtqAhg+O6OnpYTx3pnR06fG7f1/EJ7ePRBjfN7Vm3j5eDz6XYr2eTElJCUaO\nHOn23+zhhx/GjBkz7FrCb731FiIjIxnVSqJpGgqFwqWm6b1Rq9U4e/aswxaMer3eJ5uotth9ug6F\npbXYvuI6h+MCoraMNygoKMDnn38OwJwq7UpzAguuZHPSNG239gpFUVi+fDm4XC5omsbRo0ddrkE+\nffp0xsIOAOvXr7cr7AAwYcIEm8IOmJuZmEwmxpvPRqMRX375JeO5ucqXX36JZ555hvH43bt344kn\nnmB9HtKwEFwTJ0ZRpW82VmmaxtEqBaalR8JoNDotjcw0m5qmabz00kuDivVua2tz+GC/9957GRfB\n279/P5566im356JWq/HZZ585HHPfffe57B71FFOSRShXc6DoZrd3QNBa7leuXEFnZ6fNa509exaX\nLl1yeLPpdDpMmTIFBw8eZLSkra+vx8qVK1FQUGDTR67X6zF9+nR8++23ePjhh7FhwwaX4+2HGiqV\nyhoit337dgwbNozR57RaLXg8nsu1+pnwj4On8V21Fh+tcmxleYLy9i48830lPlyeh8rKSjz11FP4\n9NNPbY5tb2/H0qVLUVRU5JUgAoshxMbf3GQygaIoj3T8sqDT6UDTNOurO3fZfLAKOcPCcNMo+3kt\nxHL/hezsbIwfPx5ff/31gNAoS4KFI/h8Pr7//nvGvsrExES7wg6Y43/37NkDkUiEt956yy1h12q1\n+POf/8x4RaFSqbB9+3a7xw0GA+66664+f5/vv//epZh+T/L111/jueeew65duxgLOwCEhoZ6RNgB\nYGyMACoTH/VK97sHuYul5zBFUcjIyLAr7AAQFRWFI0eOeC06jMfjQaPROLSYFQoFo2QqSwCEJ+Hz\n+X4j7AAwf7gM35axW44gKMXdIn5Go9FmPZysrCxGNVtcLVPg7Ib84osvBpW9GRoaivnz5zN26QiF\nQvT09Nh1r/B4PPzhD3+wCiFN03jvvfes7iwmfPfddy6Nd4Xbb7/d6k6jaRoFBQWMH2wmkwk//fQT\n63MaNTIPC/Ni8R3LP0QmHK1SYlo683uSSfP08+fPM8qWtkdnZ6c1GofH4+HKlSt2wzOFQiHUajXj\n8M29e/e6lGfRn507dw4oBa3T6XD8uOfL7brK2IRwNLZ1YP9x9lrwBZ249/T0YPLkydBoNOByuXj9\n9dftli61d5NVVFS4VIv8+PHjuHjxot3j9fX1aG9vx5133om1a9daP7Nnzx7G17CwdOlSxlEsISEh\nWLt2rUPrbfr06dbzWcIfhw8fzng+GRkZLo13FYtAnTlzBm+88QZjP7LJZMJLL70EhYJ9//ivhkeh\n4Ir8/9s787imrrSP/8IuS4AAZXNBkVVeXIpSiRWlWK1ra6tWW8Vax7duo5Y61XmVUYpb61aVSq0y\n2mlpxXZoi7Y6IIILWGVpqyImKrIjsgUkCdnO+0eaDIEsNwugeL+fj5/2cO899yS5eXLOc57n9/So\nHEF5kxB8kRQBbrY4e/asVvG7ixcv6lQbVWBhYWFU6GxVVZXSuNvZ2SEuLk7jJMfa2pqytAEgd0NQ\n/bzV4e3t3eW7UlZWhq+//trgPrsLMwYDo10JrjWabsXZ54y7tbU1srKyKEVWvPnmm2q/JJcuXcKF\nCxco37OiokJrrdCsrCykpqaCyWQqZ8n29vZGhfaZspAvIUSZeObv74/x48dTvnbo0KFKWQVTkp6e\nrpIMZ2dnh5UrV1J2Z1lYWOCbb77pFpE4H2cbNFQ9wPmbZSbvWxOXHzSD7eMEMwYDbW1tWje7y8vL\nKf+oBQYG6qU8qu56bUqkxrB161ajQidnzpzZpRaxn5/fE1vW8q9Tx+D3ejHq2wxfrXSkz26oZmRk\n4NGjR1iwYIHGcyoqKtC/f/9u9+91hBCCS5cuISIiwmC/cEpKCm7cuIEdO3ZQOv/w4cOws7PDokWL\n1B4/efIkUlNTMW/ePL0UHbsrnIwQgg8++ABbt259YhLiOvPPnGLcE1ohYbLuUm6mYEVaCd57wRuh\nnqaLVyeEdMuzf+DAAQQGBuLll19We/zYsWMQiUR6SXoYg1Qq7fHMdENJzK2EBUOG/x3btUrdM72h\nyuVyle4UX19fnYlKAwYM6FHDDshdH999951ynB3L/1Hltdde0yttesaMGVrDImfPno2tW7di+/bt\nEAgElPrk8/kIDw+nXNlHHxgMBvbs2aPWsF+/fh1ffPEF5b5u3bqlVTHRUN5iB+JegxB3KRZiNoaa\nlnY8ahMj2IRqqiKRCJGRkUaFP27btk2tAF50dLTW1dzUqVMpF1e5ffu2UZrwjx49wvjx4yGTyZCY\nmAgul2twXz3BJB8bnCooA6/N+O9VnzLuly9fVioHDhkyhJK7oGO8sEAgQFxcHOUNy/z8fMTGxmo8\n3t7eju3bt3fZBDxw4IBSOTEmJkbvDZ5+/frpNevv37+/1uggS0tLhISEICsri3ISkq2tLbKzszVm\nRnYX27Zt02u14ObmhqFDTT+7trIww+xhrvj8UvcbiwxuI170ccKliznKPRt1lJWVUZYPsLKyQkpK\nisFJdQAwcuRItRnQwcHBWqObPD09Kd934MCBmDbN8PoPbm5u+Omnn2BmZgYvLy+9SkX2Bv5ernjR\n3wMZ942XuTDfsmXLFuOHRJ3S0lKVeoemZOTIkQgKCgKPx6NsdLhcLrZt24bXXnsNQqEQTU1NOjXR\nFbBYLAwZMkTjg8zn81FeXq5VQnX8+PHw8/MzaAWRnZ0NFotFOaSrpKQELBary71aW1thbW2NS5cu\nwd7enrIrpDtCyeLj4yGRSDRKWIwfPx7jxo2j/H7Z2dnB19fXlENUIm2sxNc3mzFuqBuc+nVPtqNA\nLMWu7DKsHTcAwUN9EBISonGvxsbGBh4eHpT91MYYdkDuv9a2uV9RUQEmk6nxs+JwOHB2dtb6WVpZ\nWRktIa0IqAgKCtJaF/ZJwYvZD0lXKzFrmJuKPHpNTQ1lAUGgj83cAbkB06ceY0BAgLKCj4ODA2XR\nIUD+ZdLm+mEymViyZInaY6WlpYiPj4erq6vBrqHc3FxK+vkKEhISuoSG1dTUIDIyEg0NDbh37x6l\nCvDnz59XUQs1JTExMVpXXF5eXmAwGBCLxXq5FGQymcnkiBWEBgdiMXsovvlN82a6sfxc0oBQT3sM\ncLKBpaUlBg7s6otVYGNjQ0l76NatW0blMjQ3N+tc3SokNyoqKjQe37x5s4piqjba29sNlg1ua2tD\nTU2NUUW4exJ/N1u4WAPHzxunFtknjHtWVhb2798PQP7rnJaWpncf+j44umRldWlKu7u7KxU2JRIJ\nMjMz9bo/APz973/XS4Dsq6++6jKL9fT0xMyZM1FRUYHly5cjJCREZz9Xr17ttkSnQYMG6Vw6y2Qy\nrF69Wq/qWBs2bDAo9FQXM4LcUFjV2i1JTWKpDN/frMO84e4oLCzUujejLRS3M99//z1+++03g8e1\nf/9+rQlUgHzfJD09XeOPEYPBwMmTJykL8iUmJuLbb7/Vd6gA5OPduXMn8vLyDLq+Nwi1bsLZMhHE\nRhRm7xPRMg0NDaiurqZc0qszQqEQY8aMwZtvvklJk0QoFGL69OlIS0tTm8EqFosxbtw4nDt3jlIo\nXnt7O1auXImDBw8aJLxl6qgHmUxGKQHGlDQ2NkIqlVLKRJVIJFi1ahV27dpFOZy0tbUV9vZdK/GY\ngo/+nYcanhCfvTPRpP2evdOA7PtN2BjhhnfffRfffPON2v2GpqYmLFq0CGlpad2WmdsRQgikUmmP\n3EuBMREvilXbk5SRqgtCCP7v3D2M9HLAnFD5vsYzGS3j4uKC4OBgHDhwgHK0R0dsbGxw9uxZStVq\nFOdnZGRolCawtLREVlYWJcMuk8lQXl6Oo0ePGmzY58yZo7OykgKhUIjVq1ejqakJH330UZflNSEE\nr7/+Ojgcjtp7dRdXrlzB4cOHKZ1rYWGBpKQkvfIEHBwcui0yamagC2oZjrhdR71OgC6kMoLUPx7i\nzeHucHR0xHfffadxI9nZ2Rnp6ek9ZmwZDAble7W0tCA+Pl6jG0cqlWLZsmU6698aE8poZmamYth7\neD5rEAwGAyvH9sfJ3x+irtWwnJan2rgLBAKlD1kkEkEmkxkcveHl5aW1DmVndBkKqvK0XC5XRfFQ\n3zKADAYDH3/8MQYPHkzpfBsbG0yZMgVSqRSXL1/uslRlMBg4dOiQ2pqba9as0Su5Sx9mzJiBzZs3\n633dyZMn9XIxnD592uTL8+HB/lg7fjA+ySmDUGL4MrojV8qaYW9ljlAP04U/xsXFGfX55eTk6FW4\nBpAn6w0aNEijcTc3N8dbb71FeRM/LS1NraSIOq5fv47z58+r/C09Pb3bkq5MjbejDQItm7HyyBmD\nrn+qjfvt27fxySefAJCHB65du1av2ZlYLMbmzZtV/Mft7e24cUO9vkNdXR3mzZun0QBLJBIkJCTo\n5Y8OCAhQ+o4lEgmioqJQX19P+XpAHvapz+ueNm0aXF1d8c9//lNt1Rtvb2+1/W3atIlysRCqdJxF\n6Tuz5vP52Lt3r17XOTg4dEvExPghzvB1tsYnZ43XBhFKZPiyoBaT+ptj9uzZGmeaPB4PCxcupJyt\n/O677xqVTcxkMvV+78zMzBATE6N1ph8ZGUk5vHXw4MGU/fQMBqPLdzUyMrLbCql3B7FTR8HK0w9F\n1frvcT3VoZCenp6Ijo5GWVmZQfGrhBA8evQII0eOVBqI4uJiJCcnY8qUKV3O79evHwICAjSOXyqV\noqysDKNHjzbIBcBgMDBt2jS9FBA7kpaWBm9vb62+RalUivv374PFYqGoqAju7u4aw9m+/fZbuLi4\nKN1PdnZ2Js9IjYuLQ1tbGwICAvS+1tLSEpGRkZRqqyrw8fGBh4eH3veigln9A3xb0oZgL2d4Mg3z\n7xJCsO9yBVi2Flj8gg/GjBmj8dm2traGl5cXZWPn5ORkVF6Cp6en1mgdXeTn58PNzU2ji+XatWvw\n8PDQut/j4eFB+fvh5eXVJYDA2tr6qQiHVNDP2goeDtY48ms1RjtrDhFWx1M5c+8YiXLjxg3s3bvX\noH4sLCwwf/58lYcpNDRUGXnTGTMzMwwfPlxjf5aWlli8eLFBm5EtLS2YPHmyUeXQHjx4oDNE8caN\nG1i6dCnq6+uRlZWFsjLN+igikQg8Hq/L6saUrFmzBpGRkQZfrxAte/z4MQoKCihfJxAI8Mcffxh8\nX3WMGzMKW2eEYs+lMjxup17opSNn7zSAW8/HX9kDYGZmpjVGn8Fg6HQlEkJw6NAhozJRL1++bBIt\noxMnTmjcG1IoklIN7W1tbUVWVpbaYwUFBTrDXh8+fIikpCRK9+ptIgY5gu2jvw7VU2ncY2NjlXVc\nw8LCtGqWq6OqqopShXXFF+LixYtIT0/XeF5TUxOuXbum1xg6w2QykZSUpNxUPXz4MOXCxgrWrVun\n0/ceGhqKOXPmwMbGBlu2bNEaSrlo0SIMHToUwcHBepW40wdXV1ejk2kAYO/evRp/lNVx69YtneF8\nhhDWn4nxg50Rm34HjXz94urv1vORnF+DSba1+CX9R43n5efn4+eff6bUp1QqBSHE4Hq4hBCkpqYa\npc6o4ODBgxpXaAwGA59//jkGDRpEqa+6ujq1hcEJITh69KjWSQsgn8FbWlo+NZur7xhQVvGpDIVs\na2vDw4cPMXjwYIPcH7/++iv++OMP/OUvf9F4jkwmQ1RUFFJTU1FbW4vHjx8jIiJC7bm//fYbTp8+\nbVRpsM4UFBTA29vbIBeCQCBATk6Oimuprq4Obm5uGqtEFRcXa1yVtLW14cyZM3qJimmjvr4esbGx\nOHbsmMkiPH7//Xe4uLg8EQWYpVIpJq/7BO7hr+Dj6QHwdtTtCqltbceGX+5i8fNecBfJnzd1+yGA\n/Hmrr69HdHS0qYfeI0gkEnC5XI0JgGKxGCUlJQaHNvdV+mwopEgkUrocbG1tERsbqzORSBPh4eFa\nDTsgd8GcPn0azz33HEJDQzUadgAYMWKESQ37999/jytXrhjsG25qakJOTo7KrGTevHkaZ6pcLhdH\njhxR+dvx48eVOj1CoRB37tzRu+6rJlxcXLB8+XKThu4NHz5cadivX7+uc+bWkTt37hic/agOc3Nz\n/Lz7fbz1vDdiT3Nxo/axxnNlhCDtZh1W/XAHM4PdMMHXGUFBQRoNOyB/3nQZ9oyMDKNWkzdv3kRJ\nSYnB12ujpKRE6yqLy+Xq5TK5du0asrOzDRYF+89//oP8/HyDrn2SeWqMe1paGg4dOgRAvkz597//\nTTn8D5Bv5FKVyAXkkTgJCQnKdlZWlopxq6ysxL59+7plWTdx4kTMmjULgHwFERMTo5fMgJeXF3bs\n2KEyS9+4caNGzZzg4OAuri1/f3+lsXRxccHmzZuVewmGvmaF356Kr9gY1q9f3yUEThunTp1CUVGR\nScdgZWWFqYGuWDNuIOLPcbDqhxKkFz/C43YJ2kRSlDYK8Gs5D++nc3GptBl/DbFE3olPNPb3+++/\nY8OGDZTvb2wN0jt37lDOndCXkJAQreX21D2P2uBwOMjJyTF4D6W767X2FjqnTsXFxThx4gSkUile\neukltcL+KSkpKCwshLW1NVasWNFFIN9Y+Hw+3FksnM7IQEJBAex8fPD8zJkIi4igvPPt6uqqdTO0\nM+7u7vDx9sbHK1bgwc2bKC8txc8+PnD/n/9B+OzZ8A8JUeqcaBt3fm4uCn76Ce2VlbDu31/ruNWd\nHxQdjYkTJ8Lb21uv/gghiIuLwxtvvIHdu3fjyy+/1PkAV1VVQSgU4ssvv1SJve9IRUUF1q1bh1On\nTqntj8/n48qFC8hMTkbL7dsQAHAOCsLE+fPx0a5dyMnJ6TJWfd8nXSQnJysjSJqbm1H066/47cwZ\njX13XHUpfrhM9WX3t5fAKmMf5sfvw4XSVnz+axXMGAy42VnCzd4KUUOdMT3IFWKRCJazZ2vux99f\np1ustbUVNjZyDRoqLpvO77uFpyfCXn0VY9hsvP766+Dz+biYmanzczHm86uoqEBycjLWr1+vtg/3\nAQNw5MgR7N69u8tnIhaLYW5urqIlJRKJYGFhoVdQw6RJk5T/397ejvb2dp37QKZ+ZrsDrT53mUyG\nNWvWYPPmzWCxWNi4cSPWrFmj4tcsLCzEuXPnsHHjRnC5XBw/fhzbtm3TeEN9fO4JCQmov3IFvjU1\nYNfUYKxYDFsAfAB5lpa44ukJ/qhR+DA5We31eXl5cHBwoKSXAsg3Tp2dnfHzvn2wLSxEVUUF+hMC\nNoAXAOW9LzMYyPP2hiAsTOO9dy1ZAtvCQsrj1nT+FXNz/GJnh/v29hhlYYGxVVVgS6WU3oeoqChs\n2rQJbm5uSv+lNqmCJUuWYNGiRcofcnUQQsDlcpVRKh3727VkCcTnzmGKQAB2h/crD8AFALf79YPf\n5MmUXjeVz1cXu5YsQfv585jy+DFeJIRS38nJyWhoaMD69esNuqcuKqqqwXJyhJ2dHXJycuDg4KDx\n+3D27Fm4ublpVRXtyDvvvIN33nmHUiUtbc9bnrc3CiUSjLKw0Pm5GPv5NTc3Y+uCBRhSXa22j8se\nHigfMAC7T5/ucu2yZcswd+5clR+ylJQU3Lp1S6sN0saPP/6IvLw87Ny5U+/3zhTPrDb09blrnbnf\nvXsXHh4eeO655wAAbDYb+fn5KsY9Pz9fGcrm5+eHtrY2NDc3G1TerKWlBdXV1QgMDAQgj2lllJQg\nrpM/1BbAS2IxXiovx1bIf0UVv5ZCoVAZy1tXV6c1JEpRXk4RfigQCCAQCGBbWIgPysuxD0DnMgG2\nAF4mBC9XVmKrmZnKvRXw+XzYFhYirpPinaZxazt/klQKdksL4traENcpIaNzfydPnkReXp7SeRdA\nxAAACThJREFUn5mZmdllBrNu3TrMmjULEydOBIfDwf3795Ubr8eOHeti+Ddt2oQZM2Yok5cYDIZK\nzdTVq1fj1VdfRUREBPoVFGBnJ/kHWwAv/fkvQSCAID+f0uvW9PlSRdH3zk4hnLr6fvvtt1XCBgsL\nC+Hr62tUSUQFhBAkfZaI0aNH49VXX0V7e7vKvgMhBK2trcpZo7m5udYVxIMHD1BaWoqJE+WaNl98\n8QWlfQxdz9uk8nLEmpvjgz8nER2Pd3zvGhoajP78rKysMKS6WnMfFRXYymCAz+eDx+Nh48aNWLZs\nGSIiIrB79+4uocPz589HW9t/ZSCys7MREhICV1dXne8LAMyaNQuTJ09WtjMyMjBixAhlbH13PrOm\nRuvapbGxES4uLso2i8VCY2Oj1nNcXFy6nKOJuro6FQXHs2fPYt26df/ty8EBU9q063VEVFUh/8+N\nv8uXL6tI7M6aNUtlFtPS0oKrV68q2zk5OVixYoWyzWaz8bCiAuyaGlwFMFbH+Nk1NcjPzcXs2bNV\nNnN+SE0FW0eBbcW1AJCfm6v1/KsAJuuQJWDX1KD87l3weDxlHoCZmZnKj1tlZSUCAgKUm3UikQhJ\nSUmorq4GIDfc9fX1KnsLCxcuVAlf27BhA2prawHIl7Bz5sxBeHg48nNzEVFVpXWMYwGwqqspv27F\n61Kcrw9U+167YoXy9QDyXIWOhiAlJUUlDDA1NVXF+Gvbf1D3vJWWliqrYkVERGDjxo3KwICLFy8i\nJiYGIpG8huakSZNU9kmqq6tx8uRJZZvH46n4xdUZ9o7jq62tRVpaGqX3ZrJUiqtajrNravBtcrLR\nnx+VsUT8+cxUVlbC3d1dGb7LZDIRFxenUsyex+OpGNUrV66o1JNNSUlR2TxXFyTQMdGroKBApZbv\nJ9u2gf3n90UThj6zJodoIS8vjxw+fFjZzsnJIceOHVM5Z8eOHeT27dvKdnx8PLl3757GPjMzM0lj\nYyNpbGwkgwYNIgCU7aCgIJX2SCcn0gYQouVfG0A2v/22/PyRI1WuHzFihGp/nY6Hh4ertCMiIojP\nn30m/PlfXff2AUhxcTGpqakh0dHRBACJ8PSkdC3b05MAIBN9fLSeT3UsLw0ZQgCQqVOnEg6HQ+bM\nmUMAkGnTphEOh0MWLlxIAJDp06cTDodD3nvvPZXjivakSZNU2pMnTyYcDocsXbqUACDR0dEq7aio\nKLL+jTcojXELQMa6uxMOh0NmhYZSumashwfhcDhkw4YNBACJjIzU2aY6Hh+AjBkzRuX6sLAwlfbo\n0aMJh8MhH374IQFARo0aRTgcDvnb3/5GAJCRI0cSDodDYmNjVY53bsfHxxMA5PnnnyccDods375d\n5fjnn39OAJDhw4cTDodDDh06pNI+ceIEAUBGjBhBOBwOOXPmjEr7p59+UmmfOnVKpf3LL7/I789i\nUXpvEnQcnz5wIKV+nmexCIfDIUVFRSrjyc/PV37fdPWx/o03SGNjIwFAhg0bRjgcjrIdHBys0g4M\nDFRpBwUFqbT9/f1V2n5+flqPd2wbMl5fX1+V/gxtZ2ZmajPXXdDqc+dwODh16pSyhmFaWhoYDIZK\nPc4jR45g2LBhYLPZAIC1a9diy5YtGt0yBQUFlCuz09DQ0NDIcXJyorz/Aujwufv6+qK2thZ1dXVg\nsVjIzc3tIroTFhaGc+fOgc1mg8PhwM7OTqu/XZ/B0dDQ0NAYhs4M1eLiYhw/flwZQTF16lRl6r8i\nhOjrr79GYWEhbGxssHz58iciS5CGhobmWabH5QdoaGhoaLqfpyZDlYaGhoaGOrRxp6GhoemD9FiF\nWyoyBs8C9fX1SExMBI/HA5PJxIQJEzBhwoTeHlavIpPJsGHDBrBYLL30U/oaQqEQR48eRXl5OcRi\nMZYvX66SMPYskZmZiezsbIjFYgQFBWHx4sW9PaQe47PPPkNRURGYTCb27NkDQJ5gefDgQdTV1cHd\n3R2rV6/WXXhFr8BJA5FKpWTVqlXk4cOHRCwWkw8++IBUVFT0xK2fOJqamkhpaSkhhBAej0eWLl36\nzL4XCtLT08mnn35Kdu7c2dtD6VUOHjxIzp8/TwghRCKRkLa2tl4eUe/Q2tpKVqxYQQQCAZFKpWT7\n9u2kqKiot4fVYxQXF5P79++T999/X/m3f/3rX+SHH34ghBCSlpZGvvrqK5399IhbpqOMgYWFhVLG\n4FnEyclJKWrFZDLh6+urs/J7X6ahoQFFRUWIiop6KgondBd8Ph8lJSWIiooCIJce6O309d5CUViE\nz+dDJBKhvb2dcgHtvkBQUFCX4jgdZV4mTJiA69ev6+ynR9wy6mQM7t692xO3fqKpra1FZWUl/Pz8\nensovcaJEyfw9ttvQ9BJk+ZZo66uDkwmE4mJibh//z78/PywZMkSgysoPc1YWVlh6dKlWLlyJSwt\nLfHKK69g6NChvT2sXoXH4ynzhxwdHSnVH6A3VHsJoVCI/fv3IyYmxqiixU8zBQUFYDKZGDx48DM9\nawfk1Zvu3buH8PBw7NixAxKJBHl5eb09rF6hpaUFR48exb59+5CYmAgOh4PCwsLeHtYTA1U56h4x\n7iwWS6Vwc0NDg8aK7s8CEokEe/bswYsvvqi14k5f586dOygoKMDKlSvx6aef4tatW8qCLM8aLi4u\nsLe3R1hYGKysrMBms01eQORp4e7du/Dz84OHhwccHBwwduxYFBcX9/awehVHR0elbEtTUxMlldIe\nMe4dZQwkEglyc3MRFhbWE7d+4iCEICkpCf3798e0adN6ezi9yoIFC3D48GEkJiZi7dq1GDZsGFat\nWtXbw+oVnJyc4OHhAS6XC5lMhsLCQo2Vs/o6gYGBuHfvHh4/fgyxWIyioiK9Cu30RcLCwpCdnQ1A\nri5KZVLYYxmq6mQMnkVKSkrwj3/8AwMHDlQurxYsWIARI0b08sh6l+LiYqSnp+PDDz/s7aH0GtXV\n1UhMTERLSwsGDhxILdytj5KdnY0LFy5AJBJh+PDhmDt3rl7VlZ5m9u/fj9u3b6O1tRWOjo6YO3cu\nXnjhBb1DIWn5ARoaGpo+yLPxU0hDQ0PzjEEbdxoaGpo+CG3caWhoaPogtHGnoaGh6YPQxp2Ghoam\nD0IbdxoaGpo+CG3caWhoaPogtHGnoaGh6YP8P6g8jHygjylsAAAAAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114013190>"
       ]
      }
     ],
     "prompt_number": 30
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "SciPy implements a Gaussian KDE that automatically chooses an appropriate bandwidth. Let's create a bi-modal distribution of data that is not easily summarized by a parametric distribution:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "# Create a bi-modal distribution with a mixture of Normals.\n",
      "x1 = np.random.normal(0, 3, 50)\n",
      "x2 = np.random.normal(4, 1, 50)\n",
      "\n",
      "# Append by row\n",
      "x = np.r_[x1, x2]"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 31
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "plt.hist(x, bins=8, normed=True)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 32,
       "text": [
        "(array([ 0.03623044,  0.04830725,  0.06038407,  0.07246088,  0.03623044,\n",
        "        0.15096017,  0.18719061,  0.01207681]),\n",
        " array([-6.09280539, -4.4367394 , -2.78067341, -1.12460742,  0.53145857,\n",
        "        2.18752456,  3.84359055,  5.49965654,  7.15572253]),\n",
        " <a list of 8 Patch objects>)"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAECCAYAAADw0Rw8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEqZJREFUeJzt3W9wVPW9x/FPstsQyB+Xs70hvawRG8ItMBiL0RlNWx3C\nOo2MDywzHS3MYBl9ENGBW0aH2Mn4J61BspQ+aNgKtGNEfUSLV2eYwaDVwUk7Q9xYx6ZFVitObDN7\n2W1IEyB/dnMfUHe6l2QTJMlZv7xfT+Ds/s7yXQbenJycPeSNj4+PCwBgVr7bAwAAZhehBwDjCD0A\nGEfoAcA4Qg8AxhF6ADDOO9WCnp4etbe3K5lMqq6uTvX19RnPHz9+XK+++qokKRAI6J577lFFRcW0\n9gUAzL6sR/SpVErhcFjbt2/Xzp079eabb6q3tzdjzaJFi/TUU0+ptbVV1dXVeu6556a9LwBg9mUN\nfTQaVXl5ucrKyuT1elVbW6uurq6MNcuWLdOCBQskSatXr1Y8Hp/2vgCA2Zc19IlEQn6/P73tOI4S\nicSk648dO6aampovtC8AYHbM2DdjP/jgAx0/flz33XffTL0kAGAGZP1mrOM46VMxkhSPx+U4ziXr\nTp8+rX379unxxx9XUVHRZe37uT/84Q8aGhq67DcAAFczn8+nm266KeuarKGvrKxUX1+fYrGYHMdR\nZ2entm7dmrHmzJkz2r17tx555BGVl5df1r7/bmhoSKtXr57O+wIA/EskEplyTdbQezweNTQ0KBQK\npS+RDAQC6ujokCQFg0EdOnRIg4OD2r9/f3qflpaWSfcFAMytvFy5TfEbb7zBET0AXKZIJKK6urqs\na/hkLAAYR+gBwDhCDwDGEXoAMI7QA4BxhB4AjCP0AGAcoQcA4wg9ABhH6AHAuCn/K0EAuFJ/HxhW\nbHDE7TEkSWXFBfpa6Ty3x5hThB7ArIsNjujRI1G3x5Aktd619KoLPaduAMA4Qg8AxhF6ADCO0AOA\ncYQeAIwj9ABgHKEHAOMIPQAYR+gBwDhCDwDGEXoAMI7QA4BxhB4AjCP0AGAcoQcA4wg9ABhH6AHA\nOEIPAMYRegAwjtADgHGEHgCMI/QAYByhBwDjCD0AGEfoAcA4Qg8AxhF6ADCO0AOAcYQeAIwj9ABg\nHKEHAOMIPQAYR+gBwDhCDwDGEXoAMM471YKenh61t7crmUyqrq5O9fX1Gc9/9tln2rt3rz755BPd\ne++9uvvuu9PPbdmyRfPnz1d+fr48Ho9aWlpm/h0AALLKGvpUKqVwOKympiY5jqPGxkatWrVKgUAg\nvaakpESbN2/WiRMnJnyNJ598UsXFxTM7NQBg2rKeuolGoyovL1dZWZm8Xq9qa2vV1dWVsaa0tFSV\nlZXyeDwTvsb4+PjMTQsAuGxZj+gTiYT8fn9623EcRaPRab94Xl6enn76aeXl5enOO+/U2rVrv/ik\nAC7L3weGFRsccXsMSdJIMuX2CFe1Kc/RX4nm5mYtXLhQvb29amlp0eLFi7V8+fLZ/CUB/EtscESP\nHpn+gdlsemLt9W6PcFXLeurGcRzF4/H0djwel+M4037xhQsXSpICgYBuueWWy/pqAAAwM7KGvrKy\nUn19fYrFYhobG1NnZ6dqamomXPv/z8UPDw/r/PnzkqSBgQF1d3eroqJihsYGAExX1lM3Ho9HDQ0N\nCoVC6csrA4GAOjo6JEnBYFD9/f1qbGzUuXPnlJ+fryNHjmjPnj06e/asQqGQpItX5qxbt07V1dWz\n/44AABmmPEe/YsUK7dq1K+OxYDCY/rnP51M4HL5kv8LCQrW2ts7AiACAK8EnYwHAOEIPAMYRegAw\njtADgHGEHgCMI/QAYByhBwDjCD0AGEfoAcA4Qg8AxhF6ADCO0AOAcYQeAIwj9ABgHKEHAOMIPQAY\nR+gBwDhCDwDGEXoAMI7QA4BxhB4AjCP0AGAcoQcA4wg9ABhH6AHAOEIPAMYRegAwjtADgHGEHgCM\nI/QAYByhBwDjCD0AGEfoAcA4Qg8AxhF6ADCO0AOAcYQeAIwj9ABgHKEHAOMIPQAYR+gBwDhCDwDG\nEXoAMI7QA4BxhB4AjCP0AGAcoQcA47xTLejp6VF7e7uSyaTq6upUX1+f8fxnn32mvXv36pNPPtG9\n996ru+++e9r7AgBmX9bQp1IphcNhNTU1yXEcNTY2atWqVQoEAuk1JSUl2rx5s06cOHHZ+wIAZl/W\nUzfRaFTl5eUqKyuT1+tVbW2turq6MtaUlpaqsrJSHo/nsvcFAMy+rKFPJBLy+/3pbcdxlEgkpvXC\nV7IvAGDm8M1YADAua+gdx1E8Hk9vx+NxOY4zrRe+kn0BADMna+grKyvV19enWCymsbExdXZ2qqam\nZsK14+PjX3hfAMDsyXrVjcfjUUNDg0KhUPoSyUAgoI6ODklSMBhUf3+/Ghsbde7cOeXn5+vIkSPa\ns2ePCgsLJ9wXADC3pryOfsWKFdq1a1fGY8FgMP1zn8+ncDg87X0BAHOLb8YCgHGEHgCMI/QAYByh\nBwDjCD0AGEfoAcA4Qg8AxhF6ADCO0AOAcYQeAIwj9ABgHKEHAOMIPQAYR+gBwDhCDwDGEXoAMI7Q\nA4BxhB4AjCP0AGAcoQcA4wg9ABhH6AHAOEIPAMYRegAwjtADgHGEHgCM87o9ADAT/j4wrNjgiNtj\nSJLKigv0tdJ5bo8BpBF6mBAbHNGjR6JujyFJar1rKaFHTuHUDQAYR+gBwDhCDwDGEXoAMI7QA4Bx\nhB4AjCP0AGAcoQcA4wg9ABhH6AHAOEIPAMZxrxt8Ybl0I7GRZMrtEYCcRejxheXSjcSeWHu92yMA\nOYtTNwBgHKEHAOMIPQAYR+gBwDhCDwDGEXoAMG7Kyyt7enrU3t6uZDKpuro61dfXX7Lm5ZdfViQS\n0bx58/TQQw9p8eLFkqQtW7Zo/vz5ys/Pl8fjUUtLy8y/AwBAVllDn0qlFA6H1dTUJMdx1NjYqFWr\nVikQCKTXRCIRnT59WqFQSKdOndLevXv105/+NP38k08+qeLi4tl7BwCArLKeuolGoyovL1dZWZm8\nXq9qa2vV1dWVsaarq0u33367JKmqqkpDQ0Pq7+9PPz8+Pj4LYwMApivrEX0ikZDf709vO46jaDSa\ndY3f71cikZDP51NeXp6efvpp5eXl6c4779TatWtneHwAwFRm5BYIkx21Nzc3a+HChert7VVLS4sW\nL16s5cuXz8QvCQCYpqynbhzHUTweT2/H43E5jjPtNQsXLpQkBQIB3XLLLZd8NQAAmH1Zj+grKyvV\n19enWCwmx3HU2dmprVu3ZqypqanR0aNHVVtbqw8//FBFRUXy+XwaHh5WKpXS/PnzNTAwoO7ubv3w\nhz+c1TdztciVu0Zyx0jgyyFr6D0ejxoaGhQKhdKXVwYCAXV0dEiSgsGgVq9erT//+c/avn27CgsL\n1dDQIEnq7+9XKBSSJJWUlGjdunWqrq6e5bdzdciVu0Zyx0jgy2HKc/QrVqzQrl27Mh4LBoMZ2xs2\nbNCGDRsyHlu0aJFaW1tnYEQAwJXgk7EAYByhBwDjCD0AGEfoAcA4Qg8AxhF6ADCO0AOAcYQeAIwj\n9ABgHKEHAONm5DbFV4OT/zukM0Ojbo+hwDXz3B4BU/DkS3/82z/dHoObziGN0E/TsVMJ/U/PGbfH\n0H9/61r9Zymxz2VnLyT11LG/uj0GN51DGqduAMA4Qg8AxhF6ADCO0AOAcYQeAIwj9ABgHKEHAOMI\nPQAYR+gBwDhCDwDGEXoAMI7QA4BxhB4AjCP0AGAcoQcA4wg9ABhH6AHAOEIPAMYRegAwjtADgHGE\nHgCMI/QAYByhBwDjCD0AGEfoAcA4r9sDAMBc8uRLf/zbP90eQ2XFBfpa6bw5+bUIPYCrytkLST11\n7K9uj6HWu5bOWeg5dQMAxhF6ADCO0AOAcYQeAIwj9ABgHKEHAOMIPQAYN+V19D09PWpvb1cymVRd\nXZ3q6+svWfPyyy8rEolo3rx5euihh7R48eJp7wsAmF1Zj+hTqZTC4bC2b9+unTt36s0331Rvb2/G\nmkgkotOnTysUCun+++/X3r17p70vAGD2ZQ19NBpVeXm5ysrK5PV6VVtbq66urow1XV1duv322yVJ\nVVVVGhoaUn9//7T2BQDMvqyhTyQS8vv96W3HcZRIJLKu8fv9SiQS09oXADD7ZuReN+Pj4zPxMjnt\nW0t8Ki+Zm/tSZPNf/1Gkfw6PuT0GgC+RrKF3HEfxeDy9HY/H5TjOtNaMjY1Nue+/8/l8ikQil/0G\n5tL1bg8gqf/0xR93rnZ3DklS4uPcmENilonkyhwSs0wg2XdKkb4rfx2fzzflmqyhr6ysVF9fn2Kx\nmBzHUWdnp7Zu3ZqxpqamRkePHlVtba0+/PBDFRUVyefzqaSkZMp9/91NN900zbcFALgceeNTnHfp\n6enR888/n75E8q677lJHR4ckKRgMSpJeeuklRSIRFRYWqqGhQYFAYNJ9AQBza8rQAwC+3PhkLAAY\nR+gBwLic+q8Ee3t79eKLLyoej8vv92vjxo3p8/255ne/+52OHj2q0dFRffOb39TGjRvdHmlCr732\nml588UX96le/UnFxsdvjXOLgwYOKRCIqKCjQ8uXL9f3vf18LFixwe6y0L8NtPM6cOaO2tjadPXtW\npaWluuOOO3THHXe4PdakUqmUduzYIcdxtGPHDrfHmdCFCxd04MABffrppxodHVVDQ4OWLVvm9lgZ\njh07prfeekujo6Navny57r///knX5lToDx06pO985zu67bbb9M477+jQoUPatm2b22Nd4oMPPtA7\n77yjn/zkJ/J6vRoYGHB7pAmdOXNG77//vr761a+6PcqkqqurtWHDBknSvn37dPjw4fS22z6/jUdT\nU5Mcx1FjY6NWrVqVcwcfXq9XmzZt0pIlSzQwMKDt27dr6dKlOTfn544cOaJAIKDz58+7PcqkDhw4\noBUrVujhhx9WMpnU8PCw2yNlGBwc1OHDh7V7924VFBTo2Wef1Xvvvacbb7xxwvU5depmwYIFGhwc\nVCqV0uDgYE4egUrS66+/rnvuuUde78V/J0tLS12eaGIvvPBCzn6l8bkbbrhB+fn5ys/P14033pjx\n2Qu3fVlu4+Hz+bRkyRJJF/8sVlZW6h//+Ie7Q00iHo+ru7tba9asydkPWp47d05/+ctftGbNGkmS\nx+PJqa8yJamgoEDSxVlHRkY0PDyctZc5dUS/ceNGPf7443rppZfkOI6eeeYZt0eaUF9fn3p6enTw\n4EEVFhZq06ZN+vrXv+72WBlOnDghx3F03XXXuT3KtL3xxhvpv1y5YKLbeESjURcnmlpfX596e3tV\nVVXl9igTam9v18aNG3P6aD4Wi6m0tFRtbW36+OOPVVVVpc2bN6fjmgsKCgr0wAMPaMuWLfrKV76i\n+vp6LV26dNL1cx765uZm9ff3X/L4fffdp7ffflvf/e53FQwGdfToUYXDYf3oRz+a6xElZZ8zmUwq\nFoupublZ77//vg4ePKgnnngip2Z85ZVX9OMf/zj9mJtHT9nmrKmpkST99re/VWFhoW699da5Hs+M\nCxcu6Oc//7k2bdqkwsJCt8e5xLvvvqvS0lJdf/31+tOf/uT2OJNKJpP66KOP9L3vfU8PPvig9u3b\np9///vfpmzfmgoGBAR04cEB79uxRUVGRfvaznykSiWj16ok/8jvnoW9qapr0ueeee06PPPKIPB6P\n1qxZo8OHD8/hZJmyzfn666/rtttuU0FBgWpqarR//36NjIzM+b/4k8346aefKhaL6dFHH5V08ch0\nx44deuaZZ3TNNdfM5YiSsv9eStJbb72l7u7uKdfNtencAiRXjI2Naffu3fr2t7+tm2++2e1xJnTy\n5Em9++676u7u1ujoqM6fP69f/OIXevjhh90eLYPf71dxcXH6IKS2tlZvv/12ToU+Go2qqqpK5eXl\nkqRbb71VPT09k4Y+p87Rr1y5Mn0O9MSJE7rhhhtcnmhiN998s7q7uzU+Pq5Tp05p0aJFOfVlXUVF\nhfbv36+2tja1tbXJcRw9++yzrkR+Ku+9955effVVPfbYYzn1eyhl3gJkbGxMnZ2d6b/8uWR8fFy/\n/OUvFQgEtG7dOrfHmdQPfvADhcNhtbW1adu2bVq5cmXORV66+D2P8vJynTp1SqlUSpFIJOda9I1v\nfEMfffSRBgcHNTo6qu7ublVXV0+6PqfO0a9fv16/+c1vdPjwYV177bVav3692yNNqK6uTgcOHNC2\nbdvk9Xr14IMPuj1SVnl5eW6PMKlf//rXGhsbU3NzsyRp2bJleuCBB1ye6iKPx6OGhgaFQqH05ZW5\neCXLyZMndfz4cVVUVOixxx6TdDGqk12BkSty+c/lli1b1NbWpoGBAVVUVOTMlWCfW7BggdavX6/W\n1laNjIyourpaK1eunHQ9t0AAAONy6tQNAGDmEXoAMI7QA4BxhB4AjCP0AGAcoQcA4wg9ABhH6AHA\nuP8Du6TInhwJDKUAAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x113ecaa50>"
       ]
      }
     ],
     "prompt_number": 32
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "from scipy.stats import kde\n",
      "\n",
      "density = kde.gaussian_kde(x)\n",
      "xgrid = np.linspace(x.min(), x.max(), 100)\n",
      "plt.hist(x, bins=8, normed=True)\n",
      "plt.plot(xgrid, density(xgrid), 'r-')"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 33,
       "text": [
        "[<matplotlib.lines.Line2D at 0x114129fd0>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAECCAYAAADw0Rw8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtgzXXjB/D3uezs7D5nmsmaMfOEGDPCEpl5jJRbco1G\nv5p7iajH00Wixzx5Css9ufRURGTMkEspzBlixEZYrLGZ3c/994fa07IbO+d8zvnu/fqn52yf7/m+\nj8fePvtePl+ZxWKxgIiIJEsuOgAREdkWi56ISOJY9EREEseiJyKSOBY9EZHEseiJiCROWd2AtLQ0\nrF27FiaTCVFRUYiJiSn3/UOHDmHbtm0AgMDAQAwYMABBQUE12paIiGyvyhm92WxGQkICpk2bhvnz\n52Pfvn3IzMwsN6ZBgwZ4++23sWDBAoSFhWHZsmU13paIiGyvyqJPT09HQEAA/P39oVQqERkZiZSU\nlHJjmjdvDnd3dwBAeHg4cnJyarwtERHZXpVFn5ubCz8/v7LXGo0Gubm5lY7fs2cPIiIi7mtbIiKy\nDaudjD19+jQOHTqEYcOGWestiYjICqo8GavRaMoOxQBATk4ONBrNXeMuX76M5cuX4/XXX4eHh8c9\nbfuHH3/8EUVFRff8AYiI6jJfX1+0b9++yjFVFn1ISAiysrKQnZ0NjUaDw4cPY8qUKeXG3Lx5EwsX\nLsSkSZMQEBBwT9v+WVFREcLDw2vyuYiI6HdarbbaMVUWvUKhQFxcHOLj48sukQwMDERycjIAIDo6\nGps2bUJhYSFWrFhRts28efMq3ZaIiOxL5ijLFO/du5czeiKie6TVahEVFVXlGN4ZS0QkcSx6IiKJ\nY9ETEUkci56ISOJY9EREEseiJyKSOBY9EZHEseiJiCSORU9EJHEseiIiiav2UYJERLV1PV+H7EK9\n6BgAAH9PFRp6u4qOYVcseiKyuexCPaYnpouOAQBY0KdZnSt6HrohIpI4Fj0RkcSx6ImIJI5FT0Qk\ncSx6IiKJY9ETEUkci56ISOJY9EREEseiJyKSOBY9EZHEseiJiCSORU9EJHEseiIiiWPRExFJHIue\niEjiWPRERBLHoicikjgWPRGRxLHoiYgkjkVPRCRxLHoiIolj0RMRSRyLnohI4lj0REQSx6InIpI4\nFj0RkcSx6ImIJI5FT0QkcSx6IiKJY9ETEUkci56ISOJY9EREEseiJyKSOBY9EZHEseiJiCROWd2A\ntLQ0rF27FiaTCVFRUYiJiSn3/V9//RVLly7FL7/8gqFDh6Jfv35l35swYQLc3Nwgl8uhUCgwb948\n638CIiKqUpVFbzabkZCQgNmzZ0Oj0WDWrFlo3bo1AgMDy8Z4eXkhNjYWx44dq/A93nrrLXh6elo3\nNRER1ViVh27S09MREBAAf39/KJVKREZGIiUlpdwYb29vhISEQKFQVPgeFovFemmJiOieVTmjz83N\nhZ+fX9lrjUaD9PT0Gr+5TCbDO++8A5lMhl69eqFnz573n5SI7sn1fB2yC/WiYwAA9Caz6Ah1WrXH\n6Gtjzpw5qFevHjIzMzFv3jw0atQILVq0sOUuieh32YV6TE+s+cTMlt7s2UR0hDqtykM3Go0GOTk5\nZa9zcnKg0Whq/Ob16tUDAAQGBqJjx4739NsAERFZR5VFHxISgqysLGRnZ8NoNOLw4cOIiIiocOxf\nj8XrdDqUlJQAAPLz85GamoqgoCArxSYiopqq8tCNQqFAXFwc4uPjyy6vDAwMRHJyMgAgOjoaeXl5\nmDVrFoqLiyGXy5GYmIgPPvgAt2/fRnx8PIA7V+b07dsXYWFhtv9ERORYLBa43ryBdhdPwcVkwLlG\noch39xadqk6RWRzkspi9e/ciPDxcdAwiyTh5rUDoMXr/vBsYdeBz9NEmw9VVhXM+DWGSy9H8WgZu\nu3sjue0T+KT7UBS52ffy6wV9miHsQS+77tOWtFotoqKiqhxj05OxRFT3uOlKMDlxOaJPfIvtHXpj\n2MsrETe4I97ecwkAIDObEXzjCkYc/BKbF4zGqqhR+KpTP5gquUSbao9FT0RW0yjnGuLX/hNnA5tj\n0Iy1uO3hc9cYi1yOSw2C8e4z09Hsegamb/0IHdOP4x/D/wGdi6uA1NLHtW6IyCo6nk/BqiWTsLlT\nP7zzzPQKS/6v0huGYMILC1Dq4oaPVsyAV3GBHZLWPSx6Iqq1iPRUzPlsHmaNfBObujwNyGQ13tao\ndME/h85E2kN/w/KPX2bZ2wCLnohq5eHM85i74V3MGvlPpDZtc1/vYZHLsejJOBxr1g7vfjYXcrPJ\nyinrNhY9Ed23oBtX8cGaN/DeoJehDanl5dMyGf7T9yW4GA2IS1pjnYAEgEVPRPdJrS9B/Np/Ynn0\naBx45DGrvKdJocDrI2aj14l96Hlyv1Xek1j0RHSfZmz9CGceehhbOj1p1ffN8/TF9Ofexmtb/gP/\nvBtWfe+6ikVPRPcs5ngyWl9Ow7/6T7bJ+59vFIovuzyN6V9/CDjGPZ1OjUVPRPck6MZVvPxNAmaN\nnI0SVzeb7WdNj+FofCMTT5w+ZLN91BUseiKqMZnZjDc2LcSqqJFIbxhi030ZlCrMHfQKXv16MTxL\nCm26L6lj0RNRjfU/mggXkxFfdnnaLvs72aQ1DrXojPG7Vtllf1LFoieiGvHLz0Fc0mrMHfQKzHL7\nrUuT0DsW0Sf3I+jGVbvtU2pY9ERUI69+vRhbHu2LjIZN7brf2x4+2PD4YLzEa+vvG4ueiKrV+eej\naH4tA6uiRgnZ/38fG4i2l06jxdWfhezf2bHoiahKCpMRU7cnYFG/l6B3UQnJUKpyw4roUZi4c6WQ\n/Ts7Fj0RVWngj9/ghk99HGrRWWiObR1i0CDvN3Q8nyI0hzNi0RNRpbyKCzB27zp88GTcPa1IaQsm\nhRIrez6H2H0bheZwRix6IqrUuD3rsL/VY3Y/AVuZ5LAnEHDrN7S+fEZ0FKfCoieiCjXKuYY+2t1Y\n9vcxoqOUMSkU2NDtGTy3/7+iozgVFj0RVej/ktfi88iBuOVZT3SUcrZF9Ebry2lo8tsvoqM4DRY9\nEd0l5PpFPHo+BRu7DhYd5S46lRqfRw7Ec/s/Fx3FabDoieguL+1eg0+7D0Wx2l10lApt6vwUuqb9\ngAa3fhMdxSmw6ImonFZXzqJF5gVs6myf9WzuR4G7FxLbR2Pwj9tFR3EKLHoiKmf8rtVY2XOUsJuj\naurLzk/jqaM7oTLoRUdxeCx6IirT9tIpNMq9ju0RfxcdpVpXHwjEucBQRJ/8VnQUh8eiJ6IyLySv\nw6qoETAplKKj1MgXXfpjyPdb+RSqarDoiQjA/2bzieHRoqPU2A9/6wDvkgK0unpOdBSHxqInIgB3\nZvOrewx3mtk8AJjlCmzq/BSe/X6L6CgOjUVPRHdm8znXsKN9L9FR7tm2DjF47OyP8C3MEx3FYbHo\niQhj96zHGiebzf+hwN0LB1p1Qd/ju0VHcVgseqI6rtWVswi+cdUpZ/N/2NqxL54+tpMnZSvBoieq\n42L3bsCn3Z+FUekiOsp9Oxn8CGQWC9pwVcsKseiJ6rDQaxlokXke2zrEiI5SOzIZvu7YB/2PJopO\n4pBY9ER12PP7NmLD44Ohc3EVHaXWdrSPRrcz38OjpFB0FIfDoieqoxpnX0H7jBP4qlM/0VGs4pZn\nPRxtFo5evFP2Lix6ojpqzLcb8fljA1Di6iY6itXcOXyzU3QMh8OiJ6qDGuZm4bGzP+KLLv1FR7Gq\no6Hh8CvIQdOsX0RHcSgseqI66LkDn2PLo0+i0M1TdBSrMssV2NWuJ/poeU39n7HoieoYv/wcRJ/4\nFp91HSQ6ik3saB+NGO0eyM0m0VEcBoueqI4ZcXATdob3dLhnwVrLpQbBuOldHx0vaEVHcRgseqI6\nxKfoNvql7MS6bs+KjmJT37TvxSUR/oRFT1SHPPv9Fux/pCuyfR8QHcWmdrd9ApHnjvCa+t+x6Inq\nCI/SIgz+YRs+eWKY6Cg2d9vDBynN2iHqp4OiozgEFj1RHTH4h234sXkEfvV7UHQUu9gRHo2+x5NF\nx3AILHqiOkCtL8GwQ5uwpsdw0VHs5vDDHdH0t0tocOs30VGEY9ET1QEDjiTiZHBrXGoQLDqK3RiU\nKnz7yOP4+4l9oqMIV23Rp6Wl4bXXXsOrr76KnTvvvrX4119/xRtvvIERI0Zg+/bt97QtEdmei1GP\nEQe/wOo6NJv/w87wnohJ3Ss6hnBVFr3ZbEZCQgKmTZuG+fPnY9++fcjMzCw3xsvLC7GxsejXr989\nb0tEtvf00Z043zAEPwc2Fx3F7k4EPwLP0iI0u54hOopQVRZ9eno6AgIC4O/vD6VSicjISKSkpJQb\n4+3tjZCQECgUinvelohsy8Wox+j9/8XKns+JjiKERS5HUtse6F3HZ/VVFn1ubi78/PzKXms0GuTm\n5tbojWuzLRFZx5MpSbjYoDHSgh4WHUWYne2i0Dt1H2Rms+gowvBkLJFEyQx6jPn2M6zsOUp0FKEy\nGjbFbXcvtLt0SnQUYaoseo1Gg5ycnLLXOTk50Gg0NXrj2mxLRLUX8PVmXKkfiJ8atxIdRbhdv8/q\n66oqiz4kJARZWVnIzs6G0WjE4cOHERERUeFYy1+evn4v2xKRlen1CFqxuM7P5v+wO+wJPHH6EJRG\ng+goQiir+qZCoUBcXBzi4+NhMpkQFRWFwMBAJCffudssOjoaeXl5mDVrFoqLiyGXy5GYmIgPPvgA\narW6wm2JyPZUGzagpHFTnGzSWnQUh/BbvQa45B+EzuePAWghOo7dySx/nYoLsnfvXoSHh4uOQeT8\nSkrgExGB1H9/jJeuOsaDRd7s2QRv77kkNMPgw18j7JfTUK9fg7AHvYRmsSatVouoqKgqx/BkLJHE\nuH7yCYxt26KgdVvRURzKnjbdEHnuCOTFxaKj2B2LnkhKioqg/vBDlM6aJTqJw8nz9MVPjVui/v66\nt9AZi55IQlxXrICxUyeYHnlEdBSHtKttFPx3fC06ht2x6IkkQpabC/WSJSjhbL5SB1pFwvf4Ucjq\n2M2bLHoiiVD/+98w9OsHc/O6t6ZNTRWr3ZEb+Thctm0THcWuWPREEiC/cgWqzz5DyWuviY7i8LJj\nnoLqq69Ex7ArFj2RBKjnzoVu3DhYGjQQHcXh5XbtDsXp05BduyY6it2w6ImcnOLUKbgcPIjSiRNF\nR3EKZlc1DDExUG3dKjqK3bDoiZyZxQK3WbPuHLLxks5NQLamHzSoTh2+YdETOTGXr76CrLAQ+lFc\n0+ZeGB9/HPKrVyG/eFF0FLtg0RM5q6IiuL/1Fkrmzwf+8uAfqoZSCf3TT9eZWT2LnshJqRctgrFT\nJxg7dxYdxSnpBw6EavNmwDGW+7KpKlevJCLHJP/lF7iuXo38gwdFR3Fapo4dgaIiKNLSYGol7TX7\nOaMncjYWC9xffhmlU6bA0qiR6DTOSy6HYdAgqDZtEp3E5lj0RE5G9fnnkN26Bd348aKjOD394MFw\n2bwZkPjzZFn0RE5EdvMm3N58E8WLFgFKHnmtLVPLloCnJxRHj4qOYlMseiIn4vbGG9APGQJTW641\nbxUyGfSDB985KSthLHoiJ+GyfTuUKSkomTlTdBRJ0Q8cCNXXXwMG6T5PlkVP5ARk16/D/dVXUbRs\nGeDhITqOpJiDg2EODoZy/37RUWyGRU/k6MxmeEyYAN3YsTBFRIhOI0lSP3zDoidycK7LlkFWXIzS\nV14RHUWy9P37wyUpCSgqEh3FJlj0RA5MceQI1IsWoejjj3mVjQ1Z/P1hioiAy65doqPYBIueyEHJ\nrl+HZ2wsihYvhjk4WHQcydMPGQLXL74QHcMmWPREjkivh+eYMdA9/zyM0dGi09QJ+j59oDhyBLIb\nN0RHsToWPZGjsVjgPm0azP7+PC5vTx4eMPTuDdWWLaKTWB2LnsjBqN99F4qzZ1GUkADI+SNqT/pn\nnoFKgodveHaHJOF6vg7ZhXrRMQAA/p4qNPR2va9tXZcuheqbb1CQmAh4elo5GVXH2K0b5BMmQJ6e\nDnOzZqLjWA2LniQhu1CP6YnpomMAABb0aXZfRa/69FOoExKQv3MnLH5+NkhG1VIqoR8wAKovvkDp\n66+LTmM1/L2QyAG4fvQR1AsXomDrVlgCA0XHqdP0zz575/CNhFa0ZNETiWSxQD13LlzXr0dBYiLM\nISGiE9V5prAwwN0dyh9+EB3Falj0RKIUFsJj7Fi47NuHgh07+BARRyGTQTdsGFSffSY6idWw6IkE\nkF+4AO/oaFg8PO6UfP36oiPRn+ifeQYuO3ZIZkkEFj2RPZlMcF2xAl59+qA0Lg7FH30EqNWiU9Ff\nWAICYOrQAaodO0RHsQpedUNkJ4ozZ+A+dSosKhUKduyAuXlz0ZGoCrqhQ+G6bh30Q4aIjlJrnNET\n2Zj855/h8cIL8Bw4ELqRI1G4fTtL3gkY+vSB4tQpyDIzRUepNRY9kS0YjXDZtQseo0bB66mnYHzk\nEdw+fhz60aN5t6uzUKthePppuH7+uegktcZDN0RW4lFSiA4ZJxCasgY+B5JhDgqCbvjwO0sZ8C5X\np6QbORIe48ah9OWXnfofaBY9Oa+iIshv3oTsxg3Uu5SFqFPpcNcVQ2U0wMVkgNJkAgBYAJhlchiV\nShgULtApVdC5qFDqokapyhUlKjeUqNQoVamhc1FBp3SFQamEUa6ERS4HLBbILBa4GnXw0JXAvbQY\n9Qty4X/7Bhre+g0hWZfQ/HoGGtzKxqngVih56u8o2LYN5tBQsX8+VGumdu1gcXeH8vvvYezaVXSc\n+8aiJ4cmu3ULijNnIL9wAYrz5yG/dAmKq1chz8wEDAaYH3gAlgcewENqT0QXWFCicoNOqYJB6QKT\nXFH2PgqzCUqzCUqjASqTAWq9Dm76UrgadFDrS+Fm+ON/66A2lEJpMkFlMsAsk0FusQAASpUqFKnd\nUezqjhwvDbJ96uM3H3/82DwC67o/i0v+QTAoVVjQpxn8HvQS9UdG1iSTQT9qFFTr1rHoqW6y9kJi\n8pISeJ05Be+TWnifTIXX2dNQ5t9GUejfUNi0GYqbhKCkb3uUNgpEacNAGL29AZkMAKA3mfFG0kWr\nZQEAWCyQW8wwy+Rl+6G6Rz9kCLznzYMsLw8WX1/Rce4Li57uW20XEpObTXjkyjl0vHAcHdJT8fCv\n53GxQTCONm6Jn4IicK79cGT6PXjn8MkfdAAuArh4A8D/HhDxZs8m952jUjIZzDJF9eNI0iz16sHY\nsydUX34J3QsviI5zX1j0ZFcepUXocu4IHk/7AZ3OH0O2jz+OhLbHJz2G4URwa5S4uomOSHQX3ahR\ncPvHP6AbN84pf7tj0ZPNuZcWo9uZ7xF98lu0u/QTTjRpjYMtu+CjPv+HbN8HRMcjqpaxa1fICguh\nSE2FKTxcdJx7xqInm5CbTeh0PgVPpuxG5/PHkNqkNXa37YHZw15HkRsvNSQnI5dDN3o0XNesQTGL\nnuq6B3Ovo/+RHeh7fDdu+NTHN+3/jvcHTMZtDx/R0YhqRT9iBLw7dIBszhynOynLoqdak5nNiDx3\nBIN/2IZWV88hMTwak8b9CxcDgkVHI7IaywMPwNCrF1QbN0I3frzoOPeERU/3TVFYgGGHNuOZw1tR\noPbEF5H98dpzb0Hncn/PSyVydLrYWHhMmgTdSy851Z2y1RZ9Wloa1q5dC5PJhKioKMTExNw1ZuPG\njdBqtXB1dcX48ePR6PcHKEyYMAFubm6Qy+VQKBSYN2+e9T8B2Z3s2jWoly1Dp0/XoSS4Ld4cOhM/\nBbV0yqsRiO6F6dFHYXF1hfLgQRi7dxcdp8aqLHqz2YyEhATMnj0bGo0Gs2bNQuvWrRH4p2daarVa\nXL58GfHx8bhw4QKWLl2KuXPnln3/rbfegifX+ZAEeUYG1P/5D1y++Qb6IUNw/Itv8MZJnehYRPYj\nk0E3dixcV692qqKv8neP9PR0BAQEwN/fH0qlEpGRkUhJSSk3JiUlBd26dQMAhIaGoqioCHl5eWXf\nt/x++zg5L/nZs/AYNw5evXvD3LAh8lNSUDJ/PkobPSQ6GpHd6QcPhvK775xq+eIqiz43Nxd+fn5l\nrzUaDXJzc6sc4+fnVzZGJpPhnXfewYwZM7Bnzx5r5iY7kJ89C4/YWHj17w9j69a4rdWidNYsWDQa\n0dGIxPHygn7oUKhXrBCdpMascjK2sln7nDlzUK9ePWRmZmLevHlo1KgRWrRoYY1dkg3JMzKgfv99\nuBw4gNIJE1D04YdcZpfoT3QvvgivqCiUTJ/uFD8bVc7oNRoNcnJyyl7n5ORA85fZXFVj6tWrBwAI\nDAxEx44dkZ5+/+uikO3JMjPhPnnynUM0Dz+M2ykp0E2e7BR/kYnsydy4MYxdusD1s89ER6mRKmf0\nISEhyMrKQnZ2NjQaDQ4fPowpU6aUGxMREYGkpCRERkbi/Pnz8PDwgK+vL3Q6HcxmM9zc3JCfn4/U\n1FQ8//zzNv0wdYW1V41U5t1C4xWLEbB1E64NGYGr276F0ccHKABQUFDpdnqT2WoZiJxN6fjx8Jg4\nEbqxYx3+Ussqi16hUCAuLg7x8fFll1cGBgYiOTkZABAdHY3w8HCcPXsW06ZNg1qtRlxcHAAgLy8P\n8fHxAAAvLy/07dsXYWFhNv44dUNtV438g6u+FMO++wojDn6JPWHdsXLScuR4+wHfl18ZsjI2WTGS\nyEmYHn0UFh8fuCQlwVDBZeeOpNpj9C1btsS//vWvcl+Ljo4u93rEiBEYMWJEua81aNAACxYssEJE\nsja52YS+x5Px4u5P8FNQC8RO+AhXHwisfkMi+h+ZDKXjx8N16VLnL3qSlkfPp2DyjmUodnXHzJH/\nxOnGLUVHInJahqeegtucOVAcPQpTx46i41SKRV9HhFy/iCk7luPB3Gv4qM//4UCrSN7JSlRbLi4o\nnTwZ6kWLULRxo+g0lWLRS5xfQS5eSlqDrmmHsTpqJDZ36geTgv+3E1mLfvhwuMXHQ3HmDEytWomO\nUyHHPlVM981VX4rYvevx34WxKFR7YPD0tfgicgBLnsja1GqUvvQS1IsWiU5SKf7US4zMbEbv1L2Y\nsGsVfgpqgTGTluJXvwdFxyKSNN3zz0MdHg75xYswN20qOs5dWPQSEp5xElO++RgmhQKvj/gHTgU/\nIjoSUd3g5QVdbCzUixah+MMPRae5C4teAoJuXMWkxOVofi0Di2PGITnsCZ5oJbIzXVwcvDt0gDwj\nA+aQENFxyuExeifmU3Qb075ejFVLJuNU41Z45tVPkNy2B0ueSACLry90L74It/nzRUe5C2f0Tkhe\nWopR+/+L5/Z/jqS2PfDMq2uQ5+lcz7AkkqLSF1+ET4cOkKelwdzSce5RYdE7E7MZqk2b0PHtOTBr\nGmPc+A9x2Z9rwhM5DC8vlE6eDLf33kPR+vWi05Rh0dfQzzeKcLPIIGz/9Y98h4f/8y9A7YKz8xdh\n+m9cE95RKeTAyWuVLwZnL1x0TgxdbCzUS5dCkZICU0SE6DgAWPQ1tudCLr5Ou2n3/YZey8CkxBV4\nMOca5seMRZu4EXjQRw1YYVEzso3bpSa8veeS6BhcdE4UtRolr70G99mzUZCY6BDnzHgy1kEF3PoN\nb/93Hj5a+RoOteiEZ6etwt423RziLw0RVU0/fDhQXAyXLVtERwHAGb3D8Sm6jef3bUTf40n4skt/\nDJzxKYrV7qJjEdG9UChQ8t57cI+Lu7OypZub0Dic0TsIV30pxuzbiC/jn4fKqMfQaauxvNcYljyR\nkzJGRsLUrh3US5aIjsIZvWgKkxFPHduJcXvW4WRwa4wd/yHXhieSiJJ33oFXjx7QDRsGS6NGwnKw\n6EWxWBD100HE7VqFbF9/vDp6Ds4+9DfRqYjIisyNG0M3bhzcZ85E0bp1wnKw6AVon56KSTtXQGEy\nYUH/yTgS2p4nWYkkqvTll+HdrRtctm+HoV8/IRlY9HbU/NcLmLhzFQJzfkXC35/HnjbdYXHwhwoT\nUS2p1ShetAge48Yh//HHYfHxsXsEFr0dPJh7HXG71qBDuhareo7Elo59YVS6iI5FRHZi7NwZhl69\n4PbOOyheuNDu+2fR25BP0W3E7t2APtrd+KLLAMwbOJVX0RDVUSVvvQXvLl2gfPJJGJ94wq77ZtHb\ngKtBh6HffYWRB75Aclh3PDttNXK9uGQBUV1m8fFB0eLF8Jg4EfmHDsGisV8nsOitSG42oY82GS/u\nXoszD/0NYyd8iCsPcNExIrrD+MQT0A8YAPepU1G0dq3dLsJg0VtJx/MpmLJjOUpUarw+4h/4qbFj\nPiSYiMQqmT0bXj17QrVuHfTPPWeXfbLoaykk6xIm71iGwJvXsLjPOHz7SFdeKklElXN1RdHy5XCb\nOxf6UaPs0hcs+vvkV5CLF5M+Qbcz32NN1HBsGv0Ur6Qhohoxt2hh1/XqWfT3yNWgw7BDmzHi4JfY\n0b4XBk//BAXuXqJjERFVikVfUxYLeqXuw4RdK3GuUXOMmbQEv/o9KDoVEVG1WPQ1oPjpJ4x5dRLy\nC0vx1rMzkdq0jehIREQ1xqKvCbMZ2j7P4N0GnbhkARE5HRZ9DZjCwnCqSAOLgEcJEhHVFqenREQS\nx6InIpI4Fj0RkcSx6ImIJI5FT0QkcSx6IiKJ4+WVRFSnKOTAyWsFomPA31OFht6udtkXi56I6pTb\npSa8veeS6BhY0KeZ3Yqeh26IiCSORU9EJHEseiIiiWPRExFJHIueiEjiWPRERBLHoicikrhqr6NP\nS0vD2rVrYTKZEBUVhZiYmLvGbNy4EVqtFq6urhg/fjwaNWpU422JiMi2qpzRm81mJCQkYNq0aZg/\nfz727duHzMzMcmO0Wi0uX76M+Ph4jBkzBkuXLq3xtkREZHtVFn16ejoCAgLg7+8PpVKJyMhIpKSk\nlBuTkpKCbt26AQBCQ0NRVFSEvLy8Gm1LRES2V2XR5+bmws/Pr+y1RqNBbm5ulWP8/PyQm5tbo22J\niMj2rLLWjcViscbbOLTHgn0R4GWfdSmq8rcHPFCgM4qOQUROpMqi12g0yMnJKXudk5MDjUZTozFG\no7Habf/PTcuLAAAGYklEQVTM19cXWq32nj+APTURHQBA3uU7/50fLjYHACD3omPkAJilIo6SA2CW\nCpiyLkCbVfv38fX1rXZMlUUfEhKCrKwsZGdnQ6PR4PDhw5gyZUq5MREREUhKSkJkZCTOnz8PDw8P\n+Pr6wsvLq9pt/6x9+/Y1/FhERHQvZJZqjrukpaXhk08+KbtEsk+fPkhOTgYAREdHAwA2bNgArVYL\ntVqNuLg4BAYGVrotERHZV7VFT0REzo13xhIRSRyLnohI4hzqUYKZmZlYv349cnJy4Ofnh5EjR5Yd\n73c03377LZKSkmAwGNCuXTuMHDlSdKQKbd++HevXr8eqVavg6ekpOs5d1q1bB61WC5VKhRYtWmDI\nkCFwd3cXHauMMyzjcfPmTSxZsgS3b9+Gt7c3unfvju7du4uOVSmz2YyZM2dCo9Fg5syZouNUqLS0\nFCtXrsSVK1dgMBgQFxeH5s2bi45Vzp49e7B//34YDAa0aNECY8aMqXSsQxX9pk2b8Pjjj6NLly74\n7rvvsGnTJkydOlV0rLucPn0a3333Hd59910olUrk5+eLjlShmzdv4tSpU6hfv77oKJUKCwvDiBEj\nAADLly/Hli1byl6L9scyHrNnz4ZGo8GsWbPQunVrh5t8KJVKjB49GsHBwcjPz8e0adPQrFkzh8v5\nh8TERAQGBqKkpER0lEqtXLkSLVu2xMSJE2EymaDT6URHKqewsBBbtmzBwoULoVKp8P777+PEiRNo\n27ZtheMd6tCNu7s7CgsLYTabUVhY6JAzUADYvXs3BgwYAKXyzr+T3t7eghNV7NNPP3XY3zT+0KZN\nG8jlcsjlcrRt27bcvReiOcsyHr6+vggODgZw5+9iSEgIbt26JTZUJXJycpCamooePXo47I2WxcXF\nOHfuHHr06AEAUCgUDvVbJgCoVCoAd7Lq9XrodLoq+9KhZvQjR47E66+/jg0bNkCj0eC9994THalC\nWVlZSEtLw7p166BWqzF69Gg0bdpUdKxyjh07Bo1Gg8aNG4uOUmN79+4t++FyBBUt45Geni4wUfWy\nsrKQmZmJ0NBQ0VEqtHbtWowcOdKhZ/PZ2dnw9vbGkiVLcPHiRYSGhiI2NrasXB2BSqXCuHHjMGHC\nBLi4uCAmJgbNmjWrdLzdi37OnDnIy8u76+vDhg3DgQMH0Lt3b0RHRyMpKQkJCQl45ZVX7B0RQNU5\nTSYTsrOzMWfOHJw6dQrr1q3Dm2++6VAZt27dijfeeKPsayJnT1XljIiIAAB89dVXUKvV6Ny5s73j\nSUZpaSkWLVqE0aNHQ61Wi45zl+PHj8Pb2xtNmjTBmTNnRMeplMlkQkZGBgYOHIgXXngBy5cvxw8/\n/FC2eKMjyM/Px8qVK/HBBx/Aw8MD//73v6HVahEeXvEtv3Yv+tmzZ1f6vWXLlmHSpElQKBTo0aMH\ntmzZYsdk5VWVc/fu3ejSpQtUKhUiIiKwYsUK6PV6u/+LX1nGK1euIDs7G9OnTwdwZ2Y6c+ZMvPfe\ne/Dx8bFnRABV/1kCwP79+5GamlrtOHuryRIgjsJoNGLhwoXo2rUrOnToIDpOhX7++WccP34cqamp\nMBgMKCkpweLFizFx4kTR0crx8/ODp6dn2SQkMjISBw4ccKiiT09PR2hoKAICAgAAnTt3RlpaWqVF\n71DH6Fu1alV2DPTYsWNo06aN4EQV69ChA1JTU2GxWHDhwgU0aNDAoX6tCwoKwooVK7BkyRIsWbIE\nGo0G77//vpCSr86JEyewbds2zJgxw6H+DIHyS4AYjUYcPny47IffkVgsFnz88ccIDAxE3759Rcep\n1PDhw5GQkIAlS5Zg6tSpaNWqlcOVPHDnnEdAQAAuXLgAs9kMrVbrcF308MMPIyMjA4WFhTAYDEhN\nTUVYWFil4x3qGP2gQYOwefNmbNmyBQ899BAGDRokOlKFoqKisHLlSkydOhVKpRIvvPCC6EhVkslk\noiNUavXq1TAajZgzZw4AoHnz5hg3bpzgVHcoFArExcUhPj6+7PJKR7yS5eeff8ahQ4cQFBSEGTNm\nALhTqpVdgeEoHPnv5YQJE7BkyRLk5+cjKCjIYa4E+4O7uzsGDRqEBQsWQK/XIywsDK1atap0PJdA\nICKSOIc6dENERNbHoicikjgWPRGRxLHoiYgkjkVPRCRxLHoiIolj0RMRSRyLnohI4v4fsQe9Tjcl\nzH0AAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114129d50>"
       ]
      }
     ],
     "prompt_number": 33
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Exercise: Cervical dystonia analysis\n",
      "\n",
      "Recall the cervical dystonia database, which is a clinical trial of botulinum toxin type B (BotB) for patients with cervical dystonia from nine U.S. sites. The response variable is measurements on the Toronto Western Spasmodic Torticollis Rating Scale (TWSTRS), measuring severity, pain, and disability of cervical dystonia (high scores mean more impairment). One way to check the efficacy of the treatment is to compare the distribution of TWSTRS for control and treatment patients at the end of the study.\n",
      "\n",
      "Use the method of moments or MLE to calculate the mean and variance of TWSTRS at week 16 for one of the treatments and the control group. Assume that the distribution of the `twstrs` variable is normal:\n",
      "\n",
      "$$f(x \\mid \\mu, \\sigma^2) = \\sqrt{\\frac{1}{2\\pi\\sigma^2}} \\exp\\left\\{ -\\frac{1}{2} \\frac{(x-\\mu)^2}{\\sigma^2} \\right\\}$$"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "cdystonia = pd.read_csv(\"data/cdystonia.csv\")\n",
      "cdystonia[cdystonia.obs==6].hist(column='twstrs', by=cdystonia.treat, bins=8)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 34,
       "text": [
        "array([[<matplotlib.axes.AxesSubplot object at 0x1140d01d0>,\n",
        "        <matplotlib.axes.AxesSubplot object at 0x11409e810>],\n",
        "       [<matplotlib.axes.AxesSubplot object at 0x11427dc90>,\n",
        "        <matplotlib.axes.AxesSubplot object at 0x114299f50>]], dtype=object)"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAmAAAAE8CAYAAABnzw3BAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtUlNe5P/DvDMidcRwsEp1SETGC9RJFkWIavGAOappk\neZI0xFNJYtsg2hhNo7mqSQxEtCHV0RxjT0PTZDXp6dGTi9FoDalRUwOM/lIHNaNGpYhEUAaQYW77\n94d1TojADJd3zzB+P2u5ljOzffezZ5jHh/fd794qIYQAEREREUmj9nUARERERDcaFmBEREREkrEA\nIyIiIpKMBRgRERGRZCzAiIiIiCRjAUZEREQkGQswIiIiIslYgAWgv/3tb7jzzjsxdOhQqNVqrFmz\n5ro2lZWVyMrKgk6nQ0pKCgoLC69rU11djbvvvhuxsbFITEzE448/DqfT2aaNxWLB/Pnzodfrodfr\n8fDDD6O5ublNG5vNhiVLliAxMRGxsbH493//d9TW1rpf//rrr6FWq3HgwIHrYli1ahWSkpK6+1YQ\nEbVr1apVUKvV1/05deqUu42sPFlaWgq1Wo3q6urrjp+bm4usrKxeHDn5CxZgAai5uRk//OEPsXbt\nWsTFxUGlUrV5/ZtvvkF6ejri4+Oxf/9+FBQUoKioCC+++KK7jc1mQ0ZGBhwOB/bs2YOtW7fiL3/5\nC375y1+2OVZ2djaOHTuGbdu24S9/+QsOHz6MO++8s02bBx98EB988AH+67/+Cx9//DGam5vx4x//\nGC6Xy6vxfDd+IqLekJCQgJqamjZ/hg4dCkB+nuyISqViDgxUggLa0KFDxZo1a9o898ILL4jvf//7\nbZ4zGAwiJiZGWK1WIYQQb775pggPDxcWi8Xd5sMPPxQhISGiurpaCCHEvn37hEqlEidOnHC3OXr0\nqFCpVOLQoUNCCCG+/vprERwcLHbv3u1uc+nSJREaGireffddIYQQp0+fFiqVSuzfv/+6+FeuXCmG\nDx/ek7eAiOg6nnKLzDz5ySefCJVKJf75z39eF8f8+fPFjBkzuj9Q8ls8A3YD2r9/P2bOnNnmudtv\nvx319fWorKx0t/nRj36E6Ohod5usrCw4nU78/e9/d7cZNmxYm0uEKSkp0Ov12L9/PwDg888/h1qt\nxvTp091ttFotJk2ahM8++0yxMRIReVJVVYXvf//7+P73v49Zs2bh4MGD7tdk5km6MbEAuwFVV1cj\nLi6uzXPXHldVVQEA/vnPf17Xpl+/ftDpdG3aDBo06Lrjx8XFtWkzcODA606hf7sNEZFsaWlpeOON\nN/Dhhx+ioKAAAPDjH/8Yn3/+OQC5eZJuTMG+DoD8k9JzDoQQnNdARD6TnZ3t/vuYMWMwb948TJ06\nFYWFhdi+fbtXx5CVw5grAxPPgN2AhgwZgvPnz7d57sKFCwAAvV7fYRu73Y76+vo2bWpqaq47/oUL\nF9q0uXjxIoQQHbbp378/AKChoeG6Y12+fBlarbbLYyQi6qq0tDT3XZAy86SnHHjtdQosLMBuQBkZ\nGdi9e3ebomjnzp2IiYlBcnKyu83BgwfR2NjobrN7926o1WqkpaW525w+fRpms9ndxmQy4dy5c5gy\nZQqAqwnN6XTir3/9q7vN5cuXcejQIXebAQMGIDY21j1n4tsOHTrkjomISEkVFRUYNmwYALl5Mikp\nCWq1+roc6HA4YDQamQMDlW/vASAlNDU1CaPRKIxGo7jpppvEokWLhNFoFF999ZUQQohvvvlGaLVa\n8fDDD4ujR4+K//3f/xUxMTHixRdfdB/DZrOJhIQEMWfOHHHkyBGxd+9eMXToULFgwYI2fWVkZIi0\ntDRx6NAh8fnnn4sJEyZcd8fOAw88IIYPHy4+/fRTYTQaRXZ2thg5cqRwuVzuNuvWrRPR0dFiy5Yt\n4vjx4+LIkSNi6dKlol+/fuLIkSMKvltEdCN67LHHxN69e8XJkyfF9u3bxX333SeCg4PF3/72NyGE\n/Dy5aNEiERcXJ/70pz8Js9ksysrKxAMPPCC0Wq37jkoKLCzAAtC1W5pVKpVQq9Xuv0+dOtXdprKy\nUmRlZYkBAwaIkSNHisLCwuuOU11dLe6++27xve99TyQkJIjHH39cOByONm0sFouYP3++GDx4sBgy\nZIh46KGHRHNzc5s2NptNLFmyRCQkJIjvfe97Yu7cuaK2trZNG5fLJV5//XUxfvx4odFoRGxsrMjK\nymp3aQoiop66//77hV6vF6Ghoe58U1pa2qaN7Dz58ssvi9GjR4vIyEgxePBgcdddd4mjR4/2/uDJ\nL6iE+M7knO/Ys2cPSktLYbfbkZycjNzcXEnn5oiI/NPOnTvxwQcfICQkBLNnz26zzAoRkTc6nQPW\n1NSEbdu24ZlnnkFBQQHOnz+Pw4cPy4qNiMjvXLlyBR999BEKCwvx0ksvYc+ePe1OsiYi6kynBVhI\nSAiAqwnHZrOhtbUVUVFRUgIjIvJHx48fR0JCAqKiohAWFoZRo0bh0KFDvg6LiPoYjwXYggULkJ+f\nj1/84he4+eabMXz4cFmxERH5neTkZJw8eRK1tbW4dOkSjEYj6urqfB0WEfUxnS7EarFYsHXrVrzy\nyiuIjIzEb37zG1RUVGD8+PGy4iMi8ithYWGYP38+fve73+HKlStITk7mQplE1GWdFmBmsxlJSUnu\nrRbS09NhMpnaLcA+//xzNDc3KxMlEfkNrVaLCRMm+DoMn0pNTUVqaioA4O2338bAgQPbbce8SBT4\nupsTOy3ARo4cid///vdoampCaGgojEYjZs2a1W7b5uZmnhkjRR2pbsSvd5g9N+wFRbOGY+zgaM8N\nb0AVFRW+DsHnGhoa0L9/f1y8eBFffPEF1qxZ02475kXqKaXzHnNdz3U3J3ZagEVERGDu3LkoKiqC\nzWbD2LFjMWrUqG51REQUKH7zm9+gubkZYWFhyM/PR0REhK9DIqI+xuNm3JmZmcjMzJQQChFR37B6\n9Wpfh0BEfRz3giQiIiKSjAUYERERkWQswIiIiIgk8zgHjIiI2uIeuUTUUzwDRkTUBdwjl4h6g8cz\nYNXV1SguLnY/vnDhAu67774O1wMjIgpk394jFwD3yCWibvFYgA0ePBhr164FALhcLjzyyCOYNGmS\n4oEREfmjb++R269fP2RnZ3OPXCLqsi5dgvzyyy8xaNCgDrfdICIKdN/eI9dgMODEiRPcHYCIuqxL\nBdj+/fsxZcoUpWIhIvJ7394jNzo62r1HLhFRV3h9F6TD4UB5eTnmzZunZDzUC85bWlHbZJPSV1RI\nEJpsTil92ZwuKf0QdaYre+QSEXXE6wLMaDRi2LBh0Gg0SsZDvaC2ySZt0+qVMxKwes9paX0R+Rr3\nyCWi3uB1AbZ//35kZGQoGQsRUZ/APXKJqKe8mgNmtVrx5ZdfIi0tTel4iIiIiAKeV2fAwsLC8Lvf\n/U7pWIiIiIhuCFwJn4iIiEgy7gVJRNQF3B2EiHoDCzAioi7g7iBE1Bt4CZKIqJu4OwgRdZfHM2BW\nqxVbt27F2bNnYbfbkZeXhxEjRsiIjYjIr3F3ECLqLo8F2NatW5GSkoJFixbB6XSitbVVRlxERH6N\nu4MQUU90WoBduXIFx44dw6JFiwAAQUFBiIiIkBIYEZE/4+4gJGPbN27BFrg6LcBqa2uh0WhgMBhw\n6tQpJCUl4aGHHkJISIis+IiI/BJ3ByEZ275xC7bA1ekkfKfTiZMnTyItLQ0FBQVwOBw4ePCgrNiI\niPwSdwchop7qtACLiYlBVFQUUlNTERISgoyMDBiNRlmxERH5pWu7g4SHh/s6FCLqozotwLRaLeLi\n4vDVV1/B5XKhoqICY8aMkRUbERERUUDyeBdkfn4+DAYDLBYL4uPj8cADD8iIi4iIiChgeSzABg8e\njDVr1siIhYiIiOiGwK2IiIi6iAtUE1FPsQAjIuoiLlBNRD3FvSCJiLrg2gLV06ZNA8AFqomoe3gG\njIioC7hANRH1Bp4BIyLqAi5QTUS9waszYPn5+QgPD4darUZQUBAKCgqUjouIyC99e4FqAMjIyMCn\nn36K2267zceR9S1K76MYFRKEJptTseMD3KeResbrS5CrVq1CVFSUkrEQEfm9by9QnZiYyAWqu0np\nfRRXzkjA6j2nFTv+tT6IusvrAkwIoWQcRER9BheoJqKe8qoAU6lUeP7556FSqTBz5kzMmDFD6biI\niPwWF6gmop7yqgB74YUXMGDAAFRVVaGgoABDhgxBcnKy0rERERERBSSv7oIcMGAAAECv12PSpEkw\nm5W7bk9EREQU6DwWYK2trWhpaQEAWCwWGI1GxMfHKx4YERERUaDyeAmyoaEBRUVFAIDo6GjMnj0b\nY8eOVTwwIiJ/xaV5iKinPBZgsbGx7gKMiIiu4tI8RNQTXAmfiKgbuDQPEfUE94IkIuoiLs1DRD3F\nAoyIqIu4NA8R9RQvQRIRdRGX5iGinvKqAHO5XHjiiSdQWFiodDxERH6NS/MQUW/w6hLkjh07oNfr\n3UmHiOhGxaV5iKg3eCzA6urqYDQacffdd+ODDz6QERMRkd/i0jxE1Bs8XoIsKSnBvHnzoFZzuhgR\nERFRb+i0qiovL4dGo0FCQgLXvCEiIiLqJZ1egjx+/DjKy8thNBpht9vR0tKCjRs3YtGiRbLiI/KJ\nIDVwpLpRSl+xUSG4SRMqpS8iIvIPnRZgOTk5yMnJAQCYTCa89957LL7ohtBgdWL1ntNS+iqaNZwF\nWB/kcrmwYsUK6HQ6rFixwtfhEFEf06WJXSqVSqk4iIj6lGt3hzMvElF3eF2ApaSkYPny5UrGQkTU\nJ1y7O3zatGmcH0tE3cJbG4mIuoh3hxNRTzF7EBF1Ae8OJ6LewM24iYi6gHeHE1FvYAFGRNQFvDuc\niHoDL0ESEfUA74Ikou7weAbMZrNh1apVsNvtCAkJQXp6OubMmSMjNiIiv5aSkoKUlBRfh0FEfZDH\nAiwkJAQrV65EaGgo7HY7VqxYgdTUVMTFxcmIj4iIiCjgeHUJMjT06irdVqsVTqcTwcGcOkZERETU\nXV5VUi6XC8uXL8e5c+eQm5uLgQMHKh0XERERUcDyqgBTq9UoKipCbW0tCgoKcPPNNyMhIaHXgzlV\n34Kv61t6/bjtGRUXiUFRcvbfO29pRW2TTUpfAGBzuqT1RXSj4bxYIuoNXbqWGBsbi1tuuQUmk0mR\nAqy8yoLXD1X3+nHb8/rcZCn9AEBtkw2/3mGW1t/KGb3/2RDRVZwXS0S9weMcMIvFgubmZgBAY2Mj\nDh8+jPj4eMUDIyLyV5wXS0Q95TFrXL58GQaDAS6XC1qtFnPmzMHo0aNlxEZE5Jc4L5aIespjARYf\nH4+XX35ZRixERH2CrHmxRBS4eN6ciKiblJ4XS6S0IDVwpLpR0T5io0Jwk0bOTW99CQswIqIusFgs\nCAoKQmRkpHte7IMPPujrsIi6pcHqxOo9pxXto2jWcBZg7WABRkTUBZwXS0S9gQUYEVEXcF4sEfUG\njwXYxYsXYTAY0NDQAI1Gg8zMTGRmZkoIjYiIiCgweSzAgoODMX/+fAwdOhQWiwXLli3D8OHDodfr\nZcRHREREFHA8LsSq1WoxdOhQAIBGo0FiYiIuXbqkdFxEREREAatLc8BqampQVVWFpKQkpeIhIvJr\nnJZBRL3B6wLMarWiuLgY8+fPR1hYmJIxERH5LU7LIKLe4FUB5nA4sH79etx6662YOHGi0jFJ0epw\nKr743DU2p0tKP9Q3yVgI8RouiNhzWq0WWq0WQNtpGSzAiKgrPBZgQgi89tpr0Ov1mD17toyYpLjU\n4sCzH5+S0tfKGVwhmzomYyHEa7ggYu/itAwi6i6PBdjx48exb98+xMfH44knngAA5OTkYNy4cYoH\nR0Tkr3w1LaPR6oBV4bPq2rBg9AvyeI8WEfWAxwJs5MiReOedd2TEQkTUJ/hyWsaZy1Y8veukYscf\nFBWColnD0T+cBRiRkrgSPhFRF/h6WoYA0GJX7gyYkscmov/DAoyIqAs4LYOIegMLMCKiLuC0DCLq\nDbzIT0RERCQZCzAiIiIiyTxegty0aROMRiM0Gg3Wr18vIyYiIiKigObxDNjUqVPx1FNPyYiFiKhP\n2LRpE37+859j2bJlvg6FiPoojwVYcnIyIiMjZcRCRNQn8BdTIuopzgEjIuoi/mJKRD3FAoyIiIhI\nMhZgRERERJJxIVYiImrjstWOry9ZFe3DpvCG4uQ/gtTAkepGxY4fGxWCmzShih1fKR4LsOLiYlRW\nVqKxsRF5eXm49957MXXqVBmxERGRD1xsduDJncpt+A0AK2ckKHp88h8NVidW7zmt2PGLZg0PzAJs\nyZIlMuIgIuoz+IspEfUUL0ESEXURfzElop7iJHwiIiIiyViAEREREUnGAoyIiIhIMo9zwEwmE0pK\nSuB0OjF9+nRkZ2fLiIuIyG8xLxJRT3V6BszlcmHz5s1YtmwZCgsLsXfvXlRVVcmKjYjI7zAvElFv\n6LQAM5vNiIuLQ2xsLIKDg5GRkYGysjJZsRER+R3mRSLqDZ0WYPX19YiJiXE/1ul0qK+vVzwoIiJ/\nxbxIRL3Br9YBG3NTFH6ZNkRKX2qVlG6IiHpV/7BgRfNkZIgaKuZHIsWphBCioxdPnDiBP//5z3j6\n6acBANu2bYNKpcJdd911Xdvy8nJcvnxZuUiJyC9otVpMmDDB12H4DPMiEX1bd3Nip2fAEhMTUVNT\ng9raWuh0Ohw4cACPPvpou21v5IRMRDcO5kUi6g2dngEDrt5u/cYbb7hvt541a5as2IiI/BLzIhH1\nlMcCjIiIiIh6F1fCJyIiIpKMBRgRERGRZN1ahuLixYswGAxoaGiARqNBZmYmMjMz8e6772Lv3r3Q\naDQAgJycHIwbN67HQdpsNqxatQp2ux0hISFIT0/HnDlz0NLSgg0bNqC2thaDBg3C4sWLERYWplh/\nSo0PuLq69ooVK6DT6bBixQrFxtZRf0qOLT8/H+Hh4VCr1QgKCkJBQYGi42uvPyXHZ7VasXXrVpw9\nexZ2ux0LFy6EXq9XbHzf7S8vLw+HDx/u9fFVV1ejuLjY/fjChQu47777MHXqVEV/NvuqTZs2wWg0\nQqPRYP369QCg+Pe4Ix3laF/FIzuHe0t23u2M7DzZGdk5rTP+mIf27NmD0tJS2O12JCcnIzc3t3uf\nleiGS5cuidOnTwshhGhoaBALFiwQ586dE++++654//33u3NIj6xWqxBCCJvNJpYuXSqqq6vFm2++\nKbZv3y6EEGLbtm3ij3/8o6L9KTm+999/X7z66quisLBQCCEUHVt7/Sk5toULF4rGxsY2zyk5vvb6\nU3J8GzZsEH/961+FEEI4HA7R3Nys6Pja60/J8QkhhNPpFD//+c/FN998o/jPZl9lMpnEqVOnxNKl\nS93P+eq96ihH+/Kzk53DvSE773ZGdp7sjOyc5i1/yEONjY1i4cKFoqWlRTidTvHSSy8Jo9HYrXi6\ndQlSq9Vi6NChAACNRoPExET3StBCoTn9oaGhAK5W5i6XC/369UNZWRluu+02AEBmZia++OILRfpz\nOp3o168fAGXGV1dXB6PRiGnTprmPr+TY2utPCKHYZ3ft+N+m5Pja66+j53rqypUrOHbsGKZNmwYA\nCAoKQkREhGLj66g/QLnvHgB8+eWXiIuLw8CBAxX/7Pqq5ORkREZGtnnOV+9VRznal5+d7Bzuiey8\n6w3ZebI9snNaV/hDHgoJCQFw9X2y2WxobW1FZGRkt+Lp8Ur4NTU1qKqqwogRI3D8+HHs3LkTe/fu\nxYgRI/Czn/3suoTUXS6XC8uXL8e5c+eQm5uLgQMHoqGhAVqtFgDQv39/NDQ09EpfHfUHQJHxlZSU\nYN68eWhpaXE/p+TY2utPpVIp9tmpVCo8//zzUKlUmDlzJmbMmKHo+NrrD1Dms6utrYVGo4HBYMCp\nU6eQlJSEBx98ULHxtdffQw89BECZ8V2zf/9+ZGRkAFD2ZzPQ+MN79e0c7ct4ZOdwT2TnXU9k58mO\nyM5pXeEPeSgkJAQLFixAfn4++vXrh+zsbCQlJXUrnh5NwrdarSguLsb8+fMRFhaGmTNnYuPGjViz\nZg3UajX+8Ic/9OTwbajVahQVFeG3v/0tdu3ahdOnT7d5XdXLe2e0158S4ysvL4dGo0FCQkKHZzB6\nc2wd9afkZ/fCCy+gqKgIv/rVr7Bt2zZUVla2eb23P7v2+lNqfE6nEydPnkRaWhoKCgrgcDhw8ODB\nNm16c3wd9afk5+dwOFBeXo709PTrXuvtzy6Q+eK9+m6O9mU8snN4Z2TnXW/IzpMdkZ3TvOUvechi\nsWDr1q145ZVXYDAYcOLECZSXl3crnm4XYA6HA+vXr8ett96KiRMnArha9alUKkREROD222+H2Wzu\n7uE7FBsbi1tuuQUmkwn9+/d3b/Nx6dIl9O/fX/H+ent8x48fR3l5OfLz8/Hqq6/i6NGj2LBhg2Jj\na6+/jRs3KvrZDRgwAACg1+sxadIkmM1mRT+7jvpTYnwxMTGIiopCamoqQkJCkJGRgcOHD0Or1Soy\nvvb6MxqNin5+RqMRw4YNc0/wl/G9CxS+fK86ytG+/uxk5/D2yM673pCdJzsiO6d5y1/ykNlsRlJS\nEuLi4hAdHY309HRUVlZ2K55uFWBCCLz22mvQ6/WYPXu2+/lLly4BuFpBf/bZZ4iPj+/O4a9jsVjQ\n3NwMAGhsbMThw4cRHx+P1NRUlJaWAgA+/fRTd5JRqr9rb25vji8nJwebN2+GwWDAkiVLMGrUKCxe\nvFixsbXX36JFixT77FpbW92n+C0WC4xGo6KfXUf9KfHZAVfn2sTFxeGrr76Cy+VCRUUFRo8ejQkT\nJigyvvb6GzNmjGLjA9qe9geg2GcXiHz1XnWUo30Vj+wc7onsvOuJ7DzZGdk5zVv+kodGjhyJkydP\noqmpCXa7HUajEWPHju1WPN1aCf/YsWNYuXIl4uPj3afa7r//fuzfvx9ff/01goODkZycjDvvvNN9\nTbQnzp49C4PBAJfLBa1Wi/T0dEybNk2xW3Q76m/jxo2KjO8ak8mE999/H8uXL5dy+/HRo0fxwQcf\nYPny5diwYQPOnDnT62Orra1FUVERALh/W8jKylJsfB31p+RnV11dDYPBAIvFgvj4eCxevBhCCMU+\nv/b627p1qyLjs1qtyM/Px8aNGxEeHg7Ad0sr+Lvi4mJUVlaisbER/fv3x7333ovJkyf75L1qL0fn\n5OTg5ptv9kk8snN4V8jOu+2RnSc9kZ3TPPG3PFRaWopPPvkENpsNY8eOxb333ovW1tYux8OtiIiI\niIgk40r4RERERJKxACMiIiKSjAUYERERkWQswIiIiIgkYwFGREREJBkLMCIiIiLJWIARERERScYC\njIiIiEgyFmBEREREkrEAIyIiIpKMBRgRERGRZCzAiIiIiCRjAUZEREQkGQswIiIiIslYgBERERFJ\nxgKMiIiISDIWYERERESSsQAjIiIikowFGBEREZFkLMCIiIiIJGMBRkRERCQZCzAiIiIiyViAERER\nEUnGAuwGpFar8fbbb0vtc9WqVUhKSpLaJxERkb9iARaAcnNzoVaroVar0a9fPwwdOhR5eXmor6/3\ndWhEREQEFmAB68c//jFqampgNpvxxBNP4E9/+hN+9rOf+TosIiIiAguwgNWvXz/ExsbiBz/4ARYu\nXIj7778fu3btgtVqva7tq6++iltuuQXR0dG46aabcP/996OmpqZNm+rqavzHf/wHhg4disjISIwd\nOxYffvih+/Xjx4/jJz/5CeLi4hAbG4u5c+fi7Nmz1/W1Y8cOTJgwATqdDnfddRdqa2vbvL59+3ak\npqYiOjoaycnJWLt2LYQQvfSuEBER+QcWYAFKpVK1eRwVFQWXywWHw9Fu2/Xr1+P//b//hw0bNuDY\nsWP46U9/6n69oaEBkyZNwoULF/D222/j6NGjeOmllxAUFAQAOHv2LCZMmIAf/OAH+J//+R+8/fbb\naG5uRlZWFlpbW93HOX/+PIqKivD666/j448/xvnz5zFr1iz36x9++CHmzp2Le+65B0ajEatXr0Zh\nYSFWrlzZ228PERGRbwkKOPPnzxczZswQQghht9vFrl27RFxcnEhPTxdCCKFSqcRbb73V4b/fsWOH\nUKlUorq6WgghxAsvvCBuuukmceXKlXbb/+IXvxAZGRltnjtz5owIDg4W27dvF0IIsXLlSqFSqURp\naam7ze7du4VKpRJ79+4VQggxZcoUMXny5DbHWbp0qQgPDxd2u70rbwEREZFf4xmwAFVaWoro6GhE\nR0cjOzsbY8aMwVtvvdVh29tvvx3x8fHQaDS45557AABnzpwBABw+fBg/+tGPEB4e3u6/NxqNKCsr\nc/cXHR2NUaNGQQgBs9nsbhceHo4f/ehH7sdTpkxBeHg4jh49CgAwmUzIzs5uc+x/+7d/g9VqxcmT\nJ7v/ZhAREfmZYF8HQMqYPHkySkpKEBwcjMGDByM4uP2P+uzZs5g1axZ+8pOf4J133sHAgQNx4sQJ\n3HHHHbDZbACuXqJ0uVwd9uVyufCzn/0MK1asuO41nU7XOwMiIiIKIDwDFqDCwsIwbNgwxMfHd1h8\nAcAXX3wBq9WK3/zmN0hPT0dSUhIqKiratBk3bhwOHDiAK1eutHuM8ePH48iRIxg2bNh1f7Rarbtd\nS0sLDhw44H782WefoaWlBSkpKQCAUaNGYceOHW2O/dFHHyEiIgKJiYldfg+IiIj8FQuwG1xSUhJU\nKhWKiopQWVmJ7du345133mnTZvHixVCr1bjzzjtx4MABnD59Gh988AF27twJAHjuuedw4sQJzJs3\nD1988QVOnz6NTz75BEuWLMHp06fdx4mIiMDq1atRXl6OsrIyPPPMM7jlllswbdo0AMCTTz6JL774\nAi+//DJOnDiBd999F2+88QaWLVvWaRFJRETU17AAC0Aqleq6uyA7MmbMGJSUlKCiogJTpkzBli1b\n8Prrr7f59xqNBocOHcL3vvc93HffffjhD3+IZ5991v26Xq9HRUUFHA4H5s6di1GjRuEXv/gFrFYr\nBgwY4I5ZFbFLAAAZu0lEQVRp8ODBWLp0KR5++GFkZWVh0KBBbc54ZWdn4y9/+Qv+/Oc/Y8KECVi5\nciVWrFiBVatW9c4bQ0RE5CdUQnS+yNKePXtQWloKu92O5ORk5ObmSgqNiEiuTZs2wWg0QqPRYP36\n9e22efvtt1FRUYHQ0FAsXLgQQ4YMkRwlEQWCTs+ANTU1Ydu2bXjmmWdQUFCA8+fP4/Dhw7JiIyKS\naurUqXjqqac6fL2iogJnzpzBunXrkJubi02bNkmMjogCSacFWEhICADgypUrsNlsaG1tRVRUlJTA\niIhkS05ORmRkZIevl5WV4bbbbgNwdf5kc3MzLl++LCs8Igognc5sDgkJwYIFC5Cfn49+/fohOzsb\nw4cPlxUbEZFfqa+vR0xMjPtxTEwM6uvr29ztS0TkjU7PgFksFmzduhWvvPIKDAYDTpw4cd0SBURE\nNxIP02aJiLzS6Rkws9mMpKQkxMXFAQDS09NhMpkwfvz469p+/vnnaG5uViZKIvIbWq0WEyZM8HUY\nPqHT6VBXV+d+XFdX1+liw8yLRIGvuzmx0wJs5MiR+P3vf4+mpiaEhobCaDS22Tz525qbm9stzCiw\nHaluxK93mD037KaiWcMxdnC0YsenrruRz4KnpqZi165dyMjIwIkTJxAZGdnp5UfmRaLA192c2GkB\nFhERgblz56KoqAg2mw1jx47FqFGjutUREZG/Ky4uRmVlJSwWC/Ly8nDPPffA6XQCALKysjB+/HhU\nVlZi2bJlCAsLQ15eno8jJqK+yuPy4pmZmcjMzJQQChGRby1ZssRjmwceeAAPPPCAhGiIKJBxJXwi\nIiIiyViAEREREUnGAoyIiIhIMhZgRERERJKxACMiIiKSzONdkNXV1SguLnY/vnDhAu67774O1wMj\nIiIios55LMAGDx6MtWvXAgBcLhceeeQRTJo0SfHAiIiIiAJVly5Bfvnllxg0aBAGDhyoVDxERERE\nAa9LBdj+/fsxZcoUpWIhIiIiuiF4vAR5jcPhQHl5OebNm6dkPNSLzltaUdtkU7QPm9Ol6PGJiIgC\nkdcFmNFoxLBhw6DRaJSMh3pRbZNN0Y2yAWDljARFj09ERBSIvL4EuX//fmRkZCgZCxEREdENwasC\nzGq14ssvv0RaWprS8RAREREFPK8uQYaFheF3v/ud0rEQEfmUyWRCSUkJnE4npk+fjuzs7Dav22w2\nbNmyBWfPnkV4eDjmzJmDiRMn+ihaIurLuBI+ERGurnO4efNmLFu2DIWFhdi7dy+qqqratCktLUVY\nWBjWrl2LRYsW4Q9/+AOEED6KmIj6MhZgREQAzGYz4uLiEBsbi+DgYGRkZKCsrKxNm4iICLS0tMDh\ncKCpqQkhISFQqVQ+ipiI+jKv74IkIgpk9fX1iImJcT/W6XQwm9veRTxlyhSUl5fj4Ycfhsvlwosv\nvig7TCIKEDwDRkTkpZ07dyIoKAhbtmzBc889h8LCQrhcXAuPiLrO4xkwq9WKrVu34uzZs7Db7cjL\ny8OIESNkxEZEJI1Op0NdXZ37cV1dHXQ6XZs2JpMJ06ZNQ2hoKJKSkjBgwACcP38eQ4YMkR0uEfVx\nHguwrVu3IiUlBYsWLYLT6URra6uMuIiIpEpMTERNTQ1qa2uh0+lw4MABPProo23ajB49GuXl5Rgz\nZgy++eYbNDU1sfgiom7ptAC7cuUKjh07hkWLFgEAgoKCEBERISUwIiKZgoKCkJeXh3Xr1rmXodDr\n9di9ezcAICsrCxkZGaiqqsKTTz4JjUaD3Nxc3wZNRH1WpwVYbW0tNBoNDAYDTp06haSkJDz00EMI\nCQmRFR8RkTQpKSlYu3Ztm+eysrLcf4+IiMCDDz4oOywiCkCdTsJ3Op04efIk0tLSUFBQAIfDgYMH\nD8qKjYiIiCggdXoGLCYmBlFRUUhNTQUAZGRk4NNPP8Vtt90mJTiiIDVwpLpRseNHhQShyeZU7Pix\nUSG4SROq2PGJiKhv6rQA02q1iIuLw1dffYXExERUVFRgzJgxsmIjQoPVidV7Tit2/JUzEhQ9ftGs\n4SzAiIjoOh7vgszPz4fBYIDFYkF8fDweeOABGXERERERBSyPBdjgwYOxZs0aGbEQERER3RC4Ej4R\nERGRZCzAiIiIiCRjAUZEREQkGQswIiIiIslYgBERERFJ5vEuSODqUhTh4eFQq9UICgpCQUGB0nER\nERERBSyvCjAAWLVqFaKiopSMhYiIiOiG4HUBJoRQMg4iIp8zmUwoKSmB0+nE9OnTkZ2dfV0bs9mM\nkpISWK1WREZGYtWqVfIDJaI+z6sCTKVS4fnnn4dKpcLMmTMxY8YMpeMiIpLK5XJh8+bNePbZZ6HT\n6fDkk09i9OjR0Ov17jbNzc3YtGkTnn76acTExMBisfgwYiLqy7wqwF544QUMGDAAVVVVKCgowJAh\nQ5CcnKx0bERE0pjNZsTFxSE2NhYAkJGRgbKysjYF2GeffYa0tDTExMQAADQajU9iJaK+z6u7IAcM\nGAAA0Ov1mDRpEsxms6JBERHJVl9f7y6sAECn06G+vr5Nm/Pnz6OpqQnPPfccnnjiCezbt092mEQU\nIDwWYK2trWhpaQEAWCwWGI1GxMfHKx4YEZG/cTqdMJlMWLp0KZYtW4Z3330XNpvN12ERUR/k8RJk\nQ0MDioqKAADR0dGYPXs2xo4dq3hgREQy6XQ61NXVuR/X1dVBp9O1aRMTE4Nx48ZBq9UCAIYNGwaT\nyYRx48ZJjZWI+j6PBVhsbKy7ACMiClSJiYmoqalBbW0tdDodDhw4gEcffbRNm4kTJ2Ljxo1obW2F\n3W7H119/jZEjR/ooYiLqy7xehoKIKJAFBQUhLy8P69atcy9DodfrsXv3bgBAVlYWhgwZgqlTp2LF\nihWw2+244447EBYW5uPIiagvYgFGRPQvKSkpWLt2bZvnsrKy2jyeOXMmZs6cKTMsIgpA3AuSiIiI\nSDIWYERERESSeVWAuVwuPPHEEygsLFQ6HiIiIqKA51UBtmPHDuj1eqhUKqXjISIiIgp4Hguwuro6\nGI1GTJs2jRtyExEREfUCjwVYSUkJ5s2bB7Wa08WIiIiIekOnVVV5eTk0Gg0SEhJ49ouIiIiol3S6\nDtjx48dRXl4Oo9EIu92OlpYWbNy4EYsWLZIVHxEREVHA6bQAy8nJQU5ODgDAZDLhvffeY/FFRERE\n1ENdmtjFuyCJiIiIes7rrYhSUlKQkpKiZCxERERENwTe2khEREQkGQswIiIiIslYgBER/YvJZMLy\n5cvx+OOP46OPPuqwndlsxk9/+lP8/e9/lxgdEQUSFmBERLi65+3mzZuxbNkyFBYWYu/evaiqqmq3\n3VtvvYVx48ZxfUQi6jYWYEREuHpWKy4uDrGxsQgODkZGRgbKysqua/fRRx9h8uTJ0Gg0PoiSiAKF\nxwLMZrPhqaeewq9//Ws8/fTT+OCDD2TERUQkVX19PWJiYtyPdTod6uvrr2tTVlaGmTNnAuDSPETU\nfR6XoQgJCcHKlSsRGhoKu92OFStWIDU1FXFxcTLiIyLyG2+88QZycnKgUqkghOAlSCLqNq/WAQsN\nDQUAWK1WOJ1OBAd7vXwYEVGfoNPpUFdX535cV1cHnU7Xps2pU6dQXFwMAGhsbMThw4cRHByM1NRU\nqbESUd/nVSXlcrmwfPlynDt3Drm5uRg4cKDScRERSZWYmIiamhrU1tZCp9PhwIEDePTRR9u02bhx\no/vvmzZtwoQJE1h8EVG3eFWAqdVqFBUVoba2FgUFBbj55puRkJCgdGwB77ylFbVNNsWOb3O6FDs2\nUaAJCgpCXl4e1q1bB6fTienTp0Ov12P37t0AgKysLB9HSESBpEvXEmNjY3HLLbfAZDKxAOsFtU02\n/HqHWbHjr5zBz4ioK1JSUrB27do2z3VUeC1cuFBGSEQUoDzeBWmxWNDc3Azg/+Y8xMfHKx4YERER\nUaDyeAbs8uXLMBgMcLlc0Gq1mDNnDkaPHi0jNiIiIqKA5LEAi4+Px8svvywjFiIiIqIbAlfCJyIi\nIpKMBRgRERGRZCzAiIiIiCRjAUZEREQkmcdJ+BcvXoTBYEBDQwM0Gg0yMzORmZkpITQiIiKiwOSx\nAAsODsb8+fMxdOhQWCwWLFu2DMOHD4der5cRHxEREVHA8XgJUqvVYujQoQAAjUaDxMREXLp0Sem4\niIiIiAJWl+aA1dTUoKqqCklJSUrFQ0RERBTwvN4L0mq1ori4GPPnz0dYWJiSMXnlis2BZrtym02r\nAAyMDFHs+ERERHTj8qoAczgcWL9+PW699VZMnDhR6Zi88k2zHb9674Rix88cNgCP3co9L4mIiKj3\neSzAhBB47bXXoNfrMXv2bBkxea1FwTNgNodyxyYi/2UymVBSUgKn04np06cjOzu7zev79u3De++9\nBwDQ6/W4++67ER/PX9aIqGs8FmDHjx/Hvn37EB8fjyeeeAIAkJOTg3HjxikeHBGRTC6XC5s3b8az\nzz4LnU6HJ598EqNHj25z1/egQYOwevVqREREoLS0FP/5n/+JNWvW+DBqIuqLPBZgI0eOxDvvvCMj\nFiIinzKbzYiLi0NsbCwAICMjA2VlZW0KsBEjRrj/Pn78ePzpT3+SHicR9X1cCZ+I6F/q6+sRExPj\nfqzT6VBfX99h+z179iA1NVVGaEQUYFiAERF1wz/+8Q/s27cP999/v69DIaI+iAUYEdG/6HQ61NXV\nuR/X1dVBp9Nd1+7MmTPYsmULli9fjsjISJkhElGAYAFGRPQviYmJqKmpQW1tLRwOBw4cOHDdJcaL\nFy9i/fr1WLx4MeLi4nwUKRH1dV4vxEpEFOiCgoKQl5eHdevWuZeh0Ov12L17NwAgKysL//3f/42m\npia8/vrr7n9TUFDgy7CJqA/yWIBt2rQJRqMRGo0G69evlxETEZHPpKSkYO3atW2ey8rKcv/9kUce\nwSOPPCI7LCIKMB4vQU6dOhVPPfWUjFiIiIiIbggeC7Dk5GROMiUiIiLqRZyET0RERCQZJ+F34ryl\nFbVNNsWOb3Nyv8lAF6QGjlQ3KtpHbFQIbtKEKtoHERH1LhZgnahtsuHXO8yKHX/ljATFjk3+ocHq\nxOo9pxXto2jWcBZgRER9DC9BEhEREUnm8QxYcXExKisr0djYiLy8PNx7772YOnWqjNiIiIiIApLH\nAmzJkiUy4iAiIiK6YfASJBEREZFkLMCIiIiIJGMBRkRERCQZCzAiIiIiyTxOwjeZTCgpKYHT6cT0\n6dORnZ0tIy4iIum8yXdvv/02KioqEBoaioULF2LIkCE+iJSI+rpOz4C5XC5s3rwZy5YtQ2FhIfbu\n3YuqqipZsRERSeNNvquoqMCZM2ewbt065ObmYtOmTT6Kloj6uk4LMLPZjLi4OMTGxiI4OBgZGRko\nKyuTFRsRkTTe5LuysjLcdtttAICkpCQ0Nzfj8uXLvgiXiPq4Tguw+vp6xMTEuB/rdDrU19crHhQR\nkWze5LvvtomJiWFOJKJu6bN7QYYGqfHLNOXmXvxAG6bYsYmo7xJC+DoEIgoAnRZgOp0OdXV17sd1\ndXXQ6XTtttVqtaioqOjd6DxQdCvrbwAngMLxCvZRf6pvH19GHzy+R86ar1BRo2wf36bVauV1JpE3\n+a4rORHwTV4kIrm6mxM7LcASExNRU1OD2tpa6HQ6HDhwAI8++mi7bSdMmNCtAIiI/IE3+S41NRW7\ndu1CRkYGTpw4gcjIyE6TL/MiEXVEJTycTzeZTHjjjTfct2XPmjVLVmxERFK1l+92794NAMjKygIA\nvPXWW6ioqEBYWBjy8vKg1+t9GTIR9VEeCzAiIiIi6l1cCZ+IiIhIMhZgRERERJL1yjIUMrcr2rRp\nE4xGIzQaDdavXw8AaGlpwYYNG1BbW4tBgwZh8eLFCAvr/WUkLl68CIPBgIaGBmg0GmRmZiIzM1Na\n/zabDatWrYLdbkdISAjS09MxZ84caf0DV1cLX7FiBXQ6HVasWCGt7/z8fISHh0OtViMoKAgFBQVS\nx221WrF161acPXsWdrsdCxcuhF6vV7z/6upqFBcXux9fuHAB9913H6ZOnSpl7Hv27EFpaSnsdjuS\nk5ORm5sr9X3vKwJlCyNP49i3bx/ee+89AIBer8fdd9+N+Ph4X4TaKW//TzKbzXjmmWfw2GOPIS0t\nTXKUnnkzDrPZjJKSElitVkRGRmLVqlXyA/XA0zhsNhu2bNmCs2fPIjw8HHPmzMHEiRN9FG372qs9\nvqvL33HRQ06nUyxatEhcuHBB2O128fjjj4tz58719LAdMplM4tSpU2Lp0qXu5958802xfft2IYQQ\n27ZtE3/84x8V6fvSpUvi9OnTQgghGhoaxIIFC8S5c+ek9S+EEFarVQghhM1mE0uXLhXV1dVS+3//\n/ffFq6++KgoLC4UQ8t77hQsXisbGxjbPyRz3hg0bxF//+lchhBAOh0M0NzdL7V+Iq9+1n//85+Kb\nb76R0ndjY6NYuHChaGlpEU6nU7z00kvCaDRKH7e/8yYHlpeXi5deekkIIcSJEyfEU0895YtQO+XN\nOI4fPy6am5uFEEJ88sknfXYc19qtWrVKFBQUiIMHD/og0s55M46mpibx2GOPiYsXLwohrv6/5G+8\nGceuXbvE66+/LoQQora2VixatEi4XC5fhNuh9mqPb+vOd7zHlyBlb1eUnJyMyMjINs99e3uQzMxM\nfPHFF4r0rdVqMXToUACARqNBYmIi6uvrpfUPAKGhoQCunpFxuVzo16+ftP7r6upgNBoxbdo092KU\nMscuvnO/iKy+r1y5gmPHjmHatGkAgKCgIEREREgdOwB8+eWXiIuLw8CBA6X0HRISAuDq+G02G1pb\nWxEZGSl93P4uULYw8mYcI0aMQEREBABg/PjxbdZE8xfe/p/00UcfYfLkydBoND6I0jNvxvHZZ58h\nLS3NvTuDP47Fm3FERESgpaUFDocDTU1NCAkJgUql8lHE7Wuv9vi27nzHe3wJsr3tO8xmc08P2yUN\nDQ3utXj69++PhoYGxfusqalBVVUVRowYIbV/l8uF5cuX49y5c8jNzcXAgQOl9V9SUoJ58+ahpaXF\n/ZysvlUqFZ5//nmoVCrMnDkTM2bMkNZ3bW0tNBoNDAYDTp06haSkJDz44IPSf+7279+PjIwMAHLe\n95CQECxYsAD5+fno168fsrOzkZSU5JPvmz/zJgd2tIWRPy1q29VcvmfPHqSmpsoIrUu8/TzKysrw\n3HPPYfPmzX73nz3g3TjOnz8Pp9OJ5557DlarFXfccQduvfVW2aF2yptxTJkyBeXl5Xj44Yfhcrnw\n4osvyg6zx7rzHQ+4SfgyvkhWqxXFxcWYP3/+dXNflO5frVajqKgIv/3tb7Fr1y6cPn1aSv/l5eXQ\naDRISEjocCsWJcf+wgsvoKioCL/61a+wbds2VFZWSuvb6XTi5MmTSEtLQ0FBARwOBw4ePCitfwBw\nOBwoLy9Henr6da8p1bfFYsHWrVvxyiuvwGAw4MSJEygvL5fSdyDq6HvTF/3jH//Avn37cP/99/s6\nlG554403kJOTA5VKBSFEn/1snE4nTCYTli5dimXLluHdd9+FzWbzdVhdtnPnTgQFBWHLli147rnn\nUFhYCJfL5euwuqyrP0c9PgPW1a05lNC/f39cvnwZWq0Wly5dQv/+/RXry+FwYP369bj11lvdkwRl\n9n9NbGwsbrnlFphMJin9Hz9+HOXl5TAajbDb7e6J2LLGPmDAAABXJ/5OmjQJZrNZWt8xMTGIiopy\n/7afkZGBTz/9FFqtVtrnbjQaMWzYMPclBhljN5vNSEpKQlxcHAAgPT0dlZWVPvl592dKbGHkC97G\neObMGWzZsgVPPfVUp5dkfMWbcZw6dcp9c0tjYyMOHz6M4OBgvzqj5804YmJiMG7cOPdZlmHDhsFk\nMmHcuHFSY+2MN+MwmUyYNm0aQkNDkZSUhAEDBuD8+fN+eaNKR7rzHe/xGbBvb9/hcDhw4MAB6T/E\nqampKC0tBQB8+umnit09IYTAa6+9Br1ej9mzZ0vv32KxoLm5GcD/JY34+Hgp/efk5GDz5s0wGAxY\nsmQJRo0ahcWLF0vpu7W11X3Z02KxwGg0Shs3cHXuX1xcHL766iu4XC5UVFRg9OjRmDBhgpT+gbaX\nHwE5P3MjR47EyZMn0dTUBLvdDqPRiLFjx0p73/sKb3Jgamoq/va3vwGAV1sY+YI347h48SLWr1+P\nxYsXuwtzf+PNODZu3AiDwQCDwYDJkydjwYIFflV8Ad6NY+LEiTCZTGhtbUVTUxO+/vprjBw50kcR\nt8+bcYwePRrl5eVwuVy4cOECmpqa+lTxBXTvO94rK+HL3K6ouLgYlZWVaGxsRP/+/XHvvfdi8uTJ\nUm6LP3bsGFauXIn4+Hj3pZecnBzcfPPNUvo/e/YsDAYDXC4XtFot0tPTMW3aNOnLAphMJrz//vtY\nvny5lL5ra2tRVFQEAIiOjkZ6ejqysrKkjru6uhoGgwEWiwXx8fFYvHgxhBBS+rdarcjPz8fGjRsR\nHh4OQN7SK6Wlpfjkk09gs9kwduxY3HvvvWhtbeUyFN8RKFsYeRrHa6+9hkOHDmHgwIEA4F4Sxt94\n83lcs2nTJkyYMMFvl6HwNI6PP/4YH330Eex2O+644w7cfvvtvgy5XZ7GceXKFbzzzjs4duwYNBoN\nsrOzMX78eB9H3da12sNisUCr1eKee+6B0+kE0P3vOLciIiIiIpIs4CbhExEREfk7FmBEREREkrEA\nIyIiIpKMBRgRERGRZCzAiIiIiCRjAUZEREQkGQswIiIiIslYgBERERFJ9v8BWlX8VEfQiW0AAAAA\nSUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114097350>"
       ]
      }
     ],
     "prompt_number": 34
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 34
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "## Regression models\n",
      "\n",
      "A general, primary goal of many statistical data analysis tasks is to relate the influence of one variable on another. For example, we may wish to know how different medical interventions influence the incidence or duration of disease, or perhaps a how baseball player's performance varies as a function of age."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "x = np.array([2.2, 4.3, 5.1, 5.8, 6.4, 8.0])\n",
      "y = np.array([0.4, 10.1, 14.0, 10.9, 15.4, 18.5])\n",
      "plot(x,y,'ro')"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 35,
       "text": [
        "[<matplotlib.lines.Line2D at 0x1143406d0>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAECCAYAAADn84z1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAD7NJREFUeJzt3G1M1fX/x/HXEQK84HDEpm4xhpkWc6V5VWoqXvxpBFtu\ndrFpS9cMpmS5bIi3croFjbEwRIV5o4t77edy606x9IeS1qZy2lyYheGSlZEKByIOl9//jZLVLwI8\nnsP3vPH5uMenD553s5777vM936/HcRxHAABzxrk9AAAgNAQcAIwi4ABgFAEHAKMIOAAYRcABwKjY\nof7h9evXVVFRoUAgIK/Xq4yMDGVkZKizs1Pl5eVqbm7WtGnTtH37diUkJIzWzAAASZ6hvgfe2tqq\n1tZWpaWlqa2tTTt37tSbb76pmpoaJSYm6umnn9axY8fU0dGhjRs3jubcAHDXG/IIxefzKS0tTZLk\n9Xo1c+ZM3bx5U+fOndPKlSslSRkZGTp79mzEBwUA/N2Iz8CvXbumpqYmzZ49W4FAQD6fT5KUlJSk\nQCAQsQEBAIMbUcCDwaDKysq0adOmf5x1ezyeiAwGABjakDcxJam3t1elpaVavny5Fi1aJOmPq+7W\n1lb5fD61tLQoKSnpX3//q6++UkdHR/gmBoC7gM/n04IFC4bcM2TAHcfR4cOHlZKSouzs7IH1hQsX\nqqamRuvWrdPJkycHwj6Yjo4OzZ8//zZHB4C7W11d3bB7hgz4pUuXVFtbq9TUVBUUFEiSNmzYoPXr\n16u8vFxvvPHGwNcIAQCja8ivEYbD8ePHuQIHgNtUV1enNWvWDLmHJzEBwCgCDgBGEXAAMIqAA4BR\nBBwAjCLgAGAUAQcAowg4ABhFwAHAKAIOAFHkTHW1itevH9FeAg4AUeJMdbVqd+/W2//974j2D/s6\nWQDA6DhVWam3GxtHvJ8rcACIErFdXbe1n4ADQJTojY+/rf0EHACixIq8PBXOmDHi/ZyBA0CUWJqZ\nKUkqrKrS/41gP1fgABBFlmZmatd//jOivQQcAIwi4ABgFAEHAKMIOAAYRcABwCgCDgBGEXAAMIqA\nA4BRBBwAjCLgAGAUAQcAowg4ABhFwAHAKAIOAEYRcAAwioADgFEEHACMIuAAYBQBBwCjCDgAGEXA\nAcAoAg4ARhFwADCKgAOAUQQcAIwi4ABgFAEHAKNi3R4AgB1nqqt1qrJSsV1d6o2P14q8PC3NzHR7\nrLsWAQcwImeqq1W7e7febmwcWCu8ckWSiLhLOEIBMCKnKitV/Jd4S1JxY6Nqq6pcmgjDXoEfPHhQ\nfr9fXq9XpaWlkqSPPvpIJ06ckNfrlSRt2LBB8+bNi+ykAFwV29U16HpMMDjKk+CWYQO+atUqZWVl\n6cCBAwNrHo9HOTk5ysnJiehwAKJHb3z8oOt9CQmjPAluGfYIJT09XRMnTvzHuuM4ERkIQHRakZen\nwhkz/ra2Ky1Ny3NzXZoIId/E/PTTT3XixAnNnj1bL7744qCRBzB23LpRWVhVpZhgUH0JCVqRm8sN\nTBeFFPDMzEw988wz6uzs1IcffqgPPvhAW7duDfdsAKLM0sxMgh1FQvoWSlJSkjwejyZMmKAnn3xS\nDQ0N4Z4LADCMkALe0tIiSerr69MXX3yh1NTUsA4FABjesEcoZWVlunjxotra2rR161Y9++yzqq+v\n15UrVxQbG6v09HRt2rRpNGYFAPzFsAHfsWPHP9ZWr14dkWEAACPHk5gAYBQBBwCjCDgAGEXAAcAo\nXicL/Il3XcMaAg6Id13DJo5QAPGua9hEwAHxrmvYRMAB8a5r2ETAAfGua9jETUxAvOsaNhFw4E+8\n6xrWcIQCAEYRcAAwioADgFEEHACMIuAAYBQBBwCjCDgAGEXAAcAoAg4ARhFwADCKgAOAUQQcAIwi\n4ABgFAEHAKMIOAAYRcABwCgCDgBGEXAAMIqAA4BRBBwAjCLgAGAUAQcAowg4ABhFwAHAKAIOAEYR\ncAAwKtbtAQAM70x1tU5VViq2q0u98fFakZenpZmZbo8FlxFwIMqdqa5W7e7deruxcWCt8MoVSSLi\ndzmOUIAod6qyUsV/ibckFTc2qraqyqWJEC0IOBDlYru6Bl2PCQZHeRJEGwIORLne+PhB1/sSEkZ5\nEkQbAg5EuRV5eSqcMeNva7vS0rQ8N9eliRAtuIkJRLlbNyoLq6oUEwyqLyFBK3JzuYEJAg5YsDQz\nk2DjHzhCAQCjhr0CP3jwoPx+v7xer0pLSyVJnZ2dKi8vV3Nzs6ZNm6bt27crgRsq+B88fAJE1rAB\nX7VqlbKysnTgwIGBtaNHj+rBBx9UQUGBjh07pqNHj2rjxo0RHRS28PAJEHnDHqGkp6dr4sSJf1s7\nd+6cVq5cKUnKyMjQ2bNnIzMdzOLhEyDyQjoDDwQC8vl8kqSkpCQFAoGwDgX7ePgEiLw7vonp8XjC\nMQfGGB4+ASIvpIAnJSWptbVVktTS0qKkpKSwDgX7ePgEiLyQvge+cOFC1dTUaN26dTp58qQWLVoU\n7rlgHA+fAJHncRzHGWpDWVmZLl68qPb2diUlJem5557T448/PuKvER4/flzz58+PyPAAMFbV1dVp\nzZo1Q+4Z9gp8x44dg64XFBSENhUAICx4EhMAjCLgAGAUAQcAowg4ABhFwAHAKAIOAEYRcAAwioAD\ngFEEHACMIuAAYBQBBwCjCDgAGEXAAcAoAg4ARhFwADCKgAOAUQQcAIwi4ABgFAEHAKMIOAAYRcAB\nwCgCDgBGEXAAMIqAA4BRBBwAjCLgAGAUAQcAowg4ABhFwAHAKAIOAEYRcAAwioADgFEEHACMIuAA\nYBQBBwCjCDgAGEXAAcAoAg4ARhFwADCKgAOAUQQcAIwi4ABgFAEHAKMIOAAYRcABwCgCDgBGEXAA\nMCr2Tn45Pz9f48eP17hx4xQTE6OioqJwzQUAGMYdBVyS9uzZo0mTJoVjFgDAbbjjIxTHccIxBwDg\nNt3RFbjH49HevXvl8XiUmZmptWvXhmsuAMAw7ijg+/bt0+TJk9XU1KSioiLdd999Sk9PD9dsAIAh\n3NERyuTJkyVJKSkpWrx4sRoaGsIyFABgeCEHvKurS52dnZKktrY2+f1+paamhm0wAMDQQj5CCQQC\nKikpkSQlJiYqOztbc+fODdtgAIChhRzwqVOnDgQcADD6eBITAIwi4ABgFAEHAKMIOAAYRcABwCgC\nDgBGEXAAMIqAA4BRBBwAjCLgAGAUAQcAowg4ABhFwAHAKAIOAEYRcAAwioADgFEEHACMIuAAYBQB\nBwCjCDgAGEXAAcAoAg4ARhFwADCKgAOAUQQcAIwi4ABgFAEHAKMIOAAYRcABwCgCDgBGEXAAMIqA\nA4BRBBwAjCLgAGAUAQcAowg4ABhFwAHAKAIOAEYRcAAwioADgFEEHACMIuAAYBQBBwCjYt0e4JYz\n1dU6VVmp2K4u9cbHa0VenpZmZro9FgBEragI+JnqatXu3q23GxsH1gqvXJEkIg4A/yIqjlBOVVaq\n+C/xlqTixkbVVlW5NBEARL+Qr8Dr6+v1/vvvq6+vT2vWrFFWVlboQ3R1DboeEwyG/GcCwFgX0hV4\nf3+/Dh06pJ07d6q4uFgnTpxQU1NTyEP0xscPut6XkBDynwkAY11IAW9oaND06dM1depUxcbGatmy\nZTp37lzIQ6zIy1PhjBl/W9uVlqblubkh/5kAMNaFdIRy8+ZNTZkyZeDn5ORkNTQ0hDzErRuVhVVV\nigkG1ZeQoBW5udzABIAhRMW3UKQ/Ik6wAWDkQgp4cnKybty4MfDzjRs3lJycPOhen8+nurq60KYD\ngLuUz+cbdk9IAZ85c6auXbum5uZmJScn68yZM3rttdcG3btgwYJQPgIAMAyP4zhOKL9YX1+v9957\nb+BrhE899VS4ZwMADCHkgAMA3BUVT2ICAG4fAQcAoyL2NcLr16+roqJCgUBAXq9XGRkZysjIiNTH\njbru7m7t2bNHPT09iouL05IlS5STk+P2WGHV39+vwsJCJScnq7Cw0O1xwi4/P1/jx4/XuHHjFBMT\no6KiIrdHCptgMKgjR47oxx9/VE9Pj7Zu3arZs2e7PVZY/PTTTyorKxv4+ZdfftHzzz8/pu7Dff75\n56qpqVFPT4/S09O1efPmwTc6EdLS0uI0NjY6juM4gUDA2bJli3P16tVIfZwrgsGg4ziO093d7bz+\n+uvOzz//7PJE4fXJJ584+/fvd4qLi90eJSK2bdvmtLe3uz1GRJSXlzvHjx93HMdxent7nY6ODpcn\nioy+vj7n5Zdfdn799Ve3Rwmb9vZ2Z9u2bU5nZ6fT19fnvPXWW47f7x90b8SOUHw+n9LS0iRJXq9X\nM2fOVEtLS6Q+zhXxf77DJRgMqq+vT7GxUfNc1B27ceOG/H6/Vq9eLWcM3+cei/9uv//+u7799lut\nXr1akhQTE6MJEya4PFVkXLhwQdOmTdO9997r9ihhExcXJ+mPv8fu7m51dXVp0qRJg+4dleJcu3ZN\nTU1NmjVr1mh83Kjp7+/Xrl27dPXqVW3evHlM/Uf0/vvv64UXXlBnZ6fbo0SMx+PR3r175fF4lJmZ\nqbVr17o9Ulg0NzfL6/WqoqJCP/zwg2bNmqWXXnppIAxjyenTp/XEE0+4PUZYxcXFacuWLcrPz9c9\n99yjrKwsPfDAA4PujfhNzGAwqLKyMm3atEkJY+ztguPGjVNJSYneffddffbZZ2r8n3eaW3X+/Hl5\nvV7NmDFjTF6h3rJv3z6VlJTo1Vdf1ccff6yLFy+6PVJY9PX16fLly3rsscdUVFSk3t5effnll26P\nFXa9vb06f/68lixZ4vYoYdXW1qYjR47onXfeUUVFhb777rt/fZo9ogHv7e1VaWmpli9frkWLFkXy\no1w1depUPfroo6qvr3d7lLC4dOmSzp8/r/z8fO3fv1/ffPONDhw44PZYYTd58mRJUkpKihYvXnxH\nL2SLJlOmTNGkSZO0cOFCxcXFadmyZfL7/W6PFXZ+v1/333+/vF6v26OEVUNDg2bNmqXp06crMTFR\nS5Ys+de2RCzgjuPo8OHDSklJUXZ2dqQ+xjVtbW3q6OiQJLW3t+vrr79Wamqqy1OFx4YNG3To0CFV\nVFRox44dmjNnjl555RW3xwqrrq6ugeOhtrY2+f3+MfP35/P5NH36dH3//ffq7+9XXV2dHnnkEbfH\nCrvTp09r2bJlbo8Rdg899JAuX76s3377TT09PfL7/Zo7d+6geyN2Bn7p0iXV1tYqNTVVBQUFkv4I\nw7x58yL1kaOqtbVVFRUV6u/vl8/nU05Ojh5++GG3x4oIj8fj9ghhFwgEVFJSIklKTExUdnb2v/5P\nYlF+fr4qKirU1tam1NRUbdy40e2RwioYDOrChQvKy8tze5SwmzBhgtavX6+SkhJ1d3dr7ty5mjNn\nzqB7eZQeAIziSUwAMIqAA4BRBBwAjCLgAGAUAQcAowg4ABhFwAHAKAIOAEb9P6PSghthTu6CAAAA\nAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114101b90>"
       ]
      }
     ],
     "prompt_number": 35
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We can build a model to characterize the relationship between $X$ and $Y$, recognizing that additional factors other than $X$ (the ones we have measured or are interested in) may influence the response variable $Y$.\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$y_i = f(x_i) + \\epsilon_i$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "where $f$ is some function, for example a linear function:\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$y_i = \\beta_0 + \\beta_1 x_i + \\epsilon_i$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "and $\\epsilon_i$ accounts for the difference between the observed response $y_i$ and its prediction from the model $\\hat{y_i} = \\beta_0 + \\beta_1 x_i$. This is sometimes referred to as **process uncertainty**."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We would like to select $\\beta_0, \\beta_1$ so that the difference between the predictions and the observations is zero, but this is not usually possible. Instead, we choose a reasonable criterion: ***the smallest sum of the squared differences between $\\hat{y}$ and $y$***.\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$R^2 = \\sum_i (y_i - [\\beta_0 + \\beta_1 x_i])^2 = \\sum_i \\epsilon_i^2 $$  \n",
      "</div>\n",
      "\n",
      "Squaring serves two purposes: (1) to prevent positive and negative values from cancelling each other out and (2) to strongly penalize large deviations. Whether the latter is a good thing or not depends on the goals of the analysis.\n",
      "\n",
      "In other words, we will select the parameters that minimize the squared error of the model."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "ss = lambda theta, x, y: np.sum((y - theta[0] - theta[1]*x) ** 2)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 36
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "ss([0,1],x,y)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 37,
       "text": [
        "333.35000000000002"
       ]
      }
     ],
     "prompt_number": 37
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "b0,b1 = fmin(ss, [0,1], args=(x,y))\n",
      "b0,b1"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 21.375000\n",
        "         Iterations: 79\n",
        "         Function evaluations: 153\n"
       ]
      },
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 38,
       "text": [
        "(-4.3500136038870876, 3.0000002915386412)"
       ]
      }
     ],
     "prompt_number": 38
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "plot(x, y, 'ro')\n",
      "plot([0,10], [b0, b0+b1*10])"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 39,
       "text": [
        "[<matplotlib.lines.Line2D at 0x113f66410>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXUAAAECCAYAAAAB2kexAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFn9JREFUeJzt3X9sVfX9x/HXbStUftx7W7bCtqbfkkKhOgWx3VQCXEFr\nkCYjOkmESdWvgSAy/Q4CNd9sIzMOpmtWcyk/Gpav4JZ8ZSHD+F1CiHRFGDOjtO6bWX5YpRnMlful\nlFvA/rw93z+cVYRe7u095557z3k+/uvx3nPeIfXF4XU+5xyPYRiGAACOkGH3AAAA8xDqAOAghDoA\nOAihDgAOQqgDgIMQ6gDgIFmxfKivr08bN25Uf3+/Ro0apXvvvVcVFRXq7u5WMBhUKBTSxIkTtWbN\nGmVnZ1s9MwBgGJ5Y16n39vZq9OjR6u/vV1VVldatW6eDBw9q/Pjx+t73vqd9+/bp6tWrWrZsmdUz\nAwCGEXP9Mnr0aElST0+PBgcHdcstt6ixsVHz5s2TJAUCAR07dsyaKQEAMYmpfpGkwcFBbdiwQWfP\nntWTTz6pr33tawqHw/L7/ZIkn8+ncDhs2aAAgJuLOdQzMjL06quvKhQKadOmTZo2bdo1/93j8Zg+\nHAAgPjGH+ufy8vJ01113qaWlRT6fT5cuXZLf71dnZ6d8Pt+w33vvvfd09erVhIYFALfx+/26++67\nY/58TKHe1dWlzMxMjR07VpcvX9b777+vp556SqWlpWpoaNDixYt16NAhlZWVDbuPq1evatasWTEP\nBgCQmpqa4vp8TKF+6dIl1dbWanBwUH6/XxUVFbrjjjs0ZcoUBYNBrVu3bmhJIwDAPjEvaUzUwYMH\nOVMHgDg1NTVpwYIFMX+eO0oBwEEIdQBwEEIdAByEUAcAByHUAcBBCHUAcBBCHQAchFAHAAch1AHA\nQQh1AHAQQh0AHIRQBwAHIdQBwEEIdQBwEEIdAByEUAcAByHUAcBBCHUAcBBCHQAchFAHAAch1AHA\nQQh1AHAQQh0AUlToSl/c38mK5UMXLlxQbW2twuGwvF6vAoGAAoGA9uzZo/r6enm9XknS0qVLNXPm\nzLiHAAB8obs/ojf/el5vn7ig/7w9vu/GFOpZWVmqrKxUYWGhurq6tHbtWk2ZMkUej0cVFRWqqKgY\nydwAgC8ZNAy98+FF/VfjPzXzm+O0/ZHpOnvqb3HtI6ZQ9/v98vv9kiSv16uioiJdvHhRkmQYRpxj\nAwC+6oP2K9r23j+UmSH95IHJKskbK0k6G+d+Ygr1L2tvb9e5c+dUXFysU6dOaf/+/aqvr1dxcbGW\nL1+usWPHxrtLAHCt85f7tPPYP9Ry/qr+veybur8oRx6PZ8T7i+tCaU9Pj2pqalRZWans7GyVl5dr\ny5Ytevnll5WRkaHdu3ePeBAAcJPu/oheb/xEz+47qQJ/tn792G2aPyU3oUCX4gj1gYEBVVdXa86c\nOSorK5Mk+Xw+eTwejRkzRg899JBaW1sTGgYAnG7QMHTgdIee/t0Jnb/Sp+2PTNcTs76h7CxzFiPG\nVL8YhqHt27crPz9fixYtGtre2dmpnJwcRSIRHTlyRAUFBaYMBQBONFxvbqaYQv3UqVM6fPiwCgoK\ntH79eknS448/rj/96U9qa2tTVlaWSkpKVFlZafqAAJDuzO7No4kp1KdPn64333zzuu133XWX6QMB\ngFN8eb354tu/rrVz/820mmU4ca9+AQBEd6P15l8fOyopxybUAcBEyejNoyHUAcAEyezNoyHUASAB\ndvTm0RDqADACdvbm0RDqABAnu3vzaAh1AIhRqvTm0RDqAHATqdabR0OoA8AwUrU3j4ZQB4AbSOXe\nPBpCHQC+JB1682gIdQBQevXm0RDqAFwtHXvzaAh1AK6Vrr15NIQ6ANdJ9948GkIdgGs4pTePhlAH\n4HhO682jIdQBOJoTe/NoCHUAjuTk3jwaQh2Ao7ihN4+GUAfgCG7qzaMh1AGkPbf15tEQ6gDSllt7\n82hiCvULFy6otrZW4XBYXq9XgUBAgUBA3d3dCgaDCoVCmjhxotasWaPs7GyrZwbgcm7vzaOJKdSz\nsrJUWVmpwsJCdXV1ae3atZoyZYoaGho0bdo0rV+/Xvv27dPevXu1bNkyq2cG4FL05jcX019tfr9f\nhYWFkiSv16uioiJdvHhRjY2NmjdvniQpEAjo2LFjlg0KwN0+aL+iH751Wn84eUE/eWCyNgQKCfQb\niLtTb29v17lz51RcXKxwOCy/3y9J8vl8CofDpg8IwN3ozeMTV6j39PSopqZGlZWV13Xn/CEDMBO9\n+cjEHOoDAwOqrq7WnDlzVFZWJumzs/NLly7J7/ers7NTPp/PskEBuAO9eWJiCnXDMLR9+3bl5+dr\n0aJFQ9tLS0vV0NCgxYsX69ChQ0NhDwAjwXrzxMUU6qdOndLhw4dVUFCg9evXS5KWLl2qRx99VMFg\nUOvWrRta0ggA8aI3N4/HMAwjGQc6ePCgZs2alYxDAUgTX+3NH7tzIr35VzQ1NWnBggUxf547SgEk\nHb25dQh1AElFb24tQh1AUsTSmx89cEDv7tihrN5eDYwerbkrV+q+8nKbJk5PhDoAS8W63vzogQM6\n/OKL+sWZM0PbqtraJIlgjwNXJABYYtAwdOB0h57+3Qmdv9Kn7Y9M1xOzvjHshdB3d+zQ5i8FuiRt\nPnNGh+vqkjGuY3CmDsB0I+nNs3p7b7g9s6fH7PEcjVAHYJpE1psPjB59w+0RHucdF+oXAAnr7o/o\n9cZP9Oy+kyrwZ+vXj92m+VNy47qBaO7KlaqaPPmabRsKCzVnxQqzx3U0ztQBjJiZ680/vxhaVVen\nzJ4eRbKzNXfFCi6SxolQBzAiVqw3v6+8nBBPEKEOIC48pyW1EeoAYsLzzdMDoQ4gKp7Tkl4IdQDD\n4jkt6YdQB3AdevP0RagDGEJvnv4IdQD05g5CqAMuR2/uLIQ64FL05s5EqAMuQ2/ubIQ64BL05u5A\nqAMuQG/uHoQ6kIZifZcnvbn7xBTqW7duVXNzs7xer6qrqyVJe/bsUX19vbxeryRp6dKlmjlzpnWT\nApAU27s86c3dK6ZQv//++7Vw4UJt2bJlaJvH41FFRYUqKiosGw7A9d7dseOaQJc+e5dnVV2d7nnw\nQXpzl4sp1EtKShQKha7bbhiG6QMBiG64d3l2jcnTD986TW/ucgl16vv371d9fb2Ki4u1fPlyjR3L\nLxFgta++y/Of/jwFH16h/502S//x7a/Tm7vciEu28vJybdmyRS+//LIyMjK0e/duM+cCMIzP3+X5\n6ahsbSt/Uk88v0OtfV1aO7Uv7veCwnlGfKbu8/kkSWPGjNFDDz2kYDBo2lAAhnfPgw/q/SujVf6J\nR7n/95G+/ZfX9WDl47wGDpISCPXOzk7l5OQoEonoyJEjKigoMHMuADcwtN48a5JeWZKvkry5kp6y\neyykkJhCvaamRidOnFBXV5dWrVqlxx57TC0tLWpra1NWVpZKSkpUWVlp9ayAa7HeHLGKKdRfeOGF\n67bNnz/f9GEAO8V6Q08ysd4c8eKOUkCx3dCTTDynBSNFqAOKfkNPskOd57QgEYQ6oOFv6Mns6Una\nDPTmMAOhDuj6G3o+F8nOtvzY9OYwE785gL64oefLNhQWas6KFZYdc9AwdOB0h57+3Qmdv9Kn7Y9M\n1xOzvkGgIyGcqQP64mJoVV2dMnt6FMnO1twVKyzr0+nNYRVCHfiX+8rLLb8oSm8OqxHqQBLQmyNZ\nCHXAQqw3R7IR6oBF6M1hB0IdMBm9OexEqAMmoTdHKiDUgQTRmyOVEOpAAujNkWoIdWAE6M2Rqgh1\nIA705kh1hDoQA3pzpAtCHbgJenOkE0IdGIaZvXkqvioPzkSoA19hdm+eaq/Kg7NxhQf4F6ueb/7u\njh3afINX5R2uq0tov8CNcKYOyNrePBVelQf3INThaslYb27nq/LgPjGF+tatW9Xc3Cyv16vq6mpJ\nUnd3t4LBoEKhkCZOnKg1a9Yom19SpInu/oj++6/n9T9JWG8+d+VKVbW1XVPBbCgs1FwLX5UH94op\n1O+//34tXLhQW7ZsGdq2d+9eTZs2TevXr9e+ffu0d+9eLVu2zLJB4U5mrxqxY715sl+VB3eLKdRL\nSkoUCoWu2dbY2KiNGzdKkgKBgDZu3Eiow1Rmrxr5W/sVbXvvnLIyPElfb56MV+UBUgKdejgclt/v\nlyT5fD6Fw2HThgKkz1aN/OIGq0aq6uriCsjzl/u08y//UEuI57TA+Uy5UMr/ILBCoqtGruvN5/Gc\nFjjfiEPd5/Pp0qVL8vv96uzslM/nM3MuYMSrRnhOC9xsxKctpaWlamhokCQdOnRIZWVlZs0ESPrX\nqpHJk6/ZtqGwUHOirBr5W/sVrXnrlP5w8oJ+8sBkbQgUEuhwlZjO1GtqanTixAldvnxZq1at0pIl\nS/Too48qGAxq3bp1Q0saATPFs2qE3hz4jMcwDCMZBzp48KBmzZqVjEPBRb7amz9250R6czhKU1OT\nFixYEPPnuaMUaYneHLgxQh1px8715kCqI9SRNujNgZsj1JHyWG8OxI5QR8qiNwfiR6gjJdGbAyND\nqCOl0JsDiSHUkRLozQFzEOqwFb05YC5CHbahNwfMR6gj6ejNAesQ6kgaenPAeoQ6LEdvDiQPoQ5L\n0ZsDyUWowxL05oA9CHWYit4csBehDlPQmwOpgVBHwujNgdRBqGPE6M2B1EOoI2705kDqItQRM3pz\nIPUR6ogJvTmQHgh1REVvDqSXhEN99erVuvXWW5WRkaHMzExt2rTJjLlgM3pzID2Zcqa+ceNGjRs3\nzoxdwWb05kB6MyXUDcMwYzewGb05kP4SDnWPx6Of/exn8ng8Ki8v1wMPPGDGXEgienPAORIO9Zde\nekk5OTk6d+6cNm3apG9961sqKSkxYzZYjN4ccJ6EQz0nJ0eSlJ+fr+985ztqbW0l1FMcvTngXAmF\nem9vrwYHB3Xrrbeqq6tLzc3Neuqpp8yaDRagNwecLaFQD4fDevXVVyVJ48eP16JFizRjxgxTBoO5\n6M0Bd0go1PPy8oZCHamJ3hxwF+4odSh6c8CdCHUHojcH3ItQdxB6cwCEugPQmwP4HKGexujNAXwV\noZ6m6M0B3AihnmbozQFEQ6inCXpzALEg1FMcvTmAeBDqKYzeHEC8CPUURG8OYKQI9RRCbw4gUYR6\nCqA3B2AWQt1m9OYAzESo24TeHIAVCPUkozcHYCVCPUnozQEkA6GeBPTmAJKFULcQvTmAZCPULUBv\nDsAuhLqJ6M0B2I1QN0mivfnRAwf07o4dyurt1cDo0Zq7cqXuKy+3aFoATkWoJ8iM3vzogQM6/OKL\n+sWZM0PbqtraJIlgBxCXhEO9paVFu3btUiQS0YIFC7Rw4UIz5kp5Zvbm7+7YcU2gS9LmM2dUVVdH\nqAOIS0KhPjg4qG3btunHP/6xcnNz9eKLL+qOO+5Qfn6+WfOlHCt686ze3htuz+zpSWi/ANwnoVBv\nbW3VpEmTlJeXJ0maPXu2GhsbHRvqVq03Hxg9+obbI9nZpuwfgHskFOoXL17UhAkThn7Ozc1Va2tr\nwkOlGqvXm89duVJVbW3a/KUKZkNhoeauWGHaMQC4AxdKo0jWevPPe/Oqujpl9vQokp2tuStW0KcD\niFtCoZ6bm6uOjo6hnzs6OpSbm5vwUHazY735feXlhDiAhCUU6kVFRWpvb1coFFJubq6OHj2q559/\n3qzZbMFzWgCks4RCPTMzU6tWrdIvf/nLoSWN6XqRlOe0AHCChDv12267Ta+88ooZs9iC57QAcBLX\nXijlOS0AnMiVoU5vDsCpXBXq9OYAnM4VoU5vDsAtHB3q9OYA3MaxoU5vDsCNHBfq9OYA3MwxoU5v\nDgAOCHV6cwD4QlqHOr05AFwrLUOd3hwAbiytQp3eHACiS4tQpzcHgNikfKjTmwNA7FI21OnNASB+\nKRfq9OYAMHIpE+r05gCQuJQIdXpzADCHraFObw4A5rIl1OnNAcAaSQ11enMAsFZSQ33NW6fozQHA\nQiMO9T179qi+vl5er1eStHTpUs2cOTPqdx79dh69OQBYaMSh7vF4VFFRoYqKipi/M39K7kgPBwCI\nQUJXJw3DMGsOAIAJEurU9+/fr/r6ehUXF2v58uUaO5aeHADsFDXUX3rpJV26dOm67Y8//rjKy8v1\n/e9/X93d3XrjjTe0e/durVq1yrJBAQA35zFM6FDa2toUDAZVXV097GeOHz9+w78gAADD8/v9uvvu\nu2P+/Ijrl87OTuXk5CgSiejIkSMqKCiI+vl4hgIAjMyIQ/23v/2t2tralJWVpZKSElVWVpo5FwBg\nBEypXwAAqYEHrgCAgxDqAOAglj/7paWlRbt27VIkEtGCBQu0cOFCqw+Zsi5cuKDa2lqFw2F5vV4F\nAgEFAgG7x7LN4OCgqqqqlJubq6qqKrvHsU1PT4927typv//97+rv79eqVatUXFxs91i2eOedd9TQ\n0KD+/n6VlJToySeftHukpNm6dauam5vl9XqHVhJ2d3crGAwqFApp4sSJWrNmjbKzs6PvyLBQJBIx\nnnvuOeP8+fNGf3+/sW7dOuPs2bNWHjKldXZ2GmfOnDEMwzDC4bDxzDPPuPrP4+233zZee+01Y/Pm\nzXaPYqtgMGgcPHjQMAzDGBgYMK5evWrzRPa4fPmy8eyzzxrd3d1GJBIxfv7znxvNzc12j5U0LS0t\nxscff2z86Ec/Gtr2xhtvGPv27TMMwzB+//vfG7/5zW9uuh9L65fW1lZNmjRJeXl5ysrK0uzZs9XY\n2GjlIVOa3+9XYWGhJMnr9aqoqEidnZ32DmWTjo4ONTc3a/78+a5+3MSnn36qkydPav78+ZKkzMxM\njRkzxuap7DFq1GeP4f7000/V19en3t5ejRs3zuapkqekpOS6u/IbGxs1b948SVIgENCxY8duuh9L\n65eLFy9qwoQJQz/n5uaqtbXVykOmjfb2dp07d05Tp061exRb7Nq1Sz/4wQ/U3d1t9yi2CoVC8nq9\nqq2t1ccff6ypU6fq6aefHgo4Nxk1apSeeeYZrV69WrfccosWLlyoKVOm2D2WrcLhsPx+vyTJ5/Mp\nHA7f9DtcKLVBT0+PampqVFlZefN+zIGOHz8ur9eryZMnu/osXZIikYg++ugjffe739WmTZs0MDCg\nP//5z3aPZYuuri7t3LlTv/rVr1RbW6vTp0+rqanJ7rFSRqyPLLc01HNzc9XR0TH0c0dHh3Jz3f34\n3YGBAVVXV2vOnDkqKyuzexxbnDp1SsePH9fq1av12muv6YMPPtCWLVvsHssWEyZM0Lhx41RaWqpR\no0Zp9uzZam5utnssW7S2tmrq1KmaNGmSxo8fr3vvvVctLS12j2Urn8839HiVzs5O+Xy+m37H0lAv\nKipSe3u7QqGQBgYGdPToUZWWllp5yJRmGIa2b9+u/Px8LVq0yO5xbLN06VJt27ZNtbW1euGFF3T7\n7bfrueees3ssW/j9fk2aNEkffvihBgcH1dTUpDvvvNPusWwxffp0ffTRR7py5Yr6+/vV3NysGTNm\n2D2WrUpLS9XQ0CBJOnToUEwngpbfUdrS0qLXX399aEnjww8/bOXhUtrJkyf105/+VAUFBUP/lIrl\njVFO1tLSorffflsbNmywexTbfPLJJ6qtrVVXV5cKCgpiW7bmUA0NDfrjH/+ovr4+zZgxQ0uWLFFG\nhjta4pqaGp04cUKXL1+Wz+fTkiVLdM8998S9pJHHBACAg7jjr0AAcAlCHQAchFAHAAch1AHAQQh1\nAHAQQh0AHIRQBwAHIdQBwEH+HwEg8WHrbxoVAAAAAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11401f250>"
       ]
      }
     ],
     "prompt_number": 39
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "plot(x, y, 'ro')\n",
      "plot([0,10], [b0, b0+b1*10])\n",
      "for xi, yi in zip(x,y):\n",
      "    plot([xi]*2, [yi, b0+b1*xi], 'k:')\n",
      "xlim(2, 9); ylim(0, 20)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 40,
       "text": [
        "(0, 20)"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAECCAYAAADn84z1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFspJREFUeJzt3X9sVfX9x/HXbQtcft1eygIkdl0RARtEHILyY5QKpEst\nCS6NmsAynHGtWFEy/ZayfJP1q3FcbeqYtEIb9Tv3xxIXjS4zm2uEL1is24B2G0kBLWuFzkEV2nu7\n2nvpbc/3D6ArWtp7b++955x7n4/EBI5X7jvQvvzwOa/7OQ7DMAwBAGwnxewBAACRIcABwKYIcACw\nKQIcAGyKAAcAmyLAAcCm0kb7l1988YVqamrk9XrlcrmUl5envLw89fX1ae/evers7NTs2bO1fft2\nOZ3OeM0MAJDkGK0H3t3dre7ubmVnZ8vn8+mpp57ST3/6Ux06dEjTp0/Xpk2b9M4776i3t1dbtmyJ\n59wAkPRG3UJxu93Kzs6WJLlcLs2bN0+XLl3SsWPHtHbtWklSXl6ejh49GvNBAQDXC3kP/Pz58+ro\n6NCCBQvk9XrldrslSenp6fJ6vTEbEAAwspAC3O/3a8+ePdq6devX9rodDkdMBgMAjG7Um5iSFAwG\nVVVVpTVr1mj58uWSrqy6u7u75Xa71dXVpfT09Bv+93/605/U29sbvYkBIAm43W7deeedo75m1AA3\nDEP79+9XZmamCgsLh64vW7ZMhw4d0n333afDhw8PBftIent7tXTp0jBHB4DxCwQH9drRz9TQ3q2n\nc7O09CaX2SOFrKmpaczXjBrgp0+fVkNDg7KyslRWViZJ2rx5s4qKirR37149/fTTQzVCALCSMxe/\nlOf/PlX2DKf2f+9WuZxjbjjYzqg1wmg4cOAAK3AAcTMwaOjNE51680SnSu6+SetvmWHLe3VNTU1a\nv379qK9JvP8lAUhaF3ou64XDn8ohqXrTQs2ePtHskWKKAAdge4Zh6EBrl2r//E/df/ssFd02S6kp\n9lt1h4sAB2BrPn9QL314Tp92++UpmKd5M6eYPVLccJgVANs63uHTo2+f0sypE1SzaeF14e3xeEyc\nLD5YgQOwHTvXA6OJAAdgK6HWA8vLy+M8WfwR4ABsIVHqgdHEHjgAy7vQc1llv2/V0XM+VW9aqA3z\nM8YMb/bAAcBEyVoPDBUBDsCSIq0HNtbX64PaWqUFAvIUFSm3pESr8vNjPK05CHAAlnO8w6eqhrNa\nM9etsrXf0sS00HZ7G+vr1bBrl55vaxu6Vt7eLkkJGeLsgQOwjEBwUPs+6lBVw1k9nZulbSsyQw5v\nSfqgtlaeq+FdcfWap61NDXV10R/WAliBA7CEaJwemBYIjHg91e8f73iWRIADMFU064HBSZOGflwx\n/D2+8iSxREGAAzBNtE8PzC0pUXl7+9A2iiTtzM5WbnHxOCe1JgIcQNzFqh547UZleV2dUv1+DTid\nyi0uTsgbmBIBDiDOYn164Kr8/IQN7K8iwAHETaT1QIyMAAcQc5weGBsEOICYSoaHC5uF30kAMcHp\ngbFHgAOIumR7uLBZCHAAUcPpgfFFgAOIimR+uLBZCHAA40Y90BwEOICIUQ80FwEOICLUA83H7ziA\nsFAPtA4CHEDIqAdaCwEOYEzUA62JAAcwKuqB1kWAA7gh6oHWRoAD+BrqgfZAgAO4DvVA++BPBoAk\n6oF2RIADoB5oUwQ4kMSoB9obAQ4kKeqB9keAA0mIemBiIMCBJEI9MLEQ4ECSoB6YePgTBBIc9cDE\nRYADCYx6YGIjwIEERD0wORDggMU11tfrg9papQUCCk6apNySEq3Kz7/h66kHJg8CHLCwxvp6Neza\npefb2oaulbe3S9KIIU49MLnwpwtY2Ae1tfIMC29J8rS1qaGu7rprgeCg9n3UoaqGs3o6N0vbVmQS\n3klgzBX4yy+/rObmZrlcLlVVVUmSfvOb3+jgwYNyua50SDdv3qw77rgjtpMCSSgtEBj6ccXVfyQp\n1e8fuk49MHmN+Sd9zz33qKCgQNXV1UPXHA6HNm7cqI0bN8Z0OCDZBSdNGvH6gNNJPRBjb6Hk5ORo\n6tSpX7tuGEZMBgLwH7klJSqfO1fSf1bfO7OztfjhR1X2+1YdPedT9aaF2jA/g/BOQhH/Xeu9997T\nwYMHtWDBAv3gBz8YMeQBjM+1G5XldXVK9fsVdDqVvmW7/vdShu6/3UU9MMlFdJcjPz9f1dXVeu65\n55SSkqJf/epX0Z4LwFWr8vO188031btilYLbKtU0OEuegnl64PbZhHeSiyjA09PT5XA4NGXKFH33\nu99Va2trtOcCMMzxDp/ePfWFZk6doJpNC+l2Q1KEWyhdXV2aMWOGBgYGdOTIEWVlZUV7LgC6/vTA\n2ucrOD0Q1xkzwPfs2aOTJ0/K5/Np27Ztuv/++9XS0qL29nalpaUpJydHW7dujcesQFKhHoixjPkV\nsWPHjq9dW7duXUyGAcDpgQgd/0sHLITTAxEOAhywAE4PRCQIcMBknB6ISBHggIk4PRDjQYDDNsI9\nF9vKeLgwooEAhy2Eey62lVEPRLTw9zXYQqjnYlvZwKChN/52QeV/OKMHl8zWT9ZlE94YF756YAuh\nnIttZdQDEQsEOGxhtHOxrYx6IGKJAIct5JaUqLy9XZ62tuvOxc4tLjZzrFFRD0SsEeCwha+eiz3g\ndCq3uNiyNzCpByIeCHDYxqr8fK3Kz5fH41F5ebnZ44yIeiDiiQAHooR6IOKNrzDYjtVW35weCLMQ\n4MA4nO8J6IXDnypFDuqBiDvurMB2PB6P2SPIMAy9/8klbf/tx1qRla7n772F8EbcsQIHwkQ9EFZB\ngMN2zNwDpx4IKyHAgRBQD4QVsXyA7cR7D/zMxS/1+DundenLfu3/3q2ENyyDAAduYLTTA61wIxVg\nCwW2E489cOqBsAMCHBjmutMDF89S0eKRTw+02oeJkJzYQoHtxGr7wucP6rmD7Xrj7xfkKZinB5bM\n5uhXWBoBDuhKPfDRt09p5tQJqtm0cMxuN3vgsAK2UGA70dy+oB4IOyPAkbTGc3oge+CwArZQYDvj\n3b7g4cJIFAQ4ksr5noD+6/ef6Og5n6o3LdSG+RkRHf3KHjisgGUHbCeS7YtQ64GAnRDgSHixOD2Q\nPXBYAVsosJ1wti/CrQcCdkKAIyEFgoPa91GHqhrO6uncLG1bkRnVo1/ZA4cVsIUC2xlr+4KHCyNZ\n8JWNhBHPhwuzBw4rYAsFtjPS9kW06oGAnRDgsLXrHi78zfg9XJg9cFgBWyiwnWvbFzxcGMmOFThs\nyax6YGN9vTxFRUo7ckSeoiI11tfH5X2BkbACh60EgoPasuO/NXH15rifHthYX6+GXbv0fFvb0LXy\n9nZJ0qr8/LjNAVzDChy2ce3hwn39g6Y8XPiD2lp5roZ3xdVrnrY2NdTVxXUO4BpW4LC8r9UDi3ab\n0jBJCwRGvJ7q98d5EuAKAhyWZqWHCwcnTRr6ccWw6wNOZ9xnASS2UGBRZtUDR5NbUqLyuXOvu7Yz\nO1triotNmgjJjhU4LMeq9cBrNyrL6+qU6vdrwOlUbnExNzBhGgIclnK8w6eqhrNaM9etsrXfiuoB\nVNGwKj+fwIZlEOCwBB4uDIRvzAB/+eWX1dzcLJfLpaqqKklSX1+f9u7dq87OTs2ePVvbt2+Xkxs5\nCaGxvl4f1NYqLRBQcNIk5ZaUxHzFyemBQGTG/E655557VFBQoOrq6qFrb731lhYuXKiysjK98847\neuutt7Rly5aYDorYi/cHVeJ5eiCQiMbcYMzJydHUqVOvu3bs2DGtXbtWkpSXl6ejR4/GZjrE1fAP\nqlwTqw+qcHogMH4R3SHyer1yu92SpPT0dHm93qgOBXMM/6BKxbDr0fygihXrgYBdjXuzkVVT4hj+\nQZXhovVBFavWAwG7imgFnp6eru7ubklSV1eX0tPTozoUzDH8gyoVV69F64MqPFwYiL6IVuDLli3T\noUOHdN999+nw4cNavnx5tOeCCWLxQRXqgUDsOAzDMEZ7wZ49e3Ty5En19PQoPT1dDzzwgFasWBFy\njfDAgQNaunRpTIZH7Hg8nnE/93F4PXD76m9SDwTC0NTUpPXr14/6mjG/o3bs2DHi9bKyssimQsKj\nHgjEB0sijCjS1beVTg8EEh0BjqgwDEMHWrtU++d/6v7Fs1S0eJZSU1h1A7FkrZOCYBnhPHXd5w/q\nuYPteuPvF+QpmKcHlswmvIE4YAWOcbH66YFAIiPAMaKx9sCpBwLmI8ARNk4PBKyBv+9iRCPtgQ8M\nGnrjbxdU/oczenDJbP1kXTbhDZiI7z6EhHogYD0EOEZ0bQ+ceiBgXQQ4bojTAwFrI8Axoid/8j/6\nfHER9UDAwghwXOdaPbDxrFe1pdQDASsjwDFkeD3wwCsv0DABLI7vUHB6IGBTBHiSox4I2BcBnqSo\nBwL2R4AnIeqBQGIgwJMMpwcCiYMATxKcHggkHgI8CXB6IJCY+E5OYNQDgcRGgCco6oFA4iPAEwz1\nQCB5EOAJhHogkFwI8ARBPRBIPgS4zQWCg3r16Gc6Qj0QSDoEuI1RDwSSG9/xNkQ9EIBEgNsO9UAA\n1xDgNkE9EMBXEeA2QD0QwEgIcIujHgjgRghwi6IeCGAsBLgFUQ8EEAqSwUKoBwIIBwFuEdQDAYSL\nADcZ9UAAkSLATUQ9EMB4EOAmoR4IYLwI8DijHgggWgjwOKIeCCCaSJA4oB4IIBYI8BijHgggVgjw\nGKEeCCDWCPAYoB4IIB4I8CijHgggXgjwKKEeCCDexhXgpaWlmjx5slJSUpSamqrdu3dHay5boR4I\nwAzjTpqKigpNmzYtGrPYDvVAAGYad4AbhhGNOWznWj3QQT0QgEnGFeAOh0PPPPOMHA6H8vPztWHD\nhmjNZVnUAwFYxbgC/Nlnn9WMGTPU0dGh3bt366abblJOTk60ZrMc6oEArGRcHbcZM2ZIkjIzM3XX\nXXeptbU1KkNZ0fEOnx59+5RmTp2gmk0LCW8Apot4BR4IBDQ4OKjJkyfL5/OpublZP/zhD6M5myVQ\nDwRgVREHuNfrVWVlpSRp+vTpKiws1JIlS6I2mBVQDwRgZREn0qxZs4YCPNFQDwRgBywpv4J6IAC7\nIMCvoh4IwG4IcFEPBGBPSR/gnB4IwK6SNsCpBwKwu6QMcOqBABJBUiUX9UAAiSRpApx6IIBEk/AB\nTj0QQKJK6ACnHgggkSVsgFMPBJDoEi7AqQcCSBYJFeDUAwEkk4RIOOqBAJKR7QOceiCAZGXbAKce\nCCDZ2TLAqQcCgA0DnHogAFxhmwCnHggA17NFgFMPBICvs3QSUg8EgBuzbIBTDwSA0VkuwKkHAkBo\nLBXg1AMBIHSWCXDqgQAQHtMDnHogAETG1ACnHggAkTMlMakHAsD4xT3AqQcCQHTE7U6hYRh6/5NL\n2v7bj7Xim+l64d5brgtvj8cTr1EAICHEZQVOPRAAoi8uK/BH3z6lmVMnqGbTwhuGd3l5eTxGAYCE\nEZcVOPVAAIi+uKzAQwlv9sABIDx83BEAbMoyAc4eOACExzIBDgAIj2UCnD1wAAiPZQIcABAeywQ4\ne+AAEB7LBDgAIDyWCXD2wAEgPJYJcABAeEwP8Mb6enmKipR25Ig8RUVqrK83eyQAsAVTH4HTWF+v\nhl279Hxb29C18vZ2SdKq/HyTpgIAezB1Bf5Bba08V8O74uo1T1ubGurqTJsJAOwi4hV4S0uLXn/9\ndQ0MDGj9+vUqKCgI/80DgRGvp/r9kY4FAEkjohX44OCg9u3bp6eeekoej0cHDx5UR0dH2L9OcNKk\noR9XDLs+4HRGMhYAJJWIAry1tVVz5szRrFmzlJaWptWrV+vYsWNh/zq5JSUqnzv3ums7s7O1prg4\nkrEAIKlEtIVy6dIlzZw5c+jnGRkZam1tDfvXuXajsryuTql+vwacTuUWF3MDEwBCYGoLRboS4gQ2\nAIQvogDPyMjQxYsXh35+8eJFZWRkjPhat9utpqamyKYDgCTldrvHfE1EAT5v3jydP39enZ2dysjI\nUGNjo5588skRX3vnnXdG8hYAgDE4DMMwIvkPW1pa9Mtf/nKoRnjvvfdGezYAwCgiDnAAgLlMPwsF\nABAZAhwAbCpmNcIvvvhCNTU18nq9crlcysvLU15eXqzeLuouX76siooK9ff3a+LEiVq5cqU2btxo\n9lhhGRwcVHl5uTIyMmz5xKPS0lJNnjxZKSkpSk1N1e7du80eKWR+v1+vvPKKzp49q/7+fm3btk0L\nFiwwe6yQfPbZZ9qzZ8/Qzy9cuKAHH3zQVve53n//fR06dEj9/f3KycnRQw89ZPZIYXnvvff07rvv\nauLEiSosLNT69etHfqERI11dXUZbW5thGIbh9XqNRx55xDh37lys3i4m/H6/YRiGcfnyZePHP/6x\n8a9//cvkicLzu9/9zvjFL35heDwes0eJyGOPPWb09PSYPUZE9u7daxw4cMAwDMMIBoNGb2+vyRNF\nZmBgwPjRj35kfP7552aPErKenh7jscceM/r6+oyBgQHjZz/7mdHc3Gz2WCHr7e01nnjiCaOnp8fo\n6+szysvLb5g9MdtCcbvdys7OliS5XC7NmzdPXV1dsXq7mJh09awWv9+vgYEBpaWZ/rmnkF28eFHN\nzc1at26dDBvfp7bj7F9++aVOnTqldevWSZJSU1M1ZcoUk6eKzIkTJzR79mx94xvfMHuUkE2cOFHS\nlT+Hy5cvKxAIaNq0aSZPFbrTp09r7ty5mjZtmpxOpxYtWqS//OUvI742Lol0/vx5dXR0aP78+fF4\nu6gZHBzUzp07de7cOT300EO2+iJ+/fXX9f3vf199fX1mjxIxh8OhZ555Rg6HQ/n5+dqwYYPZI4Wk\ns7NTLpdLNTU1+sc//qH58+fr4YcfHgoWO/nwww/1ne98x+wxwjJx4kQ98sgjKi0t1YQJE1RQUKBb\nbrnF7LFClpOTo9dee02dnZ2aMGGCmpubddttt4342pjfxPT7/dqzZ4+2bt0qp81OGUxJSVFlZaVe\neukl/fGPf1TbsAdPWNnx48flcrk0d+5cW65gr3n22WdVWVmpJ554Qm+//bZOnjxp9kghGRgY0Jkz\nZ3T33Xdr9+7dCgaD+uijj8weK2zBYFDHjx/XypUrzR4lLD6fT6+88op+/vOfq6amRh9//LGtPg3u\ndDq1detWvfrqq3rxxReVk5Mjh8Mx4mtjugIPBoOqqqrSmjVrtHz58li+VUzNmjVL3/72t9XS0qK5\nXzk90YpOnz6t48ePq7m5Wf39/err61N1dbUef/xxs0cLy4wZMyRJmZmZuuuuu9Ta2qqcnByTpxrb\nzJkzNW3aNC1btkyStHr1ah0+fFhr1641ebLwNDc36+abb5bL5TJ7lLC0trZq/vz5mjNnjiRp5cqV\namlp0dKlS02eLHTLli0b+vr59a9/fcO//cdsBW4Yhvbv36/MzEwVFhbG6m1ixufzqbe3V5LU09Oj\nv/71r8rKyjJ5qtBs3rxZ+/btU01NjXbs2KFFixbZLrwDgcDQ9o/P51Nzc7Ntfv/dbrfmzJmjTz75\nRIODg2pqatLtt99u9lhh+/DDD7V69WqzxwjbrbfeqjNnzujf//63+vv71dzcrCVLlpg9Vli8Xq+k\nK22+o0eP3nAbK2Yr8NOnT6uhoUFZWVkqKyuTdCVY7rjjjli9ZVR1d3erpqZGg4ODcrvd2rhxoxYv\nXmz2WBG50V+/rMzr9aqyslKSNH36dBUWFtrqm7C0tFQ1NTXy+XzKysrSli1bzB4pLH6/XydOnFBJ\nSYnZo4RtypQpKioqUmVlpS5fvqwlS5Zo0aJFZo8VlhdffFG9vb1yOp0qLS294U1wPkoPADbFJzEB\nwKYIcACwKQIcAGyKAAcAmyLAAcCmCHAAsCkCHABsigAHAJv6f2ORRlKEPAhyAAAAAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114376450>"
       ]
      }
     ],
     "prompt_number": 40
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Minimizing the sum of squares is not the only criterion we can use; it is just a very popular (and successful) one. For example, we can try to minimize the sum of absolute differences:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "sabs = lambda theta, x, y: np.sum(np.abs(y - theta[0] - theta[1]*x))\n",
      "b0,b1 = fmin(sabs, [0,1], args=(x,y))\n",
      "print b0,b1\n",
      "plot(x, y, 'ro')\n",
      "plot([0,10], [b0, b0+b1*10])"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 10.162463\n",
        "         Iterations: 39\n",
        "         Function evaluations: 77\n",
        "0.00157170444494 2.31231743181\n"
       ]
      },
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 41,
       "text": [
        "[<matplotlib.lines.Line2D at 0x11438fad0>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXMAAAECCAYAAAAMxDf2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtcU/f9P/AXchUkCRcBBTHKLamtV7ReJqJWWsW2Ktbf\narexdp1WrVsv/rx0363+1u9vtt/O7wREBelaa7d1brZ+123t6LTeAC8IrVXwDpoAIQIhICQhl/P9\no60PbRUhJJxcXs+/6mnIeYnhxcnJ+3yOjyAIAoiIyK0NEDsAERH1HcuciMgDsMyJiDwAy5yIyAOw\nzImIPADLnIjIA/h19z+bmpqQn58PvV4PiUSC9PR0pKenY8+ePThw4AAkEgkAYOnSpRg7dmy/BCYi\nou/qtsz9/PyQnZ0NuVyOtrY2vPzyy0hMTISPjw/mz5+P+fPn91dOIiLqRrdlLpPJIJPJAAASiQQJ\nCQloaWkBAPBaIyIi19Hjc+YajQZqtRrJyckAgE8++QQvvvgitm/fjo6ODqcFJCKie/PpyeX8RqMR\nGzduRFZWFiZOnHjzHLrBYMDu3bths9mwYsWK/shLRER30O1pFgCwWCzYvHkzpk+fjokTJwIApFIp\nACA4OBgPP/ww8vLy7vr1x44d45E7EVEvyWQyTJgwoceP77bMBUHAjh07EBcXh8zMzJvbdTodwsLC\nYLVacfToUcTHx9/1OTo6OjB+/PgeByIiIqCioqJXj++2zM+fP48jR44gPj4ea9euBQA8+eSTKCkp\nQW1tLfz8/KBUKpGdnW1/YiIi6rNuy1yhUODPf/7zd7aPGzfOaYGIiKj3eAUoEZEHYJkTEXkAljkR\nkQdgmRMReQCWORGRB2CZExF5AJY5EZEHYJkTEXkAljkRkQdgmRMReQCWORGRB2CZExG5GJsdd3Jj\nmRMRuZDLzZ148aMLvf66e96cgoiInK+zy4rdFQ3Yf0mHp1OHAJ29u6kPj8yJiEQkCAKO1rbip3ur\n0W6yojBLgbmKyF4/D4/MiYhEomk3Ib9UjYb2LqxLH47RQ0Ltfi6WORFRPzNbbdh7Rou/ntZi8ego\n/OqhEfD37duJEpY5EVE/Ot1wA3klKkSHBiBvQQqGhAY65HlZ5kRE/UBvtKDoRB1O1bVj5eQ4TJNL\n4ePj47DnZ5kTETmRTRDwrwstePtkPWYlhqEoS4ngAF+H74dlTkTkJDUtBuSWqGC1Cdg0NwEJEcFO\n2xfLnIjIwQxmK/5QqcG/LrQge8IQzFNEYIADT6ncCcuciMiByq7qsa1MjftjQlC4SIGwYP9+2S/L\nnIjIAbQ3upBfpoaq1YiX0uIxbqj9M+P2YJkTEfWBxSbgwzNa/PmLRiy4Pwq/mCVHQB9nxu3BMici\nstPZxhvIPapCeLA/ch5LQazUMTPj9mCZExH1UpvRgrdO1uOEqg3PTY5F2giZQ2fG7cEyJyLqIUEQ\n8OnFFrx1sh5pI8JQtFiJECfMjNuDZU5E1APXdEbklqhgsFjxWkYCkgc7b2bcHixzIqJuGC02/KlS\ng3+eb8YPx8cgUxEJ3wHinlK5E5Y5EdFdnFDpsbVUDcXgYOxYpEBEP82M24NlTkT0LU0dXdh+rA6X\nmw342bRhSI2TiB3pnljmRERfs9oE/E/Vdfzp80Y8qozEuhnDEeDnHjdkY5kTEQGo1nYgt0QFSaAv\nfvdoEuKkQWJH6hWWORF5tRsmC35f3oDSq61YNikWMxPCRJ8ZtwfLnIi8kiAIOHBZh53H6zBVLsPO\nLCVCA923ErtN3tTUhPz8fOj1ekgkEqSnpyM9PR0GgwF5eXnQarWIjo7G6tWrERTkXm9JiMh7qVqN\nyCtVod1kxatzRkIZFSJ2pD7rtsz9/PyQnZ0NuVyOtrY2vPzyy0hMTMTBgweRkpKCtWvXYt++fdi7\ndy+eeuqp/spMRGSXLosN73/RiI+qm/Dk2Gg8ft9gl5wZt0e3H9PKZDLI5XIAgEQiQUJCAlpaWlBe\nXo4ZM2YAANLT03Hy5EmnByUi6otydRuWfXAOV1uN2L4wBYvuj/KYIgd6cc5co9FArVYjOTkZer0e\nMpkMACCVSqHX650WkIioL5o7zSg4psa56514fmocJg2Tih3JKXpU5kajEVu2bEF2dvZ3zo2746e+\nROT5rDYBf69uwnuVGsxLicBLacMR5CYz4/a4Z5lbLBZs3rwZ06dPx8SJEwF8dTTe2toKmUwGnU4H\nqdQzf9MRkXu60NSJnKPXEOTni99mJmJ42ECxIzldt2UuCAJ27NiBuLg4ZGZm3tyempqKgwcPYsGC\nBTh06NDNkiciElNHlxXvlDfgcI0OP5k4FHOSwr3m7EG3ZX7+/HkcOXIE8fHxWLt2LQBg6dKlyMrK\nQl5eHtasWXNzNJGISCyCIOBwTSt2HKvDpGES7MxSQhLkvjPj9vARBEFw5g7279+P8ePHO3MXROTF\n6ttM2FqqQnOHGT/73jCMih4kdiSHqKiowOzZs3v8eO/61UVEHqPLasOe01rsO6PF/xkTjYX3R8HP\ng0YNe4tlTkRup7K+HXklKsTLgrBtoQJRgwLEjiQ6ljkRuQ1dpxmFJ+pwRtOBlVPiMGU4J+m+wTIn\nIpdnEwT881wzdp1qwMPJ4SjMUmCgv2vcSNlVsMyJyKVdbu5EzlEVfAf44L/mJWJEuOfPjNuDZU5E\nLqmzy4p3Kxpw4JIOz0wciozkcAzwkplxe7DMiUh0pcXFOFxQAD+TCebAQAz+4WocMERiQmwodi5W\nQuplM+P28NyFCojILZQWF+PIhg1447PPsLL6CrrkD+EfF25gfsh1vJw2nEXeQyxzIhLV4YICvHZN\nhbdnPonsn23D2Jov8embz0D1br7Y0dwKf+URkajaBsXgqRcKMbSlAbtyVyJWpwEA+BqNIidzLyxz\nIhJFq8GMohP1+DL1Cfz6L/+NmWeO4taPN628FWWv8DQLEfUrmyDg4/PNWLb3HEIDffFSkhnFHXW3\nFfk6uRzTly0TLaM74pE5EfWbmhYDco6qYBMEbJqbgISIYABxCBwgYH1hIXyNRliDgpC2bBmmZmSI\nHdetsMyJyOkMZiveq9Cg+GILsicMwTxFxG0z41MzMljefcQyJyKnKruqR36ZCqNjBqFwkQJhwf5i\nR/JILHMicgrtjS7kl6mhajXi5bThGDc0VOxIHo1lTkQOZbEJ+OCMFnu+aMTC+6Pwi1lyBPhy1sLZ\nWOZE5DBnNTeQU6JCZIg/ch9PwVBJoNiRvAbLnIj6rM1owVsn63FS1YbnJsdi+giZ19xI2VWwzInI\nboIg4NOLLXjrZD1mjAzDzsVKhARwnXExsMyJyC5XdQbklqhhstjw2sMJSI4MFjuSV2OZE1GvGC02\n/LFSg4/PN+OH42OQqYiErxffSNlVsMyJqMdOqPTYWqqGYnAwdixSIIIz4y6DZU5E93S9owvby+pw\npcWAn08bhglxErEj0bewzInorqw2AfvOXsf7XzTiUWUk1qcPR4AfZ8ZdEcuciO6oWtuBnKMqSIN8\n8btHkxAn5ZK0roxlTkS3aTdZ8PbJBpRea8WySbGYmRDGmXE3wDInIgBfzYwfuKzDzuN1mCaXoShL\niUGBrAh3wX8pIoKq1Yi8UhVumKzYOGckFFEhYkeiXmKZE3mxLosN73/RiI+qm7B0bDQeu28wZ8bd\nFMucyEuVq9uwtVSFxIhgbF+YgsiQALEjUR+wzIm8THOHGTuOq3H+eieenxqHScOkYkciB2CZE3kJ\nq03A36ub8F6lBvMUEXg5bTiCODPuMVjmRG6mtLgYhwsK4GcywRIYiLTly+95/8wL1zuRU3INA/18\nsTkzCfFhnBn3NCxzIjdSWlyMIxs24I2ampvb1tfWAsAdC72jy4p3yutxpKYVP5k0FA8lhnNm3EPd\ns8y3bduGyspKSCQSbN68GQCwZ88eHDhwABLJV+szLF26FGPHjnVuUiLC4YKC24ocAF6vqcH6wsLb\nylwQBBy60oqC43V4MF6CwiwlJEE8dvNk9/zXnTlzJubOnYutW7fe3Obj44P58+dj/vz5Tg1HRLfz\nM5nuuN3XaLz533V6E7aWqtDSacZ/zJZjVPSg/opHIrpnmSuVSmi12u9sFwTBKYGI6O4sgXe+p6Y1\nKAhdVhv2fNGIfWev4/tjorHg/ij4cWbca9j9vuuTTz7BgQMHkJycjB/96EcICeEVY0TOlrZ8OdbX\n1uL1W061rJPLEfejVXjug3OIlwVh20IFogZxZtzb2FXmGRkZWLx4MQwGA3bv3o13330XK1ascHQ2\nIvqWb86Lry8shK/RiE5JBPTzn8PZTglWTonFlOGcGfdWdpW5VPrVCyY4OBgPP/ww8vLyHBqKiO5u\nakYGJs+Zg3+ea8auUw14JDEc/zkuBgP9eSNlb2ZXmet0OoSFhcFqteLo0aOIj493dC4iuovLzZ3I\nOaqC3wAf/Ne8RIwIHyh2JHIB9yzzLVu2oLq6Gm1tbVixYgWeeOIJVFVVoba2Fn5+flAqlcjOzu6P\nrERerbPLil0VDfjskg7PTByKjORwDODMOH3tnmX+wgsvfGfbrFmznBKGiL5LEAQcrdVj+zE1JsSG\nYudiJaScGadv4SuCyIU1tJuQX6pGY3sXNsyU44EYzozTnbHMiVyQ2WrDX7/UYu+XWjwxOhqvPjQY\n/r5cFIvujmVOXs+ehauc6XRDO3JL1BgSGoCtC1IQE3rnC4WIbsUyJ6/W24WrnKnVYMbOE/X4vL4d\nK6fEYepwKRfFoh7j+zbyaocLCm67mhL4auGqI4WF/ZbBJgj4+FwTlu09B2mQH4oWKzFNLmORU6/w\nyJy8Wk8WrnKmK80G5JaoIEDAprkJSIgI7pf9kudhmZNX627hKmcymK3YXaHBpxdb8OPUIZibEsGZ\nceoTnmYhr5a2fDnWjxhx27Z1cjmmL1vmtH2WXm3FT/dWo9VgRmGWApmKSBY59RmPzMmrfXvhKmtQ\nENKWLXPKh5+N7V3YVqaGSm/EmrThGDs01OH7IO/FMievNzUjw6mTKxabgA++1GLP6UYsuj8Kv5gt\nRwBnxsnBWOZETnRGcwO5JSpEhvgj9/EUDJVwZpycg2VO5ARtRguKTtSjXN2G5ybHYvoIjhqSc7HM\niRxIEAR8erEFb52sx4yRYdi5WImQAK4zTs7HMidykKs6A3JL1DBZbPjPhxOQFMmZceo/LHOiPjJa\nbPhjpQYfn2/GD8fHIFMRCV/eSJn6GcucqA+OX9Nja6ka90WHYMciBSKC/cWORF6KZU5kh+sdXdhe\npkZNixEvTh+G8bESsSORl2OZE/WC1SZg39nr+NPnGjw+ajDWp8sR4MeZcRIfy5yoh6q1Hcg5qoI0\nyA9bHktGnNS567cQ9QbLnOge2k0W/P5kPcqu6bH8wVikjwzjzDi5HJY50V0IgoD9l3QoOlGHaXIZ\nirKUGBTIHxlyTXxlEt3BtVYj8kpU6OiyYuOckVBEhYgdiahbLHOiW5gsNvzpcw3+Xt2Ep8bF4LH7\nBnNmnNwCy5zoa+XqNuSVqJAUGYwdixSIDAkQOxJRj7HMyes1d5ix45gaF5o6sWpqHCYNk4odiajX\nWObktaw2AR9VN+EPlRrMU0RgzYzhCOTMOLkpljl5pQvXO5FTcg3B/r7YnJmE+DDOjJN7Y5mTV+no\nsuLt8nocrWnFs5NiMTuRM+PkGVjm5BUEQcDBK60oPF6HB+MlKMxSQhLElz95Dr6ayePV6Y3IK1Wj\n1WDGL2ePwH3R/TszXlpcjMMFBfAzmWAJDETa8uVOvecoeSeWOXmsLqsNe75oxL6z1/H9sTFYOKr/\nZ8ZLi4txZMMGvFFTc3Pb+tpaAGChk0Pxo3vySJV17Xjug3O43GzAtoUKLH4gSpSLfw4XFOD1W4oc\nAF6vqcGRwsJ+z0KejUfm5FFaOs0oOF6HqsYOrJwShynDxZ0Z9zOZ7rjd12js5yTk6Vjm5BGsNgH/\nPNeEdys0eCQ5HC9kKTDQX/wbKVsCA++43RrEUUhyLJY5ub1LTZ3IKVHBf4AP3sxMhDxsoNiRbkpb\nvhzra2tvO9WyTi5H2rJlIqYiT8QyJ7fV0WXFu6ca8NllHX4yaSjmJIVjgIvNjH/zIef6wkL4Go2w\nBgUhbdkyfvhJDnfPMt+2bRsqKyshkUiwefNmAIDBYEBeXh60Wi2io6OxevVqBPFtI/UTQRBwpLYV\nO8rqMCEuFDsXKyF14ZnxqRkZLG9yuntOs8ycOROvvPLKbdv27t2LlJQU/Pa3v0VSUhL27t3rtIDk\nnUqLi/F6VhZ+O38+Xs/KQmlxMQCgoc2E//jXFeyu0GDDLDleThvu0kVO1F/u+VOgVCqh1Wpv21Ze\nXo6NGzcCANLT07Fx40Y89dRTTglI3udOs9lrr6lwWB+McqMET4yOxqL7B8Pfl5O1RN+w65BGr9dD\nJpMBAKRSKfR6vUNDkXc7XFBwW5GfGjkGtQt+jvaL9di6eiJiQu88IULkzfr8/pSLFJGjfTOb3RIi\nQ27mcpQnjMGav+WjWCog5pUlIqcjck12vU+VSqVobW0FAOh0OkilXMyfHMccGIgPJ83D918ugqyj\nFXs2P4P0syWw8UN2oruy68g8NTUVBw8exIIFC3Do0CFMnDjR0bnIS11pNuDi4+tQce0qtheuRZLm\nCgDOZhPdyz3LfMuWLaiurkZ7eztWrFiBJUuWICsrC3l5eVizZs3N0USivjCYrdhdocGnF1vw9KSR\nkES34q3P5fAdGcPZbKIe8BEEQXDmDvbv34/x48c7cxfk5kqvtmJbmRqjh4Tip5OGImygv9iRiERX\nUVGB2bNn9/jxHNAl0TS2dyG/TIU6vQlr0oZj7NBQsSMRuS2WOfU7i03AB19qsed0I7IeiMIvZ4/g\nzDhRH7HMqV+d0dxATokKg0P8kfd4CoZIODNO5Agsc+oXeqMFRSfqcErdjuemxGK6XMZrFIgciGVO\nTiUIAoovtuCtE/WYmRCGnYuVCAkQf51xIk/DMienqdUZkFuigtkq4P8/koCkyGCxIxF5LJY5OZzR\nYsMfKjX45Hwzfjg+BpmKSFHuv0nkTVjm5FDHrumRX6rGfdEhKFikQHgwZ8aJ+gPLnBxCe6ML28vU\nqNUZ8eL0YRgfKxE7EpFXYZlTn1htAj48ex3vf67B46MGY8NMOQL8ODNO1N9Y5mS3am0Hco6qIA3y\nQ85jyYiVclVDIrGwzKnX2k0W/P5kPcqu6bH8wTikj+TMOJHYWObUY4IgYP8lHYpO1OF7I2QoylJi\nUCBfQkSugD+J1CPXWo3IK1Gho8uK/5cxEimDQ8SORES3YJlTt0wWG/70uQb/ONeMp8bF4FElZ8aJ\nXBHLnO7qpKoNW0tVSI4Mxo6FCkSEcGacyFWxzOk7mjvM2H5MjYtNnXh+6jBMHMaZcSJXxzKnm6w2\nAX+ruo4/ft6ITEUE/u+M4QjkzDiRW2CZEwDg/PWvZsZDAnyxeX4S4mWcGSdyJyxzL3fDZMHb5Q0o\nqW3Fs5NiMTsxjDPjRG6IZe6lBEHAwSs6FByvw5R4KXYuViKUM+NEbos/vV6oTm9EbokaeqMZv5o9\nEvdFc2acyN2xzL1Il8WGP59uxP+cvY7vj43BwlGDOTNO5CFY5l6ioq4NeSVqjAgPwraFCkQNChA7\nEhE5EMvcw7V0mlFwvA5VjR1YNTUOk+OlYkciIidgmXsoq03AP841YXeFBo+kRODF6fEI4sw4kcdi\nmXugi02dyC1Rwd/XB29mJkIeNlDsSETkZCxzD9LRZcW7pxpw8IoOP5k4FHOSwjkzTuQlWOYeQBAE\nHKltxY6yOqTGSbAzSwlJEP9pibwJf+LdXH2bCVtLVbjeYcYrs+S4P2aQ2JGISAQsczfVZbXhr6e1\n+OCMFktGR2PRA1Hw48w4kddimbuhL+rbkVuiQqw0EPkLFIgO5cw4kbdjmbsRncGMncfrcFpzAyun\nxGHqcJnYkYjIRbDM3YBNEPDx+Wa8U96AOUnh2JmlxEB/X7FjEZELYZm7uMvNncgrUQMA3pibiJER\nnBknou9imbsog9mK3RUafHqxBU+nDsEjKREYwJlxIrqLPpX5qlWrMHDgQAwYMAC+vr7YtGmTo3J5\nLUEQUHJVj+1laowdGorCLAXCBvJGykTUvT4fmW/cuBGDBnG22RE07Sbkl6pR32bC2hnDMWZoqNiR\niMhN9LnMBUFwRA6vZrEJ2PulFn853YisB6Lwq4dGwN+Xi2IRUc/1qcx9fHzw61//Gj4+PsjIyMBD\nDz3kqFxe40vNDeSWqBAVEoC8x1MwRBIodiQickN9KvPXXnsNYWFhUKvV2LRpE2JjY6FUKh2VzaPp\njRYUnajDqbp2rJgch+/JpVwUi4js1qf38mFhYQCAuLg4TJo0CZcuXXJIKE9mEwR8cr4ZP/1rNYID\nfLEzS4npI2QsciLqE7uPzE0mE2w2GwYOHIi2tjZUVlbi6aefdmQ2j1PTYkBeiQpmm4DfPJKAxMhg\nsSMRkYewu8z1ej3efPNNAEBoaCgyMzMxZswYhwXzJAazFX+s1OCTCy3InjAEc1MieCNlInIou8s8\nKirqZpnT3R27pkd+qRqjokNQsEiB8GDOjBOR4/EKUCfR3ujC9jI1anVGvDQ9HuNiOTNORM7DMncw\ni03AvjNavP9FIxaMGowNM+UI4I2UicjJWOYOVNXYgdySa5AN9EfOY8mIlQaJHYmIvATL3AHajBa8\ndbIeJ1RtWPZgLNJHctSQiPoXy7wPBEHAvy+1oOhEPdJGyFC0WImQAK4zTkT9j2Vup2s6I/JKVejo\nsuK1jAQkD+bMOBGJh2XeSyaLDX/8XIN/nmvGU+Ni8KgykjPjRCQ6lnkvnFS1YWupCsmRwdixUIGI\nEM6ME5FrYJn3QFNHF7Yfq8Pl5k6snjYMqXESsSMREd2GZd4Nq03A36qu4w+VGjx632CsnTEcgZwZ\nJyIXxDK/i3PaDuSWqBAS4Iv/fjQZ8TLOjBOR62KZf8sNkwVvlzegpLYVP30wFrMSwjgzTkQuj2X+\nNUEQcPCKDgXH6zA1Xoadi5UIDeS3h4jcA9sKQJ3eiNwSNfRGC159aCSUUSFiRyIi6hWvLvMuiw3v\nf9GIv1Vdx5NjY7Bg1GDOjBORW/LaMj+lbkNeqRojw4OwbaECUYMCxI5ERGQ3ryvzlk4zCo7Xoaqx\nA89PjcOD8VKxIxER9ZnXlLnVJuAf55qwu0KDuSkReHF6PII4M05EHsIryvxiUydyjqoQ4OeDNzMT\nIQ8bKHYkIiKH8ugy7+iyYtepBhy6osNPJg7FnKRwzowTkUfyyDIXBAGHa1pRcKwOqXES7MxSQhLk\nkX9VIiIAHljm9W0mbC1VoanDjF/MkmNUzCCxIxEROZ3HlHmX1Ya/nNbiwzNaLBkTjUX3R8GPM+NE\n5CU8osw/r29HbokKw6RByF+gQHQoZ8aJyLu4dZnrDGbsPF6H05obWDklDlOHy8SOREQkCrcsc5sg\n4OPzzXinvAEZSeHYmaXEQH/eSJmIvJfblfnl5k7klqjgAx+8MTcRIyM4M05E5DZl3tllxe6KBvz7\nkg7PpA7BwykRGMCZcSIiAG5Q5oIgoOSqHtvL1Bg3NBQ7sxSQDeSNlImIbuXSZa5pNyG/VI2G9i6s\nSx+O0UNCxY5EROSSXLLMzVYb9p7R4q+ntch6IAq/emgE/H25KBYR0d24XJl/qbmB3KMqRA0KQN7j\nKRgiCRQ7EhGRy3OZMtcbLSg6UYdTde1YMTkO35NLuSgWEVEPiV7mNkHAvy604O2T9ZiZGIaiLCWC\nA7xnZry0uBiHCwrgZzLBEhiItOXLMTUjQ+xYRORmRC3zmhYDcktUsNgE/OaRBCRGBosZp9+VFhfj\nyIYNeKOm5ua29bW1AMBCJ6JesbvMq6qqsGvXLlitVsyePRtz587t8dcazFb8oVKDf11oQfaEIZib\nEuGVN1I+XFBwW5EDwOs1NVhfWMgyJ6JesavMbTYbtm/fjl/+8pcIDw/Hhg0b8MADDyAuLu6eX1t2\nVY9tZWqMig5B4SIFwoK9d2bcz2S643Zfo7GfkxCRu7OrzC9duoSYmBhERUUBAKZNm4by8vJuy1x7\nowvbytS41mrES9PjMS6WM+OWwDtP6liDgvo5CRG5O7uGt1taWhAREXHzz+Hh4Whpabnr4/9yuhEr\nPzyHxMhg7FikYJF/LW35cqwfMeK2bevkckxftkykRETkrvrlA9BTde3IeSwFsVLOjN/qm/Pi6wsL\n4Ws0whoUhLRly3i+nIh6za4yDw8PR3Nz880/Nzc3Izw8/I6PlclkWIJWNF4+i0b7Mnq0oMhIzHnl\nldu2VVRUiJSGiFyFTNa7+zPYVeYJCQnQaDTQarUIDw9HaWkpfv7zn9/xsRMmTLBnF0RE1As+giAI\n9nxhVVUV3nnnnZujifPmzXN0NiIi6iG7y5yIiFwHlyIkIvIALHMiIg/g1NHEvlzy70mampqQn58P\nvV4PiUSC9PR0pKenix1LVDabDevXr0d4eDjWr18vdhzRGI1GFBUV4dq1azCbzVixYgWSk5PFjiWK\nf//73zh48CDMZjOUSiV+/OMfix2p32zbtg2VlZWQSCTYvHkzAMBgMCAvLw9arRbR0dFYvXo1grq7\noFBwEqvVKjz//PNCY2OjYDabhTVr1ggqlcpZu3NpOp1OqKmpEQRBEPR6vfDss8967ffiGx999JGQ\nk5MjvP7662JHEVVeXp6wf/9+QRAEwWKxCB0dHSInEkd7e7uwcuVKwWAwCFarVfjNb34jVFZWih2r\n31RVVQlXrlwRXnrppZvbdu/eLezbt08QBEH48MMPhffee6/b53DaaZZbL/n38/O7ecm/N5LJZJDL\n5QAAiUSChIQE6HQ6cUOJqLm5GZWVlZg1axYEL/78vbOzE+fOncOsWbMAAL6+vggO9q6VQ78REBAA\n4KvvSVdXF0wmEwYNGiRyqv6jVCoREhJy27by8nLMmDEDAJCeno6TJ092+xxOO81yp0v+L1265Kzd\nuQ2NRgO1Wo2kpCSxo4hm165d+MEPfgCDwSB2FFFptVpIJBLk5+fjypUrSEpKwjPPPHOz2LxJQEAA\nnn32Wayo7H3+AAACEUlEQVRatQr+/v6YO3cuEhMTxY4lKr1ef/PCIalUCr1e3+3j+QFoPzIajdiy\nZQuys7O7P/flwU6dOgWJRIIRI0Z49VE5AFitVly+fBkPPvggNm3aBIvFgrKyMrFjiaKtrQ1FRUX4\n3e9+h/z8fFy4cIFXQt+iJ3ddc1qZ9+aSf29gsViwefNmTJ8+HRMnThQ7jmjOnz+PU6dOYdWqVcjJ\nycHZs2exdetWsWOJIiIiAoMGDUJqaioCAgIwbdo0VFZWih1LFJcuXUJSUhJiYmIQGhqKKVOmoKqq\nSuxYopJKpWhtbQUA6HQ6SKXSbh/vtDK/9ZJ/i8WC0tJSpKamOmt3Lk0QBOzYsQNxcXHIzMwUO46o\nli5diu3btyM/Px8vvPACRo0aheeff17sWKKQyWSIiYnBxYsXYbPZUFFRgdGjR4sdSxQKhQKXL1/G\njRs3YDabUVlZiTFjxogdS1Spqak4ePAgAODQoUP3PAh06hWgvOT/K+fOncOrr76K+Pj4m2+Xli5d\nirFjx4qcTFxVVVX46KOPsG7dOrGjiKa+vh75+floa2tDfHz8vcfPPNjBgwfx2WefoaurC2PGjMGS\nJUswYIB3nAnesmULqqur0d7eDqlUiiVLlmDy5Mm9Gk3k5fxERB7AO37tERF5OJY5EZEHYJkTEXkA\nljkRkQdgmRMReQCWORGRB2CZExF5AJY5EZEH+F/v1qgWqcLbdgAAAABJRU5ErkJggg==\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11438fb50>"
       ]
      }
     ],
     "prompt_number": 41
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We are not restricted to a straight-line regression model; we can represent a curved relationship between our variables by introducing **polynomial** terms. For example, a cubic model:\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$y_i = \\beta_0 + \\beta_1 x_i + \\beta_2 x_i^2 + \\epsilon_i$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "ss2 = lambda theta, x, y: np.sum((y - theta[0] - theta[1]*x - theta[2]*(x**2)) ** 2)\n",
      "b0,b1,b2 = fmin(ss2, [1,1,-1], args=(x,y))\n",
      "print b0,b1,b2\n",
      "plot(x, y, 'ro')\n",
      "xvals = np.linspace(0, 10, 100)\n",
      "plot(xvals, b0 + b1*xvals + b2*(xvals**2))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 14.001110\n",
        "         Iterations: 198\n",
        "         Function evaluations: 372\n",
        "-11.0748186039 6.0576975948 -0.302681057088\n"
       ]
      },
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 42,
       "text": [
        "[<matplotlib.lines.Line2D at 0x114440890>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXsAAAECCAYAAAAfE3cCAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlcVXX+P/AX3MsO914uyCJyBREEHXdsMxW1MHKpyeo7\nWpPN/Pzm2GrpJFmOTlaY5USDqFkzTTnNotO3muZbZoqY608R0go12QQUuCx3YbmXu53vHyZToxJw\nOZy7vJ6Phw8fHM45n7ciLw+f81l8BEEQQEREHs1X6gKIiEh8DHsiIi/AsCci8gIMeyIiL8CwJyLy\nAgx7IiIvIHfm4qamJuTn58NgMEChUCAjIwMZGRkwmUzIy8uDVqtFdHQ0HnvsMQQGBvZXzURE1Es+\nzoyz1+v10Ov1SEhIgNFoxPLly7FmzRoUFhYiLCwMd9xxBz788EO0t7fjvvvu68+6iYioF5zqxlGp\nVEhISAAAKBQKJCUloaWlBUVFRZg2bRoAICMjA8ePH3e6UCIi6rt+67Ovr69HbW0tUlJSYDAYoFKp\nAABKpRIGg6G/miEioj7ol7A3m83Izc3FokWLruib9/Hx6Y8miIjICU69oAUAm82GjRs3YsqUKZg0\naRKAS0/zer0eKpUKOp0OSqXymtcfPXoU7e3tzpZBRORVVCoVJk6c2OPznQp7QRCwdetWDBkyBLNn\nz+46np6ejsLCQtx5553Yv39/138CV9Pe3o4JEyY4UwYRkdcpLi7u1flOhf3Zs2dx4MABaDQaPP30\n0wCAhQsXYv78+cjLy8OKFSu6hl4SEZF0nBp62R/27t3LJ3sioh4QBAECAEEATn5ZgpkzZ/b4Wqf7\n7ImI6EoWmwPGThsMZhuMnXa0dtrQ1mlHm8WO9k47Oqx2dFgd6LDYYbY5YLY50Pnd71a7AKvdAYtd\ngM0hwC4IsDsEOATAB4CPD/DS+N7Vw7AnIuqFTpsDTe0WNLZb0dhuQXOHFc3tNrSYrGjpsEJvskFn\nssJiF6AIlEEZIIciUI6wABlC/eUIDZAhxF8GVZAcIf4yBPnJEOTni0C5LwLkvgiQ+cJP7gN/mS/8\nfH0g/+6XzNcHvj7/HuE4oH32REQD4fDu3fjijTcg7+yELSAAU5cswU2ZmaK0ZXcI0LZbUGfsRF2r\nBfXGTtS3WlDfZkFDqwXtVjsig/0QGeKPyBA/RAb7ISbMH6OiQ6AOlkMV5IfwIDlC/WUuNfScYU9E\nLu3w7t048MwzeLmysutYdlUVADgV+O0WO6r1ZlTrzajRm1Gj70StwYz6NguUgXLEKQIQGxaAWIU/\nbkpQIjo0ANFh/ggPksPXhUK8pxj2ROTSvnjjjR8EPQCsr6xE9rZtPQp7i92BGr0ZFS0mVLaYUaUz\noarFjDaLHfGqAGhUgdCoAnFLshpDlAGIVQQgUO55CwIz7InIpck7O696XGY2X3HMZLWjvNmEc00d\nKGs2oby5A7WGTsSGBSBRHYhEdRDmpg1CgjoQ0aH+bvmE3lcMeyJyabaAgKsetwYF41xTB85o23Gm\nsQPfNnWgvtWChPBAJEcEY1R0CO4YOQgJ4YHw98An9d5i2BORS5u6ZAmyq6qQ3dCMr4aOxMmho/DR\niIloH5KCisLzSI0KRlpUCO4cdSnY/WQM9qth2BORS2pqt+BkXRu+Dk7Fqce34rYOG1S6WiiMFzFn\nXDTmZ41FiL9M6jLdBsOeiFyCrsOKkoutOFnXhpN1bWjrtGF0TChGx4Yia/YoJKmDIPP1nj72/saw\nJyJJmKx2fFXfhhMXWlFyoRVN7VaMjg3FuNjQS33t6kCveoEqNoY9EQ0IQRBQpTPjeI0RRReMONvY\ngeSIYEwcEoanpmiQHBnMJ3cRMeyJSDRmmwMlF1pxtNqA47VGyHx8cF28Aj8dFYWxsaEIZp/7gGHY\nE1G/au6w4sh5A45WG/B1fRuSI4NxfbwC80cPR7wywKWWEPAmDHsiclqtwYyDVXocrjKg1tCJSfEK\n3DJcjeyMoQgNYMy4An4ViKjXLve/H6jU40CVHq2dNkweqsKiibEYExvKse4uiGFPRD1W2WLC/god\nvqjUw2J3YEqCCk/erEFqVDBHzrg4hj0RdeuisROF5ToUVujQZrFjWqIKv542FKmDgtn/7kYY9kR0\nBZ3Jii8q9Nhb1oK6VgumDVPh8cnxGBkdwid4N8WwJyIAl7bRO1JtwJ5zLfi6oR3Xxytw/4QYTIhT\nQM7x726PYU/kxQRBwJnGDnz2bTMOVOoxPCIYtyarsWpGAoL8OAbekzDsibyQrsOKz8tasPvbFtgc\nAmalqLHlp6mICvWXujQSCcOeyMNca79Wu0PAiQtG7DrbjJKLbZg8VIllN8djVHQIX7R6AafDfvPm\nzSgpKYFCocDGjRsBADt27EBBQQEUCgUAYOHChRg3bpyzTRHRj7jafq1PanXYbwjGN3YVVIF+yEqN\nwPKpQ7k8sJdxOuynT5+OrKwsbNq0qeuYj48P5syZgzlz5jh7eyLqhcv7tQoAjg8fj3/cOA8nk8Yj\n7OuzWPPYAiRHBktdIknE6bBPS0uDVqu94rggCM7emoh6SbADf518F96/cS787DbcfeQjrNmxAS9N\nHI/kyP8ndXkkIdH67Hft2oWCggKkpKTggQceQEhIiFhNEXm9ap0ZH5U24kDmcshLj+K5f2zE2Kqv\ncbkn3h4YKGl9JD1RFrDIzMzEpk2b8OKLL8LX1xfvvvuuGM0QeTWHIOBYjQHPfFqGX39yDopAOR5P\n6IDjyHsY972gX5mQgCkPPSRprSQ9UZ7slUolACA4OBizZs1CXl6eGM0QeSWzzYHPv23GB980IkDu\ni7t+Mgi/HTYM/jJfALFQyHOQvW0bZGYz7IGBmPrQQ7gpM1PqskliooS9TqdDeHg47HY7Dh48CI1G\nI0YzRF6lpcOKj0ob8cmZZoyMDsGymzUYHXPlsMmbMjMZ7nQFp8M+NzcXp0+fhtFoxNKlS3HPPfeg\ntLQUVVVVkMvlSEtLw6JFi/qjViKvVK034x+ntDh0Xo+MYeHInZuMOCX74Kl3nA77ZcuWXXFsxowZ\nzt6WyGVca5KS2Eob2vH3Uw043dCOeSMj8cd7RkIZyHmQ1Df8l0PUjatNUsquqgIAUQJfEAQU1bbi\n7ycb0NBmwT1jovDM9AQEyrkZCDmHYU/UjcuTlL5vfWUlsrdt69ewdwgCDlUZ8Ncv62F1CPivMdGY\nnhQOGVebpH7CsCfqhryz86rHZWZzv9zf7hBQWKHD375sQKCfL+6fEIMbNEquGU/9jmFP1A1bQMBV\njzs7ScnuEFBQ3oK/lDQgPEiOJTfEYWJcGBckI9Ew7Im6MXXJEmRXVWH997pyViYkYGofJynZHQL2\nlrXgL182IDLYD0/cHI+xsaEMeRIdw56oG5f75Z2dpGR3CNhXrsN7JfWICPbDkzfHY+zgMDFKJroq\nhj3Rj3BmkpJDEHCgUo93T9RBGSjHEzfHYxxDniTAsCcSgSAIOFptxDsn6uAn88HSG4ewT54kxbAn\n6men6lrxh+MXYbI68GB6LG7UKBnyJDmGPVE/KW/uwB+OX0StoROLJsYiYxjHyZPrYNgTOam+tRN/\nKqrDlxdbsXB8DLJGRMBPxhmv5FoY9kR9ZDTb8Jcv67HnXAvuGDUIj0+ORzD3dSUXxbAn6iWLzYGP\nShux45QWUxJVeHN+GsKD/aQui6hbDHuiHhIEAfsr9PjD8YsYFhGEjXOSoVFxqWFyDwx7oh44rW3H\n1qO1sNoFrJiq4YQocjsMe6JuaNss+MPxi/iqrg0PpsfilmQ1Fykjt8SwJ7oKs82Bnaca8OE3jZib\nFollN6chyI8vX8l9MeyJvkcQBHxRqcebxy4gbVAINt+Ziugwf6nLInIaw57oO5UtJmw+Uguj2Yan\npw3FmFj2y5PnYNiT12vrtOHd4nrsK9fh5xNiMDs1ckBnvkq1xy15F4Y9eS1BELCnrAV/OHYR12uU\neOvutAHf0Hug97gl78WwJ69U2WJC3qEaWOwC1t46DKlRIZLUMVB73BIx7MmrmKx2bC+ux+fnWrBo\nYiyyRkRIuliZ2HvcEl3mdNhv3rwZJSUlUCgU2LhxIwDAZDIhLy8PWq0W0dHReOyxxxDo5J6dRM4Q\nBAGHzhuw5Ugtxg4Ow7b5qQgPkn6JA7H2uCX6T04vzTd9+nSsWrXqB8fef/99jBgxAq+++iqSk5Px\n/vvvO9sM0Q8c3r0b6+fPx6tz5mD9/Pk4vHv3Nc/Vtlmw9vNKvH38Ip6eNhRPTxvqEkEPfLfHbWLi\nD46tTEjAlD7ucUt0LU4/2aelpUGr1f7gWFFREdauXQsAyMjIwNq1a3Hfffc52xQRgJ6/1LQ7BHz4\nTSP++mU9fvqTKDw7MwH+Lrb0cH/tcUv0Y0TpszcYDFCpVAAApVIJg8EgRjPkpXryUrOsqQOvHaxG\niL8Mr89LQZzSdbtFnNnjlqinRH9By+3YqL9191LTbHNg+4k6fH6uBYuvG4xbk9X8N0gEkcJeqVRC\nr9dDpVJBp9NBqVSK0Qx5qWu91GwcPAK/+p/TGDEoBG+4yAtYIlchSgdmeno6CgsLAQD79+/HpEmT\nxGiGvNR/vtRsDQzBvAfXoPzGBfjVDUPwzPQEBj3Rf3D6yT43NxenT59Ga2srli5dinvvvRfz589H\nXl4eVqxY0TX0kqi/fP+lZrNqKE6Pm4fRkX549q7xCOG2gERX5SMIgiBlAXv37sWECROkLIHckNFs\nw+YjtTitbcdTU7iZCHmf4uJizJw5s8fncwYtuZ2DVXpsOlyDaYnh2HpXKteZJ+oBhj25DaPZhvwj\ntTjb2IHnZiTiJzGhUpdE5DYY9uQWjpw34PeHajA1UYWtd6UiUO5ak6OIXB3Dnlxau8WOrUdrcbKu\nDc9M54YiRH3FxyNyWV9ebMWv/ucMZL4+2PrTVAY9kRP4ZE8up9PmwB+LLuJAhR7LpsTjunhOyiNy\nFsOeXEpZUwdeLjyPoeGB2HpXKhQDvHMUkafidxK5BLtDwM6vGvD+V4341Q1xmJEUzjVtiPoRw54k\n19Bqwcv7q+ALH+TfOQJRof5Sl0TkcRj2JKmCshZsOXoB94yOwvzRUZJuEUjkyRj2JIl2ix2bDtfg\nbGMHXrotCcmRwVKXROTROPSSBtxpbTse/uAMAuS+yL9zBIOeaADwyZ4GjN0hYMepBnzwdSMenxyP\nmxNVUpdE5DUY9jQgmtuteHl/FewOYBNfwhINOIY9ie5YjQEbv6jG3LRILBgXw5ewRBJg2JNorHYH\n3i6qQ2GFDs/OSMSYWK5SSSQVhj2Jor61Ey8VVEEZKMeWn6ZCyZmwRJLidyD1u0NVeuQerMF/jbk0\ndp4zYYmkx7CnfmO1O/DW8Ys4XGXA85nDkBYVInVJRPQdhj31i4ZWC14oqER4kBz5d47gAmZELobf\nkeS0YzUGvLq/GveMicLd7LYhckkMe+ozu0PAu8V1+PxcC35zC/eEJXJlDHvqE53Jipx9VfABkH/n\nCIQH+UldEhF1Q9Swf+SRRxAUFARfX1/IZDLk5OSI2RwNkNKGdrxQUIlbk9V4YEIsJ0kRuQHRn+zX\nrl2L0FD+eO8JBEHAP0ub8F5JPZ6aqsENGm4XSOQuRA97QRDEboIGgNnmQO6BalTpzHh9XgpiFQFS\nl0REvSBq2Pv4+OD555+Hj48PMjMzccstt4jZHInkorETz++pwDB1EHLnpSBQzpWxidyNqGG/bt06\nhIeHo7a2Fjk5OYiLi0NaWpqYTVI/uzys8r7xMZg3MpLDKonclKhhHx4eDgAYMmQIrrvuOpSVlTHs\n3YQgCPjbyQZ8VNrIYZVEHkC0n8c7OzthMpkAAEajESUlJdBoNGI1R/2ow2LHur2VOHLegE13jGDQ\nE3kA0Z7sDQYDXnnlFQBAWFgYZs+ejbFjx4rVHPWTC4ZOrN1TgbRBIciengB/GfvniTyBaGEfFRXV\nFfbkHopqjdhQeB73T4jB3DT2zxN5Es6gJQiCgPe/bsQ/TjXguZkJGBMbJnVJRNTPGPZezmJzIPdQ\nDSpbTHh93ghEh3FvWCJPxLD3Ys0dVjy/pwKRIf743ZxkBPnJpC6JiETCsPdS3zZ14LefVyBrRAQW\njo+BL/vniTwaw94LfVGhQ97hWjw+OR5TElVSl0NEA4Bh70UEQcB7JfX49Gwzcm5LwvDIYKlLIqIB\nwrD3Ep02BzZ+cR71rRb8/o4RiAjm+vNE3oQzZryArsOKpz85BwHAK7OTGfREXohP9h6ussWE3+yu\nwK3Javx8QgwnShF5KYa9BztWY8Ar+6ux9IY4zBiulrocIpIQw95D/bO0EX8pqcfaWxMxKpoLmRF5\nO4a9h7E7BGw7dgFFNUb8bm4KBnNHKSICw96jmKx2rC88jw6LHbnzUhAWwC8vEV3C0Tge4tKImzKE\n+svw0m1JDHoi+gEmggeo1pnx7GflyExR4/7xHHFDRFdi2Lu5U3VteGFvJRZfNxiZKRFSl0NELoph\n78b2leuw+Ugtnpk+FBPiFFKXQ0QujGHvhgRBwM6vtPjwm0a8nDUcwyKCpC6JiFwcw97N2B0Cth69\ngJN1rXh9XgoGhXCzESL6cQx7N2KxOfDy/vMwmm343ZxkhHLEDRH1EIdeuonWThuyd5XBF8CLtyUx\n6ImoV5gYbqCx3YJVu8oxIS4MS66P465SRNRrDHsX99H/7sVbFTJoyo9AX1OEo0uW4KbMTKnLIiI3\nI1rYl5aW4p133oHdbsfMmTORlZUlVlMe6+8fF2B7pQyr/rkFs4s/BwBkV1UBAAOfiHpFlD57h8OB\nLVu2YPny5Vi/fj0KCgpQW1srRlMe61iNAe9W+2PDX9d3BT0ArK+sxIFt2ySsjIjckShhX1ZWhpiY\nGERFRUEul2Py5MkoKioSoymPtOdcCzZ+UY3xR/+MyWePXfF5mdksQVVE5M5ECfuWlhZERPx76r5a\nrUZLS4sYTXmc97/S4u2ii3jl9mSEdjRe9Rx7YOAAV0VE7o5DL12EIAj44/GL+N8zTXhtbgo04YGY\numQJshMTf3DeyoQETHnoIYmqJCJ3JcoLWrVajebm5q6Pm5uboVZzW7xrsTsEbDpcg3NNJrw2NwXK\nwEtflssvYbO3bYPMbIY9MBBTH3qIL2eJqNdECfukpCTU19dDq9VCrVbj8OHDeOKJJ8Royu1Z7Q5s\nKDwPvdmGDbcPR7C/7Aefvykzk+FORE4TJexlMhmWLl2KV199tWvo5ZAhQ8Royq2ZrHY8v6cS/nJf\nvDgrCf5y9qoRkThEG2c/cuRIbNiwQazbu722Thue+6wCccoAPDVFA5kvZ8USkXg4g1YCOpMVq3aV\n4yfRoVh6I5c/ICLxMewHmLbNguxPy5AxLBw/n8AtBIloYDDsB9AFQyeyPy3DHaMG4e7RUVKXQ0Re\nhGE/QKp0Jqz6tBz3TYjB7NRIqcshIi/DsB8A3zZ1YPVn5VhyfRxmDOd8AyIaeAx7kX3T0Ia1n1di\n2c3xmJygkrocIvJSDHsRnbzYihcKqvD0tKGYFK+Quhwi8mIMe5EU1RrxcuF5PDsjAeMGh0ldDhF5\nOYa9CI6cN+B3B6qx9tZEjIoOlbocIiKGfX87UKlH3qEavDBrGEYMCpG6HCIiAAz7frWvXIc3jtYi\nJysJSRHBUpdDRNSFYd9P9pxrwVvHLyAnazgS1UFSl0NE9AMM+36w+9tmvF1Uhw1ZydCEcxcpInI9\nDHsnfXqmCdtL6rHh9uGIVzHoicg1Meyd8K/TTfjrl/V45fbhiFMy6InIdTHs++jj0kb8/VQDXpmd\njMGKAKnLISLqFsO+D/5Z2ogdpxrwyu3JiGXQE5Eb4D54vfTP0kbsPKVl0BORW2HY98LloN9w+3AG\nPRG5FYZ9D/3rdBN2nGpg0BORW2LY98D/nrk06mYDu26IyE0x7H/Ep2eb8ZeSS0HPUTdE5K44Gqcb\nu79txvbiuu/G0TPoich9iRL2O3bsQEFBARSKSxt2LFy4EOPGjROjKdHsLWu5tAQCJ0wRkQcQJex9\nfHwwZ84czJkzR4zbi66wXIc3j13Ay1lcAoGIPINoffaCIIh1a1EdrNJjy9FavDRrOIaGc/VKIvIM\novXZ79q1CwUFBUhJScEDDzyAkBDX38jjWI0Bvz9YgxdvS8KwCAY9EXmOPof9unXroNfrrzi+YMEC\nZGZm4u6774bJZML27dvx7rvvYunSpU4VKrbiC0a8sr8az2cOQ3IkNx4hIs/S57BfvXr1j54THByM\nWbNmIS8vr6/NDIhTdW3I2Xcea25JRFqU6/8EQkTUW6L02et0OgCA3W7HwYMHodFoxGimX5zWtmPd\n3kqsmp6An8Rwc3Ai8kyi9Nm/9957qKqqglwuR1paGhYtWiRGM04ra+rAmt0V+PU0DcbHhUldDhGR\naEQJ+0cffVSM2/ar8zoTnvusHI9Njsd18UqpyyEiEpVXLpdw0diJZz4tx+Lr4jAlUSV1OUREovO6\nsG9st2DlJ2VYOD4GtySrpS6HiGhAeFXY60xWrPykDPNGRmJOWqTU5RARDRivCfvWThue+bQcGcPC\ncc+YaKnLISIaUF4R9iarHas/q8DY2FD8fEKM1OUQEQ04jw97i92B3+6pRLwqAEtuiIOPj4/UJRER\nDTiPDnu7Q8D6fVUI9pNh2c0a+DLoichLeWzYC4KA3IPVMFkdyJ4+FDJfBj0ReS+PDHtBELDt/19A\njb4Tv7klEf4yj/xjEhH1mEduS/i3kw04caEVr85ORpCfTOpyiIgk53Fh/6/TTdh1thm/m5sCRaDH\n/fGIiPrEo9Jwf4UO75XUY+OcZEQE+0ldDhGRy/CYzuwTtUbkH67Fi7OSMFgRIHU5REQuxSPC/oy2\nHesLz2P1LYncTpCI6CrcPuyr9Was/bwCy6dqMJqbjxARXZVbh31juwXP7irHLycNxg0arklPRHQt\nbhv2rZ02rNpVjrkjI5GZEiF1OURELs0tw95sc+A3uyuQHheGe0ZHSV0OEZHLc7uwtzsE5BRUISbM\nH/99PRc2IyLqCbcKe0EQ8PtDNbDYHXhqChc2IyLqKbcK++3F9Shr7sDqmYnw43o3REQ95jYzaP91\nugkF5S14bU4Kgv253g0RUW+4RdgfPq/Hn4vrsHFOCsK5DAIRUa/1OeyPHDmCnTt34sKFC8jJycGw\nYcO6PvfJJ5+goKAAMpkMv/jFL5CamtrnAksb2vHagRq8MGsY4pRcBoGIqC/63PGt0WiwYsUKjBw5\n8gfHa2trsW/fPqxfvx7Lly9Hfn4+HA5Hn9qo0Zvx2z0V+PU0DUYMCulrqUREXq/PYR8XF4fBgwdf\ncfz48eOYPHky5HI5oqKiEBMTg7Kysl7fv6XDimc/K8cv0gfjunjOjiUicka/D2nR6XSIiPj3jNaI\niAi0tLT06h4mqx3PfVaOW5PVuG0EZ8cSETmr2z77devWQa/XX3F8wYIFSE9P73EjvZn4ZHcIeLGg\nCkkRQbh/fEyPryMiomvrNuxXr17d6xuq1Wo0Nzd3fdzc3Ay1Wt2jay9PmnIIAp64WcPZsURE/aTf\nu3HS09Nx6NAh2Gw2aLVa1NfXY/jw4T269m8nG3CuqQPPzUiE3JdBT0TUX/o89PLYsWN4++23YTQa\nkZOTg8TERKxatQpDhgzB9OnTsXLlSshkMjz88MM9ekLfW9aCT840I3ceJ00REfU3H0EQBCkL2Lt3\nL2QxyXixoAobZg9HQjh3miIi+jHFxcWYOXNmj893iQVmXiyowjMzEhj0REQicYmw/+/rB2P84DCp\nyyAi8lguEfa3JnMsPRGRmFwi7ImISFwMeyIiL8CwJyLyAgx7IiIvwLAnIvICDHsiIi/AsCci8gIM\neyIiL8CwJyLyAgx7IiIvwLAnIvICDHsiIi/AsCci8gIMeyIiL8CwJyLyAgx7IiIvwLAnIvICDHsi\nIi/AsCci8gLyvl545MgR7Ny5ExcuXEBOTg6GDRsGANBqtXjyyScRFxcHAEhJScHixYv7p1oiIuqT\nPoe9RqPBihUr8Oabb17xuZiYGGzYsMGpwoiIqP/0OewvP7kTEZHr63PYd0er1WL58uUICwvDz372\nM6SmporRDBER9VC3Yb9u3Tro9forji9YsADp6elXvUatVmPLli0IDQ1FSUkJNmzYgPz8fAQFBfVP\nxURE1Gvdhv3q1at7f0O5HKGhoQCA8ePHY9CgQairq+t6gfufVCoViouLe90OEZE3U6lUvTq/37tx\njEYjQkND4evri4qKCtTX1yM6Ovqa50+cOLG/SyAiov/gIwiC0JcLjx07hrfffhtGoxHBwcFITEzE\nqlWrcPToUezcuRO+vr6IiYlBZmYmRo8e3d91ExFRL/Q57ImIyH1wBi0RkRdg2BMReQFRxtn3VGlp\nKd555x3Y7XbMnDkTWVlZUpYjmaamJuTn58NgMEChUCAjIwMZGRlSlyUph8OB7OxsqNVqZGdnS12O\nZMxmM9566y1UV1fDarVi6dKlSElJkbosSezZsweFhYWwWq1IS0vDgw8+KHVJA2bz5s0oKSmBQqHA\nxo0bAQAmkwl5eXnQarWIjo7GY489hsDAwGvfRJCI3W4XHn30UaGhoUGwWq3CihUrhJqaGqnKkZRO\npxMqKysFQRAEg8EgLF682Gv/Li77+OOPhddff11Yv3691KVIKi8vT9i7d68gCIJgs9mE9vZ2iSuS\nRmtrq/Dwww8LJpNJsNvtwksvvSSUlJRIXdaAKS0tFSoqKoSnnnqq69j27duFDz/8UBAEQfjggw+E\nP//5z93eQ7JunLKyMsTExCAqKgpyuRyTJ09GUVGRVOVISqVSISEhAQCgUCiQlJQEnU4nbVESam5u\nRklJCWbMmAHBi8cPdHR04MyZM5gxYwYAQCaTITg4WOKqpOHv7w/g0t+JxWJBZ2dn13web5CWloaQ\nkJAfHCsqKsK0adMAABkZGTh+/Hi395CsG6elpQURERFdH6vVapSVlUlVjsuor69HbW0tkpOTpS5F\nMu+88w7uv/9+mEwmqUuRlFarhUKhQH5+PioqKpCcnIxf/vKXXcHnTfz9/bF48WI88sgj8PPzQ1ZW\nFoYPHy4iUtsoAAACI0lEQVR1WZIyGAxdE6uUSiUMBkO35/MFrQsxm83Izc3FokWLuu9782AnTpyA\nQqFAYmKiVz/VA4Ddbkd5eTmuv/565OTkwGaz4ciRI1KXJQmj0Yi33noLr732GvLz8/Htt99y5v33\n+Pj4/Og5koW9Wq1Gc3Nz18fNzc1Qq9VSlSM5m82GjRs3YsqUKZg0aZLU5Ujm7NmzOHHiBB555BG8\n/vrr+Oabb7Bp0yapy5JEREQEQkNDkZ6eDn9/f0yePBklJSVSlyWJsrIyJCcnIyYmBmFhYbjxxhtR\nWloqdVmSUiqVXWuX6XQ6KJXKbs+XLOyTkpJQX18PrVYLm82Gw4cPX3NxNU8nCAK2bt2KIUOGYPbs\n2VKXI6mFCxdiy5YtyM/Px7JlyzBq1Cg8+uijUpclCZVKhZiYGJw7dw4OhwPFxcUYM2aM1GVJIjU1\nFeXl5Whra4PVakVJSQnGjh0rdVmSSk9PR2FhIQBg//79P/qQKOkM2tLSUvzpT3/qGnp5++23S1WK\npM6cOYM1a9ZAo9F0/Ti2cOFCjBs3TuLKpFVaWoqPP/4YK1eulLoUyVy8eBH5+fkwGo3QaDQ/PrzO\ngxUWFmLfvn2wWCwYO3Ys7r33Xvj6ekdPdG5uLk6fPo3W1lYolUrce++9uOGGG3o19JLLJRAReQHv\n+G+RiMjLMeyJiLwAw56IyAsw7ImIvADDnojICzDsiYi8AMOeiMgLMOyJiLzA/wH+XthljT1tmAAA\nAABJRU5ErkJggg==\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11445dbd0>"
       ]
      }
     ],
     "prompt_number": 42
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Although polynomial model characterizes a nonlinear relationship, it is a linear problem in terms of estimation. That is, the regression model $f(y | x)$ is linear in the parameters.\n",
      "\n",
      "For some data, it may be reasonable to consider polynomials of order>2. For example, consider the relationship between the number of home runs a baseball player hits and the number of runs batted in (RBI) they accumulate; clearly, the relationship is positive, but we may not expect a linear relationship."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "ss3 = lambda theta, x, y: np.sum((y - theta[0] - theta[1]*x - theta[2]*(x**2) - theta[3]*(x**3)) ** 2)\n",
      "\n",
      "bb = pd.read_csv(\"data/baseball.csv\", index_col=0)\n",
      "plot(bb.hr, bb.rbi, 'r.')\n",
      "b0,b1,b2,b3 = fmin(ss3, [0,1,-1,0], args=(bb.hr, bb.rbi))\n",
      "xvals = arange(40)\n",
      "plot(xvals, b0 + b1*xvals + b2*(xvals**2) + b3*(xvals**3))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 4274.128398\n",
        "         Iterations: 230\n",
        "         Function evaluations: 407\n"
       ]
      },
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 43,
       "text": [
        "[<matplotlib.lines.Line2D at 0x114476750>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAECCAYAAADw0Rw8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlY1Oe9NvB72B2YBVBARIIiImZRUUyMWlCyGlNNbDyt\nplnapD2XhoZGa2zSJm3SRnPUBEWy1DRb05w2CdET3yZN4gJZcGE1KmpERHZGYJgZ1mFmnvcPIo0K\nCMMwv9/M3J/ryh8MM8w3j3Dz8KwKIYQAERG5LS+pCyAiopHFoCcicnMMeiIiN8egJyJycwx6IiI3\nx6AnInJzPgN98qWXXkJxcTHUajW2bNkCAOjo6EBmZiZ0Oh3Cw8ORlpaGgIAAAMDHH3+Mffv2wdvb\nGw8++CCmTJky8v8HREQ0oAF79AsWLMATTzxx0WPZ2dmIj4/H5s2bERcXh+zsbABAdXU19u/fj40b\nN2LNmjXIysqCzWYbucqJiGhQBgz6hIQEBAYGXvRYQUEBkpOTAQApKSnIz88HAOTn52Pu3Lnw8fFB\nWFgYIiIiUFZWNkJlExHRYA15jN5gMECr1QIANBoNDAYDAECv1yM0NLT3eaGhoWhubnZQmUREZK9h\nTcYqFIphfZ6IiEbegJOxfdFoNGhpaYFWq4Ver4dGowEAhISEoKmpqfd5TU1NCAkJ6ffrHDx4EG1t\nbXaUTETkubRaLWbOnDmk1ww56GfNmoWcnBwsXboUubm5SEpK6n1869atWLx4MZqbm1FfX49Jkyb1\n+3Xa2tqQmJg41LcnIvJoRUVFQ36NYqDTKzMyMnDixAmYTCZoNBosX74cN9xww4DLK/fu3du7vDIh\nIaHfN967dy+DnohoiIqKipCamjqk1wwY9COJQU9E9B82IXDqfDtClb4IC/Lr93n2BP2Qh26IiMgx\nOrqtKKwx4VClAYcqjdAE+GDVnKgBg94eDHoiIifStZpxsNKAg5UGlDa0IX5MIG6IVmPF9AiMVfuP\nyHsy6ImIRpDFJlDa0Ib8aiPyqwxobOvG7PFq3DY5FE8unIBAP+8Rr4FBT0TkYE1t3ThcbUR+lREl\ntSZEqPyQNF6NtBvHY0pYILy9nLvHiEFPRB5PmZ4Or7IyCKUS7Tt2QHy3P2iwuq02nNC1Ib/ahPwq\nI863mZEYqcIN0Wo8cmMUQpS+I1T54DDoicjjeZWVwTcvr+eD9HS0vfHGgM8XQqDG2IXCahMKqo04\nWt+KKE0AZkapkHZjlCS99oEw6Inc1HB7qZ5EKJUAAMuMGWjPyOjzOaYuC0pqW1FYY0RhtQlWm8DM\nKBVSJ4VgbfJV0ATIN07lWxkRDctQe6merH3HDiA9He0ZGb2/EM1WG0ob2lBcY0JRrQmVLZ24JjwI\nM6NUuOvqMYjWBrjMeV4MeiI3NZheKvUQGg1Mr7+O8qYOFH3TgOIaE0p1bbhKG4AZ41R4KCkSCeGB\n8PN2zUv5GPREbqqvXir9hxACtcYuFNe2oqTWhCN1rVD5eyNxnAqLE0bjyYUxCPJ3j4h0j/8LIrqM\n0GhkMVwjp7mCxjYzimtNKPku3IUApo9TYfZ4NX5x/TiH70iVCwY9EY0oKecKDJ0WHKn7T7AbOi2Y\nNlaFGZFB+PG0cERp/F1mnH04GPREQySnHqorcOZcQWuXBUfr21BSZ8KRWhPqTWZcGxGEaWODsGhB\nDCaGjoKXBwT7pRj0REPE1SxDM5JzBR3dVhxvaMORWhNK6lpR2dKJKWMCMT0yCI/Oi0bcaCV8ZLSe\nXSoMeqIh4mqWoXHkXIHZYkOprg1H6nqGYs40dWDS6FGYPlaFh2dHYkqY666MGUkMeqIh4moW57HY\nBE6db0NJbSuO1JlwUteOmOAATItU4d4ZEZgaHohRviN/KJirY9ATDZFcVrO4I5sQONPUgZLvVsYc\nb2jFWLU/po0NwrJrwnBNRJBTTnt0Nwx6IpKMEAJVLV0oqTP1rmXXBvhgeqQKt8WHYl2KvI8WcBVs\nQSJyqvNtZhTX9AR7cW0rvL2AGZEqzI3RYvWc8QgNlPakR3fEoCeiEdXaZUHJd5OnRTUmGDstmBap\nwoxIFVbOGItItZ9HrGWXEoOeiBzKYhM4oWtDYbURRTU9h4FNDQ/E9EgVfrsgBrEeupZdSgx6oktw\nQ9TQCCFQZehCUY0Jhd+dzR6p9sfMKDUeTIrE1S58GJi7YNATXYIboq6stcuC4tpWFFQbUVBtBAAk\njnONs9k9Ef81iC7BDVGXswmBsqYOFFT1BPuZ5g5cHR6IpCg1ll0bhvEecmaMq2LQE11CDhui5DB8\nZOy09PbYC6pNCPL3RtJ4NVbMiMC1EUHw9+FwjKtg0BNdQg4boqQYPhJCoELfiUNVBhyuNKK8uQPX\njQ3C7PEa/HTmWIxV+Y94DTQyGPREMuSs4aMuiw0ltSYcqjLicJUBCihwfbQaP5kegWljg+DHXrtb\nYNATydBIDh+1dHTjUJUReecMOFJrQmyoEtePV+PPt8a61D2oNHgMeiIZcvTwUY2hCwfOtSCv0oDy\npg4kjlNjfowWa+ZHQ80VMm6P/8JEbkh8t0rmq4oW5J0zwNhpwQ3RGvzXdeGYEanikIyHYdATuQkh\nBE6db8eXZ1vwZUULvBTAvBgtfj0vGlPClNyN6sEY9EQuzCYETura8eVZPb6saIGftxfmT9Di6Zsm\nYGLIKI63EwAGPZHLEULg5Pl25JzpCfdAP2/Mj9Hi2VtiERPMyVS6HIOeyEWc03dg3xk9cs7o4e2l\nQMrEYGy8bRKigwOkLo1kjkFPJGMNJjNyyvXYf0YPY6cFKbHB+F3qBEwK5bAMDR6Dnkhm2sxW5JTr\nsfd0MypbOjFvghar5ozDNRFBnFAlu9gd9Hv27EFOTg66u7uRkJCABx54AB0dHcjMzIROp0N4eDjS\n0tIQEMA/K4muxGoTKK414fPTzThcZcSMSBXuuS4cs6JU8OURvzRMdgV9a2srdu7ciS1btsDPzw/P\nP/88SkpKcOzYMcTHx2PdunXYtWsXsrOzsXLlSkfXTOQ2qlo68fnpZuw53YxgpQ9uiQvF6jlR3MRE\nDmVXV8HPzw8A0N7eDrPZjK6uLgQGBqKgoADJyckAgJSUFOTn5zuuUiI30dFtxccnG5H+0bf4zb9O\nw2IT+PNtschaOgVLrh7DkCeHs+s7ys/PDw899BBWr14NX19f3H777YiLi4PBYIBWqwUAaDQaGAwG\nhxZL5MrKGtvxr5ON+OJsC66NCMKPp4cjKUoNby+Ou9PIsivojUYjXnvtNbz44osIDAzECy+8gMLC\nwouewxUBRD2995wzevzrZBNaOrtxW/xovHr3FIwO9JO6NPIgdgV9WVkZ4uLiEBERAQCYM2cOTpw4\nAY1Gg5aWFmi1Wuj1emh41ya5IEdc+nGmqR3/OtGE3LN6XBMRhPtmRmDmOPbeSRp2Bf2UKVPwxhtv\noLW1Ff7+/iguLsaiRYsAADk5OVi6dClyc3ORlJTk0GKJnMHeSz+sNoGvz7Vg17HzqG81Y1F8KHvv\nJAt2Bb1SqcSyZcuwadMmmM1mTJs2DVdffTUmTZqEzMxMrF27tnd5JZGrGeqlH4ZOCz451YjdpY0I\nV/lh6TVjMPcqLXvvJBsKIYSQ4o337t2LxMREKd6aaEAKgwHKQVz6Ud7UgV3Hz+OrihbMjdFgydQx\nmDRa6cRKyRMVFRUhNTV1SK/hOi6iSwx06YdNCByqNOLDYzrUGLqwOGE0Xr8nAdpRvk6ukmjwGPRE\ng9BttWH/GT3e/0YHX28F7rkuHPMnaOHD4RlyAQx6ogG0mXs2N+08dh7RwQFYNScK0yODuHyYXAqD\nnqgPze3d2Hn8PD452YjEcSo8c8tEjr+Ty2LQE31Pg8mMfxypxxdnW7AgNhiZS+MxVuUvdVlEw8Kg\nJwJQb+rC/5Y04KuKFtwxZTT++iP5T7A6YmMXeQYGPXm0OlMX/vFdwC9OGI037pnqMoeK2buxizyP\na3xHEzlYnbEL75bU48A5g8sF/AVD3dhFnsu1vrOJhqnBZMY7xXU4cM6AO6eOwesuGPAXtO/YAQxi\nYxeRa36HEw2RodOCd0vqsed0c08PfvlUqPxd+9t/oI1dRN/n2t/p5FKkmDzs6LYi+9h57DqmQ0ps\nMHYsS0CIUt6TrESOxqAnp3Hm5GG31YZPTjXh3eJ6XDc2CFt/GI9xGi6TJM/EoCenccbkoU0I5Jbr\n8VZhHSLV/vjTrbHc6EQej0FPTjPSk4fHG1rxysEaCAE8Oi8aMyJVDn8PIlfEoCenGanJQ12rGX/N\nr8XRulb8LCkSCycFw4tn0RD1YtCTy+q02PD+Nw3Ydfw8fjh1DNLnjccoX2+pyyKSHQY9uRwhBHLK\nW/Da4RpMDQvES0unIFzF6/qI+sOgJ5fybWM7Xj5QjS6LDesXxODaiCCpSyKSPQY9uYQ2sxVvFtTi\ny7MteGBWJG6OC+GdrESDxKAnWRNCILe8Ba8eqsH10Wr8ZVmCyx5ZQCQV/sSQbNUau7A9rwpNbd34\nXWoMrg7nMA2RPRj05DSDPQLBbLXh/W902HlMh+XTwnH3NWG8m5VoGBj05DSDOQLhSK0J276uwjiN\nP7K4mobIIRj05DQDHYHQZrbiL4dqUFBtxKo5UZgbo5WiRCK35CV1AeQ52nfsgHnJErR++OFFwzYF\n1Ub88sMTUCiAvyxLYMgTORh79OQ0lx6B0Ga24tWDNSiuNeHX86IxM0otYXXUF95L6x7YoydJHK4y\n4BfZJ+DjpcArd09hyMvUhXkVvz17oExPl7ocshN79ORUrV0WvHqoBiW1rVj7g6swYxxPmJQz3kvr\nHtijJ6fJrzLiF9kn4evthVfvnsKQdwH9zauQa2GPnkac2WLDjsO1yDvXgt8ksxfvSngvrXtg0NOI\nOtvcgQ37KxCtDcArd09x+Qu5AU5Qkutx/Z86kiUhBHYdP493Sxrw8OyeQ8gUbnIZiDPvviVyBAa9\nh3BmL7S5vRubvzgHU5cVGXdOdrtLuTlBSa6Gk7EewlnL5A5WGrBq50lMHq3Ei24Y8gAnKMn1sEfv\nIUa6F2q22PCXwzU4VGnEk6kT3PpCEE5QkquxO+g7Ozvx2muvobKyEt3d3Vi1ahWioqKQmZkJnU6H\n8PBwpKWlISAgwJH1kp3ad+wA0tPRnpHh8F5onakLz+45iwiVP16+Kx5BbjDhSuROFEIIYc8Lt2/f\njqlTp2LhwoWwWq3o6urChx9+CJVKhSVLlmDXrl1oa2vDypUr+3z93r17kZiYOKziSXoHzhnwwpeV\nWDE9HEuvHuM2E65EclVUVITU1NQhvcauMfr29nacPHkSCxcuBAB4e3tDqVSioKAAycnJAICUlBTk\n5+fb8+XJBVhtAq8drsH2vCr88eaJuOuaMIY8kUzZ9Te2TqeDWq1GVlYWysvLERcXhwcffBAGgwFa\nbc/JgxqNBgaDwaHFkjw0tXfjuX0V8PNW4KW7pkDDq/2IZM2uHr3VasWZM2dw/fXXY8OGDbBYLDhw\n4MBFz2Hvzj0V15qwetdJzIgMwp9ujWXIE7kAu35KQ0NDERQUhFmzZgEA5s6di9zcXGi1WrS0tECr\n1UKv10PDpWduwyYE/lHSgI9Kz2NdylVIHMfTJolchV09eq1Wi4iICJw+fRo2mw1FRUW49tprMXPm\nTOTk5AAAcnNzkZSU5MhaSSLtZiv+uOcsDlcZsX1pPEOeyMXY/Xf36tWrkZWVBaPRiOjoaKxcuRJC\nCGRmZmLt2rW9yyvJtdUZu/DU5+WYGhaI3y2Mga8399gRuRq7l1cOF5dXyl9xrQkb91dgxfQI/HDq\naM67EMmAPcsrOZNGlxFC4KPSRrxbUo/1C2IwI5LHChO5MgY9XaTbasP2vGqc0LUh487JGKt2v7Nq\niDwNg5566Tu68eyes1AH+CDjzslQ+nlLXRIROQCDngAAZ5ra8fTn5bg5LhQ/TYyAF8fjidwGg55w\nuMqATbmVSLsxCj+YGCx1OUTkYAx6D/evk434W2EdnrllIhLCAqUuh4hGAIPeQ9mEwJsFdfjibAu2\nLHbPC0KIqAeD3gOZrTZs+aISDSYztv5wMs+rIXJz3OboYUxdFjzxyRl0W214ftEkhjyRB+BPuQep\nN3Xhd5+WY1aUCg/PHgdvL66sIfIEDHoP8W1jO57+rBzLrwvDXdeESV0OETkRg94DFNUYsWH/OTw6\nbzzmxWj7fI4yPR1eZWUQSiXad+xw+L2yRCQdjtG7ua8qWrBh/zk8ddOEfkMeALzKyuCblwe/PXug\nTE93YoVENNLYo3cD/fXGP/u2Ca/n1+K522IRN1o54NcQyp7PW2bMQHtGxojXTETOwx69G+irN/7h\nMR3eLqrDpjvirhjyANC+YwfMS5ag9cMPOWxD5GY8ukfvLuPS3++Nt734It4urENOuR4vLJ6MsCC/\nwX0NjQZtb7wxkmUSkUQ8ukfvLuPSF3rjxuxsZJW24kClAVsWxw065InIvXl00LvLuPSop5+GtbEJ\nL277CGd0JmxaNAnBo3ylLouIZMKjg95dxqW7yyvwVOzNMBg7sHX3Cwjy9+gROSK6hEcngjuMS5st\nNvz+xp9CVVOJZ47vRtcH74/I+7jLfAaRJ/LoHr2r67LY8PTn5VDOuBa/bz2Krg/eH7EAdpf5DCJP\n5NE9eld2IeQ1AT5Yl3wVum59fUTfz13mM4g8EXv0LujSkHfG4WTuMp9B5InYo3cxnRYbnv6sHMGj\nfPAbJ4U84B7zGUSeij16F9JpseGpz84gROnckCci18YevYu4EPKjlb5Y8wOGPBENHoPeBXR0W/HU\nZ+UYE+SHNfOjLwt5Ln0kooFw6EbmzN9NvIb1E/IAlz4S0cAY9DJmsQk8u/csQkuP4qlNj0D94/+C\nwmC47Hlc+khEA2HQy5TVJvA/ORUAgKdz30RA3tf99ti59JGIBsKglyEhBLZ9XQV9hwW/S50A71EB\nAPrvsV9Y+siQJ6K+MOiHSZmejqDFixG4fHmfwypDfb0QAjsO1+Jscwf+ePNE+Pt4scdORMPCoB+m\n4U6EXvr6v5c0oLDaiD/dGgulnzcA9tiJaHi4vHKYhjsR+v3Xv7P6j9h7uhlbFsdBHcB/GiJyDPbo\nh2m4wyoXXv/BljeRXWbExtsnIUTJS0OIyHHYbRym4Z4BIzQafPL7F/DGwWpsviMO4Spe/0dEjjWs\noLfZbFi/fj1CQkKwfv16dHR0IDMzEzqdDuHh4UhLS0NAQICjanVLhdVGbM+rxobbYxGlYVsRkeMN\na+jm448/RlRUFBSKnt2a2dnZiI+Px+bNmxEXF4fs7GyHFOmuzjS1Y2POOfwudQJiQ5VSl0NEbsru\noG9qakJxcTEWLlwIIQQAoKCgAMnJyQCAlJQU5OfnO6ZKN9RgMuP3n5Yj7cYoXDc2SOpyiMiN2R30\nb731Fu699154ef3nSxgMBmi1WgCARqOBwY515Z7A2GnBk5+ewY+uC8MPJgZLXQ4RuTm7gr6wsBBq\ntRoTJkzo7c1f6sJwjrsb6oYps8WGP+wpR1KUCndfE+aEConI09k1GXvq1CkUFhaiuLgY3d3dvZOw\nGo0GLS0t0Gq10Ov10HjABp8LG54AAOnpA67AsQmB53PPIVTpi4evH+ekConI09kV9CtWrMCKFSsA\nAKWlpfjoo4+QlpaGd955Bzk5OVi6dClyc3ORlJTk0GLlaLAbpoQQePVgDQwdFjx3eyy8POQvHiKS\nnkM2TF0Yplm2bBm+/fZbrF27FqdPn8ayZcsc8eVlbbAbprKP6lBUa8Ifbp4AP2/uUyMi51GI/gbZ\nR9jevXuRmJgoxVs73f4zeuw4XIOMOycjLIgboojIfkVFRUhNTR3Sa7gzdoR9U2fCSweq8T+LJjHk\niUgSHEMYQTWGLvxpbwV+u+AqTAgZJXU5ROShGPQjpLXLgqc+O4P7Zo5F4ji11OUQkQdj0I8Aq03g\nuf0VSBynxuKE0VKXQ0QejkE/Al49VAMhgP++gWvliUh6DHoH+38nGlFQbcSTC2Pg7cW18kQkPa66\ncaDiWhPeLqzDi3fGIcifTUtE8sAevYPUGDqxYV8FnlgYg3E8V56IZIRB7wCtXRb8/rNy3DdzLKZH\nqqQuh4joIgz6YbLaBP60rwKzorjChojkiUE/TK8crIaXAvglT6MkIpli0A/DZ982oaDahCcWcIUN\nEckXg95OpxvbseNwLTYUvoeIZUsHffEIEZGzMejtYOy04Jk9Z/HIjVGYdLwAvnl58NuzB8r0dKlL\nIyK6DIN+iKw2gQ37KzB/ghbJE4MHffEIEZFUGPRD9HZRHSw2gZ8nRQIY/MUjRERS4fbNIcg714I9\np5uxfWl87+Sr0GgGvCeWiEhqDPpBqjZ04sUvq/DMLRMRPMrXqe+tTE+HV1kZhFKJ9h07+JcDEQ0J\nh24GoaPbij9+fhYPzBqLhLBAp7+/V1kZJ3yJyG4M+isQQmDLF5WYEqbEovhQaWrghC8RDQOD/gqy\nj+pQZ+pC2o3joVBIsymKE75ENBwcox/AN3WteP+oDtt+GA8/H+l+J3LCl4iGgz36frR0dGNjTgXW\n/CAa4So/qcshIrIbg74PNiGwKbcSC2ODMXs8h0qIyLUx6PvwwVEdWs0WPDArUupSiIiGjUF/idKG\nNnzwjQ5PLJgAH55ISURugJOx32PqsmDD/gqkzx/vUuPy3FBFRANhj/47F9bL33iVBjdepZW6nCHh\nhioiGohbB70yPR1BixcP6qz4/yttxPk2M34+2/XG5bmhiogG4tZBP9ie7reN7fh7cT2eXDgBft6u\n1yTcUEVEA3HrMfrB9HTbzFY8t6/nEpFItb8zy3MYbqgiooG4Xvd1CK7U0xVCIOOrSsyIVCF5YrAE\nFRIRjTz37tFfoaf7yakmVOo7sW1J/IjVwBUxRCQ1t+7RD6Ta0InX82vx5MIJ8B/Bc2y4IoaIpOaR\nQW+xCTyfcw73zRyL6OCAEX0vroghIql5ZND/vbgeKn9v3JkwesTfiytiiEhqdo3RNzY2IisrCwaD\nAWq1GikpKUhJSUFHRwcyMzOh0+kQHh6OtLQ0BASMbI95qEob2vDxyUa8dNcUp5wvzxUxRCQ1u4Le\nx8cH999/P2JiYmA0GrFmzRpMmjQJOTk5iI+Px7p167Br1y5kZ2dj5cqVjq4ZgH2TnO1mK57PqUDa\n3PEIVTr33lciIqnYNXSj1WoRExMDAFCr1YiNjUVzczMKCgqQnJwMAEhJSUF+fr7DCr2UPZOcrxys\nwXVjgzAvxrWOOCAiGo5hL6+sr69HdXU1Jk+eDIPBAK22J0Q1Gg0MVzh2YDiGOsn5dUULjtSZ8PJd\nU3of49JHIvIEw5qM7ezsREZGBu6///7LxuJHevx7KJOcTe3d2PZ1FR5PiYHSz7v3cS59JCJPYHfQ\nWywWbNmyBfPnz0dSUhKAnl58S0sLAECv10Mzgj3kC5OcVwr5nlMpz2HRlNGYGh548ee49JGIPIBd\nQS+EwCuvvIKoqCjccccdvY/PmjULOTk5AIDc3NzeXwBS2n2iEaYuK1bOiLjsc1z6SESewK4x+lOn\nTuHLL79EdHQ01q1bBwBYsWIFli1bhszMTKxdu7Z3eaWUKvWd+FtRPV68M67P26K49JGIPIFCCCGk\neOO9e/ciMTFxxL6+xSbw66w9WHLqayzRlXKylYjcQlFREVJTU4f0GrfdGfvPIw0INjbjR+9u42Qr\nEXk0tzy98mxzB3YdP483Tn4GBTjZSkSeze2C3mIT2JR7Dj9LioTqzhdg9rGhPSODwzZE5LFkG/T2\nbmZ6/5sGaAJ8cNvkEAiFgpOtROTxZDtGb89mprPNHfjw2Hn8en60Uw4sIyJyBZIGfeDy5VD0c0zC\nUDczWW0CW76oxIOzxiIsyM+hdRIRuTJJg36g3vpQNzO9f7QBgX7euD0+1NFlEhG5NEnH6AfqrQ9l\nM9M5fQeyj57H9iXxHLIhIrqEpD16Rxw9YLUJbP6iEvfPHItwFYdsiIguJWnQO2LJY/ZRHUb5euGO\nKRyyISLqi2xX3QxGpb4T7x/V4TGusiEi6pfLBn3PkM053JcYgQiVv9TlEBHJlstumNp1/Dz8fbxw\nR8JoiSokInINsu3RD7RhStdqxv+W1CN93nh4cciGiGhAsg36/jZMCSGQ+XUVllcWIH7ljwbcdEVE\nRDIO+v42TH1Z0YJ6kxk/Pfh/vO+ViGgQZBv0fd0J22a24uUDNXh03nj4nz0DALCpVOh45hmpyiQi\nkj3ZBn1f/ppfi+uj1bgmIgi2qCgAgJfJhFFPPSVxZURE8uUyQV/a0Ia8cy34eVIkAECo1QB4qQgR\n0ZW4RNBbbAIZX1Xiv6+Pgsq/Z0XoUA89IyLyVLJdR/9973/TgDGBfkieqO19bCiHnhEReTLZnkev\nTE9H0OLF0N//S2R/04C0uVE85oCIyA6yPY/eq6wMPnl52ByRhJ+eyuUxB0REdpLvefRKJT5JvAkt\noyNw50PznFwZEZH7kDToB5pIrdv+CrZ+UIpnbo+DV7C2z+cQEdGVSTp0o3z44X7H6N94aw9Sq77B\njMfTeMQBEdEwyHKMvrShDYcCwrHqzed4xAER0TBJGvR9jdFbbQLb86qw6nQOgrrauSGKiGiYJA16\nr4oKKIzGix775FQTAny9cFvebggfnz6fQ0REgydt0Ov1CLr99t6PDZ0WvFVYh0fmjIf3+fNQWCyX\nPYeIiIZG2svBAbS+9lrvx6/n12JBbDAmho4C/Px6nqNUovWTTySqkIjI9Uka9AoAQQ89BAA4db4N\nhyoNuC8xAgBg2rcP1shIGA8cgG38eAmrJCJybZKuoxdeXmj95z9hEwLb86rxs6RIBH13aJlt/HgY\njx2TsjwiIrcgbY/eZsOozZvx6akmeCsUuCkuRMpyiIjckuRj9A0/vhdvFNThkRujLrroWxMTA+3o\n0dCGh8Pr+HHpiiQicnEOH7opLS3FW2+9BavVitTUVNw+wIoZBYB33/sK8372M0warbz4c62tUNhs\ngM0G1c03w1Bb6+hSiYg8gkN79DabDS+//DLWrFmDjRs3Yt++faiuru73+ScjJ2Hv/DvxwMyxl3/S\n2xsAIBTDLZ1rAAAFyUlEQVQKmD7/3JFlEhF5FIcGfVlZGSIiIhAWFgYfHx/MnTsXBQUF/T7/+Xt/\niwemjYE64PI/LMy33gqhUMAyezbEd/fDEhHR0Dk06JubmxEaGtr7cUhICJqbm/t9vq29E3dv6/ti\nb6/mZiiEgO+hQzzrhohoGCRdXrlu1zZ06c72+Tmh7Bmz51k3RETD49CgDwkJQVNTU+/HTU1NCAnp\ne8mk9sgR1L+ZhXoAKCq6/Anr1/f8BwBnzjiyTCIil6XVDv1+DocGfWxsLOrr66HT6RASEoK8vDw8\n+uijfT535mOPOfKtiYioHwohhHDkFywtLcWbb77Zu7xy0aJFjvzyREQ0RA4PeiIikhdJd8YSEdHI\nY9ATEbk5SZZXDuWYBCmtXr0ao0aNgpeXF7y9vbFhwwapSwIAvPTSSyguLoZarcaWLVsAAB0dHcjM\nzIROp0N4eDjS0tIQEBAguzrfe+897Nu3D2q1GgCwYsUKTJ8+XbIaGxsbkZWVBYPBALVajZSUFKSk\npMiuPfurU27taTab8Yc//AHd3d3w8/PDnDlzsHjxYtm1Z391yq09gZ4TB9avX4+QkBCsX7/evrYU\nTma1WsUjjzwiGhoaRHd3t1i7dq2oqqpydhmDsmrVKmEymaQu4zKlpaWivLxcPPbYY72P/e1vfxO7\ndu0SQgixc+dO8c4770hVXq++6nzvvffE7t27JazqYnq9Xpw9e1YIIYTBYBAPPfSQqKqqkl179len\n3NpTCCE6OzuFEEKYzWbx2GOPidraWtm1pxB91ynH9ty9e7fYunWr2LhxoxDCvp91pw/dDPWYBKkJ\nGc5VJyQkIDAw8KLHCgoKkJycDABISUlBfn6+FKVdpK86AXm1qVarRUxMDABArVYjNjYWzc3NsmvP\n/uoE5NWeAODv7w8A6OzshM1mg6+vr+zaE7i4TqvVCl9fXwDyas+mpiYUFxdj4cKFvXXZ05ZOH7rp\n65iEsrIyZ5cxKAqFAs888wwUCgVuueUW3HTTTVKX1C+DwdC7kUKj0cBgMEhcUf/+/e9/Y9++fZg8\neTLuu+++Pn8ZSKG+vh7V1dWYPHmyrNvz+3WeOnVKdu1ps9nw+OOPo6qqCg888ABGjx4ty/bsq05A\nXt+fb731Fu699150dHT0PmZPW3IydgDPPvssNm3ahF/96lfYuXMnTpw4IXVJg6L43rn+cnPLLbdg\n+/bt+POf/wwvLy+8/fbbUpcEoKdXl5GRgfvvv/+y8U45teeldcqxPb28vLBp0yZs27YNn376Kc6e\nvfiYE7m0Z191yqk9CwsLoVarMWHChH7/yhhsWzo96IdyTILUgoODAQBRUVGYPXu2bP/yAHp+s7e0\ntAAA9Ho9NBqNxBX1TaPRQKFQQKlU4tZbb5VFm1osFmzZsgXz589HUlISAHm2Z391yq09LwgLC8OM\nGTNQWloqy/a84NI65dKep06dQmFhIVavXo2tW7fi+PHjyMzMtKstnR703z8mwWKxIC8vD7NmzXJ2\nGVfU1dXV++eS0WhEcXExoqOjJa6qf7NmzUJOTg4AIDc3tzcI5Eav1wMArFYrvvrqK8nbVAiBV155\nBVFRUbjjjjt6H5dbe/ZXp9za02g0oq2tDQBgMplQUlKC6Oho2bVnf3VeCFA5tOeKFSvw8ssvIysr\nC+np6bj66quRlpZmV1tKsjPWFY5J0Ol02LRpEwBApVJhzpw5uPnmmyWuqkdGRgZOnDgBk8kEjUaD\n5cuX44YbbpDV8rXv12k0GqHVanHPPfegtLQUFRUV8PHxQUJCApYsWWLXIU2OcvLkSTz99NOIjo7u\n/TN4xYoViI+Pl1V79lXnT37yE3z99deyas/KykpkZWXBZrNBq9Vizpw5WLhwoeyWV/ZX5/bt22XV\nnheUlpZi9+7dePzxx+1qSx6BQETk5jgZS0Tk5hj0RERujkFPROTmGPRERG6OQU9E5OYY9EREbo5B\nT0Tk5hj0RERu7v8DLdrDpSm4gIwAAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11438f110>"
       ]
      }
     ],
     "prompt_number": 43
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Of course, we need not fit least squares models by hand. The `statsmodels` package implements least squares models that allow for model fitting in a single line:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "import statsmodels.api as sm\n",
      "\n",
      "straight_line = sm.OLS(y, sm.add_constant(x)).fit()\n",
      "straight_line.summary()"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "html": [
        "<table class=\"simpletable\">\n",
        "<caption>OLS Regression Results</caption>\n",
        "<tr>\n",
        "  <th>Dep. Variable:</th>            <td>y</td>        <th>  R-squared:         </th> <td>   0.891</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Model:</th>                   <td>OLS</td>       <th>  Adj. R-squared:    </th> <td>   0.864</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Method:</th>             <td>Least Squares</td>  <th>  F-statistic:       </th> <td>   32.67</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Date:</th>             <td>Mon, 24 Jun 2013</td> <th>  Prob (F-statistic):</th>  <td>0.00463</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Time:</th>                 <td>21:24:18</td>     <th>  Log-Likelihood:    </th> <td> -12.325</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>No. Observations:</th>      <td>     6</td>      <th>  AIC:               </th> <td>   28.65</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Df Residuals:</th>          <td>     4</td>      <th>  BIC:               </th> <td>   28.23</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Df Model:</th>              <td>     1</td>      <th>                     </th>     <td> </td>   \n",
        "</tr>\n",
        "</table>\n",
        "<table class=\"simpletable\">\n",
        "<tr>\n",
        "    <td></td>       <th>coef</th>     <th>std err</th>      <th>t</th>      <th>P>|t|</th> <th>[95.0% Conf. Int.]</th> \n",
        "</tr>\n",
        "<tr>\n",
        "  <th>const</th> <td>   -4.3500</td> <td>    2.937</td> <td>   -1.481</td> <td> 0.213</td> <td>  -12.505     3.805</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>x1</th>    <td>    3.0000</td> <td>    0.525</td> <td>    5.716</td> <td> 0.005</td> <td>    1.543     4.457</td>\n",
        "</tr>\n",
        "</table>\n",
        "<table class=\"simpletable\">\n",
        "<tr>\n",
        "  <th>Omnibus:</th>       <td>   nan</td> <th>  Durbin-Watson:     </th> <td>   2.387</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Prob(Omnibus):</th> <td>   nan</td> <th>  Jarque-Bera (JB):  </th> <td>   0.570</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Skew:</th>          <td> 0.359</td> <th>  Prob(JB):          </th> <td>   0.752</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Kurtosis:</th>      <td> 1.671</td> <th>  Cond. No.          </th> <td>    17.9</td>\n",
        "</tr>\n",
        "</table>"
       ],
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 44,
       "text": [
        "<class 'statsmodels.iolib.summary.Summary'>\n",
        "\"\"\"\n",
        "                            OLS Regression Results                            \n",
        "==============================================================================\n",
        "Dep. Variable:                      y   R-squared:                       0.891\n",
        "Model:                            OLS   Adj. R-squared:                  0.864\n",
        "Method:                 Least Squares   F-statistic:                     32.67\n",
        "Date:                Mon, 24 Jun 2013   Prob (F-statistic):            0.00463\n",
        "Time:                        21:24:18   Log-Likelihood:                -12.325\n",
        "No. Observations:                   6   AIC:                             28.65\n",
        "Df Residuals:                       4   BIC:                             28.23\n",
        "Df Model:                           1                                         \n",
        "==============================================================================\n",
        "                 coef    std err          t      P>|t|      [95.0% Conf. Int.]\n",
        "------------------------------------------------------------------------------\n",
        "const         -4.3500      2.937     -1.481      0.213       -12.505     3.805\n",
        "x1             3.0000      0.525      5.716      0.005         1.543     4.457\n",
        "==============================================================================\n",
        "Omnibus:                          nan   Durbin-Watson:                   2.387\n",
        "Prob(Omnibus):                    nan   Jarque-Bera (JB):                0.570\n",
        "Skew:                           0.359   Prob(JB):                        0.752\n",
        "Kurtosis:                       1.671   Cond. No.                         17.9\n",
        "==============================================================================\n",
        "\"\"\""
       ]
      }
     ],
     "prompt_number": 44
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "from statsmodels.formula.api import ols as OLS\n",
      "\n",
      "data = pd.DataFrame(dict(x=x, x2=x**2, y=y))\n",
      "cubic_fit = OLS('y ~ x + x2', data).fit()\n",
      "\n",
      "cubic_fit.summary()"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "html": [
        "<table class=\"simpletable\">\n",
        "<caption>OLS Regression Results</caption>\n",
        "<tr>\n",
        "  <th>Dep. Variable:</th>            <td>y</td>        <th>  R-squared:         </th> <td>   0.929</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Model:</th>                   <td>OLS</td>       <th>  Adj. R-squared:    </th> <td>   0.881</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Method:</th>             <td>Least Squares</td>  <th>  F-statistic:       </th> <td>   19.50</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Date:</th>             <td>Mon, 24 Jun 2013</td> <th>  Prob (F-statistic):</th>  <td>0.0191</td> \n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Time:</th>                 <td>21:24:18</td>     <th>  Log-Likelihood:    </th> <td> -11.056</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>No. Observations:</th>      <td>     6</td>      <th>  AIC:               </th> <td>   28.11</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Df Residuals:</th>          <td>     3</td>      <th>  BIC:               </th> <td>   27.49</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Df Model:</th>              <td>     2</td>      <th>                     </th>     <td> </td>   \n",
        "</tr>\n",
        "</table>\n",
        "<table class=\"simpletable\">\n",
        "<tr>\n",
        "      <td></td>         <th>coef</th>     <th>std err</th>      <th>t</th>      <th>P>|t|</th> <th>[95.0% Conf. Int.]</th> \n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Intercept</th> <td>  -11.0748</td> <td>    6.013</td> <td>   -1.842</td> <td> 0.163</td> <td>  -30.211     8.062</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>x</th>         <td>    6.0577</td> <td>    2.482</td> <td>    2.441</td> <td> 0.092</td> <td>   -1.840    13.955</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>x2</th>        <td>   -0.3027</td> <td>    0.241</td> <td>   -1.257</td> <td> 0.298</td> <td>   -1.069     0.464</td>\n",
        "</tr>\n",
        "</table>\n",
        "<table class=\"simpletable\">\n",
        "<tr>\n",
        "  <th>Omnibus:</th>       <td>   nan</td> <th>  Durbin-Watson:     </th> <td>   2.711</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Prob(Omnibus):</th> <td>   nan</td> <th>  Jarque-Bera (JB):  </th> <td>   0.655</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Skew:</th>          <td>-0.809</td> <th>  Prob(JB):          </th> <td>   0.721</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Kurtosis:</th>      <td> 2.961</td> <th>  Cond. No.          </th> <td>    270.</td>\n",
        "</tr>\n",
        "</table>"
       ],
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 45,
       "text": [
        "<class 'statsmodels.iolib.summary.Summary'>\n",
        "\"\"\"\n",
        "                            OLS Regression Results                            \n",
        "==============================================================================\n",
        "Dep. Variable:                      y   R-squared:                       0.929\n",
        "Model:                            OLS   Adj. R-squared:                  0.881\n",
        "Method:                 Least Squares   F-statistic:                     19.50\n",
        "Date:                Mon, 24 Jun 2013   Prob (F-statistic):             0.0191\n",
        "Time:                        21:24:18   Log-Likelihood:                -11.056\n",
        "No. Observations:                   6   AIC:                             28.11\n",
        "Df Residuals:                       3   BIC:                             27.49\n",
        "Df Model:                           2                                         \n",
        "==============================================================================\n",
        "                 coef    std err          t      P>|t|      [95.0% Conf. Int.]\n",
        "------------------------------------------------------------------------------\n",
        "Intercept    -11.0748      6.013     -1.842      0.163       -30.211     8.062\n",
        "x              6.0577      2.482      2.441      0.092        -1.840    13.955\n",
        "x2            -0.3027      0.241     -1.257      0.298        -1.069     0.464\n",
        "==============================================================================\n",
        "Omnibus:                          nan   Durbin-Watson:                   2.711\n",
        "Prob(Omnibus):                    nan   Jarque-Bera (JB):                0.655\n",
        "Skew:                          -0.809   Prob(JB):                        0.721\n",
        "Kurtosis:                       2.961   Cond. No.                         270.\n",
        "==============================================================================\n",
        "\"\"\""
       ]
      }
     ],
     "prompt_number": 45
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Exercise: Polynomial function\n",
      "\n",
      "Write a function that specified a polynomial of arbitrary degree."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 45
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "## Model Selection\n",
      "\n",
      "How do we choose among competing models for a given dataset? More parameters are not necessarily better, from the standpoint of model fit. For example, fitting a 9-th order polynomial to the sample data from the above example certainly results in an overfit."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "def calc_poly(params, data):\n",
      "        x = np.c_[[data**i for i in range(len(params))]]\n",
      "        return np.dot(params, x)\n",
      "    \n",
      "ssp = lambda theta, x, y: np.sum((y - calc_poly(theta, x)) ** 2)\n",
      "betas = fmin(ssp, np.zeros(10), args=(x,y), maxiter=1e6)\n",
      "plot(x, y, 'ro')\n",
      "xvals = np.linspace(0, max(x), 100)\n",
      "plot(xvals, calc_poly(betas, xvals))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 7.015262\n",
        "         Iterations: 663\n",
        "         Function evaluations: 983\n"
       ]
      },
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 46,
       "text": [
        "[<matplotlib.lines.Line2D at 0x1145b5dd0>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAECCAYAAADn84z1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl4VOWhP/DvLJlMlplMFpJAQkjIRkRkC1BkC6BBJNYF\nlyu0F/VRKKLWCjeEXr2XahXalIqGyFJ/z612eX56tdhWEaIgi6BUICgYCCQkkED2TGYmk9nn/P4I\n5AeSdTLJmZP5fp4nYg5nMt8gfD28533fIxMEQQAREUmOXOwARETkGRY4EZFEscCJiCSKBU5EJFEs\ncCIiiWKBExFJlLK7n7Tb7Vi/fj0cDgdUKhWmT5+OnJwcWCwWFBQUoL6+HjExMXj22WehVqsHKzMR\nEQGQ9TQP3GazITAwEA6HA3l5eVizZg327t0LjUaDe++9Fx999BHMZjOWLl06WJmJiAi9GEIJDAwE\nAFitVrjdbgQEBODYsWOYM2cOACArKwvffPPNwKYkIqKbdDuEAgButxtr165FVVUVHnvsMURFRcFg\nMECn0wEAwsLCYDAYBjwoERHdqMcCl8vlyM/PR319PTZs2ID09PQbfl4mkw1YOCIi6lqPBX5NdHQ0\nJk6ciJKSEoSFhaGlpQU6nQ56vR5hYWFdvu7rr7+G2Wz2SlgiIn+h0+kwefLkbs/ptsCNRiMUCgVC\nQkJgMplw8uRJPP7448jMzMT+/ftx33334cCBA5gyZUqXX8NsNmPSpEmefQdERH7qxIkTPZ7TbYG3\ntLSgsLAQbrcbOp0OOTk5GDduHFJSUlBQUIA1a9Z0TCMkIqLB1eM0wv7au3cvr8CJiProxIkTmD9/\nfrfncCUmEZFEscCJiCSKBU5EJFEscCIiiWKBExFJFAuciEiiWOBERBLFAicikigWOBGRRPV6Mysi\nIuqc0y3gisGGxjY7Gs0OKOUyzE0OH/DdWlngRET90GJx4MU9F2CyORGjUSEqOADlTRaU1Jvx9PR4\nyAewxFngREQeqm+1Y92nZZiZqMNjmcM7rrjNdhde2lOO3x24iNWzR0EhH5gS5xg4EZEHqg1WrP74\nPO5Kj8TjU0bcMFwSolLgtYUpaLE68creCthd7gHJwAInIuojo9WJ3E/KsGRiLB66LabTc9RKOX51\n52i0OVzYXdo0IDlY4EREfbTt6GXMSNRhYXpkt+cFKOT46aTh2Hm6Ae4B2LmbBU5E1AfHqo04VdOK\nJ6YM79X5t8aEIESlwNFLRq9nYYETEfWSxeHCG19W4eczRyIoQNGr18hkMiweNwx/O13v9TwscCKi\nXvrjsRqMGx6KzHhtn143Kykcl402nG9s82oeFjgRUS+ca2jDgQt6/GxaXJ9fq5TLcN9Y71+Fs8CJ\niHrh3RM1WDoxFlq1Z8tn7k6PxL+qjGg0272WiQVORNSDs/VmVDRbsKCHWSfdCQ1UYn5KBP5Z0ui1\nXCxwIqIe/Lm4Fo9OiIVK0b/KnJscjqNVBi+lYoETEXXr2tV3dlpEv79WWlQwak12tFgcXkjGAici\n6tafi2vxb+Nj+n31DQAKuQzjYkPxXU2rF5KxwImIuuSNse8fmjBCg+IrJq98LRY4EVEX/nqyFo94\n6er7mgkjQnHyCq/AiYgGzGWDDWfq25Cd5r2rbwBIighCq92F+tb+TydkgRMRdeIfJQ24Ky0CaqV3\na1Iuk2H88FCc9MIwSrcz0hsbG1FYWAiDwQCtVousrCxkZWXh/fffx759+6DVti8nXbJkCSZMmNDv\nMEREvsBsd+HzsmZsvX/MgHz9CSM0OFnT2u+r+24LXKlUYtmyZUhMTITRaMTq1auRkpICmUyGnJwc\n5OTk9OvNiYh80WfnmzFxhAbRoaoB+foTRoTirydrIQhCv56b2e3fDXQ6HRITEwEAWq0WycnJaG5u\nBgAIA7C3LRGR2NyCgL9/34D7xg4bsPeI0wYCAC4bbf36Or0e3KmtrUV1dTXS0tIAALt378YvfvEL\nbN26FWazuV8hiIh8xTdVRgQFyDE2JmTA3kMmk7UPo/RzNkqvCtxqtWLz5s1YtmwZ1Go1srOzsWXL\nFrz66quQy+V49913+xWCiMhXfHT16rs/Qxu9McELNzJ7LHCn04lNmzZh1qxZmDJlCgAgLCwMMpkM\nwcHBWLBgAcrKyvoVgojIF1QbrChvsiArOXzA32tinAYnr5j6NRzdbYELgoBt27YhPj4eixYt6jiu\n1+sBAC6XC19++SUSEhI8DkBE5Ct2nW1CdlqEVxfudGVYiApKhQwNZs/3Rel2FkppaSkOHTqEhIQE\n5ObmAgAeffRRHD58GJWVlVAqlcjIyMCyZcs8DkBE5AvsLjc+O9+MzfekDtp7JoYHoVJv8Xi2S7cF\nPmbMGLz33ns3HZ84caJHb0ZE5KuOVBqQFKFGXJh60N4zMVyNimYrpo4M8+j1XIlJRATgk7ONWDQm\nalDf89oVuKdY4ETk96oNVlzUW3H7KM+uhD2VGK5Gpd7q8etZ4ETk9z4924Q7UyMQMAg3L683KlyN\n6hYrXG7PZqKwwInIr127eblwjHd3HeyNoAAFIoIDcMXDFZkscCLya19dNGBUuBrxg3jz8nrt4+Ce\nDaOwwInIr31a2oSFXnziTl+1j4N7diOTBU5EfqvOZMf5xjbMSNSJliExwvMbmSxwIvJbReebMDc5\nHIFefmhDXySGB6GymVfgRES95hYEFJ1rxl1efmRaX8WHBaKu1Q67093n17LAicgvnbxiQmigAilR\nwaLmCFDIMVwTiCpD34dRWOBE5Jd2lzaJfvV9jacLeljgROR3jFYnvqk2Ye4gbBvbG6MiPJtKyAIn\nIr/zRbkeU+I10Kq73c9v0CSFqz26kckCJyK/s/tcExb4yPAJ4PliHhY4EfmVssY2tNpcmBinETtK\nh1iNCi1WJ9rsrj69jgVORH5l97n2p+7IB/iZl32hkMuQoAvExZa+XYWzwInIb9idbuwv1yM71XeG\nT64ZFR6Ei30cRmGBE5HfOHyxBSlRwYjRePYIs4EUG6pCXau9T69hgROR39hd2uxTNy+vF6tRoc7U\nt21lWeBE5BdqTTaUN7VhxiA/dae3okNVqGvt2xPqWeBE5BeKzjVjbnI4VCJuXNWdmFAV6lp5BU5E\ndAO3IKDovG/N/f6hqJAA6NucfXq8GguciIa84ssmaAKVom9c1Z0AhRxhQUo0mns/jMICJ6IhT+yn\n7vRWbB+HUVjgRDSktVgcOH7ZhHk+snFVd6L7OJWQBU5EQ9rn55sxfVQYQgN9Y+Oq7sRoVKgzscCJ\niCAIAnaVNuFuCQyfANdmorDAiYjwfZ0ZMgBjY0LEjtIrHEIhIrpq19WblzIf2riqO7EaFer7UODd\nDgo1NjaisLAQBoMBWq0WWVlZyMrKgsViQUFBAerr6xETE4Nnn30WarW63+GJiLyl1ebEVxcNWD51\nhNhRei06RIUGswNuoXdzwbstcKVSiWXLliExMRFGoxGrV69GSkoK9u/fj/T0dOTm5uKjjz7Chx9+\niKVLl3rlGyAi8oZ95XpkxmmgCwoQO0qvqZRyaFQKNLf1bi54t0MoOp0OiYmJAACtVovk5GQ0Nzfj\n2LFjmDNnDgAgKysL33zzTf9SExF5kSAI2HW2EQvHSOPm5fX6Mg7e6zHw2tpaVFdXIy0tDQaDATqd\nDgAQFhYGg8HgWVIiogFQUm+GzSlgwgjfeepOb/VlKmGvCtxqtWLz5s1YtmzZTWPdUrk5QET+4+Mz\njViUEeVTT93prb5MJeyxwJ1OJzZt2oRZs2ZhypQpANqvultaWgAAer0eYWG+uT0jEfkfg9WJo5eM\nyE6NEDuKR6JDez8TpdsCFwQB27ZtQ3x8PBYtWtRxPDMzE/v37wcAHDhwoKPYiYjEtqe0CdNHhUGr\n9v2Vl52J1XjpCry0tBSHDh3C6dOnkZubi9zcXJw8eRKLFy/GuXPnsGbNGpw/fx6LFy/2SnAiov5w\nCwI+OduInIwosaN4LDq092Pg3f4vasyYMXjvvfc6/bnc3Ny+JyMiGkDHq00IUSkwZpjvbhvbkxhv\nDaEQEUnJx2far76lPLkiKECBwF4+NYgFTkRDQq3JhtN1rZgrgW1jexKjUfXqPBY4EQ0J/yhpxIK0\nSAQFKMSO0m8xoSxwIvITFocLe8414ce3SPfm5TVHiopw8Ys9vTqXBU5EkvfZ+WaMH65BrCZQ7Cj9\ncqSoCIfWrcPD3x3r1fkscCKSNLcgYOfpBtx/6zCxo/Tbwe3bsbGiAsP1db06nwVORJL2TZURQQFy\n3CqRhzZ0R2lrf6BxSs2FXp3PAiciSdv5fQMeuDVa0lMHr3EGtg8Bxelre3U+C5yIJKtSb0Gl3oLZ\no3ViR/GK2StWIC8pqdfnS3OzACIiAO9/V48fZwyDSjE0rkVvz84GAOTt2IE7e3H+0Piuicjv1Jns\nOHrJMCSmDl7v9uxsrP3gg16dywInIkn64FQdFqZHIjTQfwcSWOBEJDl6iwP7yvV44NZosaOIigVO\nRJLz0ekGzEkKR0SwdB5YPBBY4EQkKWa7C5+cbcRDt/n31TfAAiciifn4TCMmx2sxXCvtZfPewAIn\nIslos7vwt9P1+LfxMWJH8QkscCKSjJ3fN2DCCA2SIoLEjuITWOBEJAlGqxM7T9fj3ycNFzuKz2CB\nE5Ek/O+pesxI1CEujGPf17DAicjnNbc5sOtsI5ZOjBU7ik9hgRORz/u/39ZhfkoEonv5qDF/wQIn\nIp9WY7Jhb1kzHuXMk5uwwInIp/3h6GXcf2s0wv181WVnWOBE5LOKr5hwvtGCh8Zx1WVnWOBE5JNc\nbgFbv6rG8mlxCFSyqjrjv/swEpHPOFJUhIPbt0Nps8EZGIjZK1agIW4iwtRKzEwMEzuez2KBE5Go\njhQV4dC6dfhNRUXHsdU1DTj25Ot4/b5bhsSzLgdKjwX+1ltvobi4GFqtFps2bQIAvP/++9i3bx+0\nWi0AYMmSJZgwYcLAJiWiIeng9u03lDcAhN+6ABEVJ5AUMVmkVNLQY4HPnTsXCxcuxJYtWzqOyWQy\n5OTkICcnZ0DDEdHQp7TZbvj869TJOJo6Gbcc/gOAp8QJJRE93hnIyMhASEjITccFQRiQQETkX5yB\n/39pfGtgMF59cDX+84NNkCk5dNITj2/t7t69G7/4xS+wdetWmM1mb2YiIj8ye8UK5CUlAQAKFi3H\ntPPHsdPRhFnLl4uczPd5dBMzOzsbDz74ICwWC/70pz/h3XffxcqVK72djYj8wO3Z2QCA5R8U4cyt\nszDtyNuYu3Fjx3HqmkcFHhbWPq0nODgYCxYsQEFBgVdDEZF/uXX2PGxtjsOLM+Ix9bm/iB1HMjwa\nQtHr9QAAl8uFL7/8EgkJCV4NRUT+wy0IyD9wETMSwzB1JOd890WPV+CbN2/GmTNnYDQasXLlSjz0\n0EMoKSlBZWUllEolMjIysGzZssHISkRD0Hvf1sFkc+HJqXFiR5GcHgv8+eefv+nYvHnzBiQMEfmX\nk1dM+Pv3DSi4Lx1KOWed9BVXYhJJSGdLzqV6s6/RbMfG/ZX4jzmjMCyE+3x7ggVOJBGdLTnPq6wE\nAMmVuMnmxC93l+OBsdGYHK8VO45kcYsvIok4uH07Nv5gyfnGigoc2rFDpESesTnd+O/PLmDiCA0e\nuo3bxPYHC5xIIn645PwahdU6yEk853IL2PBFJYaFqLDiR3HcqKqfWOBEEnH9kvPrudTqQU7iGZdb\nwO8PXYLF4caa2QmQs7z7jQVOJBHXLzm/Zm1ioiSWnNucbry8twLNbQ6svzMJAQpWjzfwJiaRRFy7\nUZm3YwcUVitcajVmL1/u8zcwzXYX/qvoAiKClXhx3miWtxexwIkk5PbsbJ8v7OvVmGz41WcVuDU2\nBE9Pj+ewiZexwIloQBys0KPgcDUenRCD+8cO4w3LAcACJyKvsjvd2H70Mr6pNuLXC0YjfdjNzxMg\n72CBE5FXCIKAIxcN2HH0MtKGBWPr/WMQolKIHWtIY4ETUb9V6i3Y9vVlNJodeG7GSK6uHCQscCLy\niCAIKL5iws7TDTjb0IYlE2Jwzy3DuCnVIGKBE1GfVLVYcfhiC/aV6SEAeGDsMLw4PwmBSk4PHGws\ncCLqkiAIqGu142x9G0obzDhWbYLJ7sTto3R4eno8xg8P5ewSEbHAiXxIm92FWpMdda126C0OGKxO\nGK1OtNpdsLsE2JxuOFwCBAgAABlkUMiBAIUcAXIZVAo51AFyBCrbP9QKWce/qxRyKBUyBMhlUMhl\nEARAgACXu32lpNnhgtnugsHiRF1re4YrRhsCFDKMGRaC9GHBeGF2AtKHBXM+t49ggROJQBAEVBts\nKG1oQ1lTG8qbLKjUW2F1uhGrUSE2VIWI4ABo1UpEBgcgITwIgYr2gg5QyHCtPwUBcAkCHK72D5vL\nDbvTDevVD7PNDZtTgPXqcadb6PiQy9r/ByCTAWqlHCEqBUJUCmjVCqRE6TpyhAcHiPuLRV1igRMN\nkuY2B45eMqD4ignf1bRCIZfhlpgQpEQG45HxWiRFBCEiSMkhCeo1FjjRAGow23GgXI8vKw242GJF\nZrwGk+O0eDxzBGI1KpY19QsLnMjLHC43vr5kxO7SJpxtMGPGKB2WTIzBhBEaqLiRE3kRC5zIS4xW\nJz4524i/lzQgTqvGXekReOmOJKg5vY4GCAucqJ8azXa892099pU340cJYXhtQQpGRwaJHYv8AAuc\nyEMGqxPvfVuHPeeasCAtEtsfGIMoPl2dBhELnKiP7E43PjhVj7+drsec0eHY8UAGIkOG7lS7I0VF\nOLh9O5Q2G5yBgZi9YoWk9iQfyljgRL10bbe97UcvIyUyCAX3pmO4tvPnVA4VR4qKcGjdOvymoqLj\nWF5lJQCwxH0AC5yoF2pNNrx5uAoNrQ48P3MkJsX5x257B7dvv6G8AWBjRQXyduxggfsAFjhRN1xu\nAf8oacBfimvx0G0xWDwu2q9221PabJ0eV1itg5yEOsMCJ+pCtcGK/AMXoZTLsfnHaYgPU4sdadA5\nAzsfInKp/e/Xwhf1WOBvvfUWiouLodVqsWnTJgCAxWJBQUEB6uvrERMTg2effRZq/gelIUIQBHxy\ntgl/PHYFP500HPfcEuW3mzfNXrECeZWV2HjdMMraxETMXr5cxFR0TY8FPnfuXCxcuBBbtmzpOPbh\nhx8iPT0dubm5+Oijj/Dhhx9i6dKlAxqUaDC0WBx4/VAVGsx2/D4nDQnh7Rcm/joT49r3mLdjBxRW\nK1xqNWYvX+4X37sU9FjgGRkZqK+vv+HYsWPHsH79egBAVlYW1q9fzwInyTtV24oNX1Ri7uhwvDg/\nEQFXl737+0yM27Oz/eL7lCKP1vgaDAbodDoAQFhYGAwGg1dDEQ0mQRDw/rd1eOXzCjw/cySemhbX\nUd5A+0yMjZ3MxDi0Y8dgRyW6Qb9vYnI3NZIys92F3+6/iGaLA1vuS0d06M0rKTkTg3yVR1fgYWFh\naGlpAQDo9XqEhYV5NRTRYKhqseLZv5ciMiQAv89J7bS8Ac7EIN/lUYFnZmZi//79AIADBw5gypQp\n3sxENOD+VWXACx+fx4PjovHcjJE3DJn80OwVK5CXlHTDsbWJiZjFmRgksh6HUDZv3owzZ87AZDJh\n5cqVePjhh7F48WIUFBRgzZo1HdMIiaRAEAR8eKoeH5yux/o7kjA2NrTH13AmBvkqmSAIwkC+wd69\nezFp0qSBfAuiXnG6BRQeqUJJnRmvLEjucsiEyBecOHEC8+fP7/YcrsQkv2C2u/DK3gooZDK8fk8a\nglUKsSMR9RsLnIa8+lY7/nNPOSYMD8XPfhQPhR/tZUJDGwuchrSKZgte3FOO+8cOw4O3xYgdh8ir\nWOA0ZH17xYRf76vE09PjMDc5Quw4RF7HAqch6cuKFrxxuAq/nJuIiXEaseMQDQgWOA05n55txDsn\narDhrmSkRAWLHYdowLDAaUh579s6fHymEZsWpSLOD/fvJv/CAqchQRAE/J9vruBolRGv35PKp8OT\nX2CBk+S5BQFbDlfjfFMbNi1KhVbN39bkH/g7nSTN5RaQf+AiGswObFyYghAu0CE/wgInybK73Hht\nXyUcLgGv3pUMtdKjvdmIJIu/40mSbE431n92AXIZsP7OJJY3+SVegZPkWBwu/FfRBUQEByB3zigu\njSe/xQInSTHbXXhxTzniwwLx/MwEljf5NRY4SYbJ5sQvd5cjLSoYq26Ph5yP8yM/xwInSTBancj7\ntAzjhofiZ9Pi+CxWIrDASQL0FgfydpVh6kgtnpgyguVNdBULnHxaU5sDa3eVYVaSDv8+KZblTXQd\nFjj5rEazHbm7yjAvJQI/mRgrdhwin8MCJ59U32pH7q7zWJgehUfG80EMRJ1hgZPPqTXZkLurDD++\nZRgeHBctdhwin8UCJ59yxWjD2l1lWDwuGveNHSZ2HCKfxgInn1FtsGLtrjIsmRiLRWOixI5D5PNY\n4OQTLumtyPu0DMsyh2NBWqTYcYgkgQVOoitvasN/7inHk1PicEcqHz5M1FsscBLVuYY2vFRUjlXT\n4zF7dLjYcYgkhQVOoimpM+O/P7uAF2YlYPqoMLHjEEkOC5xEUXzFhNf2VSJ3zihMGakVOw6RJPWr\nwFetWoWgoCDI5XIoFAps2LDBW7loCDt6yYDfHbyEl+Yn4rbhGrHjEElWv6/A169fj9DQUG9kIT9w\n8IIeW45U4+Xs0ciIDhE7DpGk9bvABUHwRg7yA3vONeF/jl3BhoXJSI4MFjsOkeT1q8BlMhlefvll\nyGQyZGdn44477vBWLhpiPjxVj53f1yP/7lSM1KnFjkM0JPSrwF955RWEh4ejuroaGzZsQFxcHDIy\nMryVjYYAQRDwzvEaHKxowe9z0hAdqhI7EtGQ0a9HeYeHt8/bjY+Px9SpU1FWVuaVUDQ0uNwCCr+q\nxr+qjNiUk8ryJvIyjwvcZrPBYrEAAIxGI4qLi5GQkOC1YCRtdpcbG76oxEW9FfmLUhEeFCB2JKIh\nx+MhFIPBgPz8fACARqPBokWLMH78eK8FI+ky21341ecXoAlU4tUFyVAp+/UXPSLqgscFHh0d3VHg\nRNc0tTnw0p5yjIkOwarp8VDI+Qg0ooHClZjkNRf1Fry45wLuSo/EkgkxfH4l0QBjgZNXfFdjwq/3\nVmL5NO4oSDRYWODUb3vLmrH968tYNy8RE0dwaTzRYGGBk8fcgoB3j9dgb5kev12UgsTwILEjEfkV\nFjh5xOp0I//ARTSZHXjz3jROEyQSAed3UZ/Vt9qx+uNzUClk+O3dKSxvIpHwCpz65LuaVrz2RQUe\nuDUaD42L5kwTIhGxwKlXBEHAP8804s8napGbNQqZ8XwIA5HYWODUI4vDhTcPV6G8yYLX70lDXFig\n2JGICBwDpx5c0lvx3D/OQSaT4c1701neRD6EV+DUpb1lzdj29WU8kTkcd6VHcrybyMewwOkmZrsL\nW45U4VxDGzby6TlEPotDKHSDM/VmPL3zLNRKOQrvH8PyJvJhvAInAO37d//lRC0+LW3CczNGYmaS\nTuxIRNQDFjihrLEN+QcuIlYbiG0PjEFEMBfmEEkBC9yP2Zxu/LW4FrtKm7BiWhzmp4TzRiWRhLDA\n/dSJy0a8ebgKqZHB2PbAGETyqptIcljgfqbBbMfb/7qCkjoznp0Rj6kjw8SOREQeYoH7CZvTjf89\nVY+dp+txT0YUnp85EkEBCrFjEVE/sMCHOJdbwBflerxzvAapUcHYcl86hmu4mpJoKGCBD1GCIODr\nS0b8z7ErCA5Q4D/mjMJtw0PFjkVEXsQCH2LcgoCjl4z468la2JxuPJ45Aj9K0HJ2CdEQxAIfIpxu\nAYcqWvDet7WQy2RYMiEWtyeGQc7iJhqyWOASZ7Q6sau0Ef8oacQITSCemDICU+J5xU3kD1jgEiQI\nAk7XmbG7tAlfXTTg9lFheCV7NPctIfIzLHAJqTHZsL9cj8/ON0Muk+Gu9Eg8NXUEdHwmJZFfYoH7\nuBqTDV9dNGB/uR41JjtmJeqwenYCbokO4TAJkZ9jgfsYh8uNM/VtOF5txFeXDGixODEtQYufThqO\niXEaKOVdl/aRoiIc3L4dSpsNzsBAzF6xArdnZw9ieiIaTB4XeElJCd555x24XC7Mnz8fCxcu9GYu\nv2F3unG+sQ3f15lxssaEkjoz4sPUmBSnwfMzE5A+LBiKbkr7miNFRTi0bh1+U1HRcSyvshIAWOJE\nQ5RHBe52u7F161a89NJLiIiIwLp16zBu3DjEx8d7O9+QYnO6cVFvRVlTG8qaLChrbEOF3ooEXSBu\niQ7BwvQo5GUlQqvu+3+Wg9u331DeALCxogJ5O3awwImGKI8KvKysDLGxsYiOjgYAzJgxA8eOHWOB\nA2izu9BodqDGZEOtyY4akw3VBhsutVjR3OZAnDYQyVHBSIkMQtZoHVKjgr2yJ4nSZuv0uMJq7ffX\nJiLf5FGBNzc3IzIysuPziIgIlJWVeS2UWARBgNMtwO4SYHe54XAJsDrcsDhdaHO4YXG40GpzwWx3\nwWRzwWhzwmBxosXqRHObA01tDrgEYFhIAGI1KsSGBiJWo8Jtw0ORoFNjuCawV8MhnnAGdr6/iUut\nHpD3IyLxDcpNzF/uLoPL3b7MWxDaf3QLgICrP149JqD934H28wS0f7T/4+rngnDD177xs+uOC9d+\n7rqvdd17X/vR5RbgEgQ4XQIcbgFyGRColEOlkCNAIUOQUo6gAAWCAuRQK+XQBCoQolJCE6hAfJga\nY2OU0KmV0AUpMSwkACEqhSizQ2avWIG8ykpsvG4YZW1iImYvXz7oWYhocHhU4BEREWhqaur4vKmp\nCREREZ2eq9Pp8CBaPEsnGtfVjx7Y2j8EA6BH+4dY1FFRuPMPf8De645dG/k+ceKEGJGIqB90up6f\nS+tRgScnJ6O2thb19fWIiIjAkSNH8POf/7zTcydPnuzJWxARUQ9kwg/HJHqppKQEf/zjHzumEd59\n993ezkZERN3wuMCJiEhccrEDEBGRZ1jgREQSNaDTCKWw3P6tt95CcXExtFotNm3aJHacLjU2NqKw\nsBAGgwGe3HxKAAAE3UlEQVRarRZZWVnIysoSO9ZN7HY71q9fD4fDAZVKhenTpyMnJ0fsWJ1yu93I\ny8tDREQE8vLyxI7TqVWrViEoKAhyuRwKhQIbNmwQO1KnrFYr3n77bVy6dAkOhwMrV65EWlqa2LFu\ncOXKFWzevLnj87q6OjzyyCM+ef/u888/x/79++FwOJCRkYHHHnus8xOFAeJyuYRnnnlGqKurExwO\nh7BmzRqhqqpqoN7OYyUlJcKFCxeEF154Qewo3dLr9UJFRYUgCIJgMBiEJ5980id/PQVBEKxWqyAI\ngmC324UXXnhBqKmpETlR5/75z38Kb7zxhrBx40axo3Tp6aefFkwmk9gxelRQUCDs3btXEARBcDqd\ngtlsFjlR91wul/DUU08JDQ0NYke5iclkEp5++mnBYrEILpdLeO2114Ti4uJOzx2wIZTrl9srlcqO\n5fa+JiMjAyEhIWLH6JFOp0NiYiIAQKvVIjk5GXq9mDPPuxZ4dVWo1WqFy+WCUul7m142NTWhuLgY\n8+bNu2lxmK/x9XxtbW04e/Ys5s2bBwBQKBQIDvbth4ucOnUKMTExiIqKEjvKTVQqFYD2X1e73Q6b\nzYbQ0M4fSD5gf7KG6nJ7X1BbW4vq6mqkpqaKHaVTbrcba9euRVVVFR577DGf/EPyzjvv4Cc/+Qks\nFovYUbolk8nw8ssvQyaTITs7G3fccYfYkW5SX18PrVaLwsJCXLhwAampqXjiiSc6isgXHT58GDNn\nzhQ7RqdUKhWefPJJrFq1CgEBAVi4cCFSUlI6PZc3MSXGarVi8+bNWLZsGdQ+us+JXC5Hfn4+3nzz\nTezZswcVP9glUWzHjx+HVqtFUlKSz1/dvvLKK8jPz8dzzz2HnTt34syZM2JHuonL5UJ5eTmmTZuG\nDRs2wOl04quvvhI7VpecTieOHz+O6dOnix2lU0ajEW+//TZef/11FBYW4ty5c12uph6wAu/Lcnvq\nHafTiU2bNmHWrFmYMmWK2HF6FB0djYkTJ6KkpETsKDcoLS3F8ePHsWrVKrzxxhv4/vvvsWXLFrFj\ndSo8PBwAEB8fj6lTp/rk32IjIyMRGhqKzMxMqFQqzJgxA8XFxWLH6lJxcTFGjx4NrVYrdpROlZWV\nITU1FbGxsdBoNJg+fXqXf4YGrMCvX27vdDpx5MgRZGZmDtTbDXmCIGDbtm2Ij4/HokWLxI7TJaPR\nCLPZDAAwmUw4efIkEhISRE51oyVLlmDr1q0oLCzE888/j7Fjx+KZZ54RO9ZNbDZbxxCP0WhEcXGx\nz/1aAu33Z2JjY3H+/Hm43W6cOHECt912m9ixunT48GHMmDFD7BhdGjNmDMrLy9Ha2gqHw4Hi4mKM\nHz++03MHbAxcoVBg5cqV+N3vftcxjdAX9wvfvHkzzpw5A5PJhJUrV+Lhhx/G3LlzxY51k9LSUhw6\ndAgJCQnIzc0F0F5EEyZMEDnZjVpaWlBYWAi32w2dToecnByMGzdO7Fjd8tVnixoMBuTn5wMANBoN\nFi1a1OUfZLGtWrUKhYWFMBqNSEhIwNKlS8WO1Cmr1YpTp05hxYoVYkfpUnBwMBYvXoz8/HzY7XaM\nHz8eY8eO7fRcLqUnIpIo3sQkIpIoFjgRkUSxwImIJIoFTkQkUSxwIiKJYoETEUkUC5yISKJY4ERE\nEvX/AC/sps0J0nhyAAAAAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114626c10>"
       ]
      }
     ],
     "prompt_number": 46
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "One approach is to use an information-theoretic criterion to select the most appropriate model. For example **Akaike's Information Criterion (AIC)** balances the fit of the model (in terms of the likelihood) with the number of parameters required to achieve that fit. We can easily calculate AIC as:\n",
      "\n",
      "$$AIC = n \\log(\\hat{\\sigma}^2) + 2p$$\n",
      "\n",
      "where $p$ is the number of parameters in the model and $\\hat{\\sigma}^2 = RSS/(n-p-1)$.\n",
      "\n",
      "Notice that as the number of parameters increase, the residual sum of squares goes down, but the second term (a penalty) increases.\n",
      "\n",
      "To apply AIC to model selection, we choose the model that has the **lowest** AIC value."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "n = len(x)\n",
      "\n",
      "aic = lambda rss, p, n: n * np.log(rss/(n-p-1)) + 2*p\n",
      "\n",
      "RSS1 = ss(fmin(ss, [0,1], args=(x,y)), x, y)\n",
      "RSS2 = ss2(fmin(ss2, [1,1,-1], args=(x,y)), x, y)\n",
      "\n",
      "print aic(RSS1, 2, n), aic(RSS2, 3, n)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 21.375000\n",
        "         Iterations: 79\n",
        "         Function evaluations: 153\n",
        "Optimization terminated successfully.\n",
        "         Current function value: 14.001110\n",
        "         Iterations: 198\n",
        "         Function evaluations: 372\n",
        "15.7816583572 17.6759368019\n"
       ]
      }
     ],
     "prompt_number": 47
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Hence, we would select the 2-parameter (linear) model."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "## Logistic Regression\n",
      "\n",
      "Fitting a line to the relationship between two variables using the least squares approach is sensible when the variable we are trying to predict is continuous, but what about when the data are dichotomous?\n",
      "\n",
      "- male/female\n",
      "- pass/fail\n",
      "- died/survived\n",
      "\n",
      "Let's consider the problem of predicting survival in the Titanic disaster, based on our available information. For example, lets say that we want to predict survival as a function of the fare paid for the journey."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "titanic = pd.read_excel(\"data/titanic.xls\", \"titanic\")\n",
      "titanic.name"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 48,
       "text": [
        "0                      Allen, Miss. Elisabeth Walton\n",
        "1                     Allison, Master. Hudson Trevor\n",
        "2                       Allison, Miss. Helen Loraine\n",
        "3               Allison, Mr. Hudson Joshua Creighton\n",
        "4    Allison, Mrs. Hudson J C (Bessie Waldo Daniels)\n",
        "5                                Anderson, Mr. Harry\n",
        "6                  Andrews, Miss. Kornelia Theodosia\n",
        "7                             Andrews, Mr. Thomas Jr\n",
        "8      Appleton, Mrs. Edward Dale (Charlotte Lamson)\n",
        "9                            Artagaveytia, Mr. Ramon\n",
        "...\n",
        "1298                  Wittevrongel, Mr. Camille\n",
        "1299                        Yasbeck, Mr. Antoni\n",
        "1300    Yasbeck, Mrs. Antoni (Selini Alexander)\n",
        "1301                       Youseff, Mr. Gerious\n",
        "1302                          Yousif, Mr. Wazli\n",
        "1303                      Yousseff, Mr. Gerious\n",
        "1304                       Zabour, Miss. Hileni\n",
        "1305                      Zabour, Miss. Thamine\n",
        "1306                  Zakarian, Mr. Mapriededer\n",
        "1307                        Zakarian, Mr. Ortin\n",
        "1308                         Zimmerman, Mr. Leo\n",
        "Name: name, Length: 1309, dtype: object"
       ]
      }
     ],
     "prompt_number": 48
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "jitter = np.random.normal(scale=0.02, size=len(titanic))\n",
      "plt.scatter(np.log(titanic.fare), titanic.survived + jitter, alpha=0.3)\n",
      "yticks([0,1])\n",
      "ylabel(\"survived\")\n",
      "xlabel(\"log(fare)\")"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 49,
       "text": [
        "<matplotlib.text.Text at 0x1145361d0>"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEPCAYAAABBUX+lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3WlsnVd62PH/ed/33stL8nLfF1FcJFGkdnm37IlHM5PM\npGmAtJj0S6f9kmImExQtUBQp0ABFv7VpiiBoJwXcJQWCdoIWCJJg0mkmHtf22J6JZcvaSYmSuO/r\nvSTv9r7n9MNDUpYt29SMSFtznx9gyJR47z28y3POeZ7nvDTOOYdSSqmfe95nPQCllFL7QwO+UkqV\nCA34SilVIjTgK6VUidCAr5RSJUIDvlJKlYjgsx7Ah/34xz9mY2Pjsx6GUko9Vmpqajh79uwnfs/n\nLuBvbGxw5syZz3oYSin1WHnvvfc+9Xs0paOUUiVCA75SSpUIDfhKKVUiNOArpVSJ0ICvlFIlQgO+\nUkqVCA34SilVIjTgK6VUidCAr5RSJUIDvlJKlQgN+EopVSI04CulVInQgK+UUiVCA75SSpUIDfhK\nKVUiNOArpVSJ0ICvlFIl4nP3G6/U58PSEoyN+Rjj6OmxVFd/1iNSSv2sNOCrj8hm4fJln3xeNoDp\ntOH55yMCfbco9VjTj7DakcvBwgLk84Zs1uBtJfzyeUM+z0MF/KUlGB/38TxHd7elqmpvxqyU2j0N\n+AqAfB5efTVgZsajpsZSKEBNjfxbba0jmdz9fWWz8P77PsXivR3Cc89F+P4eDLxEWQuTk4ZCARoa\n3M5rtS0MYWMDEgkoK3u4+15eho0NQ3W1+1xO1LkcZDKQTEJl5Wc9mseLBnyFtTA0ZLh40cM5j5kZ\nw4kTRXp6HLEYtLe7ndX+J8nnIZ2WP7eDPUjwmJiAIDA0NTlyOZiZ8fA86Oy0Dx2QPmh9HVZXDWVl\njlQKFhcNQeBoagJjPv52a2tw44ZHJmPo7Izo6YF4/Kcfx6OWTsPoqIdz0NVlPxLQb970GB2VGXRs\nzPLkkxHOwe3bPlHkWF42OGdIJBwnT0bU1e3ucWdmDJcv+zgnz+OZM+Gub7sfMhl47z2fbNYjFrOc\nOBHR2PhZj+rxoQG/xC0vw5UrPuPjHtmsoakpZGHB48KFALC88EL4wEBoLayugu9DdTVsbsoHcX3d\nIx6PWF52bGx4lJc7ysocN28GWGuorLSsrjrGxgJ833HokCGVcgQBHDxoHxhcsllYWDAEAbS03Jt8\n5ufh7bd9wKO83JLLGXI5w8oKHD5see65iHhcgnsYyo7F9+X/X3kl4Ic/DNjYMBw9GvHFLxY4fZoH\n7kIyGXn8ZFIe/8MTSaEgAXhoyFBdDU89Fe2qyB2GMDVlKBahudmxuQlLSzJ5jY/75HLe1mskO6Qw\nhOlpg7WGubkPPj8eFy86rl6Vj3NDg+PuXY+WFktlpeHuXairiz59QMDsrEwUMj7D4qJHXZ3d1W1/\nVpmMrN6rqz9+8p2bM2Sz8rwUix6Tk47Gxv0Z388DDfgl7sYNn40NWc35vuXSpYD5eY+TJ0P+1//y\nmZtzfO1rEW1t925jLVy+7DE7K108fX0Rnud27ieT8chkoLzcAZJSsNbgeY6xMcP6usf6uiEeN7z2\nmuHwYcfMjKGtLeKrX40oL4c7dwwzM3KbzU2PIJBAtLwcceyYZWEB3nwzxvXrHhUVjs5Ow+3bPhsb\njuVln8XFiNFRSKUc2azH6qpHS4vjy18uUijA1aseMzM+6bQE3fb2iCiynDrlSCQk8Pi+1CKuXfOI\nIg9rYXMzoqnJMT3tYYzsUMbHPf7yL2MMDXmAYXKyyNe/XqSi4pOf++vXPaanZYa5csViDExPeyQS\nEI87GhsdIGmb27cNb70VEEUeBw5ELC8bGhsd1hpmZhwLC4bpaUinffr7Q5aWYGXFp7bWUV1tuXTJ\nkE57NDQ4Dh+2901szsHEhCGTkQllYsJQUeFobIREwj1w7JubcrvtnzGbhYsXPYaHferqHM8/H1JR\nIZNhRcWn139GRw2vvBKQyxkOHrScPx9irdzug8H/wxNyLPbJ96vupwG/xOXzjrffjpHPO2ZnZaW9\ntOTx5psxjhyJGB/3uXnTUl8v6R3Pg5UVmJ2VT55zhrt3fXp7Q27dMty5E9DQEDI/79PYCLGYIxaz\n1NQ4pqcNd+8a8nlHc7OjujpiY8Pjhz/0qa2FoaGAtbUiZ86EXLzoc/VqjDt3wBiPL3yhyOnTltlZ\nj/5+y+SkTxA4YjHHzIys8CFiejpGMikpo7t3Pbq7LZOTho4OWFvzaGyMePJJSyIB2awjCAzV1ZbR\nUQ/P80gmiyQSHlNT8v2zs4aVFbmf+nrH5KTH9LRjY0Mmu3TaYYysqKPIYIykRSYn4ciRj3/enYPx\ncY8rV2BszCOR8EilHGtrPtY6WlsjikWLMYbWVsf16z7z8x7OGcLQp6cnpLHR4pyhUPC4ds1nednD\nOcvQkME5GUdrK/T3w/R0wMYGTEyAc47Dh91OEB4dNQwP+2QyhrExqKpyrKwYurtDOjo+GvBHRuD6\ndZ8wlJ3UsWOO4WHDm2/GKBQM09MOa6Gy0hFFUgs4dSr6xDrQW28FLCzIyv3qVQ/f9/E8WUAcP34v\nbdPa6rh2TV6vxkbHU0/p6v5h7FvA/853vsPFixepqqri937v9/brYdUncI6tVaWhttYRjxtGRz2y\nWVnFj48bjh2LuHDBp6IiIpPxqKx01NVZNjakkOt54PuOdFr69peWDMmkRxQ5PM8RRbJSDQLL5mZA\nWZlhedlw5w7091vKygwNDZahoRjGGBYWDD/5iQS3q1d9rJXV9oULAYcOFWlqsgQBBIGkdtbXpUaw\ntORx9GhEJmNJpSy3bvnE44Zbt2RMhw4V2dz0KBQM5eVw7lxxpzhZW2uZnIQw9Jibi1FVZZmb87l9\n26O93RGPO8bHDamUpaLCsr4u3Uezs4br12McPhxx+HCRuTnZBXhe9KnFxFwOFhclnba87NPeHrGw\n4LG6agBJ83R3O4aGPNbXYWrKw/dltZvNys5lcNCRzzsuXPCZmvJYXDQ0NMDamvyMZ86E5HKGpSXJ\n68/OekxPy/O/vh5x+nRELCYpL+cca2uStpqYMFRVGaanPTY3LanUvXEvL8Mf/3GC99/3qa6GJ58s\n0tBQJJczRJHsSIyRyezgQdktra0ZZmYsPT0P3i1sPx/j4z7FItTUWJaXI+rrIYoMQ0MeiYRlbs4j\nnXbkcoZUSnZ/MzOGurqPv191v30L+C+99BJf/epX+Q//4T/s10N+bhQKMDIiBcKGBnnjf1JBcT84\nB1eueCwuOlpaQmIxQ2enI502tLc7EglHebklk3E45/GDH8SprHR0dFjefddjbc1jacnwwgtFuros\ns7OSU5dUiMX3fcbH/a1VvKWvz3Lpks/CgsfGhqGx0XL7doKpKcPgYEhFhWVjQz7Ew8Pywe/oiFhb\ng7Y2QzzuqKmJOHFCVnRtbZb33ouxsuLR0WEZGLDE45bOzoh83tHaarhwIaCpyRGGhpERn56eiCCw\nzM3B2JhhZUWCRToNVVWwuWmZnzcsL8fJZg3z8x6Tk5azZ0NGRnycg74+qK21rK76TEz4VFQ4bt6U\nFfbQUMCRI0UOH3bcuOGzsuI4csTel3ZwTlJEN296LC05Wloc6+uWujrLwoLB932MgSiSQOz7Euyl\n/iFptxMnLCdPWuJxqaPU1EAiYYkin+Fhn/p6y9qaYWPDkEw6zp3L8Zd/mWBsLKC62mKMY2pKnre2\nNodzcPWqTApra1BXJzsHaw23bnm0t1tqa2WyGR42XLvms7EhC4OxMcOtW1IsLxRkxxiLSZpvYcEn\nnzdUVdlP3O0AVFVZysstm5uGqqqIYtFw8aJPIgGDg5Z335VzIUtL8O67HvX1YIxPZaVjcHB39Qm1\njwH/6NGjzM/P79fDfa7cueMxPi4pkJUVQ1lZRHv7Z7sqWVuTAl0i4cjnpUh78GCec+ci/vqvA9bX\nPRoaDD09ESMjhvV1Gf/yckQ+L504VVVw6VJAFDnGxx2plGN01KO3V4qYra2SU15cjDDGEIYSZJeW\nDN3djp/8RNIosZjj2LGQKPJIpw2ZjMfmpqwMT56UVepzzxU4e9axuGhYW5MulqamkJ4emJjwiMVg\nZSXGzIxHbW3EoUOWhQWL7ztqaiyJhKOiwpLPG27ccLz/vk+h4LG4KKeIb93ymZvzOHUqoqoqYn4+\noK0tIp2W16+lRXYDs7MBvb1FrLU0NkrX0V/9VcDsrLdVyPa5fFnqEZOTkEw6envvvdbz8/D66z6T\nkxK8cjlpnYwiR3Oz1EaiSG4XRZIaKRYNra2WQ4ciamrgxRcjslkYGvIIQ0cYWsbH49TVyW0WF+V5\nfOqpkIqKiLk5KYy3tMjhufV18DzZgQEYY2hujhgbM6TTAQsLhqefllrH8LDP6KhPS0vEE09YslnZ\n1S0syJ8NDdJNVCh4eJ6knw4cKFJfb5ibM1utoYZY7JPf79XV0Ngor08q5SgWZWeVz8vubTulEwSO\nxUWf1VVLLGY4fnxvPh+fplCQ+sFnvXB7WJrD3wcbGx98Vxiy2c9sKDt8H7JZw/S0z6uvxrDWUF7u\nE4aGfF4CxsIC9PdLKkFW7YYokmC/uenh+5ZCwbC+7lhdNayvS9ojk/Gor7ccOCBFt2TSsLbmYa2j\nutqRyWyne+R5WVvz8LyQjo6IzU3D6qplZmY7pxvinBQx33pLdgi+D6mU3UlnhKHsGmIxx+amIYpi\nDA5mefppCVgSpAyjowEHDhSJIshkfO7cMVRWeuTzjgMHIjzPsLgILS1QKBgqK2VHIfl2H2OkY6W6\n2tHbawlDx/q6R3t7SC4XsLAQEIaG8nJ336E1uBfsVlelmGqtBDPPk2BfU2N4//1gp211c9NQUWFY\nWLCAvxOge3oc09Pwgx/EWF31aGuzVFVFDA6GbG5Kusb3pdhaWWm5ft3HOY+REZ+uLsvKiuHppx29\nvRFNTTKmREL+XF4O2NjwKBaleNzUJLuufN5jZsbjwIE8QSApvY4OQ11dRHNzRG2tpL+CQCaBVErq\nHv390ioKkMvd/zx82MaGFN1zOSgrMzzxREihIB1UiYTb6q4ylJVZWltDVlY8Kioiysr2N4dfLMpu\naHFRdlzHj396+u7zRC+etg+kbUze7L7vPhc5x1QK6utlXBJ8JN1QXe0wxm7lix3t7ZaZGW8nEBw7\nFnLoUERZmXS/XLsWMDUlJ3M3Nz1WVjyWljzq6hwHD0Z0dUU880yR9nY5bVtTY3nxRUt5uaSN6uoi\n6uslMLzzjk8yGZFOe4yPe1RVWaLIUCgYnPN4992AiQmf0VGPGzd8lpcNMzMBq6uG8nK7teI1rK9D\nsSh57akpj1u3JCBduuQzPy87lYkJw+KiFDqzWQnEkpYwOCepq/p6SS+NjHi0tTkaGkJOngzp7JQW\nys1NSW9sbnocO1akrS3iiSfkT5DXuqnp/oBUUwPt7dFOB1MiYbZSYh6VlZbJSY/JSY9CwTEyIm2m\nfX1FNjcl4FVWOoaGZDeysWEYG/PwfUNdnQTV7Z3XE09EVFVZWlrknIIUex3d3RF1dffqLwDd3ZaK\nCnk9xsZkRT07K/e7fXmN1VWpHczPB0SRobc3pKnJkUpFOGe36gxgrRTn29oioki6s0AO732S1VU4\nfDiiq0ue9yhia/cJJ09GdHZGO3WhtTVvq/MqYGxsf0/zTU7KjmZsTLqZRkf39eF/ZrrC3wcHDjji\ncVmB1dY6ams/6xGJQ4csd+/6PPNMSKHg0doqgffECSkoVldbhoc9OjvlA7exwdZJ3Ihs1lFVZTlz\nRtoxT5wImZvziMcN6bThy1+OeOGFkJoaqKuD5WXHoUOS5pie9jh0KOL8eekG6eiIuH07oLJSVrzJ\npGNgQFJHExM+3d0RxaKkN6QtzxCGsntwTnYX2azh2DFHMhlx4ID05FvrUSw6cjmPmhrpFInHI2pr\nt1tFtyc5SWvITkZOcG5swPXrMTY34aWXCjQ0OP723w45cECeu7k5+H//L87GhrQzNjYa/s7fyVIs\nQlWVnBlobf3ouYKmJnjyyZCODkNjo+G992JkMh6JhKO93ZHLheTzcPRoxOSkz/q6tLG2tFjef19O\nQvf0SGpncVFy/UHgeOaZInfuJKioMORyMD/v7dQFmposhw8XSKVkMisWPW7dMqRSIU1N8lycO2eZ\nmnI0NDh831FfL6mwTEZSTM3N0ilTKEB5OUxOBtTUWGpqpCOoqsoShvLa5/M+p09HHD8ebb3nLfX1\nn/xeNMZw/XpAJmNwznL6dMjQkOwaCwVpCPB9maTv3g22mgVgasoHwj34dDzYzIzh+98PKBZlx5JI\nyCLocaEBf5+0tMAnbWk/C9ev+9y65ROLOay19PWFjI0FvP++z/XrAfX1lqefLlJZKSvF8XFJ1SST\nEiSmp30SCUNra8S5cxErKx7l5dDUJIXOnp57j2WMdICsrMhjlpdL/l+Cq+T3u7tDikWfYtEwO+uR\ny8EXvlCkrS0kkTCcOhWxtGS2gr7k87/0pZDZWcOpUyGFAmSzPvX1kMvJ7qCqymN6WlJQV67ASy9B\nba3sulIpSTGtrcnBp6amiGzWkEpBV5fjxg35+8VFnxMnQhIJOSw1M2OYmJCWzcZGSy7nsbxsSKdj\n5HKyCmxuhpUVS0VFyMGDH3weYHBQgvvNm5KWSac9Dh4s0tkZ0tQUkUw6fvzjgFjM0tTkcfBgxLvv\nBiSThoUFn1zOcPp0gfp6n1TK8eSTljt3pJ1ydFTSSZub0vr6wgsF5uZ8VlakjrS8bKiqKnD0qNkJ\nWiDjfeaZkHh8+2spOCcS8pwcPy6TTEODHOIqL5dLZRhjKBalqDw5GVBV5XYmp/5+SzptCEOZfD7p\ntHZ7u+X4cVlUSJePvA61tdLJlEjITqGqyhGLRRgjqb3u7v0t2G5uylkLAN+XCelxsm8B//d///e5\nceMGmUyGb33rW3z961/npZde2q+HVx9SLMLQkE88DuPjki/v65MiZXm5rO59X4LxwICjvNxRVydF\nSt+X9r9cTlaXXV2W6WlDX5+jv7+ItRJ44d6HsbJSDgdJjtcxNeXT27u97ZcAk816JBIRR46EJBLS\nyXToUJGJiQBjHE1NkiJpaZHLMVy+HHDzJrS0WFIpw+3bUjh9/32PEyck91ssGrq7pQumUJCieTot\nZwk6OiTd0tIiHT6ZTIze3iKxmCORsBw7Bhcv+pSXS396KiWFyTCEZDKipyfkypUYzc2yIvV92TEs\nL/tbhU057HXw4EeD0narZWWltHFGkfx8P/xhwOysHJhKJKCpKaK+Xk4tJ5OSl19akpW0tdIHL5NM\nQGWlZX4+BhhqaiLeeiugv7/I4GDEq68GpFKO9XXD1JTPsWPFj6QWT5+WFsz1dUN9vWV1VSbX8nI5\naHbgQMTJkyEzMwGjox5VVVIwDkOP6mrZbVVVWeJxx8YGLC7KRDA2Jq9/Z+fHL3haWuS+ANbWJOUU\nBDJJGAPxuCWb9dncdHz960UWF6W4OzCwv6vr1lZLe3tIPi81i+330ONi3wL+P/kn/2S/HkrtgnNQ\nV+cYG5OCXKEg11AZHIzY2AjZ2JBLH4AlFnO8+GLE8nLE8HBAFMGpUyGDg95OgXB7pbx9DZ2qquhD\nj2dYXJTOjYYGad2rr3fMzTmqq+XEakUFvPBCRFubo7PTMjTks7Hhs7rqMTAQUVlpSCTg1CnJ8RaL\n8hjFIluHwhwTE3IdmKEhKCuTierixYDWVg/fd9y54whD6Ox0/MVfeBQKEEUe3/hGgbIyQyIhh5uO\nHo149VXp2mlslINeR49K51AYwvq6t9UlEtLc7Ojpkb7xuTmPbHa7H/3jr0HkeXKNoosXZQUcjxsu\nXHCMjwdMTfksLVmefbbA2bMhqRQ8/3yRTEY6mhob7dZzIe2mAwPh1ilnWaVPT/s76anx8Ri+HxGL\nSV2lpibizJmIp5766EGoWAyOHpUAZi386Z/Kbsxaea8cOxZtnVIOWF6WHyybNfzdv1ugo0PuPwwh\nHpcd2wd3tIXCJ78f+/ulrlMsGurq5PTydoF+cFC6rGZnIZmUNGMUma1rNn1yMfhRk7MPIZOTPnV1\ncg2jx4mmdEpUPC6HZvL5gOvXJT86P+9hjKzuEglZdR87Jkf+5Vo3UF8vXTNBAMPDslJtbXX09UEq\nFbG4KId+urvvrXycg8lJj4EBy/q6HP55/vmQ5uYI5wwzM9J9c/x4SFeX9IEb49PaarHWsbrqcfWq\nR10d9PdHO/nbU6ekH312dvtiaDFGR6WjZXDQceuWpCIk7ywXVxsYcMRiHtXVbmt1ZmhpcczNeZw8\n6djYsDQ3W6anJd9eVbXddSSdIrGY5M6Xl+WyCG1tlv5+S1ubjGdmZrvLxqOiwtLb++CA0NwMBw+G\n9PV5GOOoqJDJ0vdlMigUpLZw4oSjqwsOHSpw65acBSgUHMXivWJlfb2cWZiY8GlqckxOylgbG+H2\nbY9z50LSaQmaBw44Xnqp+JGLsX2YMdJhtN1JtbEhwXxzU/5+u/smnTZbaR7L4KDd2sXJhLx9bZ9E\nwm5dJuLjBQFbB7Pk++rqLJmMnGHYvnxDfb3lnXcMly8HbG56O/3++50qPXPGcubM47Wy36YBv4T1\n9EAQhNy5Y7hxI0Zbm3xQJQA55ubg6aeliLu9GvzgqcvTp+8PZtXVcoinrMzdd9jIGPmvrQ3Onw+5\nedPQ0gLW+uRy0mroeXIRsFxO0gotLbL7APnw53IeqZR8+LdPCG/fd2urTACHDztWViRNNDpqeOml\niOZmOHbM4vuW5eVgZ8Xd2ysFRQmg0p45MBDS2Ag3bhgOHvRoayuyvGzo6AjxPMjlJIgfPGior5ee\n9jCUltWuLgkAra2OL34xJJ02VFW5ndbHD/N9eOIJy/h4yOqqdOY89VRIWZm0PZ46FXHq1L3WyfZ2\n6e4B6b8fG5OU1+HD0U7RVQ5xOc6dg2vXAmZmfH75l4s0NUnNoqNDrkO0W62t8jNGkby2co0fGBiI\nuH1bnshTp+6dxI3FoK3tXvBNJkOyWbm0wsO2Lvo+D5yU8nlDYyPk8zIZSBfR/gbfbPbe5Zk/+Hl4\nHGjAL3EHDsA3vhEyNGS3CrHwJ3+SwPcNx48XqaiwO6v8T5JOs3Ma0hhHf39EV9e9D39/f8S1a4Z4\nXFa3m5vSJuicFIK3r0Ozra/P7ly8rLVVVuHAJ6ZIKivh2LFoq5PIcf58tPOB3NyEy5eliJhKSVpk\nasqxsuJx+HDESy9JB478Ahj5WPi+TDzPPy8/fy4nl3V45x25QuepU9Jeefbs/emRpiZoavr0VWdT\nE/zqr0bMz0se3lrH0aMRlZUSIBsaeOD1Z/r7LR0dkt8uL5e/k3rHvcd89tmQtbWQy5c9cjmfRMI+\nVL7ZGDhyRA5yRZHUORoa5Hn+2tcKjIz4xOOOU6fuP0n8QdKh9GhX3+3t8tql09IEsD3R7pdMRt7n\nuZykCE+dCh+ryzNrwFf09EgOGuDP/syjqcmxtuaYm/Pp7rY49+kfqsXFez3bzkmXTVfXvR1ASwvU\n1YXMz8P16wF26y5nZ+XiY8ZAT0+0c238WEwKktLy5zE5KQXEI0eiBwb9+no4cMDieR4dHXIQ6YOr\nr/JyuWxxPg+zszA8HDAw4MhmQ44etTvtlpWVkoLY/llqatzO1Rq3A9uZMxEzMzLujg73M13Pv7XV\n0dr68EHx01bMvi8B9+mnLZublvLyB08en6StzVFbGxKG8njbE/KBA3DgwGeTu+7qcpw/HzI3Z6ip\nkU6i/TQ3Z3YuWx1FhslJ77G6PLMGfHUfCb6OZNJjbs6QyZidk5ifRIKeFCtBeuk/LB6XVWsi4chm\n5ftOnrRbedgHb4+ljVFSJkHw8b+9yRgYGLB0d28fGvvo90iPvxRcQTqGKiq2i35ua9xw9qwEdM+T\nSeTDKivlDMPjIJl8+ED/4dt/nngeHDny6dfm2Ssfvszz4/Z7nh+z4aq9dugQ1Nc7Fhfh0KGIgYFo\nV9cLaW11bG5aZmflNOjHBcSyMgmos7MSwNvb3cemBD5otzng3QSomhrH1NS9Tpqamvsnp6oqKdYq\n9WHt7Y7V1YjFRblybE/P4/U+0YCv7tPb6/jVXy2yuGgpK7P09+8u3WCM5N37+j79eysroa/vszuE\n1tnp8P2ITEauhS+H4pT6dLGYFKrD0D52q3vQgK8+JB6Hp56yrK7K5Xc/j7/E+lGQbpLP18ln9fh4\nHIM9aMBXDxAEkmtXSv180atlKqVUidCAr5RSJUIDvlJKlQgN+EopVSI04CulVInQgK+UUiVCA75S\nSpUIDfhKKVUiNOArpVSJ0ICvlFIlQgO+UkqVCA34SilVIjTgK6VUidCAr5RSJUIDvlJKlQgN+Eop\nVSI04CulVInQgK+UUiVCA75SSpUIDfhKKVUiNOArpVSJ0ICvlFIlQgO+UkqVCA34SilVIjTgK6VU\nidCAr5RSJUIDvlJKlQgN+EopVSI04CulVInQgK+UUiVCA75SSpUIDfhKKVUiNOArpVSJ0ICvlFIl\nQgO+UkqVCA34SilVIjTgK6VUidCAr5RSJUIDvlJKlQgN+EopVSI04CulVInQgK+UUiVCA75SSpWI\n4OP+4bvf/S7GGJxzABhjHvh9v/7rv743I1NKKfVIfWzAX1pa2gnyURTx9ttvU11dTXd3N3fv3mVt\nbY3nnntu3waqlFLqZ/OxAf/b3/72zv//p//0n/it3/qt+wL822+/zaVLl/Z2dEoppR6ZXeXw3333\nXZ555pn7/u7JJ5/kwoULezIopZRSj96uAn5dXR3f+973KBQKABQKBb7//e9TX1+/p4NTSin16Hxs\nSueDvvnNb/K7v/u7fPe736WlpYXZ2Vmqq6v5Z//sn+31+JRSSj0iuwr43d3d/MEf/AE3b95kZWWF\n2tpaDh8+TBDs6uZKKaU+Bx66D98Yw8DAAGEYksvl9mJMSiml9sCulujj4+P8m3/zb8jlchQKBZ57\n7jmuX7/Oa6+9xj/9p/90r8eolFLqEdjVCv/ll1/mS1/6Ei+//PJOGmdgYIChoaE9HZxSSqlHZ1cB\nf3x8nF+5vul5AAAgAElEQVT8xV/E8+7/9nw+vyeDUkop9ejtKuA3NTVx7dq1+/7u8uXLtLa27smg\nlFJKPXq7yuH/vb/39/iDP/gDnnvuOcIw5OWXX+btt9/mH//jf7zX41NKKfWI7GqFf/bsWf7Vv/pX\neJ7HwMAAzjn+5b/8l5w6dWqvx6eUUuoR2dUKP51O093dzW/8xm/s9XiUUkrtkV0F/N/8zd9kcHCQ\n559/nqeeeoqysrK9HpdSSqlHbFcpne985zucPn2aH/zgB/zGb/wGv//7v8+FCxeIomivx6eUUuoR\nMW77N5zs0vz8PG+++SY/+tGPWF1d5b/8l//ySAf0yiuvcObMmUd6n0op9fPuvffe4/z585/4PQ99\naYV0Os3a2hqZTIaKioqfenBKKaX2165y+BMTE7z55pu8+eabFAoFnn32Wf75P//n9PX17fX4lFJK\nPSK7Cvi/8zu/w9NPP80/+kf/iMHBwY+cuFVKKfX5t6uA//LLLxOLxfZ6LEoppfbQxwb8119/nRdf\nfBGAN95442Pv4Itf/OKjH5VSSqlH7mMD/ptvvrkT8F9//XWMMQ/8Pg34Sin1eHjotsy9pm2ZSin1\n8B5ZW+Z/+2//jZGRkUcyKKWUUp+NXf9S2t/93d8lHo/zwgsvcO7cOdra2vZyXEoppR6xXad0rLVc\nvXqVH/3oR7zzzjs0NTVx7tw5fuVXfuWRDkhTOkop9fAe6Ulbz/M4ceIEv/mbv8nv/d7vUVlZyR//\n8R//zINUSim1P3ad0snlcvzN3/wNb775JteuXWNwcJBvf/vbezk2pZRSj9CuAv6///f/nosXL9Ld\n3c25c+f49re/TVVV1V6PTSml1CO0q4Df29vLN77xDRoaGvZ6PEoppfbIp+bwoyjif//v/011dfV+\njEcppdQe+dSA7/s+XV1d2oevlFKPuV2ldF544QVefvllnnvuOQ4dOoTv+zv/duzYsT0bnFJKqUdn\nVwH/z//8zwF49dVXefXVV+/7t//4H//jox+VUkqpR25XAV+DulJKPf70N5kopVSJ2NUK/1vf+tbH\n/tsf/uEfPrLBKKWU2ju7Cvi/9Vu/dd/Xd+/e5bXXXuMXf/EX92RQSimlHr1dBfzBwcGPfH306FH+\n6I/+iC996Ut7MjCllFKP1k+dwy8vL2diYuJRjkUppdQe2tUK/7vf/S7GGLavpLy2tsbly5c5derU\nng5OKaXUo7OrgL+0tHTf77RNJBL82q/92s7vvFVKKfX5t6uA/4UvfIHGxkaam5tZXV3lL/7iLxge\nHubs2bPU1NTs9RiVUko9ArvK4f/n//yfdy6n8Ed/9EfMzs6Sy+X4kz/5kz0dnFJKqUdnVyv8lZUV\nGhoaCMOQS5cu8Z3vfAdrLb/927+91+NTSin1iOwq4Hd0dDAzM8PMzAw9PT0kk0mKxSLpdHqvx6eU\nUuoR2VXAP3/+PP/6X/9rCoXCziGs4eFh2tvb93RwSimlHp1dBfwvfvGLPPHEExhjSKVSANTV1fHN\nb35zTwenlFLq0dn1LzH/8O+wbWtre+SDUUoptXf0aplKKVUiNOArpVSJ0ICvlFIlQgO+UkqVCA34\nSilVIjTgK6VUidCAr5RSJUIDvlJKlQgN+EopVSI04CulVInQgK+UUiVCA75SSpUIDfhKKVUiNOAr\npVSJ0ICvlFIlQgO+UkqVCA34SilVIjTgK6VUidCAr5RSJUIDvlJKlQgN+EopVSI04CulVInQgK+U\nUiVCA75SSpUIDfhKKVUiNOArpVSJ0ICvlFIlQgO+UkqVCA34SilVIjTgK6VUidCAr5RSJUIDvlJK\nlQgN+EopVSI04CulVInQgK+UUiVCA75SSpUIDfhKKVUiNOArpVSJ0ICvlFIlIvisB6BUKXMOZmcN\nxSI0NjqSyc96ROrnmQZ89ZlwDoy5/+9yOYgiqKj4bMb0WRga8hgb8wBDRYXliSeiTw361sL8PESR\nobHREY/vy1DVzwEN+OqBogh8f2/u+/XXPV59NUYy6fiVXylw9ChMTBiGhnycgwMHLP399oG3zeXg\nxg2P1VUJdv39luAxfRc7BzMzEuwBNjY81tY+PeBfu+YxNSUvTm2t5ezZaN+fg/l5WF831NQ46ur2\n97HVT+8x/aiovXT5smF+3iMWs/T1OdrbH919j4zA//yfcfJ5KR9tbBh++7fz3LzpE0US+EZHPZqb\nLbW1H7393bsec3MS7CYnobzc0dPjKBYhn4dk8uMnqpUVCVKplKOm5qcb//o6ZLOQSkEiAek0eJ58\n/bCMgWTSUSiYra8tniePUVn54NvkcjA25jEzY7BWJolDh6J9DbpTU4arV32cM3ie4/TpkMbG/Xt8\n9dPTgK+YnjZMTXkkEpZMBv70T+OAR7Fo6e21/PIvh/T2up/qvt3WzbbTNxsb8mcs5vB9WFuTAOo+\ncPfZLCwvQxB8NJAWCvd/XSwa0mnHxYs+uZysOE+ejCgru//7Fhbg/fcDosjg+47Dh0M2Nz2cg85O\nu6uA/cH7KC+3pFKWuTkfY+DQoYienod/jo4di7h5EwoFR3k5XL4cEEXQ3m4ZHLQfSXsFgewK5ue3\nJ0yLffBmaM8sLBick4FZa1he9mhs3OdBqJ+KBvwSt7IiKYLt1fFrr8WIIkinHfm8x4EDjtu3fdrb\nw48E0Q+bmoKlJUMyCQcPOhYWDMPDEpgOH7a0tztiMfB9x6VLAcmk5R/+w5C6Oujri7h50yedhlzO\ncfOmx/vvQ1ubo6bGcPCgJZmElhbLxITH5qahstLS1GS5e9cjnzdsbMh/9fURfX33j21+3tvZQRSL\nhh/9KGBqSgL+sWMhx445cjlDba2lqenBP9/ExL1dyPy8x9ycRyolk9Xt2z4dHeFD59MrK6G9PSIM\n4cqVgCCQHcrkpKG1Ferr7//+MJQJylpDFEEqZblxw6O6Gg4dsvtS9L2/xuJIJn+6xYDafxrwS1Q+\nD1evGm7d8shkYHnZkEoZGhoigsDjxo2AykrDzAz09lref98wM2M4eNBx+LBjelo6S1pbHbW1ktP9\nP/8n4O7dgFTK8tJLRTIZjzCUgH/jhmFjI+THPw7wfcfJkyGVlZZsFv7rf40TBI5jx4qsr/vcuOFz\n7VpAbS309oacPWvZ2DA88USE70MYWqLIp6zMEQTgnGNszOPOHQng8bilrMySy0F9vYyvrOxeUMpm\n4fZtw5UrspouFCzXrhnicY+aGsvXvlakrg5WV2FzE8rLoaEBgsARRfJ3xSL3BXfP+2gRejeGhz1G\nRz2CQHZa2ayHtXDgQHTfrmd9Xbp5gsBRVeXo6YlIp+HWLUM26+P7jkIBnnhi71faBw9awhDSaUN9\nvaOjQx779m3D6qpHba2lv//hJoHNTbh502Njw9DWZunu1klkL2jALzHz87Cw4DE1ZRgZMdy9axge\nDnY+aM3NEUNDAe3tliiyhKEhnbb8j/9RxvKyT1NTxFe+UiCZNNy541Ne7vhbf6vIzAz8+McxwtDg\n+x4VFY6BgWjncfN5GBvz8Tz4yU9iRJGhtzdkYcHQ3Ay1tbCxEePOHUcUGRYXPZaWLEeOSBqorEwK\nyW+9FXDtWgA4NjYM7e0hjY2WkRHDwoJHMmm5fNkwMeHT2mqYmID+fsvhwxEdHRFLS4ayMsfUVJyf\n/CTAOUdDQ0ChAI2NsLbmMTzsEY9LMJ6c9Kirczz3XEhLi+WVVwJmZjx6eiJOnSqSyQR4HvT3R8Ri\nn/7cF4uGujpHIiE/1927HsYYwJJOeywtyQQzP292CrHZLLz7rk82K5NnU5PkzEdGDGtrAUNDMv5s\ntkgqZdnY8GlstHR23h80czm2dkOyU2pp+eneQ7EYHD16/8QyMmK4eDFgdNTDGMeXvxzy5JO7n3yG\nh+/VZoaHDRUV4cfutNRPTwN+CVlehosXA5wzvPeeh3OOigrHwoJHTY1jdNTHGEc2Ky1/xvisrzvC\n0GN+3pDNGqqrpaB7967P1FRAsSiF17NnC6yuGubmPGIxx8AAtLZaxsclSLW1WVZWDPX1IV/4gty+\np8cyPu6Tychq9sqVgM1NQ2dnRFWVpaPDcueOIZPxefHFImtrUnQVhsVFtn4Guf9EQgLH0lKM2tqI\nS5c8CgWPzc2Qd9/16O8vkk77lJdDJgNdXRG+74gix/q6R6FgqK2VlXMm4/jRjwLGxgIqKhwrKxLU\nR0Z8EglYWoKVFY9f+IUQ3+dTUzm3b0vax1rJ/1dUyK5qYsIjlXI0NkoRdnDQUlYmE9x2vSKdZifY\ny+soQTWTMfi+YX1d0kpTUx5XrngY47GwAGVlEY2N7Ky+r14NyGQMLS2OuTmPRCK8rzCez8tKu6yM\nh04NrawYRkel48g5w9CQx/Hj9lPTgNs2NrZrAjAyIsG/psYwOBjS1cWnTqZqd/Yt4F+/fp3//t//\nO1EUcf78eb761a/u10P/3LNWUgqfZGTE49o1j6tXZfWXSjkmJuSwT2Ojo6rKEovJlvyZZ0JGRgLy\neaiuhosXfc6cKbCxEVAsSuC/ejUgkYC1NcN77/m0txuOHg2JxSQ3X1VlOXoUGhtDnJMV/MWLHouL\nkrooFOR2VVXQ0OC4etWnqkrywYuL8Eu/VODttwMqKiCbdVy65NPfb6mvt2QyHuk0NDXJKjaRgKNH\nI77/fUNVlaR5RkcDgsDQ3Cz58TfeiDM/71FbC5WVIb29EQsLPmVlcOiQpJ+M8TAGrl6VncjSEsTj\nsnKfmZHJzvMkgK6t+UTR/S2Us7Pyb/X1Hz1LcOeOz9WrAfm8o6rKcOCAjLu9PWJ62tDaajlzxjI1\n5VEsytfbnUTl5VL3WF83LC/LLiSRMKTT0s6aTDqWljwqKy0XLnhUVvqUl3scPCgB/+5dj6kpj5kZ\nSd/FYjLBbGwYamtlF5DJwHvvyS4ikbCcPh09VCdTTY1lbU3qPqmUparq4VJcra2WW7cMo6OGa9c8\nEgmPbNawuQnZrOX4cS0KPwr7EvCttfzhH/4hv/M7v0NdXR3/4l/8C44fP05HR8d+PPzPraUlCU5h\naOjqsvT1PfhDMT8vAT+dNoyNeSwuetTXW06dKrK8bGlqCnjnnYDmZssv/VKBGzc8JiY8VlY8jhyx\nxGIRR444XntN+t/r6qQ4WF0tRdhDhyIWFz3u3vUIAkc2awDJ+V+4IHn1lhbHyorP2prHtWsxGhsd\n4+M+hw+HnDpVZH3d8NprMcrKoK/Pks2GtLQ40mkAD9+PiCI4fDgiFpOc8cCA3QmsTU3Sj3/pkk9j\no+PwYUs+7zh9OuL11wOckzbK7RSS70e88EKefN5sTZiG+nrL3bs+Y2OGdNrjySdD/vqv42SzUlT2\nfcfiohRLq6os5eXS1ZTJSD3k0iXZPR05EvGlL0X3Bf2FBcPaGuRyHlFkaWuzZLNym3jc0dcXEYaG\nmhqDtY6WFumtv3XLsLRkqK6OmJ0NqKqyDA/HyGQMVVWWKPI4erTIzIzP1JRPY2NEebmlUGCrwOzY\n3JR0mEyWPoWCIRaLqK6+l/IZHZX3RSIhz/fEhKOmZvdB1vfhzBnHzZuW8nL5eeS+dqe311FZGbK2\nFuD7cOuWhKa5OXkfqEdjXwL+yMgILS0tNG0l5Z5//nkuXLigAf9ndO3avbzuyIgUyz7c1QGSNwbD\n6qpskY2Bzs6IuTkoFGKMjnocPRpRXh5hjKyQq6sld3z1qsff//uGiQnDzIzH7KysxKurI7q7Hem0\nwfctCwsSYFZXDR0d0rL4f/+vz/S0Dzhu35YukurqkFTKMT9vKBYNfX0Rxkh+P583bG5Km6XvWxYX\npeXvzh0oFmVyKSuDYtHDWsO1a4YwjGhokFbFigpobpYOlr/5G5+BgSLpNJw4EZFIFLh+PWBtzaOm\nRp6r4eEYqZSksEZHfXzfI5l0NDZKMF9clOcuimB83NDTY4gix+KiTyzmmJnxuXjRUShY3ngjxiuv\nxDFGUj9tbVl6emR1nkxKgXNoyMdaWf0//XSRv/qrOJubHtXVlgsXYjQ3O5qapNXx8uWAq1cd6bRH\nfb3DGAdYGhosNTWWiQmfzU2pWczNGW7dCjhxosjCgqGqSorV2wG9sdExPy9/lpdHdHZG9Pbea0Vd\nXYVbtzxGRgzl5VBb62hoeLj34tqaT22t49lnpW7zsJ07YShpHc+DRMLh+24r/cVHzmM4J+/NWExT\nPQ9rXwL+8vIy9R+IRHV1dYyMjOzHQz+W7tyRPHlFhePQoQfnQZ2DMPzgntkQhg++v7o6R2WlpbbW\ncO2a9I3H445s1pHJSBDJZn2qqiwrK9Ljffu2oaHB8dxzRZLJkCjy6OuLaGlxlJdbwHDjhk8qZSkv\n9zhxosAbbxjW1nxiMchkDJOT0s3jnKG/P2R83BCLeTz3XJHVVY+WlohCwXD7thQre3stuZxhbg6M\n8ZmZke6VujrI5yWFsbLi4Zxs9W/fDlhd9WhoiJib8xkeNsTjcqkBz4PKSsOxY4b5eZlQfvzjOLEY\nTE56PP98kTfeiNHdHdLRAcbIzuWddwL6+2FtzXHuHDvP6Y0bPsePW9bXZceyuuoxPe1RXm5xzmy1\nbMrrMjTkcfVqwOuv+7S1WX7pl4pbRVUJ/LW1hoUFSKc91tcNlZUyoUlQl3/zfUl7zcz4JBIhhYLH\n8LAhk5EJvrpaOoWSSUssJjuQ+npLImHIZmUnMTrqE4tFdHQ44vGQlRWzUwPJZu+lcyYmZLKsqYH3\n3pN6Ti7nqK62HDr06e/XTEZ2EPm8FMSdg6qq3b3Xt9265TE25lMsQirl+MpXClgLAwNFjh6VlNrk\npEc8breeR49EwnH8uNWTvg9Bi7afMzMzhps3fWRFLnnQY8c+urU2Bg4ejHa+t67u49/4ySScPRtx\n82aM5WUJMrdvG86di6isDKmutiwv++Rykjqpr7cMDERks/Lh933D3bsB168H1NdbvvKVkD/7szgz\nMx6VlR7GhCQSUgTNZqGpKWJ83KO3t8j0dAxjpOOkrMyRSjmuX/ew1sNay/R0wOHDIc8+G/G978Xw\nffjVXy2STod0dAS89VaMmhpHLObuK2QuLxvC0BCLQRR5jI4a6usNq6vyPNTXy+rv7l1HJiOppjCU\nILq+LoG1okJW911d0dbpVulUisUgkZADWk1Ncvr1zJkinheRSjlaWyV9ZIykVdJpw8BAEc+TFEt1\ndYS1EsDv3PG5dq1IOm2oqICKCsfsrBSJOzsj3nsvYHlZ8u2Dg5b1dfk5YjGpj/i+nA8YGzMcOuSI\nxx2jo95WO6l06Rw4UGRqyrC4GJBIOA4etESR48oVn0wGenokxTU15bGwIBPG4qKjrEzOQGzn2hMJ\nOfewuQlzcwHvvWeori5+pFvGWjmE5pzsYLY7iFZWHF1d0p21vUMIQ3Z12YelJRlEXR309zsSCdnR\n5fM+4+N2q+VWzltcvOgTj8sZhiAo8vzzmt/frX0J+HV1dSwtLe18vbS0RJ1Oyw+UzcL2tVUANjc/\nvvLV0+OoqQkJQ9n2ftL2Npnc7rWXD7TnGRKJCOc8btyIsZ1zr6ryGRryqayE2tpoawUrXRiJhASZ\nbBYaGy35vHTkpFKwuirF3FwOrl0L6OoqMDMjKzFjJPft+4ZcTgqGY2OGQsEnDB2dnfDKKz7l5dJn\nPjzs86UvFZmchOPHQ8rLZRIpFqUHfGNDWjA7OyUAr66ydczf4py0nHZ0WCorLQcPRrzySkBDQ0Rd\nnSOXk3RDLGbJ5w19fY4TJ4q8+mqCS5d8mpsldz015ZPNGvJ5ef6knlEkikIKBUNjo6W52fLEE7Ia\nnprydgrdR4/C/LzsVqqqHGEI9fURUeSxseHR3i4tmePjHl1dkv7K5w0NDZYzZ2BxUWoRiYShuzvi\nwIEQ3w+oqTHE45bqasP4uE8+Dw0Nlupqqac0NVmuXQsYGQn4ylfyNDQ4wGNyUnaKUg8RskuSFtGu\nLsvqqiGZtBSLAeXlADLBrqx4NDXZD9xO0nySqoNEwpLNengeNDdvT5LbdQ2fjQ15rgYHP/maRzU1\n8joWi+B5ctVQz5O0340bUF4uO9hMxjA15XPwoNRPZBwa8HdrX66H39vby+zsLPPz84RhyFtvvcUT\nTzyxHw/92Kmvl2Ak3H0ftgepq4Ompt3lMjs7LZcueVy7FjA+7lMsGqqrpftjbMzjypWAdNpw/nye\nykoJ6tPTPkEAUeRYW/PI5QwVFZIntlaCWlmZdGckEoaxMSkiV1RIuiCVki16c7Pj1i1ZlS8uSu4/\nnZYTuCCnVpNJyduOjvrE4x7JJKys+Cwuyu2CQCaupqaI06eL9PZGBIHUHM6ejejslDbP7S6i27d9\nEgnH2bMRhQIMDoacPl3kxIkQaw3Hj4c0NkZcuRIjm5U0yfKyPM5TT4VcvSoHycbHA37yk4BYTNII\nhw9HtLVZvvCFiOpqaG6Gu3d9PM8Qixnefz/AOUn5xOPSsTI15XP7dsDCghy0kgKyTE7JJIyNma3J\nXnYnZWVua4dnSCS8rcssSG47n5fgl8+z1WkkhXJjDKlURFOTve8qmomEwxhoarqXV4/F7E6OP5WC\nZ5+N+OpXQ86fL9LZaTl6NCKZlG6uD9rc3L7gm9jYkEkc5DIZ+bwE+zt3PNbWPMLQbBWUP7llp6HB\nUizKYqShwd136KyiQg7TgdRwWlsjQJ6L5ubowXeoHmhfVvi+7/Otb32Lf/fv/t1OW6YWbB+suhqe\nfDJiaUm6HZqbH919J5OWI0csuZxcbGxx0aO9vUh9vSUel9WbXMHRZ3XVYYxPRYUlDB1nzkQYE3Lg\nQERDg6WtTS5cNjEhfeGFQoAxUnTL5STHfeKEnIqtrw+5c8dndVUKsE1NjslJR7FomJw0PPlkyPnz\nPn/+5zGMgV/+5ZA7d2THUVFhqatzWwVHePttn9dekzRWV1fESy+FrK7KJHHsWMgrr8SJxRwTEz6Z\njGFoKODQIbmP4WFJFVy+7DM87HPlikd3t6G52TE56bOw4FNZ6SgvL5JMOhIJOcFaU+N4+ukiqZSh\nu1vSPWBYWZH7lQ4YSdfIpR0sra2WykrHkSMRmYwhl/NobpYoFobgnEdVlWN6WjpiOjrsTt57YwPW\n1z2amyW3PzMj6bftE67f+560z+bzMikfOWKprCwyPOzT1QW9vUVyOcP8vKO7W1JFAEeOWCoqpMOp\nqcndd/0g35e8+4svysSZyUiOv63t/oAvhdJ7F3xLJmX3cPOmXMsoDA3vvusRBPcH+I+rL20bHfVJ\nJmXys9ZQWenI5+V08/Hjcm2khQUHOFpafObmZLd68qSu7h/GvuXwBwYG+Lf/9t/u18M91qqqoKrq\n0beiHTwoQSgIPCorI5qbHcvL0lY5NSVpgcZGSxA4WlrgjTckZ9/dbTl2rEhtrRR7NzagpcWwsGBI\npw1Hj0ouvL7eUllpqK2VD+rRo9DSUiCdhnfeibG05LO+bjBGJov1dUN5ucfERIxEIuQf/APp2Ekk\nIjIZn/p6y8aGrPwbGuSDffOmRxTJCnN83GdpSdpRCwXLzIzhF36hyMWLATU1jsHBkKoqybMfP245\neVI6Wjo7La+8In3wyaRcNiEeh/JyS19fRHm5Y37e48SJIk1Nlvp6x7lzBWIxyZ1vy2TkoFdlpePL\nX85v9ecbOjoiFhcNQeBRKEjw7OuTtEk+b+juLpLNOqanpdAbj8t1h7ZX+NtBdXzcbJ0qhro6y7PP\nOtbWJDinUjIBplKWsjJDb6/j+PHC1iUzfObnZYK5ft3jyJECNTVSyD5w4JPfV74PfX0SWB8kHpcL\nvg0NyeLg8GFLa6sU/+NxKajncj4tLSHZrCGKJFX0MK2V1hr6+qS+8MFDbdu7ja6uiM1NqTno7wJ4\nOFq0LSGHDsFXvlJkbs4Sizl6eyPeftsnm5UUQnm5o61NPqg//KGP70unzvXrHuXlPq+9Fqe5OeJr\nXyvS2OhIpSQ4xuOSWqqoCLcuHSyFu81Nn2efjbh1y9DcbDHGUCxKUbSuzm1NHnIBsuvX4xw4IIHv\nzBkpavq+FKY7Oy3PPBOSTMpEsc05t7USlxOqDQ1QVlakqgomJ2UiaGyEjg63VTCVa/+0tEA+L0Er\nmXRkMnD4cEhHh+XWLZ+ZmYCJCUldnT2bJ5/3eeut+FZvueSX43HL/LwUn8HR3x/xzW/mKRblANb8\nfIxYLGK7HtPdLS2vcjnniOVln4WFkM1NyOelA2r78FwiAb3/v727D4qq3OMA/j27sAosy7IgL/Ii\nb4sFyNtVGtmcq1A2KTNUjtaUM1qjNYQ25VjRNDWVU5ak40tkM2EzNI1/yTjoZGPlZSbTvCms95K8\nXEG44gVElnWXkJfdc577xwOrm4C7JB3g/D7/LXv28Nsd+J2zz/N7fk+iiH/8wxdDQyrMmyfi9Glf\nGI3DrlWw0dG8S6afn4TQUBGRkQLmz2ewWIDr11Wu1skAb/oWHX3/hj7Cwviw2p34N8TRu3r+jSwx\ncfTv4d4rdxMSRNTV8TLYkBA24TAlv+D9+fehRJTwFcTPD8jNlWCz8VJPrRbo6BDR0OADmw0ICJDQ\n1aVGXJwDkZHiSD8dXt2iUgkwGkWEhfF2DL6+fKI4P5+Ph2s0DJ2dDKmpfFx9aEgFf3+eFKKiGEwm\nJ9raGCSJl3X+73+85DItbQjR0QLmzePNwSIjGSwWHwgCMDzMV+b+7W9OxMXx4a4HHhAhSXzIIyXF\nifh4NtKWga8RkCQ+0btwIV/mHx4u3TUs0dXFLzLh4RLq6nzg68vH4fv71YiM5JOmgYF8Avn3331h\ntfK6f6sVyMhwIjtbQmsr7yXECbBaBWRl8d8zMMDLTCWJL3xKT3dCqwVyc0UEBvJGaOfPM8TGivj3\nv30QFychLU1023cgMJDf1Wu1vLeQJPEJTZ0OyM4Wce4cL8vNypKQlMQnPQF+4Q0O5nMC/DwMfn5T\nP+xhNPIL0GjrhvnzefWPp4k5LAwwmfjEPF9ZPP6xV68K6OpSwd+fITHxr+kQOltQwleY0T4tAC+v\ni72lZqAAAAzVSURBVIsDUlJEBAZK0GgkpKdLaGxUIzNTxL/+xWv2c3OdaG/nLXgliSfenByeeEcr\nLxoagPPn56Czkw9bhIc7XD30/f2BvDwRN27wuYK+Pt5bRq0GMjJ4pYfFws+vUjHU14+2imAjHTnh\nWuaflsawYIHTLZn09fG7WoC/rr9fDZOJV/eM1XLCbhcgiirExEiIiHC6ar9v3RLQ1CQgNlaAzSYh\nIUGESsV79gAYqfHnJZN8gxJe3gm4J7aEBF7ZxLtJSoiJcW8zoNXenmRescIJg4G5ykhHGQxARoaE\nf/6TV8CkpfE2CT4+/IIWEMCTeESE5NYCQaUC/v53J3x9GaxWXslkNE79SlU/PyAz889dWO782xxP\ndzdQX8/ncHp7ef0/jeN7jhK+gl27JqC9nXfGDA7mm27k5DBEREjo6OB3naGhDDExEi5c8MHAAG8p\nYDTy2vQ7k6nDwUsYefLhd113JrDRGvRRsbGi2/hserqIzk5eBRMT48T332vAGENSkvvEnCDcvahn\ntIf86MSgWs1/Nl5/ofBwhtZWBklSYe5cvo9sV5cKosjfq1rNN1KJiOCVRYLAm7YlJUkwGvm3lvnz\nGRwOEVYrnzyMi7v93nx8+ATpRDyZp8nLcyIpiY+VR0XdvrguWMAna3k//Ltfp9UCK1eKYEycVMvm\n6WxwkE+Yj+rrm2VvcIpRwlcw/s8DaDS8HXBgIG+0Zbfzni5BQRIyM/mYe2ioE7//Loy0Vbj7XCEh\nfBy2r08FjYbXdk/kj1/DIyPZSLnd6OPhkX729y459fMDUlNF/Oc/PMMvXHj3jld3Sk7mQyWDgxhp\nHMeHd267nYhTUhhSUsYuMVmwgC80miqCwJP7WHit/L1fP9vwRXgSHA4+d0J9drxDCV/BQkMl/Pe/\nqpFWyAwhIXzR02ibBotFjZs3+cRncDBcS/HHEhnJkJ4uobOTQavFuI3cPOXtnrN/vGBMRBD4vAKZ\neXQ6Xrbc0yO5VgYTz1HCVzCDAViyhNexBwTwhllXrjBXjx5BYB6XvfFNQCQ88MAUBkwIpq5sWQko\n4SucXn+7wgMAFi0S0dDAK0Li46Uxh28IITMTJXzixmDg5XGEkNnnL+mlQwghRH6U8AkhRCEo4RNC\niEJQwieEEIWghE8IIQpBCZ8QQhSCEj4hhCgEJXxCCFEISviEEKIQlPAJIUQhKOETQohCUMInhBCF\noIRPCCEKQQmfEEIUghI+IYQoBCV8QghRCEr4hBCiEJTwCSFEIabdFod6vR61tbVyh0EIITOKXq+/\n5zECY4y2fyeEEAWgIR1CCFEISviEEKIQlPAJIUQhKOETQohCTKsqnfr6elRUVEAUReTn5+Pxxx+X\nOySPff755zCbzdDpdNi9e7fc4Xitp6cHZWVlsNls0Ol0WL58OZYvXy53WB4ZHh7Ge++9B4fDAY1G\ng6VLl6KgoEDusLwmSRJKSkpgMBhQUlIidzheKS4uhp+fH1QqFdRqNXbu3Cl3SF4ZHBxEeXk5rl69\nCofDgaKiIiQnJ8sdlkc6Ojqwd+9e1+Pr16/j6aefxqpVq+4+mE0ToiiyLVu2sOvXrzOHw8G2b9/O\n2tvb5Q7LY/X19ezKlSts27ZtcocyKVarlbW2tjLGGLPZbGzTpk0z6vMfHBxkjDE2PDzMtm3bxjo7\nO2WOyHvHjx9n+/btYx9//LHcoXjt5ZdfZn19fXKHMWkHDhxgp06dYowx5nQ6WX9/v8wRTY4oimzz\n5s3sxo0bYz4/bYZ0mpubERERgbCwMPj4+MBkMuHChQtyh+WxBx98EAEBAXKHMWl6vR5xcXEAAJ1O\nh8TERFitVnmD8sKcOXMA8Ds1URTh4zOtvrzek8VigdlsRl5eHtgMrZSeqXHfunULjY2NyMvLAwCo\n1Wr4+/vLHNXk1NXVITw8HKGhoWM+P23+K3p7exESEuJ6bDAY0NzcLGNEytXV1YVr167BaDTKHYrH\nJEnCm2++ifb2dmzcuHHcP/jpqqKiAuvXr8fAwIDcoUyKIAj44IMPIAgCVq5ciUceeUTukDzW3d0N\nnU6HsrIyXLlyBUajES+88AI0Go3coXntzJkzePjhh8d9ftrc4ZPpYXBwEHv37sWGDRswd+5cucPx\nmEqlQmlpKfbv34+TJ0+itbVV7pA8VlNTA51Oh/j4+Bl7l7xjxw6UlpbilVdewdGjR9HQ0CB3SB4T\nRREtLS146KGHsHPnTjidTvzyyy9yh+U1p9OJmpoaLF26dNxjpk3CNxgMsFgsrscWiwUGg0HGiJTH\n6XRi9+7dWLZsGZYsWSJ3OJMSFhaGrKws1NfXyx2Kx5qamlBTU4Pi4mLs27cPly5dwmeffSZ3WF4J\nDg4GAERHRyMnJ2dGfTsPCQmBVqvF4sWLodFoYDKZYDab5Q7La2azGQkJCdDpdOMeM20SfmJiIrq6\nutDd3Q2n04mzZ89i8eLFcoelGIwxfPHFF4iOjsbq1avlDscrdrsd/f39AIC+vj5cvHgRsbGxMkfl\nuWeffRYHDx5EWVkZXn31VaSmpmLLli1yh+WxoaEh11CU3W6H2WyeUZ+/Xq9HREQELl++DEmSUFtb\ni/T0dLnD8tqZM2dgMpkmPGbajOGr1WoUFRXh008/dZVlRkdHyx2Wx/bu3YuGhgb09fWhqKgI69at\nw4oVK+QOy2NNTU04ffo0YmNj8cYbbwDgiSgzM1PmyO7t5s2bKCsrgyRJ0Ov1KCgowKJFi+QOa9IE\nQZA7BK/YbDaUlpYCAAIDA7F69WpkZGTIHJV3iouLUVZWBrvdjtjYWDz33HNyh+SVwcFB1NXV4aWX\nXprwOGqeRgghCjFthnQIIYRMLUr4hBCiEJTwCSFEISjhE0KIQlDCJ4QQhaCETwghCkEJn8waxcXF\nqKur+9PnaWhowIcffuh63NzcjI8++ggbNmy47w39ent78dprr0GSpPt6XkLGQgmfzCr3Y9HS0aNH\n3XqJHz58GEajERUVFfd99bfBYEBMTAzOnTt3X89LyFgo4RNyh7a2NnR2diIrK8v1s56eHixcuHBS\n5xNF8Z7HPPbYY6iqqprU+QnxxrRprUDI/eJ0OvHNN9+4Oh4uXboU69evd/XIr6qqwokTJ+Dv74+1\na9di37592L9/P8LDw/Hbb78hMTHRda6tW7eiu7sbu3btglqtxqFDh3D69GkcO3YMFosFQUFBKCws\ndLUDvnTpEg4cOICnnnoK3377LYxGI4qLi1FVVYVTp06hv78fixYtwubNm6HVagEASUlJaGtrw61b\nt2ZsH3YyM9AdPplVGGOorKxEU1MTSktLUVpaisuXL6OyshIAcPHiRRw/fhzvvPMOPvnkE5w/f97t\n9R0dHYiIiHA9PnDgAEJDQ1FSUoKKigr4+PggKCgIb731Fr766is888wzKC8vd2vHbLPZ0NLSgvff\nfx8vvvgivvvuO5w5cwZbt27Fnj17AACHDh1yHT9nzhwEBwfj2rVrU/nREEIJn8w+P//8M/Lz86HT\n6aDT6ZCXl4effvoJAHD27FlkZmYiOjoaGo0G+fn5bq+1WCyuVr/jyc7OdtuZLTk52a3/uyRJWLt2\nLfR6PTQaDX744QcUFhYiOTkZer0eTz75JM6dO+c2URsSEoKenp77+CkQcjca0iGzjtVqRUJCgutx\nQkKCa7vGmzdvurW+jY+Pd3vtvHnz0NvbO+H5zWYzjhw5gs7OTjDGMDQ0hLS0NNfzQUFBbjtu3bhx\nA19++aXbXb1arYbNZnNdXCwWy4zbpYvMPJTwyawTHByMlpYWV9JvaWlxbaaj1+vR1tbmOvaPO2NF\nRUWhqalp3HM7HA7s3r0bzz//PFasWAGVSoV3333XbacqtVrt9prQ0FCsW7cOubm5Y55zaGgIVqt1\nRrUDJzMTDemQWcdkMqG6uhp2ux12ux3V1dVYtmwZACA3NxcXL16E2WxGd3c3Tpw44fba1NRUtLS0\nTHj+uXPnIjAwEMPDw6iursbly5cnPP7RRx/FsWPH0NjYCEmSYLfb3er5m5ubERcXRxO2ZMrRHT6Z\nVQRBwJo1azAwMIDXX38dAK/SWbNmDQAgMzMTBQUFOHjwIPz8/PDEE0+gpqYGvr6+AIDY2FhERUWh\ntrYW2dnZd53f19cXGzduxJEjR1BeXo6cnJx77jK0atUq145ivb29CAoKgslkctX0nzx5EoWFhffz\nYyBkTLQBClG02tpa7Nq1C4cPH4ZKxb/wNjY2orKyEm+//faU//7e3l7s2LEDe/bsmXE7XZGZhxI+\nUZxff/0VWVlZaG9vx9dffw2tVovt27fLHRYhU46GdIji/PjjjygrK4NarUZKSgo2bdokd0iE/CXo\nDp8QQhSCqnQIIUQhKOETQohCUMInhBCFoIRPCCEKQQmfEEIUghI+IYQoxP8Bsm9c+GHwnHwAAAAA\nSUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11452bdd0>"
       ]
      }
     ],
     "prompt_number": 49
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "I have added random jitter on the y-axis to help visualize the density of the points, and have plotted fare on the log scale.\n",
      "\n",
      "Clearly, fitting a line through this data makes little sense, for several reasons. First, for most values of the predictor variable, the line would predict values that are not zero or one. Second, it would seem odd to choose least squares (or similar) as a criterion for selecting the best line."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "x = np.log(titanic.fare[titanic.fare>0])\n",
      "y = titanic.survived[titanic.fare>0]\n",
      "betas_titanic = fmin(ss, [1,1], args=(x,y))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 277.621917\n",
        "         Iterations: 55\n",
        "         Function evaluations: 103\n"
       ]
      }
     ],
     "prompt_number": 50
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "jitter = np.random.normal(scale=0.02, size=len(titanic))\n",
      "plt.scatter(np.log(titanic.fare), titanic.survived + jitter, alpha=0.3)\n",
      "yticks([0,1])\n",
      "ylabel(\"survived\")\n",
      "xlabel(\"log(fare)\")\n",
      "plt.plot([0,7], [betas_titanic[0], betas_titanic[0] + betas_titanic[1]*7.])"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 51,
       "text": [
        "[<matplotlib.lines.Line2D at 0x1148a1ed0>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEPCAYAAABBUX+lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeYXdd53/vv2vucM733jsE0DMCCygKCpFlUKIkiZD2x\nHee6PM5jxyYZl8TXsXMtx08eSZYoi5YoklJC2ZJz7YROpGtKsmQ9skQQJECAAAhg0AaDOr23c2bm\n1L3Xun+sAUiAADgkp2Lezz8EiME5awrevfZvvWttZYwxCCGEuOk5Sz0AIYQQi0MKvhBCrBJS8IUQ\nYpWQgi+EEKuEFHwhhFglpOALIcQqEVjqAVxt//79zMzMLPUwhBBiRcnPz2fLli03/JhlV/BnZmbY\nvHnzUg9DCCFWlMOHD7/rx0ikI4QQq4QUfCGEWCWk4AshxCohBV8IIVYJKfhCCLFKSMEX4jqMgUTC\n/leIm8Gya8sUK1tXl2JiQpGTY1izxuC68/O64TAMDDgEAobiYsP0tCIUMpSWzs/rXy0eh+PHXSYn\n7edy220+mZkL815CLBYp+GLe9Pcr2ttdQDE4CODR0PDBp8exGBw+7JJIOChl2LNHUV4OYGhq8ufl\nPa7W0+MwNmZvgCcnFZ2dhvXr9by/z2IJh2FqSpGba8jNffePn5mxdze5uRCQKnHTkG+lmDdTUwpQ\naG1jkEhEAR+8GE9OQmeng+8rsrJgcNChpETjuoq+PoeGBv8Dv8fV9FW13Z//t1g0IyNw9GgA31e4\nrmHTJo/i4ut//NAQHD8ewPMU+fmaTZt80tIWb7xz5ftw7pzD5KSioMDQ0KDn7Y7yZiUFX8yb/HzN\nxIRDT49LLGbYvl2RTEIoZP88mYSeHoXnKSorNTk513+teBxSKcjMhMFBCIcVMzOK7GwIBt+KijIy\nFuZzqazU9PcrEgmHtDRNdfUHm91rDaOj9tfFxeDMrp5NTEA8rsjLM3OKjC6tK6SlQTQKIyOKYBAq\nKszl17za0JBDInHpe6EYGnIoLr7+59PZ6eJ5CoDJSYehIU1t7bUv3PG4LbozM4rSUk19/eIteHR2\nKi5etD8IExMQCBjWrpUFlxuRgi8+MGNgbAw8DwoLNVNTisxMOHXKIT0d7rnHJxqFEyccIhEHY2z8\nc/vtPhMTCteF6mpzOToYHrb5eSqlyMw0dHYqMjIM2dmGnBxNdbXPyEiAQMBQWfnBp949PTA87JCb\nq2losMU4Jwduv90nFvMpLHzrwuL70NenSKWgtNQwPKwYHHTIyjK0tOhrXoCMgVOnFAMDLr6vKC/3\naWzUnDnj0NHhkJenyMzUbN3qk519/XHOzLz1NczMNHieIRZzAUMkomltvXYR1xo6OhzicUhPh7o6\n74Zfj6svHNe7kIAt9r29l4quIiPDm43bIBKBsTH7vbv0/+ZTLKau8Xsp+DciBV98IF1dcPKkQ0eH\nS0YGFBb6nDmjCIddcnMNDQ0+R47AwIDL974XxHEUGzd6VFTAm2+6+L4DGEZGfGpqDDk5cP68Syrl\nkEjAwYMuWVmGWMzm91VVmqEhl+PHXXp7HY4c8XnkkSSbNnHN2/mREejrc8jKgtpaTTBoZ9rG2Jl2\nXx/86EdBRkYc0tMNjzyS5JZb4PRph64uB6WgpcWnrs4Wkvb2twrcmTOaZFKRlqaYmgKl4Pbbryy6\nyST89KcuBw4EKCkxNDf7DA/bO52JCRtHTE8ramocRkY02dnXLlgDA/CDHwTp7HSprvYxBkpKnNk8\nXjE4qGhtvfb3yHEMJSWayUmHgoJ3jz0aG31mZiCZtLP2iorrF9GZmbcXXUU0aotuJGK/d6mU/f42\nN/vzPvsuLtb09TkYo1DKUFS0ctdYFosUfPG+DQ7C+fOK730vjUOHXHJyNLff7hAKGY4fdykqMoRC\nAcrKDCdPusRiDhMTCmMCZGamyMiwxcLz4JVXgrS2GrKyNMGgIZmECxegq8ulsTGFUj6hkCInR9PX\nF2R01MH34fRpl6KiIMXFKdaseWts3d22OP/0p0FcF/Ly4M47U5SWmtmCrSgr00SjPkePurS1uTiO\njUpqapJ0djqAwhg4c8ahtNTm2MPDoJTBGIPv24J+Kd++esYJ0NbmcPBggN5el8FByMrSTE05tLe7\nXLyoqK83NDd7DAwYqqvt3xkZgfZ2F62hsVGTkWH41rdCtLcH6O936OmBhgZNJAIlJVBVZcjKuvJ9\nR0bg7FmXeNy+Z3m5prLSjtlxFKmUob/frrdUVBjS09/6uwUFsG2bvSsrKLj2hfSSsjKfiQkYG3Mw\nxtDaajhyxF4s29td0tMNGRmKrCzD2rXzuxBSXg6u611ejL7RuoSwpOCL9y0atTO6c+ccMjIgP9/G\nDFVVmoceSpJIGEZGAmRn+0SjNsqprtYUFGhqazXJpJ25j4/bmKKnR1NS4lBR4dPXZxgcVGzcmJwt\nci5r1/oMDDi4rqanJ0hXl2LdOp/paTh2zKWmxsd1obMTdu0KMDSk6Oiw0VBNjSY93SU3V1NYCL5v\nUAp8X9HW5mKMjY+6u+1dizG2MAcCNhvfvTtAWpohHlecOKHwPJdUys4yMzMNxkB5+TsLWiSiCARs\njHP+vEtnp8P0NPT2uihli25xsSIjQ9HTo8nMhO5uh3jc5iinTikKCz2Gh22kEw5DLOayYYNPc7Nm\nZMQlPV2zfv1b7z09DW++GeDYMfu5h0KaTZs8fF+RnW2orta0tTn097u4LgwN+Wzdqi9HaiMjtisq\nGlVUVBg2b/Yvr8NcYi+2dj0gmYTMTHvReOONAIGAYmbGxj1VVYZoFKanF2b2XVICJSUS48zVohX8\n559/niNHjpCbm8uXv/zlxXpbsYAKCgxKGUpLNR0dNp/u63MJh12Ki31aWw1nz6YoKFCsW+fR3u5S\nWWkLVXOz5tixAO3tdsFvcBBiMYfRUUMoZGeX0ajDvn0OyaQhI8POTsfHFQUFmpISH2MUxcV2Bp5K\nKaqr7Yzz1VcDtLUFyM/XZGVpursDs4XUJS1NcfZsgKIiQ1mZz913+zQ2+kxNOXieYWYGzp936OpS\ntLUFKS31yciAO+6wxf7MGUVJieHNNx1ycuxFo7fXoabG48gRl+5uOyuvrLRFqK5Oc+yYJh63s+r0\ndMPkpENfnyIUstl9PK44fVrR3R3izBkNKJqaDIGAAewFx3UVIyMOhYWadet8Kit9MjMV9fWaNWuu\nzP7jcZun+z6kpdmLUV4erFvnkZEBU1Nw4ECAoSEHxzGsX28oLtakp9u1ikOH3NkuHejthbKydy7G\nnj8PP/tZiKkpxfg43Hmnfe1YTKGUjczWrfNJT7eL+SUlErcsB4tW8B944AEeeeQRnn322cV6S7HA\nCgqgvh7Wrk1RU+OTTBr6+tzZhVlb4DZuNNTX24XDnTuTBIN2VjY9beOOtDRDf7+d0cbjhrw8TTis\nOHcugO/bmXgyaTt0xscdzpzR3Hqr5q67PC5eVPT3B8jJMQSDduF1ctJw9qxLZ6dLWhps2uRRVaWp\nqdHE44ZIxKWgwBZB+3dsgerrs3l9U5PPj3/skJPjkJvrU1Rk6Ox0iEQ0BQWglCI/31BSYnBdQ2+v\nQygEo6MuWtsZ8cyMIjfXIzsbGhsNn/pUkoMHXUZGArz2WoCtW31aWjyGhhR5eRCJ2Pfq6wugNeTl\naXp77UUuI0NRWAgNDT5TU/aOKhKxUYznaUZHXUIh2/nU1GSLak4O5Of7+L7DyIiivFyTk2Mud0XZ\nr69ibEyRnq6YnoacHEN7u0tFhU9Pj0s4bBfeIxF78bi64Pf1ubNtuOB5ly5GPiUldlNcMGgIhxXJ\npMLzuGny9aSn+ebBfh5uLKS5ZOXtxFu0gt/a2srw8PBivZ1YJDk5kJmp6O1VRCIOhYWGjIwUiYRD\ndbUtwOnpdkb/9l2xExPQ3++SmalnYwHFpk0+vq8ZHHQ4dcoWnbo6TXGxTzyu6O52SU+3GXpbWwCl\nDENDivFxl7KyFKBJpRzS0hQNDR6xmKGoyObLkYjm1KkQFRWGQ4dc1q3TnDxpY6DiYp+HHtIoZS9Y\nSiny8mxccuiQS3W14cgRw7Ztmttv9zh71iGVMjiOjSvKyzUdHQ7nzgUpKzM0NXnccQeXZ911dfDT\nn0I47KC1g9YeWVmGwkJFerohN9d2KI2MKMbGAoRCdkNZcbGH1g5vvBFicNAlO9veUXV2upw6ZT+H\n0VGIRAKMjto1htpau6aQnm47p6JRheM4eJ4ikTCEQjA8bAgEbGQVj0N9vaavzxCN2o6j0lLD6Khd\n7C0rMxQWvrNY5+fbCx5AXp4hGDRcuOCwfr29azpxQrFvX4hIxHYwrVmjqa+f/6I/MmL3f+TkGEpK\n5v3lr9AXTvC5ly9SnpNGZW7o3f/CMiQZvnjfxsehrc1GINPTLlrbwjU1ZTt2jh51yc62s9NEQrF9\nu08yaRdpMzOhttanp8ehpsYnP992WRQXe7zxRjrxuCKRUIyMKDZtsu2OnmcX506etEV5aMihuVnz\n+usBlFIUFSW54w4PpcB1XRoa7J/19Sny80N4niE93eeeewzRqEMkYiOaeNzhzBmHWMyhudljehqO\nHAnS2upz7pzC9y91zxhcV1Nfb6OP3l5Ffr6dBQ8MBIhGFYGAIZGwPfJFRfbrND0NiYRiaEgRi9lZ\n+sSEy/i4XTfYsCFJXp7NuW1fuUJrA7gMDir6+yE93c7A7U5Ze6fyk584pKW5nDtnZ+COk6C42Gdw\nEA4dChCN2g1qiQScPeswMGDvKEZHNRcvBunvt107Z8+61NRoQiHbd19erlm/PkVFhY3tKivf+b1v\nadFcuODR1eWQmQlaG8bHXdraFHV1KSIRu1M5EFCzO5UDQHJef/4GB+HgwQDT03ZtYts2b0HaPwF2\nX5jg2dd7+ZXN5TzaWoxS71ygXwmk4Iv3bWhIMTTkcvGiPfZgw4YUPT022pietm2Q4TAcP+6wdi2c\nP+/T12cLWna25tZbPYqLHVIp220TjQZIpaCw0KOoyCGVcsjJsYU+HDZs3mw7Mi69fl+fQyxmM/Wc\nHMOePUEcB9auNRw4YC8Yg4MuyaRCKXuXUFAAo6OGCxdcHEeTSLi0tQUpL9cMDtr3isVs1p6ZaTtk\nIhFIpQxKKWIxh8lJh0OHAsTjio4OxYMPeriuoaXFZ+1au4j79kXOYBCCQYXv2yLh+4qeHjv2QMAu\n7GZkQHW1R1GRxnEUkQi4rl0jSEtzGBhwZheZ7cdXVRmCQYfeXru7eWLCroGMjGiOHnVm7xbs+kh1\ntUdaGvi+w/i4XfyNRg2lpQbPg4ICTUGB4cQJyMqyX9f77/doabHdP9fqwx8YgKkpe2fW12fHY4wt\n7kND9vtrjI3rsrM1BQXzv1X53Dnbnvv2tszy8vm9i0h6mm+80cebvRE+99EGmotXXozzdlLwbyJT\nU3bBLjeXRdkKr5RBa1i/3ieRMGRkaMrKHA4dcsnL00SjdlPVwIBCa4fqamb7zm3skpnpYYzh/PkA\nkQhUVhoOHAjwcz/nceedHsePBwgGDfv2BcnLMzzwQILiYk1XV4j+fpfGRtvVYozGGEU06jA6ai9C\n4TBkZtrNVCMjLtGow2OPJTl50sYb1dU+4+M2X56chFTKxkeX2hirqgxdXYoHH0wxMaEIBhW9vYbK\nSgfft7PmqSnb0jg2pti2LUVvr0tamuGOO/wr4qv0dAgG7eJqTo5d5K6u9pmYcEhP15SW2jjF82xB\nzs+Hhx7ymJmB0lI4dixAV5dLcbEmHHaoqtLk5urZllCHRMJebAIBG/l0d1/ad2AvRA8/nEJrhda2\nv7K62mf7do89e0KEQtDa6pOebqio0Ghtd/0a45CTc/0i3dnpsn9/EN+3Y8rK8klLM2Rk2LguHLad\nW1VVly6A899Jk0jY/7qu/TlMJOZ31t0XjvPZlzupyk3j+U+tIyu08s9tkIJ/kxgctOef2NY7zZYt\n/oIdO3BJfr5936Ehl1gM7r3X4Hk+JSUueXmGsjJNTo5Paakt/GfOBNi/P4hSirIy+3G7dwfIyLCz\n3+Jijes6TE0pams1kYjH0aMungcTEw779gVoaUlx770+oZCdOZaU+Hieorc3QHNzCt+3G7YGB+1F\nJjPT5xd/0SM9XbN/f4DhYdudsnatR3m5T3m5z44ddpaalcVs5OKSk2PYtEnz/e+HiEYVaWnwy7+c\nICfHLnr29TmEwzYDX7/eY2zMZceOJB/6kCE/327CeruSEp+KigCnTzvEYpqmJo9k0gU0ExOKwcEA\nY2PQ0ODR2mooKFB86EM+p07B+Li9OBw54hAKKbZs0eTmGhxH09CQJJWyX7vt230KCmyUlEhwuTOm\nr88hI8MW8lDIUFYG2dmGW27xKCjQTE87vPpqgL4+l6oqTSLhk5Z245my59m9CLGYQ26u/V7X1GiM\nAWPs99Dz7C7bvDxm20znd/ZdU6PZv98wMuJSVORTUzN/r7/r/ATP7+vlVzeX84kVHOFcbdEK/le+\n8hXa29uZmprid37nd/iFX/gFHnjggcV6+5teV5d7OTKYnrbnn6xZs7D9yVorqqoUb75pSE9XnD9v\nC0Z/vwYMWVmGvj6HkhIIhQzDw85sX7o9WiGVskXZ9t07FBcbKipSxGIO6el2YbOuzjA0ZAuV6zok\nk0EmJ21BmpiAhgYoL09RWmpn6eGwme1occnKskcgHDsWoL7eB+zGrUvRyEc/mqS83DA25rBlC+zb\n55Kdbe9A9uyBT3wiSUaGbW0MBAyxmMJx7ELqxo0+PT22E0VrG/XYDqBrH1tQWGgjiETCkJ7usHt3\nkOpqTVqaIpm0u1+zs2F8PMjQUIqyMnvnMTUFIyMBJiYcNm/WpKd75OXZrpuTJ0NkZ9u2zaYmu1MZ\nYONGj7w8h6Ehh+PHHUpLbc//xz6WZN06w/nzivPnA5dnxOfPO1RWemRn22ho/Xq7WHsjWVn2ezIz\nY9ctGho87rnHvvbgYIDCQrtYn56uSE//4GcRXYvjwLp1mulpG+nNx7EKCU/zjf29HOmf5i8+2kDj\nCo9wrrZoBf/3f//3F+utVqWrN8YsxpG2OTk2Ny0stLlteblm/3539tgCu1t2zRpNY6MhmTSkUg5l\nZZrubne2s8IhLw9OnQqyY0eCX/7lFMbYLfldXTYfLizU1NbaRV/bFmno6gowMuKgNQwOGmpqFI88\nksJxFAMDttWypgYcRzM8bDdnpaUZmpttR9DYmKGpSWOMQyrl09vrXJ6Jep7B8+zhYlqDUpqsLJvD\n5+TYLqDGRo++PpfKSjs7TibtHUxurmF83Bb3q1VU2NbEnBzbnaS1PWemrMyeERQKaXxfkUwafN8u\n7h48GMDzNFNTzG76sh1RpaWamRmXmRnbahkK2YvRxIRtlb3lFkNRkc/f/32AmRmX/n7bSx+P2xl3\nZqbtmmlvdwkGDaWlPllZ9kTSnBxDLPbuPz+5uYr16zXRqF1QLyiwHVu1tYbxcU0goGlutl0/6elm\nQfrw43FFVpbdxQuKZPKD3UX0huN89med1OSn8dzOlpsiwrmaRDo3iYYGe/5JLGaPDLjR+SfzJSfH\nbsEfGUkyPOyQn+9TU2P/0V286JCVpSkr0zQ2+uTkwMGDdsEyGFSUlvqcOWMjEd83ZGUpysrszFtr\nxaFD9jiCpiaPyUnF+vUp7rvPFr+xMYfubhgetmsFg4MuhYUeeXl2YXV62h7GFo3aWV9rq8L3Db6v\nGRvTzMw4l4vvyIhLe3sAY6CuzqeqSpORocnLUxw9GmDHDo9AwHblFBUZHMdepO65J0VXl/0cR0ac\n2ZMrHaan/WsW/Lo6+PSnk7zyii32hYW2Iyc729Da6uM4tjAWF3uEwy7O7Erp9LRDa6tPebnN5sFu\nSCso8Pn0pzW9vQFmZuwF//BhlzvusF/raJS3fY0V09M23x8ZYXYB116UlYLt2+35Rw0NHiUlhnDY\n7ga+1GV0LWVlmjVr7EUkFHqrk6ewEO6+2+foUbtobPv8XQ4eNNTX3/jQtveqrEwzMOBcPva5tPT9\nF/td58d5fl8fv7algo+vK7ppIpyrScG/SeTm2lMpPc/ORhdLQQGsWQOFhYZz5xzq6ny6uly2bfMA\nu4OzsdHGFcXFPgcOGPLybPdHMgmFhUkCAbuzVGs7O9daXb4TGBqyu3MzMhRbt+rZg8f82TPxPSor\nzeXdnWBnmENDiq4u28KZng4TE/acFXsUgV1U9H3bu+26mvJy27XT12f40IdSaG1bIPPyXAoK7EJ4\nNOrMzvhtt8vdd9uOkDNn0giH7Uywr8/Bu05Ncxz40Ic0paWaXbsMExM2bqqrs3cQO3akLp+Hc+CA\n/TOwO2QbG3327bP7AcCumRQWMruI65OV5ZCbayOyqSkb9/i+Q0WF4d57PUZGFEVFmkjE4fBhRUWF\nT3OzYWbGJxCwF+7KSrvBbXLSboZ7N2VlsGWLRzjskJOjr2iHzMiwXUmu+1bRvBQ3zqeSErvD91If\n/lwe7HK1hKf5+v5e2vqn+cIjDTQU3VwRztWk4N9ElFrcYg/2H/f69T4dHQ5bthgOH7a93ZGIwnUd\n1q41lzcg5eXBgw9qamvtJqOJCRvneB5UV6cuxwhZWdDUpEmlfHJyNOvXe5SX2wXB0lLYvNljcNDu\nvi0uZnZW/taYgkF7oBgoHMceodzQYAiHITtbEQr5ZGXZWWlnJzz4YILWVtvbn5lp+MQnfKamfMbH\n4eJFB3Boa7M7bmtrfTZvtjPJkhI7S56ZsS2It9124weFKAW33mqjpt5euy+hpsY+srGs7K2PW7/e\nv3x4WkODT22tYWzMY3DQmY2fbD+96yq2bfMYHbUHxLnupSwbKio0/f0uZWV2g1RBAWht7xCMgdxc\nTVqaPcmyosLM7nPQeJ79nK51l3K10lKuO6tuatKcP293E2dmwu23p979Bd+H3Fwbpb0fPZNxPvfy\nRWrz03n2Jo1wriYFX3xglZWGigrbwuf7Dm1tDqWlmro6n1tvvfJjXddu2gkE4PXXXZqb7d+7eFER\ni0FZmWF42LZZBgIe5eUG11U0NLzV+XLLLZCfn+LsWRel7Jktb7/QFRQYBgdtwb+0njA6qjh50u4B\nUMo+9SkjA1pbIRz22bfPIRSyC93Z2TZzBzvW/fsVO3YY4nGbmV8qhtnZ8PGPJ2lrCxAI2OL3bs/Y\ndV247TbNbbdd/2MqKgylpR7GvJWlb9nis2+f7T6qrNT09jqXO6MaGz2SyUtHKNiPz82Fu+6yMd/o\nKLMbn976s7VrfUZHNWlp9v0utfOmUvZicaOH08xFKGS/7rGYvYjO5QKymH52bpxv7O/j17dW8LGW\nmzfCuZoUfDEvlLKPxovF7Fb7VMouSF7vNjsjw56vE43aWWdxsT2R0XVh40Z7eJrj2NezC6ZX/v3q\naqiq8i+/99vV1RkCAZ/paXtEQnk5HD1qNygBGGPPor80Ow0GndmHhyh832V4+K2Zsn1921mUnW3H\nZMzb3wuKiz1SKTvG+XrE3tWvU1wMH/2oz9q1PocOBZmctK2ro6Mu5eUeLS3vnGlnZHB5QdVx9OVH\nAdbW2ieGvf1zzMiwHS/zZXhYkUo5s1GPoqvLveZpoost7mmef72XE0OrI8K5mhR8MW9iMfswkEuP\nwwsGrz9rqqy0m4sOH7bHDt97b+pykVOKy3n2jfYS3GhSZiOdtwqa3TFqZh/YYVsGL7Gbgt7aTvr2\nDpX8fHukc2+v3ena2Oi/Iza7+iz6hRIMwoYNMD5uj3i+NI53e96u69r1i8V09QVrOTxrtnsyzmd/\ndpH6wgyefayFzFUQ4VxNCr6YN4WFhmBQX37K0bt1TdjDyJI4zsK3kdbV6dmnVdlFxtFRe3CaPYrB\n7gqenlazu2DfPruHDRvs+f1KvfNOYyk0NfkcP65mF57tTt3lxu5A9hkett1HTU1LO7v/6dlx/tsb\nffzG1go+uooinKtJwRfzJjfXtmmOjek5P8f06v0DCyWRsO916Qjh0VH7kI6cHDtDv/NOH62vfW6M\nUryvDpCFUl4O2dkeiQSzffhLPaJ3cl37uMdEwj5W8kbPxV1IcU/z3Os9nBya4YuPNLK2aIG3ny9z\nUvDFvPogXRMLKRi00U0yaWd2oZB5R6FcqqL0fmRnc8MHni8Xi3Gm0/V0TcT47MudNBZl8NzOFjKC\nqy/CuZoUfLEqpKfDrbf6nD9vf9/YeOMWSrGy/eTMGC8c6OffbqvkI82FqzbCuZoUfLFq2OefLn2n\niFg4sZTPc6/30j48w1Mfa6S+cHVHOFdbQTexQghxfZ0TMX73e2fQwLM7W6TYX4PM8IUQK96lCOc3\n76jkw803OARolZOCL4RYsWIpn6+93suZkShf+ngjawpkVn8jEukIIVaki+Mx/v33zuAAX3usWYr9\nHMgMXwixohhj+PGZcf7moEQ475UUfCHEihFL+Tyzt4dzYzH+8uON1Mms/j2RSEcIsSJcHI/xxEsd\nBBzF1x5rkWL/PsgMXwixrBlj+HHHGH9zaIB/d2cVDzcts7OWVxAp+EKIZSua9Pnq3h4ujsf48seb\nqC1IX+ohrWgS6QghlqULYzGe/F4H6QGHZx5rkWI/D2SGL4RYVowx/KhjjG9LhDPvpOALIZaNmaTP\nV/d00zUR58ufaKI2X2b180kiHSHEsnB+LMqTL3WQGXJthCPFft7JDF8IsaSMMfzw9Bh/++YAj99d\nxQMNEuEsFCn4QoglM5P0+cqebnomE/zVo01U58msfiFJpCOEWBLnRqM88VIH2SGXr36yWYr9IpAZ\nvhBiURlj+Kf2Uf7H4UEev7uaBxoKlnpIq4YUfCHEoplJ+vzVa930hhN85dEmqmRWv6ik4AshFsWZ\n0Siff/kim6tyeeb+OkIBSZQXmxR8IcSCMsbw/VOj/N2RQZ7cXs39ayXCWSpS8IUQC2Ym6fPlV7sZ\nnErwlUebqcpLW+ohrWpyTyWEWBBnRqI8/o+nKcwMSLFfJmSGL4SYV8YYvndqlL8/Msi/v6ea++ol\nwlkupOALIebNdMLj6de6GZxK8tVPNlOZK7P65UQiHSHEvDg9PMPjL3VQlBniK1LslyWZ4QshPhBj\nDC+dHOFKOwdEAAAgAElEQVR/Hh3i9+6pYUd9/lIPSVyHFHwhxPs2lfD48qvdjM6keOaTzVTIrH5Z\nk0hHCPG+nB6e4fF/7KAsO8TTjzZJsV8BZIYvhHhPjDH8fydGeLFtiN/bUcOONRLhrBRS8IUQcxaJ\n2whnPJbimceaqciRWf1KIpGOEGJO2odneOKlDspzQzz9iSYp9iuQzPCFEDdkjOG7x4f538eG+f17\na9heJxHOSiUFXwhxXZG4x5d2dxGOezzzWDPlMqtf0aTgCyGu6dTQDJ/fdZH76gv4s60VBF1JgFc6\nKfhCiCtoY/jO8WG+c2yYP7i3lrvr8pZ6SGKeSMEXQlx2KcKJJDy+9lgLZTmhpR6SmEdS8IUQAJwc\nnObzuzq5f20Bv7GtkoCjlnpIYp5JwRdildPG8H+ODfPd48P8h/tquatWIpyblRR8IVaxcNzjqVe6\nmEn6PLuzhdJsiXBuZlLwhVilTsxGOA82FPDrWyXCWQ2k4Auxymhj+N/HhvjHEyP8x/tquaNGIpzV\nQgq+EKvIZCzFU7u7iKU0X3tMIpzVRgq+EKvEsYFpvvBKJw81FvJrWyokwlmFpOALcZPTxvDi0SG+\nd0oinNVOCr4QN7GJWIqnXuki4Wme3dlCSZZEOKuZFHwhblLHBqb4wq4uPtRUyK9uqcCVCGfVk4Iv\nxE3G14YX24b4wakR/vD+OrZW5y71kMQyIQVfiJvIRDTFF17pwtOGZ3e2UCwRjngbKfhC3CSO9k/x\nxVe6+EhzIb+yWSIc8U5S8IVY4Xxt+F9HB/mn9lGJcMQNScEXYgUbj6b4wiudGAPP7VxHUVZwqYck\nljEp+EKsUEf6p3jqlS4eaSni32wqlwhHvKvrFvwXX3wRpRTGGACUuvYP0y/+4i8uzMiEENfka8Pf\nHxnkRx2j/NH9dWyukghHzM11C/7Y2NjlIu/7Pvv27SMvL4/6+nouXrxIOBxm+/btizZQIYSNcP5i\nVycwG+FkSoQj5u66Bf+JJ564/OtvfOMbPPnkk1cU+H379tHW1rawoxNCXHa4L8JTu7v4WEuxRDji\nfZnTY+jffPNN7rrrriv+37Zt2zh06NCCDEoI8RZfG/72zQGe2t3Ff7p/jeyaFe/bnAp+YWEhP/zh\nD0kmkwAkk0l+/OMfU1RUtKCDE2K1G5tJ8Z9+dI6TQ9M8v3Mdm6pylnpIYgWbU5fOb//2b/OlL32J\nF198kfLycgYHB8nLy+MP//APF3p8Qqxah3oj/OXuLj7RWsy/3igRjvjg5lTw6+vreeaZZzhz5gwT\nExMUFBTQ3NxMICBdnULMN18b/sfhAX5yZpw/fmANGytlVi/mx3uu2Eop1q9fTzwex/M80tPTF2Jc\nQqxKYzMpPr+rk4CjeH5nCwXShSPm0ZwKfnd3N1/84heJx+Mkk0m2b9/OqVOn2L17N3/wB3+w0GMU\nYlW4FOE8ur6EX7q9TCIcMe/mtGj7wgsv8PDDD/PCCy9cjnHWr1/P6dOnF3RwQqwGvjb8zcF+nn61\nm//84BppuRQLZk4Fv7u7m4985CM4zpUfnkgkFmRQQqwWIzNJ/u8fnuXMaJTnPtXCbRWS14uFM6eC\nX1paysmTJ6/4f8eOHaOiomJBBiXEanCgJ8yTL3WwrSaXz3+0gYIMyevFwppThv9Lv/RLPPPMM2zf\nvh3P83jhhRfYt28fv/u7v7vQ4xPipuNrw7ffHOBn58b5fx6s57aK7KUeklgl5jTD37JlC3/+53+O\n4zisX78eYwx/+qd/ysaNGxd6fELcVIank/zhD89yfizK8ztbpNiLRTWnGX4kEqG+vp7f/M3fXOjx\nCHHTOtAT5suvdvOpW0r4hdvKcK5zAq0QC2VOBf/xxx9nw4YN3HPPPdxxxx3Sey/Ee+Bpw7cO9rPr\nwgSfeaieW8plVi+WxpwK/vPPP8/rr7/Ov/zLv/DCCy+wZcsWduzYwaZNm3Bdd6HHKMSKNTyd5PMv\nd5IVcvn6p9aRly6708XSUebSE07maHh4mL1797Jnzx4mJyf567/+63kd0M9+9jM2b948r68pxFLY\n3x3m6Ve7+fStpfyr20olwhEL6vDhwzz00EM3/Jj3PN2IRCKEw2GmpqbIysp634MT4mblzW6k2n1h\ngv/ycD0bJMIRy8ScCn5PTw979+5l7969JJNJ7r77bv7oj/6IxsbGhR6fECvK0FSSz++6SG5agK9/\nah25EuGIZWROP42f+cxnuPPOO/mt3/otNmzY8I4dt0II2NcV5q9e6+Zf3VbKp2+VCEcsP3Mq+C+8\n8ALBoOwCFOJaUr7mbw7281rnJP/lQ/VsKJMIRyxP1y34r776Kvfddx8Ar7322nVf4MEHH5z/UQmx\nQgxOJfjcy53kpwd4fqdEOGJ5u+5P5969ey8X/FdffRV1ndtTKfhitXq9a5K/eq2HX5yNcK73b0SI\n5eI9t2UuNGnLFMtdytd882A/r3eG+c8PrqG1VLrVxNKbS1vmnFZfv/Wtb3Hu3Ll5GZQQK9nAVIL/\n8E9nGYwkeW5nixR7saLMOXD80pe+RCgU4t5772XHjh1UVlYu5LiEWHb2dE7y1T09/NLtZfz8LSUS\n4YgVZ86RjtaaEydOsGfPHg4ePEhpaSk7duzg0UcfndcBSaQjlpuUr/nmgX5e75IIRyxf87rT1nEc\nbrvtNm677TbGx8d57rnn+Lu/+7t5L/hCLCcDEduFU5QV5PlPtZCTJl04YuWa809vPB7nwIED7N27\nl5MnT7JhwwaeeOKJhRybEEvqtYuTPLO3h1/eWMbODRLhiJVvTgX/6aef5siRI9TX17Njxw6eeOIJ\ncnNzF3psQiyJpK954Y0+3uiJ8NmPrKWlRCIccXOYU8FvaGjgV3/1VykuLl7o8QixpPojCT738kVK\ns0I8v7OFbIlwxE3kXdsyfd/nO9/5Dnl5eYsxHiGWzKsXJ/i975/hQ01F/NnD9VLsxU3nXX+iXdel\nrq6Oc+fO0drauhhjEmJRJT3Nfz/Qx8GeCJ/7SAPNJZlLPSQhFsScpjD33nsvL7zwAtu3b6epqemK\np1zdcsstCzY4IRZaX9hGOOU5aTwnEY64yc3pp/v73/8+ALt27WLXrl1X/Nlzzz03/6MSYhG8cn6C\n5/b18iuby3m0tVi6cMRNb04FX4q6uJkkPc033ujjzd4In/toA83FEuGI1UHuX8Wq0heO89mXO6nK\nTeP5T60jK+S++18S4iYxp4L/O7/zO9f9s69//evzNhghFtKu8xM8LxGOWMXmVPCffPLJK35/8eJF\ndu/ezUc+8pEFGZQQ8ynhab6xv5cj/dP8xUcbaJQIR6xScyr4GzZseMfvW1tb+fa3v83DDz+8IAMT\nYj70TMb53MsXqclP57mdLRLhiFXtfWf4mZmZ9PT0zOdYhJhXL58b5+v7+/i1LRV8fF2RRDhi1ZtT\nwX/xxRdRSnHpJOVwOMyxY8fYuHHjgg5OiPcj4Wme39fLsYFpvvBIAw1FEuEIAXMs+GNjY1fMjtLS\n0vj5n//5y8+8FWK56J6M87mfXaSuIJ1nJcIR4gpzKvj3338/JSUllJWVMTk5yQ9+8AM6OjrYsmUL\n+fn5Cz1GIebkZ+fG+cb+Pn59awUfa5EIR4irzemZtt/85jcvH6fw7W9/m8HBQeLxOP/wD/+woIMT\nYi7inubpV7v5+yODfOGRBj6+TlouhbiWOc3wJyYmKC4uxvM82traeP7559Fa88d//McLPT4hbqh7\nMs5nf3aR+sIMnn2shUyJcIS4rjkV/OrqagYGBhgYGGDt2rVkZGSQSqWIRCILPT4hrutfzo7x39/o\n5ze2VvBRiXCEeFdzKvgPPfQQ//W//leSyeTlTVgdHR1UVVUt6OCEuJa4p3nu9R5ODs3wxUcaWVuU\nsdRDEmJFmFPBf/DBB9m6dStKKXJycgAoLCzkt3/7txd0cEJcrWsixmdf7qSxKIPndraQEZQIR4i5\nmvPGq6ufYVtZWTnvgxHiRn5yZowXDvTzb7dV8pHmQolwhHiP5LRMsezFUj7Pvd5L+/AMT32skfpC\niXCEeD/m1JYpxFLpnIjxu987gwae3dkixV6ID0Bm+GJZMsbwk7PjfPNAP795RyUfbi5a6iEJseJJ\nwRfLTizl87W9PZwZjfGljzeypkBm9ULMB4l0xLJycTzGky914CjF1x5rlmIvxDySGb5YFowx/PjM\nOH9zUCIcIRaKFHyx5GIpn2f29nBuLMZffryROpnVC7EgJNIRS+rieIwnXuog4Ci+9liLFHshFpDM\n8MWSMMbwzx1jfOvQAP/uzioebipc6iEJcdOTgi8WXTTp89W9PVwcj/HljzdRW5C+1EMSYlWQSEcs\nqvNjUZ78XgfpAYdnHmuRYi/EIpIZvlgUxhh+1DHGtyXCEWLJSMEXC24m6fPVPd10TcT58ieaqM2X\nWb0QS0EiHbGgzo9FefKlDjKCro1wpNgLsWRkhi8WhDGGH54e42/fHODxu6t4oEEiHCGWmhR8Me9m\nkj5fea2bnnCCv3q0ieo8mdULsRxIpCPm1bnRKE+81EF2mstXP9ksxV6IZURm+GJeGGP4Qfso/+/h\nQR6/u5oHGgqWekhCiKtIwRcf2EzS5+nXuukLJ/jKo01UyaxeiGVJIh3xgZwZjfLES6fJSw/wzCeb\npdgLsYzJDF+8L8YYvn9qlL87MsiT26u5f61EOEIsd1LwxXs2nfB4+rUeBqcSfOXRZqry0pZ6SEKI\nOZBIR7wnZ0aiPP5SB4WZASn2QqwwMsMXc2KM4aWTI/zPo0P8+3uqua9eIhwhVhop+OJdTSc8vvxq\nN0PTSb76yWYqc2VWL8RKJJGOuKHTwzM8/lIHxVkhviLFXogVTWb44preHuH87j013Fufv9RDEkJ8\nQFLwxTtMzUY4ozMpnvlkMxUyqxfipiCRjrhC+/AMj/9jB2XZIZ5+tEmKvRA3EZnhC8BGON89McI/\ntA3xeztq2LFGIhwhbjZS8AWRuI1wxmMpnnmsmYocmdULcTOSSGeVax+e4YmXOijPDfH0J5qk2Atx\nE5MZ/ipljOG7x4f538eG+f17a9heJxGOEDc7KfirUCTu8aXdXYTjHs881ky5zOqFWBWk4K8yJ4em\n+YtdndxXX8Cfba0g6EqqJ8RqIQV/ldDG8J3jw3zn2DB/cG8td9flLfWQhBCLTAr+KhCejXCmEh5f\ne6yFspzQUg9JCLEEpODf5E4OTvP5XZ3cv7aA39hWScBRSz0kIcQSkYJ/k9LG8H+ODfPd48P8h/tq\nuatWIhwhVjsp+DehcNzjqVe6mEn6PLuzhdJsiXCEEFLwbzrHB20XzoMNBfz6VolwhBBvkYJ/k9DG\n8A9tQ7x0coT/eF8td9RIhCOEuJIU/JvAZCzFU7u7iKU0X3tMIhwhxLVJwV/hjg1M84VdnTzUVMiv\nbamQCEcIcV1S8FcobQwvHh3ie6ckwnk/kkkYG1O4rqGkBJRcJ8UqIAV/BZqIpXjqlS4SnubZnS2U\nZEmE816kUnD4sMvkpAMY1qzRrFunl3pYQiw4OUhlhWnrn+KJf+yguTiTL328SYr9+zAxwWyxB1D0\n9jr4/pIOSYhFITP8FcLXhv/VNsQ/nRrhD++vY2t17lIP6bqMgbEx++uiouURlxgDU1PgupCWBkoZ\njLEDC4UMjkx9xCogBX8FmIim+MIrXXja8OzOFoqX8aw+mYRXXglw8aIiL89wyy2aW265dlziefbC\nEAjYC8NC0RqOH3cYGHBwHGht9Vm3zqOz0yUYhHXr/GVxURJioUnBX+aO9k/xxVe6+EhzIb+yuQJ3\nmXfhnDih2L/fxXUVExOGUAjWrNFkZ1/5cZ4HR464jI3ZHH3tWk1z88Lk6GNjMDDgArb4nz3r8nM/\n51FXt/JyHK3tRdXepSz1aMRKIwV/mfK14X8dHeSf2keXfYSTSsHwsCIehzffdOjoAFDU19viFLjG\nT9nkJITDCscxaK3o7nZYu1Zf82MBZmZgaEjhulBVZa77cddiC6MB1OzvzZyL5cgIDAw4JJNQXa0p\nL5/7+863qSloa3OJRhUFBYbbbvNJk2fXiPdACv4yNB5N8YVXOtEantu5jqKs4FIP6boSCdi926Wv\nzyEchkgEGhs1qZTBdQ2bN/ukp1/5d4yBnh6Ho0cd4nEoK9OsWaOvm6PH43DokEssppieVpw753PL\nLZpIRDEy4pCRAU1N/jvuIi4pKoKaGk1fn4PrQmurvlzwjYELFxQTE4rsbMPatQaA8XF7kblwwaWj\nI0A4rKir89m61WPdOjNPX70bS6Wgu1uRSCiKijRnzigGBhxyc21LaWenT1qaIhiEigpZhxDvTgr+\nMnOkb4qndnfx0ZYi/q9N5cs6wtEa2tpshDMzA2lphoEByMmBWMxh48YkjmMIhyEUgowM8H04fx5O\nn4aREUVHR4DaWk1WVgrf1yQSkJ5uZ+WDg9Df75JKGSIRxfnzLsPDitFRl74+j95eRXMzZGfbiGjb\ntisjmnPnFL29ikQCKio0DQ2ayko7jkv6++H0aZfubhetIRpNEo06tLUFGBszZGXZ4h8I2M6egQHF\n2rU2qrpaOGy/Jvn5145bpqYgGoXc3CvHcLVEAjo7HS5cUGit0Nqwb59LWpqiq8uhvNxQXa1pawuQ\nm6sAQySiaW19/5FYMmkvLp6nKC/X5L/LI45tNOYwOqrIyDAEAoZ43KGsTFNXtzgXRPHeScFfJnxt\n+Psjg/yoY5Q/ur+OzVXLN8K5xGbjhkQCTp50SU83FBfDqVOK8+cDDA05ZGXFCAQU4JCToxkddejo\nUKSnKzzP0NiYIhRSTE7Cnj0OqZQtGrW1mv37FZGIvQCMjiqiUYhGbXS0f7/N/5NJn6oqTXr6lUVm\nZATa212OHnXp7lY0NRm2bk1hjL0DuWRqSnHokCIchpkZRTgcJBQyJJPguooTJxySSUUoBHV1SYaG\nHE6dgsxMw8SEQ0aGoaZG09MDIyN2/FVVdqFaKVtIQyEYHoa2tgC+r8jI0GzZcv07klOnXM6ds3dA\nXV2K8nJ7gbnrLo+8PM3kpKKy0hAKvdVaOjioaG19/9/LU6cUvb0uU1OK7GzFAw9cf3wAPT2Kixft\nusixY4rCQkNeHoyPKzIyPEpKYP9+hwsXXIqLNdu3++TkvP/xifkhBX8ZGIum+MKuTmA2wslcvhHO\nJb4P7e0O09Oa9naXiQmH5mafzk7FzIxtdRwfV5w54xCJBJiedsjM1HieLYDHj7tkZRkqKjSgGB5W\nrFtnZ7QDAy6+b2ewe/aEyMnx+fSnU4TDivFxQzTqUFJiyM312bMnQE6O5rd+K/mO8bW1ubS1uSQS\nCtf1ufVW6O21F5vCQpvjJxKGoSHFyZNBCgs1NTU+vb0uWit8X5Ofb6ioSBEIQHe3Q2uroaPDZWhI\nsW6dZnRU8d3vBhkZUTQ0aG67zaevz6GiQtPZ6TIxocjJsfGW79tpfyzmMDSkyc5+50zYGGhvVxw4\n4HDiRBDPg+xsj85OeyGZmlLU1dmo7OhRdbm1NCvrvX3/tLYz+lhMUVCgGR5W7Nvnkkg45OZqKis1\nW7Zcf6Yej6srfh2LQV6e/V7GYooTJ+DllwOAQ2eni1Lw4Q+vvEXym40U/CV2uC/CU7u7+FhLMf9m\nmUc4l0SjMDBgZ9p9fQG6uhxAEY/bYwpKS2F62sYWSjn09CiiUUVNDfT3O5SU2KKfl+dTXKwZH3co\nKDBXbH4aGoKXXw4yMwORSIBTp1I0NPiEw1zu/unvD1Bf7zM15XDypMsjj1wZaUxOKrSGoiJNMGgY\nG1OAJpl0mZkxuK6iq8tGLNXVHr7voLWhvj7JhQshqqo009Pw5pshqqs9jLF9/LGYvRswRvPmmwHO\nn3cJheDkSYfKSkNhoWFgQDE66lweB2h83+B5kJ6u6e52iEZtNFNQYMebSNiZdleXw9iYQ06OYXIS\nCgo04+P2cwkGFYGAJiMD1q+3FxfPM5SV6ct3E5d0dSkmJ+0FZ82aKzP+Cxcczp2zM/TubhtVXepk\nmppyZsd+/QJdUmI/B99XZGdrEgnD6dMuJSUe4TC0tweYmHDJz7cX1omJG7+eWByLVvBPnTrF3/7t\n3+L7Pg899BCPPPLIYr31suRrw98dGeSfO0b5T/evYVPVyrjfnZ6GgwddolGH9nbDzAzceqvH8LBD\nIKC4994kb77p0thoZ9mjo4rWVp+DBx26ulxycqCnx2bc27YZTpwIMjWlKCtLEQj4RKOKigrN4CCU\nldkF24wMn+Zmn8OHQ0xMOHieLYJpaYZUynasRKOKVMq+n+PYi0dLi8foaICzZ11KSxVjY7B9u09p\nqc+xY0EmJhySSY3WDoODDlNTDuvWQXGxprU1wcAAvPpqCK1helpRUqI5exbKygwFBT6DgzaX19oW\n62AQwNDY6ON5imTSjj8tDbQ2vPaay8yMQ16eYfNmu14xOqq46y6fjAx79zE25lJaqunvd8jL82hp\nMaSna7Ztg9paPTvjtxeemhqD7/ucOePS3h5kYECzebNPKAR9fYr2dhdQDAwAeJcXpAEmJt6aWPi+\nIj0diot9tLaZfF7ejXP4wkK44w6PyUlFfj4MD7skkxpjbCSVk2OIxw1TU5Cbq6mvl2K/HCxKwdda\n8/Wvf53PfOYzFBYW8id/8ifceuutVFdXL8bbLztjMyn+YlcnjgPP71xH4QqIcC4ZGVF4HrOzSptR\n5+drMjIMsRh0dbkcOxa8vJBaWqoJhQxr1/okEopQyFBcrOjvV0QihokJRSTicP68y8aNqcuFMisL\nlNJ0dgZoaLAxzokTAfr6AnjepTsJn4sXAxQW+uzY4XP0qMP4uO3rLykxRCL2v8PDNl5KT3fZu9el\nuTnK4cOB2RmtZsMGzYYNHn19Dlo7dHUFiUQ08bhdNB4ft7PxxkafU6cC9Pcbtm9PkZ4O27Zp+vps\nx9CmTZodOzwqKqCtzS5ox2L2QlFU5DA+HsAYGwmFQh733KOJxxWdnXYGHIspUilDMqkIBOzXNi9P\n8+EPewDs2RPE9xV33KEvRzidnS5aX7qTcBgf9ykvtxeoS22oYNcqbGuqlZdnLu+Gdl1DRYVPbW2Q\nyUmorfVZv/7dF4Dz8uzr9Pa6hEL2ezs05KCUfc1HHvHQGhobfVpbZSF3OViUgn/u3DnKy8spLS0F\n4J577uHQoUOrsuAf6o3wl7u7+ERrMf9648qIcN4uEjEcPOhy8GAA34cPfzjO+fMBwuHA7IzWZ8cO\nj7NnA0QihqIiw/Hjtq2xvh4OHAhQWmpoavJIJGBszGF8XLF2rS1yaWmGw4cDTExoEgnF3XcnGRpy\nicXsLNx1DRkZtoCDjT4qK+0dQXGxQ2+v/RitbafJ3r0uJ0+6bN2aornZtn729Sl6ehxSKQCHwUEb\nw6xb59PV5RAMKjzPYft2n/FxNbsGoDhxIsDwsHP5HJ4PfzjB+fMuVVUGzzNkZ2tGRiAWU3R02EXl\niQkuF8CBAYXj2PWD6WnF6KghkVD88z+nobXdoFZS4jE2FiCZtEc/jI8rurvtgmpjo4/r2khtasp2\nQwWD9i7CMrg2lSEvT6OUM5vxG/Lzryy4DQ0a17V3RkVFhjNnbPSTlaXJybEXm7kqL9ezFxR7cUsm\n7a9DIcOmTR7FxR/kJ07Mp0Up+OPj4xS9be98YWEh586dW4y3XjZ8bfgfhwf4yZlx/viBNWysXPwI\nJxyGc+ds+2Fdnc/s9XfO+voUvb2wf3+A/n6XYNDQ328XOPv6FMYY7roLenttFt7S4mOMYcMGuxA6\nOelQUqKJRBwmJuzCZn6+wXEMa9d6nD0LQ0O2sOfnG0ZGHJqa7Mzd8wxNTT4jIy6ZmZqqKp/Dh13i\ncdt2aYzDnj0wOBggFoO6Ok1NjUdRkc/OnT7nzrm8+mqAsjJNWZlPQ4PPzIxDImEXjhMJO6bhYcPM\njEsqZY9cWLtWc/68LWpDQ4qxMYfiYsPFiy4XL7oMDNh4JBhUnD7tsH69T02NIRxWnD4dIJFg9nNN\nEgjYCGf7do/WVo/paRel7BpGTo5h794A993nzV4EQvi+4tZbfW69NcXZswHa2myMopRiyxY7A1+/\n3ufkSUgmFTU1mpIS+72yG8Q8wmGHrCxDdfWVBd91oaHBAAZjbGtqWRlcuit4L4fJNTQYsrI84nF7\n8YjF7B1Gfr6hsPC9/YyJhSWLtotgdCbJ53d1EnQcnt/ZQsESRDiXulaiUTs7DYcVd9/tvafujokJ\n20WTlQW5uXYB0nFs3DI2Zot5V5dDTY2P59nIJDvbcOyYQzLpsmGDRyjkE42GiMftzHfz5hTDww7j\n41Bba2Og/n6HzEyf3FxNMGg3Zk1OKoqLDVNTmrw8jeMYams14bBtySws1CSTDo5jcByF62q0vrSI\nabhwwaWkRDM56bB3b5Bbb/Xp67MXlaIizZEjDi0tmooKGBszZGTYghoKGVpaNMGgZvNmw6FDtr20\ntlZjjKGoCI4etfsDtmzxmZ62bargk5mp8X1FWpq92N5xh23rdF1DOGxz7vZ2l2TSdimlpdmF7u5u\nl5YW+/7RKExPB3njjSDRqO2A2rkzNdslYygogB07fLTm8qKs79tdycb8/+2de3BU5f3/X+ecvSSb\nZHezuWwSQkjIDRLuAgVSWoVqv16+P6qMtHacr7ajnVFk2jp2tO3Y2jqVVgrVamqnxbZ0Ov5THQeZ\n2ulUv1gRsUoIXwjhkoSEBELIPRty2z3nPL8/nmQx3ASKnEie139Jzp79sCTv5zmfy/uRO/lPmkrW\nNCgokLUAIeSQ1+V4G3V3y+6ijAw5t5CSApmZsrW1s1PWMFRL5sTgmgh+KBSiayxhCHR1dRGaJEv/\nWArnv8sy+NrcsGMpnFgMRkbOvLdpyp3x2YLf3y9TBIEA5wwXpaQIvF5YtCjGnj0uDEPmtauq3GRm\nCoJBmc44dMjF0aMGpaUm7e0GgYDg8GGZsnG7DaZNEyxaFKWuzqCz06C7W6OsTJCSInfmLS02mqaR\nmerg314AABgWSURBVCno7dXw+wWapvF//ycXkL4+jWPHZIrD6zVHBc3GtqXtQH+/nD4tKbHx+aC1\nVaO4OEZvr8x3hMOCkRGbzEwxagfhwu+3SEsT7Njhpq1Npp+6uuR9kpNNOjsNFi8eISlJ7pR7e7V4\ncXRoSMPng4YGg/5+g2PHNFJS7NGUlZwfWLJEY8cOF0lJgsxMmd5paZFPM2VlJpYlOHLERSRiEA7L\nllTbhilTLAzDoqzMorlZxzB0vF4NTZNx9PXJGYiREVnUnT5dsH+/Tnu7jmlqpKdbzJtnn3dQ7OMU\nFAhCIRPTlINjY6mhi9HaqlFXp3HggEznTZki6w2BgOxk2rPHoL9fLnCzZ5uO2lIoJNdE8AsLC2lr\na6O9vZ1QKMT777/Pt7/97Wvx1o5h2YItVSd5q66bH6zIZ062s1uchATZStfWJv+SU1Lsc3ZdJ05o\n1NTIXV4gYDN//nhbhLw8uasfHLQJh6NEozIP7PXKIu7p04IlS0w++MBFMCiYOdNi506dG24QJCTI\n1I3XK7tompq0+M7cNPXRQSbZehgICLxewfHjOunpMgU0fbrF7NkW3d1y2Ck72+bECY32doPiYotA\nQOfUKQiFbBIT5UlWY4XDV1/VmT9fo7MT5s61mDYtxrvvehHCJilJxjBnjk1zs4HHI2Ps7NQRQmdg\nQKO11Y3PZzM0JLthkpNtiork00d6OpSXm0SjMt/e06Nz6pRGKARpaQKPR+a3u7vlDtznk0Nb9fUG\n6eli9DMQuN2CYNBk2jSBEDbFxRaDg5CTY1FT46KnRw6ORaMydVZXp+N229TXG0QicmtfV6fh9Zp0\ndMii+IkTOp2dBo2NJmVlFmVlZ3L8PT1ygRIC8vMtMjLkIn+ptLVBTY1OdbVBU5NOKCQYHDTIz7dZ\ntEj29ff3y7gsSy7QWVmqU8dprongG4bBQw89xC9/+ct4W+b1XLDtGIiy/n+b8Lh0Ku8sJTVxYnTh\nzJplEwrJlsWsLDHaRniGxkY9PsjT16fT2WmPy/1qmnxUT0oSdHYaRCIGOTlRCgtNOjoMQiGbnh4b\nvx8MQw4l/dd/mWRk2KSmCpqbDXbvdqHrsHKlbG3cvdtFYiL099sUFQnq66VQ9PZqaJpM0YTDcnRf\n0+TOcWhIo7xcmqElJloUFzM6gSpTVomJNoahMW+eoKZG59gxF14vTJsWIyvLwufTyM+3aW3VaGrS\nSErSqKpyEQrJnHZqqo0QGj6fbE8cGZGpkV27XLhcGv39BkeOaPzP/8TIzIzy+useWlshO1sbLdTq\nZGbKadvjx2WKpq9P59Qpg5QUMz5wlpcnmD5d+uCkpgoiESm6Qkjfnq4ujfZ2nYoKE9MUlJaa5OTY\n9Pcb8QL2+OKqTLkJIdNivb3ys2xsNAiFIBiU9QXTlOm94WEpyD09EAwKEhNl4VjT5JTywADk5AiK\ni+1zrCL6+uT7aJocvDp6VB9dvOXvy9lPCJfyxKD49LlmOfyysjKeffbZa/V2jvFhSx8b323mK+UZ\nfHVuGH0Cedi6XHKXfiHGLwDign+kzc0GNTUuBgbk7t7nk901hYUmJ04YGIbF8LDO4KBMyxw+bHDi\nhJtAQJCebpOQICcza2pctLbK06ZCIZ28PIhELHp63LjdEInYowIk7Qg6OzViMQ2vVxudYLVYsEAj\nI4PR/n3ZnWMYZ3rW33vPxf79Mp+Rk2ORnGzGLZvHBsR27zbo6DDw+00WLozR0uLC45EL4NSpNrGY\nRk6OzeCgFLjBQdl6GA6DyyXnDEIhjYYGjZQUeQ6AxyO45ZYYTU0a+/bZNDe7SEsT8dbU8nKb7Gwx\nemaAtDFoaNDo6NCYMsUmHNbYt89gaAhqa11Eoxrp6XDggCc+5drfD8uXmzQ2yq6YlBSbcFj25h88\nqNPXJ3v6x7yJZFeS7MCRnTSyBrN/v0F+vsy/RyKyjiBtq+HoUUFKiiA7+9zfm337DFpbDZqbdebM\nkdYJqanyuuxsQVeXRXu7TkKCLLgrnEcVba8Spi3YsruVtxt6+OGKAuZkX8SIZIJSWmqxb5/M9efk\nSPE4m64uOWiTm2sRiWgkJen8+9/SIyY1NcbgoM6777qJRnVKSmJUV0sLhdRUi1hMY8YMgWlKUZRF\nSzG6ENkUFsre+2nTbJqbBcuXi9FpXUE4LFMmQ0Ny8Kq4WOPGGy1M0yA5WaarZHeN3I3m5MgnmdRU\nQUqKTX+/7HPPy7NHjdl0Wls1WlsNsrKgs1OKkm3rjIzI1x87pvPRR25mzTJpadFYtszm+HEN27b4\n3OdMpk6FDz+UqR+3G2xb9vX7fPL18+bZlJWB2y0wDFnUnjZNDkfNm2fFjeLGiq2FhYLCQlmIbWyU\nxm8dHS5cLkFGhoVh2Lhc8slG0+SikpMjSEszR4fRZIG0oABuv92iulrQ2iptp93uM/+fiYky3dTR\noWFZctEa8yIaGpJzFmfQLtCiKRfY4WGbhQvl01lenkVysiwmGwbMnWsTjcqisXLynBgowb8KtJ+O\n8sz/NuHzyC6c4ARJ4VwuwSAsX25hmmfv9s8gPVh0RkY0vF6B3y9YtMikocFFT4+LG26waGzUGRgQ\nzJxpc/gwFBXJcf2cHJkiMgzpyDgyIlMnXq9g1SqpMtnZsGJFlMZGnW3bPOi6QNN0srKkqLS3yx1r\nQoJg8WLw+eTO8dQp6OiwCYWkGJaWWgQCMH26zenTMbq7DWbONFm0yKKtTWPfPmmrXFJicvSoi9Wr\nY3z0kYvcXDm9u2+ffM/ycovERLngFBSYLFggi8T5+XLX7PVKoZSdKfKJJDFRDpq98YaLpiadQMBm\nyZIRYjGZt589W6Y4fL7zf8YlJTaBgCwM+3zmqDDLz87rtejpkTYJsgZw/g6YoiLZSTQ0JIvwH3fo\n1DSYM8fi5EmZgvF6BdGoVORAQBaVDx2SPj0JCTZpaecu/ImJ0igvKUlaLKSm2kydKhegj/NJxWLF\ntUUJ/n/Iv5v72LSjmTtnZbBmzsRK4VwJmnZhsQdwuWRa5tQpHZ9P7hTHcu6mqVNVJQWruloehrJi\nhcngoJzeXLDAHs2Ta0SjUkgSE2Xx07LgyBGN4WGNsjI5IJWVJQu6sRjEYoL8fGlZYBiCJUvscYIZ\nDsOCBfKpIyVFxId9li2zyM+3MU2TrCzpp3PsmE5fn0YgILtwRkY02tp0kpI0/H5pgFZXZ4x61chh\nqXDYoqvLoLdXw+22R32ApLAOD0uvoJtussjOlh0x+/bp7N8v/7z6+3XCYVi2TLbBflI+W9NkH312\nts3goI7XK7upWloMvF5ZmM7MFEybZl/0/8rjGfMsOvdnbveZ9F44LMVf1+XhMl6v7EwaHpa2Fedb\nmHJzBUNDFp2dGsXFFsXFtjqM5TOAEvwrxLQFf/yole1He3hyZQGzsj57KZwrweORffFjOV2vVyMv\nz8KyNFwuCyE0MjNtZs+WqYwZM2LMmiUFKz1d+rybppzoPHLEFbfgPXjQIC9POkpqmk5pqcnChTY1\nNXKXmZ+v8YUvRKmtjZGcDLNnn7vrTEvjnN1ocjKUlMjv7d8vC5gHD8rd/eCg/PdUVEQ5ehTy8qTA\nFRRoTJ1qMm2aOdpKKu2bu7vl0FosptPSIhe+5GRYssSKFzDH+LibJMj5Av9lOl6npspTtkwTDhzQ\nCIc1LEvDtm0KCs49NvJKSUqCoqLxn5vsw79wvUfXobTUprT06sSguDYowb8CxlI4SR6Dl+6cQSBh\n8nyM4bA07TpxQqZiSksFliXw+axRszRBNCpbIqXbo05BwZnd39ghHdJ3R8RnAzweETc9k6kS+MIX\nYhQXS6fL8nKLUAg+//kr92Tp6ZGdJWNPCUVFFrouHTHz8w18PtlKWlQk4vlwiaCxUaOz84yIn71L\nP/vBrqTE4sAB2Yfu9dqUlppcLjNmyPRVJAK2rcfz4ELI9lWF4nKZPEp1lfiguY9N7zazenYmd8/J\n/MyncC4XTZOiXVJix0Vv0SJ5CIlpwt69Olu2eLFtnfR0izlz7Pih2x8nMREWLrRobZWLQzAIO3Z4\nRgd4BAsXyrRBUZF50Xz35SDH/gVZWdLzxuuFhASNI0dcgMbp05CbC1lZ54rzlCmC7m5pU+zzCQoK\nLq64U6fCPfdEaW+X3jnZ2Zcfr8dD/GD3Q4fk0xFIS2U1uaq4EpTgXyKmLfjDR63862gPP/5SAeWT\nJIVzIT6+w5VtjnLnXV8P5eVSUEMhaT1wodRDSgpxC4HWVml9YJoaSUmCoSEplFdT2EpLpQ3D1Kmy\nEJuZCY2NcOzYmeMM5YEs5+LxwA03yM4aj+f8RxieTUaGtBu4GsyYYRMOS/vh1NRLe3+F4myU4F8C\np/qjPLO9Eb/XxUt3zsA/iVI4l0tamuz06euzANktcyni5HKNGX5Jgfw02vhcrjHDsDNMmwa9vTEG\nBuRCU1h48Z27k4XJsYNSFIorRSnXJ9A1GGPd1sPcPSeT1bMnXwrncpkxQxp5JSXJlMylpjKKiy1q\nauRAUDgsu1CuBSkp8LnPSe/7hISLdygpFJ91lOB/Amk+N8//vxKy/arn7FKQAnr5U5UZGVBRYRGL\nyXz9tVxX3W4l9IrJgRL8S0CJ/bVhrG9coVB8OqiBZ4VCoZgkKMFXKBSKSYISfIVCoZgkKMFXKBSK\nSYISfIVCoZgkKMFXKBSKSYISfIVCoZgkKMFXKBSKScKEG7wKBoPs2bPH6TAUCoXiM0UwGPzEazQh\nxLUxLVEoFAqFo6iUjkKhUEwSlOArFArFJEEJvkKhUEwSlOArFArFJGHCdekA7Nq1i7/+9a+cOHGC\n9evXM336dMdiqa2tZcuWLViWxcqVK7n11lsdiwXgN7/5DdXV1fj9fjZu3OhoLGN0dnZSWVlJX18f\nfr+fG2+8kRtvvNHpsIhGozz11FPEYjE8Hg9Lly7ljjvucDosAGzb5oknniAUCvHEE084HQ5r164l\nMTERXdcxDIP169c7HRLDw8Ns3ryZ5uZmYrEYDz30ECUlJY7F09raynPPPRf/+tSpU3z1q1/ltttu\ncywmgLfeeot33nmHWCzGzJkzuf/++y98sZiAHD9+XJw4cUI89dRToqGhwbE4LMsSjzzyiDh16pSI\nxWLiscceEy0tLY7FI4QQtbW14ujRo+LRRx91NI6P09PTIxobG4UQQvT19YkHHnjA8c9pjOHhYSGE\nENFoVDz66KPi5MmTDkck2bZtm3j++efFz3/+c6dDEUII8fDDD4v+/n6nwxjHCy+8IN5++20hhBCm\naYqBgQGHIzqDZVniwQcfFB0dHY7G0d/fLx5++GExNDQkLMsSzzzzjKiurr7g9RMypTNlyhRycnKc\nDoP6+nqysrLIzMzE5XJRUVHB7t27HY1p5syZJCUlORrD2QSDQfLz8wHw+/0UFhbS09PjbFCjeEcP\noR0eHsayLFwu5x9qu7q6qK6uZsWKFYgJ1BU9kWIZHBzk0KFDrFixAgDDMPD5fA5HdYb9+/cTDodJ\nT093NA7P6IlBg4ODRKNRRkZGSE5OvuD1zv/2T2C6u7tJS0uLfx0Khaivr3cwoolPW1sbx48fp7i4\n2OlQAJk6efzxx2lpaeH+++93/A8UYMuWLdx7770MDQ05HUocTdP46U9/iqZp3HLLLXzpS19yNJ72\n9nb8fj+VlZUcPXqU4uJivvnNb8YFzml27tzJ5z//eafDwOPx8MADD7B27Vrcbje33norRUVFF7ze\nMcF/+umn6e3tPef799xzDwsXLnQgIsV/yvDwMM899xz33XcfCQkJTocDgK7rbNiwgfb2dtavX09p\naSkFBQWOxVNVVYXf76egoIADBw44FsfZPP3006SmpnL8+HHWr1/PlClTmDlzpmPxWJZFQ0MDd911\nFw8++CC/+93v2LVrF1/84hcdi2kM0zSpqqri3nvvdToUIpEImzdv5le/+hVJSUls2rSJPXv2sGDB\ngvNe75jgP/nkk0699SUTCoXo6uqKf93V1UUoFHIwoomLaZps3LiR5cuXs2jRIqfDOYfMzEzmz59P\nbW2to4J/+PBhqqqqqK6uJhaLMTQ0xIsvvsgjjzziWEwAqampAOTm5rJ48WLq6+sdFfy0tDSSk5Pj\nm7+Kigr+9a9/TQjBr66uZvr06fj9fqdDob6+nuLiYrKysgBYunQptbW1FxT8CZnDnygUFhbS1tZG\ne3s7pmny/vvvq6eP8yCE4Le//S25ubncfvvtTocTJxKJMDAwAEB/fz979+4lLy/P0Zi+/vWv89JL\nL1FZWcl3vvMdysvLHRf7kZGReHopEolQXV3t+OcUDAbJysqirq4O27bZs2cPc+bMcTSmMXbu3ElF\nRYXTYQAwY8YMGhoaOH36NLFYjOrqaubOnXvB6yekl86HH37IH//4RyKRCD6fj4KCAn7wgx84Ektt\nbS1/+tOf4m2ZTrdgPffccxw8eJD+/n4CgQBr1qzhpptucjSmQ4cO8eMf/5i8vDw0TQOksM2bN8/R\nuJqbm6msrMS2bYLBIEuXLo0XAScCtbW1bNu2jccff9zRONrb29mwYQMAKSkpLF26lJtvvtnRmEC2\nQVZWVhKJRMjLy2PdunWOpwqHh4dZu3YtL774IomJiY7GMsY777zD9u3biUajzJ07lzVr1qDr59/L\nT0jBVygUCsXVR6V0FAqFYpKgBF+hUCgmCUrwFQqFYpKgBF+hUCgmCUrwFQqFYpKgBF+hUCgmCUrw\nFdcNa9euZf/+/f/xfQ4ePMjPfvaz+Nf19fU888wz3HfffVfdPK+7u5vvfve72LZ9Ve+rUJwPJfiK\n64qxwa//hNdff33cgN0rr7xCcXExW7ZsueqT1qFQiKlTp/LBBx9c1fsqFOdDCb5C8TGampo4efIk\n8+fPj3+vs7OT0tLSK7qfZVmfeM2Xv/xltm7dekX3VyguB2WPrLjuME2Tv/zlL+zatQuQhlL33ntv\n3At/69atvPnmm/h8Pu6++26ef/55fv3rXxMOh6mpqaGwsDB+r3Xr1tHe3s6zzz6LYRi8/PLL7Nix\ngzfeeIOuri4CgQCrVq2K2wkfOHCAF154gbvuuou//e1vFBcXs3btWrZu3crbb7/NwMAAs2fP5sEH\nH4z7lhcVFdHU1MTg4OCE8nxXXH+oHb7iukIIwWuvvcbhw4fZsGEDGzZsoK6ujtdeew2AvXv3sm3b\nNp588kl+8Ytf8NFHH417fWtra9x5EOCFF14gPT2dJ554gi1btuByuQgEAnz/+9/nD3/4A1/72tfY\nvHkzjY2N8df09fXR0NDAT37yE771rW/x97//nZ07d7Ju3To2bdoEwMsvvxy/3uv1xq2JFYpPEyX4\niuuO9957j5UrV+L3+/H7/axYsYJ3330XgPfff5958+aRm5uLx+Nh5cqV417b1dUVtwq+EAsWLBh3\nClpJSQkHDx6M/9y2be6++26CwSAej4d//vOfrFq1ipKSEoLBIHfeeScffPDBuEJtWloanZ2dV/FT\nUCjORaV0FNcdPT094w6+nz59evzIxd7e3nE2u2d742dkZNDd3X3R+1dXV/Pqq69y8uRJhBCMjIww\na9as+M8DgcC4k7U6Ojr4/e9/P25XbxgGfX198cWlq6trQpzGpbi+UYKvuO5ITU2loaEhLvoNDQ3x\ng2uCwSBNTU3xaz+eigF5nvLhw4cveO9YLMbGjRv5xje+wU033YSu6/zoRz8adx6sYRjjXpOens6a\nNWtYtmzZee85MjJCT08Pubm5l/XvVCguF5XSUVx3VFRUsH37diKRCJFIhO3bt7N8+XIAli1bxt69\ne6murqa9vZ0333xz3GvLy8tpaGi46P0TEhJISUkhGo2yfft26urqLnr9zTffzBtvvMGhQ4ewbZtI\nJDKun7++vp78/HxVsFV86qgdvuK6QtM0Vq9ezdDQEN/73vcA2aWzevVqAObNm8cdd9zBSy+9RGJi\nIl/5yleoqqrC7XYDkJeXx5QpUy54Lqjb7eb+++/n1VdfZfPmzSxevPgTTz+67bbb4qeCdXd3EwgE\nqKioiPf0/+Mf/2DVqlVX82NQKM6LOgBFManZs2cPzz77LK+88kr8lKBDhw7x2muv8cMf/vBTf//u\n7m6efvppNm3adFWGxhSKi6EEXzHp+PDDD5k/fz4tLS38+c9/Jjk5mccee8zpsBSKTx2V0lFMOt56\n6y0qKysxDIOysjIeeOABp0NSKK4JaoevUCgUkwTVpaNQKBSTBCX4CoVCMUlQgq9QKBSTBCX4CoVC\nMUlQgq9QKBSTBCX4CoVCMUn4/2d6zkaaHuNXAAAAAElFTkSuQmCC\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11481e050>"
       ]
      }
     ],
     "prompt_number": 51
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "If we look at this data, we can see that for most values of `fare`, there are some individuals that survived and some that did not. However, notice that the cloud of points is denser on the \"survived\" (y=1) side for larger values of fare than on the \"died\" (y=0) side."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Stochastic model\n",
      "\n",
      "Rather than model the binary outcome explicitly, it makes sense instead to model the *probability* of death or survival in a **stochastic** model. Probabilities are measured on a continuous [0,1] scale, which may be more amenable for prediction using a regression line. We need to consider a different probability model for this exerciese however; let's consider the **Bernoulli** distribution as a generative model for our data:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$f(y|p) = p^{y} (1-p)^{1-y}$$ \n",
      "</div>  "
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "where $y = \\{0,1\\}$ and $p \\in [0,1]$. So, this model predicts whether $y$ is zero or one as a function of the probability $p$. Notice that when $y=1$, the $1-p$ term disappears, and when $y=0$, the $p$ term disappears.\n",
      "\n",
      "So, the model we want to fit should look something like this:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$p_i = \\beta_0 + \\beta_1 x_i + \\epsilon_i$$"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "However, since $p$ is constrained to be between zero and one, it is easy to see where a linear (or polynomial) model might predict values outside of this range. We can modify this model sligtly by using a **link function** to transform the probability to have an unbounded range on a new scale. Specifically, we can use a **logit transformation** as our link function:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$\\text{logit}(p) = \\log\\left[\\frac{p}{1-p}\\right] = x$$"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Here's a plot of $p/(1-p)$"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "logit = lambda p: np.log(p/(1.-p))\n",
      "unit_interval = np.linspace(0,1)\n",
      "plt.plot(unit_interval/(1-unit_interval), unit_interval)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 52,
       "text": [
        "[<matplotlib.lines.Line2D at 0x114849d50>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAECCAYAAAAFL5eMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGLtJREFUeJzt3WtwXOWBp/F/q1t3S2qdtmWBhAzWGGPAE7BlwCNTGCty\nxQRmhpollXizFdck+0EOLihMrU1SEJKwa5Uvs84GS4kzVYuSwJdhhxTMBhhjF6xTGpLoQgXTxqQx\nli3bctvdurbU6tvZD8LCim1du3X68vyqqKhbr7rfOglPvXnP6dM20zRNAQDSSpbVEwAAxB9xB4A0\nRNwBIA0RdwBIQ8QdANIQcQeANOSYakBTU5M6OztVXFysffv2XXPMK6+8oo6ODuXm5mrr1q2qqKiI\n+0QBANM35cr9wQcf1Pe+973r/r6jo0NdXV3au3evtmzZoqamprhOEAAwc1PGfcWKFSosLLzu79va\n2vTAAw9IkpYtW6ZAIKC+vr74zRAAMGNz3nP3+/1yuVzjj10ul/x+/1xfFgAwB3E5ocodDAAguUx5\nQnUqhmHI5/ONP/b5fDIM47rj33//fQUCgbm+LQBkFKfTqdWrV097/JzjXlNTo7ffflu1tbX65JNP\nVFhYKKfTed3xgUBAq1atmuvbAkBG6ejomNH4KeO+f/9+HT9+XAMDA2poaNBjjz2maDQqSaqvr9eq\nVat0/Phxbd++XXl5eWpoaJjdzAEAcWOb71v+Hj58mJU7gLRgmqaiphSOxhSOmgp9/p/hqKlwLKbQ\n5Z+jMYVjYz9n2226r6pkxu/V0dGhurq6aY+f87YMAMyX2cT0izFfPHf578ceX/67z18zdsXvP3/d\nsde5+u/CUVM2m5Rtz1KO3absLJuy7VnKttvGHtuzPn/ui5/LFuTMKu4zRdwBXNeVMZ0Qt+vEdEJs\nkySmY7/Luvo5R5YKr3iN8b+//FpZl//mi5+/eJ0vXsueZbP6v6ZrIu5AEklETCesXK8T0wmvS0zT\nAnFHRrsc01AkNiFo14pe6IpVJTFFsiPuSFmmaSoQiqo/GFFfMKK+kYj6g2P/9I2MPdcfjGhwNEJM\nkXGIO5LGdGN9+fmBYETZdptK8hxy5jtUkjf2jzPPoUULcrRsYYFK8hwqyrWPR5SYIlMQdyRM3GKd\nnz0e67+MeI6DryQAroW4Y9omxPoacf7LgPcHI8qx2/4iyNkqyXcQayDBiDsUCEV1ui8o/3A4brF2\n5jtUkkusAasQ9wwSCEXV1RtUV++ITvUFdbo3qK7eoIZCUd3kzNXCgpyxaOc7VHZFrJ2fP0esgdRB\n3NPQ9SIeCEdV5cxTlTNPS0rztLqiSFXOPJUtyFGWjZOKQDoh7iksEIrqVO+ITvcGdapvLOCniTgA\nEfeUQMQBzBRxTzIx09SfLw2rrXtQx3qGJmynLHHmqerziC9x5mvRgmwiDuCaiHsS8AXCaj87oLbu\nAXWeG5Izz6HVlUX6uzsW6ZZSIg5g5oi7BULRmI71DKmte1Dt3QO6NBzW3TcWaXVlsb5zT4XKFuRY\nPUUAKY64zwPTNNXdP6q27gG1nx3bbrm5NF+rK4v05P1VunVhAR+BBxBXxD1BAqGoOs8Oqu3sgNq7\nBxU1TdVUFGvjMkM71i9RUS6HHkDiUJg4O+kb0evHL+r/nezTbWUFWl1RrEfvWKQqZ55s7JsDmCfE\nPQ7C0Zh+d6pPr7sv6cJgSA+tWKh//k8rZBRkWz01ABmKuM+Bdyik//vxJb11wqclpXn6hzvLtHZJ\nCfvnACxH3GfINE11nhvU6+5L+rBnSBuqDe15aJmqSvOsnhoAjCPu0xSNmfr3P/v1L3+6oOwsmx65\nfZF2rF+i/Gy71VMDgKsQ92n4qGdIB/6jW3mOLD25rkoryws5OQogqRH3SVwMhPTPfzinD3uG9F/v\nqdD6pU6iDiAlEPdrCEVievVDr/71mFcPr1ioJ9etYPsFQEoh7lcwTVOtXf06+PuzWmrk66d/v1w3\nFOVaPS0AmDHi/rnhUFT/8+hpfdYb1BPrbtKqimKrpwQAs0bcJZ3uDeqH75zUneUL1PT3y/kqOQAp\nL+Pj/t7JXr3Y2q1vr7lRX1nusno6ABAXGRv3SMzUL/5wVv/R1a//8ZVqLVtYYPWUACBuMjLufSNh\n/eidz1SQY9eLf7dcxXkZeRgApLGMq1rfSFj/7bce3XNTsf5xzY18wxGAtJRRcb8c9r9ZUqJvrb6B\nDyQBSFsZc1kIYQeQSTIi7oQdQKaZclvG7XarpaVF0WhUdXV12rRp04Tfh0IhHTx4UKdPn1Z+fr4e\nfvhhrVmzJmETnqmRcFTPvPWp1hJ2ABlk0pV7LBZTc3Oztm/frsbGRh05ckTd3d0Txrz77rvKy8vT\n7t279fjjj+uXv/ylTNNM6KSnyzRN/dPR01pq5GsLYQeQQSaNu8fjUXl5ucrKyuRwOFRbW6u2trYJ\nYwoKCjQyMqJIJKKhoSHl5OQkTUT/5UOvzg+E9ETtTUkzJwCYD5Nuy/j9frlcX3xq0zAMeTyeCWPW\nrVun9vZ2ffvb31YsFtMLL7yQmJnOUHv3gP71mFf/62+5nQCAzDPn6r311luy2+06ePCgnnvuOTU2\nNioWi8VjbrN2fnBUu9/r0vcevFllC3IsnQsAWGHSuBuGIZ/PN/7Y5/PJMIwJY9xut9atW6fc3Fwt\nW7ZMpaWlOn/+fGJmOw0x09Sed7v02Moy/fUNRZbNAwCsNGncq6ur1dPTI6/Xq0gkotbWVtXU1EwY\ns3LlSrW3tysWi+nChQsaGhpSRUVFQic9mX87fkkxU3r0zjLL5gAAVpt0z91ut6uhoUF79+4dvxSy\nsrJShw4dkiTV19ertrZW3d3deuaZZ1RcXKwtW7bMx7yvqWdwVL9sP69/euRW2bM4gQogc9nMeb5u\n8fDhw1q1alXcX9c0Te1881PdXbFAX/9SedxfHwCs1NHRobq6ummPT5vLSN7x+DU4GtFjKxdbPRUA\nsFxaxH00EtP/bjuvx//mJrZjAEBpEvfXPvLqtkWFun1xodVTAYCkkPJx7w9G9OqfvPrHNTdYPRUA\nSBopH/dXOnu0vrpUlSV5Vk8FAJJGSsfdNxzWOx6//vNdXB0DAFdK6bj/5phXG6pLVVqQbfVUACCp\npGzcA6GofnvCp39YySdRAeAvpWzcf/vxJdVUFqu8KNfqqQBA0knJuEdipl47dlGPsWoHgGtKybi/\n39Wv8qIc/dXCAqunAgBJKSXj/tsTl/TQbQutngYAJK2Ui/uFwZBOXBzW/bc4rZ4KACStlIv725/4\ntKG6VLl8dR4AXFdKFTJmmvr3P/v0leWuqQcDQAZLqbgf9waU77Cr2sWJVACYTErF/d1P+/RAdanV\n0wCApJcycY/GTB39rFfrl3IiFQCmkjJx/1PPkIyCbO7+CADTkDJxbz3Vr3U3s2oHgOlIibibpqn3\nT/frvqoSq6cCACkhJeJ+qjcoU6ZuMdiSAYDpSIm4X16122x8+TUATEdKxP0PZwZ0701syQDAdCV9\n3IdDUX3qG9HKGxZYPRUASBlJH/cPe4a0fFGB8riXDABMW9IXs+PcoFZVFFk9DQBIKUkf986zg7r7\nRuIOADOR1HHvD0bkHQppGd+4BAAzktRxd18IaEVZoexZXAIJADOR1HH/sGdId5ZzlQwAzFRSx/2j\nC0O6c3Gh1dMAgJSTtHEfjcR00h/U8jLiDgAzlbRx/9Q3oipnLte3A8AsJG05T1wMaPlCVu0AMBuO\nqQa43W61tLQoGo2qrq5OmzZtumqMx+NRS0uLgsGgCgsL9fzzz895Yh9fHObDSwAwS5PGPRaLqbm5\nWc8++6wMw9AzzzyjlStXqrKycnxMIBBQU1OTvv/978vlcmlgYCAuEztxcVjfuGtxXF4LADLNpNsy\nHo9H5eXlKisrk8PhUG1trdra2iaM+d3vfqd7771XLpdLklRcXDznSQVCUfmHw7qJr9QDgFmZdOXu\n9/vHoy1JhmHI4/FMGHP+/HlFo1E999xzCgaDeuSRR3T//ffPaVKf+oa11Mjnw0sAMEtT7rlPJRqN\nyu1269lnn9Xo6KheeOEF3XvvvcrJyZn1a37qG9FSV/5cpwYAGWvSbRnDMOTz+cYf+3w+GYYxYYzL\n5dJdd90lp9OpxYsXa+nSpXK73XOalMc3or8i7gAwa5PGvbq6Wj09PfJ6vYpEImptbVVNTc2EMWvW\nrJHb7dbo6KiGhoZ06tQp3XbbbXOa1Ke+EVUTdwCYtUm3Zex2uxoaGrR3797xSyErKyt16NAhSVJ9\nfb0qKir04IMPaufOnQqHw3rkkUeUlzf7E6GRmKnu/qCWlBJ3AJitKffcb7/9du3evXvCc/X19RMe\nb9y4URs3bozLhM71j2phYQ6fTAWAOUi6gp7qHdHNpVwCCQBzkYRxDxJ3AJijpIt7V19QS4g7AMxJ\n0sX9TF9QVU7iDgBzkVRxj8ZMnRsY1Y3FuVZPBQBSWlLF/cJQSM58h/Kz7VZPBQBSWlLF/UxfUJXc\nLAwA5iyp4n52YFQ3lbAlAwBzlVxx72e/HQDiIanifm5gVBWs3AFgzpIq7me5UgYA4iJp4h6JmfIF\nwlq8YPb3gQcAjEmauHuHQjIKspVtT5opAUDKSpqS9gyOqryIVTsAxEPSxP38YIi4A0CcJE3cewZD\nKi/iZCoAxEPSxN07FOJkKgDESdLE/cJgSIvZlgGAuEiauLNyB4D4SYq4h6Mx9QUjchVkWz0VAEgL\nSRH3S8NhleY7ZM+yWT0VAEgLSRH3i0NhlbElAwBxkxRxvxQIaWEhWzIAEC9JEfeLgbAWFbJyB4B4\nSYq4XwqEtIiVOwDETZLEPSwXcQeAuEmKuPuGw1pYwLYMAMRL0sSda9wBIH4sj3vMNNU3EpFR4LB6\nKgCQNiyPe38wooIcO1/SAQBxZHlR/cNhGfms2gEgnpIg7hEZ7LcDQFxZH/eRsEqJOwDElfVxHw7L\nxbYMAMSV5XHvHYnImc/KHQDiyfK4942M3e4XABA/U8bd7XZrx44devrpp/Xmm29ed5zH49HXv/51\n/f73v5/RBMZW7sQdAOJp0rjHYjE1Nzdr+/btamxs1JEjR9Td3X3NcS+//LLuuusumaY5own0jURU\nyrYMAMTVpHH3eDwqLy9XWVmZHA6Hamtr1dbWdtW4N998U/fdd5+Ki4tnPIG+YETOPFbuABBPk8bd\n7/fL5XKNPzYMQ36//6oxbW1t2rhxoyTJZpv+V+VFY6YGRyMqJu4AEFdzPqH60ksvafPmzbLZbDJN\nc0bbMgOjERXl8t2pABBvky6ZDcOQz+cbf+zz+WQYxoQxJ0+e1P79+yVJg4OD+uCDD+RwOFRTUzPl\nm/cHIyph1Q4AcTdpWaurq9XT0yOv1yvDMNTa2qonnnhiwpgXX3xx/OempiatXr16WmGXxk6mEncA\niL9Jy2q329XQ0KC9e/cqGo2qrq5OlZWVOnTokCSpvr5+Tm8+wModABJiyrLefvvt2r1794Tnrhf1\nrVu3zujNx7Zl7DP6GwDA1Cz9hGr/aJQrZQAgASyNO9syAJAYlse9OJe4A0C8WRv30YiK2XMHgLiz\nNO6Do1EVsXIHgLhLgm0ZVu4AEG+s3AEgDVkW92jM1HA4qsIcVu4AEG+WxT0QGgs7Nw0DgPizLO6D\no1EtYNUOAAlhYdwj7LcDQIJYFvehUFQLuFIGABLC0m2ZIrZlACAhLD2hysodABLD0j13TqgCQGJY\nvHLnhCoAJIKlJ1T5ABMAJIZ1K/dR4g4AiWLtpZDEHQASwvLbDwAA4o+VOwCkIcviPhyKqiDH0jsO\nA0DaYlsGANKQJXGPxEyFY6byHKzcASARLKnr8OerdpuNe7kDQCJYEvdAKKqCbLZkACBRrFm5h6Mq\n5GQqACSMRXGPsXIHgASybM89n7gDQMJYti3DNe4AkDgWnVBlWwYAEsmSuI+EoyrIZuUOAIliUdxj\n7LkDQAJZt+fOyh0AEsa6lTv3lQGAhGHPHQDS0LS+odrtdqulpUXRaFR1dXXatGnThN8fPXpUr7/+\nuiSpsrJSjz76qKqqqq77eiPhmPIcrNwBIFGmXD7HYjE1Nzdr+/btamxs1JEjR9Td3T1hzOLFi/XD\nH/5Qe/bs0Ze+9CX9/Oc/n/Q1R8IxVu4AkEBTFtbj8ai8vFxlZWVyOByqra1VW1vbhDG33nqrCgoK\nJEmrVq2Sz+eb9DWHw3xCFQASacq4+/1+uVyu8ceGYcjv9193/DvvvKOamppJXzMYiXEvdwBIoLgW\n9tixYzp69Ki+8Y1vTDpu7GoZ4g4AiTJlYQ3DmLDN4vP5ZBjGVeO6urp08OBB7dixQ4WFhZO+5kg4\nqnxW7gCQMFMWtrq6Wj09PfJ6vYpEImptbb1q2+XSpUvat2+ftm3bpvLy8infNBiJKY89dwBImCkv\nhbTb7WpoaNDevXvHL4WsrKzUoUOHJEn19fV69dVXNTQ0pF/84hfjf7Nr167rv6bNJkcWX7EHAIli\nM03TnM83PHz4sP77Rw79n//y1/P5tgCQ0jo6OlRXVzft8ZZsfHOlDAAkFnEHgDRkTdz5dCoAJJRF\nK3eulAGARGJbBgDSENsyAJCGWLkDQBqypLK5xB0AEoqVOwCkIeIOAGmIuANAGmLPHQDSEHEHgDRE\n3AEgDbHnDgBpyJLK5tj5og4ASCRW7gCQhqxZuRN3AEgoTqgCQBqyJu524g4AiWTRyp0TqgCQSGzL\nAEAasuhSSOIOAIlkSWXtWWzLAEAisYQGgDRE3AEgDRF3AEhDxB0A0hBxB4A0RNwBIA0RdwBIQ8Qd\nANIQcQeANETcASANEXcASEOOqQa43W61tLQoGo2qrq5OmzZtumrMK6+8oo6ODuXm5mrr1q2qqKhI\nyGQBANMz6co9FoupublZ27dvV2Njo44cOaLu7u4JYzo6OtTV1aW9e/dqy5YtampqSuiEAQBTmzTu\nHo9H5eXlKisrk8PhUG1trdra2iaMaWtr0wMPPCBJWrZsmQKBgPr6+hI3YwDAlCaNu9/vl8vlGn9s\nGIb8fv+kY1wu11VjAADzKy4nVE3TjMfLAADiZNITqoZhyOfzjT/2+XwyDGPGY67kdDrV0dEx2/kC\nQEZyOp0zGj9p3Kurq9XT0yOv1yvDMNTa2qonnnhiwpiamhq9/fbbqq2t1SeffKLCwsJJJ7F69eoZ\nTRAAMHM2c4o9FbfbrZdeemn8UsiHHnpIhw4dkiTV19dLkl5++WV1dHQoLy9PDQ0NqqysTPzMAQDX\nNWXcAQCph0+oAkAaIu4AkIamvP1AvEznNgbpqqmpSZ2dnSouLta+ffskSSMjI/rpT38qr9erxYsX\na9u2bcrLy7N4pol36dIlHThwQP39/SouLtb69eu1fv36jDweoVBIzz//vMLhsHJycrR27Vo9/PDD\nGXksLovFYtq5c6cMw9DOnTsz9lh897vfVX5+vrKysmS327Vr166ZHwtzHkSjUfPxxx83L1y4YIbD\nYfPpp582z5w5Mx9vnRTcbrd58uRJ86mnnhp/7le/+pX5m9/8xjRN03zttdfMX//611ZNb1719vaa\nn332mWmaptnf329+5zvfMc+cOZOxxyMYDJqmaZqhUMh86qmnzHPnzmXssTBN03zjjTfMn/zkJ2Zj\nY6Npmpn778nWrVvNwcHBCc/N9FjMy7bMdG5jkM5WrFihwsLCCc9deduG9evX649//KMVU5t3TqdT\nN998sySpuLhY1dXV8vv9GXs8cnNzJUnBYFCxWEzZ2dkZeyx8Pp86Ozu1YcOG8Q9GZuqxkK7+cOhM\nj8W8bMtc6zYGHo9nPt46afX3949/HqCkpET9/f0Wz2j+9fT0qLu7W7feemvGHo9YLKYdO3bozJkz\n2rJlixYuXJixx6KlpUXf/OY3NTIyMv5cph4Lm82mH/3oR7LZbNq4caO+/OUvz/hYzNueO67PZrNZ\nPYV5FwwGtX//fn3rW9+6at8wk45HVlaW9uzZI6/Xq127dmn58uUTfp8px6K9vV3FxcW65ZZb9NFH\nH11zTKYcC0n68Y9/rNLSUnV3d2vXrl1X3UZ9OsdiXuI+01sUZIKSkhL19fXJ6XSqt7dXJSUlVk9p\n3kQiEe3bt0/333+/1qxZIymzj4cklZWV6e6775bb7c7IY3HixAm1t7ers7NT4XB4/ORhJh4LSSot\nLZUkVVZW6p577pHH45nxsZiXPfcrb2MQiUTU2tqqmpqa+XjrpFVTU6N3331XkvTee++NRy7dmaap\nn/3sZ6qsrNRXv/rV8ecz8XgMDAwoEAhIkgYHB/XBBx+oqqoqI4/F5s2b1dzcrAMHDujJJ5/UHXfc\noW3btmXksRgdHR3fmhoYGFBnZ+es/ncxb59QvdZtDDLF/v37dfz4cQ0ODqqkpERf+9rXdN9992Xk\nJV4ff/yxfvCDH6iqqmr8/1pu3rxZy5cvz7jjcfr0aR04cECxWExOp1Nr167Vhg0bMvbyv8vcbrfe\neOMN7dixIyOPhdfr1Z49eyRJRUVFWrt2rerr62d8LLj9AACkIT6hCgBpiLgDQBoi7gCQhog7AKQh\n4g4AaYi4A0AaIu4AkIaIOwCkof8PmaI/Q4spIzgAAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x11488eed0>"
       ]
      }
     ],
     "prompt_number": 52
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "And here's the logit function:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "plt.plot(logit(unit_interval), unit_interval)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 53,
       "text": [
        "[<matplotlib.lines.Line2D at 0x1148baf90>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAECCAYAAADuGCyPAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8lNWhPvAnCzNDJpkkkz2ZhMSYQMRICEGgASHE2CJQ\nKV6tUD+Vtt7ehmq9P1DZbhQVBSVUWllcflWpqFxtXdCKCmERGheSCesgMNnIPmEmy0yWySzv/QOb\nGglJIJl5Z3m+/+CQQ+YBkseX8573HB9BEAQQEZHb8xU7ABERjQwWOhGRh2ChExF5CBY6EZGHYKET\nEXkIFjoRkYfwH2zAtm3bUFZWBoVCgU2bNvU75q233oJarYZUKsXSpUsRFxc34kGJiGhgg16h5+Tk\nYPXq1Vf8uFqtRnV1NQoLC7FkyRJs27ZtRAMSEdHQDFroaWlpkMvlV/x4SUkJZs6cCQBISUlBR0cH\nWltbRy4hERENybDn0A0GA8LCwnpfh4WFwWAwDPfTEhHRVRqRm6LcPYCISHyD3hQdjFKphF6v732t\n1+uhVCqvOP6rr75CR0fHcN+WiMirhISEYNKkSQOOGXahZ2Vl4bPPPkN2djbOnTsHuVyOkJCQK47v\n6OhAZmbmcN+WiMirqNXqQccMWuibN2/GmTNn0N7ejvz8fNx1112w2WwAgLy8PGRmZuLMmTNYvnw5\nZDIZ8vPzh5+ciIiumo+zt88tKiriFToR0Q+0d1tR22aG0WzFlITgyz6uVquRm5s74OcY9pQLEREN\njcVmR4OxB7Vt3ahtNaOmrRu1bWbUtplhsdmhCpYhLTKg30IfChY6EdEIEgQBrV1W1LSZLxV3mxk1\nrZd+1HX0IEI+CqpgGVTBUoyNkOPW65VQhcigHO0PHx+fYb03C52I6Br0WO2oa//uKrv1UnnXfHe1\n7esDxH9X2qoQKX48NgzxwVLEKKSQ+DluCy0WOhHRFQiCgIudlh9Mj3SjptUMQ5cF0YESqEJkiA+W\n4qaYIMwdFw5ViAzBMnGqlYVORPQdk9mKk40dOFZvxKkmE2pazRg9yrd3iiQ+WIrMuCDEB0sRHSSF\nn+/wpkhGGgudiLxWZ48Np5pMOFZvwvEGI2rbzEiLlGNCTCCWTlMhMXQ05BI/sWMOGQudiLxGt9UO\nzfcKvNLQjbERAZgQE4jfTVVhbESAQ+e4HY2FTkQeq8dqxxldB443mHCswQjtxS4kh43GhJhALMmK\nxQ2Rckj93bfAf4iFTkQewy4IONvcCXWdEccbjDjb3ImEEBkyYgKxOCMa46PkGD3KfaZQrhYLnYjc\nXqWhC/vLW3CwvAVSf19kqYKw8MZIpEcHutUc+HCx0InILTUYzThY3oID5S3o6LEhJzkUa/OScJ1y\n9LAf0HFXLHQichstXRYcrmzFfm0L6trNmJEUgj9kx+OGKDl8vbTEv4+FTkQuraPHhuLqVhwob8EZ\nXSemxCuweGIUMuMU8HexdeBiY6ETkUvSNHXgg9M6fFPTjptiApGXEoaC3CSPvqk5XCx0InIZNruA\nI1Wt+PtJHdq6rVgwPgIP/CgeCpEepXc3/FMiItGZzFbsOavHh5pmRAZK8PMJUZiaEOxyj9a7OhY6\nEYmmod2M9083o0hrQJZKgcdyr0NqRIDYsdwWC52InO5Uowl/P6nDyUYT5owNw4sLxyFCLhE7lttj\noROR05xt7sCrR+vRZOrBwhsj8eisMbzJOYJY6ETkcBdauvF6aT2+1XXi3sxo3JYaxiWHDsBCJyKH\n0Zl68Ia6AV9daMddN0VixaxEj9oMy9Ww0IloxLV2WbDreBP2njdgXlo4XrsrDYFS1o2j8U+YiEZM\nj9WOd0/q8P4pHWYlh+KVO9OgDBgldiyvwUInohFRWtuOLcW1SAyV4YU7xiJGIRU7ktdhoRPRsOg7\nLHjx61p8q+vE73+kwtSEYLEjeS0WOhFdE5tdwG5NM94sa8TcceFYfssYyHjDU1QsdCK6amd0HXjh\nnzWQS/zwx3mpSAiViR2JwEInoqvQY7Xj9dIG7NcacP/Ncci9PtRrD5NwRSx0IhoS7cVOPHuoGvHB\nMrx0ZxqCuQOiy+HfCBENyGYX8M6JJrx3qhn/NYVX5a6MhU5EV1TXZsbGQ9WQ+Ptg64KxiAzkBlqu\njIVORJcRBAGfnNXj9ZIGLM6Iwh3jI3hmpxtgoRNRH10WGzYfqUF1Sxc2zU3hChY3wkWjRNSruqUL\nD354DhI/H/zpp2NZ5m6GV+hEBAAo0hrw4ld1uP/mWPw4NUzsOHQNWOhEXq7HaseLX9WhrN6IDXOS\nkRzGI+Dc1aCFrtFosGPHDthsNuTm5mLOnDl9Pt7T04OXX34ZFy5cwOjRozFv3jxMnjzZYYGJaOTo\nOyxYu68CEXIJtiwYC7mEpwe5swEL3W63Y/v27SgoKIBSqcSqVauQnp4OlUrVO+bgwYOQyWR47rnn\n0NzcjCeffBJZWVlcp0rk4s41d2LtvgrMTwvHPROi+D3rAQYsdK1Wi+joaERGRgIAsrOzUVJS0qfQ\nAwIC0NXVBavVCpPJBIlEwi8MIhd3qKIFW4pr8dD0eExPDBE7Do2QAQvdYDAgLOzfN0eUSiW0Wm2f\nMdOnT0dpaSl+85vfwG63Y926dY5JSkTDJggC3lA34vPzes6Xe6Bh3xT99NNP4efn1zuPvmHDBmzd\nuhW+vlwRSeRKzFY7Cg9Vo8nUgz//dCxPEvJAA7auUqmEXq/vfa3X66FUKvuM0Wg0mD59OqRSKVJS\nUhAaGoqGhgbHpCWia9LebcXKPVr4+ACFc1NY5h5qwEJPTk5GY2MjdDodrFYriouLkZWV1WdMeno6\nSktLYbfb0dTUBJPJhLi4OIeGJqKh05l6sOzj80iLlGNlTiIkPITCYw045eLn54f8/HwUFhb2LltU\nqVTYu3cvACAvLw/Z2dmora3FqlWroFAosGTJEmfkJqIhqDR0Yc1n5Vh4YyT+Iz1S7DjkYD6CIAjO\nfMOioiJkZmY68y2JvNKJBiOeKqrC0mlxyElWDv4LyKWp1Wrk5uYOOIZPihJ5oOLqVjx/uAarcsYg\nM04hdhxyEhY6kYc5UN6CF7+qxdM/TkZqBJclehMWOpEH+fSsHjtKG7BhzvVIUo4WOw45GQudyEN8\neLoZ75xowsa510MVzG1vvRELncgDvHO8Cf/49iI2zUtBdJBU7DgkEhY6kZvbdbwRn58zYNO8FITL\neeanN2OhE7mxd0404bOzBhTOTUGYnE9/ejs+Mkbkpv52UodPvr2IjXOvZ5kTABY6kVt6/5QOH2ma\n8dztnGahf+OUC5Gb2a1pxnunmlE4NwWRgSxz+jcWOpEb2XfegF3Hm7BpXgqigljm1BenXIjcxJGq\nVvz/b+qw/ifJiOHSROoHr9CJ3IC6rh1/OlKDp3+SjDGhfAKU+scrdCIXp2nqwPoD1SjITUJqOPdm\noStjoRO5sKqWLqzdW4FHZibgpphAseOQi2OhE7konakHaz4tx2+nxOHm+GCx45AbYKETuSCj2Yo1\nn5ZjwfgI3JrCwyloaFjoRC7GbLXj8c8rMEkVxGPj6Kqw0IlciM0uYP2BKkQESvDbKXHw8fEROxK5\nERY6kQt56es6dPTY8PAtCfBlmdNV4jp0Ihfx/ikdyuqMeH5+Ckb58VqLrh4LncgF/LOqFe+c0OH5\n+SkIlPLbkq4Nv3KIRPatrgObj9Tg6R8n87QhGhb+u45IRE3GHqzdV4FlMxKQGsGnQGl4WOhEIuns\nseGxz8vxH+lRmDaGDw7R8LHQiUTwr+WJ4yLluPPGCLHjkIdgoROJ4C9H69FtteOBH6m41pxGDAud\nyMk+PatHcXUbCnKTuDyRRhRXuRA50elGE/5ytB5/nJcChYzffjSyeHlA5CQ6Uw+e2l+JR2YmID5E\nJnYc8kAsdCIn6LbasXZvBe68MZJb4ZLDsNCJHEwQBGz6ohpjQmXcPZEcioVO5GD/e6IJjcYe/Pf0\nBK5oIYfiXRkiBzpa044PTjdjyx1jIfXn9RM5Fr/CiBykvt2MjYeqsWZ2EsLlErHjkBcY9Apdo9Fg\nx44dsNlsyM3NxZw5cy4bo9VqsWPHDnR3d0Mul2Pt2rWOyErkNrosNqzdW4F7M6ORHs3Dnck5Bix0\nu92O7du3o6CgAEqlEqtWrUJ6ejpUKlXvmI6ODmzbtg1r1qxBWFgY2tvbHR6ayJUJgoA/fnEBqeEB\nmJ8WLnYc8iIDTrlotVpER0cjMjIS/v7+yM7ORklJSZ8xR44cwZQpUxAWFgYAUCgUjktL5Ab+flKH\neqMZf8iO501QcqoBr9ANBkNvUQOAUqmEVqvtM6ahoQE2mw2PPfYYuru7MX/+fMyYMcMxaYlc3PF6\nI949qcOffzoWEt4EJScb9ioXm80GjUaDgoICmM1mrFu3DlOmTIFEwptA5F2aO3qw/mAVHp05BlFB\n/Pon5xvwEkKpVEKv1/e+1uv1UCqVfcaEhYUhIyMDISEhiIqKwnXXXQeNRuOYtEQuymKzY11RJe64\nIQKTVJx2JHEMWOjJyclobGyETqeD1WpFcXExsrKy+oyZPHkyNBoNzGYzTCYTqqqqMG7cOIeGJnI1\nL31dh5DRo/DzCVFiRyEvNuCUi5+fH/Lz81FYWNi7bFGlUmHv3r0AgLy8PMTFxSEnJwcrV66ExWLB\n/PnzIZNx4yHyHvu1BpTUGrF1wVj48iYoichHEATBmW9YVFSEzMxMZ74lkcNUtXThkX9osWFOMpLD\neCYoOY5arUZubu6AY3gbnugadfbY8OS+SvznzbEsc3IJLHSiayAIAp4/fAHp0YG4LTVs8F9A5AQs\ndKJr8KHmIurazfj9NNXgg4mchIVOdJXO6DrwZlkjCnKT+PAQuRR+NRJdhfZuK57ZX4X/nh6PGIVU\n7DhEfbDQiYbILgh47lA1ZiSFIDsxROw4RJdhoRMN0TsnmmAy2/DrybFiRyHqFwudaAhONJjw/qlm\nrMlNhL8vHx4i18RCJxpES5cFGw5U4eFbxiCCJw+RC2OhEw3AZhew4UA18lKVmBzPTbfItbHQiQbw\n9rFG2OwCfpkZI3YUokGx0ImuoKzeiI+/vYhVsxPhx3lzcgMsdKJ+GDoteO5gNVbMTERYwCix4xAN\nCQud6AdsdgHrD1RhztgwTIwLEjsO0ZCx0Il+4M2yRgDALyZGi5yE6Oqw0Im+p6zOiD1n9ViVw3lz\ncj8sdKLvGDotePbQpUOelZw3JzfEQifCv+fN544L57w5uS0WOhEuzZv7+ACLMzhvTu6LhU5eT13X\njk/OXsTKWZw3J/fGQievpu+04LlDl9abc96c3B0LnbzWpX1aqnD7WM6bk2dgoZPX2vndvDnXm5On\nYKGTVyqtbcenZ/WcNyePwkInr6PvsGDjF9VYMYvrzcmzsNDJq9jsAp45UIV548KREct5c/IsLHTy\nKn8tbYC/rw8Wcb05eSAWOnmNozXt2HvegJU5YzhvTh6JhU5eobmjB4VfVGNlTiJCR3PenDwTC508\nntUu4Jn9VVgwPgI3xQSKHYfIYVjo5PFePVoPucQPP58QJXYUIodioZNH+2dVKw5XtuLRmWPg68N5\nc/JsLHTyWA3tZmw+UoPVsxOhkPmLHYfI4Vjo5JF6rHY8VVSJX0yMRlqkXOw4RE7BQiePtO2rWsQq\npLjjhnCxoxA5DQudPM7n5/Q40WDCshkJ8OG8OXmRQQtdo9FgxYoVePjhh7Fnz54rjtNqtbjnnnvw\n9ddfj2hAoqtRoe/CK9/U47FbkxAg8RM7DpFTDVjodrsd27dvx/Lly7Fhwwbs378ftbW1/Y578803\nkZGRAUEQHBaWaCAdPTY8WVSJ302NQ2LoaLHjEDndgIWu1WoRHR2NyMhI+Pv7Izs7GyUlJZeN27Nn\nD6ZOnQqFQuGwoEQDEQQBhYeqMSkuCLnXK8WOQySKAQvdYDAgLCys97VSqYTBYLhsTElJCW677TYA\n4JwlieKdEzroOy34r6lxYkchEs2wb4q+/vrrWLx4MXx8fCAIAqdcyOnK6ox4/5QOBbcmQeLH+/zk\nvQZ82kKpVEKv1/e+1uv1UCr7/nO2oqICmzdvBgAYjUYcO3YM/v7+yMrKckBcor50ph48e7AKK3MS\nESGXiB2HSFQDFnpycjIaGxuh0+mgVCpRXFyMhx56qM+YLVu29P73tm3bMGnSJJY5OUWP7dLDQwvT\nI3lYBREGKXQ/Pz/k5+ejsLAQNpsNubm5UKlU2Lt3LwAgLy/PKSGJfkgQBGwtrkWEXIK70iPFjkPk\nEnwEJ096FxUVITMz05lvSR7o4zMX8aGmGX/+aSpGj+J6c/J8arUaubm5A47hjkXkdk43mrCjtAGb\n56ewzIm+h0sCyK3oOyxYt78Kj8xMQFywTOw4RC6FhU5u4183QeenhePm+GCx4xC5HBY6uQVBEPDC\nP2ugDPDHPRk8eYioPyx0cgsfnG7G+YudeIQnDxFdEW+KkstT17Vj1/EmbOaKFqIB8QqdXFpdmxkb\nDlRjdU4iYoKkYschcmksdHJZHT02PL63AvdmRmMCnwQlGhQLnVySzS5gXVElMmID8dMbIsSOQ+QW\nWOjkkl786tJBKvlTVSInIXIfLHRyObs1zVDXGbFmdiL8fLmihWiouMqFXEpJbTveLGvE8/NTESjl\nlyfR1eAVOrmMSkMXnj1Yjf/JTUKsgitaiK4WC51cgr7DgoLPy7F0WhzSowPFjkPklljoJLouiw0F\nn5dj7rhw5CTzgGeia8VCJ1HZ7AKe2V+FlPAA3DOBe7QQDQcLnUQjCAK2FNfAahfwYHY8fLhHC9Gw\nsNBJNDvLGnG2uRMFuUnw5/JEomHjujASxT++vYgirQHPz0tFgIQbbhGNBBY6OV1xdSveUDdg09xU\nhAaMEjsOkcdgoZNTnWo04fnDNXj6J8mIC+Zac6KRxDl0chrtxU48ua8SK2eNQWp4gNhxiDwOC52c\n4kJrN/7n83L8ITsek1QKseMQeSQWOjlck7EHq/Zo8eusWExPChE7DpHHYqGTQxk6LVixR4u7borC\nbalhYsch8mgsdHKYtm4rVu7R4tYUJRaM5yEVRI7GQieHaO+2YsUn5zEtIRi/yOAj/UTOwEKnEdfe\nbcWKPVpMVimwJCuGj/QTOQkLnUaU0XxpmmVibBB+PTmWZU7kRCx0GjEmsxWr9pQjPSYQ/3kzy5zI\n2VjoNCLauq149BMtboiS43dT4ljmRCLgo/80bPpOC1bu0WJqQjB+zTlzItGw0GlYdKYerPhEi7wU\nJRZPjBY7DpFXY6HTNatvN2PFJ1osGB+BO9MjxY5D5PVY6HRNKg1dWPNZORZnRGNeWrjYcYgILHS6\nBicajFhXVIX8aXE81JnIhQyp0DUaDXbs2AGbzYbc3FzMmTOnz8cPHz6M3bt3AwBUKhV+9rOfISEh\nYeTTkui+qGzBC/+sxeqcREyMCxI7DhF9z6DLFu12O7Zv347ly5djw4YN2L9/P2pra/uMiYqKwhNP\nPIGNGzdiwoQJeOmllxwWmMTz4elmbP+yDhvmJLPMiVzQoIWu1WoRHR2NyMhI+Pv7Izs7GyUlJX3G\npKamIiDg0oEFmZmZ0Ov1jklLohAEAa8drceHmmb8cX4KksN4OAWRKxp0ysVgMCAs7N/bniqVSmi1\n2iuO37dvH7KyskYmHYnObLWj8Itq6Ew9+OO8FISM5hmgRK5qRJ8UPXXqFA4fPoxFixaN5Kclkeg7\nLFj+8Xn4+fhg4+0scyJXN+gVulKp7DOFotfroVRevrKhuroaL7/8MlavXg25XD6yKcnpzjV3Yu2+\nCsxPC8c9E6L49CeRGxj0Cj05ORmNjY3Q6XSwWq0oLi6+bErl4sWL2LRpEx588EFER/NpQXd3qKIF\naz4rx9JpKizKiGaZE7mJQa/Q/fz8kJ+fj8LCwt5liyqVCnv37gUA5OXl4W9/+xtMJhNeeeWV3l+z\nfv16xyanEWezC9hZ1oi95/XYMCeZNz+J3IyPIAiCM9+wqKgImZmZznxLGoKWLgs2HKiGXRCwOicR\noQGcLydyJWq1Grm5uQOO4ZOihFONJjxzoAp51yvxy0kx8PPlFAuRO2KhezFBEPD3kzq8c0KH5bck\nYEpCsNiRiGgYWOheymS2ovCLC9B3WvDCHWMRFSQROxIRDRNPLPJCx+uNyH//LCLko7BpXgrLnMhD\n8Ardi/RY7Xi1pB6HKlrx/2bE4+Z4TrEQeRIWupfQXuzEswerkRAqw4sLxyFYxr96Ik/D72oPZ7ML\n+N/jTXj/dDN+NzUOs5ND+aAQkYdioXuwqpYuPH/4AmT+vti6YCwiAzlXTuTJWOgeqMtiw1tljfj0\nnAG/zIzG3LRw+PKqnMjjsdA9THF1K7Z/WYcbo+V4aeE4KPnEJ5HXYKF7iEajGdu+rEVtmxnLbknA\nxFieKETkbVjobs5is+NvJ3X4+0kd7kyPxP/kJkHix8cLiLwRC91N2QUBhypasaO0AfHBUrywYCxi\ngqRixyIiEbHQ3YwgCCipNeLVknr4+/rgoex4HthMRABY6G7ldJMJrx5tQGuXBb+aHIvsMcFcU05E\nvVjobqDS0IXXSxqg1Xfil5NicOv1Sm5xS0SXYaG7sAst3dh1vBEltUb8fEIU1sxOhMSfNzyJqH8s\ndBcjCALUdUa8d6oZWn0n5t8Qgdd+FA+5xE/saETk4ljoLqLHasf+8ha8d0oHAFh4YyQevzWJV+RE\nNGQsdJG1dFnw8ZmL+PjMRVwfFoDfTY3DxNgg3uwkoqvGQhdJpaEL759qxpGqVtxyXQg23p6ChFCZ\n2LGIyI2x0J2orduKw5Wt2F9uQH27GfPTIvDa3Tdwb3IiGhFsEgfrstjwZXUbDpS34FRTByargnBX\nehSyVEEYxUf0iWgEsdAdwGKzo7TOiAPlLfimph3jo+TISQ7F6tmJGD2Kq1WIyDFY6CPELgg41diB\nA+UGHK5sRUKIDDnJocifGoeQ0dzClogcj4U+DBabHeeaO1Fc3YYDFS1QSP2Qk6zE1gXjEBXE04GI\nyLlY6FfBZhdw/mInjjUYcbzehDO6DsQqpJisUuDpHycjSTla7IhE5MVY6AOw2QVUGLpwvN6I4w0m\nnGrqQIR8FCbEBGFeWjhW5SRCwRUqROQi2EbfIwgCqlq6cey7Aj/ZaEKwzB8ZMUHIS1Fi2S0JCOV8\nOBG5KK8udEEQUNtm7i3w4w0mBIzyxYSYINySFIIHfxSPMDkLnIjcg1cUuiAIMHRaUdPWjdo2M2q/\n+1Gr74Sfjw8mxAbh5ngFfjslDpGBvJlJRO7Jowq922pHXVs3alovlXbNd+Vd12bGKD9fxAdLoQqW\nQRUixYSYICSGyhAdJOG+KUTkEdyu0O2CgGaTpc/V9r8KvLXbitggKVTBUqhCZJgUF4Q7boiAKljK\nm5dE5PFctuU6emyoazPjQmt37xTJv6625VI/xAfLLhV3sAw3xyugCpYhKlDCk3yIyGuJXuhdFhtO\nNpp6r7Jr28yoaetGR48dcQrppWmSEBmmjQlGfHAU4oKlPOyBiKgfgxa6RqPBjh07YLPZkJubizlz\n5lw25q233oJarYZUKsXSpUsRFxc35ABGsw3vnWpGfLAUiaGjMT0xBPEhMoTLR8GXc9tEREM2YKHb\n7XZs374dBQUFUCqVWLVqFdLT06FSqXrHqNVqVFdXo7CwEOfPn8e2bdvw9NNPDzlAZKAEG+Zcf+2/\nAyIiAgAMuH+rVqtFdHQ0IiMj4e/vj+zsbJSUlPQZU1JSgpkzZwIAUlJS0NHRgdbWVsclJiKifg1Y\n6AaDAWFhYb2vlUolDAbDgGPCwsIuG0NERI43IicsCIIwEp+GiIiGYcA5dKVSCb1e3/tar9dDqVRe\n9ZjvCwkJgVqtvta8REReKSQkZNAxAxZ6cnIyGhsbodPpoFQqUVxcjIceeqjPmKysLHz22WfIzs7G\nuXPnIJfLB3zjSZMmDTE+ERFdDR9hkPkSjUaD119/vXfZ4u233469e/cCAPLy8gAAb775JtRqNWQy\nGfLz8/usgiEiIucYtNCJiMg98Nh5IiIPwUInIvIQou3l8tFHH2Hnzp34y1/+gsDAQLFiXNGuXbtQ\nWloKAEhISMCSJUsQFBQkcqrLvfHGG1Cr1ZBIJEhLS8Pdd9+NgIAAsWNd5ssvv8S7776Luro6rF+/\nHtddd53YkfoYyhYXYtu2bRvKysqgUCiwadMmseNc0cWLF7F161a0tbVBoVBg1qxZmDVrltixLtPT\n04O1a9fCYrFAIpFg2rRpmDdvntix+mW327Fy5UoolUqsXLnyygMFETQ3Nwvr1q0Tli5dKhiNRjEi\nDKqzs7P3v999911h165dIqa5suPHjws2m02w2WzC9u3bhZ07d4odqV+1tbVCXV2dsHbtWqG8vFzs\nOH3YbDbhgQceEJqamgSLxSI8/PDDQk1NjdixLqPRaISKigph2bJlYkcZUEtLi1BZWSkIgiC0tbUJ\n999/v0v+eQqCIHR3dwuCIAg9PT3CsmXLhIaGBpET9e+jjz4S/vSnPwkbNmwYcJwoUy5//etfce+9\n94rx1kM2evRoAIDNZkN3dzdGjXLNo+huuukm+Pr6wtfXFxkZGX2eCXAlcXFxiI2NFTtGv4ayxYUr\nSEtLg1wuFzvGoEJCQpCYmAgAUCgUSE5ORktLi7ihrkAqlQIAuru7YbPZ4O8v+ga0l9Hr9SgrK8Ps\n2bMHfYjT6emPHj0KpVKJMWPGOPutr9rbb7+Nffv2ITY2Fo8//rjYcQZVVFSE2bNnix3D7fS3xYVW\nqxUxkedobGxEbW0tUlJSxI7SL7vdjhUrVqCmpgZLlixBeHi42JEus2PHDtx7773o6uoadKxDCv2p\np57qd4OuRYsW4YMPPsCaNWt6f26w/+M40kA5s7KysGjRIixcuBBvv/02du7ciSVLljg/JAbPCQDv\nvfceZDIZpk2b5ux4vYaSk7xHd3c3Nm/ejPvuuw8ymUzsOP3y9fXFxo0bodPpsH79eowdOxZJSUli\nx+pVWloKhUKBpKQknD59etDxDin0goKCfn/+woUL0Ol0eOSRRwBcujJauXIlnnnmGQQHBzsiyoCu\nlPP7pFK4AxwEAAABxElEQVQpZs+ejRdeeMEJifo3WM6DBw+irKxsSL8fRxL7/a/V1W5fQYOzWq3Y\ntGkTZsyYgcmTJ4sdZ1CRkZGYOHEiNBqNSxX62bNnUVpairKyMlgsFnR1dWHLli144IEH+h3v1CmX\nhIQEvPLKK72vf//73+PZZ591yVUuDQ0NiImJgc1mw5EjR5CQkCB2pH4dO3YMu3fvxhNPPAGJRCJ2\nHLc0lC0uaOgEQcCLL74IlUqFuXPnih3nitrb2+Hn5we5XA6j0Yhjx47hV7/6ldix+li8eDEWL14M\n4NJKrN27d1+xzAGRj6DzceETid566y3U19dDIpFg/PjxuO+++8SO1K9XX30VVqsVTz31FAAgNTUV\n999/v8ipLvfNN9/gtddeQ3t7O9avX4+kpCSsXr1a7FgAAD8/P+Tn56OwsLB32aIrbl+xefNmnDlz\nBkajEfn5+bj77ruRk5MjdqzLnD17FocPH0ZCQgIeffRRAJeKKSMjQ+RkfbW2tmLr1q2w2+0ICQnB\nvHnzkJ6eLnasAQ3WmXz0n4jIQ/BJUSIiD8FCJyLyECx0IiIPwUInIvIQLHQiIg/BQici8hAsdCIi\nD8FCJyLyEP8HxY2pL+qB/hIAAAAASUVORK5CYII=\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114614390>"
       ]
      }
     ],
     "prompt_number": 53
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "The inverse of the logit transformation is:\n",
      "\n",
      "<div style=\"font-size: 150%;\">  \n",
      "$$p = \\frac{1}{1 + \\exp(-x)}$$"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "So, now our model is:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$\\text{logit}(p_i) = \\beta_0 + \\beta_1 x_i + \\epsilon_i$$"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We can fit this model using maximum likelihood. Our likelihood, again based on the Bernoulli model is:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$L(y|p) = \\prod_{i=1}^n p_i^{y_i} (1-p_i)^{1-y_i}$$"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "which, on the log scale is:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$l(y|p) = \\sum_{i=1}^n y_i \\log(p_i) + (1-y_i)\\log(1-p_i)$$"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We can easily implement this in Python, keeping in mind that `fmin` minimizes, rather than maximizes functions:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "invlogit = lambda x: 1. / (1 + np.exp(-x))\n",
      "\n",
      "def logistic_like(theta, x, y):\n",
      "    p = invlogit(theta[0] + theta[1] * x)\n",
      "    # Return negative of log-likelihood\n",
      "    return -np.sum(y * np.log(p) + (1-y) * np.log(1 - p))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 54
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Remove null values from variables"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "x, y = titanic[titanic.fare.notnull()][['fare', 'survived']].values.T"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 70
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "... and fit the model."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "b0,b1 = fmin(logistic_like, [0.5,0], args=(x,y))\n",
      "b0, b1"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "output_type": "stream",
       "stream": "stdout",
       "text": [
        "Optimization terminated successfully.\n",
        "         Current function value: 827.015955\n",
        "         Iterations: 47\n",
        "         Function evaluations: 93\n"
       ]
      },
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 71,
       "text": [
        "(-0.88238984528338194, 0.012452067664164127)"
       ]
      }
     ],
     "prompt_number": 71
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "jitter = np.random.normal(scale=0.01, size=len(x))\n",
      "plot(x, y+jitter, 'r.', alpha=0.3)\n",
      "yticks([0,.25,.5,.75,1])\n",
      "xvals = np.linspace(0, 600)\n",
      "plot(xvals, invlogit(b0+b1*xvals))"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 72,
       "text": [
        "[<matplotlib.lines.Line2D at 0x114b65a10>]"
       ]
      },
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAYEAAAD9CAYAAABazssqAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VPW9//HXOWe27MkkhCBhJyxqQAOCMUWFiBZRb20f\nvX08tIty7f0Vl1uvbd1uaa3LD6vwq0uR1l7vr9TW/nrb23sfWq2KcUHBLSQqSliSsAWyQGayTZJZ\nzvn+/jhhICwhQGAmM5/n45HHZM6cc+b7ncD3/T3f851zNKWUQgghRFLSY10AIYQQsSMhIIQQSUxC\nQAghkpiEgBBCJDEJASGESGISAkIIkcQcsS7AQR988AGBQCDWxRBCiGElOzubWbNmnfL2JwyBZ555\nhurqajIzM1m5cuUx13nhhReoqqrC7XZz6623Mnr0aAA2b97MmjVrME2T8vJyFi1adNz3CQQClJSU\nAJBy000YH32E3taGZRio3FyswkLMefPQ29qIfOlLqIwMzNJSPLfeit7SAoZB8PbbMRcsAMCoqkLz\n+1FOJ2ZpKTid0fc6+Jq+aRNq8mQwTbT2dti/H00prAkT7PebO/eocjqfew69sRGVkkJo6VJITT30\nYVZUoIXDEAxiFRQcc/sjy3Cs8g2FkynLcJGIdRLidFVVVZ3W9icMgfnz57No0SJ++ctfHrcAu3bt\nYsWKFWzfvp1nnnmGRx55BMuyWL16NcuWLcPr9XLfffdRXFxMYWHhCQulUlOhqQmwx6tUIAC7d2PU\n1IBSGC+9hJowgciVV6K/9x56RweEw3i2bcMqLsYsKQHDQE2Zgr5pE8amTZjFxdHGVvP70bdswbF+\nPdrf/obKycHKzUX3+8HhQK+uJvzNb2KsW3dUA60Fg+jNzSjA9dxzmDNngseD1tmJXlODGjUKlZZm\nl2EAmt+PFg6jdXVBVdWQN2jK6UTr6kK53Scsy5nifOEFtMZGcLsJLVnSLzBPxWDqdKbDVYhEc8IQ\nmD59Oi0tLcd9vbKykssuuwyAoqIiAoEAbW1ttLS0UFBQQH5+PgBlZWVUVlYOGAIHG12Vnt5vuQYY\nAH4/AKqrC9XSgnPzZvD7oyc2VGMjWiiE3t2NCoXQ/vM/oasLxo9Ha20Fw8AsK0M5nRg1NWjd3Wht\nbeDz4aipQek6jBiBecklGNu2YY0fj/HHP6J6etB6ejBnzECrq0Pfsyd61KDv3Im+aRNaejqRGTPA\n4yF83XUDNj5GVRX6pk3o9fVoSmFOmACBAOa8eRibNg3YiBlVVegffxwtjzlv3rHfy+NBa2jAmj79\nuOU40/SNGzHa2yESAY+H0C23nNb+zNJSOzBLSo77+Z7pcBUi0Zz2OQGfz0dubm70eW5uLj6f76jl\nXq+X2traAfel+/1QVYW+ffuA66lIxG74+0LhIE0p6OhAtbejpaWhd3ZCby9s3YrhdBIpLwf6GpPn\nnkNrbobGRoxwGOV2g8OBNWYMxpYtmBdcgHI4UCNH4nj1VfT2dozaWpSuo23ZAp2dGDt2QHo6pKVB\nKITjvfeIzJqF+/77UaNGYV5wwTEbac3vt4ehtm4FXbePZKqqIC0N49NP0fx+sKxoaB25raOmBq2v\nPCG3+6h1ALTOTgAcGzZgbN9u98TPcq/YaG5Gb2lBGQbmxImnv79Nm9C6ujDef/+4vXxt587ocJ25\ncOFpv6dIXEN9pDpcDcmJ4SG7/FBDA1pKCnpl5YDTlgac0hQK2UGQnQ2hEKq3FzwerPx8zAsvtNdx\nOrHy8tAbG9F7egD7aIP0dLTWVkLf+hZaQ4O9D9NECwQgEkGFw+iBAPh86KYJStn77wubyGWXoft8\n6Pv2YbW1oVkWpKUd1Rs92FDhcGDl54NlYU2bhllSgvO//gt9/377qOSSS46qnrZzJ1p9PVokcqg+\nfQ4fClGaZoeJpqHy8jAO6xWfrX/85ogR9tHIuHFgGMdc52SGbwbTyzfef98O6+xsO4T7gl+II+kb\nN2J0dNhthttN6LvfRSlFxFKYCkxL2T9KYVlgqqOfW+rQupZSWAosy348+LqlQB32XCkOrdv33FR2\nO2r1PSqI/h59xN6P4uA+7OXnnubncNoh4PV6aW1tjT5vbW3F6/USiUSOuXwgqqgIzbLQQqEB17M4\nFASKvga8jwboLS1YHg9WTw+aYUB6Omr0aPvcwNy59pDK3r12g3JwP5EIqrcX66KLcP7tbxAKoe/a\nRfjqqzGLi9F6elCmaR+FvPGGPcQBaLpu/4FGjLCHhrq7wedD03XMa6455ti1GjMGbetWe+hqwwbM\noiKUy2XXbeRItLY2rIICcBz959Hr6tCamqC3F23cuH5BYFRWRo8i1IgRduPq9aI8nn7lMDZutI8+\nDvvHfyZohgGZmWi6Dtqhv9LhDb/W04Om1KCGbwZ1TuDjj+3hwIYGHH//u4RAHItYimDEIhSx6DXt\nx6B5aFnIVIRN+zF0xGPYtAibyv6xDv5uEbHsZRFLHfG7RcSy39Pse80s+hoRpWHqOhHdiflcNZYC\nQwOHrmHoGrpmPxo6GNqh57qGvVyj3zK9bx09upzoc007tL6m0W89XQMNDV0HnYOv29toWl+7pml9\nj/2Xn+5E/9MOgdmzZ/Paa69RVlbGtm3bSEtLIzs7m4yMDJqammhpacHr9bJhwwa+//3vD7gv5fHY\njdgJjiyObPSP4nDYjaSuowWD4PejNTdHGw7N70e3LHSXy+7h9+1H6+hAffIJ6DqkpuLYvRtt/377\nPEJWFubEiTgqKyEnB6u5GTQNzeVCZWaicnLs925uBocDpevoe/cet54qM9Me/srPRw8GcXz2GWRl\noTIyUIaBSk8/qqcPYLz7LprPhxYMohoacD3//KGhnu5uO6w0Dbq7MefPR9uyxT6iObyHHYlAdzfK\n4cCcMmXAz/p0WOecg9bRgTVyZL8jgcN79MbLL9tHTB4PPY88MuD+BnNOgJ4etEDADh65QO6QUUoR\nNBXdIZNA30932CQQsugOm3SHTHrCFj0Ri56wSXfYoidk0hOx6A1bBE37sTfS9xM2UYDboeMydDwO\nHZehRZ+7+567Dj4a9nKnoUWfpzk1nIaGs2+5Q+97rus4dA2HoeHU7eUHnx9s3B26hmvdO6S+/jrq\n0nmw6CoMlyvawA4nVVVNp7X9CUPgiSeeoKamho6ODpYuXcrXv/51TNMEYOHChZSUlFBTU8MPfvAD\nPB4PS5cuBcAwDJYuXcqKFSuiU0RPODMoEsHKy7MbsQEM9KoCe3w/Pd2eYeRwQGoqKi0t2nAopxMr\nMxN17rnoNTUQCNj7VMo+h5Cejt7VZc8kMk3UhAlgmpCaSuTSS9F278axcaO9blub3ctNTUX19tq9\n/O5uGDUKNXJkv2GYg8zSUoyaGqzmZox9+1AjRmAWFWGWlKC1t6N6elCFhdEjl351Nwy7F+BwoHV3\n9xvqMWfMgKoqrGnTUKmpGJ99Zp9bCAYhHI7WP7x4MY6XX8acPx/zGENOQ8W84IJDQ11z5hz6Gx3W\no7cmTMDYsweVkYHrr38ldPPNx9+h03niE72jRsHOnVheL2rSpCGqSeJQStEbsWjvjdDRa9qPwQgd\nvRHaeyN0Bk26QiadwQhd0d/tRl/TIM1pkOYySHXp9qPTINVlkObU8TgNUp06ualOUpy6/eMw8Djt\nRt7j0KO/ux06Tl2LbYN7xeUY3syBOxVJ4IQhcOedd55wJzfeeCM33njjUcvPPfdcHnvssUEXRu/s\nxEpLs3uN4fAx11EpKRAK2Y1zSord8zv8da8Xq6gIXC601la03l7MvDyCd98dXccsLcX8+9/RDQNr\n/Hgcr7xinz8ArEmTUGPGoBobsUaNInz99eihkD0EMWcOOJ0Y1dVY3d32sIzLBZmZ6I2NhGfNQnV1\noft8RC677PhTRZ1OQkuW4PrVr1DjxtnDN3l54HSiPB6s8eOPO+RhFhejBYNYhkHoppv6vYc5b559\nDqLvuVFTg5o82T5BflgYmfPnQ1bWGf/H3688h73P4T16V22tPWSVmkroG9847fcMX3MNvPwykXnz\nCN1002nvb7gImRat3WF8gTCt3fZPW08Ef08Ef0+Ytt6+x54IuqaR6THIdDvI8jjI9DjIdDvI9BiM\nyfaQ7jLIcBukuw0yXA7S+353GYl1gYHBTDRIBnHzjWHgUMM3eTJ8/nl0uZWSYvfk8/PROjuxxoxB\na2xEy8hA27YNenvtI4DUVKzp0wnddBN6czPa1KkYlZWEv/1tjLo6zLw8e4dOJ9b8+Wg1NVgFBWht\nbaj6eqzzzyf0rW9hzp5t90q/8Q37H8YRQxChJUvA7YbeXozqavT9+4nMmGE35LpOeNQotECAcHn5\n8f9hOZ2YM2ei+/2HAoYTD3n0Pvww7pUrCf7Lv9h1Ony9I3rKZnHxof0fHiiD6VEPheO9z2HLQ0uW\n4PrTn+zPeghOUIduuw3y8oZsf/EgYikOBEK0dIVp6QrR0hWiuSvE/kAIX3eYA4EwPWGLnFQHeaku\nvKlOclMdZKc4mZafSk6Kk+wUB9kpDnJSnHgcidWYnyqZTmzT4uXOYhUVFZQUF9s97RdfxPOjH9mz\nZCZOpPdHP0Lfuxe9rQ3900+JzJ0LDod9BOD343jhBSgoQI0ciVVURHjxYsyLL8b1/POovDxUWpo9\nPfTwbw2vWxdtICOlpYca/ZNpOMJhXL/5DVpXF+Z556FSUtA7O+19DhQAh21vnGiM+3Sc6f2LIdMV\njLCvM0RjR5B9fT+NHSEaO4P4eyJkpzgYme4iv+9nZLqLEWlO8tKceFOdZHkc6MNsLDvW+rUBg/n/\nGqeqqqooP40JEPEVAgd7q+Ewzt/9Dv2LL1ATJhD6p3/C+OADHFVV9kyavDzMCy+MfhPY9dvf2mPM\npokqLgbTtC8rUFJy/EZwqBrIw/cD0uiK47KUorkrxJ62Xna3Bfsee2loDxIyLUZluDkn02U/Zrk5\nJ8NNQaaLEWkuHLo08EMuQTpJiRkCHOM6MYNo0AkETq4nLsQZ0tEboc7XQ31rDzt8PdT7etjTHiTD\nbTA228OYLA9js93279keclIcw25WiogPpxsCcXVO4HBHzQkfaBz74Gvh8ImnEAoxxHzdYbbu72bL\n/gB1rXbD3x02mehNYWJuCueOTGPx9DzGZXtIdR37S3NCxErchsCg5oQf6Wyd8BRJqydssnV/N9v2\nd7Nlfzdb9wfojVhMHZHK1BFpLJqay8TcFArSXdKzF8NC3IaANOgiHnT0RviiOcCmpi42NXWxy9/L\nRG8KU/NTmTchi1vmnMOoDGnwxfAVvyEgRAwEQibV+zr5ZF8nmxq7aO4KMS0/jeKCdL47ZzTTRqTi\nkimWIoFICIikZlqK7Qe6qdzbycaGDup9PZybn8aFozP413ljmZyXKjNzREKTEBBJpysY4cM9HXyw\nu52qvZ14U53MHp3BjRcWUFyQjlt6+iKJSAiIpNAaCLNhVxsbdrVT0xJgxqh0Ssdl889zRzMizRXr\n4gkRMxICImG1dIV4u97P+p1tNLQHuagwk6un5fGTKyaQ4pSpmkKAhIBIMF3BCO/uaKOi1s9Ofw9f\nmpDNt0pGMXNUOs4EuwCaEENBQkAMeyHT4qM9HbxZ66N6XxclozO4/vwRXDQmM+GufCnEUJMQEMNW\nQ3svL9cc4I1aP+NzPCyY7OWueWNJd8s/ayEGS/63iGElbFq8v6udv205wE5fL1dNzeWp66YwKtMd\n66IJMSxJCIhhoaUrxMtbDvDa1lbGZHtYPC2PS8ZnyXCPEKdJQkDEtbrWbv7zsxYqGzoon+zlsauL\nGJvjiXWxhEgYEgIi7iil2Li3kz9/1sKetl6+cv4I/qVsDGlyBU4hhpyEgIgbEUvxTr2fP3/WgqkU\nXy/OZ/6kHJnaKcQZJCEgYs60FG/V+Xm+qpG8NBc3zx7FRWMy5XaJQpwFEgIiZiyleG9HG7+raiLD\nbXDXvLHMPCcj1sUSIqlICIizTinFh3s6WLOxEUPT+N7Fo5k1OkOuyS9EDEgIiLPqs8Yu/v2jvQQj\nFt+ZPYrSsVnS+AsRQxIC4qxo6gzym4/2sW1/N0suGsVlE3NkzF+IOCAhIM6onrDJ//u0mZdrDvCV\n8/O5+7Jxcr1+IeKIhIA4IyyleLPWz398vI+Z56Sz+qvT5Lr9QsQhCQEx5GoPdPPU+j0o4MflEzh3\nZFqsiySEOA4JATFkghGL56saeW2bj3+66ByunOKVcX8h4pyEgBgS1fs6efK9PRTlpfDsV6eRk+qM\ndZGEEIMgISBOS2cwwrMf7qVqbye3XzKG0nFZsS6SEOIkSAiIU7Zuh59n3m9g3vhsnv3adLnAmxDD\nkISAOGmBkMnT6/ew7UA3y8oncN7I9FgXSQhximTCtjgpm5q6+N5ft5DqMnjm+mkSAEIMc3IkIAYl\nYime39jIa9ta+f6XxsrYvxAJQkJAnFBDey+PvrWL7BQHq6+XmT9CJBIJAXFcSile3drKcx/v49uz\nRnHt9Dy52JsQCUZCQBxTb8TiqfV72H6gm5XXFDEuJyXWRRJCnAFyYlgcZW97kDtf3IplKZ66booE\ngBAJTI4ERD8bdrXxi3f38K2SAhn+ESIJSAgIwL7P7283NvJmrY8Hr5zI9Hy56JsQyUBCQODvCbP8\nrZ1oaKz6ylSyU2T2jxDJQkIgydW39vCTtXWUT/Ly7VmjMHQZ/hEimUgIJLEPdrezct1ubi0tZP6k\nnFgXRwgRAycMgc2bN7NmzRpM06S8vJxFixb1e/3FF1/kvffeA8A0Tfbu3ctzzz1HWloat912Gykp\nKei6jmEYLF++/MzUQpwUpRR//Xw/f97ULOP/QiS5AUPAsixWr17NsmXL8Hq93HfffRQXF1NYWBhd\n57rrruO6664DYOPGjbzyyiukpR1qVB544AHS0+X6MvEiYil+uWEPNc0Bnrx2KiMz5JaPQiSzAb8n\nUFtbS0FBAfn5+TgcDsrKyqisrDzu+u+99x5lZWX9limlhqak4rR1BiP826u1HAiE+T/XTpEAEEIM\nHAI+n4/c3Nzoc6/Xi8/nO+a6wWCQTz/9lLlz50aXaZrGgw8+yN13380bb7wxREUWp2JfR5Dvv7iN\n8d4UfrZwolz7XwgBDOGJ4Y0bNzJt2rR+Q0EPPfQQOTk5NDQ0sHz5ckaPHs306dOH6i3FIG0/0M2y\n1+u48YICrj13RKyLI4SIIwMeCXi9XlpbW6PPW1tb8Xq9x1x3/fr1Rw0F5eTYM04KCwuZM2cOtbW1\np1tecZKq93Zy/6t13F46RgJACHGUAUNg0qRJNDU10dLSQiQSYcOGDcyePfuo9bq7u6mpqeGiiy6K\nLgsGg/T09ADQ0dFBdXU1Y8eOHeLii4Gsq/fzv9/ayY8XjOdLE7JjXRwhRBwacDjIMAyWLl3KihUr\nolNECwsLWbt2LQALFy4E4KOPPmLmzJm4XIdONLa3t/P4448DkJGRweLFi5k5c+aZqoc4woub9/PH\nT5p5dNEkJuWmxro4Qog4pak4mb5TUVFBSUlJrIsx7CmleL6qiTfrfCz/8mRGZbpjXSQhxBlUVVVF\neXn5KW8v3xhOIKalWLWhgS37A/zimilyBzAhxAlJCCQI01I89s4ufN1hHl9cJFNAhRCDIiGQACKW\nYvlbO+kJmzx81STcDrlXkBBicCQEhrmQafFIxU4spXjgiom4JACEECdBQmAYC0UsfvbGDtwOjR/P\nn4DTkAAQQpwcaTWGqd6IxbLX60l16dy/QAJACHFq5EhgGOoJm/zk9XpGpDn5waXj5EYwQohTJt3H\nYaY7ZHL/q3UUZLgkAIQQp02OBIaRnrDJj1+vY2y2h+9/aQy6JgEghDg9ciQwTAQjFj9dW885GW4J\nACHEkJEQGAZCpsWDb+wg2+PgX+eNlQAQQgwZCYE4F7EUj7y5E7dD4+7Lx8s5ACHEkJIQiGOmpXj0\nrZ1YluK++eNxSAAIIYaYhECcMi3FinW7CIRMlpXL9wCEEGeGtCxxSCnFU+v3cCAQ5qcL5VIQQogz\nR6aIxhmlFL/5aB87/T08umgyHgkAIcQZJCEQZ/7fp81UNnSwYnERKU65HLQQ4sySEIgjL285wN+3\ntvKLa6aQ6ZE/jRDizJOWJk6sq/fz+6omViwuIjdN7ggmhDg7ZMA5DlQ2dPDLDQ08fNVERmfJPYGF\nEGePhECM1bQE+Pnbu/jJFROYlJsa6+IIIZKMhEAM7fT38MDaen502VjOL0iPdXGEEElIQiBGWrpC\n3P9qHf9r7mjmjMmKdXGEEElKQiAGOnoj3P9qHV87P58Fk72xLo4QIolJCJxloYjFA2vruagwg68V\n58e6OEKIJCchcBaZluLRt3eSl+bku3NHx7o4QgghIXC2KKVY/UEDnUGTH142Tu4JIISIC/JlsbPk\nPz9rYVNjF//n2im45IqgQog4ISFwFryx3cdLNft54toppLnkekBCiPghIXCGVTZ08OyHe3l88WTy\n0lyxLo4QQvQj4xJnUF1rNz9/exfLrpjAuJyUWBdHCCGOIiFwhuwPhFj2ej23lRZSLN8GFkLEKQmB\nMyAQMln2Wh3/cO4ILp+UE+viCCHEcUkIDLGIpXjkzR1Mz0/jH2fIl8GEEPFNQmAIKaV4ev0eNDRu\nv2QMmnwXQAgR5yQEhtCfPmtm24Fu/m3BeAxdAkAIEf9kiugQeavOx99qDvDktVNJle8CCCGGCQmB\nIbCpqYtn3t/LY1dPlltDCiGGFRkOOk1723t5uGIH91w+jgle+S6AEGJ4kRA4DR29Ef7ttXq+M2sU\nswszY10cIYQ4aRICpyhkWjzwRj1l47K4elperIsjhBCnRELgFCil+MW7u8n2OPmnOefEujhCCHHK\nJAROwR+qm2hoD3L35XJfACHE8HbC2UGbN29mzZo1mKZJeXk5ixYt6vf6F198wWOPPcbIkSMBmDt3\nLl/72tcGte1wVFHr47VtPp68bgoeh2SoEGJ4GzAELMti9erVLFu2DK/Xy3333UdxcTGFhYX91jv3\n3HO55557Tmnb4WRTUxe/+sCeCupNlamgQojhb8CubG1tLQUFBeTn5+NwOCgrK6OysvKo9ZRSp7zt\ncLG3PcjDFTu4V6aCCiESyIAh4PP5yM3NjT73er34fL5+62iaxrZt27jrrrtYvnw5DQ0Ng952uOjo\njbDs9Tq+PWsUs2QqqBAigZz2oPaECRNYvXo1jz32GHPmzOHnP//5UJQrboRNiwff2MHFY7NYLFNB\nhRAJZsAQ8Hq9tLa2Rp+3trbi9Xr7rZOSkoLb7cbhcLBgwQICgQBdXV2D2jbeKaX4xXt7yHAb3CJT\nQYUQCWjAEJg0aRJNTU20tLQQiUTYsGEDs2fP7rdOW1tb9JzAxo0bcblcpKenD2rbePfCJ83s9vdy\nz/zxMhVUCJGQBpwdZBgGS5cuZcWKFdFpnoWFhaxduxaAhQsX8sEHH7B27Vp0XWfcuHHcfffdA247\nXLxV5+fvWw/w5HVTZSqoECJhaepYU3tioKKigpKSklgXA4Avmrt4YO0Ofr5oMhNzZSaQECJ+VVVV\nUV5efsrbSxf3CI0dQR56Ywc/umysBIAQIuFJCBymMxjhx6/VccOFBcwZkxXr4gghxBknIdDn4FTQ\n2WMyue7cEbEujhBCnBUSAhyaCprqMvjnOaNjXRwhhDhrJASAP/RNBb338nFyg3ghRFJJ+nsMV9T6\neG1rK09eN4UUp9wgXgiRXJI6BD5rtK8K+vhiuSqoECI5Je1w0J42+wbx980fx/gcmQoqhEhOSRkC\nbT1hlr1ex5KLzqFktFwVVAiRvJIuBIIRiwfW7uCyCTl8eWruiTcQQogEllQhYFqKn7+9k5EZLr4z\ne1SsiyOEEDGXNCGglOLXH+6lM2jyg0vHylVBhRCCJJod9F+f76d6Xye/uKYIl5E02SeEEANKihB4\np97PXz9v4Ylrp5DuTooqCyHEoCR8i7ipqYtfbmjg0UWTyE93xbo4QggRVxJ6XGS3v5eH3tjBvZeP\nY1JuaqyLI4QQcSdhQ8DXHebfXqvjljnnMKtQvgsghBDHkpAhEAiZ/Pi1Oq6a4uXKKfJdACGEOJ6E\nC4GQafGzN+qZOiKVGy8siHVxhBAiriVUCJiW4rG3d5HuMrj9kjFo8l0AIYQYUMKEgFKK1R800N4b\n4d7Lx8t9AYQQYhASZoroHz5p5vOmACuvKcLlSJhsE0KIMyohQuDlLQdYu62VX1w7hTSX3BhGCCEG\na9iHwHs72ni+qpGVi6fIjWGEEOIkDesQ+KyxkyfX7+F/f3kSo7PcsS6OEEIMO8N28Hzr/gAPVezk\n/gXjKcqTbwMLIcSpGJYhsMPXw09er+eueWO58JyMWBdHCCGGrWEXAnvbe7n/1Tq+d3EhpeOyYl0c\nIYQY1oZVCLR0hbj373V8e9Yo5k/KiXVxhBBi2Bs2IeDrDnPPK7Vcf/4IFsm9gYUQYkgMixDo6I1w\n799rKS/y8tXz82NdHCGESBhxHwKBkMn9r9ZxUWEmN14wMtbFEUKIhBLXIdDdd0noKSNSuWXOOXJB\nOCGEGGJxGwLdfUcA43M83H5JoQSAEEKcAXEZAgcDYILXwx1lY9AlAIQQ4oyIuxCQABBCiLMnrq4d\ndDAAJnpTuL2sUAJACCHOsLg6EpAAEEKIsyuuQkACQAghzq64CgEJACGEOLviKgQkAIQQ4uyKqxAQ\nQghxdkkICCFEEpMQEEKIJHbC7wls3ryZNWvWYJom5eXlLFq0qN/r7777Li+++CIAhYWFXH/99Ywd\nOxaA2267jZSUFHRdxzAMli9ffgaqIIQQ4lQNGAKWZbF69WqWLVuG1+vlvvvuo7i4mMLCwug6I0eO\n5Gc/+xmpqam8/fbb/PrXv+aRRx6Jvv7AAw+Qnp5+5moghBDilA04HFRbW0tBQQH5+fk4HA7Kysqo\nrKzst86UKVNITbVv9F5SUkJra2u/15VSQ1xkIYQQQ2XAIwGfz0du7qG7eHm9Xmpra4+7/htvvMHs\n2bOjzzVN48EHH0TTNK688kquuOKKISiyEEKIoTJk1w76/PPPeffdd3n44Yejyx566CFycnJoaGhg\n+fLljB7RgZTfAAAQLUlEQVQ9munTpw/VWwohhDhNAw4Heb3efsM7ra2teL3eo9bbtWsXzz77LPfc\ncw9paWnR5Tk59s3gCwsLmTNnzoBHEUIIIc6+AUNg0qRJNDU10dLSQiQSYcOGDf2GewAOHDjAypUr\nueOOOygoKIguDwaD9PT0ANDR0UF1dXV01pAQQoj4MOBwkGEYLF26lBUrVkSniBYWFrJ27VoAFi5c\nyF/+8he6urr4zW9+E91m+fLltLW1sWLFCgAyMjJYvHgxM2fOPMPVEUIIcTI0FSfTdyoqKigpKYl1\nMYQQYlipqqqivLz8lLeXbwwLIUQSkxAQQogkJiEghBBJTEJACCGSmISAEEIkMQkBIYRIYhICQgiR\nxCQEhBAiiUkICCFEEpMQEEKIJCYhIIQQSUxCQAghkpiEgBBCJDEJASGESGISAkIIkcQkBIQQIolJ\nCAghRBKTEBBCiCQmISCEEElMQkAIIZKYhIAQQiQxCQEhhEhiEgJCCJHEJASEECKJSQgIIUQSkxAQ\nQogkJiEghBBJTEJACCGSmISAEEIkMQkBIYRIYhICQgiRxCQEhBAiiUkICCFEEpMQEEKIJCYhIIQQ\nSUxCQAghkpiEgBBCJDEJASGESGISAkIIkcQcsS7A8RhVVRiVldDdjTljBua8eeB0xrpYQgiRUOIy\nBIyqKhx/+AOOujpUdjYEg5CWhjl3bqyLJoQQCSUuQ0Dz+9G7u9F6elChEMyYgVlSctz1jaoqNL8f\n5XRilpbKEQPymQghBicuzwkY69ahv/YafPop+rZtqEAA16pVGG++CeGwfaRQUYGxbh2Ew2h+P1o4\njO73Y1RVnfr7HrHf4WyoPhMhRGI74ZHA5s2bWbNmDaZpUl5ezqJFi45a54UXXqCqqgq3282tt97K\n6NGjB73tkYyqKowPPkBva0MD8Plw/e53WFdcgbF1K+abb0JmJpphoO3di/PZZ9FDIczzzsOcNQuz\npCTaC9Z27kSNGYPyeI7qDR+rp3yw4dS6uqCqCnPuXJwvvIDW2AhuN6ElSyA1dfCfbgwppxOtqwvl\ndg94FHUmydGIEPFvwBCwLIvVq1ezbNkyvF4v9913H8XFxRQWFkbXqaqqYteuXaxYsYLt27fzzDPP\n8Mgjjwxq22PR/H60jRvtADi4rLUVx5/+hEpLQ9c0yMsDjwc6O+31g0H0t9+G669H27cPra0NzTCg\nqwtt2zZURgZGTQ3mhReidXainE6Mzz9H6+wEywLDwCwrQ9u5E72xEZWSgrlwof3ejY04du6Etja0\n6mqs2bPRd+xAFRRgXnABpKdH93kyDd3pNpAn2t4sLbWDrKQkZo2vUVmJ5vf3+4yFEPFlwBCora2l\noKCA/Px8AMrKyqisrOzXkFdWVnLZZZcBUFRURCAQoK2tjZaWlhNueyTnc8+htbfbjcZhDo5ZaYEA\nAKqrC03XsSzr0GuA489/hpdfBrcbCgogEECzLHC7CZeX4/rb36CgAK2tDfx+NLcbKz8fLrnE3u+Y\nMdDVBeEwrv/7fzGLi3G88grGrl0opxNr7lxcf/0rdHdDbq49ZNTWhpaTA6aJXleHGjt2UA275vej\nb9mC5vdj1NTYRxkn0Vgf66il/4fpBKcTx7p1seuJHzyvo2n9Fp/JIwQ5+hDi5Ax4TsDn85Gbmxt9\n7vV68fl8A66Tm5uLz+cb1LZHcnz4od1oD0BhN/gcFgAHGYDR3Y3R2YleX28fCfT0oPl8GJWV6Lt2\nYbzzDnplJdqBA3Yv1TDQ6+txVFTgeOstaGvD8dFHaH4/jvXr0To6wDTRTBOjuhpcLrRIxD5h7XRC\nXh5aTw8Eg2hdXYMahzeqqtA3bcL49FNQCpWXd9Lj9srphGBwwOGeWJ8XMGfMwEpPt4fp5sw5Zrlc\nf/zjkJ6HMSorMSorcaxfj/HRR6e9PyES3ZDMDlJKDcVu0F95Beuw4DgWbcBX+0QiqLQ00DQ0QPUd\nDdDVZQ8nhUKY+/ejAL23F23iRPTOTrSmJvTmZjRNw1FZSWTGDOjstBvqzk6siRPRu7uxRo7EGj0a\nlZJiN/z79xNZuBCVkYHe2QkNDWgpKRjr1h2zN6r5/ajJk1G1teB2o9LSTnrcfjDDPcc7L3DWesvp\n6ZCSgjriPMrh5dICAfv7IEM0ZKRt345x4ADKMKJHeEKI4xvwSMDr9dLa2hp93traitfrHdQ6g9n2\nSEY4jOP110+qAsfV3g5uN5bDgXXOOZCfDx4PyjSxPB5wODA0DePAAZwvvIDx1lvgcEBODsrlQimF\nduAAavJkSEsDrxe9tRUtFEL19mJedZX93OHAGj8elZeHOW8eVkEBqqgIzbKO2wNXTieYJpEvfxmV\nnw+ahvH++yfXE3Y67SGgI052H96rNktLsQoKiJSX91vvbB0haJ2dqEmT0Ds7+7+Px4PW0IByuaJD\nRoRCQ/KeatQolMtl/80dcTkDWoi4MmAITJo0iaamJlpaWohEImzYsIHZs2f3W2f27NmsW7cOgG3b\ntpGWlkZ2dvagtj2S0jTC3/jGaVbJprvddsOi6+gtLWh1dWAYKE2zh5wiEZRloXQdlZWF1taGMgws\nr5fw17+OOW4c5pVX2j3ZlBTo7UXv6oJIBM2ycP32txiffoo1ciTm+efbwx19DbO+Zw96ZSX69u2Y\nxcVHlS3aOF91FdaYMWhKnVSDfLyprP2GWR59FNdTT2F8/PFR4TKYoaShcLz3OTwcSEk55pDRqTIv\nuACrqAhz7twh2Z8QiW7ArpJhGCxdupQVK1ZEp3kWFhaydu1aABYuXEhJSQk1NTX84Ac/wOPxsHTp\n0gG3HYjyejHPO4/BDk5Y2MNDxxoisjIyICUFzeVCaRrWqFHokYg9a6i3Fy01FSIRrLQ01MSJmJMn\nQ0oKkYsvto8gCgrQOzuJzJxpHzFs347avx/ldKLy8sDlAocDx9q19Kxa1a+nbRUWond1oQoLMTZt\nOuZJ24PLTmUq5/FOCvcbZnG70Xt7we/H9ac/Ebr55uj2Z2vm0PHe5/Byhm+6yf6MBlGWwQxjmfPm\n2d8uj+GsKCGGE00N1YD+aaqoqODSu+4iXFaGY/VqjOOspwBrzBj79/x8HBs39nuN9HQsr5fIvHkY\n+/ah1daicnII//M/4/zLX+wx/O5uInPmoPX0EPrKVzDq6lAjR6LS0g4NnfR9KY1AAMeHH+J86SV7\n3Dori0huLrrDAU4n4auuwho3rl9Db6xbh+73o9zuo4ZijtL3PifTaB13/4fty/XrX6M3NaFSUwne\neWd8fb/hFOoM4KioQAuHIRjEKiiQy4gIgT1Nv7y8/JS3j6tBU5WWRvBf/9WehfPBB4eWc6i3b51z\nDuEbbsD80pdwPfOMPV4fCGC53ZiXXooaMSJ6kpa338bQdcL/8A9owSDdzz6L+6mnCC5diuvVVwl9\n4xuQmop5rEapr7dufPQRKj0dKysLDTuAen/2MzxPP415wQWozMyjevAn1dM+7KhgsI67/8P2FVqy\nxD4C6KtjXDmFOkN8fAFOiEQTV0cCc7duxZo4EXw+Ur73PfvLXB4PlteLFolAVhbW9OkElyzBvPRS\nHC++iPP3v0c7cACzpITgsmUYW7ZEGwjXf/wHKi+vfw//JB3sfeobNqDV12Neey3W+PHRbybLsMPJ\nO+XZSad4BCFEIkusI4GcnGgDHv7qV3F+8gnm+PGErr8ex3vvQU6OfVnp0lJ7/exsIjfe2G9Y5PAe\nZmjJktNuNA72PsnMxLz++kPTOU+xNysG8UW345HPXIghFzdHAhvffJO2+CiKEEIMG9nZ2cyaNeuU\nt4+bEBBCCHH2xeWlpIUQQpwdEgJCCJHEJASEECKJSQgIIUQSi4spoqdyB7J48swzz1BdXU1mZiYr\nV64EoKenh6effpqWlhZGjhzJHXfcgcfjAeCVV17hzTffxDAMbr75ZqZNmxbL4p/QgQMHWLVqFe3t\n7WRmZnL55Zdz+eWXJ0wdQ6EQDzzwAOFwGJfLRWlpKddcc03C1A/sG0Tde++9eL1e7r333oSq2223\n3UZKSgq6rmMYBsuXL0+o+vX29vLv//7v7N69m3A4zK233kphYeHQ1U/FmGma6vbbb1fNzc0qHA6r\nH/7wh2rPnj2xLtZJ2bx5s6qvr1d33XVXdNnzzz+v/ud//kcppdR///d/q9///vdKKaX27NmjfvjD\nH6pwOKyam5vV7bffrkzTjEm5B8vv96sdO3YopZRqb29Xt9xyi9qzZ09C1bG3t1cppVQoFFJ33XWX\n2rdvX0LV76WXXlJPPvmkevTRR5VSifXv89Zbb1WdnZ39liVS/Z5++mlVUVGhlFIqEomoQCAwpPWL\n+XDQ4Xcvczgc0TuQDSfTp08nLS2t37LD77h2+eWX8/HHHwPw8ccfU1ZWhsPhID8/n4KCAmpra896\nmU9GdnY248ePByAzM5NJkybh8/kSqo5utxuwe12WZeF0OhOmfq2trVRXV7NgwYLovT8SpW4HqSNm\nuidK/bq7u9myZQsLFiwA7AtzpqamDmn9Yj4cdKw7kMXzH2Ww2tvbyc7OBiArK4v29nYA/H4/RUVF\n0fUO3oltuGhqaqKhoYEpU6YkVB0ty+Kee+5hz5493HTTTeTl5SVM/dasWcM3v/lNenp6ossSpW4A\nmqbx4IMPomkaV155JVdccUXC1K+lpYXMzExWrVpFfX09RUVF3HzzzUNav5iHQDLQtIHvh3ai1+NF\nb28vTzzxBN/5znei448HDfc66rrO448/TktLC8uXL2fq1Kn9Xh+u9du4cSOZmZlMmDCBL7744pjr\nDNe6HfTQQw+Rk5NDQ0MDy5cvZ/To0f1eH871M02Turo6vvrVr/Ld736XZ599lvfff7/fOqdbv5iH\nwKncgWw4yMrKoq2tjezsbPx+P1lZWcDwrW8kEmHlypXMmzePiy66CEi8OgLk5+dz4YUXsnnz5oSo\n39atW9m4cSPV1dWEw+HoCdNEqNtBOTk5ABQWFjJnzhxqa2sTpn65ubmkp6dHb8hVVlbGO++8Q3Z2\n9pDVL+bnBE7lDmTDwezZs3n77bcBeOedd6IN5+zZs1m/fj2RSISWlhaampqYPHlyDEt6YkopfvWr\nX1FYWMjixYujyxOljh0dHQQCAQA6Ozv55JNPGDt2bELU74YbbmD16tWsWrWKO++8k/POO4877rgj\nIeoGEAwGo8NcHR0dVFdXJ8zfDuzzcQUFBWzfvh3LsqiqqqK4uJhZs2YNWf3i4tpBmzdv5re//W10\niujVV18d6yKdlCeeeIKamho6OzvJysriH//xH7n44osHnMJVUVERncI1ffr0GNdgYFu2bOGnP/0p\nY8eOjR5a3nDDDUydOjUh6rh7925WrVqFZVlkZ2dTWlrKggULTjjNcLjU76DNmzfz0ksvcc899yRM\n3VpaWnj88ccByMjIoLS0lIULFyZM/QD27dvHqlWr6OjoYOzYsdxxxx0opYasfnERAkIIIWIj5sNB\nQgghYkdCQAghkpiEgBBCJDEJASGESGISAkIIkcQkBIQQIolJCAghRBKTEBBCiCT2/wGJhXuq+OX5\nBgAAAABJRU5ErkJggg==\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114b5c510>"
       ]
      }
     ],
     "prompt_number": 72
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "As with our least squares model, we can easily fit logistic regression models in `statsmodels`, in this case using the `GLM` (generalized linear model) class with a binomial error distribution specified."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "logistic = sm.GLM(y, sm.add_constant(x), family=sm.families.Binomial()).fit()\n",
      "logistic.summary()"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "html": [
        "<table class=\"simpletable\">\n",
        "<caption>Generalized Linear Model Regression Results</caption>\n",
        "<tr>\n",
        "  <th>Dep. Variable:</th>          <td>y</td>        <th>  No. Observations:  </th>  <td>  1308</td> \n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Model:</th>                 <td>GLM</td>       <th>  Df Residuals:      </th>  <td>  1306</td> \n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Model Family:</th>       <td>Binomial</td>     <th>  Df Model:          </th>  <td>     1</td> \n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Link Function:</th>        <td>logit</td>      <th>  Scale:             </th>    <td>1.0</td>  \n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Method:</th>               <td>IRLS</td>       <th>  Log-Likelihood:    </th> <td> -827.02</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Date:</th>           <td>Mon, 24 Jun 2013</td> <th>  Deviance:          </th> <td>  1654.0</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>Time:</th>               <td>21:38:17</td>     <th>  Pearson chi2:      </th> <td>1.33e+03</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>No. Iterations:</th>         <td>6</td>        <th>                     </th>     <td> </td>   \n",
        "</tr>\n",
        "</table>\n",
        "<table class=\"simpletable\">\n",
        "<tr>\n",
        "    <td></td>       <th>coef</th>     <th>std err</th>      <th>t</th>      <th>P>|t|</th> <th>[95.0% Conf. Int.]</th> \n",
        "</tr>\n",
        "<tr>\n",
        "  <th>const</th> <td>   -0.8824</td> <td>    0.076</td> <td>  -11.684</td> <td> 0.000</td> <td>   -1.030    -0.734</td>\n",
        "</tr>\n",
        "<tr>\n",
        "  <th>x1</th>    <td>    0.0125</td> <td>    0.002</td> <td>    7.762</td> <td> 0.000</td> <td>    0.009     0.016</td>\n",
        "</tr>\n",
        "</table>"
       ],
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 74,
       "text": [
        "<class 'statsmodels.iolib.summary.Summary'>\n",
        "\"\"\"\n",
        "                 Generalized Linear Model Regression Results                  \n",
        "==============================================================================\n",
        "Dep. Variable:                      y   No. Observations:                 1308\n",
        "Model:                            GLM   Df Residuals:                     1306\n",
        "Model Family:                Binomial   Df Model:                            1\n",
        "Link Function:                  logit   Scale:                             1.0\n",
        "Method:                          IRLS   Log-Likelihood:                -827.02\n",
        "Date:                Mon, 24 Jun 2013   Deviance:                       1654.0\n",
        "Time:                        21:38:17   Pearson chi2:                 1.33e+03\n",
        "No. Iterations:                     6                                         \n",
        "==============================================================================\n",
        "                 coef    std err          t      P>|t|      [95.0% Conf. Int.]\n",
        "------------------------------------------------------------------------------\n",
        "const         -0.8824      0.076    -11.684      0.000        -1.030    -0.734\n",
        "x1             0.0125      0.002      7.762      0.000         0.009     0.016\n",
        "==============================================================================\n",
        "\"\"\""
       ]
      }
     ],
     "prompt_number": 74
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Exercise: multivariate logistic regression\n",
      "\n",
      "Which other variables might be relevant for predicting the probability of surviving the Titanic? Generalize the model likelihood to include 2 or 3 other covariates from the dataset."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 74
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "## Bootstrapping\n",
      "\n",
      "Parametric inference can be **non-robust**:\n",
      "\n",
      "* inaccurate if parametric assumptions are violated\n",
      "* if we rely on asymptotic results, we may not achieve an acceptable level of accuracy\n",
      "\n",
      "Parmetric inference can be **difficult**:\n",
      "\n",
      "* derivation of sampling distribution may not be possible\n",
      "\n",
      "An alternative is to estimate the sampling distribution of a statistic *empirically* without making assumptions about the form of the population.\n",
      "\n",
      "We have seen this already with the kernel density estimate."
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Non-parametric Bootstrap\n",
      "\n",
      "The bootstrap is a resampling method discovered by [Brad Efron](http://www.jstor.org/discover/10.2307/2958830?uid=3739568&uid=2&uid=4&uid=3739256&sid=21102342537691) that allows one to approximate the true sampling distribution of a dataset, and thereby obtain estimates of the mean and variance of the distribution.\n",
      "\n",
      "Bootstrap sample:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$S_1^* = \\{x_{11}^*, x_{12}^*, \\ldots, x_{1n}^*\\}$$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "$S_i^*$ is a sample of size $n$, **with** replacement.\n",
      "\n",
      "In Python, we have already seen the NumPy function `permutation` that can be used in conjunction with Pandas' `take` method to generate a random sample of some data without replacement:"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "np.random.permutation(titanic.name)[:5]"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 75,
       "text": [
        "array([u'Honkanen, Miss. Eliina',\n",
        "       u'Andersen-Jensen, Miss. Carla Christine Nielsine',\n",
        "       u'Geiger, Miss. Amalie', u'Becker, Master. Richard F',\n",
        "       u'Johnson, Mr. Malkolm Joackim'], dtype=object)"
       ]
      }
     ],
     "prompt_number": 75
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Similarly, we can use the `random.randint` method to generate a sample *with* replacement, which we can use when bootstrapping."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "random_ind = np.random.randint(0, len(titanic), 5)\n",
      "titanic.name[random_ind]"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 76,
       "text": [
        "659              Baclini, Miss. Marie Catherine\n",
        "1029                        Moran, Mr. Daniel J\n",
        "1129                  Petterson, Mr. Johan Emil\n",
        "556                 Sharp, Mr. Percival James R\n",
        "1045    Myhrman, Mr. Pehr Fabian Oliver Malkolm\n",
        "Name: name, dtype: object"
       ]
      }
     ],
     "prompt_number": 76
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "We regard S as an \"estimate\" of population P\n",
      "\n",
      "> population : sample :: sample : bootstrap sample\n",
      "\n",
      "The idea is to generate replicate bootstrap samples:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$S^* = \\{S_1^*, S_2^*, \\ldots, S_R^*\\}$$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Compute statistic $t$ (estimate) for each bootstrap sample:\n",
      "\n",
      "<div style=\"font-size: 120%;\">  \n",
      "$$T_i^* = t(S^*)$$\n",
      "</div>"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "n = 10\n",
      "R = 1000\n",
      "# Original sample (n=10)\n",
      "x = np.random.normal(size=n)\n",
      "# 1000 bootstrap samples of size 10\n",
      "s = [x[np.random.randint(0,n,n)].mean() for i in range(R)]\n",
      "_ = hist(s, bins=30)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "display_data",
       "png": "iVBORw0KGgoAAAANSUhEUgAAAXsAAAECCAYAAAAfE3cCAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFNBJREFUeJzt3X9s1PXhx/FXKSuFdneXdqFVm4ZKSwtmw0AbMMT0hs5F\n3BI2EpMVEzRh+0ag2Qy1Y0wHRmf5BlDMecpMEyVzSxbTQDTBZAO5jkUW+wuTrYC2Ml0Fdl/649qD\ntne9fr5/EDoRuF4//fR67fv5+M/ru9eX0M+Lz70/78/7k2ZZliUAwKw2Z7oDAACmHmUPAAag7AHA\nAJQ9ABiAsgcAA1D2AGCAufG++Nprr6mtrU0ul0v79++XJA0ODsrn8ykYDCovL0/V1dXKzMyUJB09\nelQffPCB0tPT9cQTT6isrGzq/w8AAOOKe2b/3e9+Vzt37rzhtYaGBpWWlmrfvn0qKSlRQ0ODJKmr\nq0snTpzQnj17tH37dvn9fo2Ojk5dcgBAwuKW/dKlS5WVlXXDa83NzaqsrJQkeb1eNTU1SZKampq0\nZs0azZ07VwsXLlR+fr46OjqmKDYAYCImPGcfCoXk8XgkSW63W6FQSJLU29ur3NzcsXG5ubnq6elx\nKCYAYDImdYE2LS1tUl8HACRH3Au0t+J2u9XX1yePx6Pe3l653W5JUk5Ojrq7u8fGdXd3Kycn57bv\n8/e//11XrlyxERkAzOXxeLRy5coJf9+Ey768vFyBQEDr169XY2OjKioqxl5/5ZVX9IMf/EA9PT26\ndOmSiouLb/s+V65c0YoVKyYcGABM1traauv70uLtenngwAGdOXNGAwMDcrvdevTRR7V69eq4Sy+P\nHz8+tvRy6dKlt/3Bx48fp+wBYIJaW1v1wAMPTPj74pb9VKLsAWDi7JY9d9ACgAEoewAwAGUPAAag\n7AHAAJQ9ABiAsgcAA1D2AGAAyh4ADEDZA4ABKHsAMABlDwAGoOwBwACUPQAYgLIHAANQ9gBgAMoe\nAAww4ccSAia62D+sYDgSd8zC7Azd4ZqXpETAxFD2QAKC4YiePtoRd8zedcWUPVIW0zgAYADKHgAM\nQNkDgAEoewAwABdogSRKZFWPxMoeOI+yB5IokVU9Eit74DymcQDAAJQ9ABiAsgcAA1D2AGAAyh4A\nDEDZA4ABKHsAMABlDwAGoOwBwACUPQAYgLIHAANQ9gBgANsboR07dkyBQEDRaFRLly7V448/rsHB\nQfl8PgWDQeXl5am6ulqZmZlO5gUA2GDrzD4cDuvw4cN65plnVFdXp4sXL+r06dNqaGhQaWmp9u3b\np5KSEjU0NDidFwBgg62yz8jIkCRdvXpVkUhEw8PDysrKUnNzsyorKyVJXq9XTU1NziUFANhmaxon\nIyNDmzdv1tatW/WNb3xDDz/8sEpKShQKheTxeCRJbrdboVDI0bAAAHtslX1/f7/q6+v18ssvKysr\nSy+99JJaWlpuGJOWluZIQADA5Nmaxuno6FBJSYny8/P1zW9+U/fdd5/OnDkjt9utvr4+SVJvb6/c\nbrejYQEA9tgq+7KyMnV2diocDisajaqtrU3Lly9XeXm5AoGAJKmxsVEVFRVOZgUA2GRrGmfBggXa\nsGGD9u7dq0gkouXLl+uee+5RcXGxfD6fampqxpZeAgCmn+119l6vV16v94bX5s+fr9ra2slmAgA4\njDtoAcAAlD0AGICyBwADUPYAYADbF2gB3Ch9jvTxhYG4YyKx0SSlAW5E2QMOCQ3F9Nyx83HH7Hqw\nKElpgBsxjQMABqDsAcAAlD0AGICyBwADUPYAYADKHgAMQNkDgAEoewAwAGUPAAbgDlrMWhf7hxUM\nR+KOyc5IVzgSG/e92OYAMx1lj1krGI7o6aMdccfserBo3C0Oro8DZjKmcQDAAJQ9ABiAsgcAA1D2\nAGAAyh4ADEDZA4ABKHsAMADr7JFyErkZamF2hu5wzUtSImDmo+yRchK5GWrvumLKHpgAyh4zUvoc\n6eMLA3HHzPYtDvgEhImg7DEjhYZi425zMNu3OOATECaCC7QAYADKHgAMQNkDgAEoewAwAGUPAAag\n7AHAAJQ9ABjA9jr7oaEh1dfX64svvlA0GtWWLVtUUFAgn8+nYDCovLw8VVdXKzMz08m8AAAbbJd9\nfX29li1bpm3btikWi2l4eFgNDQ0qLS1VbW2tjhw5ooaGBm3cuNHJvAAAG2xN41y9elVnz57V2rVr\nJUnp6elasGCBmpubVVlZKUnyer1qampyLikAwDZbZ/bBYFAul0t+v1+fffaZSkpK9MQTTygUCsnj\n8UiS3G63QqGQo2EBAPbYOrOPxWLq7OzUqlWrVFdXp5GREZ06deqGMWlpaY4EBABMnq2yz83NVXZ2\ntsrLy5WRkaE1a9bo9OnT8ng86uvrkyT19vbK7XY7GhYAYI+tsvd4PMrPz9enn36q0dFRtba26tvf\n/rZWrlypQCAgSWpsbFRFRYWTWQEANtlejbN161b5/X719/ersLBQGzdulGVZ8vl8qqmpGVt6CQCY\nfrbL/s4779Rvf/vbm16vra2dVCAAgPO4gxYADEDZA4ABKHsAMABlDwAGoOwBwACUPQAYgLIHAAPY\nXmcPYOqkz5E+vjAQd0wkNpqkNJgNKHsgBYWGYnru2Pm4Y3Y9WJSkNJgNmMYBAANQ9gBgAMoeAAxA\n2QOAASh7ADAAZQ8ABqDsAcAAlD0AGICyBwADcActMIslsu2CJC3MztAdrnlJSITpQtkDs1gi2y5I\n0t51xZT9LMc0DgAYgLIHAANQ9gBgAMoeAAxA2QOAASh7ADAAZQ8ABqDsAcAAlD0AGIA7aJE0F/uH\nFQxHxh0XiY0mIQ1gFsoeSRMMR/T00Y5xx+16sCgJaQCzMI0DAAag7AHAAJQ9ABiAsgcAA1D2AGCA\nSa3GGR0d1Y4dO5STk6MdO3ZocHBQPp9PwWBQeXl5qq6uVmZmplNZAQA2TerM/ujRoyooKFBaWpok\nqaGhQaWlpdq3b59KSkrU0NDgSEgAwOTYLvvu7m61tbVp7dq1sixLktTc3KzKykpJktfrVVNTkzMp\nAQCTYrvsDx06pMcee0xz5vz3LUKhkDwejyTJ7XYrFApNPiEAYNJslX1LS4tcLpeKiorGzuq/7vrU\nDgBg+tm6QHvu3Dm1tLSora1N0Wh07MKs2+1WX1+fPB6Pent75Xa7nc4LALDBVtlXVVWpqqpKktTe\n3q53331X1dXVevvttxUIBLR+/Xo1NjaqoqLC0bAAAHsc2Qjt+pTNhg0b5PP5VFNTM7b0EsDskMiu\npQuzM3SHa16SEmEiJl32y5Yt07JlyyRJ8+fPV21t7aRDAUg9iexaunddMWWforiDFgAMQNkDgAF4\neAkckch8Lk+gAqYPZQ9HJDKfyxOogOnDNA4AGICyBwADUPYAYADKHgAMQNkDgAFYjQNA6XOkjy8M\nxB3D0tmZjbIHoNBQTM8dOx93DEtnZzamcQDAAJQ9ABiAaRyMi60QgJmPsse42AoBmPmYxgEAA1D2\nAGAAyh4ADEDZA4ABKHsAMABlDwAGoOwBwACUPQAYgLIHAANQ9gBgAMoeAAxA2QOAASh7ADAAZQ8A\nBqDsAcAAlD0AGICHlwBwTPoc6eMLA3HHLMzO0B2ueUlKhOsoewCOCQ3F9Nyx83HH7F1XTNlPA6Zx\nAMAAlD0AGICyBwAD2Jqzv3z5svx+v0KhkFwul7xer7xerwYHB+Xz+RQMBpWXl6fq6mplZmY6nRkA\nMEG2yn7u3LnatGmTFi1apP7+fm3fvl3FxcUKBAIqLS1VbW2tjhw5ooaGBm3cuNHpzACACbI1jePx\neLRo0SJJksvl0uLFi9XT06Pm5mZVVlZKkrxer5qamhwLCgCwb9Jz9pcuXVJXV5eWLFmiUCgkj8cj\nSXK73QqFQpMOCACYvEmV/dDQkA4cOKBNmzbdNDeflpY2qWAAAOfYLvuRkRHt379f999/vyoqKiRd\nO5vv6+uTJPX29srtdjuTEgAwKbbK3rIsHTx4UAUFBXrkkUfGXi8vL1cgEJAkNTY2jv0jAACYXrZW\n45w7d04nT55UYWGhamtrJUlVVVXasGGDfD6fampqxpZeAgCmn62yLysr05/+9Kdbfu16+QMAUgcb\noRnsYv+wguHIuOMisdEkpAEwlSh7gwXDET19tGPccbseLEpCGgBTib1xAMAAlD0AGIBpnFkqkfl4\n5uIxHRJ5mpXEE62cRtnPUonMxzMXj+mQyNOsJJ5o5TSmcQDAAJQ9ABiAsgcAA1D2AGAAyh4ADEDZ\nA4ABKHsAMABlDwAGoOwBwACUPQAYgLIHAANQ9gBgAMoeAAxA2QOAAdjieAZir3oAE0XZz0DsVQ9g\nopjGAQADUPYAYACmcZIkkXl2nrkJ/Fciz6rlmEkcZZ8kicyz88xN4L8SeVYtx0ziKPsUksiZjMRK\nGwATR9mnkETOZCRW2gCYOC7QAoABOLMHMGNxETdxlD2AGYuLuIljGgcADEDZA4ABKHsAMABlDwAG\ncPwCbXt7uw4dOqRYLKYHHnhADz/8sNM/AgAwQY6e2Y+Ojur111/X9u3btWfPHn3wwQfq6upy8kcA\nAGxw9My+o6ND+fn5WrhwoSRpzZo1am5uVkFBgZM/xhEXQsMKDY/EHePJnMuSLQCzgqNl39PTo9zc\n3LH/zsnJUUdH/M2/psuZ/7ui/w18HnfM8w/dnVDZ8+QoYOZL5DjOzkhXOBKLOyZVb+Iy9qaqopz5\n+p9Vd8Udk5edkdB78eQoYOZL9DieqTdxpVmWZTn1Zp988oneeecd/frXv5YkHT58WGlpaVq/fv1N\nY1taWtTX1+fUjwYAI3g8Hq1cuXLC3+fomf3ixYt16dIlBYNB5eTk6MMPP9TPf/7zW461ExYAYI+j\nZ/bStaWXb7311tjSy3Xr1jn59gAAGxwvewBA6uEOWgAwAGUPAAZI2tLLU6dO6Z133tGXX36puro6\n3X333bccN93bLQwODsrn8ykYDCovL0/V1dXKzMy8adyxY8cUCAQUjUa1dOlSPf744ymZc2hoSPX1\n9friiy8UjUb15JNPasmSJSmXU7p2B/aOHTuUk5OjHTt2JC1jojkvX74sv9+vUCgkl8slr9crr9c7\n5dkSOSb++Mc/qrW1VfPmzdOWLVt0113xlxVPR86TJ0/q3XfflSQVFBToRz/6kQoLC1Mu53UdHR16\n5pln9NRTT2nVqlVJTplYzo6ODh06dEhDQ0PKysrS7t27b/+GVpJ0dXVZX375pbV7926rs7PzlmNi\nsZi1bds26z//+Y8VjUatmpoa69///neyIlqWZVm///3vrSNHjliWZVmHDx+23n777ZvGDAwMWFu2\nbLEGBwetWCxmvfjii1ZbW1vK5bQsy/L5fNbx48cty7KskZER68qVK0nLaFmJ57Qsy3rvvfesV155\nxdqzZ0+y4o1JJGdvb691/vx5y7IsKxQKWZs3b57y389EjomWlhbrxRdftCzLsj755BNr586dU5rJ\nbs5z586N/f6dOHEiZXNeH7d7926rrq7OOnXqVErmDIfD1lNPPWVdvnzZsqxrv5PxJG0a56677tKd\nd94Zd8xXt1uYO3fu2HYLydTc3KzKykpJktfrVVNT001jMjKu3Wx19epVRSIRDQ8PKzs7O+VyXr16\nVWfPntXatWslSenp6VqwYEHK5ZSk7u5utbW1ae3atbKmYc1AIjk9Ho8WLVokSXK5XFq8eLF6e3un\nNFcix8RXs5eUlOjKlStJv4clkZxLliwZ+/1bsWKFuru7k5ox0ZyS9P7772v16tVyuVxJzygllvNv\nf/ubVq1aNbZrwXhZU2rO/lbbLfT09CQ1QygUksfjkSS53W6FQqGbxmRkZGjz5s3aunWrfvazn6m0\ntFTFxcUplzMYDMrlcsnv92v79u06ePCgIpH4t4NPR05JOnTokB577DHNmTM9v5KJ5rzu0qVL6urq\nUklJyZTmSuSY+PqY3NzcpB83Ez12jx07pvLy8mREu0Gif57Nzc166KGHJElpaWlJzXg9w3g5L168\nqHA4rN/85jeqra3VyZMn476no3P2zz///C3PKH7yk59My1/s7cTL+VW3+0vu7+9XfX29Xn75ZWVl\nZemll15Sa2urVqxYkVI5Y7GYOjs79eMf/1g//elP9cYbb+jUqVNjZ4GpkrOlpUUul0tFRUX65z//\n6Wi2r5pszuuGhoZ04MABbdq06bbXH5JtOj4N2fWPf/xDJ0+e1AsvvDDdUW7prbfeUlVVldLS0mRZ\nVsr+2cZiMbW3t+vZZ5/V8PCwXnjhBa1atWps5uHrHC37Z599dlLfn5OTc8NHu+7ubuXk5Ew21k3i\n5XS73err65PH41Fvb6/cbvdNYzo6OlRSUqL8/HxJ0n333af29nbHy36yOXNzc5WdnT32D+2aNWvU\n2NjoeNlPNue5c+fU0tKitrY2RaNRDQ4O6tVXX9W2bdtSKqckjYyMaP/+/br//vtVUVHhaL5bSeSY\nSNZxE0+iGT7//HO98cYb2rlzp7KyspIZUVJiOT/77DMdOHBAkjQwMKDTp09r7ty5ST1hTSRnbm6u\n7r333rFPpHfffbfa29t177333vI9U2oa56vbLYyMjOjDDz9M+ieC8vJyBQIBSVJjY+MtD+iysjJ1\ndnYqHA4rGo2qra1Ny5cvT7mcHo9H+fn5+vTTTzU6OqrW1lZ95zvfSbmcVVVVev311+X3+/WLX/xC\n99xzj+NF70ROy7J08OBBFRQU6JFHHklKrkSOifLycv31r3+VdG1/qqysrLECSJZEcl6+fFn79+9X\ndXX12IlSsiWS89VXX5Xf75ff79fq1au1efPmpPdQIjkrKirU3t6u4eFhhcNh/etf/1JZWdlt3zNp\nd9B+9NFHevPNN9Xf368FCxaoqKhIO3fuVE9Pj373u9/pV7/6laTp327hdkvwvp4zEAjoxIkTikQi\nWr58uR599NGkzjcnmvPChQvy+/3q7+9XYWFh3KWP05nzuvb2dr333nv65S9/mbSMieY8e/asdu3a\npcLCwrGpnqqqqtueSTnlVsfEX/7yF0nS9773PUnSH/7wB7W2tiozM1NPPvnktDxDYrycBw8e1Ecf\nfaRvfetbkq4tGKirq0u5nF/12muvaeXKldO29HK8nH/+85/1/vvvKxqN6oc//KG+//3v3/b92C4B\nAAyQUtM4AICpQdkDgAEoewAwAGUPAAag7AHAAJQ9ABiAsgcAA1D2AGCA/wdPPCdgnZxMZQAAAABJ\nRU5ErkJggg==\n",
       "text": [
        "<matplotlib.figure.Figure at 0x114b4d550>"
       ]
      }
     ],
     "prompt_number": 77
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Bootstrap Estimates\n",
      "\n",
      "From our bootstrapped samples, we can extract *estimates* of the expectation and its variance:\n",
      "\n",
      "$$\\bar{T}^* = \\hat{E}(T^*) = \\frac{\\sum_i T_i^*}{R}$$\n",
      "\n",
      "$$\\hat{\\text{Var}}(T^*) = \\frac{\\sum_i (T_i^* - \\bar{T}^*)^2}{R-1}$$\n"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "boot_mean = np.sum(s)/R\n",
      "boot_mean"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 78,
       "text": [
        "-0.15933323217972145"
       ]
      }
     ],
     "prompt_number": 78
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "boot_var = ((np.array(s) - boot_mean) ** 2).sum() / (R-1)\n",
      "boot_var"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 79,
       "text": [
        "0.044061864233632578"
       ]
      }
     ],
     "prompt_number": 79
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "Since we have estimated the expectation of the bootstrapped statistics, we can estimate the **bias** of T:\n",
      "\n",
      "$$\\hat{B}^* = \\bar{T}^* - T$$\n"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "boot_mean - np.mean(x)"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 80,
       "text": [
        "-0.00067633809837364112"
       ]
      }
     ],
     "prompt_number": 80
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Bootstrap error\n",
      "\n",
      "There are two sources of error in bootstrap estimates:\n",
      "\n",
      "1. **Sampling error** from the selection of $S$.\n",
      "2. **Bootstrap error** from failing to enumerate all possible bootstrap samples.\n",
      "\n",
      "For the sake of accuracy, it is prudent to choose at least R=1000"
     ]
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Bootstrap Percentile Intervals\n",
      "\n",
      "An attractive feature of bootstrap statistics is the ease with which you can obtain an estimate of *uncertainty* for a given statistic. We simply use the empirical quantiles of the bootstrapped statistics to obtain percentiles corresponding to a confidence interval of interest.\n",
      "\n",
      "This employs the *ordered* bootstrap replicates:\n",
      "\n",
      "$$T_{(1)}^*, T_{(2)}^*, \\ldots, T_{(R)}^*$$\n",
      "\n",
      "Simply extract the $100(\\alpha/2)$ and $100(1-\\alpha/2)$ percentiles:\n",
      "\n",
      "$$T_{[(R+1)\\alpha/2]}^* \\lt \\theta \\lt T_{[(R+1)(1-\\alpha/2)]}^*$$"
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "s_sorted = np.sort(s)\n",
      "s_sorted[:10]"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 81,
       "text": [
        "array([-0.84783322, -0.729463  , -0.70891663, -0.70277966, -0.70118232,\n",
        "       -0.69761647, -0.68948506, -0.68308688, -0.67812924, -0.66995858])"
       ]
      }
     ],
     "prompt_number": 81
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "s_sorted[-10:]"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 82,
       "text": [
        "array([ 0.28296582,  0.29250432,  0.30557177,  0.31954429,  0.32994401,\n",
        "        0.33001289,  0.33514567,  0.34787314,  0.41920685,  0.48525756])"
       ]
      }
     ],
     "prompt_number": 82
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [
      "alpha = 0.05\n",
      "s_sorted[[(R+1)*alpha/2, (R+1)*(1-alpha/2)]]"
     ],
     "language": "python",
     "metadata": {},
     "outputs": [
      {
       "metadata": {},
       "output_type": "pyout",
       "prompt_number": 83,
       "text": [
        "array([-0.55827684,  0.22701275])"
       ]
      }
     ],
     "prompt_number": 83
    },
    {
     "cell_type": "markdown",
     "metadata": {},
     "source": [
      "### Exercise: Cervical dystonia bootstrap estimates\n",
      "\n",
      "Use bootstrapping to estimate the mean of one of the treatment groups, and calculate percentile intervals for the mean."
     ]
    },
    {
     "cell_type": "code",
     "collapsed": false,
     "input": [],
     "language": "python",
     "metadata": {},
     "outputs": [],
     "prompt_number": 83
    }
   ],
   "metadata": {}
  }
 ]
}