Gradient Descent Intutive understanding

gradient-descent-intutive-understanding.ipynb

{
  "nbformat": 4,
  "nbformat_minor": 0,
  "metadata": {
    "colab": {
      "name": "Gradient Descent Intutive understanding",
      "version": "0.3.2",
      "provenance": [],
      "collapsed_sections": [],
      "include_colab_link": true
    },
    "kernelspec": {
      "name": "python3",
      "display_name": "Python 3"
    }
  },
  "cells": [
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "view-in-github",
        "colab_type": "text"
      },
      "source": [
        "<a href=\"https://colab.research.google.com/gist/machinelearning147/c09f95db9a49f6fd21bcd27fa5e09769/gradient-descent-intutive-understanding.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>"
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "eJbVEriNZqr2",
        "colab_type": "text"
      },
      "source": [
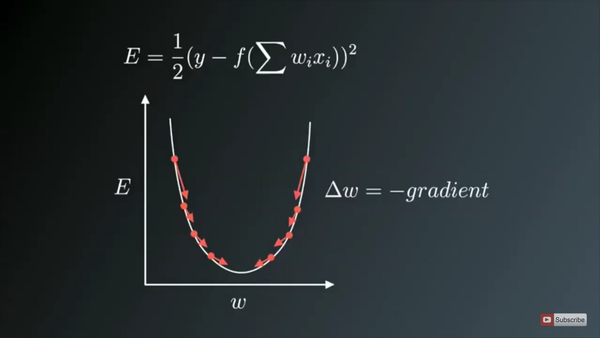
        "**Gradien Descent - Mathematical understanding**"
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "-Z8SQ3aOYz9o",
        "colab_type": "text"
      },
      "source": [
        "$f(x) = 2x^2 cos(x)$\n",
        "\n",
        "\n",
        "$f^{'}(x) = 4xcos(x) - 2x^{2}sin(x) $\n",
        "\n",
        "Parameter update rule: \n",
        "\n",
        "$x(t+1) = x(t) - \\alpha\\times f^{'}(x(t))$"
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "Q60spymnnYDF",
        "colab_type": "text"
      },
      "source": [
        "![alt text](https://i.pinimg.com/564x/ca/38/af/ca38af9b8fc5bce4eb2c6ddbdd4b32e0.jpg)\n",
        "\n",
        "\n"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "aR_BA4UDZ51V",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "# import required packages\n",
        "import numpy as np\n",
        "\n",
        "import matplotlib.pyplot as plt\n",
        "%matplotlib inline"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "zrw7zHiAZmta",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "# define helper functions\n",
        "\n",
        "# Objective/ Cost function\n",
        "def f(x):\n",
        "    return 2 * x * x * np.cos(x)"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "PRV0KhbiaOLI",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "# Derivative function for the Cost \n",
        "def df(x):\n",
        "    return 4 * x * np.cos(x) - 2 * x * x * np.sin(x)"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "aFi7_pc6dlcE",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "# Helper function to visualization\n",
        "def draw_update(ax, t, x_new):\n",
        "    ax.plot(x_new,f(x_new), 'ro')"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "YJrEcujCd61f",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "# parameter update function\n",
        "def param_update(x_t, alpha, slope):\n",
        "    \"\"\" \n",
        "    slope = f'(x)\n",
        "    \"\"\"\n",
        "    return x_t - alpha*slope"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "NdnjfCE_pGkt",
        "colab_type": "text"
      },
      "source": [
        "![alt text](https://pic1.zhimg.com/v2-ad943c338270e34bed0b67222f245168_b.png)"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "fZ_l6eZsaA_L",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "# let's visualize the cost function in given window [-5, 5]\n",
        "t = np.linspace(-5, 5)"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "tdORPf3baJjw",
        "colab_type": "code",
        "outputId": "93253205-1cac-464b-bda2-1416b7360089",
        "colab": {
          "base_uri": "https://localhost:8080/",
          "height": 269
        }
      },
      "source": [
        "plt.plot(t, f(t))\n",
        "plt.grid(True)"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "display_data",
          "data": {
            "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAD8CAYAAAB0IB+mAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3Xd4XFeZ+PHvmdGo92pVy0W2465Y\ncXoiB9KckMQpu6GEZMNiwsL+FlhagN9v92HZXToshH3YPCxLAguGFBNSnMQpipPYJrYs9ybZkVWt\nYtXRqM6c3x+aUQTIVpm5c+/ceT/Po8fWzHjOexL71Zlz3/sepbVGCCGE/TnMDkAIIUR4SMIXQogo\nIQlfCCGihCR8IYSIEpLwhRAiSkjCF0KIKCEJXwghooQkfCGEiBKS8IUQIkrEmB3AZNnZ2bq0tNTs\nMGZtYGCApKQks8MIK5lzdIi2OUfqfKurqzu11jnTvc5SCb+0tJS9e/eaHcasVVVVUVlZaXYYYSVz\njg7RNudIna9S6sxMXheSLR2l1M+VUu1KqcOTHvtnpVSzUmq//2tjKMYSQggxN6Haw/8FcNMUj/9A\na73W//VCiMYSQggxByFJ+FrrHUBXKN5LCCGEMYyu0vm0Uuqgf8snw+CxhBBCXIAKVT98pVQp8JzW\neqX/+zygE9DAvwD5WusHp/hzm4HNAHl5eeu2bNkSknjCye12k5ycbHYYYSVzjg7RNudIne+GDRuq\ntdYV073OsIQ/0+cmq6io0FKlExlkztEh2uYcqfNVSs0o4Ru2paOUyp/07Sbg8PleK4QQwnihKsv8\nDbALWKqUalJKfQz4tlLqkFLqILAB+GwoxppKc88g33v5BGfODRg1hBBCGObnb73L8wdbDR8nJDde\naa0/OMXD/x2K956JXs8oP36tjovyU5mfFXl3yQkhotvP3jzNZQuzuGV1/vQvDoIteukUpMcD0NIz\naHIkQggxO16fpq1/mHx/HjOSLRJ+WoKLBJeT1t4hs0MRQohZae8fwuvT5KclGD6WLRK+Uor89Hha\ne2WFL4SILC094wvVAlnhz1xBWsLEfzghhIgUgYWqrPBnIT9NVvhCiMjTGljhS8Kfufz0BNr7hxn1\n+swORQghZqyld5DEWCepCcZ3q7dNwi9Ii0draOuTbR0hRORo7RkiPy0epZThY9km4eenj38ckkod\nIUQkae0dpCDd+O0csFHCL0iTWnwhRORp6R1f4YeDbRK+rPCFEJFmZMxHp3s4LBU6YKOEnxwXQ0p8\nDK2ywhdCRIi2viG0Dk8NPtgo4YO/Fl9W+EKICBHYgpYV/hwUyN22QogIEtiClou2c5CfnjBxE4MQ\nQlhdi3+BKls6c1CQFs+5gRGGRr1mhyKEENNq6RkkLcFFYqzxN12BzRJ+YB9MKnWEEJEgcNNVuNgr\n4fs/FkmljhAiErT0DoVt/x5slvADzYekUkcIEQlaewcjb4WvlPq5UqpdKXV40mOZSqntSqla/68Z\noRjrQualyQpfCBEZBke89HhGI3KF/wvgpj977MvAq1rrMuBV//eGinc5yUqKlRW+EMLyWib64EfY\nCl9rvQPo+rOHbwce8//+MeCOUIw1HTn5SggRCQIl5OG66QrAyFqgPK11q//3Z4G8qV6klNoMbAbI\ny8ujqqoqqEFdo0PUNfcH/T6z4Xa7wzqeFcico0O0zTmc832zaRSAxhMHGG4Mz+XUsBR/aq21Ukqf\n57lHgUcBKioqdGVlZVBjvd57mKdrmgn2fWajqqoqrONZgcw5OkTbnMM53wOv1MLhk9x+w7XExTjD\nMqaRP1balFL5AP5f2w0ca0J+egL9Q2O4h8fCMZwQQsxJa+8g2cmxYUv2YGzC/wNwv//39wPPGDjW\nhHyp1BFCRIDxPvjh27+H0JVl/gbYBSxVSjUppT4GfBO4XilVC7zf/73hAiVOUqkjhLCy1p7w1uBD\niPbwtdYfPM9T7wvF+8+GrPCFEJGgtXeIKxdnh3VMW91pC5CXGo9SssIXQlhX39Ao7uGxsK/wbZfw\nXU4HuSlxssIXQljWRA1+GO+yBRsmfBjfx2+Rm6+EEBYVOOmqMEx98APsmfDT5CAUIYR1vddWQVb4\nQctPi6eldxCtp7zXSwghTNXaM4RDQW5KXFjHtWfCT09gaNRHj2fU7FCEEOIvtPQOkpcaT4wzvCnY\nlgm/wH/lW/bxhRBWFO6TrgJsmfADV75lH18IYUWtvYNhr9ABmyb8wApf2iQLIaxGa01r79BEngon\nWyb87OQ4XE4lN18JISyna2CE4TFf2Ct0wKYJ3+FQ5KXGy81XQgjLafUvRAvCXIMPNk34MF6LLyt8\nIYTVBG66khV+CMlRh0IIKwqs8PNlhR86+WkJnO0dwueTm6+EENbR0juIy6nITgrvTVdg44RfkB7P\nqFfTOTBsdihCCDGhtWeIeWnxOBwq7GPbNuEH9sekFl8IYSWtvYOm7N+DrRO+/25bqdQRQlhIS485\nNfgQohOvLkQpVQ/0A15gTGtdYfSYIEcdCiGsx+vTnO0bMuUuWwhDwvfboLXuDNNYAGQkuoh3OaQW\nXwhhGR39w3h9emJBGm623dJRSo33xZcVvhDCIgINHc3a0glHwtfAy0qpaqXU5jCMNyE/PV46Zgoh\nLGPiaEOTLtoqow8JUUoVaq2blVK5wHbg77XWOyY9vxnYDJCXl7duy5YtIRv7Z4eGOdLp5QcbEkP2\nnlNxu90kJycbOobVyJyjQ7TN2ej5vvjuKFtOjPDIdYkkx4auLHPDhg3VM7k+avgevta62f9ru1Jq\nK7Ae2DHp+UeBRwEqKip0ZWVlyMbeN3KCnS11XHX1NYYeNFBVVUUo444EMufoEG1zNnq+O/qPknC6\ngVuur0Qpm9XhK6WSlFIpgd8DNwCHjRxzsvz0BHwa2vrl5ishhPnG++DHm5LswfgVfh6w1T+5GODX\nWusXDR5zQqAWv7VnkEKTrooLIURAS+8QBSbt34PBCV9rfRpYY+QYFyK1+EIIK2ntGWTJkhzTxrdt\nWSb86QpfCCHMNOr10eEeNu2mK7B5wk+Jd5GW4KKpWxK+EMJcLT2DaA1FkvCNU5yZQEOXx+wwhBBR\nLpCHijONLRO/ENsn/JLMRBq7JeELIczV2DW+01CSJQnfMMWZiTR1DcpBKEIIUzV0eXA5FfNSzWmr\nANGQ8DMSGfH6aOuXSh0hhHkauzwUZSTiNOHgkwDbJ/wS/35ZwznZ1hFCmKehy0NRhrn3A0VNwm+U\nSh0hhIkauz0T+cgstk/4BekJOBRSqSOEME3v4Cg9nlFJ+EaLjXGQn5ZAoyR8IYRJAvlHEn4YFGdK\nwhdCmKep2/wafIiShF+SmShbOkII01jhpiuIooTf3j/M4IjX7FCEEFGooctDWsJ4qxczRUXCD/xU\nbZI7boUQJmjoGjR9/x7CcOKVFRRPlGZ6KMtLMTkaMVM9nhFOtrmJcSpS42NIiXeREh9Dgstp2gES\n4Tbm9dE/NEb/0Bh9Q6O4h8fITo5jYXYSDhNv4BGz09TlYVm++bknKhK+3Hxlfe7hMQ4393KwqYeD\nTb0cbOo973WXGIciJT6GhTnJlBens7YknbXF6RSmJ0TsDwLPyBiHmnrZ39jD/sYeDjX3cs49wuDo\n1NuQyXExrChIZU1xOquL0lhdmE5xZuTO3868Pk1T9yDXr8gzO5ToSPhZSbEkuJw0dMnNV1ZztneI\n77x0gq01TQTaHRWmJ7C6KI0Pri/hovwUtIa+odGJlW7/0Ci9g6McP9vPL3ef4WdvvQtAdnIca4vT\nuaQ0g6vKsrloXqplV8HdAyO8faqTnafOUdPQw8m2frz+/wAlmYmUl2QwLzVu4lNNctx7n3BaegY5\n1NzLgaZefvF2PSNeHwALspP40k3LuHFFniR+C2nrG2LE65MtnXBRSkmljsV4RsZ4dMdp/uuN03h9\nmvuvKOWaJTmsKkwjOzluxu8z6vVxvLWf/Y3d1DT0UNPYwyvH2mDb+A/6Kxdnc1VZNleXZZNv4tFy\nw2Nequu7ebOuk7dqOznc0ovWkBIXw9qSdN5/0SLWFo9/UsmawfzvqSgGYGTMx8m2fvY39vDYznoe\n+lU1ly3M5Gu3LGdlYZrR0xIzMFGhkxEFCV8pdRPwH4AT+JnW+ptGjzmV4sxEuWhrAT6fZmtNM995\n6QRn+4a4ZXU+X75p2ZzL1VxOB6uK0lhVlMZ9l48/drZ3iLfqOnmrtoO36s7xhwMtACzMSWJ9aSYV\npZlcUppBSWaiYSvhgeExahp62FPfxd4zXVSf6WZo1EeMQ1Feks5n3reEq8qyWVOURoxz7rUTsTEO\nVhamsbIwjXsvKeY3exr5wfaTfOCRt7jr4iK+cONS8kzsziisc9MVGJzwlVJO4CfA9UATsEcp9Qet\n9VEjx51KSWYiO091orWWj7smOdzcy8NPH+JQcy9ritJ45EPlVJRmhnyceWnx3L2uiLvXFaG15vjZ\nft6q7WTX6XNsO3yWLXsaAchJieOS0gwuLslgQXYS87MSKcpIJN7lnPFYWmva+4dp6PJw5pyHIy29\n7K3v5mhrH16fxqHgovxU7r2khKsWZ3PZoiyS44z5ZxfjdHDfZfO5fW0BP3mtjv95u57nD7by6esW\n88lrF1l2e8vuGrs8ONR7Z2ybyegV/nqgzn+YOUqpLcDtQNgTfnFmAp4RL+cGRma1ZSBCo/pMN/f/\n/B2S4pz88K/XctuagrAkIKUUF+WnclF+Kh+/ZiE+n6auwz2+8q7vZk99Fy8cOvsnf2ZeajwlmYkU\nZSYQF/Ne8m9tGealrkOApr1vPMk3dnsYGvVNvCbe5aC8OINPVS6iojST8pJ0UuLDW3udGu/i4Y0X\n8eFL5/Pv247xnZdO0Njl4d82rZKkb4KGLg/5aQnExphfBa+0Nu5gEKXU3cBNWuu/9X9/H3Cp1vrT\nk16zGdgMkJeXt27Lli2GxLK/fYwf7hvma5fFszh95iu4mXC73SQnJ4f0Pa1uNnOu6/by3b1DpMUp\nvrQ+nsx48//iT9Y3omn3+Ojw+H8dHP+1c1DjnfTPQ/t8KMd47KmxipwERW6iIifRQW7C+K/ZCYoY\nCyVVrTVP143y7KlRrimK4YEVsThm8Qk32v5uGzHfb+weJMYBX15v3Ap/w4YN1VrriuleZ/pFW631\no8CjABUVFbqystKQcQrb+vnhvh3klC6jcm1hSN+7qqoKo+K2qpnOufpMFz98fQ/z0hPZsvly5qVF\n7n5ypP5/rqzULNh+kh+9VkdBfv6sVvqROue5MmK+X3j7FTYszqGyck1I33cujE74zUDxpO+L/I+F\nXZH/Crk0UQuf6jNdfPS/3yE3NZ7ffPyyiE72kUwpxWevXwJK8aNXa9Ea/v1O2d4Jh8ERLx39w5a4\nYAvGJ/w9QJlSagHjif5e4EMGjzmlhFgnOSlxUpoZJnvru7j/55LsrUIpxWffXwYwnvTRfPPO1ZL0\nDdZokS6ZAYYmfK31mFLq08BLjJdl/lxrfcTIMS+kJDNx4uR4YZxAss9Ljec3my+TskCLUErxueuX\noID/8K/0v3WXJH0jNVqkS2aA4Xv4WusXgBeMHmcmSjITeefdLrPDsLX2/iE+/vheSfYW9tnrlwDj\nSX9RbjIPXbvI5Ijsq8FCNfgQJd0yA4ozEmjtHWRkzDf9i8Wsaa15+KlDDIx4efSj6yTZW9hn3l/G\njSvy+P7LJzlxtt/scGyroctDYqyTrKRYs0MBoi3hZybi09DSI9s6RniyuolXj7fzxRuXsjjX/M6A\n4vyUUvzbplWkxMfwud/tl0WQQRq7PIbe0T1bUZXwSya1SRah1dwzyNefPcqlCzJ58MoFZocjZiAr\nOY5/u3MVR1r6eOT1OrPDsaXGrsGJCkEriK6En+VvkyyVOiHl82m+8MQBfFrz3XvWyEXACHLjinnc\nWV7IT16v40Bjj9nh2IrWmgb/Ct8qoirh56XEE+t0SMIPsV/uPsPOU+f42q3LLVONIGbun25bQW5K\nHJ/73X6GztN/X8xep/88g5JM83voBERVwnc4FEUZCXLzVQi92znAv287RuXSHO69pHj6PyAsJy3B\nxbfuWs2pjgG++9IJs8OxjYkKnSzrLIKiKuHD+IVbqcUPDa9P84+/209cjJNv3bXaMhemxOxdsySH\nj1xWwn+//S67T58zOxxbCLRjt0If/IAoTPgJsqUTIo/uOM2+hh6+fvsKKcG0ga9svIiSzES+8OQB\n3MNjZocT8QJHqspFWxOVZCbSOzh+RJ6Yuw6Pjx9sP8ktq/K5bU2B2eGIEEiMjeF796yhqXuQH71a\na3Y4Ea+hy0NuShwJsaHtzhuMqEz4IE3UgvWHU6Og4Gu3XiRbOTZSUZrJpvJCHttZT1vfkNnhRLTG\nbmtV6EAUJvxiSfhBO93h5q3mMe67bL6p58QKY3zmfUvw+jQ/kdr8oDR2DVquai1qE77s48/dD16p\nJdYJn6yUHix2VJKVyF9dUsxv3mmgwyN34M7FyJiPll5J+KZLjXeRnuiShD9Hx1r7ePZAC9fPd8lR\nkTb299ctRik1vnUnZq25ZxCtrdM0LSDqEj742yR3S2nmXHx/+0lS4mO4eUF4z2kV4ZWflsBHLp3P\nW81jnO5wmx1OxGm0WJfMgKhM+OO1+LLCn639jT1sP9rG5qsXkuSSC7V293cbFuFyjm/hidlpmOiD\nb61rXNGZ8DMSaer24PUZd4C7HX3v5RNkJsXyN1dJc7RokJ0cxw3zXTx7oIVjrX1mhxNRGrs8xDod\n5KVY6/6UqEz4JZmJjHo1Z6XsbMb+ePocb9Z28slrF5EcZ/i5OcIibl7gIiU+hu9vP2l2KBGloctD\nUWaC5RoJGpbwlVL/rJRqVkrt939tNGqs2ZJa/NnRWvPdl0+QmxLHfZfPNzscEUZJLsXHr17I9qNt\n7JdumjNmxRp8MH6F/wOt9Vr/lyWOOYT39tWkUmdmdtR2sqe+m7+/bjHxLuvcNSjC48GrFpCR6OJ7\nL0tjtZlqOOexVA+dgKjc0ilIT8ChZIU/E1prvvfyCQrTE/jrS0rMDkeYIDkuhk9WLuLN2k7+KI3V\nptXrGaVvaCwqV/ifVkodVEr9XCmVYfBYM+ZyOihIlyZqM1F1ooODTb38w/vKiI2JyvWBAD56eSm5\nKXH86DWp2JnOexU61kv4Suu5V6oopV4B5k3x1FeB3UAnoIF/AfK11g9O8R6bgc0AeXl567Zs2TLn\neGbjO3sG8YzBP10efNmU2+0mOTk5BFFZz3f3DtHU7+O71yYQM+kClJ3nfD7RPufnTo3wZO0o/3pl\nAoUp9vzhH4r/x7tbx/jpgWH+5coEisP032nDhg3VWuuKaV+otTb8CygFDk/3unXr1ulw+adnDuuL\n/u827fP5gn6v119/PfiALKiuvV/P/9Jz+j9eOfkXz9l1zhcS7XM+5x7WZV99QX/l6YPmBWSwUPw/\n/t5Lx/WCLz+nh0bHgg9ohoC9ega52MgqnfxJ324CDhs11lwszk3GM+KlpVdKM8/n8Z31xDodfHC9\n7N0LyEyK5fY1BTy9r5lej7RcOJ/adjfzs5KIi7FegYORnze+rZQ6pJQ6CGwAPmvgWLNWljv+sa22\nrd/kSKypf2iUJ6ubuHV1Pjkp0jNHjLv/ilIGR708Ud1odiiWVdvuZnGuNbf+DEv4Wuv7tNartNar\ntda3aa1bjRprLsryUgCoa5c+IVN5srqJgREv919RanYowkJWFqZxSWkGj+2qlzvVpzDq9VHfOTCx\noLQae155mYHMpFiykmIl4U/B59M8vusM5SXprClONzscYTEPXLGAxq5BXj/ebnYolnPm3ABjPk1Z\nniR8y1mUm0ytJPy/8EZtB+92DvCArO7FFG5Ykce81Hh+sbPe7FAsp7ZtPJ8szkkxOZKpRXXCL8tN\npq7dHagkEn6P7awnJyWOm1fmT/9iEXVcTgf3XT6ft+o65RrYnwnsGCzKTTI5kqlFfcLvHRylwz1s\ndiiWcbrDTdWJDj5y6Xy50Uqc172XFBMb4+CxXfVmh2Ipte1uijISSIy1ZoPBqP4XvTjXf+G2TbZ1\nAh7fdQaXU/HBS4vNDkVYWFZyHLcFSjQHpUQzwMoVOhDlCT9wYaVOTvQBwD085i/FLCDXYn28hfU8\ncEUpnhEvT+yVEk0Ar09zusNt2QodiPKEn5sSR0p8zMSFlmj3VHUT7uExKcUUM7KyMI2K+Rk8vuuM\nlGgCTd0ehsd8lOVa84ItRHnCV0pRlptMbbtcePL5NI/trGdtcTprpRRTzNADV5bS0OWh6oSUaE5U\n6Fi0JBOiPOHDeIsFqcWHN+s6OS2lmGKWblwxT0o0/QIl3rKHb2FluSl0ukfoHhgxOxRTbXmngayk\nWDauklJMMXMuf6+lN2s7o/58ibp2N3mpcaTGu8wO5byiPuEvlgu3dA2M8MqxNu4oL5RSTDFrd1cU\noRQ8ta/J7FBMVdfeb+n9e5CEz+KcQBO16E34v69pZtSruaeiyOxQRAQqTE/gykXZPLG3CV+UXrzV\nWlNn8ZJMkIRPYXoCCS5nVO/jP1HdxKrCNJbNSzU7FBGh7qkoorlnkN1RegRia+8QAyNeSfhW53Ao\nFkdxpc7h5l6OtfbJ6l4E5cYV80iJj+GJ6ujc1glcsLVyDT5Iwgfe66kTjZ6sbiI2xsFtawrMDkVE\nsHiXk9vWFLDtcCt9Q9F3522gp1Cg7bpVScJnvGtma+8Q/VH2F3V4zMvv9zdzw/I80hNjzQ5HRLh7\nKooZGvXx/EFLHX0RFqc63GQmxZKZZO1/R5Lwee9j2KmOAZMjCa9Xj7XT4xnlngrpmyOCt6YojbLc\n5KhstVDbZv0LthBkwldK3aOUOqKU8imlKv7suYeVUnVKqRNKqRuDC9NYgY9h0dbq9Ym9jeSnxXPV\n4myzQxE2oJTinooi9jX0RNUWqdaa2nZr99AJCHaFfxi4E9gx+UGl1HLgXmAFcBPwn0op653o61ec\nkUCs0xFVf0nP9g7xxskO7ry4EKdDmR2OsIk7ysf/PkXTmbcd7mF6B0ftv8LXWh/TWp+Y4qnbgS1a\n62Gt9btAHbA+mLGMFON0sDAnKaoS/tM1Tfg03L1OtnNE6OSmxLNhaQ5P72tmzOszO5ywqJuo0LH2\nBVswbg+/EJj8I77J/5hlLY6i4w611jy5t4n1pZksyLbmyTwict1TUUxH/zA7ajvMDiUsJhK+hZum\nBUx7LItS6hVg3hRPfVVr/UywASilNgObAfLy8qiqqgr2LefE5RmhsWuUl199nVjn7LY43G63aXHP\nRW23l9OdQ2yYNzrnuCNtzqEgc54Zp0+TEgv/ua0Gx9nIOldhLvOtOjpMQgwcrd7FMWXt7dFpE77W\n+v1zeN9mYPJeQZH/sane/1HgUYCKigpdWVk5h+GCN5DZyta6fRRedDErCtJm9WerqqowK+65ePGp\ngyTGtvC5ezaQFDe3o9gibc6hIHOeub/yHOXxXfWsvuQKy5cqTjaX+f7Xyd0sK/CyYcOVxgQVQkZt\n6fwBuFcpFaeUWgCUAe8YNFZITJx+ZfNtHc/IGM8dbGXjqvw5J3shpnNPRRGjXs0z+6dc59lKpFTo\nQPBlmZuUUk3A5cDzSqmXALTWR4DfAUeBF4FPaa29wQZrpNKsJJwOZfsmatsOncU9PMY966SVgjDO\nsnmprCpM43d77d1qocczQqd7OCIu2ELwVTpbtdZFWus4rXWe1vrGSc/9q9Z6kdZ6qdZ6W/ChGis2\nxsH8rETbr/Cf2tfE/KxE1i/INDsUYXP3VBRxrLWPoy19ZodimLoIOPRkMrnTdhK7H3fY2jvIrtPn\n2FReiLL4xSUR+T6wuoAYh2JrjX1X+ZFwytVkkvAnKctNof6ch5Exe9YPP7O/Ba3hjrWWrpAVNpGR\nFEvl0lye2d9i20POa9vcJLicFKYnmB3KjEjCn6QsLxmvT1N/zn49dbTWbN3XzMUl6ZRK7b0Ikzsv\nLqS9f5idpzrNDsUQte39LM5NxhEhd6tLwp9kUY59K3WOtfZzoq2fTeWyuhfhc92yXFLiY9haY89q\nnVMRcMrVZJLwJ1mUk4xS9jzucGtNEzEOxa2rpe+9CJ94l5NbVuXz4uGzeEbGzA4npPqHRmnpHZKE\nH6kSYp0UZyTa7sKt16d5Zn8LlUtzyYigm2CEPdxRXohnxMv2o21mhxJSgXbqkVKDD5Lw/8JiG55+\ntfNUJ+39w9x5sWzniPBbX5pJYXoCT++z17ZOpJVkgiT8v7B0XgqnOtwMjVr6PrFZ2VrTTEp8DNct\nyzU7FBGFHA7F7WsLeLO2g47+YbPDCZmjLX3EuxyUZCaaHcqMScL/M2uL0xn1ao7Y5GYRz8gYLx4+\nyy2r8ol3WfZIAmFzm8oL8Wn4w4EWs0MJmZrGblYXphPjjJw0GjmRhkl5cToANQ3dJkcSGi8facMz\n4uUOqc4RJirLS2FlYaptbsIaHvNypLmP8pJ0s0OZFUn4fyY3NZ7C9ARqGnvMDiUkttY0U5iewPpS\naaUgzLWpvIjDzX22OEr0aEsfI16fJHw7KC9JZ39D5Cf89v4h3qzt4Pa1BRFzY4iwrw+sycehsEVN\nfo0/P5SXZJgcyexIwp9CeUkGzT2DtPcNmR1KUJ490IpPIzdbCUvITYnn6rIcntnfgi/CWy3UNPZQ\nkBZPXmpkHfAiCX8KgY9pkb6ts7WmiZWFqZTlRUbrVmF/m8oLae4Z5J36LrNDCcr+xu6IW92DJPwp\nLc9PxeVUEx/bIlFtWz+Hm/vYVC5974V13LAij8RYJ7+P4G2djv5hGrsGWVscWfv3IAl/SvEuJ8sL\n0iK6UmdrTTMONb5vKoRVJMbGcNOKeTx/qDVi73XZ3xjYv5eEbxvlxekcbOplzBt5rZJ9/lYKV5Xl\nkJsSWXuMwv42XVxI/9AYrx5rNzuUOalp6CbGoVhZOLuzr61AEv55lJekMzjq5UQElpDtPn2O5p5B\n7pJWCsKCrliUzbzUeJ7aF5k1+TUNPSwvSI3IGxmDPdP2HqXUEaWUTylVMenxUqXUoFJqv//rp8GH\nGl4X+y/IROI+/pP7mkiJi+HGFfPMDkWIv+B0KO4oL+SNk5HXasHr0xxo6pm4QTPSBLvCPwzcCeyY\n4rlTWuu1/q+Hghwn7IoyEshVb0YAAAAQuklEQVROjo24hD8w7G+lsFpaKQjruntdob+La2RdvD3Z\n1o9nxBuRFToQ/CHmx7TWJ0IVjJUopVhbnEFNY2RduN12+CyeES93rZPqHGFdi3NTWFOUxpPVkbWt\n894NV9G5wr+QBUqpGqXUG0qpqw0cxzDlJemc7higxzNidigz9lR1E/OzEqmYH5krEBE97lpXxPGz\n/Rxp6TU7lBmraegmMyk2ojpkThYz3QuUUq8AU20Gf1Vr/cx5/lgrUKK1PqeUWgf8Xim1Qmv9Fy0o\nlVKbgc0AeXl5VFVVzTh4ozm6xsvGHn9+B6tzzv+fyu12WyLuzkEfu04PsmmxizfeeMPQsawy53CS\nOYdW5ojGqeA/ntnNhy6KM2SM2Zpuvm8f91Cc6DD835dhtNZBfwFVQMVcnw98rVu3TltJ/9CoXvDl\n5/T3Xz5xwde9/vrr4QloGj965aSe/6XndMO5AcPHssqcw0nmHHqfeHyvvvjrL+uRMa+h48zUhebb\n4xnR87/0nP7xqyfDF9AMAXv1DHK1IVs6SqkcpZTT//uFQBlw2oixjJQcF8OSvJSIaLGgtebpmmYu\nXZBJcYR+3BTR5651RZwbGOGNEx1mhzKtA42R2TBtsmDLMjcppZqAy4HnlVIv+Z+6BjiolNoPPAk8\npLWOyOYZ450zuy3f7GlfQzfvdg5wt1ysFRGkcmkOWUmxEVGTX9PQg1KwuijybrgKCLZKZ6vWukhr\nHae1ztNa3+h//Cmt9Qo9XpJ5sdb62dCEG37lxRn0DY3x7rkBs0O5oCerm0lwObl5lbRSEJHD5XRw\n+9pCXj3WbvniiP2N3ZTlJpMS7zI7lDmTO22nMdE508L1+EOjXp472MLNK+eRHDftdXghLOWudYWM\neH08a+HjD7XW1DT2UF4cuds5IAl/WotykkmJi7F0I7XtR9voHxqT2nsRkVYUpLFsXgpP7rPuTVj1\n5zz0eEYjtv4+QBL+NBwOxdqSdEuv8J+sbqIgLZ7LF2aZHYoQc3L3uiIONPZQ127N3lWBBV8kX7AF\nSfgzUl6czvGzfXhGxswO5S+09Y0fY7jp4kI5xlBErNvXFuJ0KJ6stuYqv6ahh+S4GBbnJpsdSlAk\n4c9AeUkGPg0Hm6x3R+Dva5rxabjzYtnOEZErJyWOa5fksLWmCa8FK+JqGrtZU5yGM8IXVZLwZyBw\nso3VtnW01jy1r4nyknQW5UT2ykOIuy4uoq1vmLfrOs0O5U8Mjng51tof8RdsQRL+jGQkxbIgO8ly\nF25rGns42eaW2nthC++7KJe0BBdb9jSYHcqfONTci9enI/6CLUjCn7Hy4nRqGnsCrSIs4fGd9aTE\nxXDHWjnoRES+eJeTv76kmJeOtHG2d8jscCYEFnqReIbtn5OEP0PlJel09A9z5pzH7FCA8YOUnz/U\nyl3rikiS2nthEx+5dD4+rfn1H8+YHcqEPfXdlGQmkpVsjQZvwZCEP0OVS3MBeOnIWZMjGffbPQ2M\nejX3XT7f7FCECJmSrESuW5rLr99pYHjM/EPO3cNjvFnbwXXLcs0OJSQk4c9QcWYiq4vSeP5Qq9mh\nMOb18avdDVxdli0Xa4XtfPSKUjrdI7x42PzF1avH2hge87HRJi1LJOHPwsZV+Rxs6qWxy9xtne1H\n2zjbN8T9l5eaGocQRrh6cTYLspN4bGe92aHwwqFWclPibHOgkCT8WbjF/1P+BZNX+Y/tqqcoI4EN\nNvmYKcRkDofivsvms6+hh0Mm3vsyMDxG1YkObl45zzY3NUrCn4XizERWFaaZmvBPnO1n9+ku7rts\nfsTfBCLE+dy1rojEWCeP76o3LYZXj7fbajsHJOHP2i2r8zlg4rbO47vqiYtx8FcVxaaML0Q4pCW4\n2FReyDMHWugeMKdt8gsHW8lJiaOiNNOU8Y0gCX+WAts62w6Hf5XfOzjK0/uauX1tARlJsWEfX4hw\n+ujlpYyM+fjt3sawjz0wPMbrJ9q5eeU8W32SloQ/S4FtnecPhj/hP1XdxOCol4/KxVoRBZbOS+Gy\nhZn8cteZsPfXCWzn3GKj7RwI/ojD7yiljiulDiqltiql0ic997BSqk4pdUIpdWPwoVrHxlXh39bx\n+TS/3H2GdfMzWFkYuUesCTEb919eSnPPIK8dbw/ruHbczoHgV/jbgZVa69XASeBhAKXUcuBeYAVw\nE/CfgUPN7cCMbZ036zp5t3OAj8qNViKKXL88j/y0+LBevLXrdg4Ef6bty1rrQJP43UCgi9ftwBat\n9bDW+l2gDlgfzFhWUpLl39Y5FL4bQx7fWU92chw3r7TXR0whLiTG6eDDl5bwZm0nde3usIz5mg2r\ncwJCuYf/ILDN//tCYPKVlib/Y7axcVU+Bxp7aOo2flvnzLkBXjvRzocuLSE2Ri67iOhy7/oSYp2O\nsK3yXzjUSnZyHJfYbDsHYNquW0qpV4B5Uzz1Va31M/7XfBUYA/53tgEopTYDmwHy8vKoqqqa7VuY\nIsvjA+DHv3+bq3OGDY37pweGiFGwwNtEVZU1Dnp2u90R8/8qVGTO5rl0noNf7z7DKlc7OYnGLXrO\n9bp59egAVxXF8OaONwwbxyzTJnyt9fsv9LxS6gHgVuB9+r3ewc3A5ELxIv9jU73/o8CjABUVFbqy\nsnLaoK3i8VNvctzj4OZkF0bFvb+xh90vvs2nNyxm041LDRljLqqqqgybs1XJnM2ztHyQDd+t4o2e\ndB7ZeLFh43zrN68w4hvm4zdWcPki+50RHWyVzk3AF4HbtNaT9zb+ANyrlIpTSi0AyoB3ghnLigLb\nOp2DPkPeX2vNN547SnZyHA9VLjJkDCEiQX5aApuvXshzB1upPmPcQUR7zo6RnRzH+gX2286B4Pfw\nHwFSgO1Kqf1KqZ8CaK2PAL8DjgIvAp/SWpvf6zTEAtU6e84aM7Vth8+y90w3/3jDEpKl572Icp+4\ndhE5KXF84/mjhhxE5BkZ42CH15bVOQHBVuks1loXa63X+r8emvTcv2qtF2mtl2qtt13ofSLV/Kwk\nVhamsufs2PQvnqXhMS/f3HacZfNSpI2CEEBSXAyfv2EJNQ09hrQpf+14OyM+bFmdEyAlH0HauCqf\n072+kFfrPL7zDA1dHr6y8SLbrjaEmK271xWzbF4K39x2nKHR0H6yfuFQK6mxyrbbOSAJP2i3ripA\nAT9+tS5k79k1MMKPXqulcmkO1yzJCdn7ChHpnA7F125ZTlP3IL8IYb/8Iy29vHykjUvznbZeYEnC\nD1JJViI3L3Dx272N7DjZEZL3/NGrtQwMj/GVjReF5P2EsJOryrK5blkuP3mtjnPu4aDfb9Tr4wtP\nHCQ9MZbbF9m7KaEk/BC4Y7GLhTlJPPz0IdzDwe3nn+pw86vdZ/jg+hKW5KWEKEIh7OUrG5fhGfXy\nw1dqg36vn1ad4mhrH9+4YwXJsfZd3YMk/JCIdSq+c/dqWnoH+ea2Y0G917+/cJx4l5PPXr8kRNEJ\nYT+Lc1P40PoSfv1OA3Xt/XN+n5Nt/fzotVpuWZ3PTVHQtkQSfoism5/Jg1cu4Fe7G9h5qnNO7/HG\nyQ5eOdbG321YRHZyXIgjFMJePvP+MhJdTr7+3LE5tU8e8/r4whMHSIl38fXbVhgQofVIwg+hz9+w\nlNKsRL781CE8I7Pb2nnjZAcP/bKahTlJPHjlAoMiFMI+spLj+PyNS9lxsoP/s6WGkbHZ3QD5s7fe\n5UBTL/982wqyomSBJQk/hBJinXzrrtU0dHn49osnZvznnj3Qwt8+tofS7CR+u/ly4l226SQthKHu\nv6KUh29exvMHW/nYY3tmvNCqa3fz/e0nuWF5Hh9Ybf+tnABJ+CF26cIs7r98Po/tqmdPfde0r//V\n7jP8ny01rC1OZ8vmy8hJiY6VhhCh8olrF/Htu1bzdl0nH/nZH+nxXPgMXK9P88UnD5DgcvKNTStR\nyt4XaieThG+AL960jML0BL705MHz3hyiteaR12r52u8Ps2FpLo8/eClpCa4wRyqEPfzVJcX854cv\n5nBzH3/9X7tp6xs672t/sbOefQ09/NMHlpObEh/GKM0nDVoMkBQXw7fuWs2Hf/ZHrv3O66wqTGN5\nfirLC1JZnp9GYUYC//bCMf77rXfZVF7It+9ejcspP3uFCMZNK/P5n79xsfnxvdz905386mOXkpEU\ny/HWfo629HK0tY+jrX0ca+1nw9IcNpXb6oiOGZGEb5ArF2fz4w+W88qxNo629PHa8XYChQRxMQ6G\nx3w8cEUp/+/W5ThsfGefEOF05eJsfv3xy3jgf97h+h/s+JMLuZlJsSzPT+Vvr17AJ65ZFFVbOQGS\n8A30gTUFfGBNAQBDo15OnO3nmH+VsSQvhQ9fWhKVf+mEMNKa4nSeeOgK/uftdylIT5j4dJ2bEhf1\n/94k4YdJvMvJmuJ01hSnmx2KELa3ODeZf920yuwwLEc2joUQIkpIwhdCiCghCV8IIaKEJHwhhIgS\nwR5i/h2l1HGl1EGl1FalVLr/8VKl1KD/nNuJs26FEEKYJ9gV/nZgpdZ6NXASeHjSc6emOutWCCGE\nOYI9xPxlrXWgW9FuoCj4kIQQQhhBaT37PtJTvpFSzwK/1Vr/SilVChxhfNXfB3xNa/3mef7cZmAz\nQF5e3rotW7aEJJ5wcrvdJCcnmx1GWMmco0O0zTlS57thw4ZqrXXFdK+bNuErpV4B5k3x1Fe11s/4\nX/NVoAK4U2utlVJxQLLW+pxSah3we2CF1rpvmrE6gDPTBW1B2cDcTj2JXDLn6BBtc47U+c7XWudM\n96KgV/hKqQeATwDv01p7zvOaKuDzWuu9QQ1mUUqpvTP56WonMufoEG1ztvt8g63SuQn4InDb5GSv\nlMpRSjn9v18IlAGngxlLCCFEcILtpfMIEAds9zcl2u2vyLkG+LpSahTwAQ9prac/DUQIIYRhgkr4\nWuvF53n8KeCpYN47wjxqdgAmkDlHh2ibs63nG7IqHSGEENYmrRWEECJKSMIPMaXUPyqltFIq2+xY\njHa+1hp2o5S6SSl1QilVp5T6stnxGE0pVayUel0pdVQpdUQp9Q9mxxQuSimnUqpGKfWc2bEYQRJ+\nCCmlioEbgAazYwmTC7XWsAV/tdlPgJuB5cAHlVLLzY3KcGPAP2qtlwOXAZ+KgjkH/ANwzOwgjCIJ\nP7R+wHiZalRcGImS1hrrgTqt9Wmt9QiwBbjd5JgMpbVu1Vrv8/++n/EEaPsTv5VSRcAtwM/MjsUo\nkvBDRCl1O9CstT5gdiwmeRDYZnYQBigEGid930QUJL8Af5uUcuCP5kYSFj9kfMHmm+6FkUrOtJ2F\nC7WZAL7C+HaOrcyitcYY8L/hjE0YSymVzHh59Wema4sS6ZRStwLtWutqpVSl2fEYRRL+LGit3z/V\n40qpVcAC4ID/BrQiYJ9Sar3W+mwYQwy58805wN9a41bGW2vYcSurGSie9H2R/zFbU0q5GE/2/6u1\nftrseMLgSuA2pdRGIB5IVUr9Smv9EZPjCimpwzeAUqoeqNBaR2ITphnzt9b4PnCt1rrD7HiMoJSK\nYfyC9PsYT/R7gA9prY+YGpiB1Piq5TGgS2v9GbPjCTf/Cv/zWutbzY4l1GQPXwTjESCF8dYatjzZ\nzH9R+tPAS4xfvPydnZO935XAfcB1k06t22h2UCJ4ssIXQogoISt8IYSIEpLwhRAiSkjCF0KIKCEJ\nXwghooQkfCGEiBKS8IUQIkpIwhdCiCghCV8IIaLE/wf+mfe2Ci70DgAAAABJRU5ErkJggg==\n",
            "text/plain": [
              "<Figure size 432x288 with 1 Axes>"
            ]
          },
          "metadata": {
            "tags": []
          }
        }
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "uq3oSArhmVGv",
        "colab_type": "text"
      },
      "source": [
        "**Local Minima 1**"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "PoromW_tcIEv",
        "colab_type": "code",
        "outputId": "07be0d5f-b764-4759-8a1c-08188850cb84",
        "colab": {
          "base_uri": "https://localhost:8080/",
          "height": 1000
        }
      },
      "source": [
        "x = -5.\n",
        "alpha = 0.05\n",
        "x_cache, dfx_cache = [],[]\n",
        "ax = plt.axes()\n",
        "t = np.linspace(-5, 5)\n",
        "ax.plot(t, f(t))\n",
        "ax.grid(True)\n",
        "for i in range(50):\n",
        "    slope = df(x)\n",
        "    x = param_update(x , alpha, slope)\n",
        "    x_cache.append(x)\n",
        "    dfx_cache.append(slope)\n",
        "    # print(x, slope)\n",
        "    if slope<0:\n",
        "        print('Go to Right|| -->> || ')\n",
        "    else:\n",
        "        print('Go to Left || <<-- ||')\n",
        "    draw_update(ax, t, x)\n",
        "print(f'Best Value: x={x}')\n",
        "print(f'Best Funtion Value: f(x)={f(x)}')"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "stream",
          "text": [
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Best Value: x=-3.643597164971067\n",
            "Best Funtion Value: f(x)=-23.27565842351116\n"
          ],
          "name": "stdout"
        },
        {
          "output_type": "display_data",
          "data": {
            "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAD8CAYAAAB0IB+mAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3Xd8XNWZ8PHfmVHvXVaXccOAiyxh\nOrHpAQIYQwILIYTselPYTSEhIey+b3Y33hRI2GzKm3USSjYkDmBMLzZgUW2wZcm9yEVWtYpllVGf\nmfP+MTNGOLJVZu7cOzPP9/PRx9LM+J7n2NKjM889RWmtEUIIEf5sZgcghBAiOCThCyFEhJCEL4QQ\nEUISvhBCRAhJ+EIIESEk4QshRISQhC+EEBFCEr4QQkQISfhCCBEhoswOYLSsrCxdWlpqdhiT1tfX\nR2JiotlhBJX0OTJEWp9Dtb9VVVUdWuvs8V5nqYRfWlrKli1bzA5j0iorK1myZInZYQSV9DkyRFqf\nQ7W/SqkjE3ldQEo6SqlHlVJtSqmdox77gVKqSSlV4/24NhBtCSGEmJpA1fAfB64Z4/FHtNYLvR+v\nBKgtIYQQUxCQhK+1fgfoDMS1hBBCGMPoWTr3KqW2e0s+6Qa3JYQQ4jRUoPbDV0qVAi9prc/xfp0L\ndAAa+A8gT2t9zxh/bwWwAiA3N7d89erVAYknmBwOB0lJSWaHEVTS58gQaX0O1f4uXbq0SmtdMd7r\nDEv4E31utIqKCi2zdEKD9DkyRFqfQ7W/SqkJJXzDSjpKqbxRXy4Ddp7qtUIIIYwXqGmZfwE2AnOU\nUo1KqS8BP1VK7VBKbQeWAt8MRFtjaeoa4Gfr9nHkWJ9RTQghhGEefe8wL29vMbydgCy80lrfPsbD\nfwjEtSeiu3+EX751gLl5KZRkht4qOSFEZPv9u4c4/4xMrpufN/6L/RAWe+nkp8UB0Nw1YHIkQggx\nOS63prV3iDxvHjNSWCT81Pho4qPttHQPmh2KEEJMSlvvIC63Ji813vC2wiLhK6XIS4ujpVtG+EKI\n0NLc5Rmo5ssIf+LyU+NP/MMJIUSo8A1UZYQ/CXmpMsIXQoSeFt8IXxL+xOWnxdPWO8SIy212KEII\nMWHN3QMkxthJiTd+t/owSvhxaA1H5catECKENHcNkJcWj1LK8LbCJuH76l8yU0cIEUpaugfJSzX+\nhi2EUcL33eGWOr4QIpQ0dw0GpX4PYZTwfSN8makjhAgVQ04XHY7gLLqCMEr4ibFRpMRFyQhfCBEy\nWruHgODM0IEwSvjgmakjI3whRKho9s3BlxH+5MlcfCFEKAnmoisIs4SfnxYvs3SEECEjmNsqQBgm\n/M6+YQaGXWaHIoQQ42ruGiAtIZqEGOMXXUGYJXzfXFYp6wghQoFnDn5wyjkQdglfFl8JIUJHc9cA\n+UFadAVhlvDlIBQhRChp6R4M2gwdCNyZto8qpdqUUjtHPZahlFqvlKr1/pkeiLZOZ9qJko6M8IUQ\n1tY/7KR7YCQkSzqPA9ec9Nj3gDe11rOAN71fGyo2yk5WUozU8IUQlhfsGToQoISvtX4H6Dzp4RuB\nJ7yfPwHcFIi2xpMnB6EIIUJAsOfgAxg5FyhXa93i/fwokDvWi5RSK4AVALm5uVRWVvrVaIxzkNpm\nt9/XmQyHwxHU9qxA+hwZIq3Pwezv240jADTs3cZgfXBupwZl8qfWWiul9CmeWwWsAqioqNBLlizx\nq63Knl3sq2rE3+tMqs3KyqC2ZwXS58gQaX0OZn+r1+9H7arlxquWEBMVnIRvZCutSqk8AO+fbQa2\ndUJ+WhyOISc9gyPBaE4IIaakpXuArKTYoCV7MDbhvwB8wfv5F4DnDWzrhBNz8aWOL4SwsJbuwaDO\nwYfATcv8C7ARmKOUalRKfQn4MXClUqoWuML7teFOzMWXmTpCCAtr7hoI6g1bCFANX2t9+ymeujwQ\n158MGeELIaxOa01L9yCXzs4OarthtdIWICc5FpuS/XSEENbVM+Ckf9gVtINPfMIu4UfZbeSmxMlc\nfCGEZQX74BOfsEv44Dv5Skb4Qghr8uWn/DQZ4ftNTr4SQlhZs3e/LynpBIDv5Cutx1zrJYQQpmrp\nGiDKpshOjg1qu2GZ8PNS4xhyuunsGzY7FCGE+Bst3YPkpsRht6mgthumCV8OQhFCWJdnDn5wb9hC\nmCZ8OQhFCGFlnoNPglu/hzBN+DLCF0JYldutOWrCtgoQpgk/MzGGmCibjPCFEJbT0TfEsMsd9CmZ\nEKYJ32ZT5KXGnZj6JIQQVuHb9kVq+AGUlxpHi4zwhRAW41sjJCP8AMpPjZcavhDCcpplhB94eWlx\nHO0ZxOWWxVdCCOto6R4gNspGRmJM0NsO34SfGo/LrWnvHTI7FCGEOKG5e5C81DiUCu6iKwjjhC8H\noQghrKjFhINPfMI24fv+QWVqphDCSpq7BoO+LbJPQE68Oh2lVB3QC7gAp9a6wug24eM74HLylRDC\nKpwuN229gxSYMEMHgpDwvZZqrTuC1BYAKXFRJMbYpaQjhLCM1t4h3Bop6QSaUoq8tHgZ4QshLMO3\nNsiskk4wEr4G1imlqpRSK4LQ3glyEIoQwkrMOvjERxl9SIhSqkBr3aSUygHWA/+ktX5n1PMrgBUA\nubm55atXrw5Y24/uHGJbu4tfLE0I2DXH4nA4SEpKMrQNq5E+R4ZI67PR/X3l8DBP7RvhN5cnkBAd\nuGmZS5curZrI/VHDa/ha6ybvn21KqbXAYuCdUc+vAlYBVFRU6CVLlgSs7Rrnft5tquXCiy8lJsq4\nNzOVlZUEMu5QIH2ODJHWZ6P7W9mzi6TYRq69cqlhbZyOoSUdpVSiUirZ9zlwFbDTyDZHy0+NR2to\n7ZE6vhDCfGYdfOJj9Ag/F1jrXVEWBfxZa/2awW2e4Lsx0tQ1QFGGsWUdIYQYT3P3gCkHn/gYmvC1\n1oeABUa2cTon5uLLjVshhAW0dA0yryDVtPbDdlomfHwnvFmmZgohTDY44uJY37Bpc/AhzBN+fIyd\nzMQYGo/LCF8IYa4m7xz8wnRJ+IYpykigobPf7DCEEBGu3puHik28nxgRCb9eEr4QwmS+gaeZE0jC\nPuEXZ8TT1DWA0+U2OxQhRASrP9ZPbJSN7KRY02KIgISfgMut5bhDIYSpGo73U5SRgM0W/INPfMI+\n4fvePkkdXwhhpvrOAVPr9xABCd/3Dyx1fCGEWbTWNHT2S8I3Wl5qPFE2JQlfCGGa4/0jOIacpq/4\nD/uEb7cpCtLjJeELIUzjyz9FJs7BhwhI+OAp6zTI4ishhEl89xCLM2WEbzhZfCWEMNPHI3xJ+IYr\nzkigs2+Y3sERs0MRQkSghs5+spJiSIwN1jHiY4uIhO/7rdrQKWUdIUTw1Xf2m37DFoJw4pUVjJ6a\neVZ+isnRiIkYGHaxu6WbfUcdRNsVyXHRpMRFkRwXTXJcFMlxUWQkxuA9ayHsDAy76Oz3vCt1DDrp\nHXTSM+iZ6ZGZGMv8wlTyUuPCtv/hpr6zn/KSdLPDiKyEL3V8a9Jas7Oph22NXWxv7GJ7Yze1bQ5c\n7tOft5yeEM2CojQWjvpIS4gJUtSB43S52dfaS01DFzX1XdQ0dHGg3cF4x01nJXkS/7yCVBYUpVJe\nnEFqQnRwghYTNuJy09w1wE0LC8wOJTISfmqCZ3TYcFwSvtVUHenkP17aQ01DF+BJ4vML07jyrFzm\nF6YxNy8ZraFncIRe70i3d3CE7oER9rZ4kuTb+2tPJMfpWYlUlKRz8awsLpqZRZaJ+5acyojLzbaG\nLt6t7WDjoWPsaOxmYMQFQEZiDAuL0rh+fj7TUmNPvKNJiv343U1z1wA7mrrZ1tDNjqYuNuxrQ2tI\njLHz1aUz+dLF04mLtpvcS+HT0jWIW5u7S6aP4QlfKXUN8AvADvxea/1jo9scS3Gm7JppJQ2d/fz4\ntb28vL2F3JRYVi47h0tnZVOYHj/pMoVjyMn2Rs/IuLq+i3W7W3m6qhGAuXkpXDIri4tnZnFuaQbx\nMcFPhFprDrb38f6BDt6t7WDToWM4hpzYFJxTkMrnzi2irDiNsqJ0ijLG739uShxlxelwgefrviEn\nO5q6eez9wzz0+j7+/GE9918zhxsW5EvJxwLqLbBLpo+hCV8pZQd+DVwJNAKblVIvaK13G9nuWIrS\nE9jX2hvsZsVJegZH+PWGAzz2Xh12m+IbV8xixaVnkBAz9W/FpNgoLpyRxYUzsgBwuTW7mrt5t7aD\n92o7ePz9Ola9c4hou2JeQSoVpRlUlKRTUZpBRmLgS0BOl5vdLT1srjvOlrpONtcdp8MxBHhGeTcs\nzOeSmZ54A1GCSYyN4vwzMjn/jEw2HjzGD1/ezddX1/DY+3X86/VzKS/J8LsNMXX1FpmDD8aP8BcD\nB7xn26KUWg3cCAQ94RdnJPDmnjbcbm3qbnWR7NUdLTz43E6O9w+zfFEh375qDtNS4wLejt2mmF+Y\nxvzCNL62dCb9w04+OtzJxkPHqKo7fuIXAMCM7EQWFaczPTuRkoxEijMSKM5MIDV+/ETsq80eOdZP\nfafnY1dzN9X1XfQPe0o0henxXDLL8+7i4plZhv/QXzAjkxfvvZhnq5t46PW9LP9/G7lhQT4/WT7f\nlHc3wpPwo+2KaSmB/16fLKMTfgHQMOrrRuA8g9scU1FGAsMuN629g6aeKRmpnq9p4pt/rWFeQSp/\nvGcx5wTxIOeEmCiWzMlhyZwcwHO26I6mbjbXdVJVd5y39rZxrGr4E38nNT6aoox4YqM+TpLd3QP8\ncs8HaK1p6x2iuWuA0feVY6JszMxO4rMVRVSUplNRkmHIL7Tx2GyKW8oLuXbeNH779iF+9VYt7b1D\n/OHuCr/eSYmpaejspzA9AbsFBppKjzcVwJ+LK3ULcI3W+u+9X38eOE9rfe+o16wAVgDk5uaWr169\n2pBYdnY4eXjLEA8sjmNORmBHOg6Hg6SkpIBe0+om0+cPmp38bvsQczJsfHNRHLFR5n/jn2zAqWnv\nd9M+oGnr93zeMaBxjfr5cLpcRNk93zvJMYrsBBs58YqcBBvZCYq0WIXNgjVzf/79I+1724j+/tsH\nAyRGK759rnG//JcuXVqlta4Y94Vaa8M+8NxWen3U1w8AD5zq9eXl5dooh9sduuS7L+mntzQE/Nob\nNmwI+DWtbqJ9XlPVoKd/7yV92/9s1H1DI8YGZbBQ/n9+rrpRT//eS/rW336gHYMT/38I5T5PhRH9\nXfBvr+vvP7s94NcdDdiiJ5CTjV5puxmYpZSarpSKAW4DXjC4zTHlp8VjU7IvfjCtqWrkvqe3cf4Z\nmTx697lSTjDRjQsLeORzC9lS18kXH9tM35DT7JAiQvfACF39I5aYkgkGb62gtXYC9wKvA3uAp7TW\nu4xs81RiomzkpcbL4qsgeaaqkW8/s40LZ2Tyhy+cKzcMLeDGhQX84rYyquqPS9IPkhO7ZEZCwgfQ\nWr+itZ6ttZ6htV5pdHunU5Qh++IHw5qqRr7zzDYumpHF7++SZG8ln1mQzy9uW0hV/XHufuwj+ocl\n6RupwUJz8CFCNk/zKZZtkg2372gvDzy7gwvOyOT3X6iQZG9B18/P579vK2PLkeP85yt7zA4nrPlW\n90vCN0FxRgJtvUMMeOdIi8Aadrr51lM1JMdF8cvby2R5v4VdNz+Pv794On/aVM87+9vNDids1Xf2\nkxofPaF1HcEQUQnf91u2UfbUMcSv3qplV3MP/3nzPDItuIeN+KT7rprDzJwk7n9mO939claEEeo7\nByxTv4cITfhSxw+8bQ1d/LryIDcvKuDqs6eZHY6YgLhoOz//7ALaHUP84EVT5lKEvYbOfkn4ZimW\nhG+IwREX33qqhpzkWP7vZ842OxwxCfML07h36UzWVjfx2s4Ws8MJKy63pvG4NQ4+8YmohJ+ZGENC\njF1Ovgqwn762j4PtfTx0ywLL1CrFxN172UzmFaTy/bU7ae8dMjucsNHaM8iIS8sI3yxKKYozZJvk\nQNp48BiPvn+Yuy4o4eJZWWaHI6Yg2m7j559dgGPIyffX7vCtihd++nhbZOvs3RVRCR88dXyZmhkY\nvYMjfPvpbZRmJvC9T59pdjjCD7Nyk/nOVXNYv7uVNVubzA4nLNRbbNEVRGLCT/eM8GUU47+VL++h\npXuAn312oWybEAbuuXg6i0sz+LcXdtHUJWVPfzV09mNTnm1drCLiEn5xRjwDIy46HMPjv1ic0qFu\nF6s3N/APl55hicOZhf/sNsXDty7A6db85NW9ZocT8uo7+8lPiyfabp00a51IgsR3AIXU8f3z7P4R\nMhJj+KfLZpkdigig4swEvnhRKS9ub2bv0R6zwwlp9RabkgmRmPBl8ZXfPjx0jJ3HXHzlUzNIipVS\nTrj5x0s9/68/W7ff7FBCWoPFFl1BBCb8wnTvCP+YJPyp0Frz8Lp9pMUqPn9BidnhCAOkJkSz4pIz\nWL+7lUNdsg3JVPQPO+lwDFlqDj5EYMKPi7aTkxwrJZ0pent/O5vrjnPDjGjZKyeMffHi6WQkxrCm\nVu51TYVvrY8kfAuQufhTo7XmZ+v2U5gez6WFUsoJZ0mxUXx1yQx2HXOz6dAxs8MJOVackgkRnPBl\nLv7kvb7rKDuauvnGFbOJssCBzMJYd55fQlqs4uHX98k05kmShG8hRRkJtPQMMux0mx1KyHC5PaP7\nM7ITuWlhvtnhiCCIi7Zzw4xothw5TqVsoTwpDZ39JMVGkZ5gra1GIjLhF2ckoDWyuGQSXtjWRG2b\ng29dOZsoC80rFsa6tDCKwvR4frZORvmT0dDp2TRNKWu9EzbsJ1cp9QOlVJNSqsb7ca1RbU2WbJM8\nOSMuN4+sr2VuXgrXnpNndjgiiKJsim9cMZudTT28tvOo2eGEjPrOforSrbPC1sfoodojWuuF3o9X\nDG5rwmSb5Ml5eksj9Z39fPuq2dikdh9xlpUVMCM7kZ+t34/LLaP88WitLbnoCiK0pJOTHEtMlE1u\n3E7A4IiLX75VS1lxGpedmWN2OMIEdpviW1fO4UCbg+drZGO18bT3DjHkdJ9Y1W8lRs+tu1cpdRew\nBbhPa3385BcopVYAKwByc3OprKw0OCSPzFhN1b4jVCa0+n0th8MRtLiD7e2GEVq6h7lzFrz99tsn\nHg/nPp9KJPc5XmuKkm08/PJ20rtrLVebDpRA/B/XHvcsVjveeIDKyjr/gwokrfWUP4A3gJ1jfNwI\n5AJ2PO8iVgKPjne98vJyHSxfenyzvvLnlQG51oYNGwJyHatxu9366kfe1lc/8rZ2u92feC5c+3w6\nkd7np7c06JLvvqTf3d9uXkAGC8T/8V8/qtcl331J13U4/A9ogoAtegI526+Sjtb6Cq31OWN8PK+1\nbtVau7TWbuB3wGJ/2gq0WblJHO7oY8QlUzNPZdOhTvYe7eWLF5WG7YhOTNz18/PITIzh8Q8Omx2K\npdW29RIbZTuxjYuVGDlLZ/R0jmV4Rv6WMSsniRGX5ojsqXNKT3xQR1pCNDcuLDA7FGEBcdF2/u68\nYt7c2yZ7UZ1GbZuDGdlJ2C04wcHIm7Y/VUrtUEptB5YC3zSwrUmbmZMEwIG2XpMjsabG4/2s232U\n2xcXy5454oQ7zivBrhR/3FhndiiWVdvqOJFfrMawhK+1/rzWep7Wer7W+gatdYtRbU3FjGxfwneY\nHIk1/e+mI4Bneb0QPtNS47jmnGn8dUsDfUNOs8OxnP5hJ01dA8yKtIRvdYmxURSkxVMrCf9vDAy7\n+OvmBq4+exoFFjqeTVjDFy8qpXfQydpqmaJ5soNtfYDnHqEVRWzCB89/Sm2rJPyTPV/TRFf/CHdf\nWGp2KMKCFhWnM68glcc/qJPtFk5S6y0Rz8xJNjmSsUV2ws9J4mC7Q1YPjqK15vEP6pibl8Li6Rlm\nhyMsSCnF3ReWcqDNwfsHZOvk0WrbHETbFSUWXHQFEZ7wZ+YkMeR0y3GHo/imYt59YYlMxRSndP0C\nmaI5ltpWB6WZiZY6uHw0a0YVJL63XXLjFnjySSgt5fyZ2Xzw23tYtuft8f+OiFixUTJFcywH2x2W\nrd9DxCd8z39MxN+4ffJJWLECjhxBocnvbiPmK1/2PC7EKcgUzU8aHHFx5FifZev3EOEJPzU+mtyU\nWLlx++CD0H/SKK2/3/O4EKcwLTWOT8/LkymaXoc7+nBrLDslEyI84QPMykmWxVf19ZN7XAivuy8s\nkSmaXr5KgZR0LGxmThIH2hyRPb2suHhyjwvh5Zui+YRM0eRAay82BdOzEs0O5ZQk4eck0TfsoqV7\n0OxQzLNyJYPRsZ98LCEBVq40Jx4RMpRS3Hl+MbVtDqobuswOx1QH2h2UZCYSG2XdrUgiPuHPkhu3\nHLjyBu6/+l56c/NBKSgpgVWr4I47zA5NhIDr5ucTH23n6S0NZodiKivvoeMjCT/Xc0e9tjVy6/hP\nVzXy8rzLGKw9BG431NVJshcTlhQbxbXz8nhxWwsDwy6zwzHFiMvN4Y4+S9+wBUn4ZCTGkJkYE7Fz\n8Z0uN89ubWLpnByyk2PH/wtCjOHWikIcQ05e22WpPRKD5sixPpxubekbtiAJH/DU8SO1pPP2/nba\ne4e4taLQ7FBECDtvegbFGQk8tbnR7FBM4ZvaPTPbunPwQRI+ENkzdZ7e0khWUowcUC78opTi1vJC\nNh46RkNn5K289VUIZuRYd4YOSMIHPDduuwdGaHcMmR1KUB1zDPHm3lZuWlhg2b0/ROhYXl6IUvBM\nVeSN8mvbHBSmx5MQE2V2KKclP+V8fOP2QIStuH2uppkRl+bWiiKzQxFhID8tnotnZvFMVSPuCNuB\ntrbNYfkbtuBnwldK3aqU2qWUciulKk567gGl1AGl1D6l1NX+hWmsSJyaqbXm6S0NLChMZc40a9cd\nRei4taKIpq4BNh6KnG2TXW7t3TTN+j9H/o7wdwI3A++MflApdRZwG3A2cA3wG6WUZVcjZCfHkhIX\ndeLwgkiws6mHvUd7uUVG9yKArjorl5S4KJ6KoDn5DZ39DDvdlp+DD34mfK31Hq31vjGeuhFYrbUe\n0lofBg4Ai/1py0hKqRM3biPF01UNxEbZuGFBvtmhiDASF23nxoUFvLbzKN0DI2aHExS+vBH2Cf80\nCoDRv+IbvY9ZlmcTtchI+IMjLp6vaebqs6eRGh9tdjgizNxaUciQ081L25vNDiUoakMo4Y97S1kp\n9QYwbYynHtRaP+9vAEqpFcAKgNzcXCorK/295NTi6B2hwzHMi+s2kBwzuZOeHA6HaXFPxYctTroH\nRpgT3TnluEOtz4EgfZ4YrTWFSYo/vLWbgoHQOhFrKv19b/sQ6bGKrZveNyaoABo34Wutr5jCdZuA\n0cXhQu9jY11/FbAKoKKiQi9ZsmQKzQVAXhur920md9aCSZ/lWllZiWlxT8Gjj35EQZqDr9y8FJtt\nascYhlqfA0H6PHF3Rx3ihy/vIX9uObND4Gamz1T6+/Od73FOcTRLlpxnTFABZFRJ5wXgNqVUrFJq\nOjAL+MigtgLixJ46YX7jtrlrgHdr21m+qGDKyV6I8SwrKyDKpsJ+QzW3W3Ogzfqbpvn4Oy1zmVKq\nEbgAeFkp9TqA1noX8BSwG3gN+JrW2tK7KuWnxpEQYw/7Ov6zWxvRGm4pl9k5wjiZSbFcPjeHtdVN\njLjcZodjmJaeQfqHXZGR8LXWa7XWhVrrWK11rtb66lHPrdRaz9Baz9Fav+p/qMaKhJk6Wmue3drk\n2fckM8HscESYu6W8iA7HMO/WtpsdimF8u+zOsvA5tqPJSttRZuYkhfX5ttsauznU0cfNiyw9YUqE\niU/NziY9IZpnt4bv8Ye+AWIorLIFSfifMCsnmaM9g/QMhuf84bVbG4mNsvHpeXlmhyIiQEyUjc8s\nyGf97taw/ZmqbXWQlRRDemKM2aFMiCT8UXy/pcOxrDPicvPi9hauOCuXlDiZey+CY1lZAUNON6/t\nOGp2KIaobesNmfo9SML/hJlhnPDf2d9OZ98wyxZKOUcEz8KiNKZnJbK2OvzKOlqH1gwdkIT/CUUZ\nCcRE2cIy4T9b3URGYgyfmpNtdigigiiluGlhAZsOH6O5a8DscAKqvXeInkFnyNywBUn4n2C3KWZk\nJ4Xd+bY9gyOs393KZ+bnyb73IuiWlRWgNTxXE16j/NoQu2ELkvD/xqycJPaH2UydV3e0MOx0c1OZ\nlHNE8BVnJlBeks7arU1hdaqcb2A40+Ln2I4mCf8kZ+Wn0NQ1QGffsNmhBMza6iamZyWysCjN7FBE\nhFpWVkBtm4NdzT1mhxIw25u6yUqKJTsp1uxQJkwS/knKvEmxpuG4yZEERlPXAJsOdbKsrAClZCsF\nYY7r5+cRY7eF1c3bmvouyorTQurnShL+SeYVpmK3Karru8wOJSCe8/6A3SSzc4SJ0hJiWHpmNs/X\nNOMMg60WjvcNc6ijj7Li0HrXLAn/JAkxUZw5LTksEr7WmrXVTVSUpMtWCsJ0y8oK6HAM8d6BDrND\n8VtNoyc/lBWlmxzJ5EjCH0NZcRo1DV24Qvwg5l3NPRxoc7BMtlIQFrD0zBxS46NPvOsMZdX1XdgU\nzC9MNTuUSZGEP4ayonQcQ04Otof2bJ1ntzYRY7dx/Tw5xlCYLzbKznXz83h9Vyt9Q06zw/FLdf1x\n5kxLITF23CNFLEUS/hgWlXjeplXXh+6NW6fLzQvbmll6ZjapCbKVgrCGZWUFDIy4eG1n6G614HZr\nahq6WBRi9XuQhD+m0swE0hKiQ7qO/+6BDjocQywrKzQ7FCFOqChJpygjPqRn6xzqcNA76KSsOLTq\n9yAJf0xKKcqK0kI64T9X3URqfDRLz5StFIR1KKVYtrCA9w920NozaHY4U7LVmxdCbYYOSMI/pbLi\ndPa39Ybktq69gyO8vuso183PIzbKbnY4QnzCTb6tFkJ0lF9df5zU+GimZyaaHcqkScI/hbLiNLSG\n7Q3dZocyaa/uOMrgiJtbyqWcI6znjOwkFhWnsWZrY0hutVBd38XCorSQPBPa3zNtb1VK7VJKuZVS\nFaMeL1VKDSilarwfv/U/1OBaUJSGUqF54/aZqkbOyEo8sWpYCKtZXl7I/lYHO5pCa0DlGHKyr7U3\nJMs54P8IfydwM/DOGM8d1FoZxmD5AAAQt0lEQVQv9H582c92gi4lLpqZ2UlUN4RWHb/+WD8f1XWy\nvLwwpJZ8i8hy/fx8YqJsrKlqNDuUSdne0IXWhOQNW/D/EPM9Wut9gQrGasqK06iuPx5SbzvXbG1E\nKc/0NyGsKjU+mqvOyuX5bc0MOV1mhzNhvgHgwsLQHOEbuWpgulKqGugB/kVr/e5YL1JKrQBWAOTm\n5lJZWWlgSJOTMDDC8f4RnnplA7mJp/7d6HA4LBG3W2ue/GCAszJs7K/5kP0GtmWVPgeT9DmwZkc7\neal/hF8+s4GKadZYwDRef9dvHSQvUVH90fvBCyqQtNan/QDewFO6OfnjxlGvqQQqRn0dC2R6Py8H\nGoCU8doqLy/XVrKnpVuXfPcl/ezWhtO+bsOGDcEJaBwbD3ZMKN5AsEqfg0n6HFgjTpeu+OF6/aXH\nNxvWxmSdrr9ut1sv+vd1+r6naoIX0AQBW/Q4+VVrPf4IX2t9xRR+iQwBQ97Pq5RSB4HZwJbJXstM\ns3KSSYyxU13fFRILmNZUNZIYY+fqs6eZHYoQ44qy21hWVsCj7x2mwzFElsX3lW/oHOBY33DI3rAF\ng6ZlKqWylVJ27+dnALOAQ0a0ZSS7TbEgRBZg9Q87eWVHC9fNzyMhxhpvj4UYz/JFhTjdmudrms0O\nZVzV3jMyQm2HzNH8nZa5TCnVCFwAvKyUet371KXAdqVUDfAM8GWtdad/oZqjrDiNPS09DAxb+8bS\nazuP0jfsYvki678TEcJnzrRk5hWkhsRsner6LhJi7MwOoSMNT+bvLJ21WutCrXWs1jpXa3219/E1\nWuuztWdK5iKt9YuBCTf4yorScbo1O5utPV94zdZGijLiObc0w+xQhJiU5YsK2N3Sw54Wax9/WF1/\nnPmFqUTZQ3e9auhGHiQLvfU6Ky/Aauoa4IODx1i+qDAkV/+JyHbDwgKi7crSo/zBERe7mntCdv69\njyT8cWQlxVKckWDpOv7arY1ojZRzREjKSIzhsjNzeK6miRGLHn+4q7kbp1uH/Op1SfgT4FmAZc2E\nr7VmzdYmFk/PoChDjjEUoWn5okI6HMO8s7/d7FDG5Pv5XxjCM3RAEv6ElBWlcbRnkJbuAbND+Rtb\n67s43NEnG6WJkLb0zBwyE2NYs9WaZZ3q+i4K0+PJSY4zOxS/SMKfAF/dzoqj/GeqGomPtnPtvDyz\nQxFiyqLtNm5YmM8bu9vo6h82O5y/UV1/POTr9yAJf0Lm5qUQE2Wz3I3bwREXL21v5ppzppEUYmdr\nCnGy5YsKGfYezWklR7sHae4eDPn6PUjCn5CYKBvzClItN8J/YVszvYNOPltRZHYoQvjt7PwUzs5P\n4clN9ZbasLDGt+AqxOv3IAl/wsqK0tjR1M2w0xqzCLTWPPFBHbNzkzj/DJl7L0KfUoovXFDKvtZe\nNh2yzjrN6vouYuw2zspPMTsUv0nCn6CK0gyGnG621FngG/HJJxkuKubFr3+KZ396B+rPfzY7IiEC\n4oaF+aQlRPPHjXVmh3LCu7UdzC9MDYvjQiXhT9CnZmcTH23n5R0t5gby5JOwYgWxTY3Y0CQdbYIV\nKzyPCxHi4qLtfO7cItbtbqW5y/xZcYc7+tjd0sM154THhoSS8CcoPsbOZWfm8Pquo7jcJtYXH3wQ\n+vs/+Vh/v+dxIcLAneeV4NaaP39Yb3YovOId4IXLLDhJ+JNw3fw8OhzDfHj4mHlB1J/ih+BUjwsR\nYooyErj8zFz+8lE9gyPmblr48vYWyorTyE+LNzWOQJGEPwlL5+R4yjrbzSvr6KJTzMgpLg5uIEIY\n6AsXlnCsb/jECNsMvnLOdWEyugdJ+JNihbLO1i9/h/6okw6KSEiAlStNiUcII1w8M4szshN5YuMR\n02IIt3IOSMKfNLPLOj9OX8TDy+9DFxeDUlBSAqtWwR13mBKPEEbwTdHc1tBFTYM561/CrZwDkvAn\nzcyyzq7mbjbXHSf/a19CHTkCbjfU1UmyF2Hp5kUFJMbY+eMHdUFvOxzLOSAJf9LiY+xcNtecss7/\nbjxCXLSNW8tlZa0If8lx0SwvL+Sl7S10OIaC2nY4lnPA/yMOH1JK7VVKbVdKrVVKpY167gGl1AGl\n1D6l1NX+h2od180Lflmnq3+Y52qaWFZWQGpCdNDaFcJMd11QwrDLzV83NwS13XAs54D/I/z1wDla\n6/nAfuABAKXUWcBtwNnANcBvfIeahwMzyjpPbWlgcMTNXReUBq1NIcw2MyeZi2dm8adNR3AG6XCU\ncC3ngP9n2q7TWju9X24CfJuy3wis1loPaa0PAweAxf60ZSWjyzrB+CZ0uTX/u+kIi6dnMDcv9Pfz\nEGIy7rqghJbuQdbvbg1Ke+FazoHA1vDvAV71fl4AjH4P1uh9LGz4yjofHTZ+b53Xdx2loXOAuy4o\nMbwtIazm8rm5FKTFs+rdQ0HZRfOlMC3nAIy7ibpS6g1grI0kHtRaP+99zYOAE5j0hi5KqRXACoDc\n3FwqKysnewlT2F2aGDv87vUqlpeMGBa30635wXsDFCQp4jv2UVm535B2JsvhcITM/1WgSJ/Nc2WB\ni8d3dfHwX9/k3GnGnf1wqN3BnhbF7WfGWKLfgTbuv5zW+orTPa+Uuhu4Hrhcf/zrtwkYPZWk0PvY\nWNdfBawCqKio0EuWLBk3aKu4snUrHx46xp1zEzEq7t+/e4i2/j08cc9iPjU725A2pqKystKwPluV\n9Nk8l7g1m/77XV6od/LPt1xi2M6VL/5hHTDCP910cViO8P2dpXMNcD9wg9Z69I5eLwC3KaVilVLT\ngVnAR/60ZUW+ss6+48bU8Y/3DfPfb9Zy6exsSyV7IYLNblM8eN1cGjoHeMLAefkfHXWFbTkH/K/h\n/wpIBtYrpWqUUr8F0FrvAp4CdgOvAV/TWpu7C5IBfLN1Nh91jv/iKfjFm7U4hpw8eO1cQ64vRCi5\nZFY2S+dk88s3D3DMgHn5hzv6aOh1h+XsHB9/Z+nM1FoXaa0Xej++POq5lVrrGVrrOVrrV093nVDl\nm61T1eoM+Gydg+0O/rTpCLctLmbOtOSAXluIUPX9a+fSP+LiF2/WBvza4Tw7x0dW2vrpunl59Ax7\nTsUJpB+9spe4aDvfvGJ2QK8rRCiblZvM7YuLePLDeg609Qbsui635rnqJmak2sK2nAOS8P122Zk5\nZMcrfvDiLgaGA1O1+uBgB2/saeWrS2eQnRw7/l8QIoJ844rZJETb+c9X9gbsmo++d5jaNgdXloT3\nKnZJ+H6Ki7ZzzzmxHDnWz8Pr9vl9PZdb88OX9lCQFs89F00PQIRChJespFi+dtlM3trbxnsBeGd9\nqN3Bw+v2ccXcHM7LC5sNAcYkCT8A5mbaufP8Yh59/zBVR/xbiPXs1kZ2t/Rw/zVziIsO728+Iabq\n7gtLKUyP54cv7/ZrE0O3W/PdNduJjbKxctk8lFIBjNJ6JOEHyPc+PZf81Hi+88z2KR/L1j/s5KHX\n97GwKI0bFuQHOEIhwkdctJ3vffpM9h7t5ZmqqW+s9sTGOjbXHef/fOZsclPiAhegRUnCD5Ck2Ch+\nsnw+h9r7eOSNya+Gdbrc/MvanbT1DvGv188N+5GGEP66bl4ei4rT+Mlr+9jT0jPpv3/kWB8/fW0f\nS+Zks3xRWO38ckqS8APo4llZ3L64iN+9c4jq+uMT/nuDIy6++uRWnq1u4ltXzqa8JMPAKIUID0op\nHrp1ATF2G5/7n41sqZt4OdXt1tz/zHaibIof3Rz+pRwfSfgB9sC1c8lNieP+Z7Yz5By/tNM7OMIX\nH9vMut2t/OAzZ/HPl88KQpRChIcZ2Uk885ULyEyK5c4/fMiGfW0T+ntPfniEDw938uB1c8lLDd9p\nmCeThB9gKXHR/OjmedS2OVj34M+htBRsNs+fT35yb7ljjiH+7ncfsrmuk//63ELullk5QkxaYXoC\nT3/5AmZkJ/EPT2zh+Zoxt+06oaGznx+9updLZmXxuXMj6/Q4SfgGWDInh5X927n85/8KR46A1p4/\n77zTc/C4UmilsOfkMPutF/jdXRXcVBYZNUQhjJCVFMtfVpxPeUk63/hrDX/cWPc3r+nuH2HjwWPc\n9/Q2FPDj5fMjppTjY9w+oxHu9ud+i8156v0+FJA20MNDL/8XtlsWwJlyELkQ/kiJi+aJexZz75+r\n+T/P76Kuo5+kuCh2N/ewp6WHpq4BwDPm+snN8ykI4xW1pyIJ3yC2xolNFbONjMCDD8IdkvCF8Fdc\ntJ3f3rmI767ZwaPvH8am4IzsJMpL0vn8BSWclZfCWfkpZCVF5gp2SfhGKS72lHEmor7e2FiEiCBR\ndhsP3zqff758JjnJccTHyAJGH6nhG2XlSkhImNhri4uNjUWICKOUoiQzUZL9SSThG+WOO2DVKkhM\nPP3roqM9vxyEEMJgkvCNdMcd4HDAV74y9vOZmfDYY1K/F0IEhdTwg+E3v/F8CCGEifw90/YhpdRe\npdR2pdRapVSa9/FSpdSA99jDE0cfCiGEMI+/JZ31wDla6/nAfuCBUc8dHOvoQyGEEObw90zbdVpr\n3wnem4BC/0MSQghhhEDetL0HGH1Y+XSlVLVS6m2l1CUBbEcIIcQUKK1Pf1qMUuoNYNoYTz2otX7e\n+5oHgQrgZq21VkrFAkla62NKqXLgOeBsrfXfbFqtlFoBrADIzc0tX716tV8dMoPD4SApKcnsMIJK\n+hwZIq3PodrfpUuXVmmtK8Z73bgJf9wLKHU38I/A5Vrr/lO8phL4ttZ6yzjXagcmuDzVUrIA/w/X\nDC3S58gQaX0O1f6WaK2zx3uRX9MylVLXAPcDnxqd7JVS2UCn1tqllDoDmAUcGu96EwnYipRSWyby\n2zWcSJ8jQ6T1Odz76+88/F8BscB67zajm7wzci4F/l0pNQK4gS9rrf073VsIIYRf/Er4WuuZp3h8\nDbDGn2sLIYQILNlaITBWmR2ACaTPkSHS+hzW/fX7pq0QQojQICN8IYSIEJLwA0wpdZ9SSiulssyO\nxWin2ksp3CilrlFK7VNKHVBKfc/seIymlCpSSm1QSu1WSu1SSn3d7JiCRSll9y4YfcnsWIwgCT+A\nlFJFwFVApBxhdbq9lMKCUsoO/Br4NHAWcLtS6ixzozKcE7hPa30WcD7wtQjos8/XgT1mB2EUSfiB\n9QiedQkRcWMkQvZSWgwc0Fof0loPA6uBG02OyVBa6xat9Vbv5714EmCBuVEZTylVCFwH/N7sWIwi\nCT9AlFI3Ak1a621mx2KSk/dSChcFwOgT6RuJgOTno5QqBcqAD82NJCj+C8+AzW12IEaRA1Am4XT7\nCgHfx1POCSuT2EvJCTwZzNiEsZRSSXjW03xjrH2wwolS6nqgTWtdpZRaYnY8RpGEPwla6yvGelwp\nNQ+YDmzzrjguBLYqpRZrrY8GMcSAO1Wffbx7KV2PZy+lcCxlNQFFo74u9D4W1pRS0XiS/ZNa62fN\njicILgJuUEpdC8QBKUqpP2mt7zQ5roCSefgGUErVARVa61DchGnCvHsp/RzPXkrtZsdjBKVUFJ4b\n0pfjSfSbgb/TWu8yNTADKc+o5Qk8+2F9w+x4gs07wv+21vp6s2MJNKnhC3/8CkjGs5dSWB5l6b0p\nfS/wOp6bl0+Fc7L3ugj4PHDZqGNKrzU7KOE/GeELIUSEkBG+EEJECEn4QggRISThCyFEhJCEL4QQ\nEUISvhBCRAhJ+EIIESEk4QshRISQhC+EEBHi/wNnxZqjVZ5vJQAAAABJRU5ErkJggg==\n",
            "text/plain": [
              "<Figure size 432x288 with 1 Axes>"
            ]
          },
          "metadata": {
            "tags": []
          }
        }
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "6SJd_c9rmQvK",
        "colab_type": "text"
      },
      "source": [
        "Local Minima 2"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "kAFKFw_viwIb",
        "colab_type": "code",
        "outputId": "72210ab8-8a51-424a-b6f2-ae118f3abfbb",
        "colab": {
          "base_uri": "https://localhost:8080/",
          "height": 1000
        }
      },
      "source": [
        "\n",
        "x = -1.\n",
        "alpha = 0.05\n",
        "x_cache, dfx_cache = [],[]\n",
        "ax = plt.axes()\n",
        "t = np.linspace(-5, 5)\n",
        "ax.plot(t, f(t))\n",
        "ax.grid(True)\n",
        "for i in range(50):\n",
        "    slope = df(x)\n",
        "    x = param_update(x , alpha, slope)\n",
        "    x_cache.append(x)\n",
        "    dfx_cache.append(slope)\n",
        "    # print(x, slope)\n",
        "    if slope<0:\n",
        "        print('Go to Right|| -->> || ')\n",
        "    else:\n",
        "        print('Go to Left || <<-- ||')\n",
        "    draw_update(ax, t, x)\n",
        "print(f'Best Value: x={x}')\n",
        "print(f'Best Funtion Value: f(x)={f(x)}')"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "stream",
          "text": [
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Best Value: x=-6.66338443154018e-05\n",
            "Best Funtion Value: f(x)=8.880138396784195e-09\n"
          ],
          "name": "stdout"
        },
        {
          "output_type": "display_data",
          "data": {
            "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAD8CAYAAAB0IB+mAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3Xl4XNV5+PHvmdEujbVYi7XLeAPv\nwmKHYEPYDAHMkpKwhjYObdMmaZMQQn5NnzRps6dNSJvykDQQkjhgMCTsNlgYMA5e5H2TbGSt1mLt\nGq0z5/eHZoQCsrXM3Ll37n0/z6NH0szonvd4eXXm3Peco7TWCCGEsD+X2QEIIYSIDEn4QgjhEJLw\nhRDCISThCyGEQ0jCF0IIh5CEL4QQDiEJXwghHEISvhBCOIQkfCGEcIgYswMYKzMzU5eUlJgdxpT1\n9vaSnJxsdhgRJX12Bqf1OVr7u3PnzlatddZEr7NUwi8pKWHHjh1mhzFl5eXlrFy50uwwIkr67AxO\n63O09lcpdWIyrwvLlI5S6ldKqWal1P4xj/2rUqpeKbU78LE6HG0JIYSYnnDN4f8auHacx3+itV4e\n+HgpTG0JIYSYhrAkfK31FqAtHNcSQghhDKOrdD6vlNobmPJJN7gtIYQQZ6DCtR++UqoEeEFrvTjw\nfQ7QCmjg34BcrfX94/zcWmAtQE5Ozop169aFJZ5I6unpISUlxewwIkr67AxO63O09nfVqlU7tdZl\nE73OsIQ/2efGKisr01KlEx2kz87gtD5Ha3+VUpNK+IZN6Silcsd8uwbYf7rXCiGEMF64yjJ/D7wL\nLFBK1Sml/hr4vlJqn1JqL7AK+FI42hpPfUcfP3rtCCdO9RrVhBBCGOZXb7/Pi3sbDW8nLAuvtNaf\nGufhX4bj2pPR6R3iZ29UcU7uDIpnRt8qOSGEsz321nEuPGsm1y/NnfjFIbDFXjp5aQkANHT0mRyJ\nEEJMjc+vaeoeIDeQx4xki4SfmhhLYqybxs5+s0MRQogpae7ux+fX5KYmGt6WLRK+UorctAQaO2WE\nL4SILg0dIwPVPBnhT15eauLoH5wQQkSL4EBVRvhTkJsqI3whRPRpDI7wJeFPXm5aIs3dAwz5/GaH\nIoQQk9bQ2UdSnJsZicbvVm+bhJ+XmoDW0NQl0zpCiOjR2NFPbmoCSinD27JNws9NG3k7JJU6Qoho\n0tjZR16a8dM5YKOEn5cqtfhCiOjT0Dkywo8E2yR8GeELIaLN4LCf1p6BiFTogI0Sfkp8DJ6EGBpl\nhC+EiBJNXf1oHZkafLBRwodALb6M8IUQUSI4BS0j/GnIk9W2QogoEpyClpu205Cblji6iEEIIayu\nITBAlSmdachLTeBU7yD9Qz6zQxFCiAk1dPSRmhhLUpzxi67AZgk/OA8mlTpCiGgQXHQVKfZK+IG3\nRVKpI4SIBg2d/RGbvwebJfzg5kNSqSOEiAaNnX3RN8JXSv1KKdWslNo/5rEMpdRGpVRl4HN6ONo6\nk1mpMsIXQkSHvkEfHd6hqBzh/xq49kOPfQ14XWs9D3g98L2hEmLdzEyOkxG+EMLyGkb3wY+yEb7W\negvQ9qGHbwIeD3z9OHBzONqaiJx8JYSIBsES8kgtugIwshYoR2vdGPj6JJAz3ouUUmuBtQA5OTmU\nl5eH1GjsUD9V9d0hX2cqenp6ItqeFUifncFpfY5kf9+qGwKg9sgeBmojczs1IsWfWmutlNKnee5R\n4FGAsrIyvXLlypDa2ty5n2cr6gn1OlNRXl4e0fasQPrsDE7rcyT7u2dTJew/yk1XX058jDsibRr5\na6VJKZULEPjcbGBbo3LTEunuH6ZnYDgSzQkhxLQ0dvaRmRIXsWQPxib8PwL3Br6+F3jewLZG5Uql\njhAiCozsgx+5+XsIX1nm74F3gQVKqTql1F8D3wWuUkpVAh8PfG+4YImTVOoIIayssSOyNfgQpjl8\nrfWnTvPUleG4/lTICF8IEQ0aO/u5ZG5mRNu01UpbgJwZCSglI3whhHV19Q/RMzAc8RG+7RJ+rNtF\ntideRvhCCMsarcGP4CpbsGHCh5F5/AZZfCWEsKjgSVf5EdoHP8ieCT9VDkIRQljXB9sqyAg/ZLmp\nCTR09qH1uGu9hBDCVI0d/bgUZHviI9quPRN+WiL9Q346vENmhyKEEB/R0NlHzowEYtyRTcG2TPh5\ngTvfMo8vhLCiSJ90FWTLhB+88y3z+EIIK2rs7It4hQ7YNOEHR/iyTbIQwmq01jR29o/mqUiyZcLP\nTIkn1q1k8ZUQwnLaegcZGPZHvEIHbJrwXS5FzowEWXwlhLCcxsBANC/CNfhg04QPI7X4MsIXQlhN\ncNGVjPDDSI46FEJYUXCEnysj/PDJTU3kZGc/fr8svhJCWEdDZx+xbkVmcmQXXYGNE35eWgJDPk1r\n74DZoQghxKjGjn5mpSbgcqmIt23bhB+cH5NafCGElTR29pkyfw+2TviB1bZSqSOEsJCGDnNq8CFM\nJ16diVKqGugGfMCw1rrM6DZBjjoUQliPz6852dVvyipbiEDCD1iltW6NUFsApCfFkhDrklp8IYRl\ntHQP4PPr0QFppNl2SkcpNbIvvozwhRAWEdzQ0awpnUgkfA28ppTaqZRaG4H2RuWmJciOmUIIyxg9\n2tCkm7bK6ENClFL5Wut6pVQ2sBH4B631ljHPrwXWAuTk5KxYt25d2Np+bN8AB1p9/GRVUtiuOZ6e\nnh5SUlIMbcNqpM/O4LQ+G93fV94fYt2RQR65IomUuPCVZa5atWrnZO6PGj6Hr7WuD3xuVkptAM4H\ntox5/lHgUYCysjK9cuXKsLW9a/AIWxuquPSyjxl60EB5eTnhjDsaSJ+dwWl9Nrq/W7oPkni8huuv\nWolSNqvDV0olK6U8wa+Bq4H9RrY5Vm5aIn4NTd2y+EoIYb6RffATTEn2YPwIPwfYEOhcDPA7rfUr\nBrc5KliL39jRR75Jd8WFECKoobOfPJPm78HghK+1Pg4sM7KNM5FafCGElTR29DF/fpZp7du2LBP+\ncoQvhBBmGvL5aekZMG3RFdg84XsSYklNjKWuXRK+EMJcDR19aA0FkvCNU5iRSE2b1+wwhBAOF8xD\nhRnGlomfie0TflFGErXtkvCFEOaqbRuZaSiaKQnfMIUZSdS19clBKEIIU9W0eYl1K2bNMGdbBXBC\nwk9PYtDnp6lbKnWEEOapbfNSkJ6E24SDT4Jsn/CLAvNlNadkWkcIYZ6aNi8F6eauB3JMwq+VSh0h\nhIlq272j+cgstk/4eWmJuBRSqSOEME1n3xAd3iFJ+EaLi3GRm5pIrSR8IYRJgvlHEn4EFGZIwhdC\nmKeu3fwafHBIwi/KSJIpHSGEaayw6AoclPCbuwfoG/SZHYoQwoFq2rykJo5s9WImRyT84G/VOllx\nG91++1vIzASlPvhwu0c+l5SMPC+EBdW09Zk+fw8OS/iyxUJ06fAO8t77beyqaefk//wS/2c+A6dO\n/eWL/P6RzydOwF132S75D/v8tPcOUnPKy/76TrYdP0VVc4+sHI8ydW1eCjPMP5PD8CMOrUAWX1lf\nz8Aw++s72VvXwd66TvbWdf7FfZe3/+chXENDk7tYMPl/7nOQkABtbVBUBN/5Dtx5p0E9CI13cJh9\ndZ3sru1gd20H++o7OdUzSN/Q+NOQKfExLMqbwbLCNJYWpLI0P43CjETTTlISp+fza+ra+7hqUY7Z\noTgj4c9MjiMx1k1Nmyy+spqTnf384NUjbKioIzhozU9LZGlBKp86v4hzcj1oDfnfb536xXt7Rz7g\ng18C99wz8q6guNjUXwDtvYO8c6yVrcdOUVHTwdGmbnyBP4CijCRKi9KZNSMeT0IsnoQYUuJjRr9u\n6OhjX30ne+o6+fU71Qz6Rt7lzM5M5sFrz+aaRTmS+C2kqaufQZ/fElM6jkj4Simp1LEY7+Awj245\nzv++eRyfX3PvxSV8bH4WS/JTyUyJ/+gPFBWNJO1QjZ0CuvvukV8Cbjf4fIb+EhgY9rGzup23qlp5\nu7KV/Q2daA2e+BiWF6Xx8XPmsLwwjeWFacwcr/8fcntZIQCDw36ONnWzu7aDx7dW88CTO7nwrAy+\ncf1CFuenhr0fYupGK3TSHZDwlVLXAv8FuIHHtNbfNbrN8RRmJMlNWwvw+zUbKur5watHONnVz/VL\nc/natWdPXK72ne/AZz4Dk53WmQwdeEvhC0ybBN8F3HXXuC+/fLyfPY3egWEqajrYXt3GjhNt7DzR\nTv+QnxiXorQojS9eOZ9L52WyrCCVGPf0b6XFxbhYnJ/K4vxU7jivkN9vr+UnG4/yiUfe5tZzC/jK\nNQvIMXF3RmGdRVdgcMJXSrmBnwNXAXXAdqXUH7XWB41sdzxFGUlsPdaK1lre7ppkf30nDz27j331\nnSwrSOWRT5dSVpIxuR8Ojrq/8IWP3riNkL/4V6MUaI3WmubuAWravJw45eVAQyc7qts52NiFz69x\nKTgndwZ3nFfEpXMzuXDOTFLijflvF+N2cfeFxdy0PI+fv1HF/71TzYt7G/n8FXP528vn4DJxl0Yn\nq23z4lIfnLFtJqNH+OcDVYHDzFFKrQNuAiKe8AszEvEO+jjVOzj+lIEw1M4T7dz7q/dIjnfzn3+1\nnBuX5U09Ad1550enW377W3j44ZHReSAJR4IGrv7xm9S2e+kf8o8+nhDrorQwnb9fOYeykgxKi9Lw\nJES29npGQiwPrT6HOy8o5j9ePsQPXj1CbZuXf1+zRJK+CWravOSmJhIXY35RpNEJPx+oHfN9HXDB\n2BcopdYCawFycnIoLy83JJDO5mEAntv0NnPT3GG9dk9Pj2FxW9VU+lzV7uOHO/pJjVc8eG4saZ2V\nbNlSGZ5A8vPh178e/TZ70ybOeuwx4pubGfJ4cA0O4u7vx4g056GPlfkuspJiyE5UZCW5yExUxLj6\ngUb8DY3sbDCg4Sn4ZL4mpi+WddtraWhs5L5Fcbim8A7Xaf+2jejv/uo+PC6s8eeoA29LjfgAbmNk\n3j74/d3AI6d7/YoVK7RRjp7s0sUPvqCfq6gL+7U3b94c9mta3WT7vKP6lF70L6/oy7//hm7s6DM2\nqNN58kmti4u1Bq3d7pHPSo18DuUjSvj9fv2jVw/r4gdf0A+u36N9Pv+kf9Zp/7aN6G/Ztzfqrzy9\nO+zXHQvYoSeRk41+j1EPFI75viDwWMQVBO6QyyZqkbPzRBv3/PI9sjzxrFt7EbNSTbp5eOedUF09\nkqaHh0c+/+Y3I1U5DqCU4ktXzecfr5zHuu21PPTsPlm4FSF9gz5augcsccMWjF9pux2Yp5SarZSK\nA+4A/mhwm+NKjHOT5YmX0swI2VE9kuyzZyTw+89eaF6yP52xvwSefPKD5H+G6Y6/SJERulcQLkop\nvvTxefzjlfP4w45avvbsXkn6EVBrkV0ygwxN+FrrYeDzwKvAIeAprfUBI9s8k6KMpNGT44VxdlS3\nce+v3iNnRgLr1low2X/Y2OTv9592EufNzZs/+D4KKaX4p6vm84Ur5/HUjjoefEaSvtFqLbJLZpDh\ndfha65eAl4xuZzKKMpJ47/02s8Owtebufj77xA5yZiTw+7UXSg24BX3pqvkA/NfrlczJTuGBy+eY\nHJF91VioBh8csnlaUGF6Io2dfQwO+yd+sZgyrTUPPbOP3kEfj96zQpK9hX3x4/O4ZlEOP37tKEdO\ndpsdjm3VtHlJinMzMznO7FAApyX8jCT8Gho6ZFrHCOt31vH64Wa+es0C5mZ7zA5HnIFSin9fswRP\nQgz/9NRuGQQZpLZt5OByqyz2dFTCL5Jtkg1T39HHt/50kAtmZ3D/JbPNDkdMwsyUeP79liUcaOji\nkc1VZodjS7VtfaMVglbgrIQ/M7BNslTqhJXfr/nK03vwa80Pb18mqzmjyDWLZnFLaT4/31zFntoO\ns8OxFa01NYERvlU4KuHneBKIc7sk4YfZb7adYOuxU3zjhoWWqUYQk/fNGxeR7Ynnn57aTf9p9t8X\nU9caOM+gyAIHnwQ5KuG7XIqC9ERZfBVG77f28h8vH2LlgizuOK9w4h8QlpOaGMv3bl3KsZZefvjq\nEbPDsY3RCp2Z1hkEOSrhw8iNW6nFDw+fX/PPT+0mPsbN925dapkbU2LqPjY/i7suLOKX77zPtuPm\n7EZqN8Ht2K2wD36QAxN+okzphMmjW46zq6aDb920SEowbeDrq8+hKCOJr6zfQ8/AsNnhRL3gkapy\n09ZERRlJdPYN0dkXxoM0HKjF6+cnG49y/ZJcblyWZ3Y4IgyS4mL40e3LqGvv46evh2k3UwerafOS\n7YknMS68u/OGwpEJH2QTtVD98dgQKPjGDefIVI6NlJVksKY0n8e3VtPU1W92OFGttt1aFTrgwIRf\nKAk/ZMdbeni7fpi7LywmN9U6FQgiPL545Xx8fs3PpTY/JLVtfZarWnNswpd5/On7yaZK4tzwtytl\nDxY7KpqZxCfPK+T379XQ4pUVuNMxOOynoVMSvulmJMSSlhQrCX+aDjV28ac9DVxVHCtHRdrYP1wx\nF6XUyNSdmLL6jj60ts6maUGOS/gQ2Ca5XUozp+PHG4/iSYjhutmRPadVRFZuaiJ3XVDM2/XDHG/p\nMTucqFNrsV0ygxyZ8Edq8WWEP1W7azvYeLCJtZedRXKs3Ki1u79bNYdY98gUnpiamtF98K11j8uZ\nCT89ibp2Lz45/GFKfvTaETKS4/jMpbI5mhNkpsRzdXEsf9rTwKHGLrPDiSq1bV7i3C5yPNZan+LI\nhF+UkcSQT3NSys4m7c/HT/FWZSt/e/kcUuINPzdHWMR1s2PxJMTw441HzQ4lqtS0eSnISLTcRoKG\nJXyl1L8qpeqVUrsDH6uNamuqpBZ/arTW/PC1I2R74rn7Imcc/C1GJMcqPnvZWWw82MRu2U1z0qxY\ngw/Gj/B/orVeHviwxDGH8MG8mlTqTM6Wyla2V7fzD1fMJSHWOqsGRWTcf+ls0pNi+dFrsrHaZNWc\n8lpqD50gR07p5KUl4lIywp8MrTU/eu0I+WmJ/NV5RWaHI0yQEh/D366cw1uVrfxZNlabUKd3iK7+\nYUeO8D+vlNqrlPqVUird4LYmLdbtIi9NNlGbjPIjLeyt6+QLV84jLsaR4wMB3HNRCdmeeH76hlTs\nTOSDCh3rJXyl9fQrVZRSm4BZ4zz1MLANaAU08G9Artb6/nGusRZYC5CTk7Ni3bp1045nKn6wvQ/v\nMHzzotDLpnp6ekhJSQlDVNbzwx391HX7+eHlicSMuQFl5z6fjtP7/MKxQdZXDvGdSxLJ99jzl384\n/o63NQ7ziz0D/NsliRRG6M9p1apVO7XWZRO+UGtt+AdQAuyf6HUrVqzQkfLN5/frc/7fy9rv94d8\nrc2bN4cekAVVNXfr4gdf0P+16ehHnrNrn8/E6X0+1TOg5z38kv76s3vNC8hg4fg7/tGrh/Xsr72g\n+4eGQw9okoAdehK52Mgqndwx364B9hvV1nTMzU7BO+ijoVNKM0/nia3VxLldfOp8mbsXkJEcx03L\n8nh2Vz2dXtly4XQqm3sonplMfIz1ChyMfL/xfaXUPqXUXmAV8CUD25qyedkjb9sqm7pNjsSauvuH\nWL+zjhuW5pLlkT1zxIh7Ly6hb8jH0ztrzQ7Fsiqbe5ibbc2pP8MSvtb6bq31Eq31Uq31jVrrRqPa\nmo55OR4Aqppln5DxrN9ZR++gj3svLjE7FGEhi/NTOa8kncffrZaV6uMY8vmpbu0dHVBajT3vvExC\nRnIcM5PjJOGPw+/XPPHuCUqL0lhWmGZ2OMJi7rt4NrVtfWw+3Gx2KJZz4lQvw37NvBxJ+JYzJzuF\nSkn4H/FmZQvvt/Zyn4zuxTiuXpTDrBkJ/HprtdmhWE5l00g+mZvlMTmS8Tk64c/LTqGquSdYSSQC\nHt9aTZYnnusW5078YuE4sW4Xd19UzNtVrXIP7EOCMwZzspNNjmR8jk/4nX1DtPQMmB2KZRxv6aH8\nSAt3XVAsC63Ead1xXiFxMS4ef7fa7FAspbK5h4L0RJLirLnBoKP/R8/NDty4bZJpnaAn3j1BrFvx\nqQsKzQ5FWNjMlHhuDJZo9kmJZpCVK3TA4Qk/eGOlSk70AaBnYDhQiplHtsX28RbWc9/FJXgHfTy9\nQ0o0AXx+zfGWHstW6IDDE362Jx5PQszojRane2ZnHT0Dw1KKKSZlcX4qZcXpPPHuCSnRBOravQwM\n+5mXbc0btuDwhK+UYl52CpXNcuPJ79c8vrWa5YVpLJdSTDFJ911SQk2bl/IjUqI5WqFj0ZJMcHjC\nh5EtFqQWH96qauW4lGKKKbpm0Swp0QwIlnjLHL6Fzcv20NozSHvvoNmhmGrdezXMTI5j9RIpxRST\nFxvYa+mtylbHny9R1dxDzox4ZiTEmh3KaTk+4c+VG7e09Q6y6VATN5fmSymmmLLbygpQCp7ZVWd2\nKKaqau629Pw9SMJnblZwEzXnJvznKuoZ8mluLyswOxQRhfLTErlkTiZP76jD79Cbt1prqixekgmS\n8MlPSyQx1u3oefynd9axJD+Vs2fNMDsUEaVuLyugvqOPbQ49ArGxs5/eQZ8kfKtzuRRzHVyps7++\nk0ONXTK6FyG5ZtEsPAkxPL3TmdM6wRu2Vq7BB0n4wAd76jjR+p11xMW4uHFZntmhiCiWEOvmxmV5\nvLy/ka5+5628De4pFNx23aok4TOya2ZjZz/dDvuHOjDs47nd9Vy9MIe0pDizwxFR7vayQvqH/Ly4\n11JHX0TEsZYeMpLjyEi29v8jSfh88DbsWEuvyZFE1uuHmunwDnF7meybI0K3rCCVedkpjtxqobLJ\n+jdsIcSEr5S6XSl1QCnlV0qVfei5h5RSVUqpI0qpa0IL01jBt2FO2+r16R215KYmcOncTLNDETag\nlOL2sgJ21XQ4aopUa01ls7X30AkKdYS/H7gF2DL2QaXUQuAOYBFwLfDfSinrnegbUJieSJzb5ah/\npCc7+3nzaAu3nJuP26XMDkfYxM2lI/+enHTmbUvPAJ19Q/Yf4WutD2mtj4zz1E3AOq31gNb6faAK\nOD+UtowU43ZxVlayoxL+sxV1+DXctkKmc0T4ZHsSWLUgi2d31TPs85sdTkRUjVboWPuGLRg3h58P\njP0VXxd4zLLmOui4Q60163fUcX5JBrMzrXkyj4het5cV0tI9wJbKFrNDiYjRhG/hTdOCJjyWRSm1\nCZg1zlMPa62fDzUApdRaYC1ATk4O5eXloV5yWmK9g9S2DfHa65uJc09tiqOnp8e0uKejst3H8dZ+\nVs0amnbc0dbncJA+T47br/HEwX+/XIHrZHSdqzCd/pYfHCAxBg7ufJdDytrToxMmfK31x6dx3Xpg\n7FxBQeCx8a7/KPAoQFlZmV65cuU0mgtdb0YjG6p2kX/OuSzKS53Sz5aXl2NW3NPxyjN7SYpr4J9u\nX0Vy/PSOYou2PoeD9HnyPuk9yBPvVrP0vIstX6o41nT6+79Ht3F2no9Vqy4xJqgwMmpK54/AHUqp\neKXUbGAe8J5BbYXF6OlXNp/W8Q4O88LeRlYvyZ12shdiIreXFTDk0zy/e9xxnq1ES4UOhF6WuUYp\nVQdcBLyolHoVQGt9AHgKOAi8Avy91toXarBGKpmZjNulbL+J2sv7TtIzMMztK2QrBWGcs2fNYEl+\nKk/tsPdWCx3eQVp7BqLihi2EXqWzQWtdoLWO11rnaK2vGfPcd7TWc7TWC7TWL4ceqrHiYlwUz0yy\n/Qj/mV11FM9M4vzZGWaHImzu9rICDjV2cbChy+xQDFMVBYeejCUrbcew+3GHjZ19vHv8FGtK81EW\nv7kkot8nluYR41JsqLDvKD8aTrkaSxL+GPOyPVSf8jI4bM/64ed3N6A13Lzc0hWywibSk+NYuSCb\n53c32PaQ88qmHhJj3eSnJZodyqRIwh9jXk4KPr+m+pT99tTRWrNhVz3nFqVRIrX3IkJuOTef5u4B\nth5rNTsUQ1Q2dzM3OwVXlKxWl4Q/xpws+1bqHGrs5khTN2tKZXQvIueKs7PxJMSwocKe1TrHouCU\nq7Ek4Y8xJysFpex53OGGijpiXIoblsq+9yJyEmLdXL8kl1f2n8Q7OGx2OGHV3T9EQ2e/JPxolRjn\npjA9yXY3bn1+zfO7G1i5IJv0KFoEI+zh5tJ8vIM+Nh5sMjuUsApupx4tNfggCf8j5trw9Kutx1pp\n7h7glnNlOkdE3vklGeSnJfLsLntN60RbSSZIwv+IBbM8HGvpoX/I0uvEpmRDRT2ehBiuODvb7FCE\nA7lcipuW5/FWZQst3QNmhxM2Bxu6SIh1UZSRZHYokyYJ/0OWF6Yx5NMcsMliEe/gMK/sP8n1S3JJ\niLXskQTC5taU5uPX8Mc9DWaHEjYVte0szU8jxh09aTR6Io2Q0sI0ACpq2k2OJDxeO9CEd9DHzVKd\nI0w0L8fD4vwZtlmENTDs40B9F6VFaWaHMiWS8D8ke0YC+WmJVNR2mB1KWGyoqCc/LZHzS2QrBWGu\nNaUF7K/vssVRogcbuhj0+SXh20FpURq7a6I/4Td39/NWZQs3Lc+LmoUhwr4+sSwXl8IWNfkVgfxQ\nWpRuciRTIwl/HKVF6dR39NHc1W92KCH5055G/BpZbCUsIduTwGXzsnh+dwP+KN9qoaK2g7zUBHJm\nRNcBL5LwxxF8mxbt0zobKupYnD+DeTnRsXWrsL81pfnUd/TxXnWb2aGEZHdte9SN7kES/rgW5s4g\n1q1G37ZFo8qmbvbXd7GmVPa9F9Zx9aIckuLcPBfF0zot3QPUtvWxvDC65u9BEv64EmLdLMxLjepK\nnQ0V9bjUyLypEFaRFBfDtYtm8eK+xqhd67K7Njh/LwnfNkoL09hb18mwL/q2SvYHtlK4dF4W2Z7o\nmmMU9rfm3Hy6+4d5/VCz2aFMS0VNOzEuxeL8qZ19bQWS8E+jtCiNviEfR6KwhGzb8VPUd/Rxq2yl\nICzo4jmZzJqRwDO7orMmv6Kmg4V5M6JyIWOoZ9rerpQ6oJTyK6XKxjxeopTqU0rtDnz8IvRQI+vc\nwA2ZaJzHX7+rDk98DNcsmmV2KEJ8hNuluLk0nzePRt9WCz6/Zk9dx+gCzWgT6gh/P3ALsGWc545p\nrZcHPh4IsZ2IK0hPJDMlLuqhuyzsAAAQtUlEQVQSfu9AYCuFpbKVgrCu21bkB3Zxja6bt0ebuvEO\n+qKyQgdCP8T8kNb6SLiCsRKlFMsL06moja4bty/vP4l30MetK6Q6R1jX3GwPywpSWb8zuqZ1Plhw\n5cwR/pnMVkpVKKXeVEpdZmA7hiktSuN4Sy8d3kGzQ5m0Z3bWUTwzibLi6ByBCOe4dUUBh092c6Ch\n0+xQJq2ipp2M5Lio2iFzrJiJXqCU2gSMNxn8sNb6+dP8WCNQpLU+pZRaATynlFqktf7IFpRKqbXA\nWoCcnBzKy8snHbzRXG0jZWNPvLiFpVmn/6Pq6emxRNytfX7ePd7HmrmxvPnmm4a2ZZU+R5L0Obwy\nBjVuBf/1/DY+fU68IW1M1UT9feewl8Ikl+H/vwyjtQ75AygHyqb7fPBjxYoV2kq6+4f07K+9oH/8\n2pEzvm7z5s2RCWgCP910VBc/+IKuOdVreFtW6XMkSZ/D73NP7NDnfus1PTjsM7SdyTpTfzu8g7r4\nwRf0z14/GrmAJgnYoSeRqw2Z0lFKZSml3IGvzwLmAceNaMtIKfExzM/xRMUWC1prnq2o54LZGRRG\n6dtN4Ty3rijgVO8gbx5pMTuUCe2pjc4N08YKtSxzjVKqDrgIeFEp9WrgqY8Be5VSu4H1wANa66jc\nPGNk58x2y2/2tKumnfdbe7lNbtaKKLJyQRYzk+Oioia/oqYDpWBpQfQtuAoKtUpng9a6QGsdr7XO\n0VpfE3j8Ga31Ij1Sknmu1vpP4Qk38koL0+nqH+b9U71mh3JG63fWkxjr5rolspWCiB6xbhc3Lc/n\n9UPNli+O2F3bzrzsFDwJsWaHMm2y0nYCoztnWrgev3/Ixwt7G7hu8SxS4ie8Dy+Epdy6Ip9Bn58/\nWfj4Q601FbUdlBZG73QOSMKf0JysFDzxMZbeSG3jwSa6+4el9l5EpUV5qZw9y8P6XdZdhFV9ykuH\ndyhq6++DJOFPwOVSLC9Ks/QIf/3OOvJSE7jorJlmhyLEtNy2ooA9tR1UNVtz76rggC+ab9iCJPxJ\nKS1M4/DJLryDw2aH8hFNXSPHGK45N1+OMRRR66bl+bhdivU7rTnKr6jpICU+hrnZKWaHEhJJ+JNQ\nWpSOX8PeOuutCHyuoh6/hlvOlekcEb2yPPFcPj+LDRV1+CxYEVdR286ywlTcUT6okoQ/CcGTbaw2\nraO15plddZQWpTEnK7pHHkLcem4BTV0DvFPVanYof6Fv0Mehxu6ov2ELkvAnJT05jtmZyZa7cVtR\n28HRph6pvRe2cOU52aQmxrJue43ZofyFffWd+Pw66m/YgiT8SSstTKOitiO4VYQlPLG1Gk98DDcv\nl4NORPRLiHXzV+cV8uqBJk529psdzqjgQC8az7D9MEn4k1RalEZL9wAnTnnNDgUYOUj5xX2N3Lqi\ngGSpvRc2cdcFxfi15nd/PmF2KKO2V7dTlJHEzBRrbPAWCkn4k7RyQTYArx44aXIkI/6wvYYhn+bu\ni4rNDkWIsCmamcQVC7L53Xs1DAybf8h5z8Awb1W2cMXZ2WaHEhaS8CepMCOJpQWpvLiv0exQGPb5\neXJbDZfNy5SbtcJ27rm4hNaeQV7Zb/7g6vVDTQwM+1ltky1LJOFPweolueyt66S2zdxpnY0HmzjZ\n1c+9F5WYGocQRrhsbiazM5N5fGu12aHw0r5Gsj3xtjlQSBL+FFwf+C3/ksmj/MffraYgPZFVNnmb\nKcRYLpfi7guL2VXTwT4T1770DgxTfqSF6xbPss2iRkn4U1CYkcSS/FRTE/6Rk91sO97G3RcWR/0i\nECFO59YVBSTFuXni3WrTYnj9cLOtpnNAEv6UXb80lz0mTus88W418TEuPllWaEr7QkRCamIsa0rz\neX5PA+295myb/NLeRrI88ZSVZJjSvhEk4U9RcFrn5f2RH+V39g3x7K56blqeR3pyXMTbFyKS7rmo\nhMFhP3/YURvxtnsHhtl8pJnrFs+y1TtpSfhTFJzWeXFv5BP+Mzvr6BvycY/crBUOsGCWhwvPyuA3\n756I+P46wemc6200nQOhH3H4A6XUYaXUXqXUBqVU2pjnHlJKVSmljiilrgk9VOtYvSTy0zp+v+Y3\n206wojidxfnRe8SaEFNx70Ul1Hf08cbh5oi2a8fpHAh9hL8RWKy1XgocBR4CUEotBO4AFgHXAv8d\nPNTcDsyY1nmrqpX3W3u5RxZaCQe5amEOuakJEb15a9fpHAj9TNvXtNbBTeK3AcFdvG4C1mmtB7TW\n7wNVwPmhtGUlRTMD0zr7Ircw5Imt1WSmxHPdYnu9xRTiTGLcLu68oIi3Klupau6JSJtv2LA6Jyic\nc/j3Ay8Hvs4Hxt5pqQs8Zhurl+Syp7aDunbjp3VOnOrljSPNfPqCIuJi5LaLcJY7zi8izu2K2Cj/\npX2NZKbEc57NpnMAJtx1Sym1CZg1zlMPa62fD7zmYWAY+O1UA1BKrQXWAuTk5FBeXj7VS5hiptcP\nwM+ee4fLsgYMjfsXe/qJUTDbV0d5uTUOeu7p6Ymav6twkT6b54JZLn637QRLYpvJSjJu0HOqs4fX\nD/ZyaUEMb21507B2zDJhwtdaf/xMzyul7gNuAK7UH+wdXA+MLRQvCDw23vUfBR4FKCsr0ytXrpww\naKt44thbHPa6uC4lFqPi3l3bwbZX3uHzq+ay5poFhrQxHeXl5Yb12aqkz+ZZUNrHqh+W82ZHGo+s\nPtewdr73+00M+gf47DVlXDTHfmdEh1qlcy3wVeBGrfXYuY0/AncopeKVUrOBecB7obRlRcFpndY+\nvyHX11rz7RcOkpkSzwMr5xjShhDRIDc1kbWXncULexvZecK4g4i2nxwmMyWe82fbbzoHQp/DfwTw\nABuVUruVUr8A0FofAJ4CDgKvAH+vtTZ/r9MwC1brbD9pTNde3n+SHSfa+eer55Mie94Lh/vc5XPI\n8sTz7RcPGnIQkXdwmL0tPltW5wSFWqUzV2tdqLVeHvh4YMxz39Faz9FaL9Bav3ym60Sr4pnJLM6f\nwfaTwxO/eIoGhn189+XDnD3LI9soCAEkx8fw5avnU1HTYcg25W8cbmbQjy2rc4Kk5CNEq5fkcrzT\nH/ZqnSe2nqCmzcvXV59j29GGEFN124pCzp7l4bsvH6Z/KLzvrF/a18iMOGXb6RyQhB+yG5bkoYCf\nvV4Vtmu29Q7y0zcqWbkgi4/NzwrbdYWIdm6X4hvXL6SuvY9fh3G//AMNnbx2oIkLct22HmBJwg9R\n0cwkrpsdyx921LLlaEtYrvnT1yvpHRjm66vPCcv1hLCTS+dlcsXZ2fz8jSpO9QyEfL0hn5+vPL2X\ntKQ4bppj700JJeGHwc1zYzkrK5mHnt1Hz0Bo8/nHWnp4ctsJPnV+EfNzPGGKUAh7+frqs/EO+fjP\nTZUhX+sX5cc42NjFt29eREqcfUf3IAk/LOLcih/ctpSGzj6++/KhkK71Hy8dJiHWzZeumh+m6ISw\nn7nZHj59fhG/e6+GqubuaV/naFM3P32jkuuX5nKtA7YtkYQfJiuKM7j/ktk8ua2Grcdap3WNN4+2\nsOlQE3+3ag6ZKfFhjlAIe/nix+eRFOvmWy8cmtb2ycM+P195eg+ehFi+deMiAyK0Hkn4YfTlqxdQ\nMjOJrz2zD+/g1KZ23jzawgO/2clZWcncf8lsgyIUwj5mpsTz5WsWsOVoC/+4roLB4aktgHzs7ffZ\nU9fJv964iJkOGWBJwg+jxDg337t1KTVtXr7/ypFJ/9yf9jTwN49vpyQzmT+svYiEWNvsJC2Eoe69\nuISHrjubF/c28tePb5/0QKuquYcfbzzK1Qtz+MRS+0/lBEnCD7MLzprJvRcV8/i71Wyvbpvw9U9u\nO8E/rqtgeWEa69ZeSJbHGSMNIcLlc5fP4fu3LuWdqlbueuzPdHjPfAauz6/56vo9JMa6+faaxShl\n7xu1Y0nCN8BXrz2b/LREHly/97SLQ7TWPPJGJd94bj+rFmTzxP0XkJoYG+FIhbCHT55XyH/feS77\n67v4q//dRlNX/2lf++ut1eyq6eCbn1hItichglGaTzZoMUByfAzfu3Updz72Zy7/wWaW5KeyMHcG\nC/NmsDA3lfz0RP79pUP88u33WVOaz/dvW0qsW373ChGKaxfn8n+fiWXtEzu47RdbefKvLyA9OY7D\njd0cbOjkYGMXBxu7ONTYzaoFWawptdURHZMiCd8gl8zN5GefKmXToSYONnTxxuFmgoUE8TEuBob9\n3HdxCf9yw0JcNl7ZJ0QkXTI3k9999kLu+7/3uOonW/7iRm5GchwLc2fwN5fN5nMfm+OoqZwgSfgG\n+sSyPD6xLA+A/iEfR052cygwypif4+HOC4oc+Y9OCCMtK0zj6Qcu5v/eeZ+8tMTRd9fZnnjH/3+T\nhB8hCbFulhWmsawwzexQhLC9udkpfGfNErPDsByZOBZCCIeQhC+EEA4hCV8IIRxCEr4QQjhEqIeY\n/0ApdVgptVcptUEplRZ4vEQp1Rc453b0rFshhBDmCXWEvxFYrLVeChwFHhrz3LHxzroVQghhjlAP\nMX9Nax3crWgbUBB6SEIIIYygtJ76PtLjXkipPwF/0Fo/qZQqAQ4wMurvAr6htX7rND+3FlgLkJOT\ns2LdunVhiSeSenp6SElJMTuMiJI+O4PT+hyt/V21atVOrXXZRK+bMOErpTYBs8Z56mGt9fOB1zwM\nlAG3aK21UioeSNFan1JKrQCeAxZprbsmaKsFODFR0BaUCUzv1JPoJX12Bqf1OVr7W6y1zproRSGP\n8JVS9wGfA67UWntP85py4Mta6x0hNWZRSqkdk/ntaifSZ2dwWp/t3t9Qq3SuBb4K3Dg22SulspRS\n7sDXZwHzgOOhtCWEECI0oe6l8wgQD2wMbEq0LVCR8zHgW0qpIcAPPKC1nvg0ECGEEIYJKeFrreee\n5vFngGdCuXaUedTsAEwgfXYGp/XZ1v0NW5WOEEIIa5OtFYQQwiEk4YeZUuqflVJaKZVpdixGO93W\nGnajlLpWKXVEKVWllPqa2fEYTSlVqJTarJQ6qJQ6oJT6gtkxRYpSyq2UqlBKvWB2LEaQhB9GSqlC\n4GqgxuxYIuRMW2vYQqDa7OfAdcBC4FNKqYXmRmW4YeCftdYLgQuBv3dAn4O+ABwyOwijSMIPr58w\nUqbqiBsjDtla43ygSmt9XGs9CKwDbjI5JkNprRu11rsCX3czkgBtf+K3UqoAuB54zOxYjCIJP0yU\nUjcB9VrrPWbHYpL7gZfNDsIA+UDtmO/rcEDyCwpsk1IK/NncSCLiPxkZsPknemG0kjNtp+BM20wA\nX2dkOsdWprC1xjDw20jGJoyllEphpLz6ixNtixLtlFI3AM1a651KqZVmx2MUSfhToLX++HiPK6WW\nALOBPYEFaAXALqXU+VrrkxEMMexO1+egwNYaNzCytYYdp7LqgcIx3xcEHrM1pVQsI8n+t1rrZ82O\nJwIuAW5USq0GEoAZSqkntdZ3mRxXWEkdvgGUUtVAmdY6GjdhmrTA1ho/Bi7XWreYHY8RlFIxjNyQ\nvpKRRL8d+LTW+oCpgRlIjYxaHgfatNZfNDueSAuM8L+stb7B7FjCTebwRSgeATyMbK1hy5PNAjel\nPw+8ysjNy6fsnOwDLgHuBq4Yc2rdarODEqGTEb4QQjiEjPCFEMIhJOELIYRDSMIXQgiHkIQvhBAO\nIQlfCCEcQhK+EEI4hCR8IYRwCEn4QgjhEP8flZJXywYd+qMAAAAASUVORK5CYII=\n",
            "text/plain": [
              "<Figure size 432x288 with 1 Axes>"
            ]
          },
          "metadata": {
            "tags": []
          }
        }
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "AnQ8mzMOnDRv",
        "colab_type": "text"
      },
      "source": [
        "Local Minima 3"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "9mXsahtOmG3N",
        "colab_type": "code",
        "outputId": "c2f0a145-7b7c-42a8-a7af-9d5223957f38",
        "colab": {
          "base_uri": "https://localhost:8080/",
          "height": 1000
        }
      },
      "source": [
        "\n",
        "x = 2.\n",
        "alpha = 0.05\n",
        "x_cache, dfx_cache = [],[]\n",
        "ax = plt.axes()\n",
        "t = np.linspace(-5, 5)\n",
        "ax.plot(t, f(t))\n",
        "ax.grid(True)\n",
        "for i in range(50):\n",
        "    slope = df(x)\n",
        "    x = param_update(x , alpha, slope)\n",
        "    x_cache.append(x)\n",
        "    dfx_cache.append(slope)\n",
        "    # print(x, slope)\n",
        "    if slope<0:\n",
        "        print('Go to Right|| -->> || ')\n",
        "    else:\n",
        "        print('Go to Left || <<-- ||')\n",
        "    draw_update(ax, t, x)\n",
        "print(f'Best Value: x={x}')\n",
        "print(f'Best Funtion Value: f(x)={f(x)}')"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "stream",
          "text": [
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Go to Right|| -->> || \n",
            "Go to Left || <<-- ||\n",
            "Best Value: x=3.6435971637604454\n",
            "Best Funtion Value: f(x)=-23.275658423511157\n"
          ],
          "name": "stdout"
        },
        {
          "output_type": "display_data",
          "data": {
            "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAD8CAYAAAB0IB+mAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3Xl8W9WZ8PHfkbzK+x7vDkkICWRx\nbNIGKE1adigQAi0MlNJ23rRv25npNrSUWToL0+nKtLTzdmhLoS3TlC3skAQasyaQOHZ2EidO4jXe\nN3mXdN4/JAWTOvEiXd0r6fl+PvpgS+Ke5yTO46Nzn3OO0lojhBAi8tnMDkAIIURoSMIXQogoIQlf\nCCGihCR8IYSIEpLwhRAiSkjCF0KIKCEJXwghooQkfCGEiBKS8IUQIkrEmB3ARNnZ2bqsrMzsMGZs\ncHCQpKQks8MIKelzdIi2Podrf6urqzu11jlTvc9SCb+srIydO3eaHcaMVVVVsXr1arPDCCnpc3SI\ntj6Ha3+VUiem876gTOkopR5SSrUrpfZNeO67SqlmpVSt73FNMNoSQggxO8Gaw38YuGqS5+/XWi/3\nPV4MUltCCCFmISgJX2v9OtAdjGsJIYQwhtFVOl9RSu3xTflkGNyWEEKIs1DB2g9fKVUGPK+1vsD3\nfR7QCWjg34B8rfXnJvn/1gPrAfLy8io2bNgQlHhCyel0kpycbHYYISV9jg7R1udw7e+aNWuqtdaV\nU73PsIQ/3dcmqqys1FKlEx6kz9Eh2vocrv1VSk0r4Rs2paOUyp/w7Vpg35neK4QQwnjBKsv8I7AN\nWKiUalJKfR74gVJqr1JqD7AG+Fow2ppMc+8wP958iBNdg0Y1IYQQhnnozWO8sKfV8HaCsvBKa33b\nJE//JhjXno6+oXEe+PMRFuWnUpoVfqvkhBDR7ddv1PPhc7K4dmn+1G8OQETspVOQngBAS++wyZEI\nIcTMuD2atoFR8n15zEgRkfDTEmNJjLXT2jdidihCCDEj7QMjuD2a/LREw9uKiISvlCI/PYHWPhnh\nCyHCS0uvd6BaICP86StISzz1ByeEEOHCP1CVEf4M5KfJCF8IEX5a/SN8SfjTV5CeSPvAKONuj9mh\nCCHEtLX0DZMUZyc10fjd6iMo4SegNZyUG7dCiDDS0jtMfnoiSinD24qYhO+f/5JKHSFEOGntGyE/\nzfgbthBBCd9/h1vm8YUQ4aSldyQk8/cQQQnfP8KXSh0hRLgYdbnpdIZm0RVEUMJPio8hNSFGRvhC\niLDR1jcKhKZCByIo4YO3UkdG+EKIcNHir8GXEf7MSS2+ECKchHLRFURYwi9IT5QqHSFE2AjltgoQ\ngQm/e3CM4TG32aEIIcSUWnqHSXfE4ogzftEVRFjC99eyyrSOECIceGvwQzOdAxGX8GXxlRAifLT0\nDlMQokVXEGEJXw5CEUKEk9a+kZBV6EDwzrR9SCnVrpTaN+G5TKXUFqVUne+/GcFo62zmnJrSkRG+\nEMLahsZc9A2Ph+WUzsPAVac9923gVa31AuBV3/eGio+xk50cJ3P4QgjLC3WFDgQp4WutXwe6T3v6\nBuAR39ePADcGo62p5MtBKEKIMBDqGnwAI2uB8rTWrb6vTwJ5k71JKbUeWA+Ql5dHVVVVQI3GuUao\na/EEfJ2ZcDqdIW3PCqTP0SHa+hzK/r7WNA5A43u7GWkIze3UkBR/aq21Ukqf4bUHgQcBKisr9erV\nqwNqq6p/P4eqmwj0OjNqs6oqpO1ZgfQ5OkRbn0PZ35oth1H767jhitXExYQm4RvZSptSKh/A9992\nA9s6pSA9Aeeoi/6R8VA0J4QQs9LaN0x2cnzIkj0Ym/CfBT7j+/ozwDMGtnXKqVp8mccXQlhYa99I\nSGvwIXhlmX8EtgELlVJNSqnPA/8JXK6UqgMu831vuFO1+FKpI4SwsJbe4ZDesIUgzeFrrW87w0sf\nD8b1Z0JG+EIIq9Na09o3wqXn5oS03YhaaQuQmxKPTcl+OkII6+ofdjE05g7ZwSd+EZfwY+w28lIT\npBZfCGFZoT74xC/iEj74T76SEb4Qwpr8+akgXUb4AZOTr4QQVtbi2+9LpnSCwH/yldaTrvUSQghT\ntfYOE2NT5KTEh7TdiEz4+WkJjLo8dA+OmR2KEEL8hda+EfJSE7DbVEjbjdCELwehCCGsy1uDH9ob\nthChCV8OQhFCWJn34JPQzt9DhCZ8GeELIazK49GcNGFbBYjQhJ+VFEdcjE1G+EIIy+kcHGXM7Ql5\nSSZEaMK32RT5aQmnSp+EEMIq/Nu+yBx+EOWnJdAqI3whhMX41wjJCD+ICtISZQ5fCGE5LTLCD778\n9ARO9o/g9sjiKyGEdbT2DRMfYyMzKS7kbUduwk9LxO3RdAyMmh2KEEKc0tI3Qn5aAkqFdtEVRHDC\nl4NQhBBW1GrCwSd+EZvw/X+gUpophLCSlt6RkG+L7BeUE6/ORil1HBgA3IBLa11pdJvw/h1wOflK\nCGEVLreH9oERCk2o0IEQJHyfNVrrzhC1BUBqQgxJcXaZ0hFCWEbbwCgejUzpBJtSivz0RBnhCyEs\nw782yKwpnVAkfA1sVkpVK6XWh6C9U+QgFCGElZh18ImfMvqQEKVUoda6WSmVC2wB/kZr/fqE19cD\n6wHy8vIqNmzYELS2H9o3yu4ONz9d4wjaNSfjdDpJTk42tA2rkT5Hh2jrs9H9ffHYGI8dGue/P+7A\nERu8ssw1a9ZUT+f+qOFz+FrrZt9/25VSG4GVwOsTXn8QeBCgsrJSr169Omht17oO80ZzHRddcilx\nMcZ9mKmqqiKYcYcD6XN0iLY+G93fqv79JMc3cc3lawxr42wMndJRSiUppVL8XwNXAPuMbHOigrRE\ntIa2fpnHF0KYz6yDT/yMHuHnARt9K8pigP/VWr9scJun+G+MNPcOU5xp7LSOEEJMpaVv2JSDT/wM\nTfha63pgmZFtnM2pWny5cSuEsIDW3hGWFKaZ1n7ElmXC+3fCW6Q0UwhhspFxN12DY6bV4EOEJ/zE\nODtZSXE09cgIXwhhrmZfDX5RhiR8wxRnOmjsHjI7DCFElGvw5aESE+8nRkXCb5CEL4QwmX/gaWYB\nScQn/JLMRJp7h3G5PWaHIoSIYg1dQ8TH2MhJjjcthihI+A7cHi3HHQohTNXYM0RxpgObLfQHn/hF\nfML3f3ySeXwhhJkauodNnb+HKEj4/j9gmccXQphFa01j95AkfKPlpyUSY1OS8IUQpukZGsc56jJ9\nxX/EJ3y7TVGYkSgJXwhhGn/+KTaxBh+iIOGDd1qnURZfCSFM4r+HWJIlI3zDyeIrIYSZ3h/hS8I3\nXEmmg+7BMQZGxs0ORQgRhRq7h8hOjiMpPlTHiE8uKhK+/7dqY7dM6wghQq+he8j0G7YQghOvrGBi\naebiglSToxHTMTzm5kBrH4dOOom1K1ISYklNiCElIZaUhBhSEmLITIrDd9ZCxBkec9M95P1U6hxx\nMTDion/EW+mRlRTP0qI08tMSIrb/kaahe4iK0gyzw4iuhC/z+NaktWZfcz+7m3rZ09TLnqY+6tqd\nuD1nP285wxHLsuJ0lk94pDviQhR18LjcHg61DVDb2EttQy+1jb0c6XAy1XHT2cnexL+kMI1lxWlU\nlGSS5ogNTdBi2sbdHlp6h7lxeaHZoURHwk9zeEeHjT2S8K2m+kQ3//b8QWobewFvEl9alM7li/NY\nWpTOovwUtIb+kXEGfCPdgZFx+obHea/VmyRfO1x3KjnOzU6isjSDSxZkc/H8bLJN3LfkTMbdHnY3\n9vJGXSfb6rvY29TH8LgbgMykOJYXp3Pd0gLmpMWf+kSTHP/+p5uW3mH2Nvexu7GPvc29bD3UjtaQ\nFGfnS2vm8/lL5pIQaze5l8KvtXcEjzZ3l0w/wxO+Uuoq4KeAHfi11vo/jW5zMiVZsmumlTR2D/Gf\nL7/HC3tayUuN5761F3DpghyKMhJnPE3hHHWxp8k7Mq5p6GXzgTYer24CYFF+Kh9ZkM0l87O5sCyT\nxLjQJ0KtNUc7BnnrSCdv1HWyvb4L56gLm4ILCtP41IXFlJekU16cQXHm1P3PS02gvCQDVnm/Hxx1\nsbe5j9++dYwfbjrE/77TwN1XLeT6ZQUy5WMBDRbYJdPP0ISvlLIDvwAuB5qAHUqpZ7XWB4xsdzLF\nGQ4OtQ2Eullxmv6RcX6x9Qi/ffM4dpviq5ctYP2l5+CIm/2PYnJ8DBfNy+aiedkAuD2a/S19vFHX\nyZt1nTz81nEefL2eWLtiSWEalWWZVJZmUFmWSWZS8KeAXG4PB1r72XG8h53Hu9lxvIdO5yjgHeVd\nv7yAj8z3xhuMKZik+Bg+fE4WHz4ni21Hu/j3Fw7wdxtq+e1bx/nH6xZRUZoZcBti9hosUoMPxo/w\nVwJHfGfbopTaANwAhDzhl2Q6ePVgOx6PNnW3umj20t5W7n16Hz1DY6xbUcQ3r1jInLSEoLdjtymW\nFqWztCidL6+Zz9CYi3ePdbOtvovq4z2nfgEAzMtJYkVJBnNzkijNTKIk00FJloO0xKkTsX9u9kTX\nEA3d3sf+lj5qGnoZGvNO0RRlJPKRBd5PF5fMzzb8H/2qeVk895VLeKqmmR9ueo91/28b1y8r4Pvr\nlpry6UZ4E36sXTEnNfg/6zNldMIvBBonfN8EfMjgNidVnOlgzO2hbWDE1DMlo9Uztc187U+1LClM\n43efW8kFITzI2REXw+qFuaxemAt4zxbd29zHjuPdVB/v4c/vtdNVPfaB/yctMZbizETiY95Pkn19\nwzxw8G201rQPjNLSO8zE+8pxMTbm5yTzycpiKssyqCzNNOQX2lRsNsXNFUVcs2QOv3ytnp//uY6O\ngVF+c1dlQJ+kxOw0dg9RlOHAboGBptJTlQIEcnGlbgau0lr/te/7TwMf0lp/ZcJ71gPrAfLy8io2\nbNhgSCz7Ol38aOco96xMYGFmcEc6TqeT5OTkoF7T6mbS57dbXPxqzygLM218bUUC8THm/+Cfbtil\n6Rjy0DGsaR/yft05rHFP+PfhcruJsXt/dlLiFDkOG7mJilyHjRyHIj1eYbPgnHkgf/7R9rNtRH//\n5e1hkmIV37zQuF/+a9asqdZaV075Rq21YQ+8t5U2Tfj+HuCeM72/oqJCG+VYh1OXfut5/fjOxqBf\ne+vWrUG/ptVNt89PVjfqud9+Xt/6P9v04Oi4sUEZLJz/np+uadJzv/28vuWXb2vnyPT/HsK5z7Nh\nRH+X/csm/Z2n9gT9uhMBO/U0crLRK213AAuUUnOVUnHArcCzBrc5qYL0RGxK9sUPpSerm/jG47v5\n8DlZPHTXhTKdYKIblhdy/6eWs/N4N5/97Q4GR11mhxQV+obH6R0at0RJJhi8tYLW2gV8BdgEHAQe\n01rvN7LNM4mLsZGfliiLr0LkieomvvnEbi6al8VvPnOh3DC0gBuWF/LTW8upbuiRpB8ip3bJjIaE\nD6C1flFrfa7Wep7W+j6j2zub4kzZFz8Unqxu4u+f2M3F87L59Z2S7K3kE8sK+Omty6lu6OGu377L\n0JgkfSM1WqgGH6Jk8zS/Etkm2XCHTg5wz1N7WXVOFr/+TKUkewu6bmkBP7u1nJ0neviPFw+aHU5E\n86/ul4RvgpJMB+0Dowz7aqRFcI25PHz9sVpSEmJ44LZyWd5vYdcuzeevL5nLH7Y38PrhDrPDiVgN\n3UOkJcZOa11HKERVwvf/lm2SPXUM8fM/17G/pZ//uGkJWRbcw0Z80DeuWMj83GTufmIPfUNyVoQR\nGrqHLTN/D1Ga8GUeP/h2N/byi6qj3LSikCvPn2N2OGIaEmLt/OSTy+hwjvLd50yppYh4jd1DkvDN\nUiIJ3xAj426+/lgtuSnx/PMnzjc7HDEDS4vS+cqa+Wysaeblfa1mhxNR3B5NU481Dj7xi6qEn5UU\nhyPOLidfBdkPXj7E0Y5BfnjzMsvMVYrp+8rH5rOkMI3vbNxHx8Co2eFEjLb+EcbdWkb4ZlFKUZIp\n2yQH07ajXTz01jHuXFXKJQuyzQ5HzEKs3cZPPrkM56iL72zc618VLwL0/rbI1tm7K6oSPnjn8aU0\nMzgGRsb55uO7Kcty8O2rzzM7HBGABXkp/P0VC9lyoI0ndzWbHU5EaLDYoiuIxoSf4R3hyygmcPe9\ncJDWvmF+/Mnlsm1CBPjcJXNZWZbJvzy7n+ZemfYMVGP3EDbl3dbFKqIu4ZdkJjI87qbTOTb1m8UZ\n1fe52bCjkf9z6TmWOJxZBM5uU/zolmW4PJrvv/Se2eGEvYbuIQrSE4m1WyfNWieSEPEfQCHz+IF5\n6vA4mUlx/M3HFpgdigiikiwHn724jOf2tPDeyX6zwwlrDRYryYRoTPiy+Cpg79R3sa/Lzf/96DyS\n42UqJ9J84VLv3+uPNx82O5Sw1mixRVcQhQm/KMM3wu+ShD8bWmt+tPkQ6fGKT68qNTscYYA0Ryzr\nP3IOWw60Ud8r25DMxtCYi07nqKVq8CEKE35CrJ3clHiZ0pml1w53sON4D9fPi5W9ciLYZy+ZS2ZS\nHE/Wyb2u2fCv9ZGEbwFSiz87Wmt+vPkwRRmJXFokUzmRLDk+hi+tnsf+Lg/b67vMDifsWLEkE6I4\n4Ust/sxt2n+Svc19fPWyc4mxwIHMwlh3fLiU9HjFjzYdkjLmGZKEbyHFmQ5a+0cYc3nMDiVsuD3e\n0f05OUncuLzA7HBECCTE2rl+Xiw7T/RQJVsoz0hj9xDJ8TFkOKy11UhUJvySTAdaI4tLZuDZ3c3U\ntTv5+uXnEmOhumJhrEuLYijKSOTHm2WUPxON3d5N05Sy1idhw/7lKqW+q5RqVkrV+h7XGNXWTMk2\nyTMz7vZw/5Y6FuWncs0F+WaHI0Ioxqb46mXnsq+5n5f3nTQ7nLDR0D1EcYZ1Vtj6GT1Uu19rvdz3\neNHgtqZNtkmemcd3NtHQPcQ3rzgXm8zdR5215YXMy0nix1sO4/bIKH8qWmtLLrqCKJ3SyU2JJy7G\nJjdup2Fk3M0Df66jvCSdj52Xa3Y4wgR2m+Lrly/kSLuTZ2plY7WpdAyMMurynFrVbyVG19Z9RSl1\nJ7AT+IbWuuf0Nyil1gPrAfLy8qiqqjI4JK+seE31oRNUOdoCvpbT6QxZ3KH2WuM4rX1j3LEAXnvt\ntVPPR3KfzySa+5yoNcUpNn70wh4y+uosNzcdLMH4O67r8S5W62k6QlXV8cCDCiat9awfwCvAvkke\nNwB5gB3vp4j7gIemul5FRYUOlc8/vENf/pOqoFxr69atQbmO1Xg8Hn3l/a/pK+9/TXs8ng+8Fql9\nPpto7/PjOxt16bee128c7jAvIIMF4+/4T+826NJvPa+PdzoDD2iagJ16Gjk7oCkdrfVlWusLJnk8\no7Vu01q7tdYe4FfAykDaCrYFeckc6xxk3C2lmWeyvb6b904O8NmLyyJ2RCem77ql+WQlxfHw28fM\nDsXS6toHiI+xndrGxUqMrNKZWM6xFu/I3zIW5CYz7tackD11zuiRt4+T7ojlhuWFZociLCAh1s5f\nfaiEV99rl72ozqKu3cm8nGTsFixwMPKm7Q+UUnuVUnuANcDXDGxrxubnJgNwpH3A5EisqalniM0H\nTnLbyhLZM0eccvuHSrErxe+2HTc7FMuqa3Oeyi9WY1jC11p/Wmu9RGu9VGt9vda61ai2ZmNejj/h\nO02OxJp+v/0E4F1eL4TfnLQErrpgDn/a2cjgqMvscCxnaMxFc+8wC6It4VtdUnwMhemJ1EnC/wvD\nY27+tKORK8+fQ6GFjmcT1vDZi8sYGHGxsUZKNE93tH0Q8N4jtKKoTfjg/Uupa5OEf7pnapvpHRrn\nrovKzA5FWNCKkgyWFKbx8NvHZbuF09T5pojn56aYHMnkojvh5yZztMMpqwcn0Frz8NvHWZSfysq5\nmWaHIyxIKcVdF5VxpN3JW0dk6+SJ6tqdxNoVpRZcdAVRnvDn5yYz6vLIcYcT+Esx77qoVEoxxRld\nt0xKNCdT1+akLCvJUgeXT2TNqELE/7FLbty+T0oxxXTEx0iJ5mSOdjgtO38PUZ/wvX8xcuPWS0ox\nxUxIieYHjYy7OdE1aNn5e4jyhJ+WGEtearzcuPX5/fYTKKWkFFNMy5y0BK5eki8lmj7HOgfxaCxb\nkglRnvABFuSmyOIr3i/FvGJxnpRiimm766JSKdH08c8UyJSOhc3PTeZIuzPqy8ue3S2lmGLm/CWa\nj0iJJkfaBrApmJudZHYoZyQJPzeZwTE3rX0jZodiqj/taGRBbrKUYooZ8U4BllDX7qSmsdfscEx1\npMNJaVYS8THWvf8V9Ql/gdy45Uj7ALsaermlskhKMcWMXbu0gMRYO4/vbDQ7FFNZeQ8dP0n4ed47\n6nVt0TuP/3h1E3abYm15kdmhiDCUHB/DNUvyeW53K8NjbrPDMcW428OxzkFL37AFSfhkJsWRlRQX\ntbX4LreHp3Y1s2ZhLjkp8WaHI8LULZVFOEddvLzfUnskhsyJrkFcHm3pG7YgCR/wzuNH65TOa4c7\n6BgY5ZZKGd2L2fvQ3ExKMh08tqPJ7FBM4S/tnp9j3Rp8kIQPRHelzuM7m8hOjpMDykVAlFLcUlHE\ntvouGrujb+Wtf4ZgXq51K3RAEj7gvXHbNzxOh3PU7FBCqss5yqvvtXHj8kLL7v0hwse6iiKUgieq\no2+UX9fupCgjEUdcjNmhnJX8K+f9G7dHomzF7dO1LYy7NbdUFpsdiogABemJXDI/myeqm/BE2Q60\nde1Oy9+whQATvlLqFqXUfqWURylVedpr9yiljiilDimlrgwsTGNFY2mm1prHdzayrCiNhXOsPe8o\nwsctlcU09w6zrT56tk12e7Rv0zTr/zsKdIS/D7gJeH3ik0qpxcCtwPnAVcB/K6UsuxohJyWe1ISY\nU4cXRIN9zf28d3KAm2V0L4LoisV5pCbE8FgU1eQ3dg8x5vJYvgYfAkz4WuuDWutDk7x0A7BBaz2q\ntT4GHAFWBtKWkZRSp27cRovHqxuJj7Fx/bICs0MRESQh1s4Nywt5ed9J+obHzQ4nJPx5I+IT/lkU\nAhN/xTf5nrMs7yZq0ZHwR8bdPFPbwpXnzyEtMdbscESEuaWyiCt3v4r9nLlgs0FZGTz6qNlhGaYu\njBL+lLeUlVKvAHMmeelerfUzgQaglFoPrAfIy8ujqqoq0EvOLo6BcTqdYzy3eSspcTPbXsDpdJoW\n92y80+qib3ichbHds4473PocDNLn6cnZsoXvb/o5ieO+qrcTJ3B//vMcOniQ9ssuC36QQTSb/r65\nZ5SMeMWu7W8ZE1Qwaa0DfgBVQOWE7+8B7pnw/SZg1VTXqaio0GbZ+l6bLv3W8/qd+q6Z/79btwY/\nIAN9+jfv6Iu+96p2uz2zvka49TkYpM/TVFqqNfzlo7Q0yNEF32z6+4kH3tB3/Hp78IOZAWCnnkau\nNmpK51ngVqVUvFJqLrAAeNegtoLi1J46EX7jtqV3mDfqOli3ohCbTTZKEwZoaJjZ82HM49Ecabf+\npml+gZZlrlVKNQGrgBeUUpsAtNb7gceAA8DLwJe11pbeVakgLQFHnD3i5/Gf2tWE1nBzhVTnCIOU\nlMzs+TDW2j/C0Jg7OhK+1nqj1rpIax2vtc7TWl854bX7tNbztNYLtdYvBR6qsaKhUkdrzVO7mr37\nnmQ5zA5HRKr77gPHaT9fDof3+Qjj32V3gYXPsZ1IVtpOMD83OaLPt93d1Ed95yA3rbB0wZQId7ff\nDg8+iC4pwYOiK3sOPPig9/kI4x8ghsMqW5CE/wELclM42T9C/0hk1g9v3NVEfIyNq5fkmx2KiHS3\n3446cYLvPr2Hi77wEP3rPml2RIaoa3OSnRxHRlKc2aFMiyT8Cfy/pSNxWmfc7eG5Pa1ctjiP1ASp\nvRehsba8kFGXh5f3njQ7FEPUtQ+Ezfw9SML/gPkRnPBfP9xB9+AYa5fLdI4IneXF6czNTmJjTbPZ\noQSd1uFVoQOS8D+gONNBXIwtIhP+UzXNZCbF8dGFOWaHIqKIUooblxey/VgXLb3DZocTVB0Do/SP\nuMLmhi1Iwv8Au00xLyc54s637R8ZZ8uBNj6xNF/2vRcht7a8EK3h6drIGuXXhdkNW5CE/xcW5CZz\nOMIqdV7a28qYy8ON5TKdI0KvJMtBRWkGG3c1R9Spcv6B4XyLn2M7kST80ywuSKW5d5juwTGzQwma\njTXNzM1OYnlxutmhiCi1tryQunYn+1v6zQ4laPY095GdHE9OcrzZoUybJPzTlPuSYm1jj8mRBEdz\n7zDb67tZW16IUrKVgjDHdUvzibPbIurmbW1DL+Ul6WH170oS/mmWFKVhtylqGnrNDiUonvb9A7tR\nqnOEidIdcaw5L4dnaltwuT1mhxOwnsEx6jsHKS8Jr0/NkvBP44iL4bw5KRGR8LXWbKxpprI0Q7ZS\nEKZbW15Ip3OUN490mh1KwGqbvPmhvDjD5EhmRhL+JMpL0qlt7MUd5gcx72/p50i7k7WylYKwgDXn\n5ZKWGHvqU2c4q2noxaZgaVGa2aHMiCT8SZQXZ+AcdXG0I7yrdZ7a1Uyc3cZ1S+QYQ2G++Bg71y7N\nZ9P+NgZHXWaHE5Cahh4WzkklKX7KM6QsRRL+JFaUej+m1TSE741bl9vDs7tbWHNeDmkO2UpBWMPa\n8kKGx928vC98t1rweDS1jb2sCLP5e5CEP6myLAfpjtiwnsd/40gnnc5R1pYXmR2KEKdUlmZQnJkY\n1tU69Z1OBkZclJeE1/w9SMKflFKK8uL0sE74T9c0k5YYy5rzZCsFYR1KKdYuL+Sto5209Y+YHc6s\n7PLlhXCr0AFJ+GdUXpLB4faBsNwqeWBknE37T3Lt0nziY+xmhyPEB9zo32ohTEf5NQ09pCXGMjcr\nyexQZkwS/hmUl6SjNexp7DM7lBl7ae9JRsY93Fwh0znCes7JSWZFSTpP7moKy60Wahp6WV6cHpZn\nQgd6pu0tSqn9SimPUqpywvNlSqlhpVSt7/HLwEMNrWXF6SgVnjdun6hu4pzspFOrhoWwmnUVRRxu\nc7K3ObwGVM5RF4faBsJyOgcCH+HvA24CXp/ktaNa6+W+xxcDbCfkUhNimZ+TTE1jeM3jN3QN8e7x\nbtZVFIXVkm8RXa5bWkBcjI34nqEJAAAQZElEQVQnq5vMDmVG9jT2ojVhecMWAj/E/KDW+lCwgrGa\n8pJ0ahp6wupj55O7mlDKW/4mhFWlJcZyxeI8ntndwqjLbXY40+YfAC4vCs8RvpGrBuYqpWqAfuAf\ntNZvTPYmpdR6YD1AXl4eVVVVBoY0M47hcXqGxnnsxa3kJZ35d6PT6bRE3B6tefTtYRZn2jhc+w6H\nDWzLKn0OJelzcJ0b6+L5oXEeeGIrlXOssYBpqv5u2TVCfpKi5t23QhdUMGmtz/oAXsE7dXP644YJ\n76kCKid8Hw9k+b6uABqB1Knaqqio0FZysLVPl37ref3Ursazvm/r1q2hCWgK2452TiveYLBKn0NJ\n+hxc4y63rvz3LfrzD+8wrI2ZOlt/PR6PXvGvm/U3HqsNXUDTBOzUU+RXrfXUI3yt9WWz+CUyCoz6\nvq5WSh0FzgV2zvRaZlqQm0JSnJ2aht6wWMD0ZHUTSXF2rjx/jtmhCDGlGLuNteWFPPTmMTqdo2Rb\nfF/5xu5hugbHwvaGLRhUlqmUylFK2X1fnwMsAOqNaMtIdptiWZgswBoac/Hi3lauXZqPI84aH4+F\nmMq6FUW4PJpnalvMDmVKNb4zMsJth8yJAi3LXKuUagJWAS8opTb5XroU2KOUqgWeAL6ote4OLFRz\nlJekc7C1n+Exa99YennfSQbH3KxbYf1PIkL4LZyTwpLCtLCo1qlp6MURZ+fcMDrS8HSBVuls1FoX\naa3jtdZ5Wusrfc8/qbU+X3tLMldorZ8LTrihV16cgcuj2ddi7XrhJ3c1UZyZyIVlmWaHIsSMrFtR\nyIHWfg62Wvv4w5qGHpYWpRFjD9/1quEbeYgs983XWXkBVnPvMG8f7WLdiqKwXP0notv1ywuJtStL\nj/JHxt3sb+kP2/p7P0n4U8hOjqck02HpefyNu5rQGpnOEWEpMymOj52Xy9O1zYxb9PjD/S19uDw6\n7FevS8KfBu8CLGsmfK01T+5qZuXcTIoz5RhDEZ7WrSii0znG64c7zA5lUv5//8vDuEIHJOFPS3lx\nOif7R2jtGzY7lL+wq6GXY52DslGaCGtrzsslKymOJ3dZc1qnpqGXooxEclMSzA4lIJLwp8E/b2fF\nUf4T1U0kxtq5Zkm+2aEIMWuxdhvXLy/glQPt9A6NmR3OX6hp6An7+XuQhD8ti/JTiYuxWe7G7ci4\nm+f3tHDVBXNIDrOzNYU43boVRYz5jua0kpN9I7T0jYT9/D1Iwp+WuBgbSwrTLDfCf3Z3CwMjLj5Z\nWWx2KEIE7PyCVM4vSOXR7Q2W2rCw1r/gKszn70ES/rSVF6ezt7mPMZc1qgi01jzy9nHOzUvmw+dI\n7b0If0opPrOqjENtA2yvt846zZqGXuLsNhYXpJodSsAk4U9TZVkmoy4PO49b4wdxV0MP+1v6uXNV\nmex7LyLG9csLSHfE8rttx80O5ZQ36jpZWpQWEceFSsKfpo+em0NirJ0X9raaHQoAj7x9gpSEGNn3\nXkSUhFg7n7qwmM0H2mjpNb8q7ljnIAda+7nqgsjYkFAS/jQlxtn52Hm5bNp/ErfH3PnF9v4RXtzb\nyi0VxSTJzVoRYe74UCkerfnfdxrMDoUXfQO8SKmCk4Q/A9cuzafTOcY7x7pMjeOP7zbi8mg+varU\n1DiEMEJxpoOPn5fHH99tYGTc3E0LX9jTSnlJOgXpiabGESyS8GdgzcJc77TOHvOmdcbdHh595wQf\nPTeHudlJpsUhhJE+c1EpXYNjp0bYZvBP51wbIaN7kIQ/I1aY1nl530naB0a566IyU9oXIhQumZ/N\nOTlJPLLthGkxRNp0DkjCnzGzp3V+t+04JZkOPnpujintCxEK/hLN3Y291Daas/4l0qZzQBL+jJk5\nrbO/pY8dx3u4c1WpbIMsIt5NKwpJirPzu7ePh7ztSJzOAUn4M5YYZ+dji8yZ1vn9thMkxNq4pUJW\n1orIl5IQy7qKIp7f00qnczSkbUfidA4EfsThD5VS7yml9iilNiql0ie8do9S6ohS6pBS6srAQ7WO\na5eEflqnd2iMp2ubWVteSJojNmTtCmGmO1eVMub28KcdjSFtNxKncyDwEf4W4AKt9VLgMHAPgFJq\nMXArcD5wFfDf/kPNI4EZ0zqP7WxkZNzDnavKQtamEGabn5vCJfOz+cP2E7hCdDhKpE7nQOBn2m7W\nWrt8324H/Juy3wBs0FqPaq2PAUeAlYG0ZSUTp3VC8UPo9mh+v/0EK+dmsig//PfzEGIm7lxVSmvf\nCFsOtIWkvUidzoHgzuF/DnjJ93UhMPEzWJPvuYjhn9Z595jxe+ts2n+Sxu5h7pSFViIKfXxRHoXp\niTz4Rn1IdtF8PkKncwCmXJevlHoFmGwjiXu11s/43nMv4AIenWkASqn1wHqAvLw8qqqqZnoJU9jd\nmjg7/GpTNetKxw2L2+XRfPfNYQqTFYmdh6iqOmxIOzPldDrD5u8qWKTP5rm80M3D+3v50Z9e5cI5\nxm0nUt/h5GCr4rbz4izR72Cb8k9Oa33Z2V5XSt0FXAd8XL//67cZmFhKUuR7brLrPwg8CFBZWalX\nr149ZdBWcXnbLt6p7+KORUkYFfev36infeggj3xupaVq76uqqgzrs1VJn83zEY9m+8/e4NkGF397\n80cM27nyud9sBsb5mxsvicgRfqBVOlcBdwPXa62HJrz0LHCrUipeKTUXWAC8G0hbVuSf1jnUY8w8\nfs/gGD97tY5Lz82xVLIXItTsNsW91y6isXuYRwysy3/3pDtip3Mg8Dn8nwMpwBalVK1S6pcAWuv9\nwGPAAeBl4Mtaa3N3QTKAv1pnx0nX1G+ehZ++Wodz1MW91ywy5PpChJOPLMhhzcIcHnj1CF0G1OUf\n6xykccATkdU5foFW6czXWhdrrZf7Hl+c8Np9Wut5WuuFWuuXznadcOWv1qlucwW9Wudoh5M/bD/B\nrStLWDgnJajXFiJcfeeaRQyNu/npq3VBv3YkV+f4yUrbAF27JJ/+Me+pOMH0vRffIyHWztcuOzeo\n1xUinC3IS+G2lcX0P/QI48UlYLNBWRk8OuN6kQ9wezRP1zQzL80WsdM5IAk/YB87L5ecRMV3n9vP\n8FhwZq3ePtrJKwfb+NKaeeSkxAflmkJEiru7d/G9lx4gtqkRtIYTJ2D9+oCS/kNvHqOu3cnlpZG9\nil0SfoASYu187oJ4TnQN8aPNhwK+ntuj+ffnD1KYnsjnLp4bhAiFiCyp//rPJI6fNoc/NAT33jur\n69V3OPnR5kNctiiXD+VHzIYAk5KEHwSLsuzc8eESHnrrGNUnAluI9dSuJg609nP3VQtJiI3sHz4h\nZqXhDEcfnun5s/B4NN96cg/xMTbuW7sEpSJ7F1pJ+EHy7asXUZCWyN8/sWfWx7INjbn44aZDLC9O\n5/plBUGOUIgIUVIys+fP4pFtx9lxvId/+sT55KUmBBZXGJCEHyTJ8TF8f91S6jsGuf+Vma+Gdbk9\n/MPGfbQPjPKP1y2K+JGGELN2333gcHzgKU9iovf5GTjRNcgPXj7E6oU5rFsRUTu/nJEk/CC6ZEE2\nt60s5lev11PT0DPt/29k3M2XHt3FUzXNfP3yc6kozTQwSiHC3O23w4MPQmkpWila03O55+q/YefF\nV0/7Eh6P5u4n9hBjU3zvpsifyvGThB9k91yziLzUBO5+Yg+jrqmndgZGxvnsb3ew+UAb3/3EYv72\n4wtCEKUQYe722+H4cZTHg7v+GO+uupo7fvMOWw+1n/3/e/RRKCtDxdj58d038D/2Q+SnRW4Z5ukk\n4QdZakIs37tpCXXtTn42xeKQLucof/Wrd9hxvJv/+tRy7pKqHCFmrCjDweNfXMW8nGSevfuHDBUU\nTV6f/+ij3vLNEydQWlPU38Gq798TcA1/ODFu27kotnphLjdXFPHL1+opzUriwrJMSjMdHziHtrl3\nmE//+h1a+ob51Z2VrDkv18SIhQhv2cnxPJ56DNvLD5Aw5ivZPHEC7rjD+wA0cPrEjfKXc95+e0jj\nNYskfIP847WLefdYN3c/sQcAR5yd8+aksLgglfk5yfzP6/U4R138/vMf4sIymbMXIlCO7/4TjJ15\nj50zztLPopwzXEnCN0iaI5ZXvv5RDrcNcKC1nwMt/Rxo7eeZ2hYGRlxkJ8fz2BdWyQlWQgTLbBP3\nLMo5w5UkfAPFxdi4oDCNCwrTTj2ntaapZ5jMpDiS4uWPX4igKSnxTuPMhMMx43LOcCY3bUNMKUVx\npkOSvRDBNkl9/lnZ7d7yziiZvwdJ+EKISOGvz8/Kmvq9sbHwyCNRlexBEr4QIpLcfjt0dsIf/gBx\ncZO/JysLfvvbqEv2IHP4QohIdPvtUZnQpxLombY/VEq9p5Tao5TaqJRK9z1fppQa9h17eOroQyGE\nEOYJdEpnC3CB1nopcBi4Z8JrRyc7+lAIIYQ5Aj3TdrPW2n+C93agKPCQhBBCGCGYN20/B0w8rHyu\nUqpGKfWaUuojQWxHCCHELCit9dnfoNQrwJxJXrpXa/2M7z33ApXATVprrZSKB5K11l1KqQrgaeB8\nrXX/JNdfD6wHyMvLq9iwYUNAHTKD0+kkOTnZ7DBCSvocHaKtz+Ha3zVr1lRrrSunet+UCX/KCyh1\nF/AF4ONa66EzvKcK+KbWeucU1+oAZrhUzhKygU6zgwgx6XN0iLY+h2t/S7XWOVO9KaCyTKXUVcDd\nwEcnJnulVA7QrbV2K6XOARYA9VNdbzoBW5FSaud0frtGEulzdIi2Pkd6fwOtw/85EA9s8Z0Ys91X\nkXMp8K9KqXHAA3xRax3Y6d5CCCECElDC11rPP8PzTwJPBnJtIYQQwSVbKwTHg2YHYALpc3SItj5H\ndH8DvmkrhBAiPMgIXwghooQk/CBTSn1DKaWVUtlmx2K0M+2lFGmUUlcppQ4ppY4opb5tdjxGU0oV\nK6W2KqUOKKX2K6X+zuyYQkUpZfctGH3e7FiMIAk/iJRSxcAVQLQcknm2vZQiglLKDvwCuBpYDNym\nlFpsblSGcwHf0FovBj4MfDkK+uz3d8BBs4MwiiT84Lof77qEqLgxEiV7Ka0Ejmit67XWY8AG4AaT\nYzKU1rpVa73L9/UA3gRYaG5UxlNKFQHXAr82OxajSMIPEqXUDUCz1nq32bGY5PS9lCJFIdA44fsm\noiD5+SmlyoBy4B1zIwmJ/8I7YPOYHYhR5ACUGTjbvkLAd/BO50SUGeyl5AIeDWVswlhKqWS862m+\nOtk+WJFEKXUd0K61rlZKrTY7HqNIwp8BrfVlkz2vlFoCzAV2+1YcFwG7lFIrtdYnQxhi0J2pz36+\nvZSuw7uXUiROZTUDxRO+L/I9F9GUUrF4k/2jWuunzI4nBC4GrldKXQMkAKlKqT9ore8wOa6gkjp8\nAyiljgOVWutw3IRp2nx7Kf0E715KHWbHYwSlVAzeG9Ifx5vodwB/pbXeb2pgBlLeUcsjePfD+qrZ\n8YSab4T/Ta31dWbHEmwyhy8C8XMgBe9eShF5lKXvpvRXgE14b14+FsnJ3udi4NPAxyYcU3qN2UGJ\nwMkIXwghooSM8IUQIkpIwhdCiCghCV8IIaKEJHwhhIgSkvCFECJKSMIXQogoIQlfCCGihCR8IYSI\nEv8fC+n+j090l4cAAAAASUVORK5CYII=\n",
            "text/plain": [
              "<Figure size 432x288 with 1 Axes>"
            ]
          },
          "metadata": {
            "tags": []
          }
        }
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "zMPLt0tGquMo",
        "colab_type": "text"
      },
      "source": [
        "**Final Observations:** \n",
        "\n",
        "1. Local Minima is not always global minima\n",
        "\n",
        "2. It depends on the initial startinig poing of the parameter\n",
        "\n",
        "3. Gradient descent will help you to navigate in the right direction to find the optimal value for the cost function\n",
        "\n",
        "**Exercises:** \n",
        "\n",
        "1. Try Changing the learning rate (alpha), such as 0.001 and 1. Observe the behaviour of your gradient descent funtion.\n",
        "\n",
        "2. Use random to generate initial x value. \n",
        "\n",
        "3. Try to solve a two dimentional optimization f(x1, x2)"
      ]
    }
  ]
}