Решение задачи №85 от UniLecs

unfinished_formula.hs

solve k =
  if k == 0
    then 0
    else extract . dropWhile (notSameOddity k') . dropWhile (notIncludes k') . enhance $ [0..]
  where
    k' = abs k
    sums = scanl (+) 0 [1..]
    enhance = zip3 (cycle [0, 1, 1, 0]) sums
    first  (x, _, _) = x
    second (_, x, _) = x
    third  (_, _, x) = x
    notIncludes k = (< k) . second
    notSameOddity k = (/= k `rem` 2) . first
    extract = third . head

assertEq x y =
    if x == y
    then return ()
    else error $ "Assertion violated: first argument is " ++ show x ++ " but second argument is " ++ show y
    
assertEq' = uncurry assertEq

main = do
    assertEq' (solve 2,  3)
    assertEq' (solve 12, 7)
    putStrLn "Tests passed"

Назовём последовательность вида
,
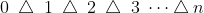где △ является + либо -, op(n)-последовательностью.
Обозначим через S(n) множество значений op(n) последовательностей при всех возможных подстановках △.
Теорема 1: для любого неотрицательного n элементы S(n) либо все чётные, либо все нечётные.
Доказательство: воспользуемся методом математической индукции.
Базис индукции: при n = 0 S(n) = {0}, т. е. все элементы чётные.
Шаг индукции: пусть все элементы S(n - 1) имеют одинаковую чётность.
op(n) можно получить, приписав △ n к op(n - 1). Любое число в S(n) получается прибавлением или вычитанием n к некоторому числу k из S(n - 1). Если n чётное, то k △ n имеет ту же чётность, что и k. Если же n нечётное, то k △ n и k имеют противоположные чётности. В любом случае оба полученных числа имеют одинаковую чётность. С учётом того, что все числа S(n - 1) имеют одинаковую чётность, получаем, что и в S(n) все числа имеют одинаковую чётность. ◼

Определим функцию

oddity(n) = 0, если все элементы S(n) чётные,
            1, если все элементы S(n) нечётные.

Теорема 2: функция oddity(n) является периодической, и её период равен 4.
Доказательство: рассмотрим величину m = n mod 4.
Если m = 0 или m = 3 (n = 4*k или n = 4*k + 3, k ∈ ℤ), то значение op(n) является суммой чётных чисел и чётного числа нечётных чисел, поэтому значение op(n) чётное.
Если m = 1 или m = 2 (n = 4*k + 1 или n = 4*k + 2, k ∈ ℤ), то значение op(n) является суммой чётных чисел и нечётного числа нечётных чисел, поэтому значение op(n) нечётное.
Так как функция n mod 4 является периодической с периодом 4, то такой же период имеет функция oddity. ◼

Обозначим

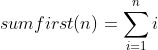
Теорема 3: S(n) — множество всех целых чисел отрезка [-sumfirst(n), sumfirst(n)] с той же чётностью, что и sumfirst(n).
Доказательство: воспользуемся методом математической индукции.
Базис индукции: при n = 0 S(n) = {0}, и все чётные точки из [-n, n] = [0, 0] = {0} принадлежат S(0).
Шаг индукции: пусть при n = k -1 ∀a: a ∈ ℤ ∩ [-sumfirst(-(k - 1)), sumfirst(k - 1)], a mod 2 = sumfirst(k -1) mod 2 ⇔ a ∈ S(k -1).

1. Рассмотрим произвольное m ∈ [-sumfirst(k), sumfirst(k)] такое, что m mod 2 = sumfirst(k) mod 2. Допустим, что m ∉ S(k).
   Если m ≥ 0, положим m̃ = m - k, иначе положим m̃ = m + k.
   Если m ≥ 0, то

0 ≤ m ≤ sumfirst(k)
-k ≤ m - k ≤ sumfirst(k) - k
sumfirst(k-1) ≤ m̃ ≤ sumfirst(k -1) (т. к. для всех неотрицательных целых k справедливо sumfirst(k) ≥ k)
Также
m̃ mod 2 = (m - k) mod 2 = (sumfirst(k) - k) mod 2 = sumfirst(k - 1) mod 2

Т. о., m̃ принадлежит множеству целых чисел отрезка [-sumfirst(k - 1), sumfirst(k - 1)] с той же чётностью, что и sumfirst(k -1). Тогда согласно посылке шага индукции m̃ ∈ S(k-1). Но тогда m = m̃ + k = op(k - 1) + k = 0 △ 1 △ … △ (k -1) + k = op(k), и, следовательно, m ∈ S(k), что противоречит нашему предположению. Следовательно, наше исходное предположение неверно и m ∈ S(k). Случай m < 0 рассматривается аналогично.
Т. о. мы получаем, что для любого m ∈ [-sumfirst(k), sumfirst(k)] такого, что m mod 2 = sumfirst(k) mod 2 справедливо m ∈ S(k).
2) Рассмотрим произвольное m ∈ S(k). В силу определения S(k) m ∈ [-sumfirst(k), sumfirst(k)].
m mod 2 = (0 △ 1 △ … △ (k -1) △ k) mod 2 = sumfirst(k) mod 2. Следовательно, m принадлежит множеству целых чисел отрезка [-sumfirst(k), sumfirst(k)] с той же чётностью, что и sumfirst(k -1) ◼

Из вышесказанного следует следующая простая идея решения: для данного k берём наименьшее n, для которого [-sumfirst(n), sumfirst(n)] включает |k|, а затем при необходимости корректируем n так, чтобы выполнялось oddity(n) = k mod 2. Согласно теореме 2, для этого понадобится увеличить n максимум на 2.
Так как компьютеры работают не с настоящими действительными числами, а с их аппроксимацией, вычислять n через неравенство sumfirst(n) >= k нежелательно, потому что при вычислении ответа используется квадратный корень, а для больших k значение квадратного корня может быть искажено отбрасыванием последних битов, не умещающихся в разрядную сетку. Во избежание ошибок подобного рода генерируется последовательность {sumfirst(0), sumfirst(1), sumfirst(2), …}, последовательные элементы которой сравниваются с k.