Created
February 7, 2021 20:42
-
-
Save CQCumbers/b71b5941ec22d88d45ecb201a133b233 to your computer and use it in GitHub Desktop.
N64 Fractal Path Tracer
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| #include <math.h> | |
| #include <stdint.h> | |
| #include <libdragon.h> | |
| typedef double vec3[3]; | |
| const double epsl = 0.0000005; | |
| // vector dot product | |
| static double dot(vec3 v0, vec3 v1) { | |
| double x2 = v0[0] * v1[0]; | |
| double y2 = v0[1] * v1[1]; | |
| double z2 = v0[2] * v1[2]; | |
| return x2 + y2 + z2; | |
| } | |
| // normalize vector v | |
| static void normalize(vec3 v) { | |
| double r = sqrt(dot(v, v)); | |
| v[0] /= r, v[1] /= r, v[2] /= r; | |
| } | |
| // reflect vector v across plane n | |
| static void reflect(vec3 v, vec3 n) { | |
| double c = 2 * fmax(0, dot(v, n)); | |
| v[0] = v[0] - c * n[0]; | |
| v[1] = v[1] - c * n[1]; | |
| v[2] = v[2] - c * n[2]; | |
| } | |
| // rescale vector v about point o | |
| static void rescale(vec3 v, vec3 o, double c) { | |
| v[0] = c * v[0] - (c - 1) * o[0]; | |
| v[1] = c * v[1] - (c - 1) * o[1]; | |
| v[2] = c * v[2] - (c - 1) * o[2]; | |
| } | |
| // position of ray at distance d | |
| static void ray_at(vec3 dir, vec3 pnt, double d, vec3 v) { | |
| v[0] = dir[0] * d + pnt[0]; | |
| v[1] = dir[1] * d + pnt[1]; | |
| v[2] = dir[2] * d + pnt[2]; | |
| } | |
| // get distance from point p to fractal | |
| // from Kaliedoscopic IFS reply 106 | |
| static double distance(vec3 p) { | |
| int maxI = 10, i = -1; | |
| double phi = 0.5 * (1 + sqrt(5)); | |
| vec3 n1 = { -phi, phi - 1, 1 }; | |
| vec3 n2 = { 1, -phi, phi + 1 }; | |
| vec3 v0 = { 1, phi - 1, 0 }; | |
| normalize(n1), normalize(n2), normalize(v0); | |
| while (++i < maxI) { | |
| p[1] = fabs(p[1]), p[2] = fabs(p[2]); | |
| reflect(p, n2), p[0] = fabs(p[0]); | |
| p[2] = fabs(p[2]), reflect(p, n1); | |
| rescale(p, v0, 2); | |
| } | |
| return (sqrt(dot(p, p)) - 2) * pow(2, -maxI); | |
| } | |
| // get number of steps to fractal from origin | |
| static int trace(vec3 dir, vec3 pnt, vec3 h, vec3 n) { | |
| int maxSteps = 255, steps = 0; | |
| double dist = 1000, total = 0; | |
| while (++steps <= maxSteps) { | |
| ray_at(dir, pnt, total, h); | |
| dist = distance((vec3){h[0],h[1],h[2]}); | |
| if (dist < epsl * 2) break; | |
| if (dist > 7) return 0; | |
| total += dist; | |
| } | |
| if (dist >= epsl * 2) return 0; | |
| n[0] = distance((vec3){ h[0] + epsl, h[1], h[2] }) - dist; | |
| n[1] = distance((vec3){ h[0], h[1] + epsl, h[2] }) - dist; | |
| n[2] = distance((vec3){ h[0], h[1], h[2] + epsl }) - dist; | |
| return normalize(n), 1; | |
| } | |
| static double halton2(unsigned num) { | |
| unsigned reversed = 0, base = 2; | |
| double inv = 1 / (double)base, invN = 1; | |
| while (num) { | |
| unsigned next = num / base; | |
| unsigned digit = num - next * base; | |
| reversed = reversed * base + digit; | |
| invN *= inv, num = next; | |
| } | |
| return reversed * invN; | |
| } | |
| static double halton3(unsigned num) { | |
| unsigned reversed = 0, base = 3; | |
| double inv = 1 / (double)base, invN = 1; | |
| while (num) { | |
| unsigned next = num / base; | |
| unsigned digit = num - next * base; | |
| reversed = reversed * base + digit; | |
| invN *= inv, num = next; | |
| } | |
| return reversed * invN; | |
| } | |
| // get cosine-weighted vector v | |
| // in hemisphere about vector n | |
| static void get_sample(vec3 n, vec3 v) { | |
| static unsigned i = 1; | |
| double u0 = halton2(i); | |
| double u1 = halton3(i++); | |
| // ray tracing gems 16.6.2 | |
| double a = 1 - 2 * u0; | |
| double b = sqrt(1 - a * a); | |
| double phi = 2 * M_PI * u1; | |
| v[0] = n[0] + b * cos(phi); | |
| v[1] = n[1] + b * sin(phi); | |
| v[2] = n[2] + a; | |
| normalize(v); | |
| } | |
| // get scene shade along ray | |
| static double shade(vec3 dir, vec3 pnt) { | |
| double hit[3], norm[3], lum = 255; | |
| for (int i = 0; i < 2; ++i) { | |
| if (trace(dir, pnt, hit, norm)) { | |
| get_sample(norm, dir), lum *= 0.875; | |
| ray_at(norm, hit, epsl * 2, pnt); | |
| } else return lum * (1 - dir[1]); | |
| } | |
| return 0; | |
| } | |
| // get camera ray from x/y fraction | |
| // uvw are orthogal unit vectors | |
| static void cam_ray(double x, double y, vec3 dir) { | |
| vec3 u = { 1/sqrt(2), 0, 1/sqrt(2) }; | |
| vec3 v = { -1/sqrt(6), sqrt(2)/sqrt(3), 1/sqrt(6) }; | |
| vec3 w = { -1/sqrt(3), -1/sqrt(3), 1/sqrt(3) }; | |
| dir[0] = x * u[0] + y * v[0] + w[0]; | |
| dir[1] = x * u[1] + y * v[1] + w[1]; | |
| dir[2] = x * u[2] + y * v[2] + w[2]; | |
| normalize(dir); | |
| } | |
| int main(void) { | |
| init_interrupts(); | |
| display_init( | |
| RESOLUTION_320x240, | |
| DEPTH_32_BPP, 2, GAMMA_NONE, | |
| ANTIALIAS_RESAMPLE | |
| ); | |
| display_context_t disp = 0; | |
| while(!(disp = display_lock())); | |
| double viewH = 1.5 / (double)240 / 4; | |
| double viewW = 2.0 / (double)320 / 4; | |
| display_show(disp); | |
| for (int y = 0; y < 240; ++y) { | |
| for (int x = 0; x < 320; ++x) { | |
| double h = viewH * (y - 120); | |
| double w = viewW * (x - 160); | |
| double lum = 0, spp = 32; | |
| for (int j = 0; j < spp; ++j) { | |
| vec3 dir, pnt = { 6/sqrt(3), 6/sqrt(3), -6/sqrt(3) }; | |
| cam_ray(w + halton2(j) * viewW, h + halton3(j) * viewH, dir); | |
| lum += shade(dir, pnt) / spp; | |
| } | |
| uint32_t color = (uint32_t)fmin(lum, 255) * 0x01010101; | |
| graphics_draw_pixel(disp, x, y, color); | |
| } | |
| } | |
| } |
Author
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
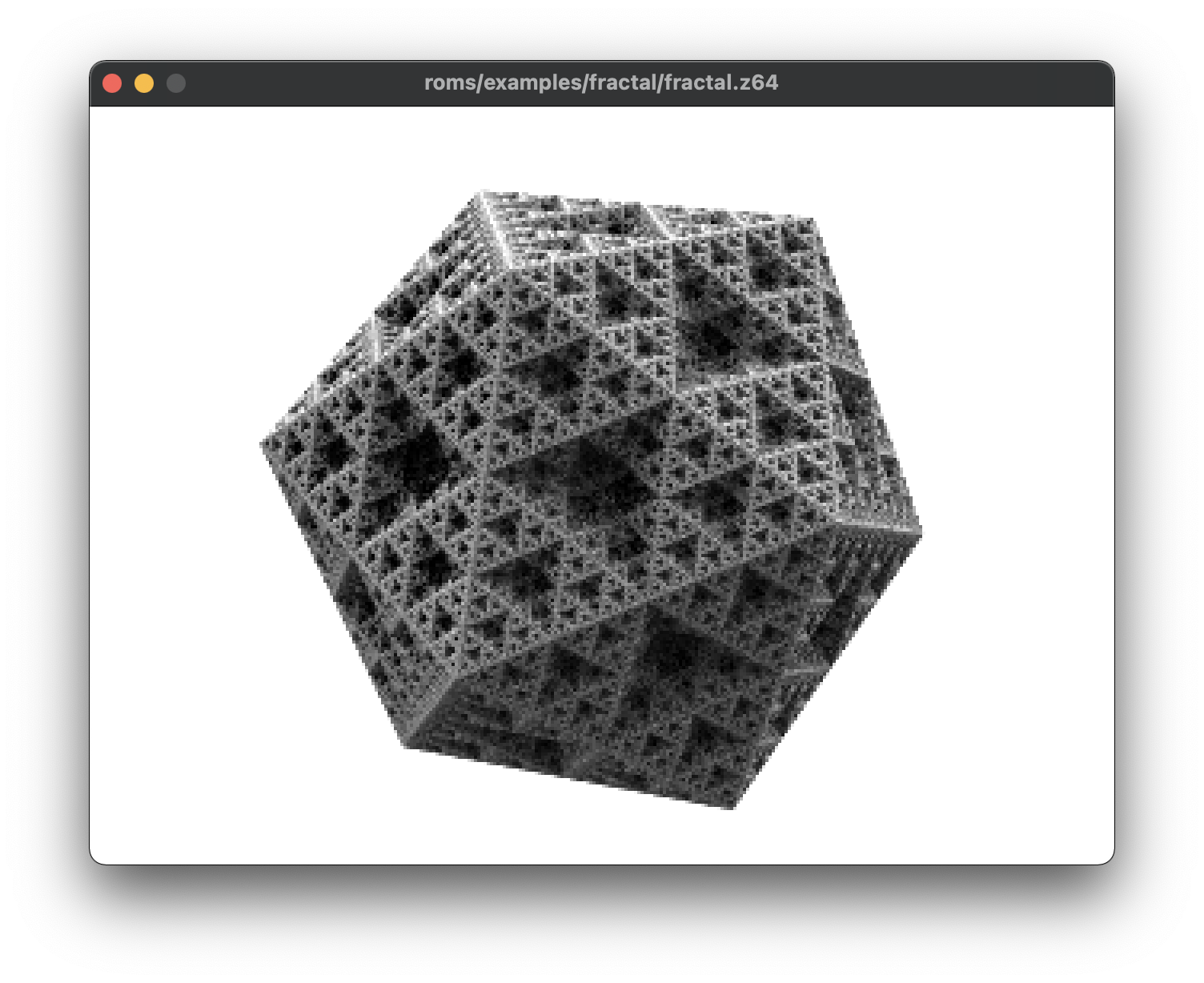
When compiled with libdragon for the Nintendo 64, this should render a Sierpinski icosahedron, as seen in the emulator screenshot: