-
-
Save JonathanMaes/52deb6c333c1033d5f5d22a25529eb31 to your computer and use it in GitHub Desktop.
| """ This script implements a class for calculating the Earth terminator. | |
| Additional functionality for calculating the boundary of the various | |
| twilight types and plotting these areas on a 2D map are also provided. | |
| -------------------------------------------------------------------------- | |
| Copyright (C) 2023 Jonathan Maes | |
| This program is free software: you can redistribute it and/or modify | |
| it under the terms of the GNU Lesser General Public License as published | |
| by the Free Software Foundation, either version 3 of the License, or | |
| (at your option) any later version. | |
| This program is distributed in the hope that it will be useful, | |
| but WITHOUT ANY WARRANTY; without even the implied warranty of | |
| MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the | |
| GNU Lesser General Public License for more details. | |
| See <https://www.gnu.org/licenses/> for the full text | |
| of the GNU Lesser General Public License. | |
| """ | |
| from datetime import datetime, timedelta | |
| import numpy as np | |
| class Terminator: | |
| def __init__(self, date: datetime = None, delta: float = 1, refraction: float = 0.83, calculate_polygons=True): | |
| """ Determines the area on Earth where the Sun is (more than) <refraction>° below the horizon at <date>. | |
| (This class has been adapted from https://stackoverflow.com/a/55653999). | |
| Arguments: | |
| @param date [datetime] (datetime.utcnow()): The time in UTC, used to calculate the position of the sun. | |
| @param delta [float] (0.1): Stepsize in degrees to determine the resolution of the polygon. | |
| @param refraction [float] (-0.83): Nighttime is considered when the sun is more than <refraction>° below the horizon. | |
| The default value corresponds to sunset, adjusted for refraction and the thickness of the solar disc. | |
| @param calculate_polygons [bool] (True): Set this to False for a small performance improvement. | |
| If False, <self.polygons> and <self.edges> are not calculated. | |
| Properties: | |
| (NOTE: all exposed properties and return-values corresponding to angles are in DEGREES) | |
| <self.date>, <self.delta> and <self.refraction> store the arguments that this class was initialized with. | |
| <self.solar_lon> and <self.solar_lat> give the longitude/latitude of the point on Earth where the Sun is at zenith. | |
| <self.terminator> contains unique coordinates of points on the terminator line. | |
| It is a tuple with two elements: (longitudes, latitudes), where each element is a 1D NumPy array. | |
| <self.edges> and <self.polygons> are intended for plotting, and are explained in the self.calc_polygons() documentation. | |
| NOTE: these two properties only exist if <calculate_polygons> is True, or after calling self.calc_polygons(). | |
| Methods: | |
| self.set_date() can be used to change the date, upon which all properties will be recalculated. | |
| self.calc_polygons() calculates the properties <self.polygons> and <self.edges>. | |
| It is called by default if <calculate_polygons> is True. | |
| Terminator.solar_position(date) for the coordinates where the sun is at zenith at a given datetime (staticmethod). | |
| Some 'private' methods that you usually won't be calling directly: | |
| Two techniques for calculating the terminator line are used: | |
| self._method_rotation() gives coordinates that are EQUALLY SPACED ON A SPHERE (poor resolution near poles) | |
| self._method_longitudes() gives coordinates with EQUALLY SPACED LONGITUDES (poor resolution near equator) | |
| self._sort() to sort all the coordinates (from _rotation and _longitudes) in clockwise order as seen from the sun. | |
| These two techniques are combined to give closely spaced coordinates both near the equator and the poles. | |
| """ | |
| if date is None: | |
| date = datetime.utcnow() | |
| elif date.utcoffset(): # make sure date is UTC, or naive with respect to time zones | |
| raise ValueError(f"Datetime instance must be UTC, not {date.tzname()}") | |
| self.delta, self.refraction = delta, refraction | |
| self.set_date(date) | |
| if calculate_polygons: self.calc_polygons() | |
| def set_date(self, date: datetime): | |
| if hasattr(self, 'date'): | |
| if date == self.date: return # No effort needed | |
| self.date = date | |
| self.solar_lon, self.solar_lat = self.solar_position(date) | |
| # Combine both methods, to get good resolution all around the terminator | |
| terminator_rotation = self._method_rotation() | |
| terminator_longitudes = self._method_longitudes() | |
| longitudes = np.append(terminator_rotation[0], terminator_longitudes[0]) | |
| latitudes = np.append(terminator_rotation[1], terminator_longitudes[1]) | |
| # Order the vertices anticlockwise as seen from the sun, because now they are not in any particular order. | |
| self.terminator = self._sort(longitudes, latitudes) # The UNCLOSED terminator line. To calculate closed polygons, use self.calc_polygons(). | |
| if hasattr(self, 'polygons'): self.calc_polygons() # Only calc_polygons() if it was already done before | |
| def _sort(self, longitudes: np.ndarray, latitudes: np.ndarray): | |
| """ Longitudes and latitudes are in DEGREES (both as input arguments and returned values). """ | |
| longitudes, latitudes = np.deg2rad((longitudes + 180) % 360 - 180), np.deg2rad(latitudes) | |
| solar_lat, solar_lon = np.deg2rad(self.solar_lat), np.deg2rad(self.solar_lon) | |
| # Convert lat/lon to cartesian vectors | |
| vec_sunlight = -np.asarray([np.cos(solar_lat)*np.cos(solar_lon), np.cos(solar_lat)*np.sin(solar_lon), np.sin(solar_lat)]) | |
| vec_vertices = np.asarray([np.cos(latitudes)*np.cos(longitudes), np.cos(latitudes)*np.sin(longitudes), np.sin(latitudes)]).T | |
| reference_right = np.cross(vec_sunlight, np.asarray([0, 0, 1])) # Rightmost point on earth as seen from the sun | |
| reference_up = np.cross(reference_right, vec_sunlight) # Northernmost point on earth as seen from sun | |
| # Determine angle of vec_vertices as seen from the sun w.r.t. reference_right | |
| projection = vec_vertices - np.tile((vec_sunlight*vec_vertices).sum(1), (3, 1)).T*vec_vertices | |
| sine = (reference_up*projection).sum(1)/np.linalg.norm(reference_up)/np.linalg.norm(projection, axis=1) | |
| cosine = (reference_right*projection).sum(1)/np.linalg.norm(reference_right)/np.linalg.norm(projection, axis=1) | |
| angles = np.arctan2(sine, cosine) | |
| # Sort clockwise as seen from the sun | |
| order = angles.argsort()[::-1] #! DO NOT CHANGE THIS DIRECTION, OTHERWISE self.calc_polygons() WILL NOT WORK CORRECTLY | |
| longitudes, latitudes = longitudes[order], latitudes[order] | |
| return np.rad2deg(longitudes), np.rad2deg(latitudes) | |
| def _method_rotation(self): | |
| """ This method returns coordinates (in DEGREES) that are EQUALLY SPACED ON A SPHERE. | |
| Reasoning: | |
| The terminator at the moment when the sun is directly above (0°N, 0°E) consists | |
| of the points (latitude, longitude). So one can then calculate where each point | |
| should move if the sun were be above (solar_lat, solar_lon) instead, by rotation. | |
| Source: rotation matrices in ℂ² from https://math.stackexchange.com/a/1847806, | |
| theta and phi are also defined according to the figure there. | |
| """ | |
| N = int(180/self.delta) | |
| longitude, latitude = np.empty(N*2), np.empty(N*2) | |
| # Fill latitudes up and then down, equally spaced | |
| latitude[:N] = np.linspace(-(90+self.refraction), 90+self.refraction, N) | |
| latitude[N:] = latitude[:N][::-1] | |
| # Fill the longitude values from the offset for midnight. | |
| with np.errstate(invalid='ignore'): # Ignore invalid values in arccos, we remove those nans later | |
| omega0 = np.rad2deg(np.arccos(np.sin(np.deg2rad(self.refraction)) / np.cos(np.deg2rad(latitude)))) # angle of sunrise/sunset from solar noon | |
| longitude[:N] = -(180 - omega0[:N]) # Negative longitudes | |
| longitude[N:] = 180 - omega0[N:] # Positive longitudes | |
| longitude, latitude = np.delete(longitude, [N, -1]), np.delete(latitude, [N, -1]) # Remove double entries | |
| # Clean x and y arrays (remove nans due to arccos, close loop) | |
| notnan = np.where(~np.isnan(longitude)) | |
| longitude, latitude = longitude[notnan], latitude[notnan] | |
| # Apply the rotation to put the sun at zenith above (lon, lat), using rotation matrices in ℂ² | |
| theta, phi = np.deg2rad(90 - latitude), np.deg2rad(longitude) | |
| d_theta, d_phi = np.deg2rad(self.solar_lat), np.deg2rad(self.solar_lon) | |
| matrix = np.matrix([np.cos(theta/2), np.exp(1j*phi)*np.sin(theta/2)]) # Represent original coords as complex number | |
| matrix = np.matrix([[np.cos(-d_theta/2), -np.sin(-d_theta/2)], [np.sin(-d_theta/2), np.cos(-d_theta/2)]])*matrix # Rotate about y-axis over -deltatheta | |
| z1, z2 = matrix # The two rows in the final matrix | |
| new_theta = 2*np.arctan(np.abs(z2)/np.abs(z1)) | |
| new_phi = (np.angle(z2) - np.angle(z1)) + d_phi | |
| new_theta, new_phi = np.asarray(new_theta).reshape(-1), np.asarray(new_phi).reshape(-1) # Matrix to array type | |
| # Clip lat/lon pairs to appropriate range (lon -180 -> 180, lat -90 -> 90) | |
| lon, lat = np.rad2deg(new_phi), 90 - np.rad2deg(new_theta) | |
| lat = ((lat + 90) % 360) - 90 # Latitude range -90 -> 270 | |
| excessive_latitudes = np.where(lat >= 90) # Latitude range -90 -> 90 | |
| lat[excessive_latitudes] = 180 - lat[excessive_latitudes] | |
| lon[excessive_latitudes] -= 180 # Because latitude at excessive_latitudes was changed | |
| lon = ((lon + 180) % 360) - 180 # Longitude ange -180 -> 180 | |
| return lon, lat | |
| def _method_longitudes(self): | |
| """ This method returns coordinates (in DEGREES) with EQUALLY SPACED LONGITUDES. | |
| Reasoning: | |
| An equation exists for the solar elevation at a given coordinate. It can be | |
| rewritten into a quadratic formula for sin(latitude), which can then be solved for | |
| any given longitude. The quadratic formula has 2 solutions, so an additional check | |
| is performed to retain only those solutions for which the original formula holds. | |
| Source: based on https://www.maplesoft.com/support/help/maple/view.aspx?path=MathApps%2FDayAndNightTerminator, | |
| which uses formulas similar to https://en.wikipedia.org/wiki/Sunrise_equation#Generalized_equation. | |
| """ | |
| solar_lat, solar_lon = np.deg2rad(self.solar_lat), np.deg2rad(self.solar_lon) | |
| refraction = np.deg2rad(self.refraction) | |
| longitudes = np.deg2rad(np.linspace(-180, 180, int(360//self.delta + 1))[:-1]) | |
| # Solve quadratic equation to find latitude(s) for given longitudes | |
| alpha = -refraction | |
| delta = solar_lat | |
| omega = solar_lon - longitudes | |
| denominator = (np.cos(delta)*np.cos(omega))**2 | |
| a = np.sin(delta)**2/denominator + 1 | |
| b = -2*np.sin(alpha)*np.sin(delta)/denominator | |
| c = np.sin(alpha)**2/denominator - 1 | |
| D = b**2 - 4*a*c | |
| valid = np.where(D >= 0) # Only at these longitudes will there be a terminator (for the given <refraction>) | |
| longitudes, a, b, c, D = longitudes[valid], a[valid], b[valid], c[valid], D[valid] | |
| # Separate in 'plus' and 'minus', due to quadratic formula having 2 solutions | |
| sine_phi_plus = (-b + np.sqrt(b**2 - 4*a*c))/(2*a) | |
| sine_phi_minus = (-b - np.sqrt(b**2 - 4*a*c))/(2*a) | |
| valid_plus = np.where(np.logical_and(sine_phi_plus >= -1, sine_phi_plus <= 1)) | |
| valid_minus = np.where(np.logical_and(sine_phi_minus >= -1, sine_phi_minus <= 1)) | |
| phi_plus = np.arcsin(sine_phi_plus[valid_plus]) | |
| phi_minus = np.arcsin(sine_phi_minus[valid_minus]) | |
| longitudes_plus = longitudes[valid_plus] | |
| longitudes_minus = longitudes[valid_minus] | |
| longitudes = np.append(longitudes_plus, longitudes_minus[::-1]) | |
| latitudes = np.append(phi_plus, phi_minus[::-1]) | |
| # Depending on the situation, up to half of these coordinates can be wrong. Therefore we do the following check. | |
| angle_to_sun = np.arccos(np.sin(latitudes)*np.sin(solar_lat) + np.cos(latitudes)*np.cos(solar_lat)*np.cos(np.abs(solar_lon-longitudes) % 360)) # See https://en.wikipedia.org/wiki/Great-circle_distance#Formulae | |
| ok = np.where(np.isclose(angle_to_sun, np.pi/2+refraction)) | |
| longitudes = longitudes[ok] | |
| latitudes = latitudes[ok] | |
| # Now that we have retained only the correct half of the solutions of the quadratic equation, we must | |
| return np.rad2deg(longitudes), np.rad2deg(latitudes) | |
| @staticmethod | |
| def solar_position(date: datetime): | |
| """ Returns tuple (longitude, latitude) in DEGREES where the sun is directly overhead at <date>. | |
| Source: Vallado, David 'Fundamentals of Astrodynamics and Applications', (2007), Chapter 5 (Algorithm 29) | |
| A more accurate coordinate can be calculated using other libraries, but the error of not accounting for the | |
| oblateness of the earth is probably the more significant factor in the error on the final terminator polygon. | |
| """ | |
| # NOTE: Constants are in degrees in the textbook, so we need to convert the values from deg2rad when taking sin/cos | |
| T_UT1 = (date - datetime(2000, 1, 1, 12, 0))/timedelta(days=1)/36525 # Centuries from J2000 | |
| lambda_M_sun = (280.460 + 36000.771*T_UT1) % 360 # solar longitude (deg) | |
| M_sun = (357.5277233 + 35999.05034*T_UT1) % 360 # solar anomaly (deg) | |
| lambda_ecliptic = (lambda_M_sun + 1.914666471*np.sin(np.deg2rad(M_sun)) + 0.019994643*np.sin(np.deg2rad(2*M_sun))) # ecliptic longitude | |
| epsilon = 23.439291 - 0.0130042*T_UT1 # obliquity of the ecliptic (epsilon in Vallado's notation) | |
| delta_sun = np.rad2deg(np.arcsin(np.sin(np.deg2rad(epsilon))*np.sin(np.deg2rad(lambda_ecliptic)))) # declination of the sun | |
| # Right ascension calculations | |
| numerator = (np.cos(np.deg2rad(epsilon))*np.sin(np.deg2rad(lambda_ecliptic))/np.cos(np.deg2rad(delta_sun))) | |
| denominator = (np.cos(np.deg2rad(lambda_ecliptic))/np.cos(np.deg2rad(delta_sun))) | |
| alpha_sun = np.rad2deg(np.arctan2(numerator, denominator)) | |
| # Longitude is opposite of Greenwich Hour Angle (GHA = theta_GMST - alpha_sun) | |
| theta_GMST = ((67310.54841 + (876600*3600 + 8640184.812866)*T_UT1 + 0.093104*T_UT1**2 - 6.2e-6*T_UT1**3) % 86400)/240 # Greenwich mean sidereal time (seconds), converted to degrees | |
| lon = -(theta_GMST - alpha_sun) | |
| if lon < -180: lon += 360 | |
| return lon, delta_sun | |
| def calc_polygons(self): | |
| """ NOTE: No calculations are done here, this method only exists for plotting on a 2D world map. | |
| When this function is called, two properties are added to this class: <self.polygons> and <self.edges>. | |
| Since it is possible that the terminator passes through the longitude boundary of ±180°, it | |
| is also possible that 2 lines or polygons are sometimes needed to fully cover the terminator | |
| or nighttime region of the Earth on a 2D map. | |
| Thus, <self.edges> and <self.polygons> are lists containing 1 or 2 elements, where each element | |
| has the same structure as <self.terminator>, i.e. a tuple of (longitudes, latitudes). | |
| -> <self.edges> is simply the terminator boundary, so just a subset of <self.terminator>. | |
| -> <self.polygons> is the same as <self.edges>, but with additional cooridinates added such that | |
| plotting <self.polygons> as a polygon will nicely cover the entire nighttime area on a map. | |
| """ | |
| lon, lat = self.terminator | |
| # To determine number of transitions, polygon must be closed and all longitudes in range [-180,180) | |
| lon, lat = np.append(lon, lon[0]), np.append(lat, lat[0]) | |
| lon = (lon + 180) % 360 - 180 | |
| # Determine the indices of the transitions through the ±180° boundary | |
| get_transitions = lambda longitudes: np.where(np.abs(longitudes[:-1] - longitudes[1:]) > 180)[0] + 1 | |
| transitions = get_transitions(lon) | |
| self.polygons, self.edges = [], [] | |
| ## CASE 0 TRANSITIONS | |
| if transitions.size == 0: # Closed shape which does not cross the 180° boundary, so just return that without further ado | |
| self.edges.append((lon, lat)) | |
| if self.refraction < 0: # Then invert this shape by adding coordinates at (±180°, ±90°) | |
| lon = np.append(lon[::-1], [180, 180, -180, -180, 180]) | |
| lat = np.append(lat[::-1], [ 90, -90, -90, 90, 90]) | |
| self.polygons.append((lon, lat)) | |
| return | |
| ## CASE 1 OR 2 TRANSITIONS | |
| # If a transition contains a coordinate at exactly -180°, then copy that latitude to 180° to get perfect 2D shape on map | |
| for i, transition in enumerate(transitions[::-1]): # Go backwards, to avoid index problems when inserting those new 180° coordinates | |
| if np.isclose(lon[transition-1], -180): # Then the transition is -180 -> 179 or something similar | |
| lon = np.insert(lon, transition, 180) | |
| lat = np.insert(lat, transition, lat[transition-1]) | |
| if np.isclose(lon[transition], -180): # Then the transition is 179 -> -180 or something similar | |
| lon = np.insert(lon, transition, 180) | |
| lat = np.insert(lat, transition, lat[transition]) | |
| transitions = get_transitions(lon) # Recalculate the transition indices, because we may have inserted 180's before if there are transitions | |
| lon, lat = lon[:-1], lat[:-1] # Remove duplicated coordinates | |
| if transitions.size == 1: # sine across the globe --> add two vertices at north or south pole at ±180° to complete the polygon on map | |
| p = lon.argsort() | |
| lon, lat = lon[p], lat[p] | |
| self.edges.append((lon, lat)) | |
| y_level = -90 + 180*(self.solar_lat <= 0) # -90 if south pole is in darkness, 90 if north pole in darkness | |
| self.polygons.append((np.append(lon, [180, -180]), np.append(lat, [y_level, y_level]))) | |
| if transitions.size == 2: # shape does not enclose north/south pole, but is cut off by the ±180° edge --> return 2 shapes, each one side of ±180° edge | |
| self.polygons.append((lon[transitions[0]:transitions[1]], lat[transitions[0]:transitions[1]])) | |
| self.polygons.append((np.append(lon[transitions[1]:], lon[:transitions[0]]), np.append(lat[transitions[1]:], lat[:transitions[0]]))) | |
| self.edges = self.polygons.copy() | |
| if self.refraction < 0: # Then invert this shape by adding coordinates at (±180°, ±90°) | |
| if self.polygons[0][0][0] > 0: self.polygons = self.polygons[::-1] # Put the western polygon first | |
| longitudes = np.concatenate([self.polygons[0][0], [-180, 180], self.polygons[1][0], [180, -180]]) | |
| latitudes = np.concatenate([self.polygons[0][1], [-90, -90], self.polygons[1][1], [90, 90]]) | |
| self.polygons = [(longitudes, latitudes)] | |
| # Close each polygon again | |
| for i, polygon in enumerate(self.polygons): | |
| self.polygons[i] = tuple(np.append(p, p[0]) for p in polygon) | |
| if __name__ == "__main__": | |
| animate = False | |
| delta = 10 # Terminator resolution in degrees (10° for testing to clearly see any glitches if they occur) | |
| date = datetime.utcnow() | |
| dusk_dawn = Terminator(date, delta=delta, refraction=-10) | |
| sunrise_sunset = Terminator(date, delta=delta, refraction=0) | |
| civil_twilight = Terminator(date, delta=delta, refraction=6) | |
| nautical_twilight = Terminator(date, delta=delta, refraction=12) | |
| astronomical_twilight = Terminator(date, delta=delta, refraction=18) | |
| twilights = [dusk_dawn, sunrise_sunset, civil_twilight, nautical_twilight, astronomical_twilight] | |
| colors = ['#FFFF55', '#888888', '#666666', '#333333', '#000000'] | |
| alpha = 1 | |
| import matplotlib.pyplot as plt | |
| def show_animation(date): | |
| import matplotlib.animation as animation | |
| fig, ax = plt.subplots() | |
| scat = ax.scatter([], [], color='y') # Show Sun at zenith | |
| fills = [ax.fill([], [], [], [], color=colors[i], alpha=alpha, edgecolor=None) for i in range(len(twilights))] # The four twilight types | |
| lines = [ax.plot([], [], [], [], color='y') for _ in twilights] # The four twilight lines | |
| ax.set_xlim(-180, 180) | |
| ax.set_ylim(-90, 90) | |
| ax.set_aspect('equal', adjustable='box') | |
| fig.tight_layout() | |
| def update(frame: int): | |
| dt = timedelta(days=2, minutes=10, seconds=np.random.random()) # Random amount of seconds to see as many cases as possible | |
| datenow = date + frame*dt | |
| for twilight in twilights: twilight.set_date(datenow) | |
| ax.set_title(str(datenow)) | |
| scat.set_offsets((sunrise_sunset.solar_lon, sunrise_sunset.solar_lat)) | |
| # Show various twilight types | |
| for i, terminator in enumerate(twilights): | |
| for j, polygon in enumerate(terminator.polygons): fills[i][j].set_xy(np.asarray(polygon).T) | |
| for j, edge in enumerate(terminator.edges): lines[i][j].set_data(np.asarray(edge)) | |
| if len(terminator.polygons) == 1: fills[i][1].set_xy([[0, 0]]) | |
| if len(terminator.edges) == 1: lines[i][1].set_data([[0], [0]]) | |
| update(0) | |
| ani = animation.FuncAnimation(fig=fig, func=update, frames=None, cache_frame_data=False, interval=32) | |
| plt.show() | |
| def show_plot(date): | |
| for twilight in twilights: twilight.set_date(date) | |
| fig, ax = plt.subplots() | |
| ax.set_title(str(date)) | |
| ax.scatter(sunrise_sunset.solar_lon, sunrise_sunset.solar_lat, color='y') | |
| # Show various twilight types | |
| for i, terminator in enumerate(twilights): | |
| for polygon in terminator.polygons: ax.fill(*polygon, color=colors[i], alpha=alpha, edgecolor=None) | |
| for edge in terminator.edges: ax.plot(*edge, color='y') | |
| ax.set_xlim(-180, 180) | |
| ax.set_ylim(-90, 90) | |
| ax.set_aspect('equal', adjustable='box') | |
| fig.tight_layout() | |
| plt.show() | |
| if animate: show_animation(date) | |
| else: show_plot(date) |
That code is not quite correct. I misunderstood y_level. There needs to be a check to make sure there is a vertex on -180 and 180 longitude. What is the code to get the latitude for -180 or 180 longitude?
That code is not quite correct. I misunderstood y_level. There needs to be a check to make sure there is a vertex on -180 and 180 longitude. What is the code to get the latitude for -180 or 180 longitude?
y_level is 90 or -90 depending on whether the north or south pole is in darkness.
The code for as_polygons probably contains some bugs and edge cases, because my main interest was the path rather than the polygon.
I do not know the code to get the latitude for 180 longitude: if such a formula exists, which gives the terminator latitude for a given longitude, then it would be much easier to use that formula for all longitudes instead of messing with these rotation matrices etc.
I don't know if such a formula exists or not, but I sadly did not find one.
I see online resources that compute the day/night polygons, but all their code is minimized. I have not been able to find anything myself. I have tried several algorithms, but there is always something lacking and I don't have sufficient math skills to figure out the rest of the problem. One idea I have thought about is to simply take the closest point to -180 and 180 degrees and then use the formula "Intersection of two paths given start points and bearings" from this site https://www.movable-type.co.uk/scripts/latlong.html to return the latitude point at -180/180 degrees. The first point and bearing could be the point closest to 180 degrees traveling to the closet point to -180+360 and the second point would be at (180, -90) with a 0 degree bearing. That should be a close approximation for the latitude at -180/180 degrees. What do you think?
@hamiltoncj I have derived an appropriate formula for terminator latitude(s) given a longitude, and consequently updated the code with a new method method_longitudes.
The idea is that there are now two possibilities for calculating the terminator:
method_rotationis how the terminator was calculated beforehand, which results in points equally spaced from each other on a sphere.method_longitudesis the new way, which gives points with equally spaced longitudes. I suppose it could be very easily adapted to calculate the latitude(s) of the terminator at a given longitude.
The difference between these two is obvious if you get close to the poles.
I also fixed the bug in as_polygons(), I hope it works well for every case now.
The two methods are shown below for delta=2, with method_rotation clearly showing that it is not the best for display on a 2D map, whereas method_longitudes is suitable.
Thanks! I will give it a try, hopefully this week.
@hamiltoncj The problem was that the method_longitudes did not return the terminator vertices in any particular order. But the as_polygons function assumes that the list of vertices it gets is ordered, such that there are no more than two pairs of successive longitudes that are further than 180° apart (i.e. where the terminator moves across the 180° line), because that is how it decides where to cut the list of vertices into separate polygons.
I solved this by adding an additional ordering at the end of method_longitudes, such that it returns the terminator polygon vertices in clockwise order as seen from the sun (so anticlockwise on the map).
Various improvements could still be made:
- Nighttimes for
refraction < 0will fill the daytime side when plotted withas_polygons, so I'll add a 'invert' optional argument toas_polygons. - As you can see,
method_longitudeshas low resolution near the equator, whilemethod_rotationhas low resolution near the poles. By combining both methods, the resolution will be good everywhere.
But I'll do that another time. I hope all the other issues are now fixed 😅
Haha, of course there is another.
That one seems to have been because the array of vertices was not closed, so I added an extra line in as_polygons to ensure that the first and last coordinates are the same. Now that specific case works again.
But the as_polygons method was written very quickly all those months ago, so it's probably better to use a plotting function in an existing library if such a thing exists. I expect the method_ functions to be correct by now, but I'm not as confident in as_polygons.
@hamiltoncj I have now combined the two methods to get good resolution both near the poles (method_rotation was bad there around equinoxes) and near the equator (method_longitudes was bad there around equinoxes).
I haven't observed any oddities in the plotting anymore (which I now changed to an animation to see as many cases as possible) with this new version of as_polygons , but I won't guarantee that it will work perfectly given the history in this comment section ;)
@JonathanMaes This is looking good and so far I have not found any other glitches. At some point it might be nice to have a function to return a sunrise_sunset line from -180 to 180 where refraction is always 0 or perhaps 0.83. I can take the polygon and simply remove the extra connecting points.
I'm going to add this to my QGIS plugin and then will test it some more and will let you know the results.
Thanks for all your help with this.
@JonathanMaes I don't know if this is consistent in all cases, but I am seeing that the first two coordinates are duplicated at the -180 boundary if it starts from there.
I realized that the first point's latitude was probably supposed to be -90 or 90, -180 to complete a polygon and then the second point is the terminator latitude, -180. For example
date = datetime(2023, 3, 28, 8, 0, 0, 0)
ss = Terminator(date, delta=4, refraction=0)
p = ss.as_polygons()
looking at the first three longitudes we have:
array([-180. , -180. , -176.
The latitudes are:
array([ 83.91401011, 83.91401011, 84.58580924,
I'm sure that first latitude should be 90.
It was because the initial array in _method_longitudes generates an np.linspace(-180, 180, N) but that final 180 eventually gets changed by the modulus operator to -180, hence the -180 point will always appear twice. Fixed now.
I'm not sure what the general rule of thumb is for polygon representation with the first and last points. In QGIS the last point should be the same as the first point to create a closed polygon, but it will draw it correctly if that is not the case. Where the code currently stands is that if the shape is closed in your code and not touching the -180,180 boundary the first and last points are the same. If it encounters the -180,180 boundary the first and last points are not the same. I think a polygon probably should be closed, but it should be consistent one way or the other.
Other than these minor issues I think your code is getting close to perfect. You may want to consider adding a license at the top such as the GNU Public License (GPL) Version 2 or any later version like QGIS does and add yourself as the author.
@JonathanMaes I never really asked, but are you fine with this code being used in the QGIS plugin released under a GNU 2 license. It is fine if you want it under a different open source license, but that would be important to include in the header comments of the code.
Thanks once again for figuring this out.
@hamiltoncj Sure, go ahead. I will be adding a license and fixing your most recent remarks in an update today or tomorrow.
I think I will (try to) make polygons consistently closed, and add an extra method or property to just get e.g. that single black line (so not closed, unless it doesn't cross the 180 boundary).
Thanks for finding all those bugs in the original code ;)
@hamiltoncj The rule I have used now for the closed-ness of the polygons is as follows:
self.terminatoris an unclosed line with no specific starting point.self.polygonsis a list of closed polygon(s) covering the nighttime areas, where the sun is more thanself.refraction° below the horizon.self.edgesis nearly the same asself.polygons, but without those additional coordinates at e.g. (±180,±90), so it purely represents the boundary line(s). Basically this is just the black line on your plot.
So basically, self.polygons can directly be used in a matplotlib plt.fill, while self.edges can directly be used in a simple plt.plot.
Note that as_polygons() was renamed to calc_polygons() and does not have a return value anymore; it now just sets the self.polygons and self.edges properties. There is also set_date() to recalculate the terminator for a different time.
The if __name__ == "__main__": block now also illustrates
self.edges, plotted as a yellow line for each terminator- that
calc_polygons()should now work correctly forrefraction < 0(so regions where the sun is above the horizon), as illustrated by the yellow terminator forrefraction=-10
Thanks again for pushing me to extend the functionality of this code to what it is now :)
This looks great. I tested it with a number of date/times and it worked flawlessly. I personally wont be needing any of the matplotlib functionality as I am creating a QGIS vector object from what your code returns. You might want to consider moving
import matplotlib.pyplot as plt
under
if name == "main":
or your sample code could be another python file. I am calling the function _solar_position(date: datetime) to get the sun location to plot. Is it normal to use an underscore for a static function? Should the underscore be there? Those are the only comments I have.
Great job and thanks for figuring this out.
Good point, I forgot that it was a staticmethod, so I removed the underscore.
You can just get the self.solar_lon and self.solar_lat values if you already have a Terminator though, so then there is no need to call Terminator.solar_position.
Do note that there are more accurate ways to calculate it using e.g. skyfield library; the current method is just an approximation to avoid adding non-stdlib dependencies.
I also finally removed the Pandas dependency, as it was only used once and could be changed to a simpler calculation with <1ms difference.
Looks good. I recognize that the solar position is more accurate using Skyfield, but I am using this in conjunction with day/night terminator. I have another implementation using Skyfield. I am hoping that at some point in time someone will implement a Skyfield version of this, but in looking at the the day/night terminator on the whole earth this is probably sufficient.
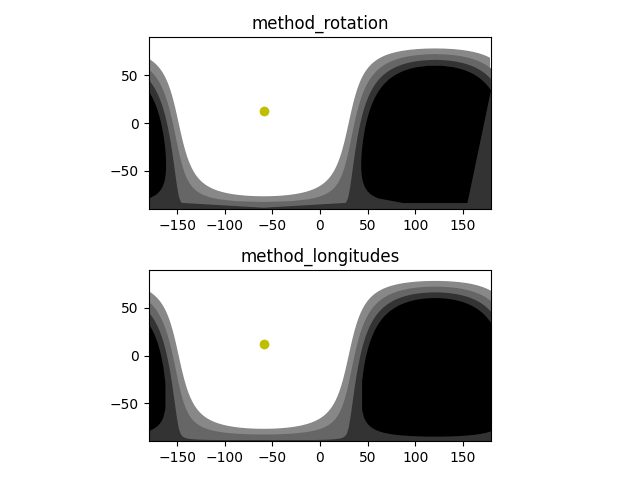
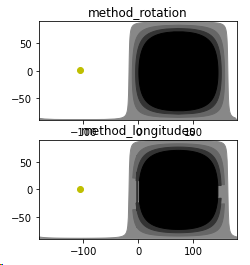
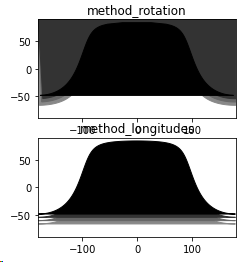
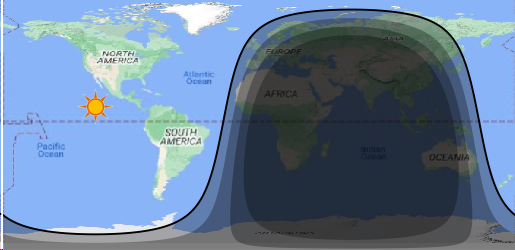
I posted this on the Skyfield thread, but should have done it here.
Jonathan, I am trying to adapt your code to work in the QGIS plugin Earth, Sun, Moon, and Planets (https://plugins.qgis.org/plugins/earthsunmoon/), at least until I can get a version that uses Skyfield. I have made one change in the code in "as_polygons". Rather than tacking on [180,-180] to the end of the array, I put [-180] and the beginning and [180] at the end. Without doing this it messes up the plots. In one case I just want the day/night terminator line and the rest of the time the polygon so I added in a check to see if I want a closed polygon generated or not. I add in extra coordinates to complete the polygon so that the drawing does not get confused in QGIS. Here are the changes for transitions.size == 1. I need to look at the other cases. transitions.size == 0 isn't working quite right. I'm not very good with NumPy so there may be a better way to make the changes.