Modern artificial intelligence systems and data algorithms that are great for modern application development, but are only sometimes fully applied to software and our daily lives.
This note/document teaches you how information breaks back into its original form, how quantum computers can perform such operations faster than classical computers, and why.
We can't have information using a single symbol, as there are no combinations to compare with it unless we divide the whole into two parts, such as 1 and 0, at the most abstract level.
We put everything in place values of two, and then compare the information and real-world data to its patterns and calculation functions (using the sum of products) that express the data, information, or mathematical calculations. This may not sound easy, but it is straightforward and anyone can understand it, as it is a basic and universal method. It may even shock you at how useful, simple, and widely implemented it is.
See Binary number for more details. Counting things in different quantities per column may seem complicated if you are learning this for the first time, but it is straightforward, and I will break it down for you in detail, providing a tool at the end.
People are generally used to counting things in ten symbols: 9 + 1 = 10.
As soon as we add 0 + 1 = 1, it becomes a 9 in a binary number, as we are at the edge of our number, using only two symbols to count zero and one.
| Eqivilent | Binary | Value |
| 0 + 1 = 1 (9) | 0 + 1 = 1 | 1 |
| 9 + 1 = 10 (90) | 1 + 1 = 10 | 2 |
| 90 + 1 = 91 (99) | 10 + 1 = 11 | 3 |
| 99 + 1 = 100 (900) | 11 + 1 = 100 | 4 |
We count the same way we usually do, except that 9 + 1 = 10 is the same as 1 + 1 = 10, using two symbols rather than ten symbols per column as 1 + 1 = 2, and there is no digit 2, so we move to the left and add a one to the next column same as 9+1=10 as there is no tenth symbol past 9.
We can convert all binary numbers into numbers composed of digits 0 to 9 and add one to determine the next binary number. 1011 + 1 = 1100 is the same as 9099 + 1 = 9100. Additionally, 9100 changes to 9900 because there are only two digits instead of ten in a binary value before adding to the next digit to the left; therefore, all other values between are invalid, except for nine and zero in scale.
Counting to 10 = 2 in binary twice makes 100 = 4, since we can only count to each digit twice instead of ten times. This also means that counting to 100 = 4 twice makes 1000 = 8 as we add a new digit to the left while counting.
We know the value 734 is 700 + 30 + 4 = 734 in much the same way that we know 1100 is 8 + 4 = 12 in binary per column.
We know that 7.34 is the same as 7 + 3÷10 + 4÷100 = 7.34. In much the same way that we know 1+1=10 is 2 in binary and that 0.1 + 0.1 = 1.0, which is 1 in value, so dividing 1 by 2 gives us the value 1÷2 = 0.5 in value from the decimal point 0.5+0.5=1. We know that 100 = 4 in binary; if we move this behind the decimal point as 0.01, we need to add 0.01 four times to reach 1.00, which represents the value of 1 in counting after the decimal point. It then has the same value as 1÷4=0.25 from the decimal point.
We then know that 0.11 is 1÷2 + 1÷4 = 0.75 from the decimal point in counting. We know that 0.01 is 1÷4=0.25 from the decimal point. We know that 11 + 1 in binary is 100 and that 0.11 + 0.01 is 1.00, the same as 0.75 + 0.25 = 1 in parts from the decimal point.
The decimal point marks a position in the number; meanwhile, the values below the decimal point are counted the same as regular numbers. This makes each place value a division out of the number of digits we use per place value, the farther away we move to the right. 7.34 is the same as 7 + 3÷10 + 4÷100 = 7.34 when using ten digits per place value from the decimal point.
Every number value can be represented in place values of two, much the same as place values of ten units away in counting to the right or left of the decimal point. You can use the following tool: rapidtables decimal to binary. This shows the steps of dividing a number up into place values of 2 when counting. Counting things in different quantities per column is part of a universal number-based conversion procedural method called radix and base. Mastering radix and base conversion is unnecessary, but a basic understanding is useful. The babyloinas used 60 symbols before moving to the left each time. This made each digit 60 times its place value each time we moved to the left or 60 to the right of the decimal point. It's that binary is as low or abstract as we can go when comparing data, which makes for easy analysis. It made possible all forms of arithmetic, math and complex hardware that run complex physics and even simulate reality.
In data science, we form the sum of products (SOP) of our program's code, math, or real-world data. We can remove all matching sums/comparisons, leaving behind the smallest logic that translates to math arithmetic and comparison logic for our program code or logic. See the following Truth table SOP. Don't worry if you still need to get it, as I will break down the terminology and make it easy to understand.
The SOP method applies to building computers as small as possible, as well as to the code running on them or to analyzing real-world data into patterns or arithmetic calculations and math theorems to run on a computer or as a dedicated digital circuit.
There are specialized software development tools that optimize code for developers and utilize the sum of products to push hardware to its limits. The code generated by these compilers for the computer to follow often does not even match the steps the developer put into the code.
At the smallest scale, we can represent all numbers as ones and zeros in a positional number system based on two digits per column rather than ten. We can even represent numbers like 3.1415 by adding a decimal point to our positional base two binary values.
| A | B | Out |
| 00 | 00 | 000 |
| 00 | 01 | 001 |
| 00 | 10 | 010 |
| 00 | 11 | 011 |
| 01 | 00 | 001 |
| 01 | 01 | 010 |
| 01 | 10 | 011 |
| 01 | 11 | 100 |
| 10 | 00 | 010 |
| 10 | 01 | 011 |
| 10 | 10 | 100 |
| 10 | 11 | 101 |
| 11 | 00 | 011 |
| 11 | 01 | 100 |
| 11 | 10 | 101 |
| 11 | 11 | 110 |
This is called creating a truth table for what you are analyzing. This is an addition in its most abstract form, using 1 and 0 to express the values.
When we have many inputs and outputs, as shown in the example below.
| A | B | Out1 | Out2 |
| 10 | 01 | 11 | 01 |
| 01 | 10 | 01 | 11 |
We join all inputs and outputs in each row to make it easier to analyze.
| Inputs | Outputs |
| 1001 | 1101 |
| 0110 | 0111 |
We convert them back into individual inputs and outputs at the end of the analysis. To form the sum of products for our data, we assign that 1 = true and 0 = false.
In English, we have a word called "NOT", which implies that if something is not true, it is false and that something that is not false is true. Another English word allows us to compare two or more statements in one sentence: "AND". If 2+3 is five and 7+1 is 8, then the sentence is true, as both comparisons are accurate; if one of the statements is false "OR" more, then the output is false = 0.
To solve the data precisely into what it is, you must compare each zero digit using "NOT" under one input combination to make them true, then use "AND" to output ONE if the combination is set.
If we have input "A" as 10 and input "B" as 01, then flipping all the zeros to ones as follows 1, NOT(0), NOT(0), 1 = 11, 11 will only be all ones if the inputs match. We then compare using "AND", which will only output a ONE if all values are ones. This limits to just one combination of the inputs.
x1 and not x2 and not x3 and x4
The values x1 to x2 are input "A", and the values x3 to x4 are input "B". The output will only be one if the input "A" is 10 and the input "B" is 01.
We take our comparison, which is only one when A=10 and B=01, and insert it into our output in places one and two, forming output 011=3. To do this, we write the comparison twice, shift to the left by one " << 1" for the second position, and to the left " << 0" for the first position; we then write this as
"(x1 and not x2 and not x3 and x4) << 1 = 10"
and add
"(x1 and not x2 and not x3 and x4) << 0 = 1".
To add digits together from the two expressions, we have the English word "OR", which is only false if all comparisons are false; this means if one comparison is true in the sentence or all-sum, the output is one. In our output, we use "OR" = "|" to combine the outputs together under the set condition.
This creates a single line that outputs the values we want to a specific set of inputs organized into expressions of "NOT", "AND", and "OR" in a three-step language.
The more digits that are ones at the output of a given input combination, the more times we have to write the same comparison and move the one output to the position of each digit of the output, then "OR" them together in one line.
You create a new line of code (expression) for input to the output of each row in the table of what you are analyzing. You then combine all separate lines with "OR". This creates the maximized version of our data or program logic.
This is the sum of product expression for our code/program, real-world data, or mathematical arithmetic logic.
This allows us to align anything we like to an absolute answer by eliminating all matching comparisons between inputs, thereby creating a combined output. You can see this done under the Log2 Int32 V3 function.
What is nice about this is that it is easy to understand and allows us to find the smallest calculations or math theorems for everything, from the smallest code for an application or program, to even the most complex ones. Additionally, it can be entirely automated with artificial intelligence, making it easier to solve extremely complex problems.
This allows us to find the smallest expression for data or any program or code, but we can still further reduce the size of our analyzed data, functions, or program code running on the computer.
It also enables us to determine the most effective way to write conversion algorithms or generation algorithms.
The last step in our analysis is to remove the combinations of xor and put them in the expression or code to shorten it. An XOR means "NOT A AND B" or "A AND NOT B", which means one or the other, but not both, are true. We call XOR a derived function as it is a combination of NOT, OR, and AND to create XOR.
This is because the sum of products for addition reduces to an XOR comparison 0+1=1, 1+0=1, which is 1 xor 0 = 1, and 0 xor 1 = 1, but 1 xor 1 is 0. When we add 1+1=10 in binary, we do 1 AND 1 = 10 for the next place value. When we take out all matching comparisons of addition in the sum of products, we end up with the pattern described here. We often call "XOR" a sum for the columns and "AND" a carry.
We then remove all (AND<<1)/XOR expressions with the addition operation in the code or use an addition logic circuit. We then replace all combinations that are "NOT(A) addition B" with the subtraction operation in the code or use a subtraction logic circuit. We replace all repeated additions that move to the left by one with multiply, and all subtracts that move to the right with divide.
Lastly, the difference between zero creates less than, greater than, and equal to. Any remaining XOR operations are equivalent to comparisons in programming code.
Relatively, all arithmetic functions are derivable from one another geometrically. There is a script at the end of this note that uses only "AND", "OR", and "NOT" to make every math operation and even comparison by implementing each derived arithmetic operation in combination with the next ones by function.
It is essential to note that the arithmetic logic for multiplying, dividing, adding, and subtracting does not change when we add a decimal point, as it is only a placeholder in our value. For example, adding four twenty-five times is 100; 0.04 added twenty-five times is 1.00, using the decimal point as an imaginary placeholder. The same applies to binary values.
You can design a simple function that translates truth tables or data into the smallest math function possible. You can even write a program that tests your program logic and code, and writes the smallest version of your program's code and logic. Optimization compilers already do an excellent job at doing this for the software developer. The resulting compiled instructions in the code do not match what the developer wrote for the logic and math of the program, usually because of auto-optimization. However, auto-optimization of gigabyte projects takes forever to compile with full optimization, so compilers resort to shortcuts and breaking down your code into smaller sections that can be auto-optimized.
This means optimizing your program's code and logic using the sum-of-products method, and further refining it by hand, as what needs to be fast is still essential.
I also found it fun breaking down "Math.sin/inverse", and "Math.cos/inverse" this way. It changes into a pattern, much like the division and multiplication functions. We can match our currently defined division and multiplication functions to the pattern to calculate sine and cosine faster as a series. Generally, we do not need to calculate it very far to be accurate, and we don't need a big logic circuit for it. This is because we are limited to the accuracy of a 64-bit floating point number, and higher accuracy is optional and generally not useful. The concept of floating-point numbers was to add a value to our binary numbers that specified the position of the placeholder in our binary numbers. The arithmetic logic for addition, subtraction, multiplication, and division remained the same universally.
Working this way, you can design all math functions and custom functions like an artist, where nothing is impossible. You can also define any function about anything in the world around you using real-world data and even derive all the math theorems we have discovered.
If you take the time to map what you want to solve, anything is possible. There are no limits to what you can solve or build the answer to. You also shouldn't need to rebuild the book of physics or calculus by analyzing what is from real-world data to what it really is.
You should be able to visualize your code and methods without resorting to automated breakdowns of your program's logic functions or auto-solving real-world data for everything in your reality.
However, it can be fun to reconstruct everything based on what we analyze in the real-world from real-world data. It can also give us a much deeper understanding when visualizing patterns/code or looking at a math formula. It also gives us a much deeper understanding of the world around us.
You can also use it to solve problems that originally had no answers in a quantum-solved way and automate the entire task. The difference is that quantum computers can use entanglement to align the answer across qubits, using measurement to give us our answer instantly.
In quantum computing, we have qubits that can be "up" or "down" as a "one", or "zero", or be both "one and zero in a superposition state". We can do the same thing with qubits as we did with "AND", "OR", and "NOT" except much faster as the qubits align to the answer using entanglement and measurement rather than us comparing everything in "AND" and "NOT," then "OR" everything together and cross out matches to outputs causing us to align to our answer. This solves all problems that are in place values of multiples of twos that require us to compare everything and find the result, known as O(n), varying time operations. This also means programming a quantum computer to do math along qubits is done differently to align to an answer. This also means some of the simpler calculations are easier to do on a digital system rather than on a quantum system. Aligning things to an absolute answer and analyzing data is faster on a quantum computer. A digital system can do such alignment and solve to an absolute answer using the sum of products (SOP) or, in reverse, using products of sums (POS) and refactoring the code or data we are analyzing, giving the smallest function for our real-world data or code. Both SOP and POS give the same smallest function or code; it's just that POS is faster when there are more ones than zeros, as we end up with fewer comparisons to reduce to get to the same smallest code or function.
We also use these methods to determine how to write complex algorithms or code in the most efficient way possible. Often, finding shortcuts allows us to avoid calculations and comparisons and reuse as much as possible when combining our outputs.
Generally, the SOP and POS methods of analyzing data and reducing code or large data from the binary back into arithmetic math functions and comparison into code and algorithms are the most abstract and straightforward we can go for data analysis and are the brute force methods for breaking everything down and combining everything back togther into functions and code or circuits to combine togther to build dedcated hardware.
Generally, we can subtract a prior number into the next to find the difference between the following number, which is much faster than a sum of products at the most abstract representation of our data or code.
We can combine the differences into expressions of our data as dimensional geometric equations, as there is a pattern that runs through all arithmetic combinations. This method generally gives us the smallest answer to the data differentially, making such alignments faster on the digital system using the defined math functions "addition", "subtraction", "multiplication", and "division".
Digital computers generally leverage this geometric structure into digital logic gates to make smaller computational combinational arithmetic logic units that can compute all math operations in a more compact package per splice in positional base two binary numbers.
If you want a faster, more modern automated method that solves all things matrixed geometrically faster without using the sum of products. You can use my Q-AI matrix: Link. It also has good documentation and shows the structure of all things and how it builds geometrically in as simple an explanation as possible.
You may also find it interesting how we can pick a single number apart into what it is see FL64 Number analysis library.
Scientifically, we know everything emerges from something simpler or abstract that creates complex systems between interacting parts called emergence.
You might also like the game of Life simulation. The game of life is a great example; see Let's Build a Computer in the Game of Life. In this video, you learn that "AND, OR, NOT" is a complete set of functional gates and what a Turing-complete system is.
You may also be interested in learning about configuration spaces; see Traversing Configuration Space.
Lastly, you may enjoy the following: In which 2swap Solved Klotski.
We know that we can solve everything or anything by mapping it this way, using the stat solve in the sum of products truth tables, or by using the differential method employed in my Q-AI matrix tool. What makes quantum computing so special is that it can solve all possibilities linearly into an answer much faster. See how quantum computing will work.
We can take emergence to its most extreme and think about the zero dimension; see the zero dimension explained.
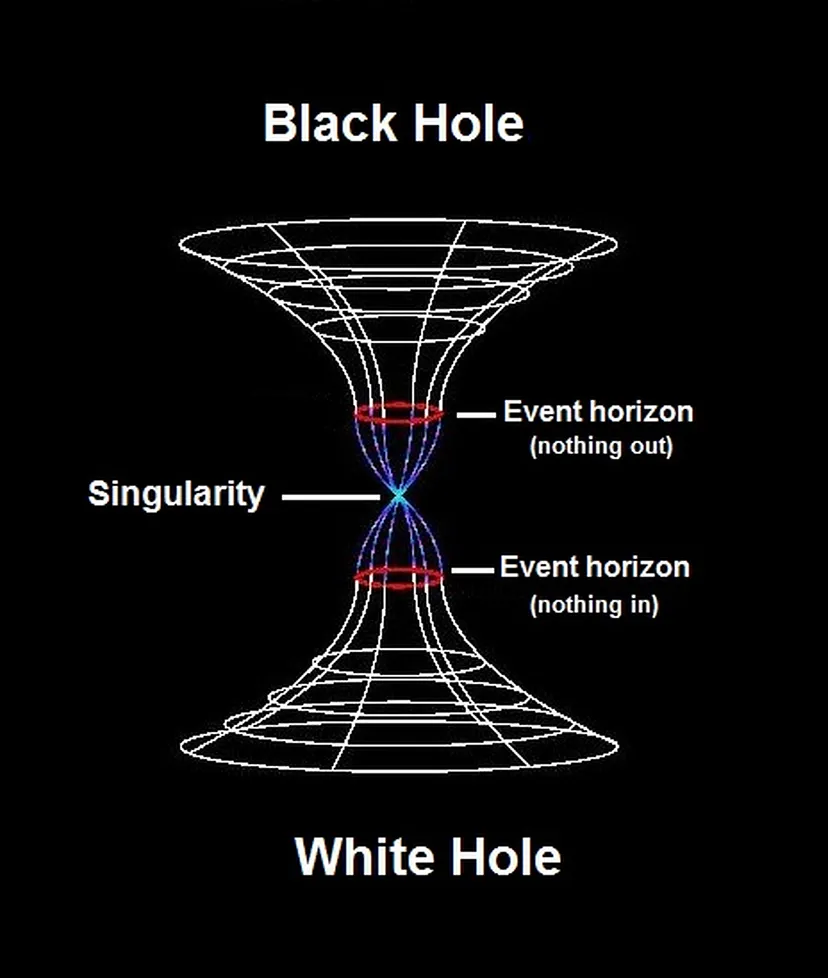
Energy is neither created nor destroyed. It just is and sums to zero. The object that contains it all is called a singularity.
If we take a circle and split it into two halves, with one half representing the positive and the other half representing the negative, the sum of the two halves equals zero. This is the initial fluctuation that begins anything at all called a quantum fluctuation, still summing to zero. It is also measurable using the Casimir effect and is the frontier of zero-point energy. An infinite and renewable form of energy research, see what if we harnessed zero point energy. The following video delves even deeper into the details, and it's also worth noting that this is a collective endeavour; see unlocking the quantum vacuum. However, I recommended watching it from the start.
Both white holes and black holes are opposite to each other and begin at the singularity.
We can think of these two extreme points as mirroring binary digits 1 and 0 from the whole (the singularity) at the most abstract level. However, within this singularity exists every possibility.
This zero, encapsulating 1 and 0, underlies the unfolding of reality from fluctuations at a singular point, embodying the wave function of the zero-point field that encompasses all known reality. Energy is neither created nor destroyed and equally sums to zero. All phenomena emerge from this void, akin to nothingness as infinite potential.
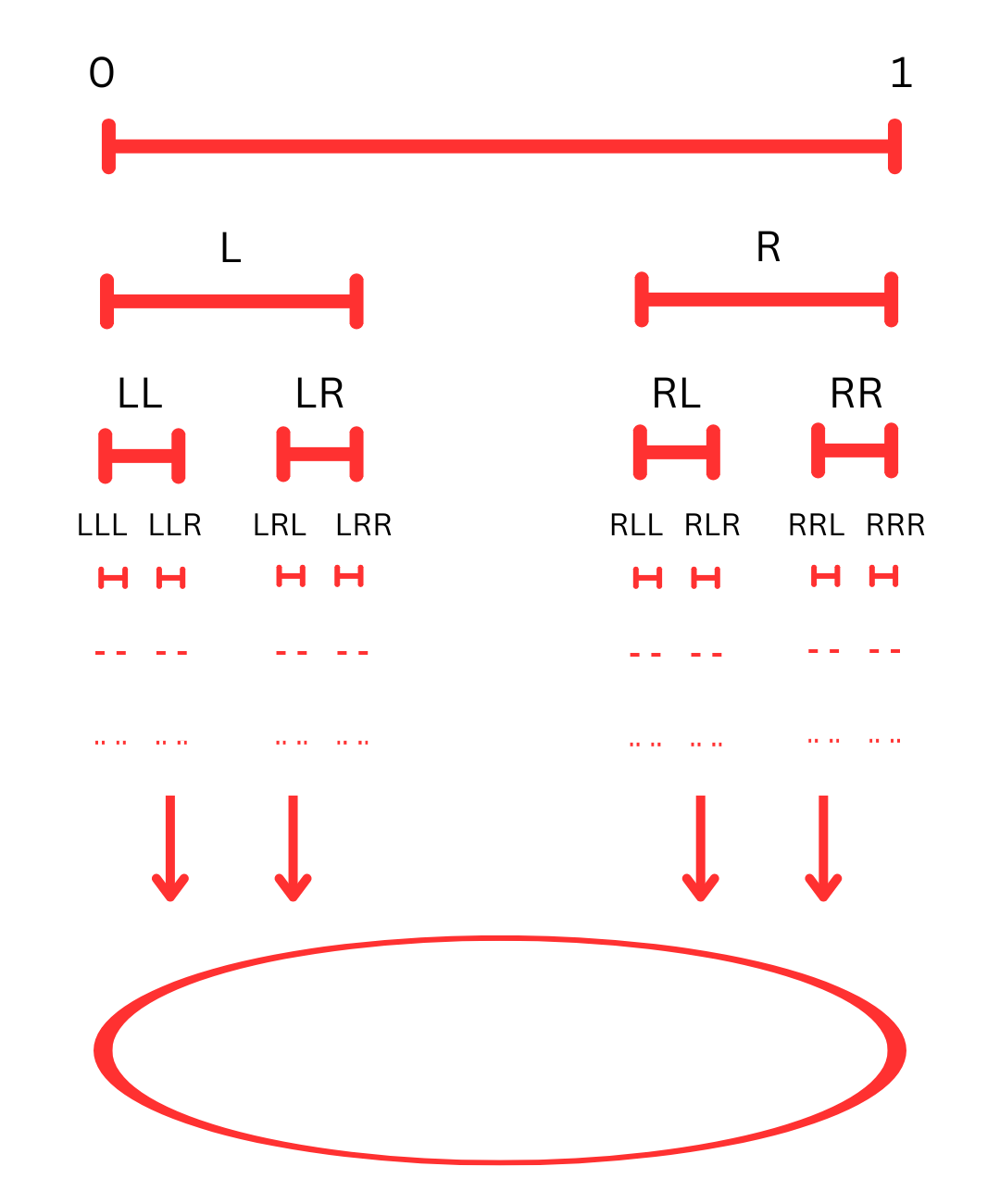
We can select paths choosing between 0=L and 1=R, much like the branching of a tree. As we navigate selecting branches, we can choose a new L=0 or R=1 that is added in continuation, while all additions contribute to zero in balance, creating perfect symmetry and expansion. We can generate all the information that comprises our current reality in a simulation spanning from a whole that contains it all, or create any song or video.
Our reality is a small place within this infinite expansion. Determining the exact path to our particular reality poses a highly complex problem. We use the microwave background of the Big Bang to map our particular universe. We have a fairly good model, but sometimes, we have to change the model to match what we did not know could exist based on observation of our emergent universe. Sending the James Webb telescope into space enables us to analyze a greater portion of our universe in greater detail, providing a more in-depth timeline of our emerging universe and everything within it.
Mind benders explains this in detail in a concept called the Library of Babel. Which turns out to be the most accurate description of what reality is and how it emerges at the smallest scale, revealing that everything is contained within a small section of what we call 'here and now'.
You may also like the following: Universe is a single whole.
Everything remains connected to a single fabric or whole, and the states of all units depend on one another and interact and create emergent properties from this whole in cause-effect relationships.
The separation between objects and particles may not exist as well, and all things are equal to zero as a single indivisible unit.
Everything spans from zero in quantum fluctuation and remains as a single invisible unit. It begins at a singularity which spans to what you call the Big Bang. The singularity existed before the Big Bang. There may be many more universes than just ours.
Alan Watts combines both scientific understanding and our existing knowledge in a simplified explanation.
Realize that everything connects to everything else (Leonardo da Vinci, 1452-1519).