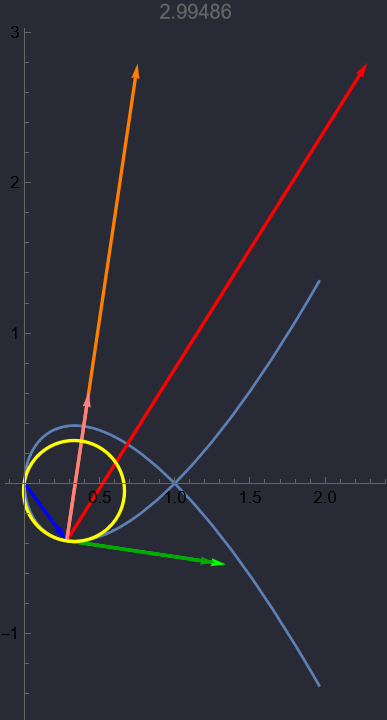
Visualisierung für beliebig parametrisierte Kurven

curves.nb

norm[x_] := Sqrt[Simplify[x . x]];

interval = 1.4;
f[t_] = {t^2, t^3 - t}; (* Kurve *)

v[t_] = D[f[t], t]; (* Geschwindigkeitsvektor *)
V[t_] = norm[v[t]]; (* Geschwindigkeit *)
a[t_] = D[v[t], t]; (* Beschleunigungsvektor *)

T[t_] = v[t]/
  V[t]; (* Tangentialvektor (Geschwindigkeitsvektor normiert) *)
nf[t_] = D[T[t], 
  t]; (* Normalvektor (aber wahrscheinlich nicht normiert) *)

k[t_] = norm[nf[t]]/V[t]; (* Krümmung *)
Nf[t_] = nf[t]/(k[t]*V[t]);(* Normalvektor *)

Manipulate[
 Show[
  ParametricPlot[{f[t]}, {t, -interval, interval}, 
   PlotLabel -> k[c]], (* Kurve *)
  Graphics[{
    Blue, Thick, Arrow[{{0, 0},  f[c]}],(* Kurvenvektor *)
    Green, Arrow[{f[c],  f[c] + v[c]}],(* Geschwindigkeitsvektor *)
    Red, Arrow[{f[c], f[c] + a[c]}], (* Beschleunigungsvektor *)
    Darker[Green], Arrow[{f[c],  f[c] + T[c]}],(* Tangentialvektor *)

    
    Orange, Arrow[{f[c], f[c] + nf[c]}], (* 
    Normalvektor aber nicht normiert *)
    Pink, Arrow[{f[c], f[c] + Nf[c]}],  (* Normalvektor *)
    Yellow, Circle[f[c] + Nf[c]*1/k[c], 1/k[c]] (* Krümmungskreis *)
    }]
  ], {c, -interval, interval}
 ]

curves3D.nb

norm[x_] := Sqrt[Simplify[x . x]];

interval = 2 Pi;
f[t_] = {Cos[t], 2 Sin[t], 0.5 t}; (* Kurve *)

v[t_] = D[f[t], t]; (* Geschwindigkeitsvektor *)
V[t_] = norm[v[t]];
a[t_] = D[v[t], t]; (* Beschleunigungsvektor *)

T[t_] = v[t]/
  V[t]; (* Tangentialvektor (Geschwindigkeitsvektor normiert) *)
nf[t_] = D[T[t], 
  t]; (* Normalvektor (aber wahrscheinlich nicht normiert) *)

k[t_] = norm[nf[t]]/V[t]; (* Krümmung *)
Nf[t_] = nf[t]/(k[t]*V[t]);(* Normalvektor *)
B[t_] = Cross[Nf[t], T[t]];
tau[t_] = -Nf[t] . -(D[B[t], t]/V[t]);
Manipulate[
 Show[
  ParametricPlot3D[{f[t]}, {t, -interval, interval}, 
   PlotLabel -> StringForm["`` - ``", k[c], tau[c]]], (* Kurve *)
  Graphics3D[{
    Blue, Thick, Arrow[{{0, 0, 0},  f[c]}],(* Kurvenvektor *)
    Green, Arrow[{f[c],  f[c] + v[c]}],(* Geschwindigkeitsvektor *)
    Red, Arrow[{f[c], f[c] + a[c]}], (* Beschleunigungsvektor *)
    Darker[Green], Arrow[{f[c],  f[c] + T[c]}],(* Tangentialvektor *)

    
    Orange, Arrow[{f[c], f[c] + nf[c]}], (* 
    Normalvektor aber nicht normiert *)
    Yellow, Arrow[{f[c], f[c] + B[c]}], (* 
    Normalvektor aber nicht normiert *)
    Pink, Arrow[{f[c], f[c] + Nf[c]}]  (* Normalvektor *)
    }]
  ], {c, -interval, interval}
 ]

Preview:

Preview 3D: