Created
February 6, 2019 13:42
-
-
Save SuperShinyEyes/63dc9c64b1efb8100bb014c1ed4450f0 to your computer and use it in GitHub Desktop.
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| def shelving(ys, cut_off, gain, mode='low'): | |
| '''Shelving filter for bass | |
| Args: | |
| ys (numpy.array): 1D signals | |
| cut_off (float): Normalized cut-off frequency. 0 < cut_off < 1 | |
| gain (float): gain in dB | |
| ''' | |
| gain = 10 ** (gain / 20) # NOTE: is it 20 or 40? | |
| wc = 2 * np.pi * cut_off / 44100 # cut_off frequency in radians(0 <= wc <= pi) | |
| tan_term = np.tan(wc / 2) | |
| gain_sqrt = np.sqrt(gain) | |
| if mode == 'low': | |
| a0_prime = tan_term + gain_sqrt | |
| a1_prime = tan_term - gain_sqrt | |
| b0_prime = gain * tan_term + gain_sqrt | |
| b1_prime = gain * tan_term - gain_sqrt | |
| else: | |
| a0_prime = gain_sqrt * tan_term + 1 | |
| a1_prime = gain_sqrt * tan_term - 1 | |
| b0_prime = gain_sqrt * tan_term + gain | |
| b1_prime = gain_sqrt * tan_term - gain | |
| a1 = a1_prime / a0_prime | |
| b0 = b0_prime / a0_prime | |
| b1 = b1_prime / a0_prime | |
| return signal.lfilter(b=[b0, b1], a=[1, a1], x=ys) |
Author
Author
Author
def shelving(cut_off, gain, mode='low'):
'''Shelving filter for bass
Args:
ys (numpy.array): 1D signals
cut_off (float): Normalized cut-off frequency. 0 < cut_off < 1
gain (float): gain in dB
'''
gain = 10 ** (gain / 20) # NOTE: is it 20 or 40?
wc = 2 * np.pi * cut_off / 44100 # cut_off frequency in radians(0 <= wc <= pi)
tan_term = np.tan(wc / 2)
gain_sqrt = np.sqrt(gain)
if mode == 'low':
a0_prime = tan_term + gain_sqrt
a1_prime = tan_term - gain_sqrt
b0_prime = gain * tan_term + gain_sqrt
b1_prime = gain * tan_term - gain_sqrt
else:
a0_prime = gain_sqrt * tan_term + 1
a1_prime = gain_sqrt * tan_term - 1
b0_prime = gain_sqrt * tan_term + gain
b1_prime = gain_sqrt * tan_term - gain
a1 = a1_prime / a0_prime
b0 = b0_prime / a0_prime
b1 = b1_prime / a0_prime
return [b0, b1], [1, a1]
gains = (4, 8, 12)
colors = ('r', 'g', 'b')
nfft = 2**14
cut_off = 1000
fig, ax1 = plt.subplots()
ax1.set_title(f'Digital filter frequency response. Cut-off @ {cut_off} Hz')
for g, c in zip(gains, colors):
b, a = shelving(cut_off=cut_off, gain=g, mode='low')
w, h = freqz(b, a, nfft, whole=False)
w *= 0.5 * sample_rate / np.pi
# plot amplitude in dB and frequency on log scale (essentially log-log)
# we were right, just looking at it wrong
ax1.semilogx(w, 20 * np.log10(abs(h)), c)
ax1.set_ylabel('Amplitude [dB]', color=c)
ax1.set_xlabel('Frequency [Hz]')
b, a = shelving(cut_off=cut_off, gain=-g, mode='low')
w, h = freqz(b, a, nfft, whole=False)
w *= 0.5 * sample_rate / np.pi
# plot amplitude in dB and frequency on log scale (essentially log-log)
# we were right, just looking at it wrong
ax1.semilogx(w, 20 * np.log10(abs(h)), c)
ax1.set_ylabel('Amplitude [dB]', color=c)
ax1.set_xlabel('Frequency [Hz]')
ax1.axvline(x=cut_off, label=f'cut-off at {cut_off} Hz', linestyle=(0, (5, 5)), color='black')
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment



gain = 10
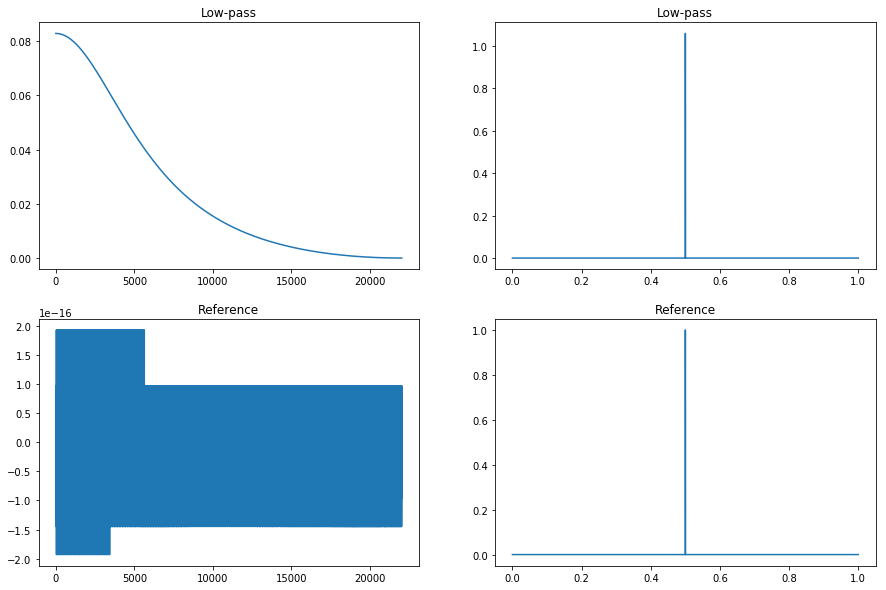
wc = np.pi / 4
gain = 100
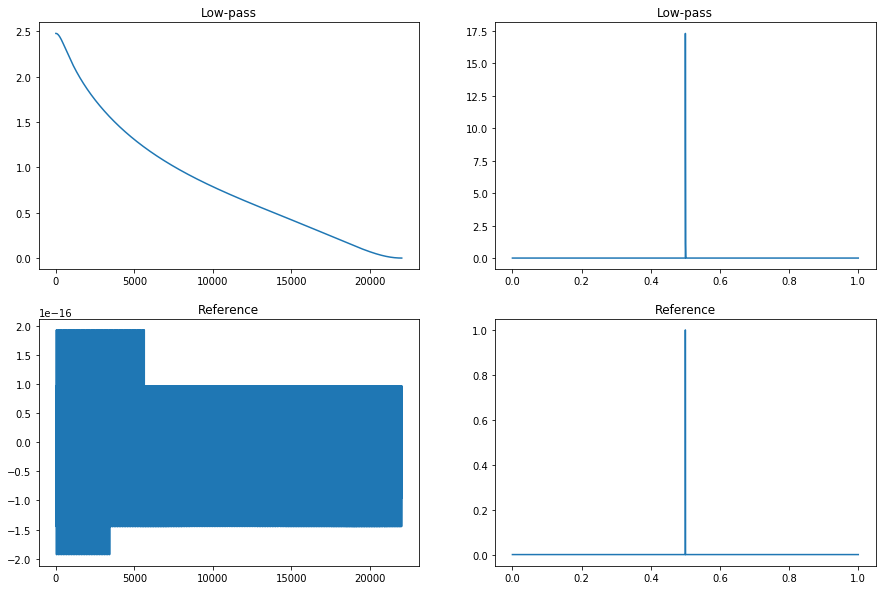
wc = np.pi / 4
gain = 1.1
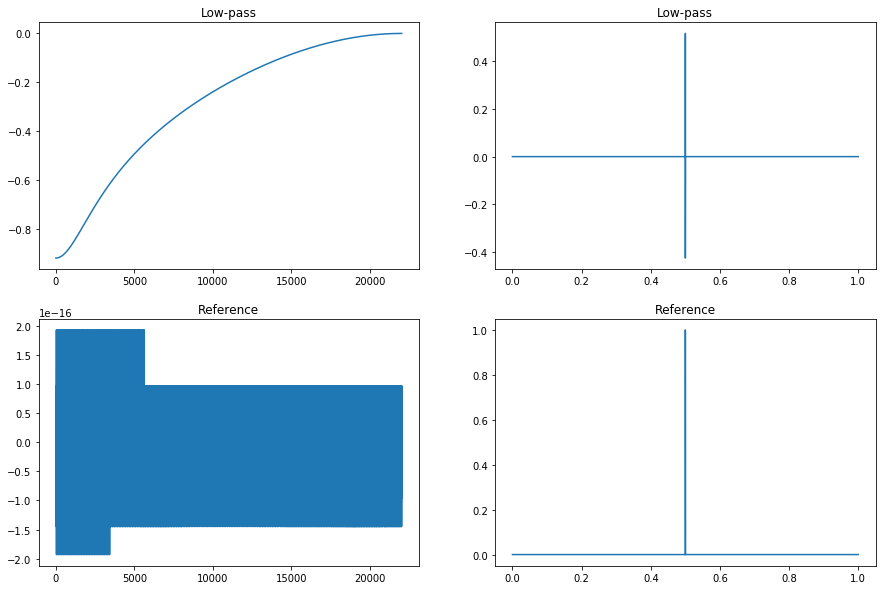
wc = np.pi / 4