Linear Regression with a circular dependent variable

circ_regression.py

# The MIT License (MIT)
# 
# Copyright (c) Alex H. Williams
#
# Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation
# files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy,
# modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all copies or substantial portions of the
# Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE
# WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR
# COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE,
# ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.

import numpy as np
import matplotlib.pyplot as plt

import scipy.stats
normcdf = scipy.stats.norm.cdf
normpdf = scipy.stats.norm.pdf

from scipy.linalg import cho_factor, cho_solve
from sklearn.base import BaseEstimator


class CircularRegression(BaseEstimator):
    """
    Reference
    ---------
    Brett Presnell, Scott P. Morrison and Ramon C. Littell (1998). "Projected Multivariate
    Linear Models for Directional Data". Journal of the American Statistical Association,
    Vol. 93, No. 443. https://www.jstor.org/stable/2669850

    Notes
    -----
    Only works for univariate dependent variable.
    """

    def __init__(self, alpha=0.0, tol=1e-5, max_iter=100):
        """
        Parameters
        ----------
        alpha : float
            Regularization parameter

        tol : float
            Convergence criterion for EM algorithm

        max_iter : int
            Maximimum number of EM iterations.
        """
        self.alpha = alpha
        self.tol = tol
        self.max_iter = max_iter

    def fit(self, X, y):
        """
        Uses EM algorithm in Presnell et al. (1998).

        Parameters
        ----------
        X : array
            Independent variables, has shape (n_timepoints x n_neurons)
        y : array
            Circular dependent variable, has shape (n_timepoints x 1),
            all data should lie on the interval [-pi, +pi].
        """

        # Convert 1d circular variable to 2d representation
        u = np.column_stack([np.sin(y), np.cos(y)])

        # Randomly initialize weights. Ensure scaling does
        W = np.random.randn(X.shape[1], 2)
        W /= np.max(np.sum(X @ W, axis=1))

        # Cache neuron x neuron gram matrix. This is used below
        # in the M-step to solve a linear least squares problem
        # in the form inv(XtX) @ XtY. Add regularization term to
        # the diagonal.
        XtX = X.T @ X
        XtX[np.diag_indices_from(XtX)] += self.alpha
        XtX = cho_factor(XtX)

        # Compute model prediction in 2d space, and projection onto
        # each observed u.
        XW = (X @ W)
        t = np.sum(u * XW, axis=1)
        tcdf = normcdf(t)
        tpdf = normpdf(t)

        self.log_like_hist_ = [
            np.log(2 * np.pi) - 
            0.5 * np.mean(np.sum(XW * XW, axis=1), axis=0) +
            np.mean(np.log(1 + t * tcdf / tpdf))
        ]

        for itr in range(self.max_iter):

            # E-step.
            m = t + (tcdf / (tpdf + t * tcdf))
            XtY = X.T @ (m[:, None] * u)

            # M-step.
            W = cho_solve(XtX, XtY)

            # Recompute model prediction.
            XW = X @ W
            t = np.sum(u * XW, axis=1)
            tcdf = normcdf(t)
            tpdf = normpdf(t)

            # Store log-likelihood.
            self.log_like_hist_.append(
                np.log(2 * np.pi) - 
                0.5 * np.mean(np.sum(XW * XW, axis=1), axis=0) +
                np.mean(np.log(1 + t * tcdf / tpdf))
            )

            # Check convergence.
            if (self.log_like_hist_[-1] - self.log_like_hist_[-2]) < self.tol:
                break

        self.weights_ = W

    def predict(self, X):
        u_pred = X @ self.weights_
        return np.arctan2(u_pred[:, 0], u_pred[:, 1])

    def score(self, X, y):
        """
        Returns 1 minus mean angular similarity between y and model prediction.

        score == 1 for perfect predictions
        score == 0 in expectation for random predictions
        score == -1 if predictions are off by 180 degrees.
        """
        y_pred = self.predict(X)
        return np.mean(np.cos(y - y_pred))


if __name__ == "__main__":
    ## Synthetic time series data

    # Params
    n_obs = 3000
    nX = 10
    n_traversals = 10
    noise_lev = 0.2

    # Create time series where dependent variable, y moves around
    # the circle at constant velocity.
    _raw_y = np.linspace(0, 2 * n_traversals * np.pi, n_obs + 1)[:-1]
    y = _raw_y % (2 * np.pi) - np.pi

    # Create predictor variables 
    X_locs = np.linspace(0, np.pi * 2, nX + 1)[:-1]
    X = np.array([scipy.stats.vonmises(loc=l, kappa=10.0).pdf(y) for l in X_locs]).T
    X += np.random.randn(n_obs, nX) * noise_lev

    ## Fit Model

    model = CircularRegression(max_iter=20)
    model.fit(X, y)

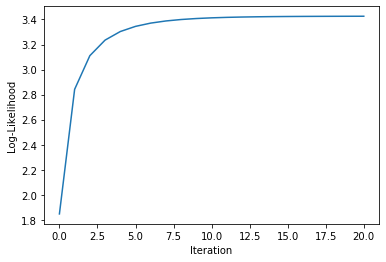
    plt.figure()
    plt.plot(model.log_like_hist_)
    plt.xlabel("Iteration")
    plt.ylabel("Log-Likelihood")

    ## Show Fit

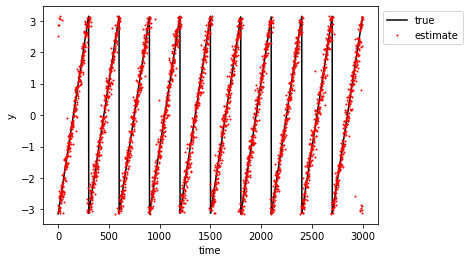
    plt.figure()
    plt.plot(y, "-k", label="true")
    plt.plot(model.predict(X), '.r', ms=2, label="estimate")
    plt.ylabel("y")
    plt.xlabel("time")
    plt.legend(bbox_to_anchor=(1,1,0,0))
    plt.show()

    ## Cross Validation Demo
    from sklearn.model_selection import cross_val_score
    print(cross_val_score(CircularRegression(alpha=1.0), X, y, cv=5))

Code Output

Cross-Validation Scores: [0.95037565 0.95037833 0.94832496 0.95862434 0.94391777]

Log-likelihood Learning Curve:

Model prediction (red) vs measurements (black):