PCA and NMF with cross-validation (using Numpy)

make_nmf_fig.py

from pca_crossval import * 
from tqdm import tqdm
import itertools
np.random.seed(1111)

m, n, r = 100, 101, 3
Utrue, Vtrue = rand(m,r), rand(r,n)
data = np.dot(Utrue, Vtrue) + .25*randn(m,n)
data[data < 0] = 0
ranks = []
train_err = []
test_err = []

rank_range = range(1,11)
repeat_range = range(10)
with tqdm(total=len(rank_range)*len(repeat_range)) as pbar:
    for rank, repeat in itertools.product(rank_range, repeat_range):
        _, _, train, test = crossval_pca(data, rank, nonneg=True)
        ranks.append(rank)
        train_err.append(train[-1])
        test_err.append(test[-1])
        pbar.update(1)
ranks = np.array(ranks)
train_err = np.array(train_err)
test_err = np.array(test_err)

fig, axes = plt.subplots(1, 2, sharey=True, sharex=True, figsize=(7, 4))
axes[0].plot(ranks + randn(ranks.size)*.1, train_err, '.k')
axes[0].plot(np.unique(ranks), [np.mean(train_err[ranks==r]) for r in np.unique(ranks)], '-r', zorder=-1)
axes[0].set_ylabel('RMSE')
axes[0].set_title('Train Error')
axes[0].set_xlabel('# of components')

axes[1].plot(ranks + randn(ranks.size)*.1, test_err, '.k')
axes[1].plot(np.unique(ranks), [np.mean(test_err[ranks==r]) for r in np.unique(ranks)], '-r', zorder=-1)
axes[1].set_xticks(np.unique(ranks).astype(int))
axes[1].set_title('Test Error')
axes[1].set_xlabel('# of components')

fig.tight_layout()
fig.savefig('cv_nmf.pdf')
plt.show()

make_pca_fig.py

from pca_crossval import * 
import itertools
from tqdm import tqdm
np.random.seed(2222)

m, n, r = 500, 501, 5
Utrue, Vtrue = randn(m,r), randn(r,n)
data = np.dot(Utrue, Vtrue) + 6*randn(m,n)
ranks = []
train_err = []
test_err = []

rank_range = range(1,11)
repeat_range = range(10)
with tqdm(total=len(rank_range)*len(repeat_range)) as pbar:
    for rank, repeat in itertools.product(rank_range, repeat_range):
        _, _, train, test = crossval_pca(data, rank)
        ranks.append(rank)
        train_err.append(train[-1])
        test_err.append(test[-1])
        pbar.update(1)
ranks = np.array(ranks)
train_err = np.array(train_err)
test_err = np.array(test_err)

fig, axes = plt.subplots(1, 2, sharey=True, sharex=True, figsize=(7, 4))
axes[0].plot(ranks + randn(ranks.size)*.1, train_err, '.k')
axes[0].plot(np.unique(ranks), [np.mean(train_err[ranks==r]) for r in np.unique(ranks)], '-r', zorder=-1)
axes[0].set_ylabel('RMSE')
axes[0].set_title('Train Error')
axes[0].set_xlabel('# of components')

axes[1].plot(ranks + randn(ranks.size)*.1, test_err, '.k')
axes[1].plot(np.unique(ranks), [np.mean(test_err[ranks==r]) for r in np.unique(ranks)], '-r', zorder=-1)
axes[1].set_xticks(np.unique(ranks).astype(int))
axes[1].set_title('Test Error')
axes[1].set_xlabel('# of components')

fig.tight_layout()
fig.savefig('cv_pca.pdf')
plt.show()

pca_crossval.py

import numpy as np
from numpy.random import randn, rand
from scipy.optimize import minimize
import matplotlib.pyplot as plt

def censored_least_squares(A, X0, B, M, options=dict(maxiter=20), **kwargs):
    """Approximately solves least-squares with missing/censored data by L-BFGS-B

        Updates X to minimize Frobenius norm of M .* (A*X - B), where
        M is a masking matrix (m x n filled with zeros and ones), A and
        B are constant matrices.

    Parameters
    ----------
    A : ndarray
            m x k matrix
    X0 : ndarray
            k x n matrix, initial guess for X
    B : ndarray
            m x n matrix
    M : ndarray
            m x n matrix, filled with zeros and ones
    options : dict
            optimization options passed to scipy.optimize.minimize
    
    Note: additional keyword arguments are passed to scipy.optimize.minimize

    Returns
    -------
    result : OptimizeResult
            returned by scipy.optimize.minimize
    """
    k = A.shape[1]
    n = B.shape[1]

    def fg(x):
        X = x.reshape(k, n)
        resid = np.dot(A, X) - B
        f = 0.5*np.sum(resid[M]**2)
        g = np.dot(A.T, (M * resid))
        return f, g.ravel()

    return minimize(fg, X0.ravel(), method='L-BFGS-B', jac=True, options=options, **kwargs)

def crossval_pca(data, rank, p_holdout=.25, tol=1e-4, nonneg=False):
    """Fits PCA or NMF while holding out data at random

        Finds U and Vt that minimize Frobenius norm of (U*Vt - data) over
        a random subset of the entries in data.

        Note: this code does not return orthogonalized factors for PCA.

    Parameters
    ----------
    data : ndarray
            m x n matrix
    rank : int
            number of components
    p_holdout : float
            probability of holding out an entry, expected proportion of data in test set.
    tol: float
            absolute convergence criterion on the root-mean-square-error on training set
    nonneg : bool
            if True, fit NMF model
    
    Returns
    -------
    U : ndarray
            m x rank matrix
    Vt : ndarray
            rank x n matrix
    train_hist : list
            RMSE on training set on each iteration
    test_hist : list
            RMSE on test set on each iteration
    """

    # m = num observations, n = num features
    m, n = data.shape

    # initialize factor matrices
    U, Vt = randn(m, rank), randn(rank, n)

    # hold out data at random
    M = rand(m, n) > p_holdout

    # initial loss
    converged = False
    resid = np.dot(U, Vt) - data
    train_hist = [np.sqrt(np.mean((resid[M])**2))]
    test_hist = [np.sqrt(np.mean((resid[~M])**2))]

    # impose nonnegativity, if desired
    if nonneg:
        bounds_U = [(0, None) for _ in range(U.size)]
        bounds_V = [(0, None) for _ in range(Vt.size)]
    else:
        bounds_U = None
        bounds_V = None

    # optimize
    while not converged:
        # update V
        r = censored_least_squares(U, Vt, data, M, bounds=bounds_V)
        Vt = r.x.reshape(rank, n)

        # update U
        r = censored_least_squares(Vt.T, U.T, data.T, M.T, bounds=bounds_U)
        U = r.x.reshape(rank, m).T

        # recprd train/test error
        resid = np.dot(U, Vt) - data
        train_hist.append(np.sqrt(np.mean((resid[M])**2)))
        test_hist.append(np.sqrt(np.mean((resid[~M])**2)))
        converged = (train_hist[-2]-train_hist[-1]) < tol

    return U, Vt, train_hist, test_hist

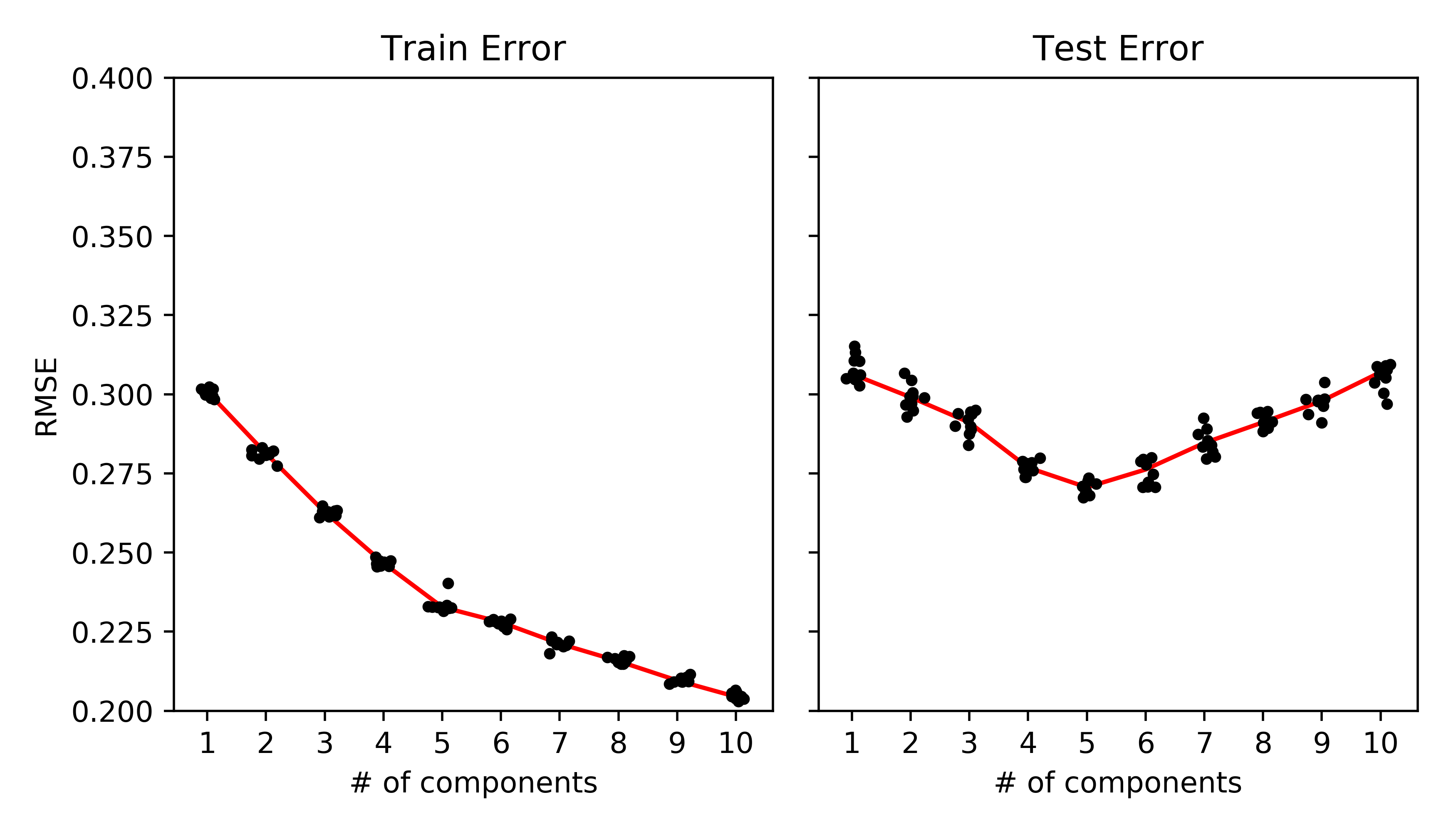
PCA example. (Takes ~3 mins on my laptop for 500x501 rank-5 matrix)

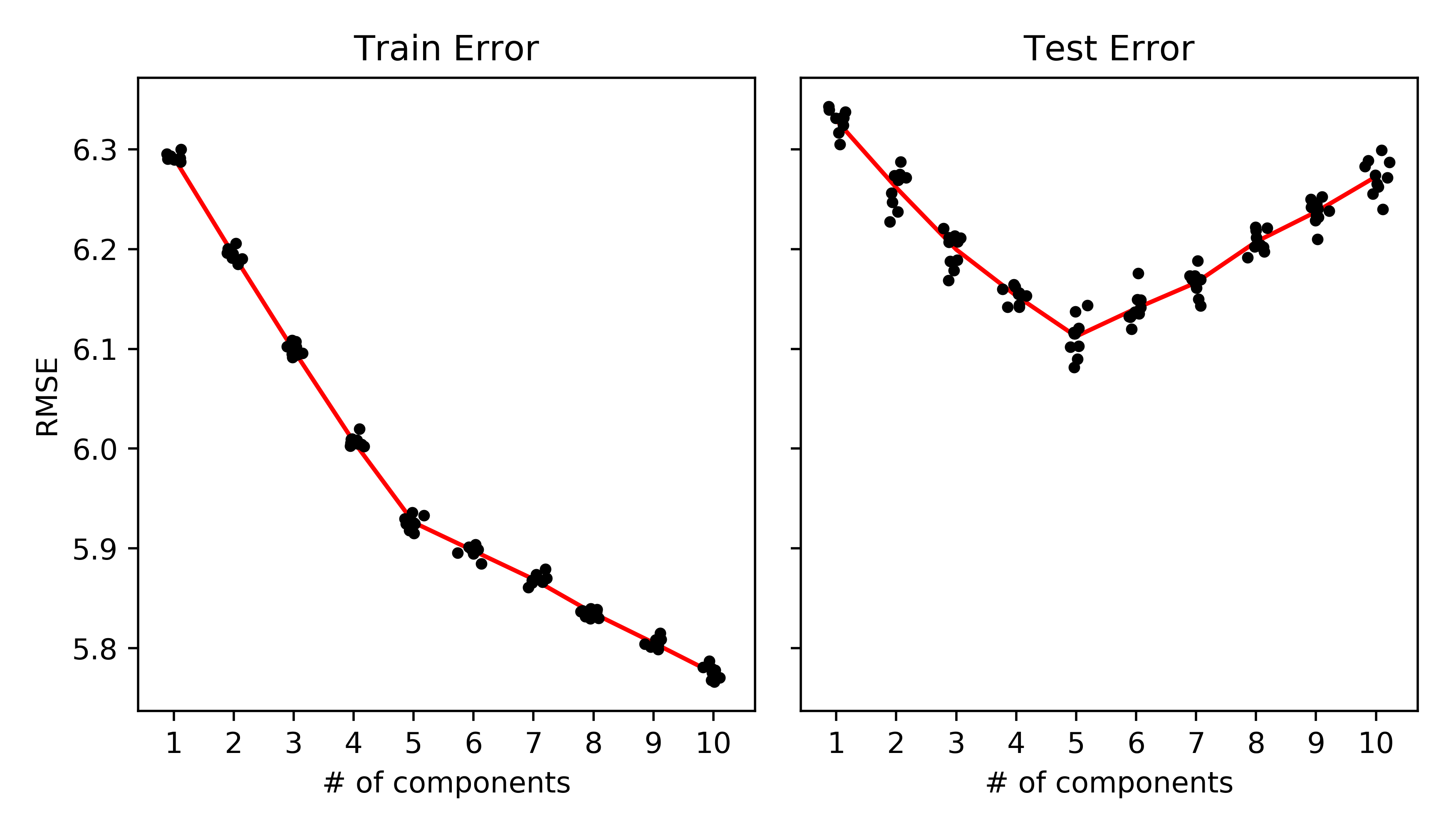
NMF example. (Takes ~30 s on my laptop for 100x101 rank-5 matrix)