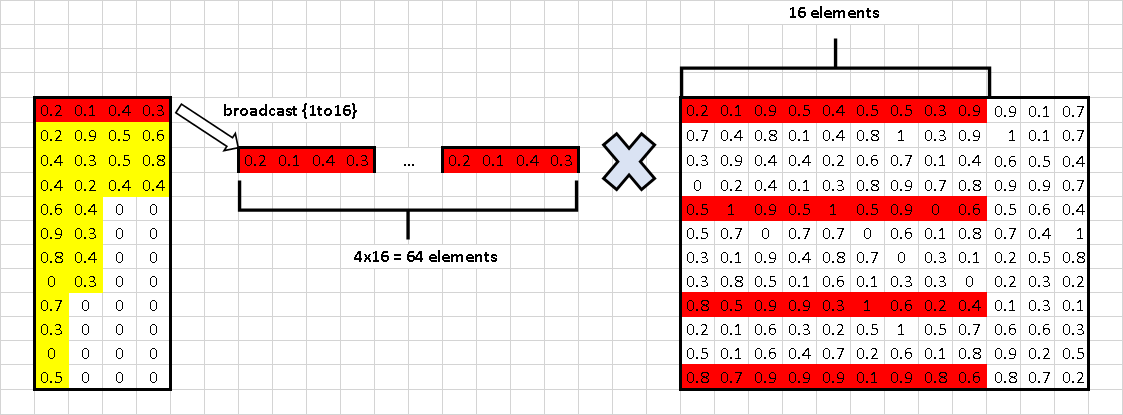
As we all know, sparse patterns must align with target ISA, especially GEMM instruction. VNNI introduces the following GEMM example:
Description Multiply groups of 4 adjacent pairs of unsigned 8-bit integers in a with corresponding signed 8-bit integers in b, producing 4 intermediate signed 16-bit results. Sum these 4 results with the corresponding 32-bit integer in src, and store the packed 32-bit results in dst. Operation
FOR j := 0 to 15
tmp1.word := Signed(ZeroExtend16(a.byte[4*j]) * SignExtend16(b.byte[4*j]))
tmp2.word := Signed(ZeroExtend16(a.byte[4*j+1]) * SignExtend16(b.byte[4*j+1]))
tmp3.word := Signed(ZeroExtend16(a.byte[4*j+2]) * SignExtend16(b.byte[4*j+2]))
tmp4.word := Signed(ZeroExtend16(a.byte[4*j+3]) * SignExtend16(b.byte[4*j+3]))
dst.dword[j] := src.dword[j] + tmp1 + tmp2 + tmp3 + tmp4
ENDFOR
dst[MAX:512] := 0
According to our kernel experiments, we defined the so-called "4x1" sparse pattern to fully utilize VNNI capability.
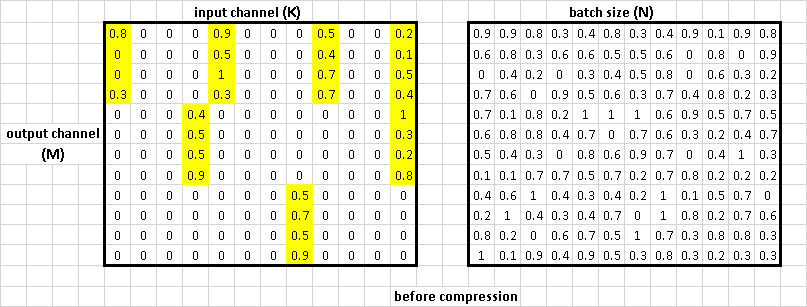
As we can see from the above picture, the sparse pattern in the weight(the left matrix) is 4x1, 4 is in output channels dims, 1 is in input channel dims. Or if we treat this as a typical GEMM, we can say 4 in M dimensions and 1 in K dimension. For the rest part of this doc, we will use GEMM concept which usually uses M, K, N for the first, second and third dimension.
but after compression, we concat each 4x1 block in the same line into some 4x4 blocks(there will be some paddings in lines that number of non-zero blocks can't be devided by 4, as we can see the second and third line in the image). then for each 1x4 elements(maybe including paddings) in a 4x4 blocks, we can broadcast them to 64 elements as 4x16 elements, which is applicable for VNNI. the "4" in each 1x4 just means accumulation dims in VNNI. for activation(the right matrix) we just pick some 1x16 blocks according to sparse index and concat them into 4x16 blocks, this is the second matrix we prepared for VNNI.
as we may know, for a typical GEMM(MxKxN) problem, a high efficency GEMM micro-kernel need to tile in (m x k x n), or take m rows of matrix A and n cols of matrix B to improve density of fma instructions, finally reduce bubbles in the assembly line. the 4x1 pattern, the "4" is so-call m in micro-kernels, and the "4" by the concat along rows is just for VNNI accumution dims.
If we have sparse weight matrix in patterns like "1x4", we can save the concat cost but lower density of micro-kernels, which will bring more harm for parformance.
comparsion between "1x4" and "4x1"
- "4x1" does tiling along M dimensions, "1x4" does no tiling along this dimensions.
- "4x1" needs concat along K dimensions, "1x4" doesn't need concat. However, the concat happens during the compression, which is offline.
As conclusion, we think "4x1" will bring higher performance, about ~2(+)x against "1x4" (estimated from differences between tiling and no tiling.)
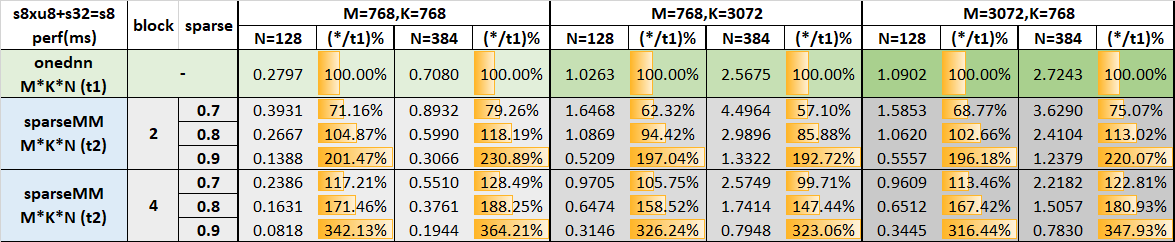
We can do a similiar simulations here. We change the "4x1" to "2x1", which means tiling along the M dimensions becomes 2 and see the impact on the performance quantitatively. from the following table, we can see about 1/3 perf drop, therever we expect more performance drop with totally no tiling here.