Leetcode 85: Maximal Rectangle

leetcode_85.md

Description

Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.

Link to the original problem

Example 1

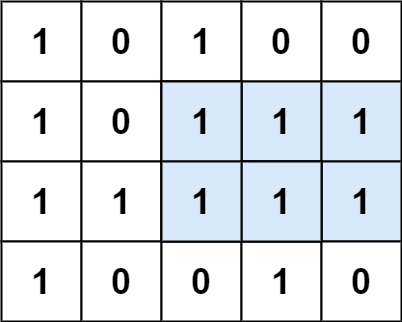
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 6
Explanation: The maximal rectangle is shown in the above picture.

Example 2

Input: matrix = [["0"]]
Output: 0

Example 3

Input: matrix = [["1"]]
Output: 1

Constraints:

• rows == matrix.length
• cols == matrix[i].length
• 1 <= row, cols <= 200
• matrix[i][j] is '0' or '1'.

Idea

1. This one is indeed a hard problem and let me see how I can introduce the idea.
2. First thing we can probably think of is the brute-force solution. However, it's not gonna be efficient. We all know why, because there're so many possibilities where the largest rectangle might locate.
3. For example, assume the matrix dimension is m * n, we can start from any index of the matrix, that are m * n possibilities. And for any of the indices, we can extend the largest rectangle's size from 1 to the rightmost columns and to the bottommost rows (assuming we only consider these directions so there are no duplicates). You can already see how inefficient this is.
4. And you'll probably also see that we might be duplicating the calculations if we are only blindly extending the matrix's dimensions, right? I mean, for example, when we start from row i and finished calculation for the largest rectangle with row size of 1, and when we try to find rectangles starting with row i and row size of 2, we would like to take advantage of the knowledge of the i row we have already calculated, right? But, how?
5. I'm not sure how either, but let's get back to the problem itself. Let's see if we can find something useful.
6. So we are trying to find the largest rectangle containing only 1s, that means the largest rectangle cannot have 0s, That also means, if there's 0 in the new row (or column) when we extend, at least for that row (or column), it won't form a rectangle of 1s. Well, duh! 🙄
7. Lol, bear with me, we are definitely getting somewhere.
8. So if we can somehow keep a record of how many 1s for each column when we extend, we can "take" advantage of previous rows' information. For example, in the figure of Example 1, for the first three rows, you can use an array of 1s like [3,1,3,2,2] to represent its current "state" (each number in the array means how many consecutive 1s ending at the bottom row). And trying to find a largest rectangle from the orignal matrix is same as finding it from this array. And it's fairly easy to keep a record of this array, right? (When you extend, if you meet a 0, it's reset to be 0; otherwise, add 1 to its current value.)
9. So now the problem is converted to finding the largest rectangle from an array such as [3,1,3,2,2].
10. We can definitely start from any of the array's index i and keep counting if we can form a rectangle with starting "height" at index i. But it's gonna be O(n2), with n being the size of the array. Let's see if we can do better than that.
11. Now this is where the magic happens.
12. You probably have already guessed, it's the "Stack", since it's the "Stack" series.
13. Also, since I didn't think of this method myself, so I'll try to explain it directly, we can always revisit it and find out the logic behind it and try to apply it in other situations.
14. In order to make it easy to understand the process, I also drew some illustrations like below, so let's see.
15. Some context first, each bar in the figures is an element in the above-mentioned array. And we will use a stack to remember "some" indices of the visited indices. The bars with dashed border are the ones that's popped out from the stack.
16. In Figure I, we visit the array at index 0, and we also enqueue its index 0 to the stack. Because we don't know if the bars we'll see are shorter or higher, so we just "wait and see".
17. And also we'll keep enqueuing if we meet higher bars from the array. Why? Because the "largest" rectangle starting from the leftmost bar can continue extending, so we don't know if we should stop now.
18. In Figure II, we enqueue two more bars since they're higher than previous ones.
19. In Figure III, we meet a bar at index i, that is shorter than previous one. Hmm, now we cannot keep extending, what do we do now?
20. We know one thing for sure that, if the largest rectangle starts from the bar before index i, it won't be able to extend to the right, because the bar at index i "failed" it. But, we can try to look backwards.
21. Also we know the bars we previously enqueued are in increasing order. That means the bars we enqueued can always extends until to the index before i. And we'll find out the largest one in backward order.
22. In Figure III, we pop the bar index at the stack top, and keep a record of its height t, and now the stack top points to the bar before t. So now we have a height, how do we find the width of the rectangle though?
23. Since we keep a record of indices in the stack, we know the index before index t. And we also know current index i. So the width would be i - (stack top) - 1. Try to apply some numbers and you'll find out why we need to do - 1.
24. As you can see from Figure IV, we know the width for our example is 1 for the first rectangle.
25. OK, let's keep going. So we compare bar height at index i with the one at index at the stack top. We find out the bar at index i is shorter, so same logic, we pop the one at the stack top. (We know we cannot extend this one further passing index i, but we know we can extend until the index before i.)
26. Similarly, we found the bar with height t, and its width now is 2, as you can see in Figure V.
27. In figure VI, as you can see, the bar at index 0 with height t is still higher than the one at index i, we keep popping out the stack. We know the height is t, but now the calculation for its width is a bit different. Because after popping out the stack, the stack becomes empty, so now the width becomes exactly i, why?
28. It's because array indices start from 0, and the width before index i is i. (You can still use our formula above, it's almost like i - (-1) - 1, if you think of the stack top points to the index before 0, which is -1.)
29. You might ask, what if the bar before i is shorter than the one at i? Very good question, the answer is also simple. It's basically the same problem again.
30. Remember we are enqueuing the indices when we meet higher bars? So suppose the bar at index 0 is shorter than the bar at index i, we enqueue index i to the stack, and don't you find it similar? We already see the same problem in Figure II. And because we record the indices onto the stack, we can always find the width correctly with our formular. And we don't care about missing some indices between 0 and i, because we know those bars are higher than bar i, and we can safely extend from index 0, until we find a shorter bar after i.
31. Careful readers might also ask, what if we meet a bar with same height as previous bar, the answer is we enqueue them, since higher bars and equal height bars function in the same way in this problem.
32. Now the complexity decreases to O(n), since we only enqueue and dequeue each index once.
33. I would say this is the magic of stack.
34. Thanks for reading. Let me know if you still find it confusing.

Solution

Javascript

const maximalRectangle = function(matrix) {
  if (!matrix.length || !matrix[0].length) return 0;

  const m = matrix.length, n = matrix[0].length;
  const arr = Array(n).fill(0);
  let max = 0;
  for (let i = 0; i < m; i += 1) {
    for (let j = 0; j < n; j += 1) {
      arr[j] = matrix[i][j] == "1" ? arr[j] + 1 : 0;
    }
    max = Math.max(max, findMax(arr));
  }
  return max;
};

function findMax(heights) {
  const stk = [];
  let ans = 0, i = 0;
  heights.push(0);
  while (i < heights.length) {
    if (!stk.length || heights[i] >= heights[stk[stk.length - 1]]) {
      stk.push(i);
      i += 1;
    } else {
      const t = stk.pop();
      const width = !stk.length ? i : (i - stk[stk.length - 1] - 1);
      ans = Math.max(ans, heights[t] * width);
    }
  }
  return ans;
}

References

1. Stack wiki page