Skip to content

Instantly share code, notes, and snippets.

@asufana

asufana/はなもげら語.md

Last active January 29, 2020 17:45
Show Gist options
  • Save asufana/f70f19a360ff35d37f2991a43e940f47 to your computer and use it in GitHub Desktop.
Save asufana/f70f19a360ff35d37f2991a43e940f47 to your computer and use it in GitHub Desktop.
Download ZIP
はなもげら語の実装
Raw
はなもげら語.md

はなもげら語

1stステップ： 10+20+30 を実現する

とりあえず整数の足し算処理ができる言語処理系を、Javaを使って作ってみる。

１．字句解析を行う

  • 文字列のソースコードから、処理に必要な文字列を抽出し、ばらばらの文字列に切り分ける処理
  • 例えば 10 + 20 + 30 //足し算 という文字列を 10 + 20 + 30 という形に切り分ける

1.1. トークン

  • 切り分けられた文字列を トークン と呼ぶ
  • 1stステップで必要なトークン種別は、10 のような数値と + のような識別子の２種類
  • トークンを Java 上で保持するためのクラスを準備する
  • 実装はこちら

1.2. 実装概要

  • 字句解析器 Lexer（Lexical analyzer）クラスを実装する
  • Lexerクラスは文字列を渡すと、下記のようにトークンのリストを返却する振る舞いをする
@Test
public void testLexer() {
    //文字列を渡すと
    final List<Token> tokens = Lexer.toTokens("10 + 20 + 30");
    //トークンリストを返却する
    assertThat(tokens, contains(new NumToken(10),
                                new IdToken("+"),
                                new NumToken(20),
                                new IdToken("+"),
                                new NumToken(30)));
}

1.3. 字句解析器の実装

  • 文字列からトークンを抽出するために 正規表現 を利用する
    • 数値の判定　：[0-9]+
    • 識別子の判定：[\\+\\-]
  • matcher.group() のマッチ位置でトークン種別を判定する
    • 数値と識別子の判定合わせた正規表現 \\s*(([0-9]+)|([\\+\\-])) において、
    • matcher.group(2) にマッチすれば、その文字列は数値トークン
    • matcher.group(3) にマッチすれば、その文字列は識別子トークン
  • 実装はこちら

２．抽象構文木

  • 字句解析によってトークンに分解されたソースコードを、
  • 構文解析によって抽象構文木（AST：Abstract Syntax Tree）を組み立てる
    • 構文解析の主な仕事は、
      • どのトークンからどのトークンまでが１つの式や文なのか、
      • どの開き括弧トークンからどの閉じ括弧トークンまでが対応しているのかなど、
    • トークン間の関係を解析すること
  • その解析結果を保持する入れ物が抽象構文木

2.1. 抽象構文木のイメージ

  • 10+20+30 の抽象構文木は下記のような構造
  • プログラムを解析し、このような構造にすることで、あとはノードを順番に辿っていくことで正しい処理を実現できる

  • たとえばピンクの線のようにノードを辿っていくと A+B/(C+D)-(E*F) が正しく計算されるように抽象構文木が構築されている例

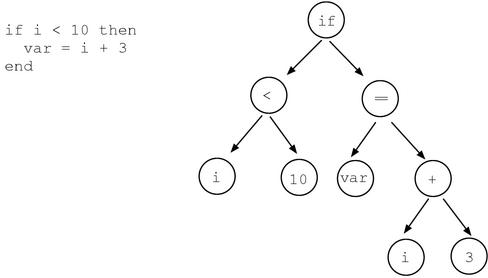
  • たとえば下記のプログラムを構文解析した例

2.2. 抽象構文木のデータ構造

  • 抽象構文木を Java 上で保持するためのクラスを準備する
  • ASTLeaf が末端のオブジェクト
    • ASTNum が NumToken を保持
    • ASTId が IdToken を保持
  • ASTExpr が + を表現するオブジェクト、ここには足し算対象の２つの ASTLeaf も保持される
  • 実装はこちら

2.3. 抽象構文木を実行してみる

  • 抽象構文木を構築する構文解析はちょっと置いておいて、
  • 解析された抽象構文木を使ってプログラムを動かしてみる

10+20 の抽象構文木の実行

@Test
public void test01() throws Exception {
    //10+20の抽象構文木を手動で作成
    final ASTNode leafLeft = new ASTNum(new NumToken(10));
    final ASTNode expr = new ASTId(new IdToken("+"));
    final ASTNode leafRight = new ASTNum(new NumToken(20));
    final ASTNode nodes = new ASTExpr(leafLeft, expr, leafRight);
    
    //実行
    final Object result = nodes.eval();
    assertThat(result, is(30));
}
  • 抽象構文木を手動で作成し、トップノードの eval() を実行する
    • eval() はインターフェース ASTNode で定義しているため、どのノードにも実装されている
    • 末端ノード ASTLeaf で eval() 実行すると、単に保持しているトークンの値を返却する
    • 演算ノード ASTExpr で eval() 実行すると、保持している演算子と２つのノードに対して決められた処理を実行する
      • たとえば ASTExpr が + と 10 20 を保持していたら、10+20 を処理する
      • ASTExpr.java

10+20+30 の抽象構文木の実行

@Test
public void test02() throws Exception {
    //10+20の抽象構文木
    final ASTNode leafLeftLeft = new ASTNum(new NumToken(10));
    final ASTNode expr = new ASTId(new IdToken("+"));
    final ASTNode leafLeftRight = new ASTNum(new NumToken(20));
    final ASTNode leafLeft = new ASTExpr(leafLeftLeft, expr, leafLeftRight);
    
    //(10+20)+30の抽象構文木
    final ASTNode leafRight = new ASTNum(new NumToken(30));
    final ASTNode nodes = new ASTExpr(leafLeft, expr, leafRight);
    
    //実行
    final Object result = nodes.eval();
    assertThat(result, is(60));
}
  • トップノードの ASTNode は、 + と 10+20 30 を保持している
  • トップノードで eval() を実行すると、
    • まず保持している２つのノードのそれぞれの eval() 値を取得する
    • その上で + 処理をするため、再帰的にノードの階層構造が処理されることが分かる

３．構文解析を行う

  • 字句解析された 10 + 20 + 30 を抽象構文木の構造に変換する処理

3.1. 文法を定義する

  • 構文解析をするためには、はなもげら語の文法を定義する必要がある
  • 例えば足し算の文法を 1 + 1 とするか + 1 1 とするかなど

3.2. はなもげら語1stステップの文法

  • 文法を言葉で構造化してみると、下記のように定義できる
    • 因子：数値
    • 項　：因子 と 因子 を 足し算できる
  • この文法を構文解析に落としこむために、BNF という記法で記述する
    • factor ::= NUMBER
    • expression ::= factor ( '+' factor )*
  • BNF を レールロード・ダイヤグラム で表現すると下記のようになる

3.3. 文法をプログラムで表現する

  • LL構文解析 を利用する
    • トップダウン構文解析手法のひとつ
    • 入力文字を左から解析していき、左端導出（Leftmost Derivation）を行うことからLL法と呼ぶ
  • LL法は 再帰下降構文解析器 として、比較的簡単にプログラムできる

3.4. 実装概要

  • 構文解析器 FirstParser クラスを実装する
  • FirstParser はトークンリストを渡すと、下記のように ASTNode を返却する振る舞いをする
@Test
public void test() {
    //字句解析
    final List<Token> tokens = Lexer.toTokens("10 + 20 + 30");
    //構文解析
    final ASTNode nodes = new FirstParser(tokens).expression();
    //実行
    assertThat(nodes.eval(), is(60));
}

3.5. 構文解析器の実装

  • BNF で定義した文法に沿って、解析プログラムを実装する
  • left となる 数値 をトークンから取得し、ASTNode とする
  • 演算子 となる 識別子 をトークンから取得し、ASTNode とする
  • right となる 数値 をトークンから取得し、ASTNode とする
  • left 演算子 right という ASTNode を作成し、left に再セットする
  • トークンがなくなるまで、2 から 5 を繰り返す
  • 実装はこちら

４．実行コマンドの作成

  • 実行可能 jar を生成する
> mvn clean package
> java -jar target/hanamogera-1.0-SNAPSHOT.jar "10 + 20 + 30"
60

2ndステップ：掛け算を実現する

１．四則計算BNFを考える

  • 四則計算を実装するには計算順序を考える必要がある（掛け算は足し算より優先する）
  • その計算順序をBNFを使って表現すると、以下のように表せる
    • 1stステップBNF
      • factor ::= NUMBER
      • expression ::= factor ( '+' factor )*
    • 新しいBNF
      • factor ::= NUMBER
      • term ::= factor ( ('*'|'/') factor )*
      • expression ::= term ( ('+'|'-') term)*
      • 最も基本的な要素は数値
      • 次に基本的な要素（優先順位の高い要素）は * と /

２．BNFに合わせて構文解析を修正する

３．実行してみる

> mvn clean package
> java -jar target/hanamogera-1.0-SNAPSHOT.jar "10 + 20 * 30 / 10"
70

3rdステップ：パーサコンビネータを作る

  • 再帰下降構文解析器はコード冗長が多い
  • BNFから分かるように文法は、小さな仕様の組み合わせから成り立っている
  • 小さな仕様をそれぞれ関数として表し、関数と関数を組み合わせて文法として表現できると良い
  • そのような高階関数的な仕組みをもったライブラリをパーサコンビネータと言う
  • たとえばパーサコンビネータ・ライブラリ Parser を利用してBNFを記述すると
//factor::= NUMBER
Parser factor = rule().number(ASTNum.class)
//expression::= factor ( '+' factor )*
Parser expression = rule().expresssion(ASTExpr.class, factor, new Operators());
  • パーサコンビネータは、小さなメソッド群をメソッドチェインして組み合わせ、BNF文法を組み立てていく
  • BNF表記をプログラム上で近いかたちで表現でき、かつ構文解析の機能性を持つ
  • ぜんぜん別件だけど、ファントムタイプについて

参考文献

Sign up for free to join this conversation on GitHub. Already have an account? Sign in to comment