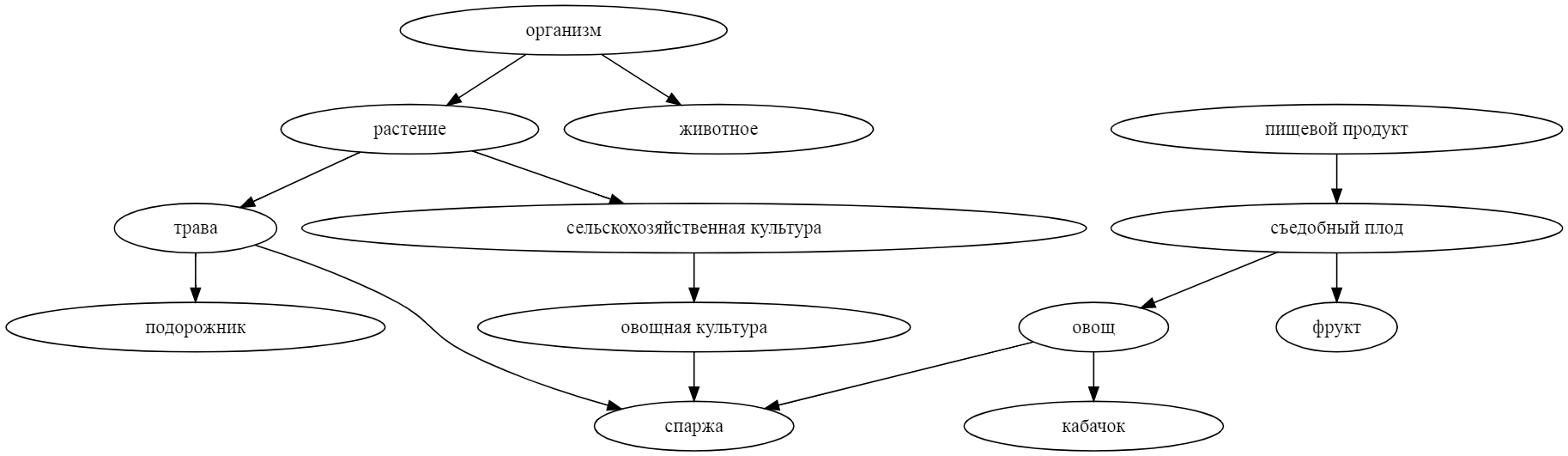
Как может машина понимать смысл слов и понятий, и вообще, что значит - понимать? Понимаете ли вы, например, что такое спаржа? Если вы скажете мне, что спаржа - это (1) травянистое растение, (2) съедобный овощ, и (3) сельскохозяйственная культура, то, наверное, я останусь убеждён, что вы действительно знакомы со спаржей. Лингвисты называют такие более общие понятия гиперонимами, и они довольно полезны для ИИ. Например, зная, что я не люблю овощи, робот-официант не стал бы предлагать мне блюда из спаржи. Но чтобы использовать подобные знания, надо сначала откуда-то их добыть.
В этом году компьютерные лингвисты организовали соревнование по поиску гиперонимов для новых слов. Я тоже попробовал в нём поучаствовать. Нормально получилось собрать только довольно примитивный алгоритм, основанный на поиске ближайших соседей по эмбеддингам из word2vec. Однако этот простой алгоритм каким-то образом оказался наилучшим решением для поиска гиперонимов для глаголов. Послушать про него можно в записи моего выступления, а если вы предпочитаете читать, то добро пожаловать под кат.
Итак, ещё раз определение: гипоним - это более общее понятие из пары, а гипероним - его частный случай. "Овощ" - гипероним по отношению к "спаржа", а "спаржа" - гипероним по отношению к "овощ". Прямых гиперонимов может быть много ("спаржа" - это не только "овощ", а ещё и "трава"). Кроме того, у гиперонимов могут быть свои собственные гиперонимы (так, "трава" - это частный случай "растения", а "растение" - частный случай "живого организма").
Готовые пары гипоним-гипероним можно найти в специальных словарях, тезаурусах, куда включены целые графы гиперонимов, таксономии. Это, например, wiktionary (питонячья обёртка), или WordNet и RuWordNet. Обычно единицей такого словаря является синсет - множество слов, обладающих примерно одинаковым смыслом. Многозначные слова входят в несколько синсетов сразу. Отношения гипоним-гипероним (и некоторые другие, например часть-целое или тема-объект темы) устанавливаются именно между синсетами.
У читателя может возникнуть закономерный вопрос: а зачем вообще в 2к20 нужны какие-то тезаурусы? Есть же машиннообученные word2vec, fastText, и даже простите BERT, почему бы не использовать их напрямую для всех задач? На самом деле, конечно, делать так можно, и все так обычно и делают. Но есть несколько "но":
- Модели, основанные на статистике со-встречаемости слов, смешивают в одну кучу разные виды связей между словами: схожесть написания, общую тему, отношения "общее/частное", "часть/целое", синонимы, антонимы... Если хочется работать с одним конкретным видом связанности слов, нужен дополнительный сигнал, и тезаурус - проверенный источник такого сигнала.
- Чисто статистические модели часто выдают непрозрачные результаты, а в некоторых задачах важна полная интерпретируемость. Опять же, проверенность словаря - решает.
- Как было видно из того же примера с кудахтаньем, статистические модели выдают довольно шумные результаты, и если есть способ дополнительно отфильтровать этот шум, то почему бы им не воспользоваться.
Кроме этих логических доводов, есть ещё и эстетические: тезаурусом в виде питонячьего пакета очень приятно пользоваться. Вы посмотрите сами, как удобно работать с синсетами:
for sense in wn.get_senses('замок'):
print(sense.synset)
# Synset(id="126228-N", title="СРЕДНЕВЕКОВЫЙ ЗАМОК")
# Synset(id="114707-N", title="ЗАМОК ДЛЯ ЗАПИРАНИЯ")Для каждого синсета можно глядеть на гиперонимы...
wn.get_senses('спаржа')[0].synset.hypernyms
# [Synset(id="348-N", title="ОВОЩИ"),
# Synset(id="4789-N", title="ТРАВЯНИСТОЕ РАСТЕНИЕ"),
# Synset(id="6878-N", title="ОВОЩНАЯ КУЛЬТУРА")]... или, наоборот, на гипонимы
wn.get_senses('спаржа')[0].synset.hypernyms[0].hyponyms
# [Synset(id="107993-N", title="АРТИШОК"),
# Synset(id="108482-N", title="СПАРЖА"),
# Synset(id="118660-N", title="ЗЕЛЕНЫЙ ГОРОШЕК"),
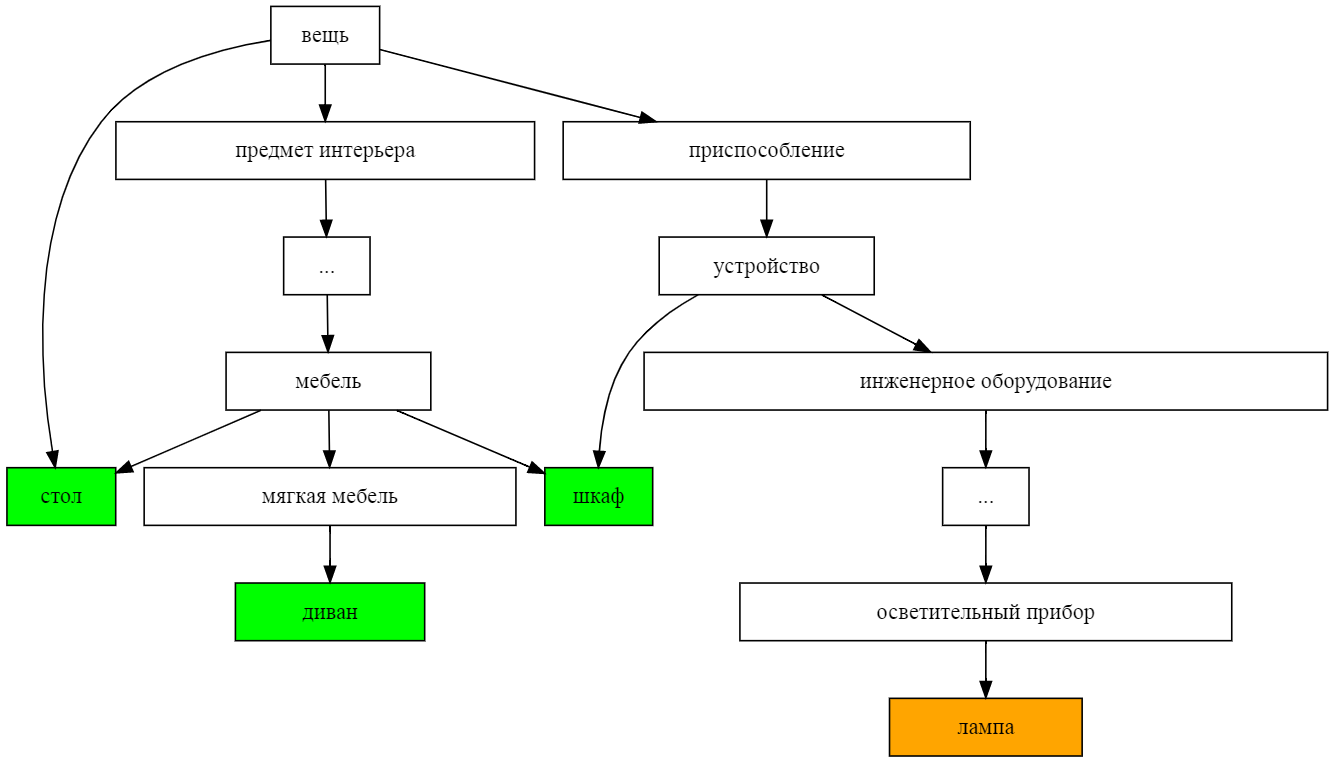
# ...Одно из забавных применений таксономии - измерение непохожести между понятиями как сумму расстояний до ближайшего общего гиперонима. Возьмём, например, такую детскую задачку: нужно исключить одно из слов ДИВАН, ШКАФ, ЛАМПА, СТОЛ. Нарисуем подграф их гиперонимов:
по картинке видно, что расстояние от "лампы" до остальных предметов - больше, чем между ними, так что она тут лишняя. А если не хочется рисовать картинки, то вычислить расстояние по таксономии можно и кодом - простым поднятием по дереву.
ДИВАН ШКАФ ЛАМПА СТОЛ
ДИВАН 0 3 10 3
ШКАФ 3 0 5 2
ЛАМПА 10 5 0 7
СТОЛ 3 2 7 0
Словари типа RuWordNet очень качественные, потому что собраны лингвистами вручную. Но поэтому же наполнение таких словарей не очень высокое. Хотелось бы научиться добавлять новые понятия в таксономии автоматически, или хотя бы полуавтоматически (машина предлагает варианты, лингвист их утверждает). Для этого компьютерные лингвисты из Сколтеха и Вышки организовали соревнование (раз два три), приуроченное к конференции Диалог, и уже даже написали про это статью. Идея соревнования: для слова, пока не включённого в таксономию RuWordNet, надо найти его гиперонимы из этой таксономии, предложив 10 вариантов. Засчитывались как прямые гиперонимы слова-запроса, так их их гиперонимы (т.е. гиперонимы второго порядка). Искались гиперонимы и оценивались результаты раздельно для существительных и для глаголов. Подробнее на данные, скрипты для оценки и бейзлайны можно посмотреть в репозитории соревнования.
Поставленная задача выглядит похоже на типичную задачу информационного поиска, только здесь нужно искать гиперонимы. А значит, можно попробовать решить эту задачу как поисковую: для входного слова-запроса отобрать кандидатов в гиперонимы, а потом переранжировать их по какой-то формуле. Конкретно у меня лучше всего взлетел как раз бейзлайновый вариант этого решения:
- Используя модель word2vec, вычислить эмбеддинги (представления в виде числовых векторов) для всех понятий в таксономии;
- Найти 100 ближайших соседей по сходству этих эмбеддингов с эмбеддингом слова-запроса;
- Заставить каждого из этих соседей "голосовать" за свои гиперонимы 1 и 2 порядка;
- Отранжировать гиперонимы-кандидаты по взвешенной сумме набранных голосов и отобрать первые 10.
Почему такое решение вообще может работать? Оказалось, что у 90% новых существительных и 99% новых глаголов есть "сёстры" в имеющейся таксономии, т.е. понятия с хотя бы одним общим гиперонимом. Эти "сёстры" по смыслу тесно связаны с запросом, а потому, согласно дистрибутивной гипотезе, часто встречаются рядом с теми же словами, рядом с которыми встречается и запрос. Значит, если сопоставить словам векторы из модели, угадывающей слово по контексту (например, word2vec, FastText, ELMO или BERT), то среди ближайших соседей слова по таким представлениям будет много "сестёр", и в качестве ответа можно использовать их гиперонимы.
Ещё несколько деталей алгоритма:
- при использовании модели w2v, для слов, не входящих в её словарь, мы искали в словаре слова с самым длинным общим префиксом и использовали их эмбеддинги;
- для представления понятий, составленных из нескольких слов, мы просто усредняли эмбеддинги этих слов (но можно придумать лучше);
- мы L2-нормализовали эмбеддинги, чтобы было удобнее искать ближайших соседей по косинусному расстоянию;
- каждый сосед голосовал за все свои гиперонимы 1 и 2 порядка, но голосам за гипероним 2 порядка давался вдвое меньший вес;
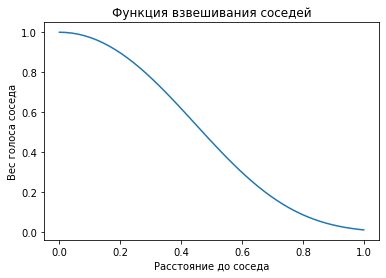
- вес каждого голоса домножался на функцию, резко убывающую при росте расстояния от запроса до найденного соседа, чтобы самые близкие соседи получили преимущество.
Здесь разобран упрощённый питонячий код моего алгоритма. Полную версию модели, которую я засабмитил на лидерборд, можно посмотреть на гитхабе, но код там довольно грязный. Более простую и опрятную версию можно запустить, склонировав себе репозиторий python-ruwordnet.
Для работы с тезаурусом я пользуюсь самописной библиотекой ruwordnet, которая скоро появится на PyPI.
from ruwordnet import RuWordNet
wn = RuWordNet()
wn.load_from_xml(root='data')Для получения векторов слов можно использовать сжатые вектора fastText (на несжатых word2vec качество выше, но и сама модель на два порядка толще). Вектор текста - нормализованная сумма векторов всех слов длиной хотя бы в 3 символа.
import numpy as np
import compress_fasttext
ft = compress_fasttext.models.CompressedFastTextKeyedVectors.load(
'https://github.com/avidale/compress-fasttext/releases/download/v0.0.1/ft_freqprune_100K_20K_pq_100.bin'
)
def vectorize(text):
vec = np.sum([ft[word] for word in text.lower().split() if len(word) >= 3], axis=0)
vec /= sum(vec**2) ** 0.5
return vecВектора всех глагольных фраз можно положить в KDTree - одну из структур данных, позволяющих быстро искать ближайших соседей.
from sklearn.neighbors import KDTree
words, vectors, synset_ids = [], [], []
for synset in wn.synsets:
if synset.part_of_speech != 'V':
continue
for sense in synset.sense:
words.append(sense.name)
vectors.append(vectorize(sense.name))
synset_ids.append(synset.id)
vectors = np.stack(vectors)
tree = KDTree(vectors)Веса для соседей, найденных в дереве, будем вычислять в зависимости от расстояния до соседа, по вот такой формуле
def distance2vote(d, a=3, b=5):
sim = np.maximum(0, 1 - d**2/2)
return np.exp(-d**a) * sim **bДля примера, попробуем вычислить гиперонимы для слова "кудахтать". Первые три найденные соседа - так себе по качеству, и гиперонимы у них неправильные, но среди 97 других соседей есть "повизгивать", "гавкать", "фырчать", и много других животных звуков.
votes = Counter()
dists, ids = tree.query(vectorize('кудахтать').reshape(1, -1), k=100)
for idx, distance in zip(ids[0], dists[0]):
for hyper in wn[synset_ids[idx]].hypernyms:
votes[hyper.id] += distance2vote(distance)
print(words[idx], [t.title for t in wn[synset_ids[idx]].hypernyms])
# БАРАХТАТЬСЯ ['ДВИЖЕНИЕ, ПЕРЕМЕЩЕНИЕ', 'ПЛЕСКАТЬСЯ В ВОДЕ']
# ГОГОТАТЬ ['СМЕЯТЬСЯ (ИЗДАВАТЬ СМЕХ)', 'РАЗРАЗИТЬСЯ (БУРНО ВЫРАЗИТЬ)']
# ГУКАТЬ ['ПРОИЗНЕСТИ, ВЫГОВОРИТЬ, ПРОГОВОРИТЬ']
# ...В результате после суммирования голосов правильный гипероним, "издать звук", лидирует с большим отрывом.
for sid, score in votes.most_common(10):
print(score, wn[sid].title)
# 0.6925543543920146 ИЗДАТЬ ЗВУК
# 0.4306341411813687 ПРОИЗНЕСТИ, ВЫГОВОРИТЬ, ПРОГОВОРИТЬ
# 0.2957854226709537 ДВИЖЕНИЕ, ПЕРЕМЕЩЕНИЕ
# ...При оценке на тестовой выборке около 40% предложенных моделью кандидатов оказались настоящими гиперонимами слов-запросов. Это на 15% хуже, чем наилучшее решение для существительных (оно использовало кучу дополнительных источников данных - wordnet, викисловарь, результаты поиска в Яндексе и Гугле). Однако моё решение оказалось наилучшим для глаголов. Скорее всего, это означает, что искать гиперонимы для глаголов - в целом непростая задачка, и никто ещё не придумал, как решать её достаточно круто. Ну, что ж ¯\_(ツ)_/¯.
Какого рода косяки делает моя модель в тех 60% случаев, когда она не права? Есть несколько важных видов ошибок:
- Попадание в тему, но неточное попадание в смысл слова. Например, для слова "заряжание" модель предсказала гиперонимы "прицеливание" и "лафет", которые тоже связаны с огнестрельным оружием, но не непосредственно с заряжанием.
- Неумение обрабатывать многозначность. Например, для слова "выгорание" модель предсказала гипероним "гореть", проигнорировав другие смыслы этого слова - потерю цвета и эмоциональное выгорание.
- Непонимание синтаксиса. Например, для фразы "прогревание больного места" модель предложила гиперонимы "больной человек" и "место в пространстве".
- Неумение работать со словообразованием, незнание фактов о мире, неумение работать с абстрактными понятиями, путаница между субъектом и объектом глагола, и ещё много разных косяков.
Более совершенная модель могла бы учитывать морфологию слов, синтаксическую структуру фраз, определения терминов из внешних источников, структуру самой таксономии, и бог знает что ещё. Лично я пытался экспериментировать с внешними источниками (Википедией), но не успел до дедлайна привести это решение в рабочий вид.
Итак, хорошая новость в том, что даже если использовать очень простую модель, 40% предложенных ею гиперонимов годятся. И это достаточно много, чтобы имело смысл соединить в один конвейер роботов и людей: роботы предлагают гиперонимы, люди их валидируют, и таксономия пополняется очень быстро.
Плохая же новость в том, что даже довольно сложные модели не смогли справиться сильно лучше, так что задачу обогащения таксономии пока что нельзя считать полностью решённой. Но на то мы и компьютерные лингвисты, чтобы не сдаваться (-: