eigen_value_decomposition.md

行列の固有値分解

行列の固有値分解

$$ A={a_{i,j}},\\ v^{(j)}={v_i},\\ V={v^{(1)},...,v^{(n)}}$$

$A$ を $\mathbb{R}^n \times \mathbb{R}^n$ とし、 $A$ の固有ベクトルを $v_1,...,v_n$, および $A$ の固有値を$\lambda_1,...,\lambda_n$ とすると, 以下が成り立つ:

$$A=V\text{diag}(\lambda)V^{-1} \tag{1}$$

ここで、 $\text{diag}(v)$ はベクトル$v$を対角要素に並べて行列にしたもの、すなわち、 $\text{diag}(v)_{i,j}:=v_i \text{ for } i = j, \text{ otherwise } 0$ である.

証明

固有値の定義より、以下が成り立つ:

$$ Av^{(1)}=\lambda_1 v^{(1)}, \\ Av^{(2)}=\lambda_1 v^{(2)}, \\ ...\\ Av^{(n)}=\lambda_1 v^{(n)} \tag{2} $$

(2)式の両辺を行列で表すと、

$$AV=V\text{diag}(\lambda) \tag{3}$$

とかけるので、右から $V^{-1}$ をかけることによって (1) 式を得る. $(\text{QED})$

これを図に可視化すると以下のようになる:

注意

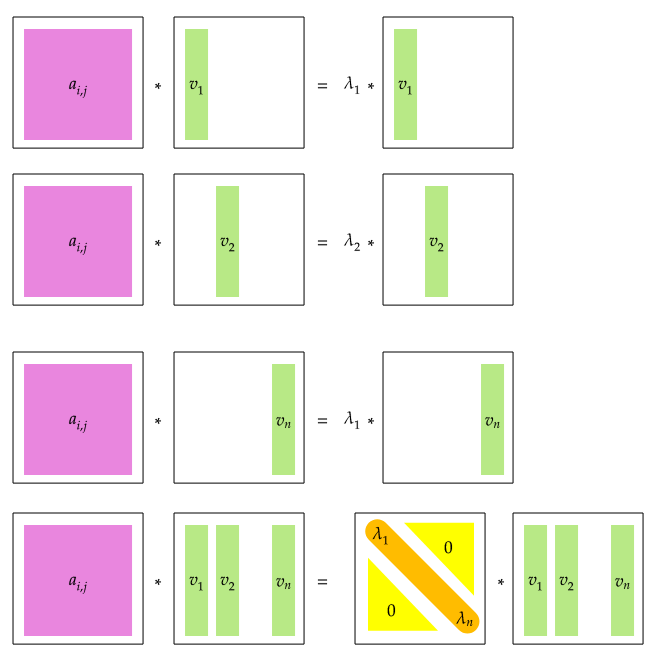
$AV=\text{diag}(\lambda)V$ は成り立たない.