En estadística, la función gaussiana (en honor a Carl Friedrich Gauss) es una función definida por la siguiente expresión, donde a, b y c son constantes.
Así pues, la distribución gaussiana actúa como la función de densidad de una variable aleatoria x con distribución normal:
Siendo el valor de la integral 1 cuando la media b=μ, desviación típica c=σ y:
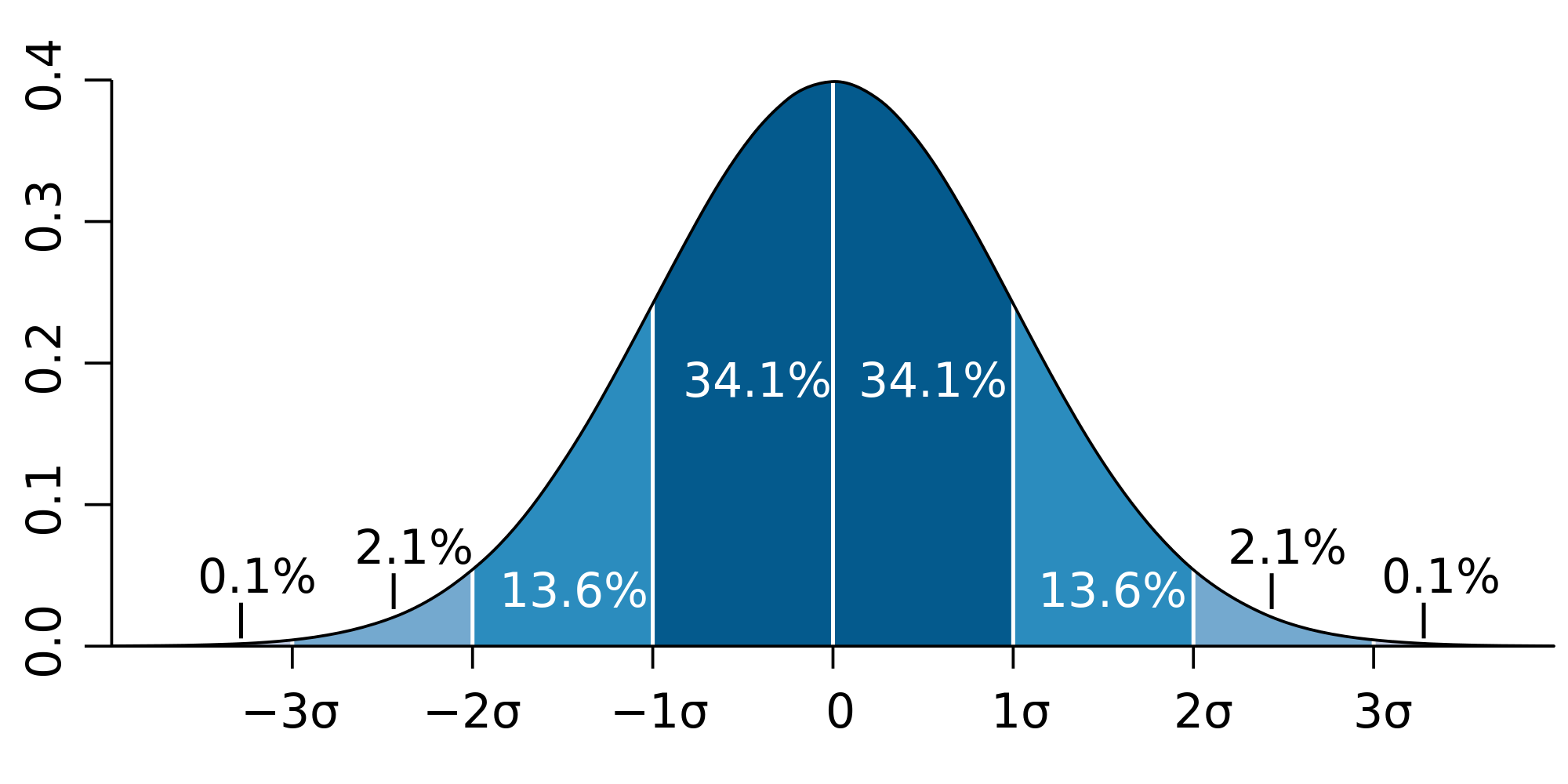
La gráfica de la función es simétrica con la forma de la campana, conocida como campana de Gauss. El parámetro a es la altura de la campana, centrada en el punto b, y con el ancho que determina c. Siendo el valor de la integral 1 cuando la media b=μ, desviación típica c=σ y:
Algunas propiedades de la distribución normal o gaussiana son:
La entropía diferencial de la distribución normal es proporcional a su varianza. Como resultado, a mayor entropía menor es la ganancia de información.
La distribución gaussiana multivariante, es una generalización de la distribución normal a dimensiones superiores. En el caso particular de dos dimensiones, la función de densidad con μ=(0,0), donde p es el coeficiente de correlación entre x e y, es:
The idea of Gaussian smoothing is to use this 2-D distribution as a `point-spread' function, and this is achieved by convolution. Since the image is stored as a collection of discrete pixels we need to produce a discrete approximation to the Gaussian function before we can perform the convolution. In theory, the Gaussian distribution is non-zero everywhere, which would require an infinitely large convolution kernel, but in practice it is effectively zero more than about three standard deviations from the mean, and so we can truncate the kernel at this point.
Kernel de convolución que aproxima una gaussiana con σ=1. El tamaño del kernel puede calcularse usando: N=3σ (99.74% de la distribución). Este caso en concreto usa: N=2σ, con σ=1, por lo que solo guarda el 95.4% de la distribución.
The convolution can in fact be performed fairly quickly since the equation for the 2-D isotropic Gaussian shown above is separable into x and y components. Thus the 2-D convolution can be performed by first convolving with a 1-D Gaussian in the x direction, and then convolving with another 1-D Gaussian in the y direction. (The Gaussian is in fact the only completely circularly symmetric operator which can be decomposed in such a way).
Con N=3*σ y σ=1, el tamaño del kernel debe ser N=7, tal que en 1D:
gauss1D =
| 0.0044 | 0.0540 | 0.2420 | 0.3991 | 0.2420 | 0.0540 | 0.0044 |
Respecto al kernel gaussiano 2D, es posible eliminar altas frecuencias de una imagen (eliminar ruido o detalles pequeños) al aplicar la máscara producto de la convolución gauss1D * gauss1D
gauss2D =
| 0.0000 | 0.0002 | 0.0011 | 0.0018 | 0.0011 | 0.0002 | 0.0000 |
| 0.0002 | 0.0029 | 0.0131 | 0.0216 | 0.0131 | 0.0029 | 0.0002 |
| 0.0011 | 0.0131 | 0.0586 | 0.0966 | 0.0586 | 0.0131 | 0.0011 |
| 0.0018 | 0.0216 | 0.0966 | 0.1592 | 0.0966 | 0.0216 | 0.0018 |
| 0.0011 | 0.0131 | 0.0586 | 0.0966 | 0.0586 | 0.0131 | 0.0011 |
| 0.0002 | 0.0029 | 0.0131 | 0.0216 | 0.0131 | 0.0029 | 0.0002 |
| 0.0000 | 0.0002 | 0.0011 | 0.0018 | 0.0011 | 0.0002 | 0.0000 |
Aplicaciones de las derivadas de la distribución gaussiana:
Base Function (0th order)
Análogamente, para el caso multivariante:
holi