Hash table in C, part 5: better hashing

README.md

Blog 2020/8/21

<- previous | index | next ->

Hash table in C, part 5: better hashing

Let's learn how to implement a hash table in C! (See also part 1, 2, 3 and 4).

Let's take a look at the importance of the hash function by comparing "terrible hash" to DJB2 and SDBM

size_t djb2Hash(void* datap, size_t length) {
    size_t hash = 5381;
    uint8_t* cursorp = datap;
    for (size_t i=0; i < length; cursorp++, i++) {
        hash = ((hash << 5) + hash) ^ (*cursorp);
    }
    return hash;
}

size_t sdbmHash(void* datap, size_t length) {
    size_t hash = 0;
    uint8_t* cursorp = datap;
    for (size_t i=0; i < length; cursorp++, i++) {
        hash = (*cursorp) + (hash << 6) + (hash << 16) - hash;
    }
    return hash;
}

Hashing the dictionary

To analyze the performance of these hash functions, we'll add all of the words (about 100,000) in /usr/share/dict/words as keys in a hash table, then look at a histogram of slot list lengths.

We'll use a function pointer so that we can easily pass in different hashing functions.

HashTable* hashTheDictionary(size_t (*hashFuncp)(void*, size_t)) {
    // open the dictionary file
    int fd = open("/usr/share/dict/words", O_RDONLY);
    assert(fd != -1);

    // get the size of the file
    struct stat statbuf;
    int err = fstat(fd, &statbuf);
    assert(err == 0);
    off_t fsize = statbuf.st_size;

    // read the file into memory.
    char* fbuff = (char*)malloc(fsize);
    assert(fbuff != NULL);
    ssize_t bytesRead = read(fd, fbuff, fsize);
    assert(bytesRead == fsize);

    HashTable* htp = HashTableMake(1);
    char* valuep = "common value";
    char* cursorp = fbuff;
    char* endp = fbuff + fsize;
    char* keyp = cursorp;
    while (cursorp != endp) {
        if (*cursorp == '\n') {
            *cursorp = '\0';
            size_t keyLength = cursorp - keyp;
            if (keyLength > 0) {
                size_t keyHash = hashFuncp(keyp, keyLength);
                HashTableSet(htp, keyp, keyLength, keyHash, valuep);
            }
            cursorp++;
            keyp = cursorp;
            continue;
        } else {
            cursorp++;
            continue;
        }
    }

    return htp;
}

void analyzeHashTable(HashTable* htp) {
    #define LENGTHS_LEN (1000)
    size_t score = 0;
    size_t lengths[LENGTHS_LEN] = {0};
    for (size_t i=0; i < htp->capacity; i++) {
        HTSlot* slotp = htp->slotspp[i];
        size_t chainLength = 0;
        while (slotp != NULL) {
            if (slotp->valuep != NULL) {
                chainLength++;
            }
            slotp = slotp->nextp;
            continue;
        }
        lengths[chainLength]++;
        score += (chainLength * chainLength);
        continue;
    }

    printf("Chain lengths histogram:\n");
    printf("length occurrences\n");
    printf("------ -----------\n");
    for (size_t i=0; i < LENGTHS_LEN; i++) {
        if (lengths[i] == 0) {
            continue;
        }

        if (i < 10) {
            printf("     ");
        } else if (i < 100) {
            printf("    ");
        } else if (i < 1000) {
            printf("   ");
        } else if (i < 10000) {
            printf("  ");
        } else if (i < 100000) {
            printf(" ");
        }
        printf("%zu %zu\n", i, lengths[i]);
    }
    printf("population: %zu, slots: %zu, empty slots: %zu, score: %zu\n",
        htp->population, htp->capacity, lengths[0], score
    );
}

int main(int argc, char** argv) {
    HashTable* htp;

    printf("\ndjb2 hash\n");
    htp = hashTheDictionary(djb2Hash);
    analyzeHashTable(htp);

    printf("\nsdbm hash\n");
    htp = hashTheDictionary(sdbmHash);
    analyzeHashTable(htp);

    printf("\nterrible hash\n");
    htp = hashTheDictionary(terribleHash);
    analyzeHashTable(htp);

    return 0;
}

Results

What we are looking for is a "short tail". The ideal hash function would give us an even distribution of hash values. That is, if we had N slots and N keys, all of our slot lists would be length 1.

Practically, some slots will be empty and others will be length > 1.

terrible hash

First, let's take a look at "terrible hash":

terrible hash
Chain lengths histogram:
length occurrences
------ -----------
     0 63741
     1 206
     2 95
     3 67
     4 55
     5 35
     6 36
     7 28
     8 28
     9 32
    10 20
    11 20
    12 13
    13 22
    14 14
    15 12
(...many rows elided...)
    82 8
    83 10
    84 12
    85 7
    86 11
    87 6
    88 8
    89 2
    90 6
    91 5
(...many rows elided...)
   266 1
   267 1
   268 2
   269 2
   272 2
   274 1
   279 1
   283 1
   288 2
   298 1
population: 102401, slots: 65536, empty slots: 63741, score: 13240151

Oof! This is truly terrible! 97% of the slots are unused, and one of the slots has a chain which is 298 elements long!!!

This hash produces a long tail, which is the opposite of what we want!

DJB2 and SDBM

Now let's compare that to DJB2 and SDBM.

DJB2 hash
Chain lengths histogram:
length occurrences
------ -----------
     0 13809
     1 21547
     2 16591
     3 8633
     4 3484
     5 1096
     6 292
     7 69
     8 13
     9 2
population: 102401, slots: 65536, empty slots: 13809, score: 263639

SDBM hash
Chain lengths histogram:
length occurrences
------ -----------
     0 13778
     1 21522
     2 16539
     3 8841
     4 3447
     5 1056
     6 275
     7 66
     8 11
    10 1
population: 102401, slots: 65536, empty slots: 13778, score: 262737

Visually:

DBJ2 and SDBM are remarkably similar in distribution!

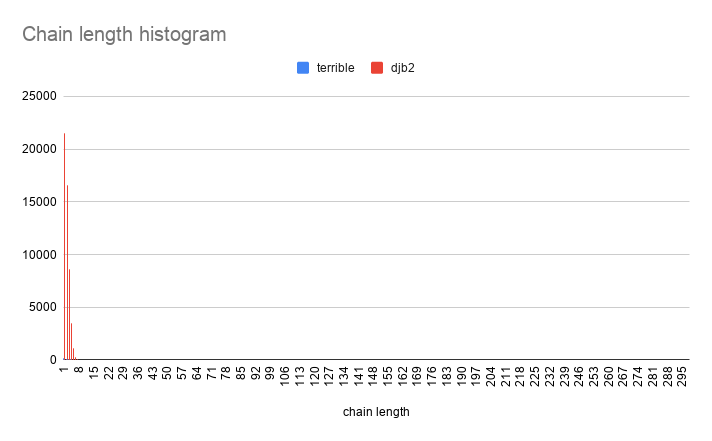
Now let's compare DJB2 to "terrible hash" :)

The difference in performance is so severe that they can't really be compared on the same graph! Let's zoom in:

Next time

In part 6, we'll take a look at using prime numbers for our slot array sizes.

HashTable.c

#include "HashTable.h"

#include <stdio.h>  // fprintf
#include <stdlib.h>  // exit
#include <string.h>  // memset
#include <stdint.h>  // uint8_t
#include <stdbool.h>  // true
#include <assert.h>  // assert

void* dmalloc(size_t size) {
    void* p = malloc(size);
    if (p == NULL) {
        perror("Error: malloc failed: ");
        exit(1);
    }
    memset(p, 0, size);
    return p;
}
#define malloc(x) dont_use_malloc_use_dmalloc

size_t terribleHash(void* datap, size_t length) {
    size_t sum = 0;
    for (size_t i=0; i < length; i++) {
        uint8_t* byte = datap + i;
        sum += *byte;
        continue;
    }
    return sum;
}

size_t djb2Hash(void* datap, size_t length) {
    size_t hash = 5381;
    uint8_t* cursorp = datap;
    for (size_t i=0; i < length; cursorp++, i++) {
        hash = ((hash << 5) + hash) ^ (*cursorp);
    }
    return hash;
}

size_t sdbmHash(void* datap, size_t length) {
    size_t hash = 0;
    uint8_t* cursorp = datap;
    for (size_t i=0; i < length; cursorp++, i++) {
        hash = (*cursorp) + (hash << 6) + (hash << 16) - hash;
    }
    return hash;
}

static HTSlot* _HTSlotMake() {
    HTSlot* sp = dmalloc(sizeof(HTSlot));
    return sp;
}

HashTable* HashTableMake(size_t capacity) {
    HashTable* htp = dmalloc(sizeof(HashTable));
    htp->capacity = capacity;
    htp->minCapacity = capacity;
    htp->slotspp = dmalloc(sizeof(void*) * capacity);
    return htp;
}

void HashTableFree(HashTable* htp) {
    for (size_t i=0; i < htp->capacity; i++) {
        HTSlot* slotp = htp->slotspp[i];
        while (slotp != NULL) {
            HTSlot* tmp = slotp;
            free(slotp);
            slotp = tmp->nextp;
            continue;
        }
    }
    free(htp->slotspp);
    free(htp);
}

void* HashTableGet(HashTable* htp, void* keyp, size_t keyLength,
    size_t keyHash
) {
    size_t slotIndex = keyHash % htp->capacity;
    HTSlot* cursorp = htp->slotspp[slotIndex];
    while (cursorp != NULL) {
        if (cursorp->keyHash == keyHash
            && cursorp->keyLength == keyLength
            && memcmp(cursorp->keyp, keyp, keyLength) == 0
        ) {
            return cursorp->valuep;
        } else {
            cursorp = cursorp->nextp;
            continue;
        }
    }
    return NULL;
}

static void _adjustCapacityIfNeeded(HashTable* htp);

void HashTableSet(HashTable* htp, void* keyp, size_t keyLength,
    size_t keyHash, void* valuep
) {
    size_t origPop = htp->population;
    size_t slotIndex = keyHash % htp->capacity;
    HTSlot* cursorp = htp->slotspp[slotIndex];
    while (cursorp != NULL) {
        if (cursorp->keyHash == keyHash
            && cursorp->keyLength == keyLength
            && memcmp(cursorp->keyp, keyp, keyLength) == 0
        ) {
            if (cursorp->valuep == NULL && valuep != NULL) {
                htp->population++;
            } else if (cursorp->valuep != NULL && valuep == NULL) {
                htp->population--;
            }
            cursorp->valuep = valuep;
            goto adjust;
        } else {
            cursorp = cursorp->nextp;
            continue;
        }
    }

    // no existing match?  append a new slot to the list.
    if (valuep != NULL) {
        HTSlot* newSlotp = _HTSlotMake();
        newSlotp->keyp = keyp;
        newSlotp->keyLength = keyLength;
        newSlotp->keyHash = keyHash;
        newSlotp->valuep = valuep;
        if (htp->slotspp[slotIndex] == NULL) {
            htp->slotspp[slotIndex] = newSlotp;
        } else {
            HTSlot* lastp = htp->slotspp[slotIndex];
            while (lastp->nextp != NULL) {
                lastp = lastp->nextp;
                continue;
            }
            lastp->nextp = newSlotp;
        }
        htp->population++;
    }

adjust:
    if (origPop != htp->population) {
        _adjustCapacityIfNeeded(htp);
    }
}

static bool _shouldShrink(HashTable* htp) {
    return htp->capacity >= (htp->population * 2);
}

static bool _shouldGrow(HashTable* htp) {
    return htp->population >= (htp->capacity * 2);
}

static void _adjustCapacityIfNeeded(HashTable* htp) {
    size_t newCapacity;
    if (_shouldShrink(htp)) {
        newCapacity = htp->capacity / 2;
    } else if (_shouldGrow(htp)) {
        newCapacity = htp->capacity * 2;
    } else {
        return;
    }

    if (newCapacity < htp->minCapacity) {
        return;
    }

    HTSlot** slots2pp = dmalloc(sizeof(void*) * newCapacity);
    for (size_t i=0; i < htp->capacity; i++) {
        HTSlot* cursorp = htp->slotspp[i];
        while (cursorp != NULL) {
            HTSlot* tmp = cursorp;
            cursorp = cursorp->nextp;
            if (tmp->valuep != NULL) {
                tmp->nextp = NULL;
                size_t slotIndex = tmp->keyHash % newCapacity;
                if (slots2pp[slotIndex] == NULL) {
                    slots2pp[slotIndex] = tmp;
                } else {
                    HTSlot* lastp = slots2pp[slotIndex];
                    while (lastp->nextp != NULL) {
                        lastp = lastp->nextp;
                        continue;
                    }
                    lastp->nextp = tmp;
                }
            }
            continue;
        }
    }
    free(htp->slotspp);
    htp->slotspp = slots2pp;
    htp->capacity = newCapacity;
}

HashTable.h

#ifndef _HASHTABLE_H_
#define _HASHTABLE_H_

#include <unistd.h>  // size_t

size_t terribleHash(void* datap, size_t length);
size_t djb2Hash(void* datap, size_t length);
size_t sdbmHash(void* datap, size_t length);

struct _HTSlot {
    void* keyp;
    size_t keyLength;
    size_t keyHash;
    void* valuep;
    struct _HTSlot* nextp;
};
typedef struct _HTSlot HTSlot;

struct _HashTable {
    HTSlot** slotspp;
    size_t capacity;
    size_t population;
    size_t minCapacity;
};
typedef struct _HashTable HashTable;

HashTable* HashTableMake(size_t capacity);
void HashTableFree(HashTable* htp);

void* HashTableGet(HashTable* htp, void* keyp, size_t keyLength,
    size_t keyHash
);
void HashTableSet(HashTable* htp, void* keyp, size_t keyLength, size_t keyHash,
    void* valuep
);

#endif

histograms.c

#include <fcntl.h>  // open
#include <assert.h>  // assert
#include <stdlib.h>  // malloc
#include <sys/stat.h>  // fstat
#include <sys/types.h>
#include <unistd.h>  // read
#include <stdio.h>  // printf
#include <stdint.h>  // uint8_t

#include "HashTable.h"

HashTable* hashTheDictionary(size_t (*hashFuncp)(void*, size_t)) {
    // open the dictionary file
    int fd = open("/usr/share/dict/words", O_RDONLY);
    assert(fd != -1);

    // get the size of the file
    struct stat statbuf;
    int err = fstat(fd, &statbuf);
    assert(err == 0);
    off_t fsize = statbuf.st_size;

    // read the file into memory.
    char* fbuff = (char*)malloc(fsize);
    assert(fbuff != NULL);
    ssize_t bytesRead = read(fd, fbuff, fsize);
    assert(bytesRead == fsize);

    HashTable* htp = HashTableMake(1);
    char* valuep = "common value";
    char* cursorp = fbuff;
    char* endp = fbuff + fsize;
    char* keyp = cursorp;
    while (cursorp != endp) {
        if (*cursorp == '\n') {
            *cursorp = '\0';
            size_t keyLength = cursorp - keyp;
            if (keyLength > 0) {
                size_t keyHash = hashFuncp(keyp, keyLength);
                HashTableSet(htp, keyp, keyLength, keyHash, valuep);
            }
            cursorp++;
            keyp = cursorp;
            continue;
        } else {
            cursorp++;
            continue;
        }
    }

    return htp;
}

void analyzeHashTable(HashTable* htp) {
    #define LENGTHS_LEN (1000)
    size_t score = 0;
    size_t lengths[LENGTHS_LEN] = {0};
    for (size_t i=0; i < htp->capacity; i++) {
        HTSlot* slotp = htp->slotspp[i];
        size_t chainLength = 0;
        while (slotp != NULL) {
            if (slotp->valuep != NULL) {
                chainLength++;
            }
            slotp = slotp->nextp;
            continue;
        }
        lengths[chainLength]++;
        score += (chainLength * chainLength);
        continue;
    }

    printf("Chain lengths histogram:\n");
    printf("length occurrences\n");
    printf("------ -----------\n");
    for (size_t i=0; i < LENGTHS_LEN; i++) {
        if (lengths[i] == 0) {
            continue;
        }

        if (i < 10) {
            printf("     ");
        } else if (i < 100) {
            printf("    ");
        } else if (i < 1000) {
            printf("   ");
        } else if (i < 10000) {
            printf("  ");
        } else if (i < 100000) {
            printf(" ");
        }
        printf("%zu %zu\n", i, lengths[i]);
    }
    printf("population: %zu, slots: %zu, empty slots: %zu, score: %zu\n",
        htp->population, htp->capacity, lengths[0], score
    );
}

int main(int argc, char** argv) {
    HashTable* htp;

    printf("\ndjb2 hash\n");
    htp = hashTheDictionary(djb2Hash);
    analyzeHashTable(htp);

    printf("\nsdbm hash\n");
    htp = hashTheDictionary(sdbmHash);
    analyzeHashTable(htp);

    printf("\nterrible hash\n");
    htp = hashTheDictionary(terribleHash);
    analyzeHashTable(htp);

    return 0;
}

Makefile

default: tests
	./tests

tests: HashTable.o tests.c
	gcc -g -std=c99 -Wall -Werror HashTable.o tests.c -o tests

histograms: HashTable.o histograms.c
	gcc -g -std=c99 -Wall -Werror HashTable.o histograms.c -o histograms

HashTable.o: HashTable.h HashTable.c
	gcc -g -std=c99 -Wall -Werror -c HashTable.c

clean:
	rm -f HashTable.o tests histograms

.PHONY: default clean

tests.c

#include "HashTable.h"

#include <assert.h>  // assert
#include <stdio.h>  // printf
#include <string.h>  // strlen, strcmp

void testMake() {
    printf("%s... ", __FUNCTION__);
    size_t capacity = 3;
    HashTable* htp = HashTableMake(capacity);
    assert(htp != NULL);
    assert(htp->capacity == 3);
    printf("OK\n");
}

void testFree() {
    printf("%s... ", __FUNCTION__);
    size_t capacity = 3;
    HashTable* htp = HashTableMake(capacity);
    HashTableFree(htp);
    printf("OK\n");
}

void testSet() {
    printf("%s... ", __FUNCTION__);
    size_t capacity = 3;
    HashTable* htp = HashTableMake(capacity);
    char* keyp = "hello";
    size_t keyLength = strlen(keyp) + 1;
    size_t keyHash = terribleHash(keyp, keyLength);
    char* valuep = "world";
    HashTableSet(htp, keyp, keyLength, keyHash, valuep);
    assert(htp->population == 1);
    printf("OK\n");
}

void testGet() {
    printf("%s... ", __FUNCTION__);
    size_t capacity = 3;
    HashTable* htp = HashTableMake(capacity);
    char* keyp = "hello";
    size_t keyLength = strlen(keyp) + 1;
    size_t keyHash = terribleHash(keyp, keyLength);
    char* valuep = "world";
    HashTableSet(htp, keyp, keyLength, keyHash, valuep);

    char* gotp = HashTableGet(htp, keyp, keyLength, keyHash);
    assert(strcmp(valuep, gotp) == 0);
    printf("OK\n");
}

void testSlotCollision() {
    printf("%s... ", __FUNCTION__);
    size_t capacity = 1;
    HashTable* htp = HashTableMake(capacity);

    char* key1p = "hello";
    size_t key1Length = strlen(key1p) + 1;
    size_t key1Hash = terribleHash(key1p, key1Length);
    char* value1p = "world";
    HashTableSet(htp, key1p, key1Length, key1Hash, value1p);
    assert(htp->population == 1);

    char* key2p = "foo";
    size_t key2Length = strlen(key2p) + 1;
    size_t key2Hash = terribleHash(key2p, key2Length);
    char* value2p = "bar";
    HashTableSet(htp, key2p, key2Length, key2Hash, value2p);
    assert(htp->population == 2);

    char* got1p = HashTableGet(htp, key1p, key1Length, key1Hash);
    assert(strcmp(value1p, got1p) == 0);

    char* got2p = HashTableGet(htp, key2p, key2Length, key2Hash);
    assert(strcmp(value2p, got2p) == 0);

    printf("OK\n");
}

void testHashCollision() {
    printf("%s... ", __FUNCTION__);
    size_t capacity = 1;
    HashTable* htp = HashTableMake(capacity);

    char* key1p = "ab";
    size_t key1Length = strlen(key1p) + 1;
    size_t key1Hash = terribleHash(key1p, key1Length);
    char* value1p = "cd";
    HashTableSet(htp, key1p, key1Length, key1Hash, value1p);
    assert(htp->population == 1);

    char* key2p = "ba";
    size_t key2Length = strlen(key2p) + 1;
    size_t key2Hash = terribleHash(key2p, key2Length);
    char* value2p = "dc";
    HashTableSet(htp, key2p, key2Length, key2Hash, value2p);
    assert(htp->population == 2);

    char* got1p = HashTableGet(htp, key1p, key1Length, key1Hash);
    assert(strcmp(value1p, got1p) == 0);

    char* got2p = HashTableGet(htp, key2p, key2Length, key2Hash);
    assert(strcmp(value2p, got2p) == 0);

    printf("OK\n");
}

void testGrow() {
    printf("%s... ", __FUNCTION__);
    size_t capacity = 1;
    HashTable* htp = HashTableMake(capacity);
    assert(htp->population == 0);
    assert(htp->capacity == capacity);

    char* key1p = "hello";
    size_t key1Length = strlen(key1p) + 1;
    size_t key1Hash = terribleHash(key1p, key1Length);
    char* value1p = "world";
    HashTableSet(htp, key1p, key1Length, key1Hash, value1p);
    assert(htp->population == 1);
    assert(htp->capacity == capacity);

    char* key2p = "foo";
    size_t key2Length = strlen(key2p) + 1;
    size_t key2Hash = terribleHash(key2p, key2Length);
    char* value2p = "bar";
    HashTableSet(htp, key2p, key2Length, key2Hash, value2p);
    assert(htp->population == 2);
    assert(htp->capacity == capacity*2);

    printf("OK\n");
}

void testShrink() {
    printf("%s... ", __FUNCTION__);
    size_t capacity = 1;
    HashTable* htp = HashTableMake(capacity);
    assert(htp->population == 0);
    assert(htp->capacity == capacity);

    char* key1p = "hello";
    size_t key1Length = strlen(key1p) + 1;
    size_t key1Hash = terribleHash(key1p, key1Length);
    char* value1p = "world";
    HashTableSet(htp, key1p, key1Length, key1Hash, value1p);
    assert(htp->population == 1);
    assert(htp->capacity == capacity);

    char* key2p = "foo";
    size_t key2Length = strlen(key2p) + 1;
    size_t key2Hash = terribleHash(key2p, key2Length);
    char* value2p = "bar";
    HashTableSet(htp, key2p, key2Length, key2Hash, value2p);
    assert(htp->population == 2);
    assert(htp->capacity == capacity*2);

    HashTableSet(htp, key2p, key2Length, key2Hash, NULL);
    assert(htp->population == 1);
    assert(htp->capacity == capacity);

    printf("OK\n");
}

int main(int argc, char** argv) {
    testMake();
    testFree();
    testSet();
    testGet();
    testSlotCollision();
    testHashCollision();
    testGrow();
    testShrink();
    return 0;
}