Get the preferred folding direction for a quad; assuming 'best' is 'contains most inner space'

about.md

Determining the fold direction of a quadrilateral.

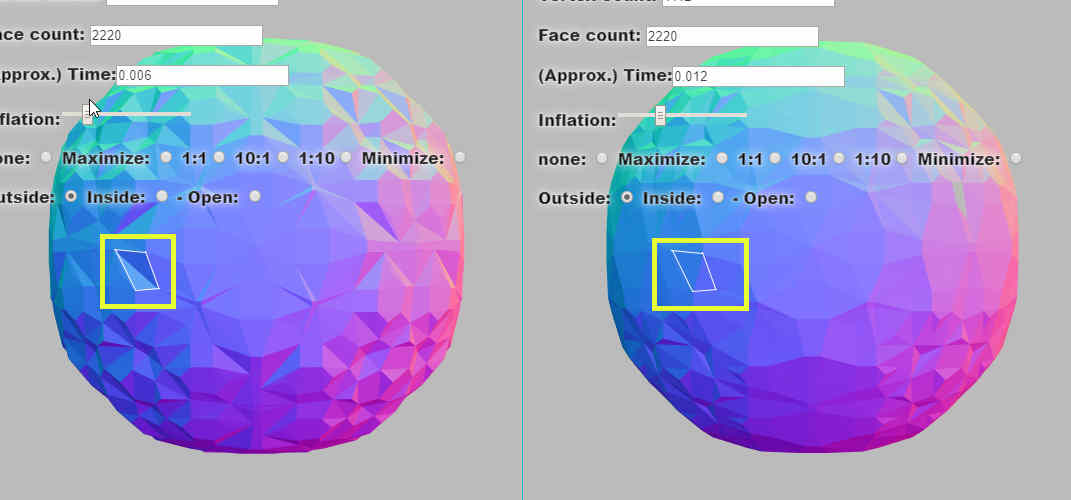
This function calculat(ed) the lengths of the diagonals of the quad p1 -> p3 and p2 -> p4, and resulted with a fold on the shortest of the diagonals. That works in some cases.

The function now calculates the nearest points on the two crossing lines of the quad and picks the line furthest along the normal passed in; this might be called 'the choice enclosing the most area'. The other choice might be more appropriate on inward curvatures and minimizations.

var direction = getFold( faceNormal, p1, p2, p3, p4 );
if( direction ) 
	GenerateTriangles( [ p1, p2, p3 ], [p1, p3, p4] );  // the common line is p1-p3
else
	GenerateTriangles( [ p2, p3, p4 ], [p2, p4, p1] );  // the common line is p2-p4
	

getFold.js

	//https://en.wikipedia.org/wiki/Skew_lines#Nearest_Points

	function getFold( faceNormal, p1, p2, p3, p4 ) {
		p1 = vertices[p1];
		p2 = vertices[p2];
		p3 = vertices[p3];
		p4 = vertices[p4];

		const del1 = [ p2.x-p1.x, p2.y-p1.y, p2.z-p1.z ];
		const d1 = [p1.x-p3.x, p1.y-p3.y, p1.z-p3.z ];
		const d2 = [p2.x-p4.x, p2.y-p4.y, p2.z-p4.z ];
		
		const l1 = 1/Math.sqrt( d1[0]*d1[0] + d1[1]*d1[1] + d1[2]*d1[2]);
		const l2 = 1/Math.sqrt( d2[0]*d2[0] + d2[1]*d2[1] + d2[2]*d2[2]);
		const n1 = [d1[0]*l1,d1[1]*l1,d1[2]*l1];
		const n2 = [d2[0]*l2,d2[1]*l2,d2[2]*l2];
		const c = [0,0,0];
		cross(c,n1,n2);
		const c1 = [0,0,0];
		cross(c1,n1,c);		
		const c2 = [0,0,0];
		cross(c2,n2,c);
	
		const dot1 = del1[0]*c2[0] + del1[1]*c2[1] + del1[2]*c2[2] ;
		// line normal 1   dot    N2 X ( N1 X N2 )
		const dot2 = n1[0]*c2[0] + n1[1]*c2[1] + n1[2]*c2[2];
		if( dot2 ){ // if dot2 is 0, division is NaN/Infinity; lines are parallel, and all points are closest...
			
			// point on (1-3) that's closest
			const closeP1 = [p1.x + (( dot1/dot2  )*n1[0]),p1.y + (( dot1/dot2  )*n1[1]),p1.z + (( dot1/dot2  )*n1[2])]

			const dot3 = -del1[0]*c1[0] + -del1[1]*c1[1] + -del1[2]*c1[2] ;
			const dot4 = n2[0]*c1[0] + n2[1]*c1[1] + n2[2]*c1[2]; // will be OK if dot2 above != 0.
			// point on (2-4) that's closest
			const closeP2 = [p2.x + (( dot3/dot4  )*n2[0]),p2.y + (( dot3/dot4  )*n2[1]),p2.z + (( dot3/dot4  )*n2[2])]

			const crossDel = [closeP1[0]-closeP2[0],closeP1[1]-closeP2[1],closeP1[2]-closeP2[2]];

			if( ( crossDel[0] * faceNormal[0] + crossDel[1] * faceNormal[1] + crossDel[2] * faceNormal[2] ) > 0 )
				return 1;
			return 0;
		}
		// fallback on length comparison
		// compare the length, and prefer to fold on the shorter one.
		if( d1[0]*d1[0]+d1[1]*d1[1]+d1[2]*d1[2] < d2[0]*d2[0]+d2[1]*d2[1]+d2[2]*d2[2] ) {
			//console.log( "YES")
			return 1;
		}
		//console.log( "NO", d1, d2)
		return 0;
	}