Опубликовано:11 ноября 2023 г. | в 16:00 (34 минуты чтения)
В этой статье мы рассмотрим внутреннюю структуру больших языковых моделей (БЯМ), чтобы получить практическое представление о том, как они работают. Для этого мы будем использовать исходный код llama.cpp, реализацию модели LLaMA от Meta на чистом C++. Лично я считаю, что llama.cpp — отличное учебное пособие для более глубокого понимания БЯМ. Его код чистый, лаконичный и понятный, без лишних абстракций. Мы будем использовать эту версию коммита.
Мы сосредоточимся на выводе данных в больших языковых моделях, то есть на том, как уже обученная модель генерирует ответы на основе запросов пользователя.
Этот пост написан для инженеров в областях, отличных от ML и AI, которые заинтересованы в лучшем понимании LLM. Он фокусируется на внутренней части LLM с инженерной точки зрения, а не с точки зрения AI. Следовательно, он не предполагает обширных знаний в области математики или глубокого обучения.
В этой статье мы рассмотрим процесс логического вывода от начала до конца, затронув следующие темы (нажмите, чтобы перейти к соответствующему разделу):
- Тензоры: базовый обзор того, как выполняются математические операции с использованием тензоров, которые потенциально могут быть перенесены на графический процессор.
- Токенизация: процесс разделения запроса пользователя на список токенов, которые LLM использует в качестве входных данных.
- Встраивание: процесс преобразования токенов в векторное представление.
- Трансформер: центральная часть архитектуры больших языковых моделей, отвечающая за сам процесс логического вывода. Мы сосредоточимся на механизме самовнимания.
- Сэмплирование: процесс выбора следующего прогнозируемого токена. Мы рассмотрим два метода сэмплирования.
- Кэш KV: распространённый метод оптимизации, используемый для ускорения логического вывода в больших подсказках. Мы рассмотрим базовую реализацию кэша KV.
Мы надеемся, что к концу этой статьи вы получите полное представление о том, как работают большие языковые модели. Это позволит вам изучить более сложные темы, некоторые из которых подробно описаны в последнем разделе.
Откройте оглавление
Будучи большой языковой моделью, LLaMA работает следующим образом: на вход подаётся текст, «подсказка», и система предсказывает, какими должны быть следующие токены или слова.
Чтобы проиллюстрировать это, мы возьмём в качестве примера первое предложение из статьи Википедии о квантовой механике. Наша подсказка:
Quantum mechanics is a fundamental theory in physics that
Языковая модель пытается продолжить предложение в соответствии с тем, что, по её мнению, является наиболее вероятным продолжением. Используя llama.cpp, мы получаем следующее продолжение:
provides insights into how matter and energy behave at the atomic scale.
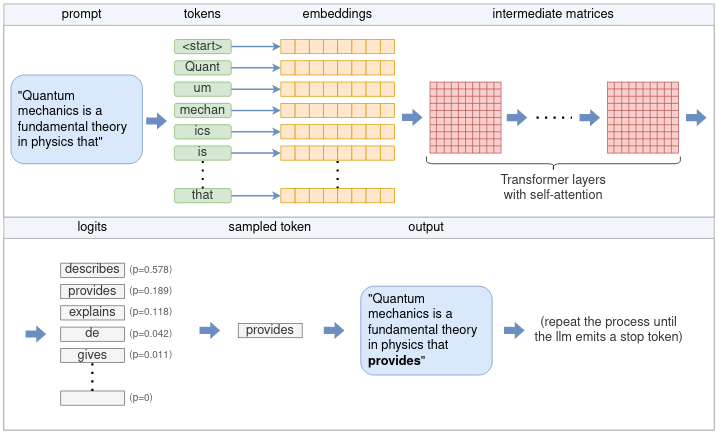
Давайте начнём с общего описания того, как работает этот процесс. По сути, LLM каждый раз предсказывает только один токен. Генерация полного предложения (или нескольких предложений) достигается за счёт многократного применения модели LLM к одному и тому же запросу с добавлением предыдущих выходных токенов к запросу. Такой тип модели называется авторегрессионной моделью. Таким образом, основное внимание мы уделим созданию одного токена, как показано на схеме высокого уровня ниже:
Полный процесс создания одного токена на основе пользовательского запроса включает в себя различные этапы, такие как токенизация, встраивание, использование нейронной сети Transformer и выборка. Об этом мы расскажем в этой статье.
Согласно схеме, процесс выглядит следующим образом:
- Токенизатор разбивает запрос на список токенов. Некоторые слова могут быть разбиты на несколько токенов в зависимости от словаря модели. Каждый токен представлен уникальным номером.
- Каждый числовой токен преобразуется в эмбеддинг. Эмбеддинг — это вектор фиксированного размера, который представляет токен в более удобной для обработки LLM форме. Все эмбеддинги вместе образуют матрицу эмбеддингов.
- Матрица встраивания служит входными данными для трансформера. Трансформер — это нейронная сеть, которая является ядром большой языковой модели. Трансформер состоит из нескольких слоёв. Каждый слой принимает входную матрицу и выполняет над ней различные математические операции с использованием параметров модели, наиболее примечательным из которых является механизм самовнимания. Выходные данные слоя используются в качестве входных данных для следующего слоя.
- Последняя нейронная сеть преобразует выходные данные трансформера в логиты. Каждому возможному следующему токену соответствует логит, который представляет собой вероятность того, что токен является «правильным» продолжением предложения.
- Для выбора следующего токена из списка логитов используется один из нескольких методов выбора.
- Выбранный токен возвращается в качестве результата. Чтобы продолжить генерацию токенов, выбранный токен добавляется к списку токенов, полученному на шаге (1), и процесс повторяется. Это можно продолжать до тех пор, пока не будет сгенерировано нужное количество токенов или пока LLM не выдаст специальный токен конца потока (EOS).
В следующих разделах мы подробно рассмотрим каждый из этих этапов. Но прежде нам нужно познакомиться с тензорами.
Тензоры — это основная структура данных, используемая для выполнения математических операций в нейронных сетях. В llama.cpp используется ggml — реализация тензоров на чистом C++, эквивалентная PyTorch или Tensorflow в экосистеме Python. Мы будем использовать ggml, чтобы понять, как работают тензоры.
Тензор представляет собой многомерный массив чисел. Тензор может содержать одно число, вектор (одномерный массив), матрицу (двумерный массив) или даже трёх- или четырёхмерные массивы. На практике больше не требуется.
Важно различать два типа тензоров. Есть тензоры, которые содержат фактические данные в виде многомерного массива чисел. С другой стороны, есть тензоры, которые представляют собой только результат вычислений между одним или несколькими другими тензорами и не содержат данных до тех пор, пока не будут вычислены. Вскоре мы рассмотрим это различие.
В ggml тензоры представлены структурой ggml_tensor В упрощённом для наших целей виде это выглядит следующим образом:
// ggml.h
struct ggml_tensor {
enum ggml_type type;
enum ggml_backend backend;
int n_dims;
// number of elements
int64_t ne[GGML_MAX_DIMS];
// stride in bytes
size_t nb[GGML_MAX_DIMS];
enum ggml_op op;
struct ggml_tensor * src[GGML_MAX_SRC];
void * data;
char name[GGML_MAX_NAME];
};
Первые несколько полей просты в использовании:
typeсодержит примитивный тип элементов тензора. Например,GGML_TYPE_F32означает, что каждый элемент представляет собой 32-битное число с плавающей запятой.enumсодержит информацию о том, поддерживается ли тензор центральным процессором или графическим процессором. Мы вернёмся к этому позже.n_dimsЭто количество измерений, которое может варьироваться от 1 до 4.neсодержит количество элементов в каждом измерении. ggml — это порядок, в котором обрабатываются строки, то естьne[0]обозначает размер каждой строки,ne[1]— размер каждого столбца и так далее.
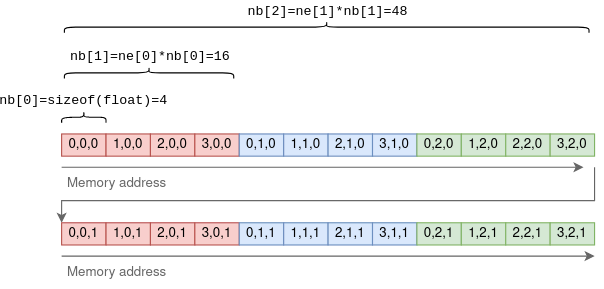
nb Это немного сложнее. Он содержит шаг: количество байтов между последовательными элементами в каждом измерении. В первом измерении это будет размер примитивного элемента. Во втором измерении это будет размер строки, умноженный на размер элемента, и так далее. Например, для тензора 4x3x2:
Пример тензора из 32-битных чисел с плавающей запятой с размерами {4,3,2} и шагами {4,16,48}.
Цель использования шага состоит в том, чтобы можно было выполнять определённые операции с тензорами без копирования данных. Например, операцию транспонирования двумерного массива, которая преобразует строки в столбцы, можно выполнить, просто поменяв местами ne и nb и указав на те же базовые данные:
// ggml.c (the function was slightly simplified).
struct ggml_tensor * ggml_transpose(
struct ggml_context * ctx,
struct ggml_tensor * a) {
// Initialize `result` to point to the same data as `a`
struct ggml_tensor * result = ggml_view_tensor(ctx, a);
result->ne[0] = a->ne[1];
result->ne[1] = a->ne[0];
result->nb[0] = a->nb[1];
result->nb[1] = a->nb[0];
result->op = GGML_OP_TRANSPOSE;
result->src[0] = a;
return result;
}
В приведённой выше функции result — это новый тензор, инициализированный так, чтобы он указывал на тот же многомерный массив чисел, что и исходный тензор a. Поменяв местами измерения в ne и шаги в nb, мы выполняем операцию транспонирования без копирования данных.
Как уже упоминалось, некоторые тензоры содержат данные, а другие представляют собой теоретический результат операции между другими тензорами. Возвращаясь к struct ggml_tensor:
opЭто может быть любая поддерживаемая операция между тензорами. Установка значенияGGML_OP_NONEозначает, что тензор содержит данные. Другие значения могут обозначать операцию. Например,GGML_OP_MUL_MATозначает, что этот тензор не содержит данных, а лишь представляет результат матричного умножения двух других тензоров.src— это массив указателей на тензоры, между которыми должна быть выполнена операция. Например, еслиop == GGML_OP_MUL_MAT, тоsrcбудет содержать указатели на два тензора, которые нужно перемножить. Еслиop == GGML_OP_NONE, тоsrcбудет пустым.dataуказывает на фактические данные тензора илиNULLесли этот тензор является результатом операции. Он также может указывать на данные другого тензора, и тогда он называется представлением. Например, в приведённой выше функцииggml_transpose()результирующий тензор является представлением исходного тензора, только с изменёнными размерами и шагами.dataуказывает на то же место в памяти.
Функция умножения матриц хорошо иллюстрирует эти понятия:
// ggml.c (simplified and commented)
struct ggml_tensor * ggml_mul_mat(
struct ggml_context * ctx,
struct ggml_tensor * a,
struct ggml_tensor * b) {
// Check that the tensors' dimensions permit matrix multiplication.
GGML_ASSERT(ggml_can_mul_mat(a, b));
// Set the new tensor's dimensions
// according to matrix multiplication rules.
const int64_t ne[4] = { a->ne[1], b->ne[1], b->ne[2], b->ne[3] };
// Allocate a new ggml_tensor.
// No data is actually allocated except the wrapper struct.
struct ggml_tensor * result = ggml_new_tensor(ctx, GGML_TYPE_F32, MAX(a->n_dims, b->n_dims), ne);
// Set the operation and sources.
result->op = GGML_OP_MUL_MAT;
result->src[0] = a;
result->src[1] = b;
return result;
}
В приведённой выше функции result не содержит никаких данных. Это просто представление теоретического результата умножения a на b.
Приведенная выше функция ggml_mul_mat() или любая другая тензорная операция ничего не вычисляет, а просто подготавливает тензоры к операции. С другой стороны, можно сказать, что она создает вычислительный граф, в котором каждая тензорная операция является узлом, а источники операции — дочерними узлами. В сценарии умножения матриц в графе есть родительский узел с операцией GGML_OP_MUL_MAT и два дочерних узла.
В качестве реального примера из llama.cpp приведу следующий код, реализующий механизм самовнимания, который является частью каждого слоя Transformer и будет рассмотрен более подробно позже:
// llama.cpp
static struct ggml_cgraph * llm_build_llama(/* ... */) {
// ...
// K,Q,V are tensors initialized earlier
struct ggml_tensor * KQ = ggml_mul_mat(ctx0, K, Q);
// KQ_scale is a single-number tensor initialized earlier.
struct ggml_tensor * KQ_scaled = ggml_scale_inplace(ctx0, KQ, KQ_scale);
struct ggml_tensor * KQ_masked = ggml_diag_mask_inf_inplace(ctx0, KQ_scaled, n_past);
struct ggml_tensor * KQ_soft_max = ggml_soft_max_inplace(ctx0, KQ_masked);
struct ggml_tensor * KQV = ggml_mul_mat(ctx0, V, KQ_soft_max);
// ...
}
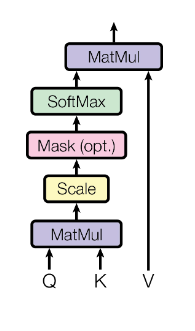
Код представляет собой серию тензорных операций и создаёт граф вычислений, идентичный тому, что описан в оригинальной статье о трансформере:
Чтобы фактически вычислить результирующий тензор (здесь он KQV), необходимо выполнить следующие действия:
- Данные загружаются в
data-указатель каждого конечного тензора. В примере конечными тензорами являютсяK,QиV. - Выходной тензор (
KQV) преобразуется в вычислительный граф с помощьюggml_build_forward(). Эта функция относительно проста и упорядочивает узлы в порядке глубины.1 - Граф вычислений запускается с помощью
ggml_graph_compute(), который выполняетggml_compute_forward()для каждого узла в порядке обхода в глубину.ggml_compute_forward()выполняет основную часть вычислений. Он выполняет математическую операцию и заполняет указательdataтензора результатом. - В конце этого процесса указатель
dataвыходного тензора указывает на конечный результат.
Многие тензорные операции, такие как сложение и умножение матриц, могут выполняться на графическом процессоре гораздо эффективнее благодаря высокому уровню параллелизма. Если графический процессор доступен, тензоры можно пометить как tensor->backend = GGML_BACKEND_GPU. В этом случае ggml_compute_forward() попытается перенести вычисления на графический процессор. Графический процессор выполнит тензорную операцию, и результат будет сохранён в памяти графического процессора (а не в указателе data).
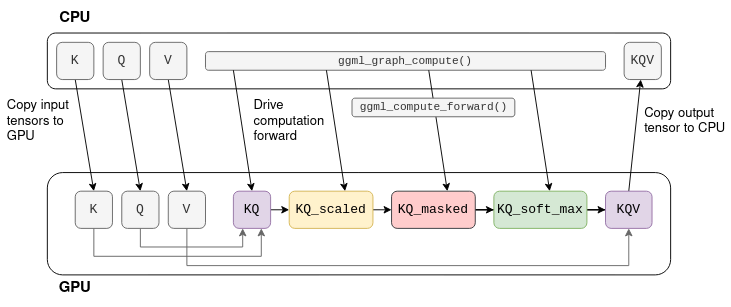
Рассмотрим граф вычислений с самовниманием, показанный ранее. Если предположить, что K,Q,V — это фиксированные тензоры, то вычисления можно перенести на графический процессор:
Процесс начинается с копирования K``Q, V в память графического процессора. Затем центральный процессор выполняет вычисления тензор за тензором, но фактическая математическая операция выполняется графическим процессором. Когда последняя операция в графе завершается, данные результирующего тензора копируются из памяти графического процессора в память центрального процессора.
Примечание: в реальном трансформере K,Q,V не являются фиксированными, а KQV не является конечным результатом. Подробнее об этом позже.
Теперь, когда мы разобрались с тензорами, можно вернуться к работе LLaMA.
Первым шагом в логическом выводе является токенизация. Токенизация — это процесс разделения запроса на список более коротких строк, называемых токенами. Токены должны входить в словарь модели, то есть в список токенов, на которых обучалась языковая модель. Например, словарь LLaMA состоит из 32 000 токенов и является частью модели.
В нашем примере токенизация разбивает запрос на одиннадцать токенов (пробелы заменяются специальным метасимволом ’ ’ (U+2581)):
|Quant|um|▁mechan|ics|▁is|▁a|▁fundamental|▁theory|▁in|▁physics|▁that|
Для токенизации LLaMA использует токенизатор SentencePiece с алгоритмом кодирования байтовых пар (BPE). Этот токенизатор интересен тем, что он основан на подсчётах слов, то есть слова могут быть представлены несколькими токенами. Например, в нашем запросе слово «Quantum» разбивается на «Quant» и «um». Во время обучения, когда формируется словарь, алгоритм BPE гарантирует, что распространённые слова будут включены в словарь как единый токен, а редкие слова будут разбиты на подсчёты слов. В приведённом выше примере слово «Quantum» не входит в словарь, а «Quant» и «um» являются двумя отдельными токенами. Пробелы не обрабатываются отдельно и включаются в токены в качестве метасимволов, если они достаточно распространены.
Токенизация на основе подслов эффективна по нескольким причинам:
-
Это позволяет магистру права выучить значение редких слов, таких как "Quantum", сохраняя при этом относительно небольшой объем словаря, представляя распространенные суффиксы и приставки в виде отдельных лексем.
-
Он изучает особенности конкретного языка, не используя схемы токенизации, специфичные для этого языка. Цитата из статьи о BPE-кодировании:
Рассмотрим такие словосочетания, как немецкое Abwasser|behandlungs|anlange «станция очистки сточных вод», для которых сегментированное представление переменной длины интуитивно более привлекательно, чем кодирование слова в виде вектора фиксированной длины.
-
Аналогичным образом он полезен при разборе кода. Например, переменная с именем
model_sizeбудет преобразована вmodel|_|size, что позволит языковой модели «понять» назначение переменной (ещё одна причина давать переменным информативные имена!).
В llama.cpp токенизация выполняется с помощью функции llama_tokenize() . Эта функция принимает на вход строку с подсказкой и возвращает список токенов, где каждый токен представлен целым числом:
// llama.h
typedef int llama_token;
// common.h
std::vector<llama_token> llama_tokenize(
struct llama_context * ctx,
// the prompt
const std::string & text,
bool add_bos);
Процесс токенизации начинается с разбиения запроса на односимвольные токены. Затем система итеративно пытается объединить два последовательных токена в один более крупный, если объединённый токен входит в словарь. Это гарантирует, что итоговые токены будут максимально крупными. Для нашего примера токенизация выполняется следующим образом:
Q|u|a|n|t|u|m|▁|m|e|c|h|a|n|i|c|s|▁|i|s|▁a|▁|f|u|n|d|a|m|e|n|t|a|l|
Qu|an|t|um|▁m|e|ch|an|ic|s|▁|is|▁a|▁f|u|nd|am|en|t|al|
Qu|ant|um|▁me|chan|ics|▁is|▁a|▁f|und|am|ent|al|
Quant|um|▁mechan|ics|▁is|▁a|▁fund|ament|al|
Quant|um|▁mechan|ics|▁is|▁a|▁fund|amental|
Quant|um|▁mechan|ics|▁is|▁a|▁fundamental|
Обратите внимание, что каждый промежуточный этап включает в себя корректную токенизацию в соответствии со словарём модели. Однако в качестве входных данных для LLM используется только последний этап.
Токены используются в качестве входных данных для LLaMA, чтобы предсказать следующий токен. Ключевой функцией здесь является функция llm_build_llama():
// llama.cpp (simplified)
static struct ggml_cgraph * llm_build_llama(
llama_context & lctx,
const llama_token * tokens,
int n_tokens,
int n_past);
Эта функция принимает на вход список токенов, представленных параметрами tokens и n_tokens. Затем она строит полный граф тензорных вычислений LLaMA и возвращает его в виде struct ggml_cgraph. На этом этапе вычисления не производятся. Параметр n_past, который в настоящее время равен нулю, можно пока не учитывать. Мы вернемся к нему позже, когда будем обсуждать кэш kv.
Помимо токенов, функция использует веса модели или параметры модели. Это фиксированные тензоры, которые изучаются в процессе обучения LLM и включаются в модель. Эти параметры модели предварительно загружаются в lctx перед началом логического вывода.
Теперь мы приступим к изучению структуры графа вычислений. Первая часть графа вычислений включает в себя преобразование токенов в эмбеддинги.
Эмбеддинг — это фиксированное векторное представление каждого токена, которое больше подходит для глубокого обучения, чем простые целые числа, поскольку оно отражает семантическое значение слов. Размер этого вектора — размерность модели, которая варьируется в зависимости от модели. Например, в LLaMA-7B размерность модели составляет n_embd=4096.
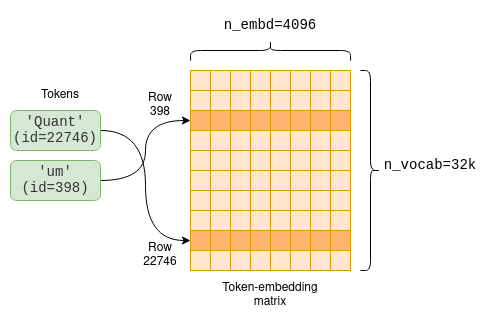
Параметры модели включают в себя матрицу встраивания токенов, которая преобразует токены во встраиваемые объекты. Поскольку размер нашего словаря составляет n_vocab=32000, это 32000 x 4096 матрица, в которой каждая строка содержит вектор встраивания для одного токена:
Каждому токену соответствует встраивание, которое было изучено в процессе обучения и доступно в виде матрицы встраиваний токенов.
Первая часть графа вычислений извлекает из матрицы встраивания токенов соответствующие строки для каждого токена.
// llama.cpp (simplified)
static struct ggml_cgraph * llm_build_llama(/* ... */) {
// ...
struct ggml_tensor * inp_tokens = ggml_new_tensor_1d(ctx0, GGML_TYPE_I32, n_tokens);
memcpy(
inp_tokens->data,
tokens,
n_tokens * ggml_element_size(inp_tokens));
inpL = ggml_get_rows(ctx0, model.tok_embeddings, inp_tokens);
}
//
The code first creates a new one-dimensional tensor of integers, called inp_tokens, to hold the numerical tokens. Then, it copies the token values into this tensor’s data pointer. Last, it creates a new GGML_OP_GET_ROWS tensor operation combining the token-embedding matrix model.tok_embeddings with our tokens.
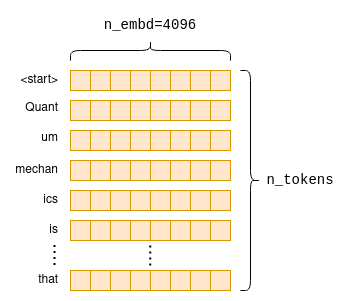
This operation, when later computed, pulls rows from the embeddings matrix as shown in the diagram above to create a new n_tokens x n_embd matrix containing only the embeddings for our tokens in their original order:
В процессе встраивания для каждого исходного токена создаётся вектор встраивания фиксированного размера. Если сложить их вместе, получится матрица встраивания подсказки.
Основная часть графа вычислений называется трансформером. Трансформер — это архитектура нейронной сети, которая является ядром большой языковой модели и выполняет основную логику вывода. В следующем разделе мы рассмотрим некоторые ключевые аспекты трансформера с инженерной точки зрения, уделив особое внимание механизму самовнимания. Если вы хотите лучше понять архитектуру трансформера, я рекомендую прочитать иллюстрированную статью о трансформере2.
Сначала мы рассмотрим, что такое самовнимание, а затем уменьшим масштаб, чтобы увидеть, как оно вписывается в общую архитектуру Transformer3.
Самовнимание — это механизм, который принимает последовательность токенов и создаёт компактное векторное представление этой последовательности с учётом взаимосвязей между токенами. Это единственное место в архитектуре больших языковых моделей, где вычисляются взаимосвязи между токенами. Таким образом, оно составляет основу понимания языка, которое подразумевает понимание взаимосвязей между словами. Поскольку оно включает в себя вычисления между токенами, оно также представляет наибольший интерес с инженерной точки зрения, поскольку вычисления могут быть довольно масштабными, особенно для длинных последовательностей.
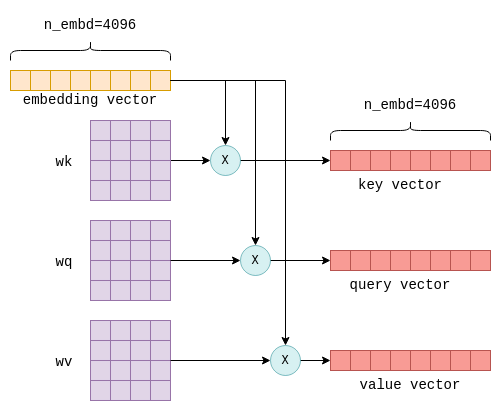
Входными данными для механизма самовнимания является n_tokens x n_embd матрица эмбеддинга, в которой каждая строка, или вектор, представляет отдельный токен4. Затем каждый из этих векторов преобразуется в три отдельных вектора, называемых «ключом», «запросом» и «значением». Преобразование осуществляется путем умножения вектора эмбеддинга каждого токена на фиксированные матрицы wk, wq и wv, которые являются частью параметров модели:
При умножении вектора встраивания токена на матрицы параметров wk, wq и wv получаются векторы «ключ», «запрос» и «значение» для этого токена.
Этот процесс повторяется для каждого токена, то есть n_tokens раз. Теоретически это можно сделать в цикле, но для повышения эффективности все строки преобразуются за одну операцию с помощью матричного умножения, которое выполняет именно эту задачу. Соответствующий код выглядит следующим образом:
// llama.cpp (simplified to remove use of cache)
// `cur` contains the input to the self-attention mechanism
struct ggml_tensor * K = ggml_mul_mat(ctx0,
model.layers[il].wk, cur);
struct ggml_tensor * Q = ggml_mul_mat(ctx0,
model.layers[il].wq, cur);
struct ggml_tensor * V = ggml_mul_mat(ctx0,
model.layers[il].wv, cur);
В итоге мы получаем K, Q и V: три матрицы размером n_tokens x n_embd, в которых векторы ключей, запросов и значений для каждого токена объединены.
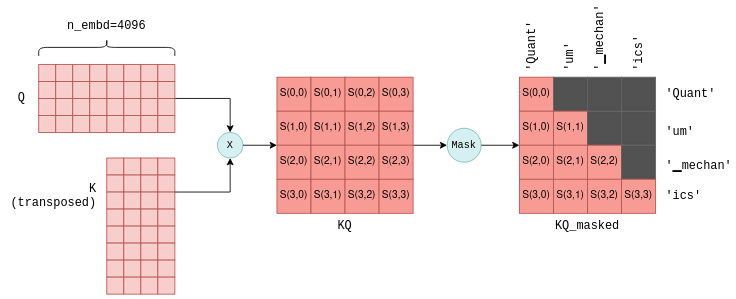
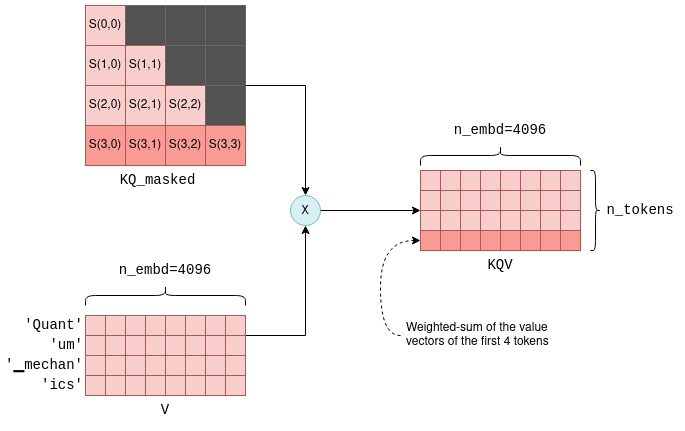
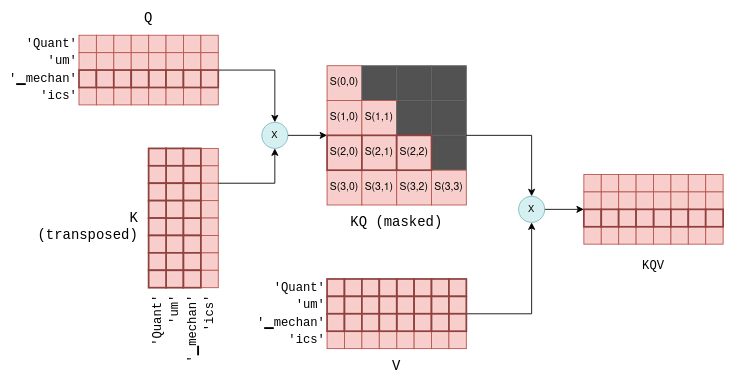
Следующий этап самовнимания заключается в умножении матрицы Q, содержащей сложенные векторы запросов, на транспонированную матрицу K, содержащую сложенные векторы ключей. Для тех, кто не очень хорошо знаком с матричными операциями, поясним, что эта операция по сути вычисляет совместную оценку для каждой пары векторов запросов и ключей. Мы будем использовать обозначение S(i,j) для обозначения оценки запроса i с ключом j.
В результате этого процесса получается n_tokens^2 оценок, по одной для каждой пары «запрос — ключ», которые объединяются в одну матрицу под названием KQ. Эта матрица впоследствии маскируется, чтобы удалить элементы выше диагонали:
Совместный показатель S(i,j) рассчитывается для каждой пары «запрос — ключ» путем умножения Q на транспонированную матрицу K. Здесь показан результат для первых четырех токенов, а также для токенов, представленных каждым показателем. На этапе маскировки сохраняются только показатели между токеном и предыдущими токенами. Для простоты промежуточная операция масштабирования опущена.
Операция маскировки — критически важный этап. Для каждого токена сохраняются оценки только для предыдущих токенов. На этапе обучения это ограничение гарантирует, что языковая модель научится предсказывать токены, основываясь исключительно на предыдущих токенах, а не на будущих. Более того, как мы подробнее рассмотрим позже, это позволяет значительно оптимизировать прогнозирование будущих токенов.
Последний этап самовнимания заключается в умножении замаскированного балла KQ_masked на векторы значений, полученные ранее5. Такая операция матричного умножения создаёт взвешенную сумму векторов значений всех предыдущих токенов, где весами являются баллы S(i,j). Например, для четвёртого токена ics создаётся взвешенная сумма векторов значений Quant, um, ▁mechan и ics с весами S(3,0)–S(3,3), которые сами были рассчитаны на основе вектора запроса ics и всех предыдущих векторов ключей.
Матрица KQV содержит взвешенные суммы векторов значений. Например, выделенная последняя строка представляет собой взвешенную сумму первых четырёх векторов значений, где весами являются выделенные баллы.
KQV Матрица завершает механизм самовнимания. Соответствующий код, реализующий самовнимание, уже был представлен ранее в контексте общих тензорных вычислений, но теперь вы лучше подготовлены к тому, чтобы полностью его понять.
Самовнимание — это один из компонентов так называемых слоёв трансформера. Каждый слой, помимо механизма самовнимания, содержит множество других тензорных операций, в основном матричное сложение, умножение и активацию, которые являются частью нейронной сети прямого распространения. Мы не будем подробно рассматривать эти операции, но отметим следующие факты:
- В сети прямого распространения используются большие фиксированные матрицы параметров. В LLaMA-7B их размеры составляют
n_embd x n_ff = 4096 x 11008. - Помимо самовнимания, все остальные операции можно рассматривать как выполняемые построчно или токен за токеном. Как упоминалось ранее, только самовнимание содержит межтокеновые вычисления. Это будет важно позже, при обсуждении kv-кэша.
- Входная и выходная данные всегда имеют размер
n_tokens x n_embd: по одной строке для каждого токена, размер каждой из которых соответствует размерности модели.
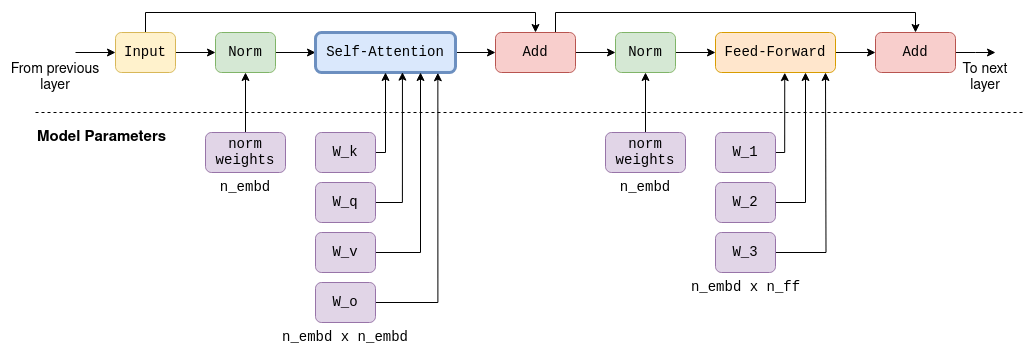
Для полноты картины я приложил схему одного слоя трансформера в LLaMA-7B. Обратите внимание, что в будущих моделях точная архитектура, скорее всего, будет немного отличаться.
Full computation graph of a Transformer layer in LLaMA-7B, containing self-attention and feed-foward mechanisms. The output of each layer serves as the input to the next. Large parameter matrices are used both in the self-attention stage and in the feed-forward stage. These constitute most of the 7 billion parameters of the model.
В архитектуре Transformer есть несколько слоёв. Например, в LLaMA-7B их n_layers=32 штук. Слои идентичны, за исключением того, что у каждого из них свой набор матриц параметров (например, свои матрицы wk, wq и wv для механизма самовнимания). Входными данными для первого слоя является матрица встраивания, как описано выше. Выходные данные первого слоя используются в качестве входных данных для второго слоя и так далее. Можно представить, что каждый слой создаёт список векторных представлений, но каждое векторное представление больше не привязано напрямую к отдельному токену, а связано с более сложным пониманием взаимосвязей между токенами.
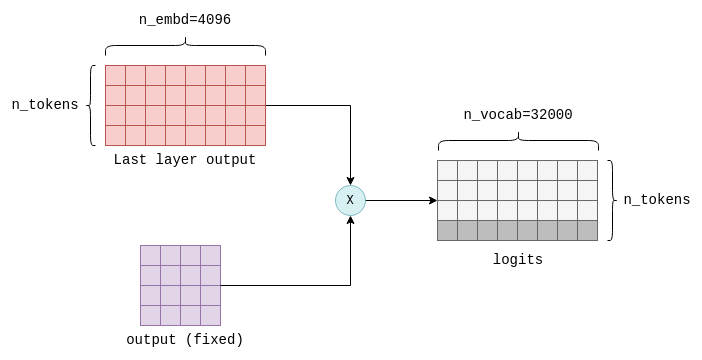
На последнем этапе работы трансформера вычисляются логиты. Логит — это число с плавающей запятой, которое представляет собой вероятность того, что конкретный токен является «правильным» следующим токеном. Чем выше значение логита, тем больше вероятность того, что соответствующий токен является «правильным».
Логиты вычисляются путём умножения выходных данных последнего слоя Transformer на фиксированную n_embd x n_vocab матрицу параметров (также называемую output в llama.cpp). В результате этой операции для каждого токена в нашем словаре получается логит. Например, в LLaMA получается n_vocab=32000 логитов:
На последнем этапе работы трансформера вычисляются логиты путём умножения выходных данных последнего слоя на матрицу с фиксированными параметрами (также называемую «выходными данными»). Интерес представляет только последняя строка результата, выделенная здесь, которая содержит логит для каждого возможного следующего токена в словаре.
Логиты — это выходные данные трансформера, которые сообщают нам, какие токены являются наиболее вероятными следующими. На этом все тензорные вычисления завершаются. Следующая упрощённая и прокомментированная версия функции llm_build_llama() обобщает все шаги, описанные в этом разделе:
// llama.cpp (simplified and commented)
static struct ggml_cgraph * llm_build_llama(
llama_context & lctx,
const llama_token * tokens,
int n_tokens,
int n_past) {
ggml_cgraph * gf = ggml_new_graph(ctx0);
struct ggml_tensor * cur;
struct ggml_tensor * inpL;
// Create a tensor to hold the tokens.
struct ggml_tensor * inp_tokens = ggml_new_tensor_1d(ctx0, GGML_TYPE_I32, N);
// Copy the tokens into the tensor
memcpy(
inp_tokens->data,
tokens,
n_tokens * ggml_element_size(inp_tokens));
// Create the embedding matrix.
inpL = ggml_get_rows(ctx0,
model.tok_embeddings,
inp_tokens);
// Iteratively apply all layers.
for (int il = 0; il < n_layer; ++il) {
struct ggml_tensor * K = ggml_mul_mat(ctx0, model.layers[il].wk, cur);
struct ggml_tensor * Q = ggml_mul_mat(ctx0, model.layers[il].wq, cur);
struct ggml_tensor * V = ggml_mul_mat(ctx0, model.layers[il].wv, cur);
struct ggml_tensor * KQ = ggml_mul_mat(ctx0, K, Q);
struct ggml_tensor * KQ_scaled = ggml_scale_inplace(ctx0, KQ, KQ_scale);
struct ggml_tensor * KQ_masked = ggml_diag_mask_inf_inplace(ctx0,
KQ_scaled, n_past);
struct ggml_tensor * KQ_soft_max = ggml_soft_max_inplace(ctx0, KQ_masked);
struct ggml_tensor * KQV = ggml_mul_mat(ctx0, V, KQ_soft_max);
// Run feed-forward network.
// Produces `cur`.
// ...
// input for next layer
inpL = cur;
}
cur = inpL;
// Calculate logits from last layer's output.
cur = ggml_mul_mat(ctx0, model.output, cur);
// Build and return the computation graph.
ggml_build_forward_expand(gf, cur);
return gf;
}
Для фактического выполнения логического вывода вычисляется граф вычислений, возвращаемый этой функцией, с использованием ggml_graph_compute() как описано ранее. Затем логиты копируются из data указателя последнего тензора в массив чисел с плавающей запятой, готовый к следующему шагу — выборке.
Теперь, когда у нас есть список логитов, нужно выбрать следующий токен на их основе. Этот процесс называется выборка. Существует несколько методов выборки, подходящих для разных сценариев использования. В этом разделе мы рассмотрим два основных метода выборки, а более продвинутые методы, такие как грамматическая выборка, будут рассмотрены в следующих публикациях.
Жадная выборка — это простой подход, при котором выбирается токен с наибольшим логитом.
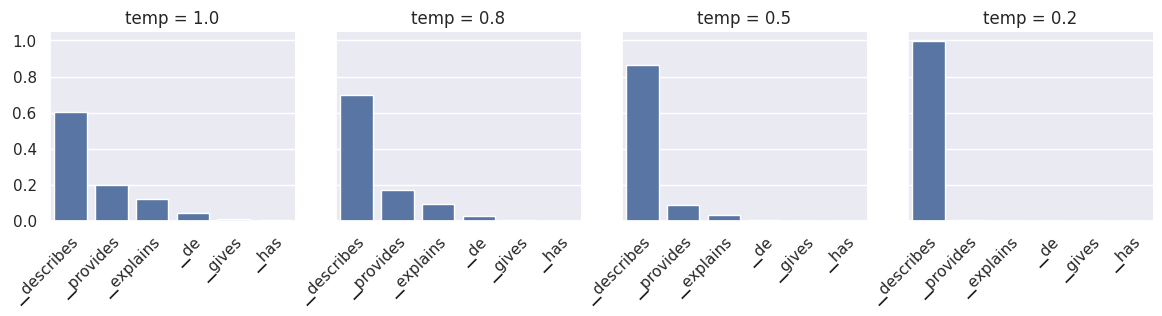
Для нашего примера наиболее высокие логиты имеют следующие токены:
жетон
логит
▁describes
18.990
▁provides
17.871
▁explains
17.403
▁de
16.361
▁gives
15.007
Таким образом, при жадной выборке в качестве следующего токена детерминированно выбирается ▁describes Жадная выборка наиболее полезна, когда при повторной оценке идентичных запросов требуются детерминированные результаты.
Выборка по температуре является вероятностной, то есть при повторной оценке одна и та же подсказка может дать разные результаты. Она использует параметр температура, который представляет собой число с плавающей запятой в диапазоне от 0 до 1 и влияет на случайность результата. Процесс происходит следующим образом:
- Логиты сортируются от большего к меньшему и нормализуются с помощью функции softmax, чтобы их сумма равнялась 1. Это преобразование преобразует каждый логит в вероятность.
- Применяется пороговое значение (по умолчанию установлено на уровне 0,95), при котором сохраняются только самые популярные токены, совокупная вероятность которых ниже порогового значения. Этот шаг эффективно удаляет токены с низкой вероятностью, предотвращая случайную выборку «плохих» или «неправильных» токенов.
- Оставшиеся логиты делятся на параметр температуры и снова нормализуются таким образом, чтобы их сумма равнялась 1 и они представляли собой вероятности.
- На основе этих вероятностей случайным образом выбирается токен. Например, в нашем запросе токен
▁describesимеет вероятностьp=0.6, то есть он будет выбран примерно в 60 % случаев. При повторной оценке могут быть выбраны другие токены.
Параметр температуры на шаге 3 служит для увеличения или уменьшения случайности. При более низких значениях температуры токены с меньшей вероятностью будут выбраны при повторной оценке. Таким образом, более низкие значения температуры уменьшают случайность. Напротив, при более высоких значениях температуры распределение вероятностей становится более «плоским», что подчёркивает важность токенов с меньшей вероятностью. Это повышает вероятность того, что при каждой повторной оценке будут выбираться разные токены, что увеличивает случайность.
Нормализованные вероятности следующих токенов для нашего примера. При более низких температурах токены с низкой вероятностью подавляются, а при более высоких — выделяются. temp=0 по сути идентично жадной выборке.
Выбор токена завершает полную итерацию LLM. После выбора первого токена он добавляется в список токенов, и весь процесс повторяется. Выходные данные итеративно становятся входными данными для LLM, и на каждой итерации список токенов увеличивается на один.
Теоретически последующие итерации могут выполняться идентичным образом. Однако для предотвращения снижения производительности по мере увеличения списка токенов используются определённые оптимизации. О них мы расскажем далее.
Этап самовнимания в трансформере может стать узким местом с точки зрения производительности по мере роста списка входных токенов для языковой модели. Чем длиннее список токенов, тем больше матриц перемножается. Каждое матричное умножение состоит из множества более мелких числовых операций, известных как операции с плавающей запятой, которые ограничены количеством операций с плавающей запятой в секунду (flops) на графическом процессоре. В арифметике логического вывода Transformer подсчитано, что для модели с 52 миллиардами параметров на графическом процессоре A100 производительность начинает снижаться при 208 токенах из-за чрезмерного количества операций с плавающей запятой. Наиболее часто используемый метод оптимизации для устранения этого узкого места известен как kv-кэш.
Подведём итог: каждому токену соответствует вектор встраивания, который затем преобразуется в векторы ключа и значения путём умножения на матрицы параметров wk и wv. Кэш kv — это кэш для этих векторов ключа и значения. Кэшируя их, мы экономим на операциях с плавающей запятой, необходимых для их повторного вычисления на каждой итерации.
Кэш работает следующим образом:
- Во время первой итерации для всех токенов вычисляются векторы ключей и значений, как описано выше, а затем сохраняются в кэше kv.
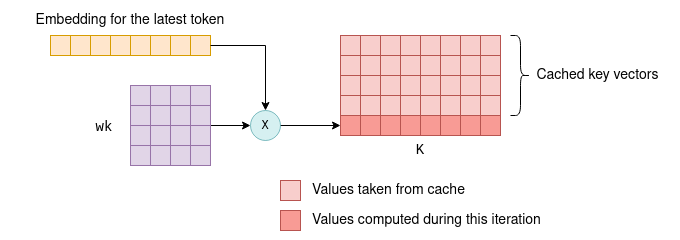
- На последующих итерациях нужно будет вычислить только векторы ключей и значений для самого нового токена. Кэш-векторы k-v вместе с векторами k-v для нового токена объединяются в матрицы
KиV. Это позволяет избежать повторного вычисления векторов k-v для всех предыдущих токенов, что может быть весьма существенно.
На последующих итерациях вычисляется только ключевой вектор последнего токена. Остальные берутся из кэша, и вместе они образуют матрицу K. Новый ключевой вектор также сохраняется в кэше. Тот же процесс применяется к векторам значений.
Возможность использовать кэш для векторов ключей и значений обусловлена тем, что эти векторы остаются неизменными между итерациями. Например, если мы сначала обработаем четыре токена, а затем пять токенов, при этом первые четыре токена не изменятся, то первые четыре вектора ключей и значений останутся неизменными между первой и второй итерациями. В результате нет необходимости пересчитывать векторы ключей и значений для первых четырёх токенов на второй итерации.
Этот принцип справедлив для всех слоёв в Transformer, а не только для первого. Во всех слоях векторы ключей и значений для каждого токена зависят исключительно от предыдущих токенов. Таким образом, при добавлении новых токенов на последующих итерациях векторы ключей и значений для существующих токенов остаются прежними.
Для первого слоя эта концепция относительно проста для проверки: ключевой вектор токена определяется путём умножения фиксированного встраивания токена на фиксированную wk матрицу параметров. Таким образом, он остаётся неизменным на последующих итерациях, независимо от добавления новых токенов. То же самое относится и к вектору значений.
Для второго слоя и последующих этот принцип не так очевиден, но всё же верен. Чтобы понять почему, рассмотрим KQV матрицу первого слоя, результат этапа самовнимания. Каждая строка в KQV матрице представляет собой взвешенную сумму, которая зависит от:
- Векторы значений предыдущих токенов.
- Баллы рассчитываются на основе ключевых векторов предыдущих токенов.
Таким образом, каждая строка в KQV зависит исключительно от предыдущих токенов. Эта матрица после нескольких дополнительных операций со строками служит входными данными для второго слоя. Это означает, что входные данные второго слоя на последующих итерациях не изменятся, за исключением добавления новых строк. Индуктивно та же логика распространяется на остальные слои.
Ещё раз взглянем на то, как рассчитывается матрица KQV. Третья строка, выделенная цветом, определяется только на основе третьего вектора запроса и первых трёх векторов ключей и значений, также выделенных цветом. Последующие токены на неё не влияют. Поэтому в последующих итерациях она останется неизменной.
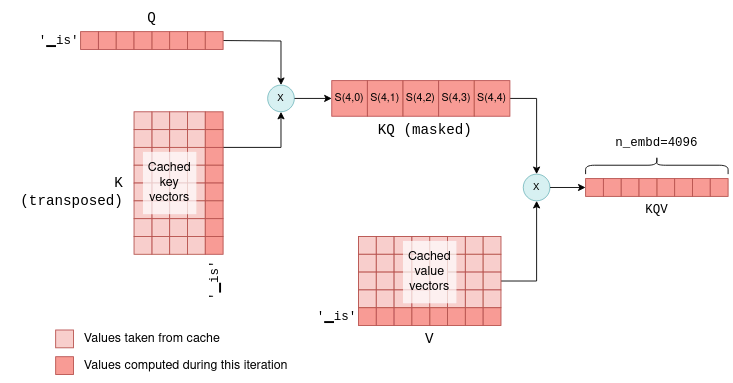
Вы можете задаться вопросом, почему мы не кэшируем векторы запросов, ведь мы кэшируем векторы ключей и значений. Дело в том, что на самом деле, кроме вектора запроса текущего токена, векторы запросов предыдущих токенов на последующих итерациях не нужны. При наличии кэша kv мы можем использовать механизм самовнимания только с вектором запроса последнего токена. Этот вектор запроса умножается на кэшированную K матрицу для вычисления совместных оценок последнего токена и всех предыдущих токенов. Затем она умножается на кэшированную V матрицу, чтобы вычислить только последнюю строку матрицы KQV . Фактически на всех уровнях мы теперь передаём векторы размером 1 x n_embd вместо матриц n_token x n_embd , вычисленных на первой итерации. Чтобы проиллюстрировать это, сравните следующую диаграмму, на которой показана более поздняя итерация, с предыдущей:
Самовнимание на последующих итерациях. В этом примере на первой итерации было четыре токена, а на второй итерации добавляется пятый токен — 'is'. Векторы ключа, запроса и значения последнего токена вместе с кэшированными векторами ключа и значения используются для вычисления последней строки KQV, которая является всем, что нужно для прогнозирования следующего токена.
Этот процесс повторяется на всех уровнях с использованием кэша kv для каждого уровня. В результате на выходе Transformer в данном случае получается один вектор n_vocab логитов, предсказывающих следующий токен.
Благодаря этой оптимизации мы экономим на операциях с плавающей запятой при вычислении ненужных строк в KQ и KQV, которые могут стать весьма существенными по мере увеличения размера списка токенов.
Мы можем изучить код llama.cpp, чтобы увидеть, как на практике реализован кэш kv. Возможно, вас не удивит, что он создан с использованием тензоров: один для векторов ключей, другой для векторов значений.
// llama.cpp (simplified)
struct llama_kv_cache {
// cache of key vectors
struct ggml_tensor * k = NULL;
// cache of value vectors
struct ggml_tensor * v = NULL;
int n; // number of tokens currently in the cache
};
При инициализации кэша выделяется достаточно места для хранения 512 векторов ключей и значений для каждого слоя.
// llama.cpp (simplified)
// n_ctx = 512 by default
static bool llama_kv_cache_init(
struct llama_kv_cache & cache,
ggml_type wtype,
int n_ctx) {
// Allocate enough elements to hold n_ctx vectors for each layer.
const int64_t n_elements = n_embd*n_layer*n_ctx;
cache.k = ggml_new_tensor_1d(cache.ctx, wtype, n_elements);
cache.v = ggml_new_tensor_1d(cache.ctx, wtype, n_elements);
// ...
}
Напомним, что во время вывода график вычислений строится с помощью функции llm_build_llama(). У этой функции есть параметр с именем n_past, который мы игнорировали ранее. На первой итерации n_tokens параметр содержит количество токенов и n_past имеет значение 0. В последующих итерациях, n_tokens устанавливается равным 1, потому что обрабатывается только последний токен, и n_past содержит количество прошлых токенов. n_pastзатем используется для извлечения правильного количества векторов ключей и значений из кэша kv.
Соответствующая часть этой функции показана здесь. Она использует кэш для вычисления матрицы K . Я немного упростил код, чтобы не учитывать многоголовое внимание, и добавил комментарии к каждому шагу:
// llama.cpp (simplified and commented)
static struct ggml_cgraph * llm_build_llama(
llama_context & lctx,
const llama_token * tokens,
int n_tokens,
int n_past) {
// ...
// Iteratively apply all layers.
for (int il = 0; il < n_layer; ++il) {
// Compute the key vector of the latest token.
struct ggml_tensor * Kcur = ggml_mul_mat(ctx0, model.layers[il].wk, cur);
// Build a view of size n_embd into an empty slot in the cache.
struct ggml_tensor * k = ggml_view_1d(
ctx0,
kv_cache.k,
// size
n_tokens*n_embd,
// offset
(ggml_element_size(kv_cache.k)*n_embd) * (il*n_ctx + n_past)
);
// Copy latest token's k vector into the empty cache slot.
ggml_cpy(ctx0, Kcur, k);
// Form the K matrix by taking a view of the cache.
struct ggml_tensor * K =
ggml_view_2d(ctx0,
kv_self.k,
// row size
n_embd,
// number of rows
n_past + n_tokens,
// stride
ggml_element_size(kv_self.k) * n_embd,
// cache offset
ggml_element_size(kv_self.k) * n_embd * n_ctx * il);
}
}
Сначала вычисляется новый вектор ключа. Затем n_past используется для поиска следующего свободного слота в кэше, и туда копируется новый вектор ключа. Наконец, матрица K формируется путём просмотра кэша с правильным количеством токенов (n_past + n_tokens).
Кэш kv является основой для оптимизации логического вывода в LLM. Стоит отметить, что версия, реализованная в llama.cpp (на момент написания статьи) и представленная здесь, не является наиболее оптимальной. Например, она заранее выделяет большой объём памяти для хранения максимального количества поддерживаемых векторов ключей и значений (в данном случае 512). Более продвинутые реализации, такие как vLLM, направлены на повышение эффективности использования памяти и могут обеспечить дальнейшее повышение производительности. Эти продвинутые методы будут рассмотрены в следующих публикациях. Более того, поскольку эта сфера развивается с молниеносной скоростью, в будущем, вероятно, появятся новые и более совершенные методы оптимизации.
В этой статье мы рассмотрели довольно много тем и надеемся, что вы получили базовое представление о полном процессе логического вывода в LLM. Обладая этими знаниями, вы сможете работать с более продвинутыми ресурсами:
- Подсчёт параметров LLM и Арифметические вычисления в Transformer позволяют детально проанализировать производительность LLM.
- vLLM — это библиотека для более эффективного управления памятью кэша kv.
- Непрерывная пакетная обработка — это метод оптимизации, позволяющий объединять несколько запросов к LLM в один пакет.
Я также надеюсь, что в будущих публикациях смогу рассказать о более сложных темах. Вот некоторые из них:
- Квантованные модели.
- Тонкая настройка LLM с помощью LoRA.
- Различные механизмы внимания (многозадачное внимание, внимание к сгруппированным запросам и скользящее внимание).
- Пакетная обработка запросов LLM.
- Грамматическая выборка.
Оставайтесь с нами!
-
ggml также предоставляет
ggml_build_backward()функцию, которая вычисляет градиенты в обратном направлении — от вывода к вводу. Эта функция используется для обратного распространения ошибки только во время обучения модели, но не во время логического вывода. ↩ -
В статье описывается модель «кодировщик-декодировщик». LLaMA — это модель только с декодером, поскольку она предсказывает только один токен за раз. Но основные концепции те же. ↩
-
Для простоты я решил описать здесь механизм самовнимания с одной головкой. В LLaMA используется механизм самовнимания с несколькими головками. Он лишь немного усложняет тензорные операции, но не влияет на основные идеи, представленные в этом разделе. ↩
-
Если быть точным, то сначала векторные представления подвергаются операции нормализации, которая масштабирует их значения. Мы не учитываем этот фактор, поскольку он не влияет на основные представленные идеи. ↩
-
Оценки также подвергаются операции softmax, которая масштабирует их таким образом, чтобы сумма значений в каждой строке оценок равнялась 1. ↩