Sethares dissmeasure function in Python

readme.md

Adaptation of Sethares' dissonance measurement function to Python

Example is meant to match the curve in Figure 3:

Original model used products of the two amplitudes a1⋅a2, but this was changed to minimum of the two amplitudes min(a1, a2), as explained in G: Analysis of the Time Domain Model appendix of Tuning, Timbre, Spectrum, Scale.

This weighting is incorporated into the dissonance model (E.2) by assuming that the roughness is proportional to the loudness of the beating. ... Thus, the amplitude of the beating is given by the minimum of the two amplitudes.

With the first 6 harmonics at amplitudes 1/n starting at 261.63 Hz, using the product model, it also perfectly matches Figure 4 of Davide Verotta - Dissonance & Composition, so it should be trustworthy.

sethares.png

sethares.py

"""
Python translation of http://sethares.engr.wisc.edu/comprog.html
"""
import numpy as np


def dissmeasure(fvec, amp, model='min'):
    """
    Given a list of partials in fvec, with amplitudes in amp, this routine
    calculates the dissonance by summing the roughness of every sine pair
    based on a model of Plomp-Levelt's roughness curve.

    The older model (model='product') was based on the product of the two
    amplitudes, but the newer model (model='min') is based on the minimum
    of the two amplitudes, since this matches the beat frequency amplitude.
    """
    # Sort by frequency
    sort_idx = np.argsort(fvec)
    am_sorted = np.asarray(amp)[sort_idx]
    fr_sorted = np.asarray(fvec)[sort_idx]

    # Used to stretch dissonance curve for different freqs:
    Dstar = 0.24  # Point of maximum dissonance
    S1 = 0.0207
    S2 = 18.96

    C1 = 5
    C2 = -5

    # Plomp-Levelt roughness curve:
    A1 = -3.51
    A2 = -5.75

    # Generate all combinations of frequency components
    idx = np.transpose(np.triu_indices(len(fr_sorted), 1))
    fr_pairs = fr_sorted[idx]
    am_pairs = am_sorted[idx]

    Fmin = fr_pairs[:, 0]
    S = Dstar / (S1 * Fmin + S2)
    Fdif = fr_pairs[:, 1] - fr_pairs[:, 0]

    if model == 'min':
        a = np.amin(am_pairs, axis=1)
    elif model == 'product':
        a = np.prod(am_pairs, axis=1)  # Older model
    else:
        raise ValueError('model should be "min" or "product"')
    SFdif = S * Fdif
    D = np.sum(a * (C1 * np.exp(A1 * SFdif) + C2 * np.exp(A2 * SFdif)))

    return D


if __name__ == '__main__':
    from numpy import array, linspace, empty, concatenate
    import matplotlib.pyplot as plt

    """
    Reproduce Sethares Figure 3
    http://sethares.engr.wisc.edu/consemi.html#anchor15619672
    """
    freq = 500 * array([1, 2, 3, 4, 5, 6])
    amp = 0.88**array([0, 1, 2, 3, 4, 5])
    r_low = 1
    alpharange = 2.3
    method = 'product'

#    # Davide Verotta Figure 4 example
#    freq = 261.63 * array([1, 2, 3, 4, 5, 6])
#    amp = 1 / array([1, 2, 3, 4, 5, 6])
#    r_low = 1
#    alpharange = 2.0
#    method = 'product'

    n = 3000
    diss = empty(n)
    a = concatenate((amp, amp))
    for i, alpha in enumerate(linspace(r_low, alpharange, n)):
        f = concatenate((freq, alpha*freq))
        d = dissmeasure(f, a, method)
        diss[i] = d

    plt.figure(figsize=(7, 3))
    plt.plot(linspace(r_low, alpharange, len(diss)), diss)
    plt.xscale('log')
    plt.xlim(r_low, alpharange)

    plt.xlabel('frequency ratio')
    plt.ylabel('sensory dissonance')

    intervals = [(1, 1), (6, 5), (5, 4), (4, 3), (3, 2), (5, 3), (2, 1)]

    for n, d in intervals:
        plt.axvline(n/d, color='silver')

    plt.yticks([])
    plt.minorticks_off()
    plt.xticks([n/d for n, d in intervals],
               ['{}/{}'.format(n, d) for n, d in intervals])
    plt.tight_layout()
    plt.show()

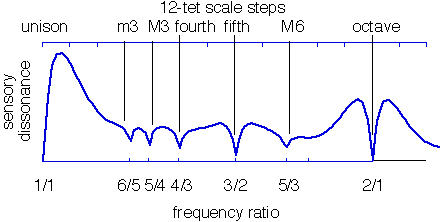
Adding more overtone and making a reasonable amplitude decay of 0.7, gives us a map of consonnance, with relative level of consonance
We can clearly see that the 5th is the most consonant, following by 4th, M3rd, M6th, m3rd, then interestingly, the subminor 3rd appear to be more consonant than the major and minor 7th which is a surprise to me
I think it makes sense that the 4th is less consonant than the 5th, after all the 4th is only a descending 5th of the octave so it kinda is consonant only by proxy

@BlueMagma2 let's put it this way, when given a standard tone like A440, and a second tone, calculate a value such that a cutoff point can separate what is consonant from what is dissonant. So that an off-tune 5ths or 4ths can be compared to on tune 3rds. The dissonace scale would need to be adjusted accordingly as well