GraphX_Programming_Guide_inJa.md

#GraphX Programming Guide 英文サイト

##概要

GraphX はグラフとグラフ並列計算処理のための新しい SparkAPI です。 GraphX​​ は、各頂点と辺にプロパティ情報を持つ「弾力性分散プロパティグラフ」を導入することにより、 Spark の RDD を拡張しています。グラフ計算処理をサポートするために、 GraphX は Pregel API を最適化した基本的な関数 (例： subgraph, joinVertices, mapReduceTriplets )を提供します。加えて、グラフ分析作業を簡単にするためのグラフアルゴリズムやビルダーを持っています。

###グラフ並列計算処理について

ソーシャルネットワークから言語分析まで、グラフデータは規模と重要性を拡大させ、多くの新しいグラフ並列計算処理機構（ Giraph や GraphLab ）の発展を後押ししてきました。 計算方式の制限やグラフ分割/分散の新しい技術の導入によって、これらの機構は大量データに対する洗練されたグラフアルゴリズム処理を、より一般的な並列データシステムより高速かつ効率的に実行することができます。

しかしながら、これらのパフォーマンスのために受け入れた制約は、典型的なグラフ分析パイプラインにおける多くの重要なステージ、つまり、グラフの構築、その構造の修正、あるいは複数のグラフをまたがる計算処理等を実現するすることを難しくしてしまっています。さらにどのようにデータを見るかは、その目的と、多くの異なるテーブルビューとグラフビューを持ちえる生データによって変わってきます。

その結果、同じ物理データの表とグラフ間を行ったり来たりしたり、簡潔かつ効率的に計算式を表現するための情報付けを各Viewのプロパティに対して行ったりする必要性がしばしば発生します。しかし既存のグラフ分析の流れでは、必ず並列グラフシステムと並列データ処理とで構成しなければならず、大規模なデータ移動と、データモデルのための冗長で複雑なプログラミングを伴ってしまいます。

GraphX プロジェクトのゴールは、並列グラフ計算処理と並列データ計算処理を複合 API によってひとつのシステムに統合することにあります。GraphX API を使うことで、データ複製や移動を行わずとも、ユーザはデータをグラフ構造とコレクション構造の両方で扱うことができるようになります。最近のグラフ並列処理システムの進化を取り入れることで、GraphX はグラフ処理の最適化を可能にしているのです。

###Spark Bagel API から GraphX に移行してください

GraphX のリリースに先だって、 Spark におけるグラフ計算処理は Pregel の実装である Begal に実装されてきました。 GraphX はよりリッチなプロパティを提供することによって グラフ API と、 Pregel の概念と性能を効率化して、メモリーのオーバーヘッドを改善しています。我々が最終的に Bagel を廃するまでは、引き続き Begal API と Begal プログラミングガイドのサポートは続けるつもりです。しかしながら、我々は Begel のユーザに対して、 GraphX API を検討することを推奨していますし、 Begal からの移行から問題あった際にはフィードバックをいただきたいと思います。

##はじめの一歩

始めるにあたってまずやっていただきたいことは、 Spark と GraphX をプロジェクトにインポートすることです

import org.apache.spark._
import org.apache.spark.graphx._
// いくつかのサンプルを稼働させるには RDD も必要になってくるでしょう
import org.apache.spark.rdd.RDD

もし Spark シェルを使っていないのであれば、 SparkContext も必要です。 Spark についてのはじめの一歩が知りたければ、Spark Quick Start Guideを参照してください。

##プロパティグラフ

プロパティグラフとは、各頂点と辺にユーザ定義オブジェクトを付加させた有向多重グラフです。有向多重グラフは、同じ接続元( source )と接続先( destination )を共有する多重並列な辺を持つ可能性のある有向グラフです。並列の辺をサポートできる機能は、同じ頂点間の複数の関係性（例えば同僚や、友人）が存在しうるシナリオのモデリングを単純化します。各頂点は 64bit 長の一意な ID （ VertexID ）をキーに持ちます。 GraphX は頂点の ID に、強制的な順序性を押し付けることはしません。同様に、辺は接続元と接続先の頂点のID情報を持ちます。

プロパティグラフは頂点型（ VD ）と辺型（ ED ）によってパラメタ化されます。各頂点と各辺それぞに関連づけられたオブジェクトの型が存在します。

GraphX は、頂点と辺の表現を、それらが double や int といった素の古い型の時に、特製の配列へ蓄積し、メモリ容量を減らすことで、最適化します。

いくつかのケースでは、同じグラフ内に、異なるプロパティ型を頂点に持たせたくなるかもしれません。これは継承によって実現できます。例えば、二つに分かれたグラフとしてユーザや製品をモデリングするには以下のようにします。

class VertexProperty()
case class UserProperty(val name:String) extends VertexProperty
case class ProductProperty(val name:String,val price:Double) extends VertexProperty

// グラフには VertexProperty を持たせます
var graph:Graph[VertexProperty, String] = null

RDD と同様に、プロパティグラフは不可変性と分散性による耐障害性を持ちます。値やグラフ構造への変換は、要求された変換に伴う新しいグラフを生成することによって 実現されます。元々のグラフの一部（例えば 影響を受けていない構造, 属性, あるいはインデックス）は、本質的に関数的なデータ構造のコストを減らしつつ、新しいグラフの中で再利用されることに気をつけてください。グラフは、人為的に分割された頂点の範囲を使いつつ、 worker をまたいで分割されます。 RDD と同様に、分割されたグラフの各パーティションは、失敗イベントの中で異なるサーバ上で再生成されます。

必然的に、プロパティグラフは各頂点と辺のためにプロパティをエンコードすることによって型化したコレクションのペアに一致します。結果的に、グラフクラスは、グラフの頂点と辺にアクセスするメンバーを含むクラスを含みます。

classGraph[VD, ED]{
	val vertices:VertexRDD[VD]
	val edges:EdgeRDD[ED]
}

VertexRDD[VD] クラスと EdgeRDD[ED] クラスは、期待的に RDD[(VertexID, VD)] クラスと RDD[Edge[ED]] クラスのバージョンを最適化したり、拡張したりします。 RDD[(VertexID, VD)] クラスと RDD[Edge[ED]] クラスの両方供、グラフ計算処理と内部最適化試行周りのために作られた追加機能を提供します。VertexRDD クラスと、 EdgeRDD クラスの API については、vertex and edge RDDsでより詳しく論じていますが、今は単純に RDD[(VertexID, VD)] クラスと RDD[Edge[ED]] クラスの形で考えておけば良いです。

###プロパティグラフ例

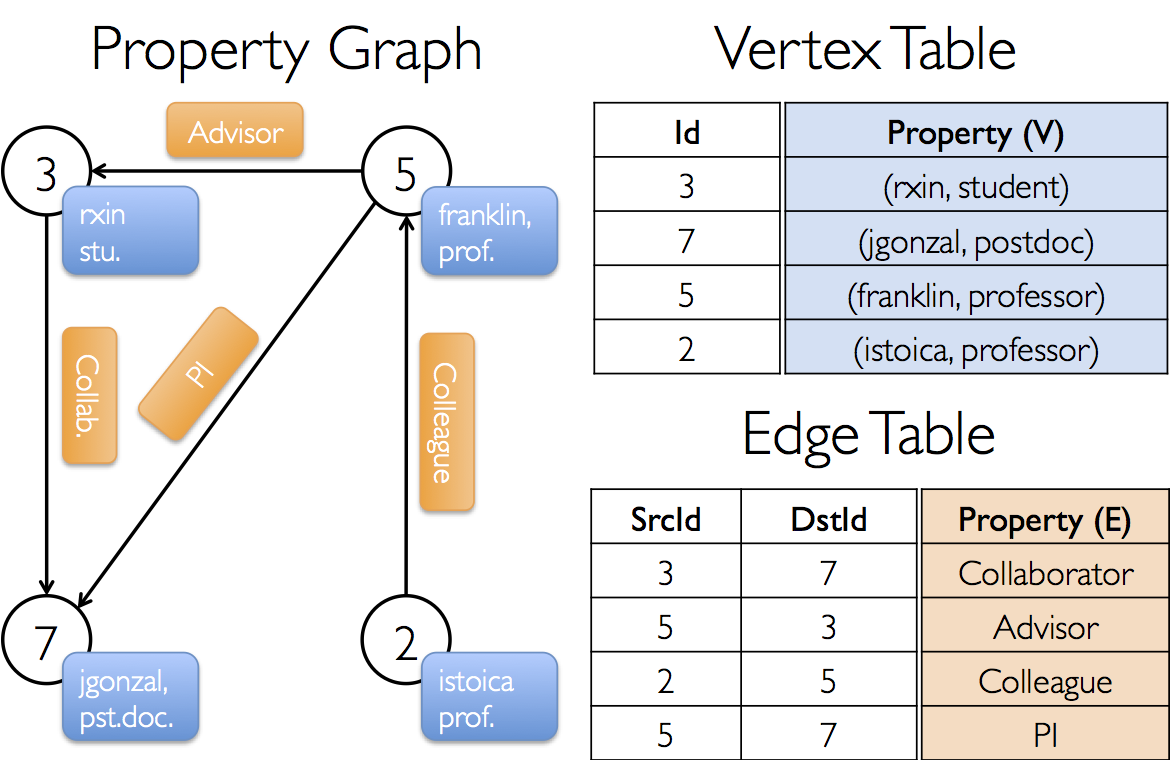
GraphX プロジェクトで、様々なコラボレーションを含むプロパティグラフを構築したいと想定しましょう。頂点の属性として、 username と、occupation を持つとします。我々は辺にコラボレーションする人の間の関係性を記述する string 情報を、辺に付加することができます。

このグラフは以下のようなGraph型となります。

val userGraph:Graph[(String, String), String]

プロパティグラフを生成するには、生ファイルや RDD、あるいは 人工ジェネレータなどからと言った風に、いろいろな方法があり、graph buildersに詳しく記載しています。おそらくもっとも一般的な方法は、Graph Objectを使う方法です。例えば、以下のコードは RDD のコレクション列から graph を構築するものです。

// SparkContext は既に構成されていると過程します。
val sc:SparkContext

// 頂点用の RDD を生成します。
val users:RDD[(VertexId, (String, String))]=
	sc.parallelize(Array(	(3L,("rxin","student")),(7L,("jgonzal","postdoc")),
	 						(5L,("franklin","prof")),(2L,("istoica","prof"))))

// 辺用の RDD を生成します。
val relationships:RDD[Edge[String]]=
	sc.parallelize(Array(	Edge(3L,7L,"collab"),
							Edge(5L,3L,"advisor"),
							Edge(2L,5L,"colleague"),
							Edge(5L,7L,"pi")))

// 不在のユーザとの関係性が存在するというケースにおける、デフォルトユーザを定義します。
val defaultUser =("John Doe","Missing")

// 初期グラフを生成します。
val graph =Graph(users, relationships, defaultUser)

この例では、 Edge ケースクラスを使っています。 Edge クラスは接続元頂点の ID を srcId 、接続先頂点の ID を dstId に持ちます。加えて、 Edge が保持するプロパティ情報として attr という値も持ちます。

graph.vertices と graph.edges をそれぞれ使うことによって、グラフを分解することができます。

val graph:Graph[(String, String), String] // 前述の例で生成されたグラフです。

// postdocs （博士課程修了者）の全ユーザをカウントします
graph.vertices.filter {case(id,(name, pos))=> pos =="postdoc"}.count

// 接続元の頂点 ID が、接続先の頂点 ID より大きい全ての辺をカウントします。
graph.edges.filter(e => e.srcId > e.dstId).count

graph.vertices は、 RDD[(VertexID, (String, String))] を継承した VertexRDD[(String, String)] を応答するので、タプル型を分解するために case クラスを使うことに気をつけてください。一方で、 graph.edges は、 Edge[String] オブジェクトを含んだ EdgeRDD を応答します。あるいは以下のように、 case クラス型のコンストラクタを使うこともできます。

graph.edges.filter {caseEdge(src, dst, prop)=> src > dst }.count

プロパティグラフの頂点と辺の情報に加えて、 GraphX はトリプレット（３つ子）情報を持っています。トリプレット情報とは、頂点と辺の情報を論理的に結合させて、 EdgeTriplet クラスのインスタンスを含む RDD[EdgeTriplet[VD, ED]] にしたものになります。この結合は、SQLで表現すると以下のようになります。

SELECT src.id, dst.id, src.attr, e.attr, dst.attr
FROM edges AS e LEFT JOIN vertices AS src, vertices AS dst
ON e.srcId = src.Id AND e.dstId = dst.Id

あるいは、以下のように図示できます。

EdgeTriplet クラスは、 Edge クラスを拡張して、接続元／接続先情報を持つ、 srcAttr や dstAttr を追加したものです。トリプレットはユーザ間の関係性を文字列で表現するために使うことができます。

val graph:Graph[(String, String), String] // 前述の例で生成されたグラフです。
// Use the triplets view to create an RDD of facts.
val facts:RDD[String]=
	graph.triplets.map(triplet =>
		triplet.srcAttr._1 +" is the "+ triplet.attr +" of "+ triplet.dstAttr._1)
facts.collect.foreach(println(_))

##グラフオペレーター

ちょうど、 RDD が map や、 filter 、 reduceByKey といった基本的な処理機能をもっているように、プロパティグラフもユーザ定義された処理機能群を持っていて、変換されたプロパティや構造から新しいグラフを生成します。コアの処理機能は実装を最適化して Graph クラスに実装されており、 GraphOps クラスに定義されたコア処理機能の構成として表現された便利な処理機能となっています。しかしながら、 Scala の Implicit のおかげで、 GraphOps クラスは自動的に Graph クラスのメンバーとして利用できます。例えば、（ GraphOps ）に定義されている各頂点の入次数を以下のように計算することができる。

入次数（ indegree ）とは、有向グラフにおいて、頂点に入ってくる辺の数のことです。逆に出次数（ outdegree ）は頂点から出て行く変数です。

val graph:Graph[(String, String), String]

// 暗黙的に GraphOps.inDegrees オペレータを使います。
val inDegrees:VertexRDD[Int]= graph.inDegrees

コア処理機能と GraphOps を分離している理由は、将来、異なるグラフを表現できるようにするためです。それぞれのグラフ表現はコア処理機能の実装を提供しなければならず、 GraphOps に定義された便利な処理機能を再利用できるようになります。

###処理機能のまとめ

以下に Graph クラスと GraphOps クラスの処理機能をリストアップしてますが、シンプルに Graph クラスのものとして表現しています。いくつかの機能はデフォルト変数や型コンスタクタについての記載を省略していたり、応用的な使い方についても省略しているので、 API リストを公式には参照するようにしてください。

/** プロパティグラフにおける機能のまとめ */
class Graph[VD, ED]{
	// 基本的なグラフアルゴリズム ========================================================================
	val numEdges:Long
	val numVertices:Long
	val inDegrees:VertexRDD[Int]
	val outDegrees:VertexRDD[Int]
	val degrees:VertexRDD[Int]

	// コレクションとしてのグラフの情報 ===================================================================
	val vertices:VertexRDD[VD]
	val edges:EdgeRDD[ED]
	val triplets:RDD[EdgeTriplet[VD, ED]]

	// グラフのキャッシュ機能 ===========================================================================
	def persist(newLevel:StorageLevel=StorageLevel.MEMORY_ONLY):Graph[VD, ED]  
	def cache():Graph[VD, ED]  
	def unpersistVertices(blocking:Boolean=true):Graph[VD, ED]  

	// 人為的にパーティションニングを変更する機能  ==========================================================
	def partitionBy(partitionStrategy:PartitionStrategy):Graph[VD, ED] 

	// 頂点と辺の属性を変換する機能 ======================================================================
	def mapVertices[VD2](map:(VertexID,VD)=>VD2):Graph[VD2, ED]  
	def mapEdges[ED2](map:Edge[ED]=>ED2):Graph[VD, ED2]  
	def mapEdges[ED2](map:(PartitionID,Iterator[Edge[ED]])=>Iterator[ED2]):Graph[VD, ED2]  
	def mapTriplets[ED2](map:EdgeTriplet[VD, ED]=>ED2):Graph[VD, ED2]  
	def mapTriplets[ED2](map:(PartitionID,Iterator[EdgeTriplet[VD, ED]])=>Iterator[ED2])    :Graph[VD, ED2]  

	// グラフ構造の変換 ================================================================================  
	def reverse:Graph[VD, ED]  
	def subgraph(
		epred:EdgeTriplet[VD,ED]=>Boolean=(x =>true),
		vpred:(VertexID,VD)=>Boolean=((v, d)=>true))
		:Graph[VD, ED]
	def mask[VD2, ED2](other:Graph[VD2, ED2]):Graph[VD, ED]  
	def groupEdges(merge:(ED,ED)=>ED):Graph[VD, ED]  

	// グラフと RDD を結合させる機能 =====================================================================
	def joinVertices[U](table:RDD[(VertexID, U)])(mapFunc:(VertexID,VD, U)=>VD):Graph[VD, ED]  
	def outerJoinVertices[U, VD2](other:RDD[(VertexID, U)]) 
	     (mapFunc:(VertexID,VD,Option[U])=>VD2)    
	     :Graph[VD2, ED]  

	// 隣接しているトリプレットのついての情報を集約 ==========================================================
	def collectNeighborIds(edgeDirection:EdgeDirection):VertexRDD[Array[VertexID]]  
	def collectNeighbors(edgeDirection:EdgeDirection):VertexRDD[Array[(VertexID, VD)]]  
	def mapReduceTriplets[A:ClassTag](
	      mapFunc:EdgeTriplet[VD, ED]=>Iterator[(VertexID, A)],      
	      reduceFunc:(A,A)=> A,      
	      activeSetOpt:Option[(VertexRDD[_], EdgeDirection)]=None)    
	      :VertexRDD[A]  

	// 反復グラフ並列計算処理 ===========================================================================
	def pregel[A](initialMsg:A, maxIterations:Int, activeDirection:EdgeDirection)(
		vprog:(VertexID,VD, A)=>VD,      
		sendMsg:EdgeTriplet[VD, ED]=>Iterator[(VertexID,A)],      
		mergeMsg:(A,A)=> A)    
		:Graph[VD, ED]  

	// 基本的なグラフアルゴリズム ========================================================================  
	def pageRank(tol:Double, resetProb:Double=0.15):Graph[Double, Double]  
	def connectedComponents():Graph[VertexID, ED]  
	def triangleCount():Graph[Int, ED]  
	def stronglyConnectedComponents(numIter:Int):Graph[VertexID, ED]
}

##プロパティオペレーター

プロパティグラフは、以下のような、RDD の map に非常に似たような処理機能を持っています。

class Graph[VD, ED]{
	def mapVertices[VD2](map:(VertexId,VD)=>VD2):Graph[VD2, ED]  
	def mapEdges[ED2](map:Edge[ED]=>ED2):Graph[VD, ED2]  
	def mapTriplets[ED2](map:EdgeTriplet[VD, ED]=>ED2):Graph[VD, ED2]
}

これらのオペレーターはそれぞれ、ユーザが定義した map 関数によって編集された頂点や辺のプロパティの新しいグラフを返します。

全てのケースにおいて、グラフ構造は影響を受けていないということに注意してください。これはこれらの処理機能の重要な特徴です。つまり、応答したグラフがオリジナルグラフの構造的なインデックスを使うことができるのです。以下のふたつのコードは論理的には同じことを意味しています。しかしひとつめのは、事前に構造的なインデックスを受け取っておらず、GraphXシステムの最適化の恩恵を受けることができていません。

val newVertices = graph.vertices.map {case(id, attr)=>(id, mapUdf(id, attr))}
val newGraph =Graph(newVertices, graph.edges)

mapVerticesを使えば、インデックスを事前に受け取ることができます。

val newGraph = graph.mapVertices((id, attr)=> mapUdf(id, attr))

これらのオペレータは、特定の計算処理や不要なプロパティを取り除くためにグラフを初期化するのにしばしば使われます。例えば、頂点のプロパティとしての出次数を持ったグラフを、 PageRank のために初期化します。

// 頂点のプロパティに出次数を持つグラフ	
val inputGraph:Graph[Int, String]=  
	graph.outerJoinVertices(graph.outDegrees)((vid,_, degOpt)=> degOpt.getOrElse(0))

// 各辺が重みを持ち、各頂点が初期のページランクであるグラフを生成
val outputGraph:Graph[Double, Double]=
	inputGraph.mapTriplets(triplet =>1.0/ triplet.srcAttr).mapVertices((id,_)=>1.0)

##構造オペレータ

現状、 GraphX はシンプルなよく使われる構造オペレータのみを提供していて、将来的にはもっと追加していこうとしています。以下に基本的な構造オペレータを示します。

classGraph[VD, ED]{  
	def reverse:Graph[VD, ED]  
	def subgraph(epred:EdgeTriplet[VD,ED]=>Boolean,               
		vpred:(VertexId,VD)=>Boolean):Graph[VD, ED]  
	def mask[VD2, ED2](other:Graph[VD2, ED2]):Graph[VD, ED]  
	def groupEdges(merge:(ED,ED)=>ED):Graph[VD,ED]}

reverse は、全ての辺の方向を逆にした新しいグラフを応答します。これは例えば、ページランクを逆方向に計算するときに便利です。なぜなら、 reverse は頂点や辺のプロパティや辺の数などをいじらず、データの移動や複製を行わずに処理を実装できるからです。

subgraph は頂点や辺に述語を与え、述語を備えた頂点と辺のみのグラフを応答します。 subgraph は、興味のある頂点と辺に絞り込んだり、リンク切れしている箇所を取り除いたりと、いろいろな場面で利用することができます。例えば、以下のコードはリンク切れを削除している処理になります。

// 頂点用のRDDを生成
val users:RDD[(VertexId, (String, String))]=
	sc.parallelize(Array((3L,("rxin","student")),(7L,("jgonzal","postdoc")),
						(5L,("franklin","prof")),(2L,("istoica","prof")),
						(4L,("peter","student"))))

// 辺用のRDDを生成
val relationships:RDD[Edge[String]]=  sc.parallelize(Array(Edge(3L,7L,"collab"),
					Edge(5L,3L,"advisor"),
					Edge(2L,5L,"colleague"),Edge(5L,7L,"pi"),
					Edge(4L,0L,"student"),   Edge(5L,0L,"colleague")))

// 不在のユーザとの関係性を持つケースとしてデフォルトユーザを定義
val defaultUser =("John Doe","Missing")

// 初期グラフを生成
val graph =Graph(users, relationships, defaultUser)

// ユーザ４（ピーター）とユーザ５（フランクリン）をコネクションを持つ（我々が情報を持っていない）ユーザ０が存在することが分かります。
graph.triplets.map(    
	triplet => triplet.srcAttr._1 +" is the "+ triplet.attr +" of "+ triplet.dstAttr._1  
	).collect.foreach(println(_))

// 不在ユーザの頂点を、それに接続している辺と同様に削除します。
val validGraph = graph.subgraph(vpred =(id, attr)=> attr._2 !="Missing")

// この validGraph ではユーザー０を削除することで、ユーザ４と５の接続が切れます。
validGraph.vertices.collect.foreach(println(_))validGraph.triplets.map(    
	triplet => triplet.srcAttr._1 +" is the "+ triplet.attr +" of "+ triplet.dstAttr._1  
).collect.foreach(println(_))

この例では頂点の述語だけ提供されていることに注意してください。 subgraph オペレータは、頂点や辺の述語が与えられていない場合、デフォルトでは true になります。

mask オペレータも、入力されたグラフの一部分を抽出したサブグラフを応答します。 mask オペレータは、 subgraph オペレータと合わせて使うことで、別の関係するグラフのプロパティ情報をベースにしたグラフ抽出を行うことができます。例えば、リンク切れを持つグラフを使って、リンク切れの無いグラフコンポーネントを実行し、正しいサブグラフを抽出することができます。

// connectedComponents を実行します。
val ccGraph = graph.connectedComponents() // 不在フィールドはもはや含んでいません。

// 不在ユーザの頂点を、それに接続している辺と同様に削除します。
val validGraph = graph.subgraph(vpred =(id, attr)=> attr._2 !="Missing")

// valid 用のサブグラフに結果を抽出します。
val validCCGraph = ccGraph.mask(validGraph)

groupEdges オペレータは、並列辺（例：同じ頂点間で重複した辺）を複数のグラフにマージします。多くのアプリケーションで、 graph のデータ容量を削減しつつ、並列辺を単一の辺に（加重を付けて）加えることができます。

Join オペレータ

RDD 上の外部列データをグラフにジョインさせたい場面はたくさんあります。たとえば、別のユーザプロパティをグラフにマージするだとか、頂点のプロパティ情報をグラフから別のグラフに持って行くだとか。これは Join を使うことで実現できます。以下に、重要な Join オペレータを挙げます。

classGraph[VD, ED]{  
	def joinVertices[U](table:RDD[(VertexId, U)])(map:(VertexId,VD, U) => VD)    
		:Graph[VD, ED]  
	def outerJoinVertices[U, VD2](table:RDD[(VertexId, U)])(map:(VertexId,VD,Option[U]) => VD2)    
		:Graph[VD2, ED]
}

joinVertices オペレータは、入力された RDD と頂点を Join させて、ユーザ定義の map 関数を Join した頂点に適用させることで得られた頂点プロパティを持つ新しいグラフを返します。 RDD でマッチングしていない頂点は、元のデータを保持しています。

もし RDD が与えられた頂点の値を一つ以上含んでいるなら、ひとつだけ使われることに注意してください。このため、後続の JOIN を大幅に高速化させるために結果の値を事前にインデックス化することによって、入力 RDD は最初にユニークにしておくことを推奨します。

val nonUniqueCosts:RDD[(VertexID, Double)]
val uniqueCosts:VertexRDD[Double] =  
	graph.vertices.aggregateUsingIndex(nonUnique,(a,b) => a + b)
val joinedGraph = graph.joinVertices(uniqueCosts)(  
	(id, oldCost, extraCost) => oldCost + extraCost)

より汎用的な outerJoinVertices は、 joinVertices と似たような振る舞いをしますが、ユーザ定義の map 関数が、頂点のプロパティ型を変更したり、全ての頂点に適用させたりはしません。なぜなら、全ての頂点が OptionType をとる map 関数を入力 RDD の中でマッチングさせるわけではないだろうからです。例えば、 outDegree を使った頂点プロパティの初期化によって PageRank のためのグラフをセットアップすることができます。

val outDegrees:VertexRDD[Int]= graph.outDegrees
val degreeGraph = graph.outerJoinVertices(outDegrees){(id, oldAttr, outDegOpt) =>  
	outDegOpt match{    
		case　Some(outDeg) => outDeg    
		case　None => 0　// 出次が無いことを、0 outDegree で示す
	}
}

上の例で使われた関数パターンを複数パラメータのリストがカリー化していることに気づくでしょう。 f(a)(b) を f(a,b) として書いているので、 a に依存せず b に影響を与える型を意味するでしょう。結果的に、ユーザ定義関数のために型の付属情報を提供する必要があります。

val joinedGraph = graph.joinVertices(uniqueCosts,  
		(id:VertexID, oldCost:Double, extraCost:Double) => oldCost + extraCost)

##近接集合

グラフ計算では各頂点の近接情報を集約させることが重要になります。例えば、各ユーザのフォロワーの人数が知りたくなったり、フォロワーの平均年齢が知りたくなったりするでしょう。多くの反復型のグラフアルゴリズム（例：ページランク、最短経路探索や接続コンポーネント）は、近接頂点のプロパティを、繰り返し集約しています。

MapReduceトリプレット

GraphX の（徹底的に最適かされた）コアとなる集約機能が、 mapReduceTriplets オペレータになります。

classGraph[VD, ED]{  
	def mapReduceTriplets[A](      
		map:EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],      
		reduce:(A,A) => A)
	:VertexRDD[A]
}	

mapReduceTriplets はユーザ定義 map 関数をとります。これは、各トリプレットに適用されて、トリプレットの各頂点に向けてメッセージを配信します。事前集約の最適化を促進するために、トリプレットの接続元や接続先へのメッセージ配信のみをサポートしています。ユーザ定義 reduce 関数は、各頂点に配信されたメッセージを結合します。 mapReduceTriplets は VertexRDD[A] を応答します。これには、各頂点に配信されたメッセージが集約されたものが含まれています。返された VertexRDD に含まれていないメッセージを頂点が受け取ることはありません。

mapReduceTriplets には activeSet というオプションがあることに注意してください。 （詳細はAPIドキュメントを参照のこと） これはmapフェーズを 与えられた VertexRDD にある頂点に隣接するへんに制限します。

activeSetOpt:Option[(VertexRDD[_], EdgeDirection)] = None

EdgeDirection は、頂点に接続しているどの辺がmapフェーズに含まれているかを特定します。もし direction が in ならば、ユーザ定義 map 関数は、アクティブセット上の接続先頂点に隣接した辺の上でのみ稼働します。もし direction が out ならば、 map 関数は、アクティブセット上の接続元頂点に隣接した辺の上でのみ稼働します。もし direction が Either なら、アクティブセット上のどちらかの頂点の辺で関数は稼働します。もし direction が both ならば、両方の頂点の辺で稼働します。アクティブセットはグラフの頂点セットから取得していなければなりません。頂点のサブセットに隣接しているトリプレットに、計算処理を制限することは、繰り返し処理の中でしばしば必要になりますし、 Pregel の GraphX 実装のキーとなるところです。

下の例では、 mapReduceTriplets オペレータを使って、各ユーザの年上フォロワーの平均年齢を計算しています。

// Import random graph generation library
import org.apache.spark.graphx.util.GraphGenerators
// Create a graph with "age" as the vertex property.  Here we use a random graph for simplicity.
val graph: Graph[Double, Int] =
  GraphGenerators.logNormalGraph(sc, numVertices = 100).mapVertices( (id, _) => id.toDouble )
// Compute the number of older followers and their total age
val olderFollowers: VertexRDD[(Int, Double)] = graph.mapReduceTriplets[(Int, Double)](
  triplet => { // Map Function
    if (triplet.srcAttr > triplet.dstAttr) {
      // Send message to destination vertex containing counter and age
      Iterator((triplet.dstId, (1, triplet.srcAttr)))
    } else {
      // Don't send a message for this triplet
      Iterator.empty
    }
  },
  // Add counter and age
  (a, b) => (a._1 + b._1, a._2 + b._2) // Reduce Function
)
// Divide total age by number of older followers to get average age of older followers
val avgAgeOfOlderFollowers: VertexRDD[Double] =
  olderFollowers.mapValues( (id, value) => value match { case (count, totalAge) => totalAge / count } )
// Display the results
avgAgeOfOlderFollowers.collect.foreach(println(_))

mapReduceTriplets オペレータが最適な状態で稼働するのは、メッセージ（あるいはメッセージの集計）がコンスタントにサイズ指定された時です。（例えば、リストや連結の代わりの少数や足し算）より正確に言うと、 mapReduceTriplets は各頂点の次数の sub-linear に理想的にはあるべきものです。

次数計算処理

集約処理としてよくあるのが、各頂点の次数の計算です。次数とは頂点に接している辺の数のことです。有向グラフを扱う中では、各頂点の入次数（ in-degree ）や、出次数（ out-degree ）、次数合計を知る必要がしばしばあります。 GraphOps クラスは次数計算のオペレータを持っています。例えば以下の例では、入次数、出次数、全次数の最大値を計算しています。

// Define a reduce operation to compute the highest degree vertex
def max(a: (VertexId, Int), b: (VertexId, Int)): (VertexId, Int) = {
  if (a._2 > b._2) a else b
}
// Compute the max degrees
val maxInDegree: (VertexId, Int)  = graph.inDegrees.reduce(max)
val maxOutDegree: (VertexId, Int) = graph.outDegrees.reduce(max)
val maxDegrees: (VertexId, Int)   = graph.degrees.reduce(max)

近接集約

あるケースにおいては、より簡単に計算処理を表現する方法として、近接頂点や拡張点の属性を集約する方法があります。これは、 collectNeighborIds オペレータや、 collectNeighbors オペレータを使うことで実現できます。

class GraphOps[VD, ED] {
  def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexId]]
  def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[ Array[(VertexId, VD)] ]
}

これらのオペレータは大変負荷がかかることに気をつけてください。情報の複製や、実際の情報のやりとりが求められるからです。可能であれば、 mapReduceTriplets オペレータを直接使うことが望まれます。

キャッシュとキャッシュ解放

Sparkでは、デフォルトではメモリに保持しつづけられません。再計算を避けるためにデータを複数使う場合は、明示的にキャッシュしなければなりません。 GraphX におけるグラフ情報も同様の挙動をとります。 グラフを複数回使う時は、忘れずに Graph.cash() を最初に呼ぶようにしてください。

繰り返し計算処理の中では、キャッシュ解放もパフォーマンスを最適化するには必要となるでしょう。デフォルトでは、キャッシュされたRDDやグラフ情報はLRU順で押し出されるまでは、メモリに保持されます。繰り返し計算処理のために、中間処理結果はキャッシュに格納されます。最終的には取り出されるにも関わらず、不要なデータがメモリにストアされて、ガベージコレクションで時間を浪費します。これは不要なり次第、中間データのキャッシュを解放することで、メモリ管理より効率化させることが可能です。これはグラフやRDDの具現化や、全ての他のデータのキャッシュ解放や、将来の繰り返し処理の中で具現化されたデータセットを使うことを、各繰り返しの中で引き起こします。 繰り返し計算処理のためには、 Pregel API を使ってください。 Pregel API は中間結果を正しく削除してくれます。

Pregel API

グラフはそもそもは再起的なデータ構造です。結果として多くの重要なグラフアルゴリズムは繰り返して各頂点を再計算して、不動点条件に到達するまで実施します。グラフ平行抽象化の範囲は、これらの反復アルゴリズムを発現することが提案されています。GraphX は Pregel ライクなオペレータ提供します。それは、 Pregel や GraphLab アルゴリズムで広く使われたものを融合したものです。

GraphX のハイレベルな Pregel オペレータはバルク同期並列メッセージングの抽象概念で、グラフのトポロジーを強います。 Pregel オペレータはスーパーステップの中で実行されます。そこでは頂点は前のスーパーステップから送られてきた入力メッセージの合計を受け取り、頂点プロパティのために新しい値を計算し、次のスーパーステップの隣接する頂点にメッセージを送信します。 Pregel とは異なる代わりに GraphLab のように、メッセージトリプレットの関数としてメッセージは並列に計算され、接続元と接続先頂点属性の両方にメッセージ計算はアクセスします。メッセージを受け取っていない頂点はスーパーステップの中でスキップされます。 Pregel オペレータは、残るメッセージが無くなったら繰り返し処理を中止し、最終的なグラフを返します。

より標準的な Pregel 実装と違って、 GraphX における頂点は近接する頂点にメッセージを送ることだけができ、メッセージの構成は、ユーザ定義のメッセージ関数を使って並列に行われることに気をつけてください。これらの構成は GraphX における追加的な最適化を許容します。

下記は、実装のスケッチだけでなく Pregel オペレータのシグネチャです。

class GraphOps[VD, ED] {
  def pregel[A]
      (initialMsg: A,
       maxIter: Int = Int.MaxValue,
       activeDir: EdgeDirection = EdgeDirection.Out)
      (vprog: (VertexId, VD, A) => VD,
       sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
       mergeMsg: (A, A) => A)
    : Graph[VD, ED] = {
    // Receive the initial message at each vertex
    var g = mapVertices( (vid, vdata) => vprog(vid, vdata, initialMsg) ).cache()
    // compute the messages
    var messages = g.mapReduceTriplets(sendMsg, mergeMsg)
    var activeMessages = messages.count()
    // Loop until no messages remain or maxIterations is achieved
    var i = 0
    while (activeMessages > 0 && i < maxIterations) {
      // Receive the messages: -----------------------------------------------------------------------
      // Run the vertex program on all vertices that receive messages
      val newVerts = g.vertices.innerJoin(messages)(vprog).cache()
      // Merge the new vertex values back into the graph
      g = g.outerJoinVertices(newVerts) { (vid, old, newOpt) => newOpt.getOrElse(old) }.cache()
      // Send Messages: ------------------------------------------------------------------------------
      // Vertices that didn't receive a message above don't appear in newVerts and therefore don't
      // get to send messages.  More precisely the map phase of mapReduceTriplets is only invoked
      // on edges in the activeDir of vertices in newVerts
      messages = g.mapReduceTriplets(sendMsg, mergeMsg, Some((newVerts, activeDir))).cache()
      activeMessages = messages.count()
      i += 1
    }
    g
  }
}

Pregel は二つの引数リストを取ることに注意してください。（例： graph.pregel(list1)(list2) ）ひとつめの引数リストは初期メッセージと、繰り返しの最大値と、送信メッセージが通る辺の方向を含む、設定パラメータを含みます。ふたつめの引数リストは、メッセージ受信と、メッセージ計算とメッセージ結合のためのユーザ定義関数を含みます。

下記のように、最短経路検索のように計算処理を表現するために Pregel オペレータを使うことができます。

import org.apache.spark.graphx._
// Import random graph generation library
import org.apache.spark.graphx.util.GraphGenerators
// A graph with edge attributes containing distances
val graph: Graph[Int, Double] =
  GraphGenerators.logNormalGraph(sc, numVertices = 100).mapEdges(e => e.attr.toDouble)
val sourceId: VertexId = 42 // The ultimate source
// Initialize the graph such that all vertices except the root have distance infinity.
val initialGraph = graph.mapVertices((id, _) => if (id == sourceId) 0.0 else Double.PositiveInfinity)
val sssp = initialGraph.pregel(Double.PositiveInfinity)(
  (id, dist, newDist) => math.min(dist, newDist), // Vertex Program
  triplet => {  // Send Message
    if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {
      Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))
    } else {
      Iterator.empty
    }
  },
  (a,b) => math.min(a,b) // Merge Message
  )
println(sssp.vertices.collect.mkString("\n"))

グラフビルダー

GraphX は RDD やディスク内の頂点と辺の集まりからグラフを構築するいくつかの方法を提供しています。デフォルトでグラフの辺を再パーティションするグラフビルダーはありません。そのかわり、デフォルトパーティションの中に辺は残っています。 Graph.groupEdges はグラフに再パーティションされることを要求します。なぜなら、一意の辺が同じパーティションに配置されるからです。ですので、 groupEdges を呼ぶ前に、 Graph.partitionBy を呼ばないといけません。

object GraphLoader {
  def edgeListFile(
      sc: SparkContext,
      path: String,
      canonicalOrientation: Boolean = false,
      minEdgePartitions: Int = 1)
    : Graph[Int, Int]
}

GraphLoader.edgeListFile は、ディスク上の辺のリストからグラフをロードする方法を提供します。それは下記のフォーマットで近接ペアリストをパースします。 # で始まるのはコメント行です。

# This is a comment
2 1
4 1
1 2

それは特定された辺からグラフを生成します。辺から仕向けれたどの頂点も自動的に生成しながら。全ての頂点と辺の属性はデフォルトは１です。 canonicalOrientation 引数は、前向き方向（ srcId < dstId ）に辺を再度仕向けさせます。これは、 connected components アルゴリズムで必要となるものです。 minEdgePartitions 引数は、生成される辺のパーティションの最小値を特定します。例えば HDFS ファイルがもっとブロックを持っていたとしても、辺のパーティションが存在します。

object Graph {
  def apply[VD, ED](
      vertices: RDD[(VertexId, VD)],
      edges: RDD[Edge[ED]],
      defaultVertexAttr: VD = null)
    : Graph[VD, ED]

  def fromEdges[VD, ED](
      edges: RDD[Edge[ED]],
      defaultValue: VD): Graph[VD, ED]

  def fromEdgeTuples[VD](
      rawEdges: RDD[(VertexId, VertexId)],
      defaultValue: VD,
      uniqueEdges: Option[PartitionStrategy] = None): Graph[VD, Int]

}

Graph.apply は頂点と辺の RDD からグラフを生成することを可能とします。重複した頂点は勝手に選択され、頂点 RDD ではなく、辺 RDD にある頂点がデフォルトの属性に割与えられます。

Graph.fromEdges は、辺の RDD からのみグラフを生成することと、その辺に接続された頂点の自動的な生成と、頂点をデフォルト値に割与えることを可能とします。

Graph.fromEdgeTuples は、辺のタプルからのみグラフを生成することと、辺の値に１を設定することと、その辺に接続された頂点の自動的な生成と、頂点をデフォルト値に割与えることを可能とします。また辺の複製、つまり、 uniqueEdges パラメータとしての PartitionStrategy の Some 値の応答 (例えば uniqueEdges = Some(PartitionStrategy.RandomVertexCut) ) もサポートします。パーティション戦略により、同一の辺は同じパーティションに共存する必要があり、そのため複製されます。

頂点 RDD と 辺 RDD

GraphX は、グラフに含まれる頂点と辺の RDD ビューを提供します。しかしながら、GraphX は頂点と辺を最適化したデータ構造の中で維持したり、このデータ構造は追加的な関数を提供したりするため、頂点と辺は、 VertexRDD 型や EdgeRDD 型としてそれぞれ応答されます。このセクションでは、これらの型の便利な追加関数のいくつかを紹介します。

VertexRDD

VertexRDD[A] は RDD[(VertexID, A)] を継承し、VertexID が一回だけ発生するという制約を追加しています。さらに、 VertexRDD[A] は型 A の属性を持つ頂点を表現しています。内部的には、再利用可能なハッシュマップデータ構造に頂点の属性を格納することで実現しています。結果的には、もしふたつの VertexRDD がひとつの VertexRDD から（例えば、 filter や mapValues で）提供された場合、そのふたつの VertexRDD は、ハッシュ評価せずに、一定時間内にジョインさせることができます。インデックス化されたデータ構造を利用するために、 VertexRDD は以下の追加関数を提供します。

class VertexRDD[VD] extends RDD[(VertexID, VD)] {
  // Filter the vertex set but preserves the internal index
  def filter(pred: Tuple2[VertexId, VD] => Boolean): VertexRDD[VD]
  // Transform the values without changing the ids (preserves the internal index)
  def mapValues[VD2](map: VD => VD2): VertexRDD[VD2]
  def mapValues[VD2](map: (VertexId, VD) => VD2): VertexRDD[VD2]
  // Remove vertices from this set that appear in the other set
  def diff(other: VertexRDD[VD]): VertexRDD[VD]
  // Join operators that take advantage of the internal indexing to accelerate joins (substantially)
  def leftJoin[VD2, VD3](other: RDD[(VertexId, VD2)])(f: (VertexId, VD, Option[VD2]) => VD3): VertexRDD[VD3]
  def innerJoin[U, VD2](other: RDD[(VertexId, U)])(f: (VertexId, VD, U) => VD2): VertexRDD[VD2]
  // Use the index on this RDD to accelerate a `reduceByKey` operation on the input RDD.
  def aggregateUsingIndex[VD2](other: RDD[(VertexId, VD2)], reduceFunc: (VD2, VD2) => VD2): VertexRDD[VD2]
}

例えば、 filter オペレータがどのように VertexRDD を応答するか注意してください。フィルターは、実態としては BitSet を使って実装されているので、インデックスの再利用し、他の VertexRDDs との迅速なジョインできる機能を保持します。同様に、 mapValues オペレータは、 map 関数は VertexID を変更することができず、そのため、おなじハッシュマップデータ構造を再利用可能になっています。 leftJoin と innerJoin はどちらも、同じハッシュマップから取得したふたつの VertexRDD をジョインする時に特定し、ポイント探索よりはむしろコスト的にリニアなスキャンによるジョインを実装することができます。

aggregateUsingIndex オペレータは、 RDD[(VertexID, A)] から新しい VertexRDD の効率的な構成のために便利です。概念的には、もし、頂点のセット上に構成された、 VertexRDD[B] を持っている場合、 RDD[(VertexID, A)] における頂点のスーパーセットになり、合成されたものと、それぞれのものの両方のインデックスを再利用できます。例えば、

val setA: VertexRDD[Int] = VertexRDD(sc.parallelize(0L until 100L).map(id => (id, 1)))
val rddB: RDD[(VertexId, Double)] = sc.parallelize(0L until 100L).flatMap(id => List((id, 1.0), (id, 2.0)))
// There should be 200 entries in rddB
rddB.count
val setB: VertexRDD[Double] = setA.aggregateUsingIndex(rddB, _ + _)
// There should be 100 entries in setB
setB.count
// Joining A and B should now be fast!
val setC: VertexRDD[Double] = setA.innerJoin(setB)((id, a, b) => a + b)

EdgeRDD

RDD[Edge[ED]] を拡張した EdgeRDD[ED] は、 PartitionStrategy の中で定義されたいろんなパーティション戦略のひとつを使ってパーティションされたブロックの中で、辺を組織します。各パーティションの中では、辺の属性と隣接構成は分割的に蓄積され、属性の変化を評価する時に、再利用を最大化します。

以下の３つの関数は、 EdgeRDD によって提供されているものです。

// Transform the edge attributes while preserving the structure
def mapValues[ED2](f: Edge[ED] => ED2): EdgeRDD[ED2]
// Revere the edges reusing both attributes and structure
def reverse: EdgeRDD[ED]
// Join two `EdgeRDD`s partitioned using the same partitioning strategy.
def innerJoin[ED2, ED3](other: EdgeRDD[ED2])(f: (VertexId, VertexId, ED, ED2) => ED3): EdgeRDD[ED3]

ほとんどのアプリケーションでは、EdgeRDD のオペレーションはグラフオペレーターを通して実現されるか、ベースとなる RDD クラスに定義されたオペレーションをあてにしています。

最適化された表現

最適化についてはこのガイドのスコープ外のことですが、よく理解することは、APIの利用と同様に、スケーラブルなアルゴリズムを狙うかもしれません。 GraphX は、頂点区切り方式を分散グラフパーティションとして採用しています。

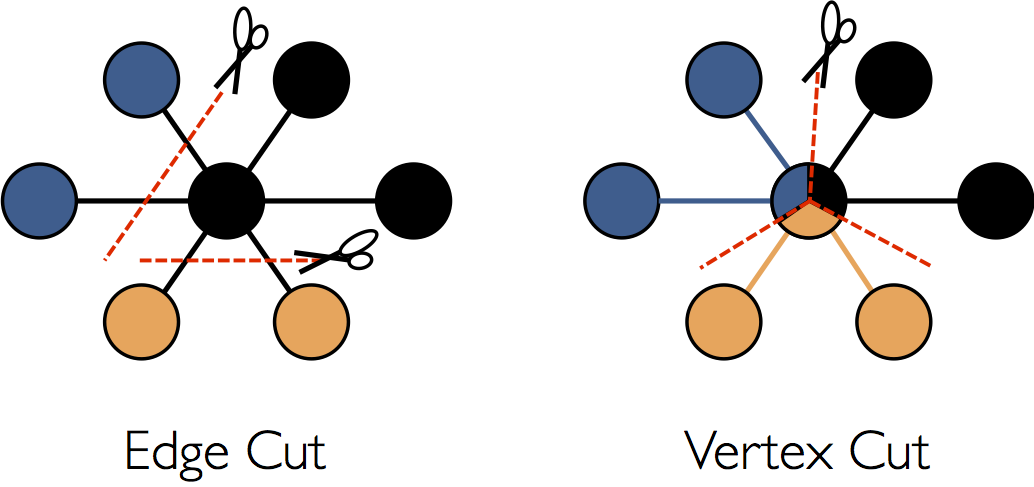
辺に沿ってグラフを分割するのではなく、 GraphX は頂点に沿ってグラフを分割します。それによって連携処理と蓄積の両方のオーバーヘッドを削減することができます。論理的には、辺をノードに割り当てることと、頂点を複数のノードに拡張させることは一致します。辺の割当は厳密には、 PartitionStrategy に依存し、様々な探索法とのトレードオフが存在します。ユーザは、 Graph.partitionBy オペレータによるグラフの再パーティショニングによって異なる戦略間で選択をすることができます。デフォルトのパーティション戦略は、グラフ構造上に提供された初期の辺のパーティショニングを使います。しかしながら、ユーザーは、簡単に 2D パーティショニングか、 GraphX に含まれる他の探索法に切り替えることができます。

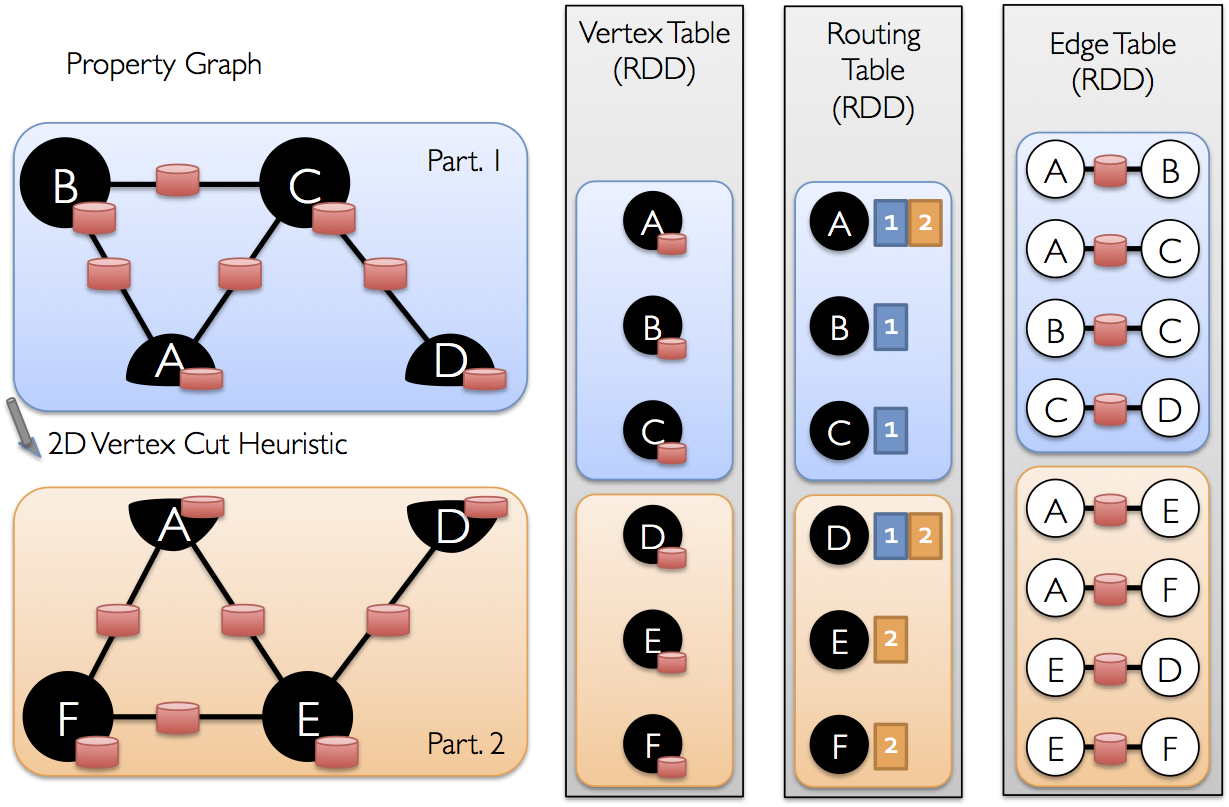
一度、辺がパーティショニングされると、効率的なグラフ並列計算へのキーとなる挑戦は、頂点属性を辺と効率的にジョインさせることになります。現実のグラフは頂点よりも多くの辺を持つのが典型的であるため、我々は頂点の属性を辺に移動させるのです。全てのパーティションが全ての頂点に隣接している辺を含んでいる訳ではないので、我々は内部的にルーティングテーブルを維持します。そのルーティングテーブルには、 triplets や mapReduceTriplets のようにオペレータに要求されたジョインを実装した時に、どの頂点にブロードキャストするかの情報を持っています。

グラフアルゴリズム

GraphX は、分析タスクをシンプルにするためのグラフアルゴリズムのセットを持っています。そのアルゴリズムは、 org.apache.spark.graphx.lib パッケージに含まれていて、 GraphOps 経由で、 Graph クラスのメソッドとして直接アクセスすることができます。このセクションでは、そのアルゴリズムについて、どのように利用するか説明します。

PageRank

ページランクアルゴリズムはグラフにおける各頂点の重要度を計算し、 u から v への辺が u により v の重要性がどのように支持されているかを推定します。例えば、 Twitter で多くのユーザからフォローされているユーザは、高いランクになります。

GraphX は、 PageRank オブジェクトのメソッドとして、ページランクアルゴリズムの静的あるいは動的な実装を提供します。静的なページランクアルゴリズムは、固定回数繰り返し実行します。動的なページランクはランクが収束するまで繰り返し処理を実行します。 GraphOps はこれらのアルゴリズムを Graph クラスから直接呼び出すことを可能にします。

GraphX は、ページランクアルゴリズムを稼働させることができる、ソーシャルネットワークのサンプルデータを持っています。 graphx/data/users.txt にユーザデータがあり、 graphx/data/followers.txt が関係性のデータになります。各ユーザのページランクは、以下のように計算します。

// Load the edges as a graph
val graph = GraphLoader.edgeListFile(sc, "graphx/data/followers.txt")
// Run PageRank
val ranks = graph.pageRank(0.0001).vertices
// Join the ranks with the usernames
val users = sc.textFile("graphx/data/users.txt").map { line =>
  val fields = line.split(",")
  (fields(0).toLong, fields(1))
}
val ranksByUsername = users.join(ranks).map {
  case (id, (username, rank)) => (username, rank)
}
// Print the result
println(ranksByUsername.collect().mkString("\n"))

Connected Components アルゴリズム

Connected Components アルゴリズムは、接続した頂点を、その中で一番小さな値のIDでラベリングします。例えば、ソーシャルネットワーク上では、　Connected Components はおおよそのクラスタとして捉えることができます。 GraphX は、 ConnectedComponents オブジェクトにこのアルゴリズムの実装を持っていて、ソーシャルネットワークのサンプルデータを使って、以下のように計算することができます。

// Load the graph as in the PageRank example
val graph = GraphLoader.edgeListFile(sc, "graphx/data/followers.txt")
// Find the connected components
val cc = graph.connectedComponents().vertices
// Join the connected components with the usernames
val users = sc.textFile("graphx/data/users.txt").map { line =>
  val fields = line.split(",")
  (fields(0).toLong, fields(1))
}
val ccByUsername = users.join(cc).map {
  case (id, (username, cc)) => (username, cc)
}
// Print the result
println(ccByUsername.collect().mkString("\n"))

トライアングルカウント

二つの隣接頂点を、その間の辺と一緒に持っている場合、頂点は三角形の一部になります。 GraphX は、 TriangleCount オブジェクトにトライアングルカウントアルゴリズムの実装を持っていて、拡張点を通る三角形の数をカウントし、クラスタリングの計算を提供します。以下のようにソーシャルネットワークのデータからトライアングルカウントを実装できます。TriangleCount は、単純かされた指標( srcId < dstId )と、Graph.partitionBy を使ってパーティショニングされたグラフを要求することに気をつけてください。

// Load the edges in canonical order and partition the graph for triangle count
val graph = GraphLoader.edgeListFile(sc, "graphx/data/followers.txt", true).partitionBy(PartitionStrategy.RandomVertexCut)
// Find the triangle count for each vertex
val triCounts = graph.triangleCount().vertices
// Join the triangle counts with the usernames
val users = sc.textFile("graphx/data/users.txt").map { line =>
  val fields = line.split(",")
  (fields(0).toLong, fields(1))
}
val triCountByUsername = users.join(triCounts).map { case (id, (username, tc)) =>
  (username, tc)
}
// Print the result
println(triCountByUsername.collect().mkString("\n"))

例

ここで、テキストファイルからグラフを構築し、そこから重要な関係性とユーザを抽出し、さらにサブグラフ上でページランクを計算し、最終的にトップユーザに関連した属性を最終的に応答したいとします。これを、 GraphX を使えば、以下のように数行で実装することができます。

// Connect to the Spark cluster
val sc = new SparkContext("spark://master.amplab.org", "research")

// Load my user data and parse into tuples of user id and attribute list
val users = (sc.textFile("graphx/data/users.txt")
  .map(line => line.split(",")).map( parts => (parts.head.toLong, parts.tail) ))

// Parse the edge data which is already in userId -> userId format
val followerGraph = GraphLoader.edgeListFile(sc, "graphx/data/followers.txt")

// Attach the user attributes
val graph = followerGraph.outerJoinVertices(users) {
  case (uid, deg, Some(attrList)) => attrList
  // Some users may not have attributes so we set them as empty
  case (uid, deg, None) => Array.empty[String]
}

// Restrict the graph to users with usernames and names
val subgraph = graph.subgraph(vpred = (vid, attr) => attr.size == 2)

// Compute the PageRank
val pagerankGraph = subgraph.pageRank(0.001)

// Get the attributes of the top pagerank users
val userInfoWithPageRank = subgraph.outerJoinVertices(pagerankGraph.vertices) {
  case (uid, attrList, Some(pr)) => (pr, attrList.toList)
  case (uid, attrList, None) => (0.0, attrList.toList)
}

println(userInfoWithPageRank.vertices.top(5)(Ordering.by(_._2._1)).mkString("\n"))