Last active
February 22, 2018 16:30
-
-
Save ispapadakis/6c3b8d549de733b82568f37f9ce85c44 to your computer and use it in GitHub Desktop.
Biconnected Component Analysis of Undirected Graph (i.e., Bridges, Articulation Points) with Condensed Tree
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| class Graph(object): | |
| ''' | |
| Undirected Graph | |
| INPUT: | |
| Node Count: Int | |
| Edges: List in format [source, end] | |
| ''' | |
| def __init__(self,n,edges): | |
| self.nodeCount = n | |
| self.label = list(range(n)) | |
| self.edgeCount = len(edges) | |
| self.edges = edges[:] | |
| self.adj = [[] for _ in range(n)] | |
| for edgeIndex, edge in enumerate(self.edges): | |
| i,j = edge | |
| self.adj[i].append([j,edgeIndex]) | |
| self.adj[j].append([i,edgeIndex]) | |
| def __str__(self): | |
| out = [] | |
| for i,row in enumerate(self.adj): | |
| out.append('{:3d}: {}'. \ | |
| format(self.label[i],[self.label[v] for v,_ in row])) | |
| return '\n'.join(out) | |
| def bridges(self): | |
| low = [None]*self.nodeCount | |
| depth = [None]*self.nodeCount | |
| art = set() | |
| bridge = set() | |
| def dfs(u, parent): | |
| nonlocal time | |
| low[u] = depth[u] = time | |
| time += 1 | |
| isArticulation = False | |
| children = 0 | |
| for v, edge in self.adj[u]: | |
| if low[v] is None: | |
| dfs(v,u) | |
| children += 1 | |
| if low[v] >= depth[u]: | |
| isArticulation = True | |
| low[u] = min(low[u], low[v]) | |
| if low[v] > depth[u]: | |
| bridge.add(edge) | |
| elif v != parent: | |
| low[u] = min(low[u],depth[v]) | |
| if parent is None: | |
| if children > 1: | |
| art.add(u) | |
| elif isArticulation: | |
| art.add(u) | |
| for u in range(self.nodeCount): | |
| if low[u] is None: | |
| time = 0 | |
| dfs(u, None) | |
| return art, bridge | |
| class disjointSet: | |
| def __init__(self, n): | |
| self.parent = list(range(n)) | |
| def find(self, element): | |
| if self.parent[element] == element: | |
| return element | |
| self.parent[element] = self.find(self.parent[element]) | |
| return self.parent[element] | |
| def union(self, x, y): | |
| x = self.find(x) | |
| y = self.find(y) | |
| if x == y: | |
| return | |
| if x < y: | |
| self.parent[y] = x | |
| else: | |
| self.parent[x] = y | |
| def bctree(graph): | |
| ''' Condense Biconnected Tree ''' | |
| _, bridges = graph.bridges() | |
| dset = disjointSet(graph.nodeCount) | |
| nodes = set() | |
| brg = [] | |
| for i,e in enumerate(graph.edges): | |
| if i in bridges: | |
| brg.append(e) | |
| continue | |
| dset.union(*e) | |
| bcAdj = {i:[] for i,lst in enumerate(graph.adj) if not lst} | |
| for e in brg: | |
| u,v = [dset.find(u) for u in e] | |
| bcAdj.setdefault(u,[]).append(v) | |
| bcAdj.setdefault(v,[]).append(u) | |
| return bcAdj | |
| if __name__ == '__main__': | |
| print("Testing...\n") | |
| print("CASE A") | |
| vertices = 8 | |
| edges = [[1,6], [6,2], [2,3], [3,5], [5,7], [7,0], [0,4]] | |
| g = Graph(vertices,edges) | |
| print('Graph Adjacency List') | |
| print(g) | |
| art, bridge = g.bridges() | |
| print('Articulation Points') | |
| print(sorted(art)) | |
| print('Bridges') | |
| print(*[edges[b] for b in bridge],sep='\t') | |
| print('Condensed Tree From Biconnected') | |
| bcg = bctree(g) | |
| for u in sorted(bcg): | |
| print('{:3d}: {}'.format(u,sorted(bcg[u]))) | |
| print('\n'*2) | |
| print("CASE B") | |
| vertices = 12 | |
| edges = [[0,1],[0,3],[1,2],[1,6],[2,3],[2,7],[3,4], | |
| [5,0],[5,8],[5,9],[8,10],[9,10],[10,11]] | |
| g = Graph(vertices,edges) | |
| print('Graph Adjacency List') | |
| print(g) | |
| art, bridge = g.bridges() | |
| print('Articulation Points') | |
| print(sorted(art)) | |
| print('Bridges') | |
| print(*[edges[b] for b in bridge],sep='\t') | |
| print('Condensed Tree From Biconnected') | |
| bcg = bctree(g) | |
| for u in sorted(bcg): | |
| print('{:3d}: {}'.format(u,sorted(bcg[u]))) | |
| print('\n'*2) | |
| print("CASE C") | |
| vertices = 10 | |
| edges = [[0,1],[1,2],[2,3],[3,4],[3,5],[4,5],[4,8], | |
| [5,6],[6,7],[5,7],[5,8],[7,8],[8,9]] | |
| g = Graph(vertices,edges) | |
| print('Graph Adjacency List') | |
| print(g) | |
| art, bridge = g.bridges() | |
| print('Articulation Points') | |
| print(sorted(art)) | |
| print('Bridges') | |
| print(*[edges[b] for b in bridge],sep='\t') | |
| print('Condensed Tree From Biconnected') | |
| bcg = bctree(g) | |
| for u in sorted(bcg): | |
| print('{:3d}: {}'.format(u,sorted(bcg[u]))) | |
| print('\n'*2) | |
| print("CASE D: Disconnected Graph") | |
| vertices = 10 | |
| edges = [[0,1],[1,2],[2,3],[3,0],[3,5], | |
| [5,6],[6,7],[5,7]] | |
| g = Graph(vertices,edges) | |
| print('Graph Adjacency List') | |
| print(g) | |
| art, bridge = g.bridges() | |
| print('Articulation Points') | |
| print(sorted(art)) | |
| print('Bridges') | |
| print(*[edges[b] for b in bridge],sep='\t') | |
| print('Condensed Tree From Biconnected') | |
| bcg = bctree(g) | |
| for u in sorted(bcg): | |
| print('{:3d}: {}'.format(u,sorted(bcg[u]))) | |
| print('\n'*2) |
Author
Author
Non-Recursive Implementation
from collections import defaultdict
class Graph(object):
# Undirected Graph
def __init__(self,n,edges):
self.nodeCount = n
self.edges = edges
self.adj = [[] for _ in range(self.nodeCount)]
for u,v in edges:
self.adj[u].append(v)
self.adj[v].append(u)
def bridges(self):
parent = [None]*self.nodeCount
low = [None]*self.nodeCount
depth = [None]*self.nodeCount
nonbridge = []
bridge = []
adj = [iter(row) for row in self.adj]
for root in range(self.nodeCount):
if depth[root] is not None:
continue
self.forestRoots.append(root)
stack = [root]
depth[root] = 0
low[root] = 0
while True:
u = stack[-1]
for v in adj[u]:
if depth[v] is None:
parent[v] = u
depth[v] = depth[u] + 1
low[v] = depth[v]
stack.append(v)
break
elif v != parent[u]:
low[u] = min(low[u],depth[v])
else:
stack.pop()
if not stack:
break
w = stack[-1]
low[w] = min(low[w],low[u])
if depth[w] < low[u]:
bridge.append([w,u])
else:
nonbridge.append([w,u])
return bridge, nonbridge
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
Test Cases
CASE A
Simple Path : All Edges Are Bridges
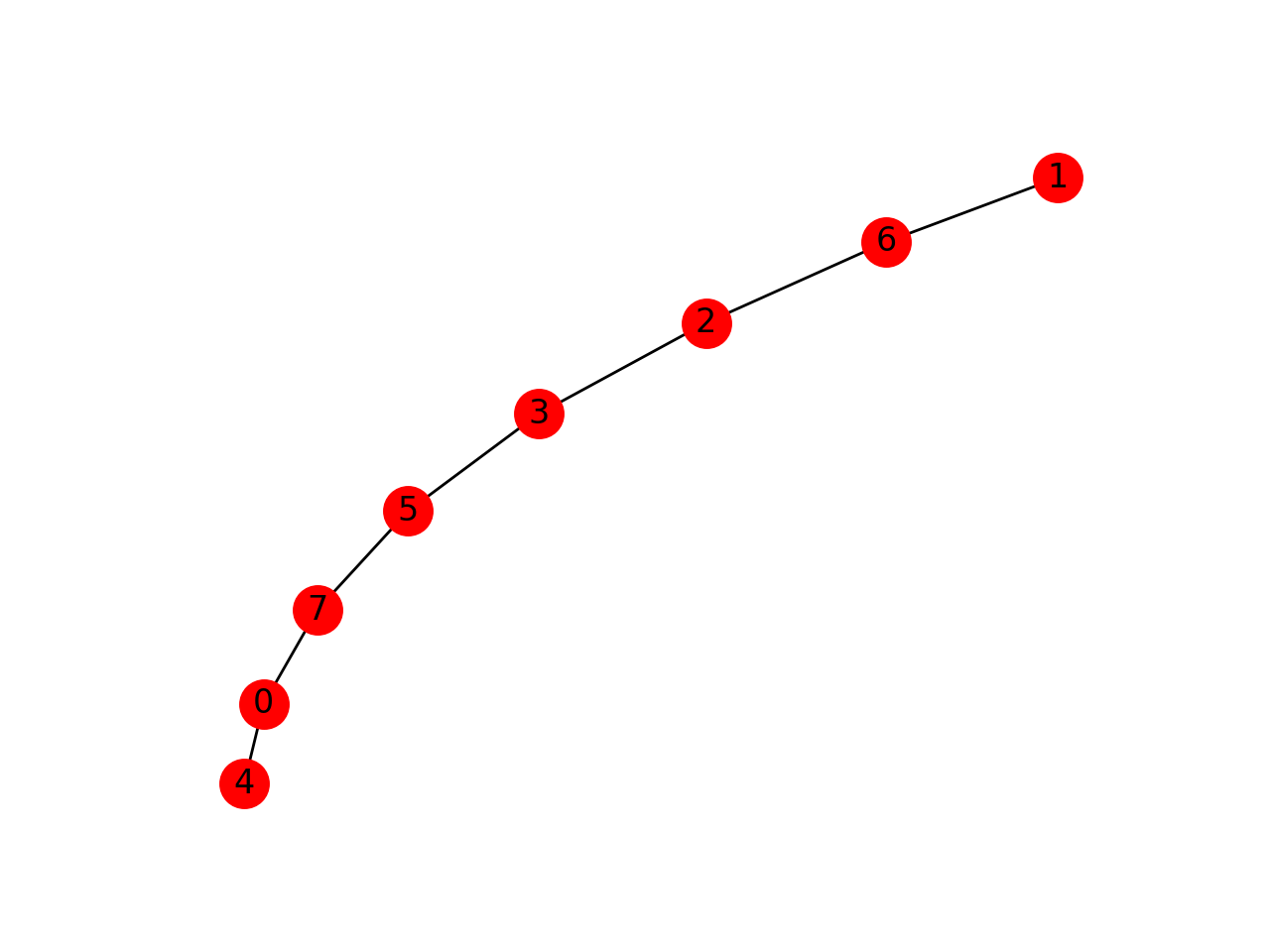
CASE B
Bridges at [11,10],[5,0],[1,6],[2,7],[3,4]
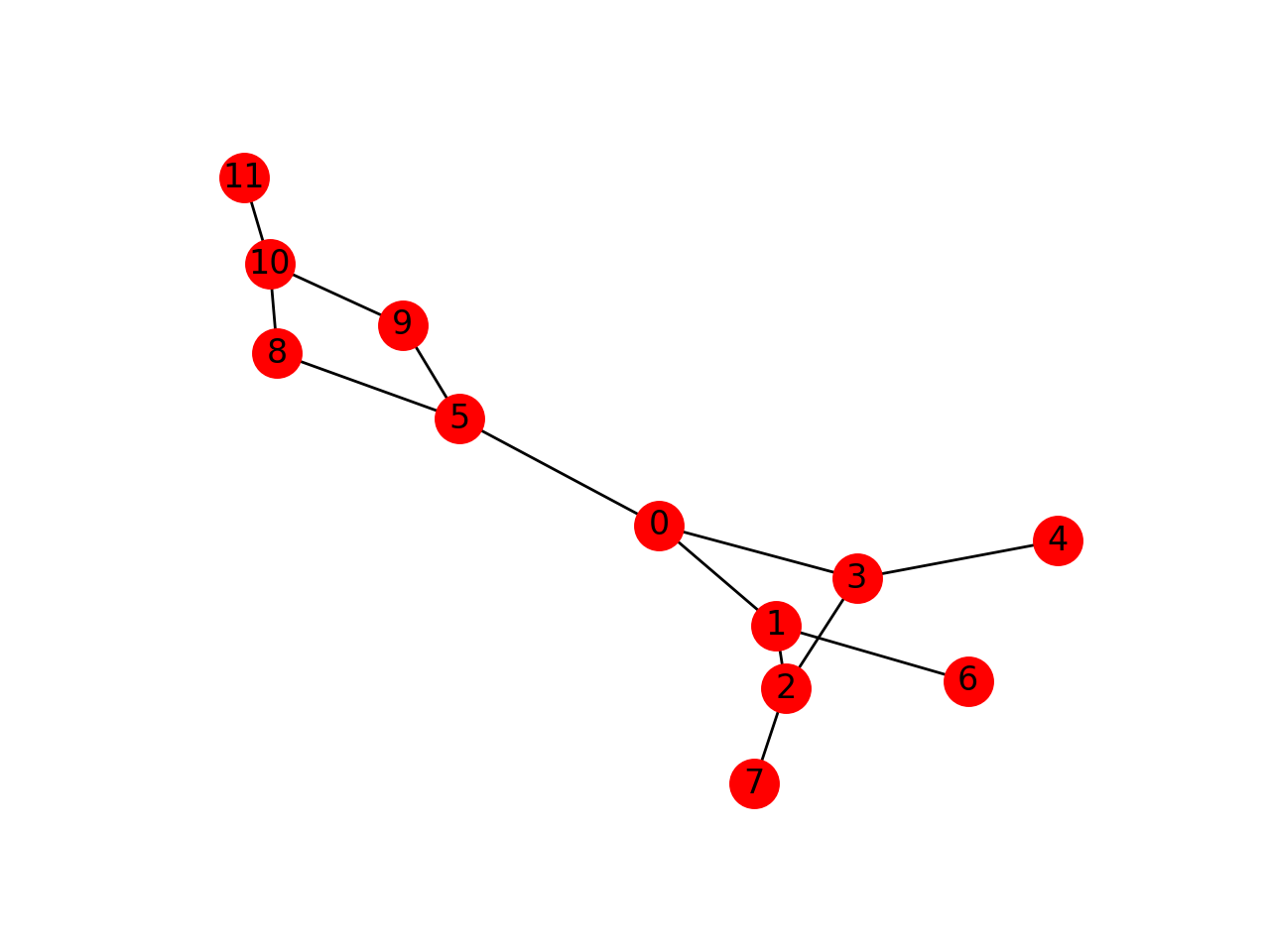
CASE C
Bridges at [0,1],[1,2],[2,3],[8,9]
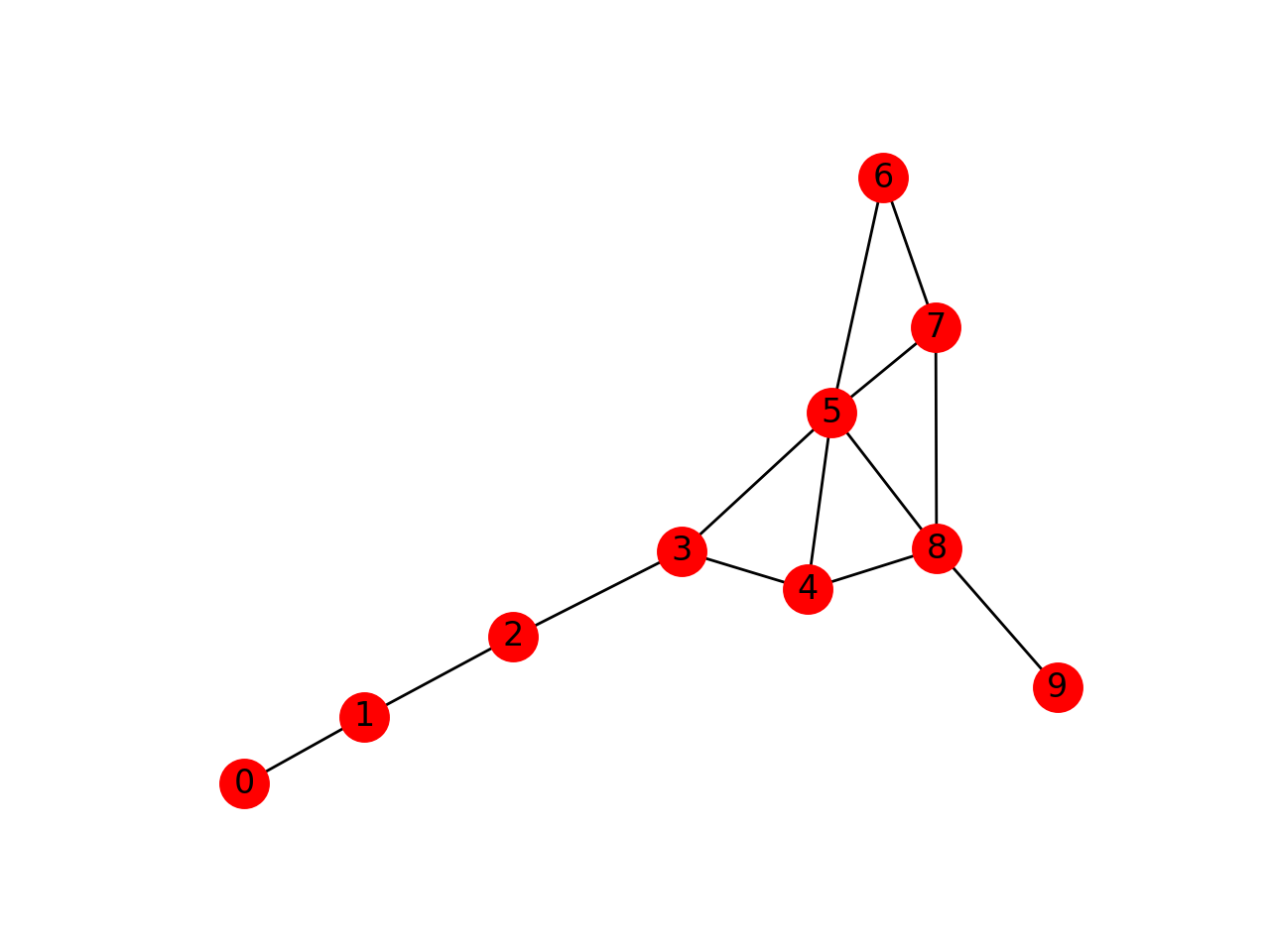
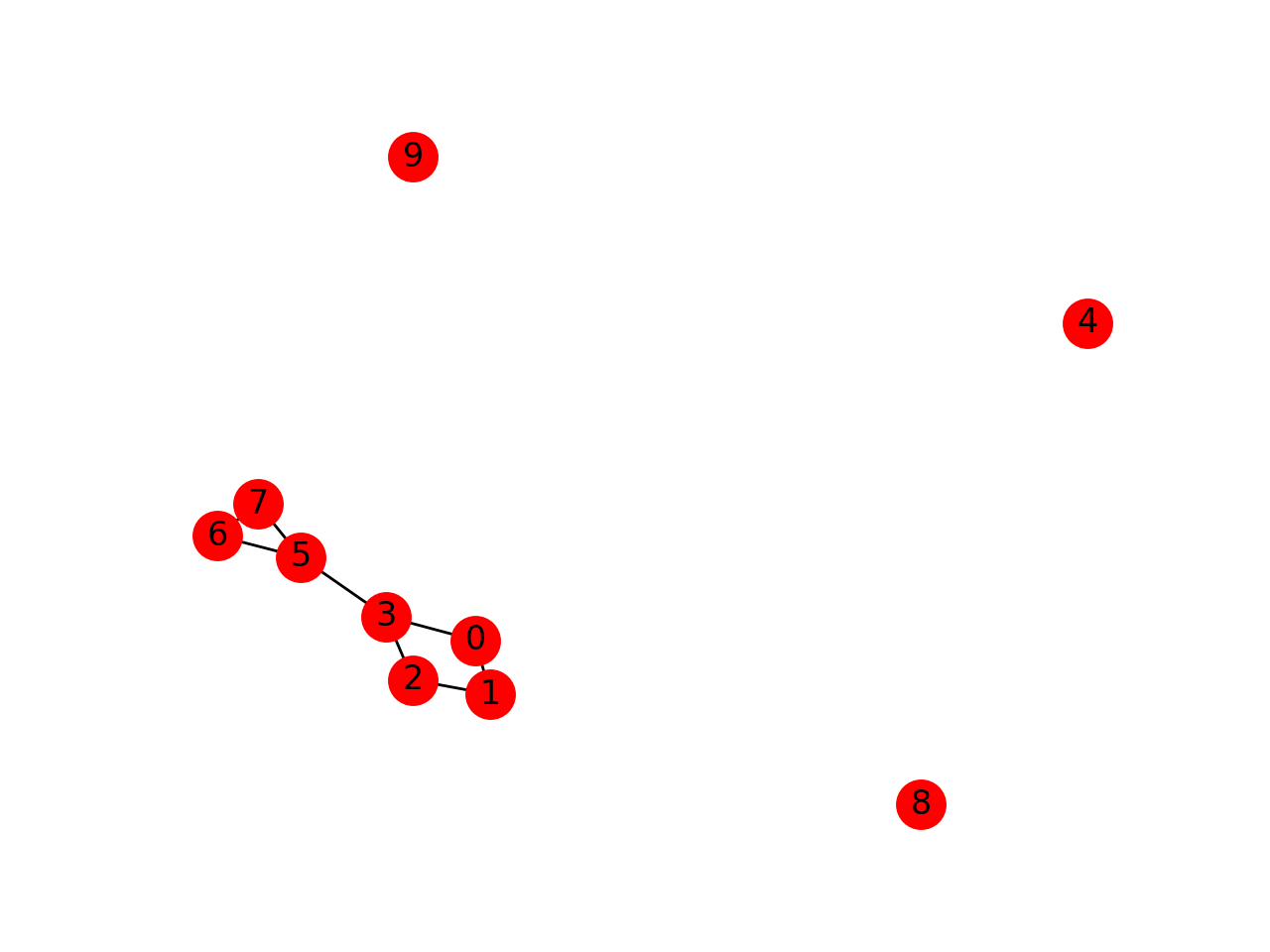
CASE D
Disconnected Graph - Bridge at [5,3]