Spacetime diagram of a relativistic tortoise and hare race

TortoiseHareRace-II.tex

\documentclass[crop=true, border=10pt]{standalone}
\usepackage{comment}
\begin{comment} 
:Title: Tortoise and Hare - Variation 2
:Author: 	    J A Miller, UAH Physics & Astronomy, [email protected]
                   2020/06/29

A race between a tortoise and hare. 

References:
1. T. Takeuchi
    https://www1.phys.vt.edu/~takeuchi/relativity/practice/problem04.html
    and
    "An Illustrated Guide to Relativity" ISBN: 9780521141000
2. Basic plot style and colors from 
    https://gist.github.com/mcnees/45b9f53ad371c38ba6f3759df5880fb1

---------------------------------------------------------------------
Problem to accompany figure
---------------------------------------------------------------------

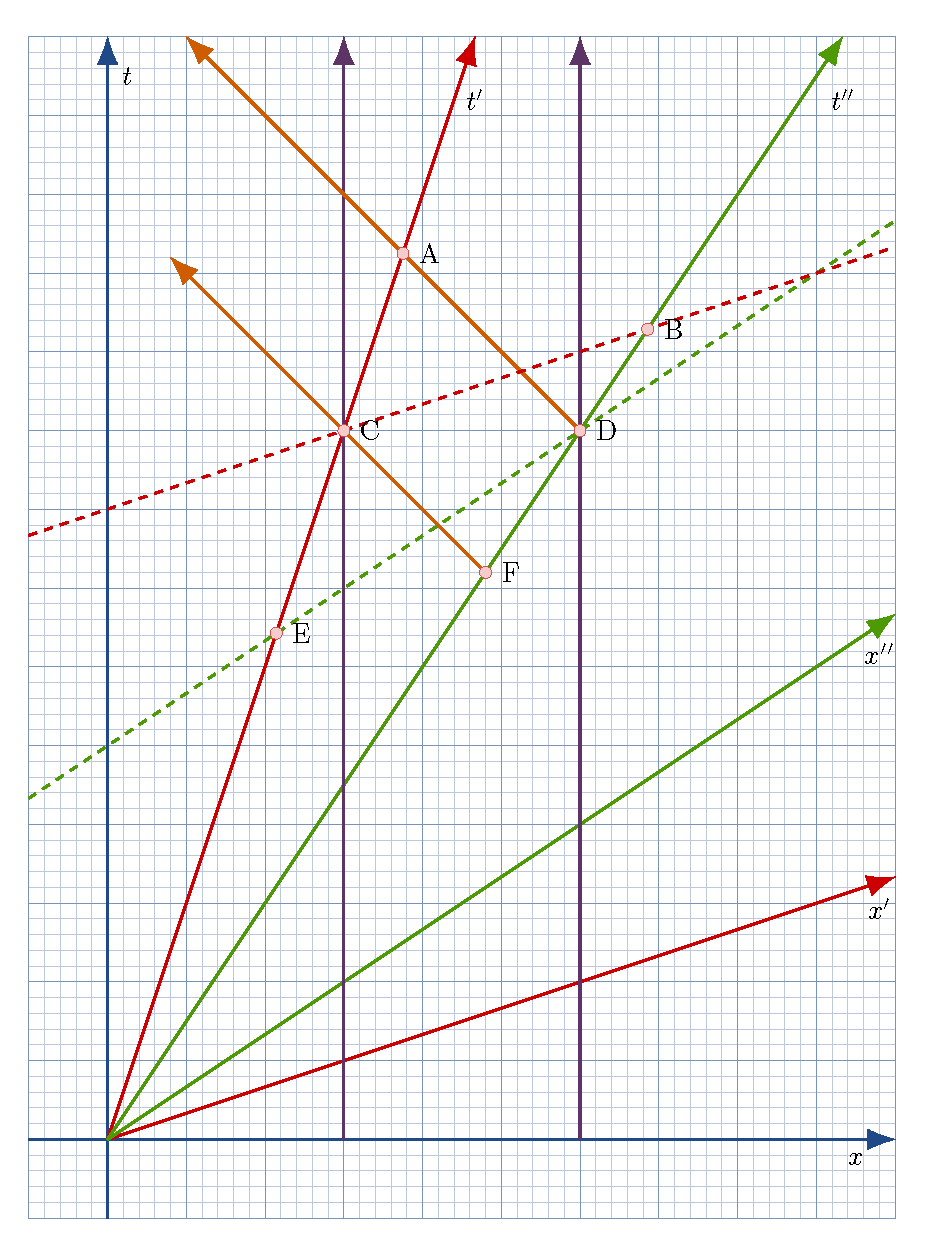
\ditem{Tortoise and Hare II}\label{exer-hareII} A tortoise and hare decide to race again. They start at the same point and both race in the $+x$ direction. The hare is twice as fast as the tortoise but the hare gives the tortoise a handicap by letting him race only half the distance. See Figure \ref{fig-hareII}.

In the ground frame both animals cross their respective finish lines at the same time. The official on the ground declares a tie.

\begin{enumerate}[label=(\alph*),nosep]
\item At which point (A through F) on the spacetime diagram does the hare cross the finish line?

\item At which point does the tortoise cross the finish line?

\item At which point is the tortoise when the hare crosses its finish line in the hare frame?

\item At which point is the hare when the tortoise crosses its finish line in the tortoise frame?

\item At which point does the tortoise actually see the hare cross its finish line?

\item What is the result of the race in the respective frames of the tortoise and the hare?

\item f the tortoise bases its conclusion on what it actually sees, will it think that it won or that it lost?
\end{enumerate}

---------------------------------------------------------------------
Figure caption
---------------------------------------------------------------------

\caption{
Spacetime diagram for the tortoise and hare race. \textit{Red arrows:} The primed frame of the tortoise. \textit{Green arrows:} The double primed frame of the hare. \textit{Purple arrows:} The worldlines of the tortoise (left arrow) and hare (right arrow) finish lines. \textit{Orange arrows:} Light rays. \texit{Dashed lines:} Lines of simultaneity in the two moving frames. For Exercise \ref{exer-hareII}.
              } 

---------------------------------------------------------------------
Solution to problem
---------------------------------------------------------------------

\ditem{Tortoise and Hare II} 
\begin{enumerate}[label=(\alph*),nosep]
\item Point D.

\item Point C.

\item The hare crosses his finish line at point D, where the time is $t_D^{\prime\prime}$ in the hare frame. All events along the line $t_D^{\prime\prime} = \gamma_h (t - v_h x)$ occur simultaneously with $t_D^{\prime\prime}$. (The quantities $\gamma_h$ and $v_h$ are the Lorentz factor and speed of the hare (or the hare frame) relative to the ground.) This line of simultaneity is parallel to the $x^{\prime\prime}$ axis, and intersects the tortoise worldline at point E. Hence, the tortoise is at point E on its worldline when the hare is done.

\item The tortoise crosses his finish line at C at some time (in his frame) $t_C^\prime$. The locus of all points simultaneous with $t_C^\prpr$ is given by $t_C^\prime = \gamma_t (t - v_t x)$, where $v_t$ is the tortoise speed in the ground frame, and is a line through point C and parallel to the $x^\prime$ axis. Thus, when the tortoise finished, the hare is at point B on its worldline and is already done.

\item The tortoise will see the hare at the hare finish line at point A along his worldline.

\item In the tortoise frame, the hare has won. In the hare frame, he has won also.

\item Based on what the tortoise sees, he would say he won! 
\end{enumerate}


\end{comment}




\usepackage{tikz}
\usetikzlibrary{arrows.meta,calc,intersections}

\usepackage{pgfplots}
\pgfplotsset{compat=1.16}

\usepackage{xcolor}
\definecolor{plum}{rgb}{0.36078, 0.20784, 0.4}
\definecolor{chameleon}{rgb}{0.30588, 0.60392, 0.023529}
\definecolor{cornflower}{rgb}{0.12549, 0.29020, 0.52941}
\definecolor{scarlet}{rgb}{0.8, 0, 0}
\definecolor{brick}{rgb}{0.64314, 0, 0}
\definecolor{sunrise}{rgb}{0.80784, 0.36078, 0}
\definecolor{lightblue}{rgb}{0.15,0.35,0.75}


% ----------------------- parameter specifications ------------------------

% the speeds of the tortoise and hare. 
\newcommand*\vt{0.33333}
\newcommand*\vh{0.66666}

% finish lines
\newcommand*\xfint{3.0}
\newcommand*\xfinh{6.0}

% graph boundaries
\newcommand*{\xa}{-1}  % lower left corner
\newcommand*{\ya}{-1}
\newcommand*{\xb}{10}  % upper right corner
\newcommand*{\yb}{14}

% x and y scales
\newcommand*{\xscale}{1cm} 
\newcommand*{\yscale}{1cm}  

% some calculations now ...

% gamma and eta factors for tortoise and hare
\pgfmathsetmacro{\gamt}{1/sqrt(1-\vt*\vt)}
\pgfmathsetmacro{\gamh}{1/sqrt(1-\vh*\vh)}
\pgfmathsetmacro{\etat}{\vt*\gamt}
\pgfmathsetmacro{\etah}{\vh*\gamh}


% ------------------------ other functions ------------------------------




% ------------------------ begin figure ------------------------------

\begin{document}

\begin{tikzpicture}[
	scale=1,
	domain=\xa:\xb,
	x=\xscale,y=\yscale, 
	axisarrow/.style=-{Latex[inset=0pt,length=10pt]},
	minor gridlines/.style={cornflower!30,step=0.2,thin},
	major gridlines/.style={cornflower!60,step=1.0,thin},
	axes/.style={cornflower,thick,axisarrow},      % unprimed axes
	primed axes/.style={scarlet,thick,axisarrow},  % primed axes
	double primed axes/.style={chameleon,thick,axisarrow},  % double primed axes
	LOS primed/.style={scarlet,thick,dashed},  % line of simultaneity in primed frame
	LOS double primed/.style={chameleon,thick,dashed},  % line of simultaneity in primed frame
	light ray/.style={sunrise,thick,axisarrow}, 
	textnode/.style={inner sep=0pt},  % for a text only node
	dot/.style={circle,draw=scarlet!70,fill=scarlet!20,inner sep=1.5pt} 
    ]
 
 
   % some coordinates   
   \coordinate (O) at (0,0); 
    
    % Draw the grid.
    \draw [minor gridlines] (\xa,\ya) grid (\xb,\yb);
    \draw [major gridlines] (\xa,\ya) grid (\xb,\yb);
    
    % Draw unprimed axes
    \draw[axes,name path=taxis] (0,\ya) -- (0,\yb);
    \node[textnode] at (0.25,\yb-0.5) {$t$};
    \draw[axes,name path=xaxis] (\xa,0) -- (\xb,0);
    \node[textnode] at (\xb-0.5,-0.25) {$x$};
    
    % Draw the primed axes (tortoise)
    \draw[primed axes,name path=tpaxis] (O) -- (\vt*\yb,\yb) node (tp) {};
	\node[textnode] at ($(tp)+(0,-0.8)$) {$t^\prime$};
	\draw[primed axes,name path=xpaxis] (O) -- (\xb,\vt*\xb) node (xp) {};
	\node[textnode] at ($(xp)+(-0.2,-0.4)$) {$x^\prime$};
	
	% Draw the double primed axes (hare)
    \draw[double primed axes,name path=tppaxis] (O) -- (\vh*\yb,\yb) node (tpp) {};
	\node[textnode] at ($(tpp)+(0,-0.8)$) {$t^{\prime\prime}$};
	\draw[double primed axes,name path=xppaxis] (O) -- (\xb,\vh*\xb) node (xpp) {};
	\node[textnode] at ($(xpp)+(-0.2,-0.5)$) {$x^{\prime\prime}$};
	
	% Draw the worldlines of the two finish lines
    \draw[plum,thick,axisarrow,name path=wtfin] (\xfint,0) -- (\xfint,\yb);
    \draw[plum,thick,axisarrow,name path=whfin] (\xfinh,0) -- (\xfinh,\yb);
    
   % Find where the worldlines cross the finish lines	, points C and D
   %   Delay labeling until the end so they are on top of crossing lines
	\path [name intersections={of=whfin and tppaxis,by=D}];
	%\node[dot,label={right:D}] at (D) {};
	\path [name intersections={of=wtfin and tpaxis,by=C}];
	%\node[dot,label={right:C}] at (C) {};
	
  	% Draw light rays and add a couple points A and F
	\draw [light ray,name path=lightfromD] (D) -- ($(D)+(-5,5)$) {};
    \path [name intersections={of=lightfromD and tpaxis,by=A}];
	\node[dot,label={right:A}] at (A) {};
	    % For next line, x and y scale must be equal to work as is
        % I find point F manually. Would be nice to use intersections somehow
   	\path let \p1=(C) in coordinate (F) at ( {\vh*(\x1+\y1)/(1+\vh)}, {(\x1+\y1)/(1+\vh)} ); 
   	%\node[dot,label={right:F}] at (F) {};  % delay label
	\draw [light ray,name path=lightfromF] (F) -- ($(F)+(-4,4)$) {};
	
	% Get the finish times in the primed frames
	\pgfmathsetmacro{\tppfinh}{ \xfinh/\etah  };
	\pgfmathsetmacro{\tpfint}{ \xfint/\etat  };
	
	% Lines of simultaneity
    \draw[LOS double primed,name path=LOSpp] plot(\x,\vh*\x + \tppfinh/\gamh);	
    \path [name intersections={of=LOSpp and tpaxis,by=E}];
    \node [dot,label={right:E}] at (E) {};
 
    \draw[LOS primed,name path=LOSp] plot(\x,\vt*\x + \tpfint/\gamt);	
    \path [name intersections={of=LOSp and tppaxis,by=B}];
    \node [dot,label={right:B}] at (B) {};   
    
  
    % Delayed labels. 
    \node[dot,label={right:D}] at (D) {};
	\node[dot,label={right:C}] at (C) {};
	\node[dot,label={right:F}] at (F) {}; 


 \end{tikzpicture}  

\end{document}