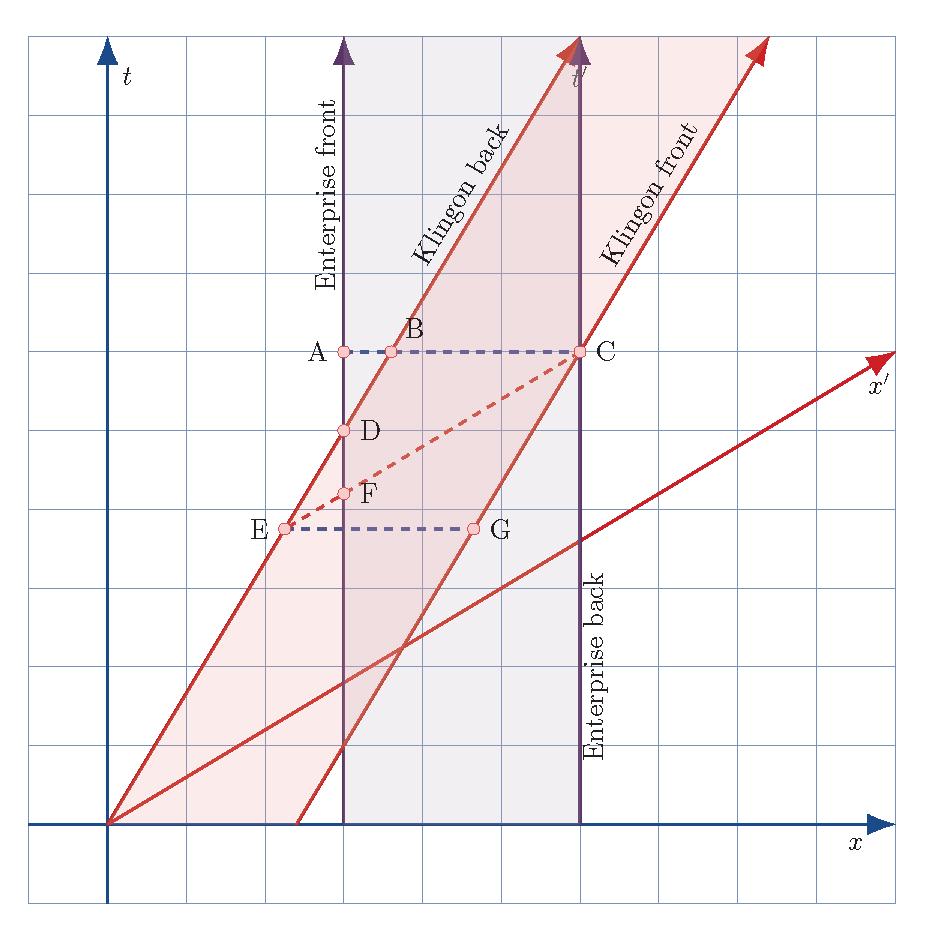
Spacetime diagram for a Klingon-Enterprise battle. The second variation. (special relativity)

KlingonEnterprise-II.tex

\documentclass[crop=true, border=10pt]{standalone}
\usepackage{comment}
\begin{comment} 
:Title: Klingons and Enterprise II
:Author: 	    J A Miller, UAH Physics & Astronomy, [email protected]
                   2020/07/01

Spacetime diagram of an Enterprise - Klingon battle. The second of a few variations.

References:
1. https://www1.phys.vt.edu/~takeuchi/relativity/practice/problem07.html
2. Basic plot style and colors from 
    https://gist.github.com/mcnees/45b9f53ad371c38ba6f3759df5880fb1

---------------------------------------------------------------------
Problem to accompany figure
---------------------------------------------------------------------

See the above reference. He has a nice, vivid description of the problem.


---------------------------------------------------------------------
Figure caption
---------------------------------------------------------------------

\caption{
Spacetime diagram of an Enterprise - Klingon battle. \textit{Blue arrows:} The unprimed frame of the stars and the Enterprise. \textit{Red arrows:} The primed frame of the Klingon ship, and the worldline of the ship front (the back of the ship is the $t^\prime$ axis). \textit{Purple arrows:} The worldlines of the Enterprise front and back. \textit{Dashed lines:} lines of simultaneity. For Exercise \ref{exer-klingonII}.
              } 

---------------------------------------------------------------------
Solution to problem
---------------------------------------------------------------------

See reference.


\end{comment}



\usepackage{tikz}
\usetikzlibrary{arrows.meta,calc,intersections}

\usepackage{pgfplots}
\pgfplotsset{compat=1.16}

\usepackage{xcolor}
\definecolor{plum}{rgb}{0.36078, 0.20784, 0.4}
\definecolor{chameleon}{rgb}{0.30588, 0.60392, 0.023529}
\definecolor{cornflower}{rgb}{0.12549, 0.29020, 0.52941}
\definecolor{scarlet}{rgb}{0.8, 0, 0}
\definecolor{brick}{rgb}{0.64314, 0, 0}
\definecolor{sunrise}{rgb}{0.80784, 0.36078, 0}
\definecolor{lightblue}{rgb}{0.15,0.35,0.75}


% ----------------------- parameter specifications ------------------------

% the speed of the primed frame  
\newcommand*\vp{0.6}

% proper length of both ships
% enterprise front will stay at x=3
\newcommand*\length{3.0}

% graph boundaries
\newcommand*{\xa}{-1}  % lower left corner
\newcommand*{\ya}{-1}
\newcommand*{\xb}{10}  % upper right corner
\newcommand*{\yb}{10}

% x and y scales
\newcommand*{\xscale}{1cm} 
\newcommand*{\yscale}{1cm}  

% some calculations now ...

% gamma and eta factors for the primed frame
\pgfmathsetmacro{\gamp}{1/sqrt(1-\vp*\vp)}
\pgfmathsetmacro{\etap}{\vp*\gamp}


% ------------------------ other functions ------------------------------

% Extract coordinate
% https://tex.stackexchange.com/questions/477075/coordinates-unit-in-pt-although-default-is-cm-in-tikz
% Example:
%  \ExtractCoordinate{x};
%  \node[above] at (\XCoord,\YCoord) {node};
\newdimen\XCoord
\newdimen\YCoord
\newcommand*{\ExtractCoordinate}[1]{\path (#1); \pgfgetlastxy{\XCoord}{\YCoord};}


% ------------------------ begin figure ------------------------------

\begin{document}

\begin{tikzpicture}[
	scale=1,
	domain=\xa:\xb,
	x=\xscale,y=\yscale, 
	axisarrow/.style=-{Latex[inset=0pt,length=10pt]},
	minor gridlines/.style={cornflower!30,step=0.2,thin},
	major gridlines/.style={cornflower!60,step=1.0,thin},
	axes/.style={cornflower,thick,axisarrow},      % unprimed axes
	primed axes/.style={scarlet,thick,axisarrow},  % primed axes
	primed major gridlines/.style={scarlet!60,thin},
	double primed axes/.style={chameleon,thick,axisarrow},  % double primed axes
	double primed major gridlines/.style={chameleon!60,thin},
	LOS/.style={cornflower,thick,dashed},  % line of simultaneity in unprimed frame
	LOS primed/.style={scarlet,thick,dashed},  % line of simultaneity in primed frame
	LOS double primed/.style={chameleon,thick,dashed},  % line of simultaneity in primed frame
	light ray/.style={sunrise,thick,axisarrow}, 
	textnode/.style={inner sep=0pt},  % for a text only node
	dot/.style={circle,draw=scarlet!70,fill=scarlet!20,inner sep=1.5pt} 
    ]
 
   % some coordinates   
   \coordinate (O) at (0,0); 
    
    % Draw the grid for the unprimed frame
    %\draw [minor gridlines] (\xa,\ya) grid (\xb,\yb);
    \draw [major gridlines] (\xa,\ya) grid (\xb,\yb);
    
    % Draw unprimed axes
    \draw[axes,name path=taxis] (0,\ya) -- (0,\yb);
    \node[textnode] at (0.25,\yb-0.5) {$t$};
    \draw[axes,name path=xaxis] (\xa,0) -- (\xb,0);
    \node[textnode] at (\xb-0.5,-0.25) {$x$};
    
    % Draw the primed axes 
    \draw[primed axes,name path=tpaxis] (O) -- (\vp*\yb,\yb) node (tp) {}; % klingon back worldline
	\node[textnode] at ($(tp)+(0,-0.5)$) {$t^\prime$};
	\draw[primed axes,name path=xpaxis] (O) -- (\xb,\vp*\xb) node (xp) {};
	\node[textnode] at ($(xp)+(-0.2,-0.4)$) {$x^\prime$};
	
	% Worldlines for Enterprise
    \draw[thick,plum,axisarrow,name path=efront] (3,0) -- (3,\yb);
    \draw[thick,plum,axisarrow,name path=eback] (3+\length,0) -- (3+\length,\yb);
	
	% Draw the worldlines of the front of the Klingons
    \draw[primed axes,name path=kfront] (\length/\gamp,0) -- (\vp*\yb+\length/\gamp,\yb);

    % Get point C. This is the "pivot" for everything else. Get its $t^\prime$ value
    \path [name intersections={of=eback and kfront,by=C}];

    % Point A
    \path let \p1=(C) in coordinate (A) at (3,\y1); 
    
    % Point B
    \draw[LOS,name path=LOSAC] (A) -- (C);
    \path [name intersections={of=LOSAC and tpaxis,by=B}];
    
    % Point D
    \path [name intersections={of=efront and tpaxis,by=D}];

    % Now the line of simultaneity through C to E
     \path let \p1=(C) in coordinate (E) at ( { \etap*\gamp*(\y1-\vp*\x1)  }, {\gamp*\gamp*(\y1-\vp*\x1)} );     
     \draw[LOS primed,name path=LOSC] (C) -- (E);
    
    % Point F
    \path [name intersections={of=LOSC and efront,by=F}];
	
	% Line of simultaneity through E to G
	% *** Since tikz uses points internally, we need to convert a pure number to cm to have the same unit as \x1
	 \path let \p1=(E) in coordinate (G) at ({\x1+((1cm/1pt)*(\length)/\gamp)}, {\y1});     
     \draw[LOS,name path=LOSEG] (E) -- (G);
	
    % Shading
	\draw[fill=plum!40,opacity=0.2] (3,0) -- (3+\length,0) -- (3+\length,\yb) -- (3,\yb) -- (3,0);
	\draw[fill=scarlet!40,opacity=0.2] (0,0) -- (3/\gamp,0) -- (\vp*\yb+\length/\gamp,\yb) -- (\vp*\yb,\yb) -- (0,0);	
	
	% Label the points
	\node[dot,label={right:C}] at (C) {};
	\node[dot,label={left:A}] at (A) {};
	\node[dot,label={above right:B}] at (B) {};
	\node[dot,label={right:D}] at (D) {};
	\node[dot,label={left:E}] at (E) {};
	\node[dot,label={right:F}] at (F) {};
	\node[dot,label={right:G}] at (G) {};

   % Hard to keep track of front and back... better label
   % These are manually set. Need to adjust for a different primed frame speed
    \node[inner sep=0pt,rotate=90] at (2.8,8) {Enterprise front};
    \node[inner sep=0pt,rotate=90] at (6.2,2) {Enterprise back};
    \node[inner sep=0pt,rotate=59] at (6.9,8) {Klingon front};
    \node[inner sep=0pt,rotate=59] at (4.5,8) {Klingon back};

\end{tikzpicture}  

\end{document}