Last active
June 27, 2022 08:47
-
-
Save jeffwillette/8bff0124df63c158c34b314298893d37 to your computer and use it in GitHub Desktop.
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| import math | |
| from typing import Any | |
| import numpy as np | |
| import pandas as pd # type: ignore | |
| import seaborn as sns # type: ignore | |
| import torch | |
| import torch.nn as nn | |
| from matplotlib import pyplot as plt # type: ignore | |
| from scipy.special import lambertw # type: ignore | |
| from torch import nn | |
| T = torch.Tensor | |
| def weight_2_norm(w: T, keepdim: bool = False) -> T: | |
| return (w ** 2).sum(dim=(-1, -2), keepdim=keepdim) # type: ignore | |
| def phi_inv(N: int) -> float: | |
| # phi_inv(N - 1) = lambertW(N / e) according to text below theorem 3.2 | |
| return np.real(lambertw(N / math.e)) # type: ignore | |
| def weight_inf_norm(w: T, keepdim: bool = False) -> T: | |
| """ | |
| in the case of 'inf' norm, the dimension which is summed is the head output dimension | |
| which is the second dimension in (H, D/H, in_D) which is how the matrices are split | |
| """ | |
| return w.abs().sum(dim=-1, keepdim=keepdim).amax(dim=-1, keepdim=keepdim) | |
| def head_split(t: T, split_size: int, split_dim: int = 0) -> T: | |
| return torch.stack(t.split(split_size, split_dim)) | |
| def lip_2_upper_bound_F(N: int, qk_weight: T, v_weight: T, o_weight: T, split_size: int) -> T: | |
| qkv_norm_prod = ( | |
| weight_2_norm(head_split(qk_weight, split_size=split_size, split_dim=1)) | |
| * weight_2_norm(head_split(v_weight, split_size=split_size, split_dim=1)) | |
| ) | |
| qkv_norm_prod = qkv_norm_prod.sum().sqrt() | |
| o_norm = weight_2_norm(o_weight).sqrt() | |
| return ( # type: ignore | |
| (np.sqrt(N) / np.sqrt(split_size)) | |
| * (4 * phi_inv(N) + 1) | |
| * qkv_norm_prod | |
| * o_norm | |
| ) | |
| def lip_2_upper_bound_f(N: int, qk_weight: T, split_size: int) -> T: | |
| qk_norm = weight_2_norm(head_split(qk_weight, split_size=split_size, split_dim=1)) | |
| head_norm = (np.sqrt(N) / np.sqrt(split_size)) * qk_norm * (4 * phi_inv(N) + 1) | |
| # print(f"{qk_norm=} {(np.sqrt(N) / np.sqrt(split_size))=} {(4 * phi_inv(N) + 1)=}") | |
| return (head_norm ** 2).sum().sqrt() # type: ignore | |
| def lip_inf_upper_bound_f(N: int, qk_weight: T, split_size: int) -> T: | |
| qk_norm = ( | |
| weight_inf_norm(head_split(qk_weight, split_size=split_size, split_dim=1)) | |
| * weight_inf_norm(head_split(qk_weight, split_size=split_size, split_dim=1).mT) | |
| ).amax(dim=0) | |
| return (4 * phi_inv(N) + (1 / np.sqrt(split_size))) * qk_norm # type: ignore | |
| def lip_inf_upper_bound_F(N: int, qk_weight: T, v_weight: T, o_weight: T, split_size: int) -> T: | |
| o_norm = weight_inf_norm(o_weight) | |
| v_norm = weight_inf_norm(head_split(v_weight, split_size=split_size, split_dim=1)).amax(dim=0) | |
| qk_norm = ( | |
| weight_inf_norm(head_split(qk_weight, split_size=split_size, split_dim=1).mT) | |
| * weight_inf_norm(head_split(qk_weight, split_size=split_size, split_dim=1)) | |
| ).amax(dim=0) | |
| return ( # type: ignore | |
| (4 * phi_inv(N) + (1 / np.sqrt(split_size))) | |
| * o_norm | |
| * qk_norm | |
| * v_norm | |
| ) | |
| class LipschitzSelfAttn(nn.Module): | |
| def __init__(self, dim: int, num_heads: int, ln: bool = True, p_norm: str = "2", c: float = 1.0, p: float = 0.0): | |
| super().__init__() | |
| self.dim = dim | |
| self.num_heads = num_heads | |
| self.ln = ln | |
| self.c = c | |
| self.split_size = dim // num_heads | |
| self.fc_qk = nn.Linear(dim, dim, bias=False) | |
| self.fc_v = nn.Linear(dim, dim, bias=False) | |
| self.fc_o = nn.Linear(dim, dim, bias=False) | |
| self.dropout = nn.Dropout(p=p) | |
| if ln: | |
| self.ln_layer = nn.LayerNorm(dim) | |
| if p_norm not in ["2", "inf"]: | |
| raise ValueError(f"{p_norm=} must be one of [2, inf]") | |
| if self.dim % self.num_heads != 0: | |
| raise ValueError(f"{dim=} must be evenly divisible by {num_heads}") | |
| self.p_norm = p_norm | |
| self.upper_bound_F_func: Any = {"2": lip_2_upper_bound_F, "inf": lip_inf_upper_bound_F}[p_norm] | |
| self.upper_bound_f_func: Any = {"2": lip_2_upper_bound_f, "inf": lip_inf_upper_bound_f}[p_norm] | |
| def weight_norm(self, weight: T) -> T: | |
| if self.p_norm == "2": | |
| return weight_2_norm(weight, keepdim=True).sqrt() | |
| return weight_inf_norm(weight, keepdim=True) | |
| def norm_weights(self) -> None: | |
| with torch.no_grad(): | |
| qk_weight = head_split(self.fc_qk.weight.data.T, split_size=self.split_size, split_dim=-1) # (H, D, D/H) | |
| self.fc_qk.weight.data = torch.cat((qk_weight / self.weight_norm(qk_weight)).split(1, 0), -1).squeeze(0).T # (D, D) | |
| v_weight = head_split(self.fc_v.weight.data.T, split_size=self.split_size, split_dim=-1) # (H, D, D/H) | |
| self.fc_v.weight.data = torch.cat((v_weight / self.weight_norm(v_weight)).split(1, 0), -1).squeeze(0).T | |
| self.fc_o.weight.data = (self.fc_o.weight.data.T / self.weight_norm(self.fc_o.weight.data.T)).T | |
| def upper_bound_F(self, N: int) -> float: | |
| with torch.no_grad(): | |
| return float( | |
| self.upper_bound_F_func( | |
| N, | |
| qk_weight=self.fc_qk.weight.data.T, | |
| v_weight=self.fc_v.weight.data.T, | |
| o_weight=self.fc_o.weight.data.T, | |
| split_size=self.split_size | |
| ) | |
| ) | |
| def upper_bound_f(self, N: int) -> float: | |
| return float(self.upper_bound_f_func(N, qk_weight=self.fc_qk.weight.T, split_size=self.split_size)) | |
| def f(self, X: T, final: bool = False) -> T: | |
| # QK represents the queries and keys which are the same input and the same linear projection | |
| Q_ = K_ = head_split(self.fc_qk(X), split_size=self.split_size, split_dim=-1) # (H, B, N, D/H) | |
| A = head_split(self.fc_qk.weight.T, split_size=self.split_size, split_dim=1) # (H, D, D/H) | |
| A = (A @ A.mT) / np.sqrt(self.split_size) # (H, D, D) | |
| # using || a - b ||^2_2 = ||a||^2_2 - 2 a^T b + ||b||^2_2 | |
| # in equation 14 the b term is equivalent to transposing ||a||^2_2 | |
| a = (Q_ ** 2).sum(-1, keepdim=True).repeat(1, 1, 1, Q_.size(-2)) # || XW ||^2_row 1^T from eq. 14 # (H, B, N, N) | |
| atb = torch.einsum("...ij,...kj->...ik", Q_, K_) # XW(XW)^T from eq. 14 --> (H, B, N, N) | |
| P_ = torch.softmax((-(a - (2 * atb) + a.mT)) / np.sqrt(self.split_size), -1) # (H, B, N, N) | |
| # any transpose is irrelevant because A is symmetric | |
| XA = torch.einsum("bij,hjk->hbik", X, A) # (B, N, D) @ (H, B, D, D) -> (H, B, N, D) | |
| PXA = torch.einsum("hbij,hbjk->hbik", P_, XA) # (H, B, N, N) @ XA where XA is (H, B, N, D) --> (H, B, N, D) | |
| if final: | |
| return torch.cat(PXA.split(1, 0), -1).squeeze(0) # (B, N, D) | |
| return PXA # type: ignore | |
| def F(self, X: T) -> T: | |
| f = self.f(X) | |
| WV_ = head_split(self.fc_v.weight.T, split_size=self.split_size, split_dim=1) # (H, D/H, D) | |
| F = torch.einsum("hbij,hjk->hbik", f, WV_) # (H, B, N, D) @ (H, in_D, D/H).mT --> (H, B, N, D/H) | |
| F = torch.cat(F.split(1, 0), -1).squeeze(0) # (B, N, D) | |
| F = self.fc_o(F) | |
| return F # type: ignore | |
| def forward(self, X: T, normalize: bool = False) -> T: | |
| F = self.F(X) | |
| if normalize: | |
| F = F / self.upper_bound_F(X.size(1)) | |
| F = X + self.dropout(F) | |
| F = F if getattr(self, 'ln_layer', None) is None else self.ln_layer(F) | |
| return F | |
| if __name__ == "__main__": | |
| def simplified_upper(p: str, N: int) -> float: | |
| if p == "2": | |
| return np.sqrt(N) * np.log(N) # type: ignore | |
| return np.log(N) - np.log(np.log(N)) # type: ignore | |
| def matrix_2(jac: T, x: T) -> T: | |
| return (jac ** 2).sum(dim=(-1, -2)).sqrt() # type: ignore | |
| def matrix_inf(jac: T, x: T) -> T: | |
| return jac.abs().sum(dim=-1).amax() | |
| def op_2(jac: T, x: T) -> T: | |
| # Lemma F.5, second equation in the paper. for the single dimension case, this is the x^t J x | |
| return (((jac @ x) ** 2).sum() / (x ** 2).sum()).sqrt() # type: ignore | |
| # second to last part of Lemms F.5, this only holds for the single dimension case. It would have to be more | |
| # complicated in higher dimensions | |
| # return ((jac * x / x) ** 2).sum().sqrt() | |
| def op_inf(jac: T, x: T) -> T: | |
| return ((jac @ x) / (x ** 2).sum().sqrt()).abs().amax() # type: ignore | |
| getter = {"matrix-2": matrix_2, "matrix-inf": matrix_inf, "op-2": op_2, "op-inf": op_inf} | |
| gpu = torch.device("cuda:0") | |
| # for norm_type in ["matrix", "op"]: | |
| for norm_type in ["matrix"]: | |
| for p in ["2", "inf"]: | |
| data: Any = {"N": [], "bound": [], "type": []} | |
| # 2 == 1.88, 10 == 5.20, 100 == 12, 300 == ? | |
| for N, lr in zip((2, 10, 100, 300), (1e-2, 1e-2, 1e-1, 1e-1)): | |
| print(f"running {norm_type=} {p=} {N=}") | |
| jac_norm_func, dim, heads = getter[f"{norm_type}-{p}"], 1, 1 | |
| model = LipschitzSelfAttn(dim=dim, num_heads=heads, ln=False, p_norm=p).to(gpu) | |
| # model.norm_weights() | |
| for lyr in [model.fc_qk, model.fc_v, model.fc_o]: | |
| nn.init.ones_(lyr.weight) | |
| def func(X: T) -> T: | |
| return model.F(X.unsqueeze(0)).squeeze(0) | |
| ub_F, ub_f = model.upper_bound_F(N), model.upper_bound_f(N) | |
| max_jacnorm = 0.0 | |
| for _ in range(50): | |
| # set x according to appendix H in the paper | |
| c = torch.rand(N, dim) * 10 | |
| x = torch.rand(N, dim) * 2 * c - c | |
| x.requires_grad_(True) | |
| x_param = nn.Parameter(x.to(gpu)) | |
| opt = torch.optim.Adam([x_param], lr=lr) | |
| for i in range(500): | |
| jac = torch.autograd.functional.jacobian(func, x_param.squeeze(0), create_graph=True).view(N * dim, N * dim) | |
| x_ = x_param.view(-1, 1).squeeze(0) | |
| jacnorm = jac_norm_func(jac, x_) | |
| if i % 50 == 0: | |
| print(f"iteration: {i} {ub_F=} {ub_f=} simplified upper: {simplified_upper(p, N):.3f}") | |
| print(f"jacobian max: {jacnorm}") | |
| opt.zero_grad() | |
| (-jacnorm).backward() | |
| opt.step() | |
| if jacnorm.cpu().item() > max_jacnorm: | |
| max_jacnorm = jacnorm.cpu().item() | |
| for n, v in zip(["ub-f", "ub-F", "jacnorm"], [ub_f, ub_F, max_jacnorm]): | |
| data["N"].append(N) | |
| data["type"].append(n) | |
| data["bound"].append(v) | |
| fig, ax = plt.subplots(nrows=1, ncols=1) | |
| df = pd.DataFrame(data) | |
| sns.lineplot(data=df, ax=ax, x="N", y="bound", hue="type") | |
| fname = f"{norm_type}-{p}-{N}" | |
| df.to_csv(f"{fname}.csv") | |
| fig.savefig(f"{fname}.pdf") |
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
The above code gives values in line with figure 2 of the original paper for the infinity norm adversarially optimized to find the least upper bound of the norm of the Jacobian.
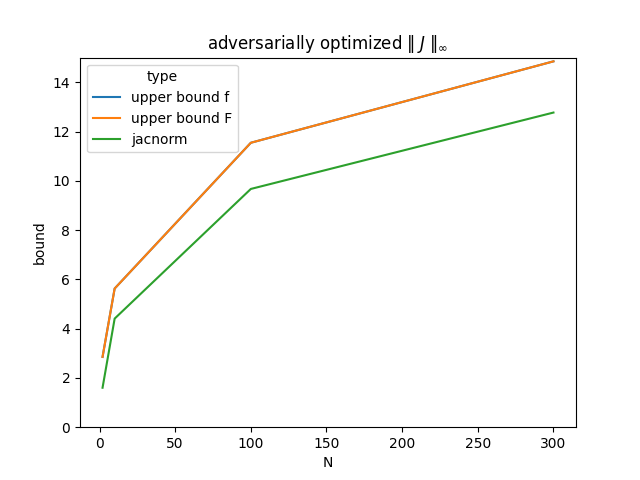
For the 2 norm (pictured in figure 8 of the paper), I had trouble getting the values to match what is depicted. If the y axis is the square root of the bound, then it starts to look correct....