Computer models can be tremendously useful in both exploring and visualizing the consequences of scientific hypotheses and comparing these predictions with data. New ideas and discoveries require new models.
In an ideal world, the necessary programming, testing, and debugging would be trivial, leaving us free to focus on the core science. In practice, however, high-quality scientific programming takes time.
Landlab was written to make the process of writing models more efficient by providing pre-built software and process components that handle many of the common tasks. The following tutorials give a flavor for what you can do with Landlab without having to reinvent the wheel. To try them out, you'll need to install Landlab.
In the first example, we will build a 2D model of the erosional degradation of a fault scarp through the process of linear diffusion. Conveniently, Landlab has a component that will calculate erosion rates due to linear diffusion, but in this example we do not take advantage of Landlab's pre-built diffusion component. After building this model without a component, we then contrast what the model would look like when using the pre-built component (see diffusion_model_with_components).
Note that >>> implies that we are on the command line in your favorite Python
frontend. We start by importing NumPy and Landlab's RasterModelGrid class:
>>> import numpy
>>> from landlab import RasterModelGridWe also need to import functions for plotting:
>>> from landlab.plot.imshow import imshow_node_grid
>>> from pylab import show, figureNext, we create a new raster grid with 40 columns, 25 rows, and a cell spacing of 10m:
>>> mg = RasterModelGrid(25, 40, 10.0)This line creates a grid object, mg. For this application, we want values of elevation, z, tied to each grid node. We can create such an array by calling the grid's add_zeros method:
>>> z = mg.add_zeros('node', 'elevation')add_zeros is one of many methods that belong to the grid object. As those familiar with object-oriented programming will recognize, a method is a function (a.k.a., subroutine) that is attached to a particular class, in this case the RasterModelGrid class. Here, the add_zeros method creates and returns a NumPy array of floating-point numbers whose length is equal to the number of nodes in the grid. We can test this by finding the length of the array:
>>> len(z)
1000As the name suggests, the value of each element in the array is initially zero. Let's create a fault scarp running diagonally across the domain by uplifting some of the grid nodes. To do this, we'll first create an array to represent the y-coordinate of the fault trace:
>>> fault_y = 50.0 + 0.25*mg.node_xHere node_x is a NumPy array containing the x-coordinate of each node.
Now, we uplift the portion of the domain where y > fault_y. We'll have this co-seismic uplift increase somewhat to the right:
>>> upthrown_nodes = numpy.where(mg.node_y>fault_y)
>>> z[upthrown_nodes] += 10.0 + 0.01*mg.node_x[upthrown_nodes]The numpy.where function finds and returns the array indices where the condition mg.node_y > fault_y is true; the resulting array upthrown_nodes contains the indices of the nodes whose elevation we want to raise. We then raise these elevations on the next line. Let's see what this looks like:
>>> imshow_node_grid(mg, z, cmap='jet', grid_units=['m','m'])
>>> show()imshow_node_grid() is part of the plotting functions that come with Landlab. We are sending imshow_node_grid the model grid and the values we want to plot, in this case z. We are specifying the colormap to be jet (red to blue) and that the units on the x and y axes are in meters. show() makes the plot pop-up on your screen.
The result looks like this:
Now we'll apply a diffusion model to calculate the degradation of the fault scarp. If you’ve taken a course in numerical computing, you may remember that an explicit solution to the diffusion equation requires time steps to be small; otherwise, the solution will become unstable (i.e., the numbers will go crazy and be meaningless). The Courant-Friedrichs-Lewy criterion states that the time step size must be smaller than Delta x^2 / K_d.
With that in mind, we start by setting a value for our diffusion coefficient, kd, and calculating a time-step size that is comfortably smaller than the maximum:
>>> kd = 0.01 # 0.01 m2 per year
>>> dt = 0.2*mg.dx*mg.dx/kd # CFL condition
>>> dt
2000.0For boundary conditions, we'll have fixed elevation values along the top and bottom sides, while the right and left sides will be no-flux boundaries. By default, all the grid edges are open boundary nodes, meaning that they are treated as fixed-elevation boundaries. To turn the right and left sides into no-flux boundaries, we use the set_closed_boundaries_at_grid_edges method:
>>> mg.set_closed_boundaries_at_grid_edges(False, True, False, True)This method allows you to specify whether each of the four grid edges—counter-clockwise from the bottom—should be closed, meaning that it is in effect a no-flux boundary.
We'll also need the ID numbers of those nodes that lie in the core of the grid, because these are the ones whose elevations we will want to iteratively update:
>>> interior_nodes = mg.get_core_nodes()This returns an array containing the ID numbers of all the core nodes (of which there are (25-2) x (40-2) = 874).
Next, we'll run 50,000 years (25 time steps) of scarp degradation. Here is our loop:
>>> for i in range(25):
... g = mg.calculate_gradients_at_active_links(z)
... qs = -kd*g
... dqsdx = mg.calculate_flux_divergence_at_nodes(qs)
... dzdt = -dqsdx
... z[interior_nodes] += dzdt[interior_nodes]*dtOur algorithm starts by calculating gradients at each of the active links, which are those that either connect two core nodes, or connect a core node with an open boundary node (top and bottom edges in this example). We then calculate the sediment fluxes associated with these links by using the transport law 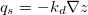
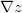
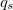
The next step is to add up the net sediment fluxes entering and leaving each cell in the grid. This is handled by a call to the grid's calculate_flux_divergence_at_nodes method. The result is the net volumetric sediment outflux per unit area for each node, which is our 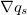
We do this operation on the next line. Finally, on the last line of the loop we calculate elevation changes (by multiplying dzdt by time-step size) and update the elevations of the interior nodes.
The following commands open a new figure window and show an image of the terrain after 50,000 years of hillslope diffusion:
>>> figure('elev_50ka')
>>> imshow_node_grid(mg, z, cmap='jet', grid_units=['m','m'])
>>> show()Here is the resulting image:
We now build the same exact model but we take advantage of Landlab's pre-built linear diffusion component.
Below is the entire code for the model which uses the pre-built linear diffusion component.
#Import statements so that you will have access to the necessary functions
import numpy
from landlab import RasterModelGrid
from landlab.components.diffusion.diffusion import LinearDiffuser
from landlab.plot.imshow import imshow_node_grid
from pylab import show, figure
#Create a raster grid with 25 rows, 40 columns, and cell spacing of 10 m
mg = RasterModelGrid(25, 40, 10.0)
#Create a field of node data (an array) on the grid called elevation.
#Initially populate this array with zero values.
z = mg.add_zeros('node', 'topographic__elevation')
#Check the size of the array
len(z)
#Create a diagonal fault across the grid
fault_y = 50.0 + 0.25*mg.node_x
upthrown_nodes = numpy.where(mg.node_y>fault_y)
z[upthrown_nodes] += 10.0 + 0.01*mg.node_x[upthrown_nodes]
#Illustrate the grid
imshow_node_grid(mg, 'topographic__elevation', cmap='jet', grid_units=['m','m'])
show()
#Instantiate the diffusion component:
linear_diffuse = LinearDiffuser(grid=mg, input_stream='./diffusion_input_file.txt')
#Set boundary conditions
mg.set_closed_boundaries_at_grid_edges(False, True, False, True)
#set a model timestep
#(the component will subdivide this as needed to keep things stable)
dt = 2000.
#Evolve landscape
for i in range(25):
linear_diffuse.diffuse(dt)
#Plot new landscape
figure()
imshow_node_grid(mg, 'topographic__elevation', cmap='jet', grid_units=['m','m'])
show()Let's go through the model with a component and compare it to the non-component version presented in the previous section.
The import statements are nearly the same, except that the model using a component has to import the LinearDiffuser class. In Landlab components are built as classes, which among other things, means that they can have both their own data and methods (methods are functions that are part of a class). The statement that imports the LinearDiffuser is repeated below:
>>> from landlab.components.diffusion.diffusion import LinearDiffuserIn this case the LinearDiffuser class is contained in a file called diffusion.py that is in the landlab/components/diffusion directory.
The code to create the raster grid (mg, an object of type RasterModelGrid), the elevation array z (or elevation field on mg), and the scarp across the landscape are all the same between the two models. Similarly, the plotting is the same between the two models.
Because the model is using the LinearDiffuser class, the code must instantiate a member of the class, or make an object of type LinearDiffuser. That step is repeated below, where linear_diffuse is an object of type LinearDiffuser.
>>> linear_diffuse = LinearDiffuser(grid=mg, input_stream='./diffusion_input_file.txt')Note that in order to initialize an object of type LinearDiffuser, a grid object must be passed, as well as an input file. If you downloaded the example code, you should also have a copy of diffusion_input_file.txt. Here is what it contains:
linear_diffusivity: in m2 per year 0.01
In this case linear_diffusivity, is a target phrases (targets for short, and there can be no spaces in a target) that Landlab is looking for in the input file when intializing an object of type LinearDiffuser. The Landlab code will read through the input file and look for each required target. Once that target is found, it ignores the text on the rest of the line (so anything following the target on the same line is a comment), and takes the value for the parameter associated with the target from the next line of text.
Note that in the model without a component, we calculated a stable dt in the model. With the component, the testing of timestep stability happens automatically, and the component will internally subdivide the timestep as necessary. Finally, the diffusion model takes the name of the grid node field that it will be diffusing. In this case, we have already added the field topographic__elevation to the code and we would like to diffuse elevation values. The component looks for a field called topographic__elevation by default, and this is why we chose this field name (though equally, we could have chosen a different field name and overridden the default in the component). You can imagine that one might use the diffusion code in a very different way, say to calculate heat transfer, and in that case we could have declared a different field name using the 'values_to_diffuse' target phrase. Setting the boundary conditions is the same between the two models.
The evolution loop in the model with the component is much shorter than the loop in the model without the component. In this case all that is needed is to call the diffuse method of the LinearDiffuser class:
>>> linear_diffuse.diffuse(dt)The diffuse method essentially does everything that was typed out explicitly in the first example. Note that because the elevation data are a field on the grid, those data do not need to be passed to the method.
Plotting the final landscape is the same between the two models and the result should be exactly the same.