Bayesian linear regression with polynomial basis functions

0.notes.md

Srry, this is a bit of an awkward format. I might move this and a few other demos to a repo.

This is code one could drop into Jupyter [1] notebook cells and draw some wicked-looking graphs. I wrote it to understand Bayesian linear regression (for this classMLPR, specifically this and this). No promises that I did it perfectly.

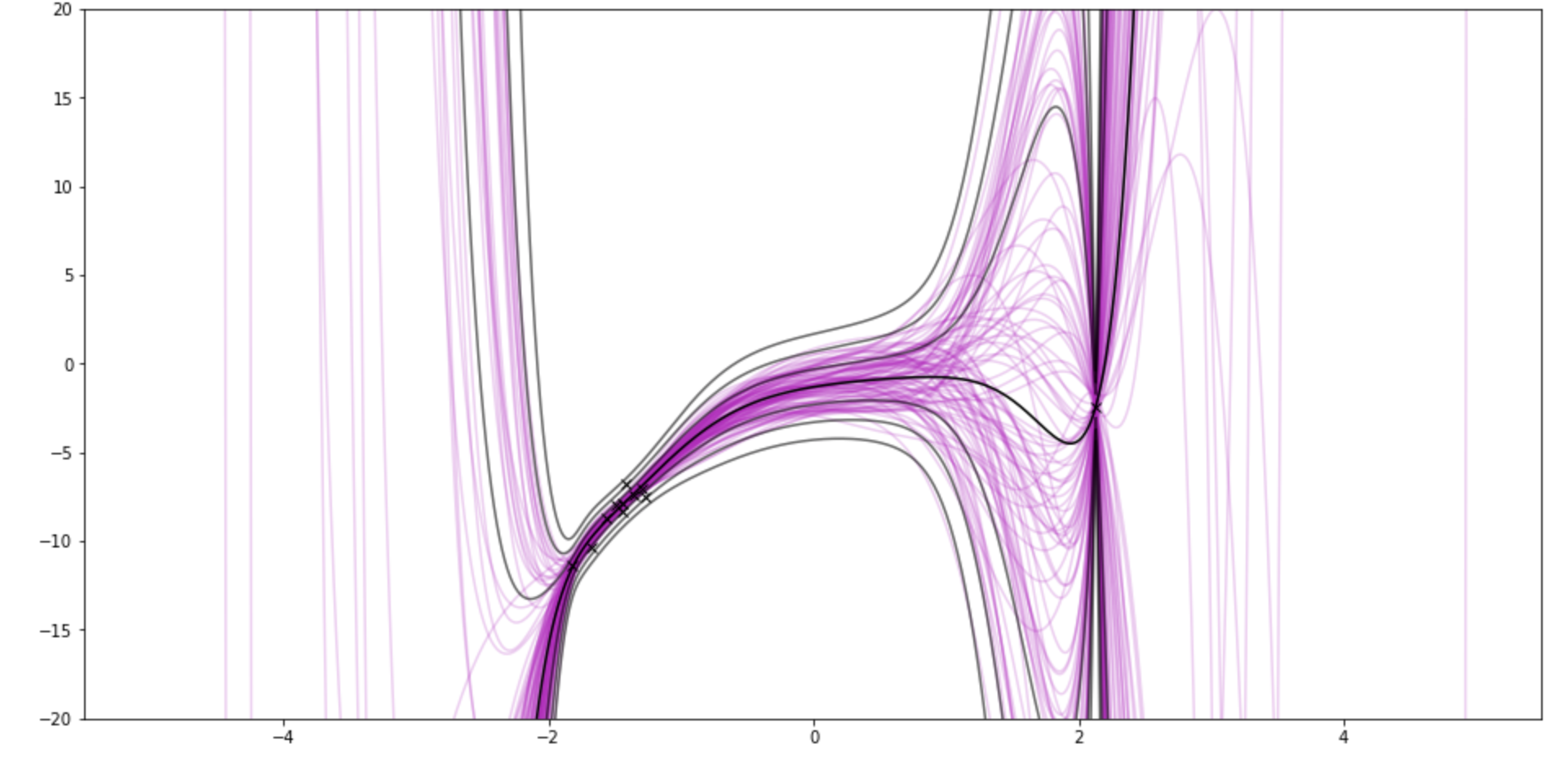
The graphs show samples from the posterior weights in pink. The black lines kinda show the posterior distribution P(y|data) by drawing lines for standard deviations away from the mean. So it goes through the points on the x-axis, asks P(y|data) for the value and uncertainty

It uses polynomial basis functions, because they are sqiggly and cool-looking.

• model_params=3 matches the underlying function (and the right noise variance sigma_y is already set)
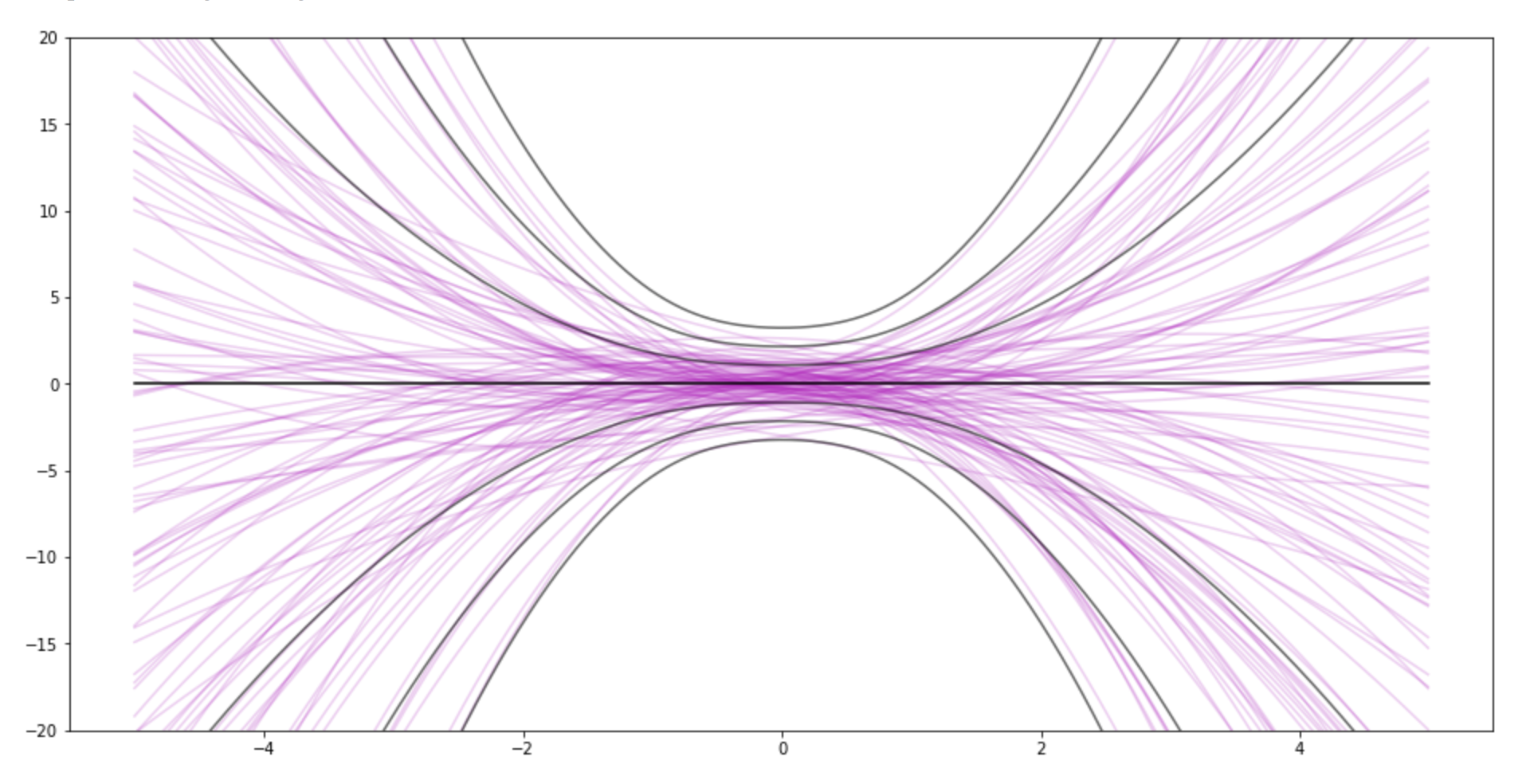
• If you set "sample size" to 0, you can see the prior. Then try messing with sigma_w. This demo uses the same sigma_w for all weights. You can also see the impact of the prior after data.
• For fun, I sample from two regions of the underlying function. So try going from sample_size 10 to 11.
  • If you set the "model–params" (number of coefficients) to 10 and sample size to 11, it pinches around the brand new point.

[1] with matplotlib, numpy, scipy

generate_data.py

import matplotlib.pyplot as plt
import numpy as np
from ipywidgets import interact, interact_manual
from scipy.linalg import cholesky
from scipy.stats import multivariate_normal

# weights for the underlying function
real_w = np.vstack((0.5, 3, -2))


def generate_noisy_samples(sample_size, actual_sigma_y, real_w):

    # sample sample_size points between -2, 2
    #X_in = np.random.rand(sample_size, 1) * 4 - 2
    # sample approx sample_size points near -2 and 2
    X_in = np.vstack((
        np.random.rand(int(sample_size / 2), 1) - 2,
        np.random.rand(int(sample_size / 2), 1) + 2
    ))

    f = np.hstack(X_in**i for i in range(len(real_w))) @ real_w
    noise = actual_sigma_y * np.random.randn(X_in.shape[0], 1)

    y = f + noise
    assert y.shape == (sample_size, 1)

    return X_in, y


all_X_in, all_y = generate_noisy_samples(
    sample_size=20,
    actual_sigma_y=.4,
    real_w=real_w,
)

plot.py

N = 100  # number of lines

grid_size = 0.01
x_grid = np.arange(-5, 5, grid_size)


def plot_example(model_params, sample_size, sigma_w):
    # For fun graphics, we use the first `sample_size` points.
    X_in = all_X_in[:sample_size]
    y = all_y[:sample_size]

    # Set our guesses of sigma
    #sigma_w = 1  # weights
    sigma_y = .4  # noisy observations

    # Set up the prior
    w_0 = np.tile(0, (model_params, 1))
    V_0 = sigma_w**2 * np.identity(model_params)

    # Compute phi for our X_in
    Phi_X_in = np.hstack(X_in**i for i in range(model_params))

    # Now compute the posterior, just reading off the formula
    V0_inv = np.linalg.inv(V_0)

    V_n = sigma_y**2 * np.linalg.inv(sigma_y**2 * V0_inv + (Phi_X_in.T @ Phi_X_in))
    w_n = V_n @ V0_inv @ w_0 + 1 / (sigma_y**2) * V_n @ Phi_X_in.T @ y
    assert w_n.shape == (model_params, 1)

    # Now let's draw!

    # Now we're ready to start plotting.
    # This is the X for the entire grid
    X = np.vstack(x_grid**i for i in range(model_params)).T

    plt.clf()
    plt.figure(figsize=(16, 8))

    # here are some posterior lines
    w = np.random.multivariate_normal(mean=w_n.flatten(), cov=V_n, size=N)
    plt.plot(x_grid, X @ w.T, '-m', alpha=.2)

    # here's the mean
    plt.plot(x_grid, X @ w_n, '-w')

    # How curvey can this be?
    var_post = np.sum(np.dot(X, V_n) * X, 1)[:, None] + sigma_y**2
    for k in np.arange(1, 4):
        plt.plot(x_grid, X @ w_n + k * np.sqrt(var_post), '-', color='0.2')
        plt.plot(x_grid, X @ w_n - k * np.sqrt(var_post), '-', color='0.2')

    # here is the prior
    #plt.plot(x_grid, X @ w_0, '-g')

    # here's f
    #plt.plot(x_grid, np.vstack([x_grid**i for i in range(len(real_w))]).T @ real_w, '-b')

    # here is samples
    plt.plot(X_in, y, 'xk')

    # here are the points used in the posterior
    plt.ylim([-20, 20])
    plt.show()


interact(
    plot_example,
    model_params=(1, 10),
    sample_size=(0, 20),
    sigma_w=(0.1, 3),
    continuous_update=False,
)

This is the prior for 3 weights (quadratic)

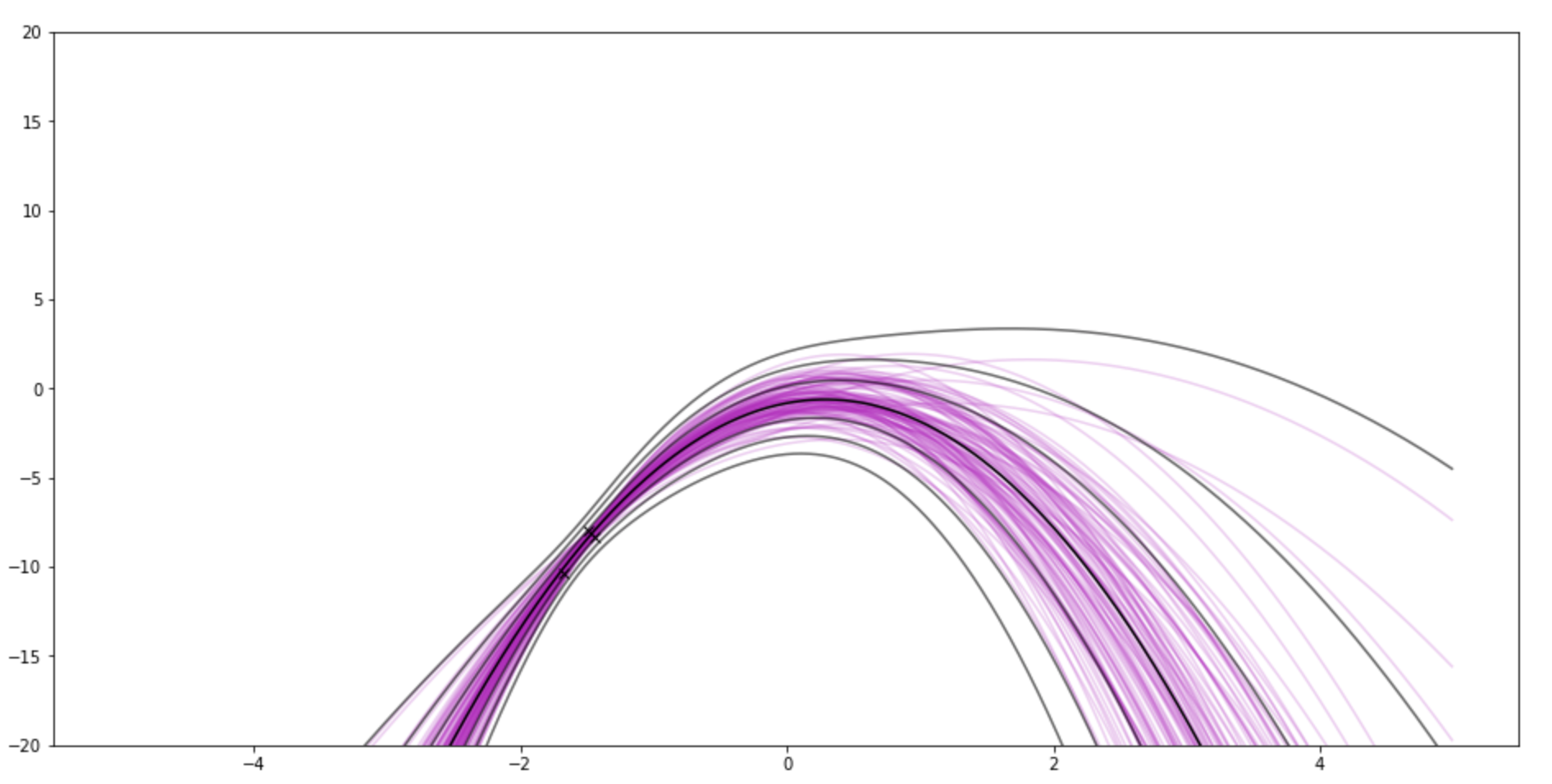
After 3 observations. There's still a little lump around 0.

After 11:

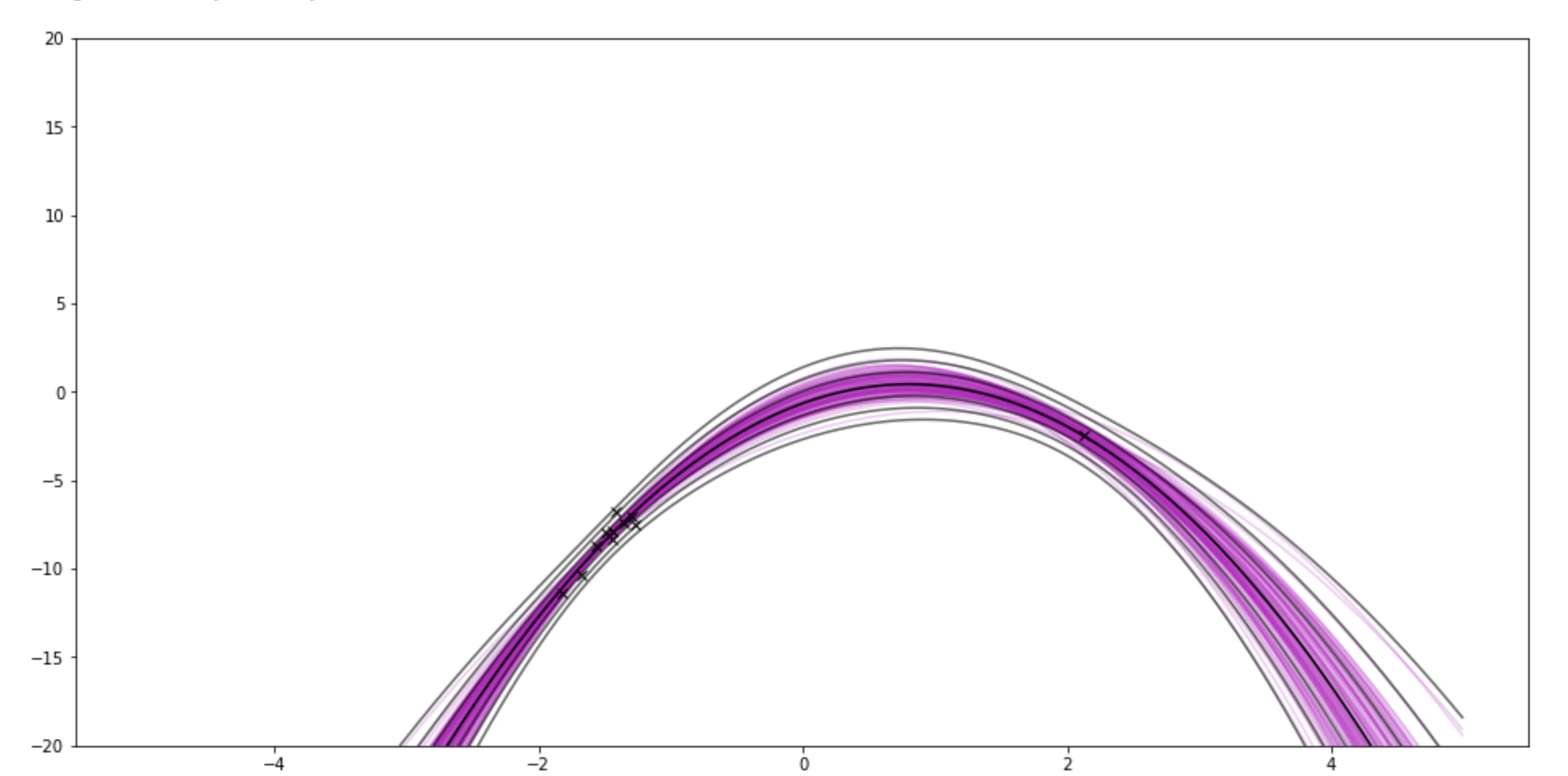
If I use 9-degree polynomial, and show 11 samples (10 from one side, 1 from another side)