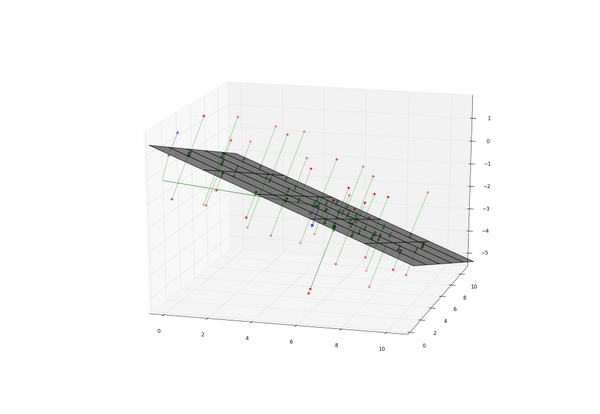
n-dimensional hyperplane (line for 2D, plane for 3D) fitting via singular value decomposition method

README.markdown

n-dimensional hyperplane (line for 2D, plane for 3D) fitting via singular value decomposition method

standard_fit.py

#!/usr/bin/env nosetests -vs
# coding=utf-8
"""
Linear algebra standard fitting module

(C) 2013 hashnote.net, Alisue
"""
__author__  = 'Alisue ([email protected])'
__version__ = '0.1.0'
__date__    = '2013-10-28'
__all__ = ['standard_fit', 'projection', 'distance', 'function']

import numpy as np

def standard_fit(X):
    """
    Find (n - 1) dimensional standard (e.g. line in 2 dimension, plane in 3
    dimension, hyperplane in n dimension) via solving Singular Value
    Decomposition.

    The idea was explained in the following references

    - http://www.caves.org/section/commelect/DUSI/openmag/pdf/SphereFitting.pdf
    - http://www.geometrictools.com/Documentation/LeastSquaresFitting.pdf
    - http://www.ime.unicamp.br/~marianar/MI602/material%20extra/svd-regression-analysis.pdf
    - http://www.ling.ohio-state.edu/~kbaker/pubs/Singular_Value_Decomposition_Tutorial.pdf

    Example:
        >>> XY = [[0, 1], [3, 3]]
        >>> XY = np.array(XY)
        >>> C, N = standard_fit(XY)
        >>> C
        array([ 1.5,  2. ])
        >>> N
        array([-0.5547002 ,  0.83205029])

    Args:
        X: n x m dimensional matrix which n indicate the number of the dimension
            and m indicate the number of points

    Returns:
        [C, N] where C is a centroid vector and N is a normal vector
    """
    # Find the average of points (centroid) along the columns
    C = np.average(X, axis=0)
    # Create CX vector (centroid to point) matrix
    CX = X - C
    # Singular value decomposition
    U, S, V = np.linalg.svd(CX)
    # The last row of V matrix indicate the eigenvectors of
    # smallest eigenvalues (singular values).
    N = V[-1]
    return C, N

def projection(x, C, N):
    """
    Create orthogonal projection matrix of x on the plane

    Args:
        x: n x m dimensional matrix
        C: n dimensional vector whicn indicate the centroid of the standard
        N: n dimensional vector which indicate the normal vector of the standard

    Returns:
        n x m dimensional matrix which indicate the orthogonal projection points
        on the plane
    """
    rows, cols = x.shape
    NN = np.tile(N, (rows, 1))
    D = distance(x, C, N)
    DD = np.tile(D, (cols, 1)).T
    return x - DD * NN

def distance(x, C, N):
    """
    Calculate an orthogonal distance between the points and the standard

    Args:
        x: n x m dimensional matrix
        C: n dimensional vector whicn indicate the centroid of the standard
        N: n dimensional vector which indicate the normal vector of the standard

    Returns:
        m dimensional vector which indicate the orthogonal disntace. the value
        will be negative if the points beside opposite side of the normal vector
    """
    return np.dot(x-C, N)

def function(x, C, N):
    """
    Calculate an orthogonal projection of the points on the standard

    Args:
        x: (n-1) x m dimensional matrix
        C: n dimensional vector whicn indicate the centroid of the standard
        N: n dimensional vector which indicate the normal vector of the standard

    Returns:
        m dimensional vector which indicate the last attribute value of
        orthogonal projection
    """
    Ck = C[0:-1]    # centroid for known parameters
    Nk = N[0:-1]    # normal for known parmeters
    Cu = C[-1]      # centroid for unknown parameter
    Nu = N[-1]      # normal for unknown parameter
    return np.dot(x-Ck, Nk) * -1.0 / Nu + Cu

#===============================================================================
#
# Unittest
#
#===============================================================================
if __name__ == '__main__':
    import doctest; doctest.testmod()

test_standard_fit.py

#!/usr/bin/env nosetests -vs
# coding=utf-8
"""

(C) 2013 hashnote.net, Alisue
"""
__author__  = 'Alisue ([email protected])'
__version__ = '0.1.0'
__date__    = '2013-10-28'

import random
import numpy as np
from functools import wraps
from functools import partial
from nose.tools import *
from nose.plugins.attrib import attr
from testconfig import config

import standard_fit

def multi(default_runs=1):
    def inner(fn):
        @wraps(fn)
        def wrapper(*args, **kwargs):
            for i in range(int(config.get('runs', default_runs))):
                fn(*args, **kwargs)
        return wrapper
    return inner

def multi_dimensional(dimension=9):
    def inner(fn):
        for d in range(1, dimension+1):
            @wraps(fn)
            def wrapper(d=d, *args, **kwargs):
                fn(*args, dimension=d, **kwargs)
            wrapper.__name__ += "_%dd" % d
            globals()[wrapper.__name__] = wrapper
    return inner

def cosine(a, b):
    """
    Calculate cosine similarity of two vectors

    Args:
        a: n dimensional vector A
        b: n dimensional vector B

    Returns:
        cosine value which 1, -1, and 0 indicates a) completely same direction,
        b) completely opposite direction, and c) orthgonal direction
        respectively.
    """
    norma = np.linalg.norm(a)
    normb = np.linalg.norm(b)
    return np.dot(a, b) / (norma * normb)

@multi_dimensional(9)
@multi(10)
@attr(matplotlib=False)
def test_standard_fit(dimension):
    # define true parameters and function
    N = np.random.rand(dimension)
    N = N / np.linalg.norm(N)
    C = np.random.rand(dimension)
    F = partial(standard_fit.function, C=C, N=N)
    E = (np.random.rand(50) - 0.5) * 0.01
    NN = np.tile(N, (50, 1))
    EE = np.tile(E, (dimension, 1)).T

    # create corresponding points with some error
    e = np.random.normal(size=50) * 0.01
    xy = np.random.rand(50, dimension-1)
    xyz = np.c_[xy, F(xy) + e]
    # shift xyz along N vector
    xyz = xyz + EE * NN

    # run standard_fit
    c, n = standard_fit.standard_fit(xyz)
    f = partial(standard_fit.function, C=c, N=n)

    # normal vector similarity check
    similarity_n = cosine(n, N)
    ok_(abs(similarity_n) > 0.99,
            "similarity_n (%f) is lower than threshold" % abs(similarity_n))

@multi_dimensional(9)
@multi(10)
@attr(matplotlib=False)
def test_function(dimension):
    # define true parameters and function
    N = np.random.rand(dimension)
    N = N / np.linalg.norm(N)
    C = np.random.rand(dimension)
    F = partial(standard_fit.function, C=C, N=N)

    # create corresponding points with some error
    xy = np.random.rand(50, dimension-1)
    xyz = np.c_[xy, F(xy)]

    # run standard_fit
    c, n = standard_fit.standard_fit(xyz)
    f = partial(standard_fit.function, C=c, N=n)

    xyz_signal = np.c_[xy, F(xy)]
    xyz_fitted = np.c_[xy, f(xy)]

    np.testing.assert_array_almost_equal(
            xyz_signal, xyz_fitted, decimal=6)

@multi_dimensional(9)
@multi(10)
@attr(matplotlib=False)
def test_distance(dimension):
    # define true parameters and function
    N = np.random.rand(dimension)
    N = N / np.linalg.norm(N)
    C = np.random.rand(dimension)
    F = partial(standard_fit.function, C=C, N=N)
    E = (np.random.rand(50) - 0.5) * 0.01
    NN = np.tile(N, (50, 1))
    EE = np.tile(E, (dimension, 1)).T

    # create corresponding points with some error
    xy = np.random.rand(50, dimension-1)
    xyz = np.c_[xy, F(xy)]
    # shift xyz along N vector
    xyz = xyz + EE * NN

    # run standard_fit
    c, n = standard_fit.standard_fit(xyz)

    D = standard_fit.distance(xyz, C, N)
    np.testing.assert_array_almost_equal(
            D, E, decimal=6)

    d = standard_fit.distance(xyz, c, n)
    np.testing.assert_array_almost_equal(
            D, d, decimal=1)

@multi_dimensional(9)
@multi(10)
@attr(matplotlib=False)
def test_projection(dimension):
    # define true parameters and function
    N = np.random.rand(dimension)
    N = N / np.linalg.norm(N)
    C = np.random.rand(dimension)
    F = partial(standard_fit.function, C=C, N=N)
    E = (np.random.rand(50) - 0.5) * 0.01
    NN = np.tile(N, (50, 1))
    EE = np.tile(E, (dimension, 1)).T

    # create corresponding points with some error
    xy = np.random.rand(50, dimension-1)
    xyz = np.c_[xy, F(xy)]
    # shift xyz along N vector
    xyz = xyz + EE * NN

    # run standard_fit
    c, n = standard_fit.standard_fit(xyz)

    projected = standard_fit.projection(xyz, c, n)

    PC = projected - c
    for i, pc in enumerate(PC):
        dot = np.dot(pc, n)
        np.testing.assert_almost_equal(dot, 0)

    distances = standard_fit.distance(xyz, c, n)
    for x, p, d in zip(xyz, projected, distances):
        norm = np.linalg.norm(p - x)
        np.testing.assert_almost_equal(norm, abs(d))

try:
    import matplotlib.pyplot as pl
    from mpl_toolkits.mplot3d import Axes3D
 
    def extend_plt3d(plt3d):
        def draw_vector(p1, p2, *args, **kwargs):
            from matplotlib.patches import FancyArrowPatch
            from mpl_toolkits.mplot3d import proj3d
            class Arrow3D(FancyArrowPatch):
                def __init__(self, xs, ys, zs, *args, **kwargs):
                    FancyArrowPatch.__init__(self, (0,0), (0,0), *args, **kwargs)
                    self._verts3d = xs, ys, zs
                    self._verts3d = [x.flatten() for x in self._verts3d]
                def draw(self, renderer):
                    xs3d, ys3d, zs3d = self._verts3d
                    xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)
                    self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
                    FancyArrowPatch.draw(self, renderer)
            xs = np.array([p1[0], p2[0]])
            ys = np.array([p1[1], p2[1]])
            zs = np.array([p1[2], p2[2]])
            plt3d.add_artist(Arrow3D(xs, ys, zs, *args,
                mutation_scale=20, arrowstyle="-|>", **kwargs))
        setattr(plt3d, 'vector', draw_vector)
        return plt3d
 
    def create_vector(top, tail=(0, 0, 0)):
        return np.array([tail, top])

    def rotate(vector, normal, theta):
        x, y, z = normal
        R = np.array([
            [0, -z, y],
            [z, 0, -x],
            [-y, x, 0],
        ])
        I = np.identity(3)
        M = I + np.sin(theta) * R + (1 - np.cos(theta)) * np.dot(R, R)
        return np.dot(M, vector)

    @attr(matplotlib=True)
    def test_plot_standard_plane():
        scale = 10
        # define true parameters and function
        O = np.array([0, 0, 0])
        N = np.random.rand(3)
        N = N / np.linalg.norm(N)
        C = np.random.rand(3)
        F = partial(standard_fit.function, C=C, N=N)
        E = (np.random.rand(50) - 0.5) * scale / 2
        NN = np.tile(N, (50, 1))
        EE = np.tile(E, (3, 1)).T

        # create corresponding points with some error
        xy = np.random.rand(50, 2) * scale
        xyz = np.c_[xy, F(xy)]
        # shift xyz along N vector
        xyz = xyz + EE * NN

        # run standard_fit
        c, n = standard_fit.standard_fit(xyz)

        # projection
        prj = standard_fit.projection(xyz, c, n)

        # find farthest point
        norms = np.apply_along_axis(np.linalg.norm, 1, prj - c)
        ind = np.argmax(norms)
        farthest = prj[ind]

        # find surface minimum and maximum value of each axis
        p1 = rotate(farthest - c, n, np.pi/4) + c
        ps = np.array([
            p1,
            rotate(p1 - c, n, np.pi/2) + c,
            rotate(p1 - c, n, np.pi) + c,
            rotate(p1 - c, n, -np.pi/2) + c,
        ])
        pmin = np.min(ps, axis=0)
        pmax = np.max(ps, axis=0)
        xmin, xmax = pmin[0], pmax[0]
        ymin, ymax = pmin[1], pmax[1]
        zmin, zmax = pmin[2], pmax[2]

        # create surface grid
        zf = lambda x, y: (n[0]*(x-c[0])+n[1]*(y-c[1])) * -1.0 / n[2] + c[2]
        mgx, mgy = np.meshgrid(
                np.linspace(xmin, xmax),
                np.linspace(ymin, ymax),
            )
        mgz = zf(mgx, mgy)

        # draw
        plt3d = pl.subplot(111, projection='3d')
        plt3d = extend_plt3d(plt3d)

        plt3d.scatter(*np.hsplit(xyz, 3), color='r')
        plt3d.scatter(*np.hsplit(prj, 3), color='g')
        plt3d.plot_surface(mgx, mgy, mgz, color="k", alpha=0.5)

        plt3d.vector(O, c, color='g')
        plt3d.vector(O, C, color='g', alpha=0.5)
        plt3d.vector(c, n+c, color='b')
        plt3d.vector(C, N+C, color='b', alpha=0.5)

        for o, p in zip(xyz, prj):
            plt3d.vector(o, p, color='g', alpha=0.5)

        pl.show()
except ImportError:
    pass