Polymers As Structure Directing Agents
Generalizing the Concept of an SDA
1. Isohedral Tiles are SDAs that Program Symmetry
2. 2D Math in a 3D World
3. Different Self-Assembly Characteristics
  1. Row 5: Gyrations (ABC)
  2. Row 4: Kaleidoscopes (*abc)
  3. Row 3: Gyroscopes (A*bc)
  4. Row 2: Frieze
  5. Row 1: Pluripotence
Conclusions
References

tl;dr

Structure directing agents (SDA) are typically small molecules added during the synthesis of materials which control their growth; for example, by templating channels and controlling aspect ratios in zeolites. However, SDAs can more broadly be envisioned as any additive which tunes, or even fully programs, the assembly of some structure. Under this definition, chaperones could be considered SDAs for protein folding.

In this body of work we reconsider the role of additives in colloidal systems which serve such a role in tuning the colloid's (self-)assembly (text available upon request if you cannot access them):

Refs. 5 and 7 are essentially reviews of the first part of this work, which the interested reader should refer to.

Colloidal materials generally derive their utility from how their constituents are arranged, rather than from the chemistry of what they are made of, so SDAs are particular useful for engineering these systems. Generally, colloidal systems rely on top-down or bottom-up assembly strategies. Top-down approaches, such as lithography, are often limited "below" by resolution limits and/or "above" by scalability concerns. Bottom-up strategies, like tuning the surface chemistry or shape of the colloid, require that the colloid itself be mutable. But what if we wish to make a material out of proteins, antibodies, or quantum dots? The chemistry of these building blocks can impart (desired) functionality to the final material, but not necessarily if the modifications to these colloids necessary to program their self-assembly are too severe. Moreover, practical issues involving synthesis also limit experimental realization.

SDAs represent a third assembly paradigm. The SDA is essentially a separate assembly machine that we program instead of the parts themselves.

Many of the graphics below have been presented at scientific conferences including:

"Stabilizing colloidal crystals by leveraging void distributions," N. A. Mahynski, A. Z. Panagiotopoulos, D. Meng, S. K. Kumar, American Institute of Chemical Engineers Annual Meeting, Atlanta, GA USA (11/2014).
"Entropic control over nanoscale colloidal crystals," N. A. Mahynski, S. K. Kumar, A. Z. Panagiotopoulos, Thermodynamics, Copenhagen, Denmark (09/2015).
"Structure-directing soft matter agents: a new twist on colloidal crystal assembly," N. A. Mahynski, Condensed Matter Theory Seminar, Johannes Gutenburg University am Mainz, Mainz Germany (06/2016).
"Entropic control over nanoscale colloidal crystals," N. A. Mahynski, S. K. Kumar, A. Z. Panagiotopoulos, American Institute of Chemical Engineers Annual Meeting, San Francisco, CA USA (11/2016).
"Polymer-mediated polymorphic control over open colloidal crystals," N. A. Mahynski, L. Rovigatti, C. N. Likos, A. Z. Panagiotopoulos, American Institute of Chemical Engineers Annual Meeting, San Francisco, CA USA (11/2016).
"Self-Assembly templates for two-dimensional colloidal crystals derived from symmetry," N. A. Mahynski, V. K. Shen, American Institute of Chemical Engineers Annual Meeting, Boston, MA USA (11/2021).

Please cite appropriately if you find this material to be helpful.

Polymers As Structure Directing Agents

Let's begin by drawing an analogy between conventional small-molecule SDAs in "hard matter" and larger molecules in "soft matter".

The Depletion Force

The "depletion force" is an effective attraction that arises in colloidal solutions when a (generally smaller) "depletant" is excluded between two approaching surfaces. For example, if two hard spheres are diffusing freely in a solvent and a small polymer is added, then when the spheres approach each other they begin to exclude the polymer from existing between them. This creates an osmotic "vacuum" which pulls the spheres together. More generally, this is regarded as an entropic effect where the polymer gains translational entropy due to the aggregation of the colloids. This is because when the colloids approach each other, the volume around their surface that normally excludes the polymer becomes shared, thus "releasing" some net volume into the surrounding medium for the polymer to exist in.

The first observation of depletion is generally attributed to reports on the "creaming" of rubber latex particles upon the addition of polysaccharides. Depletion plays a role in organizing materials in crowded environments, such as biological cells, and can be used to rationally design interactions between colloidal particles of different shapes. Askaura and Oosawa were the first to produce an explanation of the phenomenon in the 1950s and provided a standard expression for the effective interaction between colloids following the first explanation:

$W_{\rm dep}(h) = -PV_{\rm ov}(h)$,

where $P$ is the osmotic pressure of the polymer depletant and $V_{\rm ov}$ is the overlap (lense) volume which can be computed from intersecting spheres. The range of depletion is given by $\delta$. For dilute polymer solutions this is typically the polymer's radius of gyration, but depending on the system there can be more complicated expressions. This simple expression is valid for small polymers when the surface-surface distance, $h$, is such that $0 \le h \le 2\delta$; formally, $W_{\rm dep}(h) = \infty$ if $h < 0$, and $W_{\rm dep}(h) = 0$ if $h > 2\delta$. Typically, $P$, is approximated assuming the polymer solution is ideal so that $P = n_b k_{\rm B}T$, where $T$ is the temperature, $k_{\rm B}$ is Boltzmann's constant, and $n_b$ is the number density of polymers. Thus, we have:

$\frac{U_{\rm AO}(h)}{k_{\rm B}T} = -n_b \frac{\pi}{6} (2\delta-h)^2(3R+2\delta+h/2)$,

where the (spherical) colloid has radius $R$. Increasing the polymer density increases the effective attraction which can induce fluid phase separation, and even crystallization, of the colloids.

Some statisical mechanics help explain the entropy interpretation of depletion. Consider a system with volume, $V$, of $N$ colloids in equilibrium with a reservoir of ideal polymer chains with fugacity, $z ={\rm exp}(\beta \mu_{\rm poly})$, where $\beta = 1/k_{\rm B}T$. For a given microstate of the system in which the colloid positions are defined by $\vec{r}^N$, the partition function of a single polymer chain is given by the total number of accessible conformations, $\Omega(\vec{r}^N; V)$. Since the polymers are ideal (non-interacting) the canonical partition function for $M$ polymers is

$Q = \frac{\left[\Omega(\vec{r}^N; V)\right]^M}{M!}$.

We can write the semigrand partition function for the entire system as:

$\Upsilon (N, z, V) = \int_V^{} {\rm exp} \left( -U_{\rm HS}(\vec{r}^N) \right) \times \sum_{M=0}^{\infty} {\rm exp} \left( M \beta \mu_{\rm poly} \right) Q d{\rm \vec{r}}^N$.

Recalling the Maclaurin series expansion of the exponential function, we may re-write this as:

$\Upsilon (N, z, V) = \int_V^{} {\rm exp} \left( -U_{\rm HS}(\vec{r}^N) + z\Omega(\vec{r}^N; V) \right) ~d{\rm \vec{r}}^N $.

This means $\Upsilon (N, z, V)$ can also be interpreted as the canonical partition function for a one-component system of colloids where the polymer fugacity sets the effective attraction strength:

$ U_{\rm eff}(\vec{r}^N) = U_{\rm HS}(\vec{r}^N) - z\Omega(\vec{r}^N; V)$.

This is a general expression which clearly articulates the connection between a polymer's accessible configuration space, $\Omega(\vec{r}^N; V)$, and the effective colloidal interaction.

The Difference Between FCC and HCP

At high polymer concentration the depletion force drives colloids to aggregate into the tightest packing possible because it releases the most net volume into the bulk for the polymer. For isotropic spheres of equal size, the highest packing as conjectured by Kepler and later proven by Hales is about 74%. However, this packing may be obtained in two different crystals: the face-centered cubic (FCC) or the hexagonal close-packed (HCP) structure. Both begin the same way. Start with a hexagonal packing of the plane then stack a copy on top of that layer so that spheres in the top layer "nest" in cavities formed by those in the lower layer. This will cover half of the "holes" you can see looking from the top down. The FCC is formed by placing a third layer to cover up the other holes which creates 3 uniquely positioned layers ("ABC"); this triplet is repeated to grow the crystal (ABCABCABC...). If the other half of the holes are not covered we obtain a repeating "ABABAB" pattern instead, which leads to the HCP structure. Of course, random choices for these layers can also be made which still result in close-packing ("ABCBABCB..."), however, they are non-crystalline.

If a polymer depletant drives the solidification of equally sized colloids, then it would seem that the above packings would be equally suitable from the polymer's perspective. However, due to slight differences in vibrational entropy, in single-component systems of hard spheres the FCC is marginally more stable than the HCP, though its magnitude was debated. In the end, the free energy difference was found to be roughly 0.001 $k_{\rm B}T$ per sphere lower in the FCC than the HCP. Experiments on hard spheres usually produce a mixture of different packings, which led to the conclusion that in principle, the FCC is always more stable than the HCP, but due to kinetic limitations and possibly gravity, the systems tend to form a random close-packed set of layers.

Consequently, the same conclusion was drawn for colloid-polymer mixtures. Importantly, this is premised on understanding the binary mixture as an effectively one-component system of attractive colloids, rather than as a two component system of mutually repulsive colloids and polymers. This follows the AO model of depletion; however, as it turns out, assumptions in the AO model can make this conclusion incorrect!

The Details of the Polymer Matter

In fact, when the polymer is sufficiently large, the HCP can be stabilized over the FCC. The reason for this has to do with the void structure of the two competing crystals. The interstices of both polymorphs can be described as forming either tetrahedral voids (TV) or octahedral voids (OV); these shapes can be obtained by connecting nearest neighbor colloid centers of mass into a platonic solid around the center of each void. The FCC and HCP have an identical number of voids per colloid (in a ratio of 2:1, TV:OV), however, they are arranged differently.

In the FCC crystal each OV is completely surrounded by TVs, whereas in the HCP, the OVs (and TVs) are arranged in "columns" where they stack on top of each other. When depletion-driven (first order) phase separation occurs in a colloid-polymer mixture, the two components asymmetrically distribute themselves. In crystallization, the solid phase contains mostly colloids with a few polymers, and the other colloidal "gas" phase is the reverse of this. Previously, the critical assumption was that the small amount of polymer in the crystal does not matter; since the AO model turns the system into an effectively one-component system it is easy to see why this seems reasonable.

However, we found that the small amount of polymer inside the crystal does make a significant difference. This is because it samples the solid's void space and its free energy is directly related to the arrangement of the voids. An OV is much larger than a TV and has roughly 6 times the accessible volume. So when a polymer partitions into the colloidal crystal, it entropically prefers to exist in an OV. When the polymer is small, it can find OVs easily and it does not "see" the neighborhood outside the OV it occupies very much. As a linear polymer gets longer, however, it eventually cannot fit into a single void and must spread out into a neighboring void. Since the HCP has "stacks" of OVs it can allow a polymer to spread out in these large OV "channels"; in the FCC, each OV is surrounded by TVs, so a large polymer is forced to enter a neighboring TV.

This confines the polymer more relative to the HCP environment, raising the polymer's free energy enough to overcome the small free energy difference between colloids in the polymorphs. Thus, the relative stability of the two crystals depends on the polymer's size! For very short chains, the FCC is still the most stable, per previous arguments. As the chain grows longer, the HCP can be stabilized instead. Increasing the length can lead to oscillations and even potentially destabilize close-packing altogether (see Ref. 6)!

This idea can be generalized. A linear polymer of the right length can be made to stabilize the HCP because a linear chain is geometrically more compatible with linear void channels than a "spherically" symmetric distribution of OVs and TVs found in the FCC crystal. In fact, a more "spherically" symmetric polymer can do the opposite. In Refs. 3 and 4 we explored the use of star polymers to stabilize the FCC over the HCP, which works for these qualitative reasons. This even works for lower density crystals (diamond-like "tetrastacks") which also have competing hexagonal and cubic polymorphs! We have also explored the case where the polymer can adsorb on the colloid in Ref. 2 - in this case, the smaller TVs tend to provide lower energy environments than the OVs (more surface area relative to volume in the void) which is favorable in this case. Remarkably, this means the TV void "stacks" now stabilize the HCP over the FCC, once again.

Overall, we conclude that the polymer's topology and energetic interactions can actually be used to rationally tune the relative stability of competing solid polymorphs. No programming of the colloids has been performed. However, the results discussed so far mostly apply when we have just two main competing structures whose voids have a characteristic difference that can be easily exploited by a complementary polymer (lock-and-key logic). The open question is: how can this sort of SDA-driven assembly paradigm be generalized?

Generalizing the Concept of an SDA

The definition of an SDA envisioned at the outset is essentially that of a "molecular engineer" who knows (1) what building blocks they will receive and (2) has all the information they need to assemble them in a certain way. There should be no explicit information in, or dependence on, the building block itself. One generalized object that can perform this operation is a "box" that can envelop some cargo, and then rely on "programming" on its exterior to self-assemble, thus organizing its cargo. In 2D, this "box" is just a topological ring.

Isohedral Tiles are SDAs that Program Symmetry

It turns out there is a remarkable connection between this very idea and crystallographic symmetry! I discuss this in more detail here. Crystals are composed of fundamental domains (FD), or asymmetric units, which are the smallest "piece" of the crystal that is duplicated in certain ways to create the pattern. Below is an illustration of the FD (black polygons) and the primitive unit cells (red polygons) for all crystal symmetries in two Euclidean dimensions (2D).

In 2D, each symmetry (aka "wallpaper") group can be described by a single, unique orbifold. This can viewed as the surface that results when the symmetrically equivalent positions on the FD are folded up to match each other. See the last link for a longer discussion and more explanation. In the image below, edge pairings are indicated for these particular FDs with colored arrows and points; approximations of a few of these orbifolds are also shown. Simply reversing this "folding" process to "cut" open the orbifolds reveals all possible isohedral tilings (distinct FDs) of the plane, which is a finite number in 2D.

These tilings have unique boundary patterns that define how parts of the tile's perimeter are actually copies of other parts, abstractly illustrated at the right. These operations instruct you on how to take a copy the entire tile and place it adjacent to the first by aligning matched pairs; repeating this fills the plane to make a pattern with the symmetry group described by the orbifold the isohedral tile (FD) resulted from by "cutting"!

This means isohedral tilings can be interpreted as ring-like SDAs which envelop some cargo, and using only the information around its perimeter, can be programmed to self-assemble the cargo into a given crystallographic symmetry! Essentially, you can think of the cargo as the "L" motif above and the SDA's is the polygon with a colored perimeter. Importantly, this means the boundary (color) pattern is derivable; moreover, the SDA shapes do not (and we will see below, arguably should not) be simple polygons!

2D Math in a 3D World

The aforementioned process of "cutting open" orbifolds is, perhaps, an abstract-sounding but remarkably simple process that I will discuss in more detail elsewhere. For now, it suffices to understand that there are 46 ways to cut open the orbifold surfaces for the 17 wallpaper groups; there are actually more isohedral tiles (93 in total) which are also derivable from orbifolds, but require a little more logic. These 46 represent boundaries that can envelop any asymmetric cargo and self-assemble it into a structure with the symmetry group that the original orbifold represents. This "asymmetric" property of the cargo is important; if the cargo has some symmetry it is possible for it to contribute this to the overall pattern in a way that results in a different symmetry group. This is almost never guaranteed, though. In fact, this usually requires very precise placement of the cargo inside the tile or other conditions to be met, so I will regard this as an exception for now. In mathematical parlance, these 46 tiles correspond to the fundamental domains of crystals (the cargo "induces" only the trivial identity symmetry), or result in a patterns whose motif-transitive proper subgroup of the orbifold's symmetry group is primitive.

Some orbifolds have only 1 way to perform a valid "cutting", while the group with the most (p2gg) has 8. The image below illustrates the 46 isohedral tiles (IH) for wallpaper groups. The IH numbering follows from Ref. [A] below. The matching rules for each tile are indicated by colors and arrows. The color of the name, however, is different and is based on practical self-assembly characteristics observed in Ref. 8.

To create a self-assembling SDA we can imagine it as a ring which has been discretized into beads, and each bead is assigned a color. Beads with the same color attract each other, while beads with different colors are repulsive hard spheres. The angles between neighboring beads can be specified to achieve a desired shape. A reasonable first attempt would be to specify the shape as one of the regular polygons used to introduce orbifolds above. In fact, for some groups this will seem to work (e.g., a rhombus for p3) and you might think that we are done. However, there is some practical information we are ignoring. Namely, that these SDAs are essentially derived from "two dimensional mathematics," but we are expecting them to work in our three dimensional world.

Observe that a pair of SDAs can always align along an edge if the second rotates 180 degrees out of plane around an in-plane axis defined by the edge itself (cf. image below). This operation always allows two SDAs to match along any edge if it is straight. Next, observe that rotation out of the assembly plane is equivalent to a reflection through a mirror normal to the plane. This changes the chirality of the ring (L vs. D). In the figure below, the red and blue layers will reverse positions ("top" vs. "bottom") if you rotate instead of reflecting, but the central colored layer where the "programming" is will be the same either way. This allows the p3 polygon to form both triplets shown; in both cases all beads are aligned so the configurations are equally favorable from an energetic standpoint. At first, this may seem inconsequential, but if we consider what the cargo inside the rings will look like, it is clear the second arrangement will not be what we intended (the D's cargo is upside down).

In fact, similar problems arise for all tiles. Since rotational diffusion is expected to be inevitable in any experimental realization, this an ever-present issue. We must have a general way to encode that an edge is intended to match with an enantiomorph of the same chirality (rotation or translation symmetry) or its opposite (a reflection symmetry). If the edges are straight, you can always match opposites (L-D) even if that is not intended. A pair of approaching SDAs will not know what to do in that case. Like Maxwell's demon, we may know the intent and could arrange the SDAs as needed, but the system is missing that information. To be true "self"-assembly, we must provide it somehow.

One way to provide this information is by giving the SDA's edges non-zero curvature. Once decided, an edge's curvature, like the color patterns, is copied to its matching pair by appropriate symmetry operations. The reader may convince themselves that this results in a situation where the correct enantiomorphs will "nest" inside each other, while the incorrect ones either form a cavity or bend away from each other preventing them from matching up their beads. Qualitatively, this process is illustrated above. Note that when a mirror symmetry is encountered, the edge is required to be straight.

Different Self-Assembly Characteristics

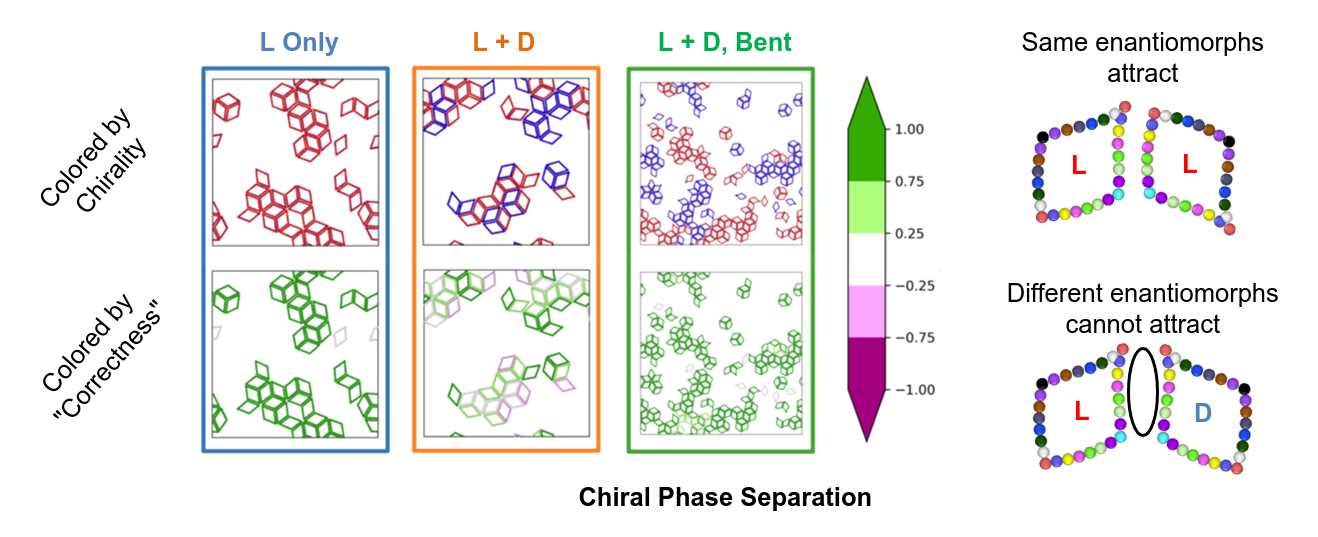
Owing to rotational diffusion we may assume that any surface will usually contain a roughly racemic (50:50) mixture of L and D SDAs. In what follows, I illustrate 3 cases from Ref. 8. If the SDA's edges are straight, defects usually arise (L+D), whereas if they are curved (L+D bent), they will assemble without confusion. In certain cases, it is ideal to have only one enantiomorph (L or D, arbitrary) but we have assumed this will be practically impossible to achieve. If we examine the resulting self-assembly behavior in molecular dynamics simulations there seem to be 5 distinct categories that emerge, which may be naturally explained by the orbifold the SDA derives from. These are organized in the pyramid at the right and rows correspond to the tile name colors I initially presented.

Row 5: Gyrations (ABC)

In row 5 we have all the wallpaper groups that contain no reflections. p2-p6 exclusively contain rotations, which is indicated in the orbifold signature by numbers without other symbols; for example, 2222 is p2 and 632 is p6. p1 is also included in this category which, in fact, contains no rotations, and is a result purely of translations. For these wallpaper groups, every SDA is surrounded by others of the same chirality. Below are results from molecular dynamics simulations illustrating the self-assembly that occurs. L/D are indicated in red/blue colors; the top row indicates raw results, while the bottom row re-colors each snapshot according to how "correctly" each SDA is oriented with respect to its neighbors. The ideal scenario for SDAs encoding for groups in this row is to have just one enantiomorph at the interface, and indeed the example snapshot below is almost entirely green (good). When a racemic mixture is simulated without bending the edges, the SDA enantiomorphs can interact at random. When the edges are bent, these incorrect L-D interactions are suppressed, while only L-L and D-D interactions are allowed. As a result, chiral phase separation (large blue/red domains) occurs.

Row 4: Kaleidoscopes (*abc)

Row 4 contains all wallpaper groups which are composed of intersecting mirrors. The orbifold signatures all start with an asterisk followed by numbers indicating the angles the mirrors form with each other; recall that each mirror creates a straight edge (no bending is allowed). For example, *632 is a 30-60-90 triangle ($\pi/6$, $\pi/3$, and $\pi/2$). In this case, each SDA is entirely surrounded by the opposite enantiomorph. Mirror edges have the unique property that, unlike every other symmetry, they create an edge which does NOT match with any other part of the SDA ring. This means that a mirror edge contains entirely unique "colors". If all edges are mirrors then all points are unique. Such structures are called "addressably complex" which is a concept central to the design of many DNA-based nanomaterials.

Row 3: Gyroscopes (A*bc)

Row 3 is made of groups which are a combination of rows 4 and 5. These groups have mirrors which create a polygon, but contain a rotation center inside. The orbifold signature reflects these features with a number (A, the order of the rotation center) followed by an asterisk and other numbers (*bc...) indicating the angles the mirrors which form the polygon make. In the example below we have 2*22, meaning there is a 2-fold rotation center (2) inside a rectangle (*22). When only one enantiomorph is present, the SDAs can only assemble around the rotation center creating the polygon. To move across the polygon's edges requires the other enantiomorph. In this example, the L enantiomorphs form dimers; for comparison, p31m (3*3) forms trimers and p4gm (4*2) forms tetramers.

Row 2: Frieze

SDAs that result from wallpaper groups in row 2 form one dimensional assemblies when only one enantiomorph is present. Essentially, they grow in a line to form "rods". This is because (almost) all ways of cutting open the orbifold result in patterns that match with the same enantiomorph in one direction, but the opposite enantiomorph in the orthogonal one. An example from p1g1 (xx) is illustrated below. This corresponds to IH43 (see above). However, p1g1 has an exception, colored orange like those in row 2! Note that IH44 has 2 pairs of edges related by glide reflections, and thus is completely surrounded by opposite enantiomorphs (akin to SDAs derived from groups in row 2).

Row 1: Pluripotence

There was one exception to the characteristic behavior in row 2. This implies that if you wanted to change the self-assembly behvior, you could simply choose to use that tile (IH44). In fact, row 1 is full of exceptions! For these groups, tiles can be found exhibiting behaviors like that of rows 2, 3, or 4, as indicated by the colors of their IH tile designation above. Ultimately, this can be traced back to the presence of crosscaps (x) in the orbifolds. A Moebius band is a related surface that results from combining a boundary with the crosscap. In fact, this is the orbifold (*x) for c1m1, which belongs to row 1. Intuitively, cross-caps and Moebius bands are "strange" things and to be brief: when strange things happen in the orbifold's topology, strange things happen in the self-assembly of SDAs which derive from them. These e[X]ceptional groups are easy to remember because their orbifold signatures all contain an "x"!

In fact, the laces on the football above should really be a crosscap so the reader will have to forgive some artistic license. Until now, the exact choice of "cuts" you make to "open up" the orbifold (football) and create an isohedral tile has not affected its self-assembly characteristics. Different cuts result in different tiles, but those tiles behave similarly. Now, the choice of cuts matters! You can choose cuts which expose different features resulting in different patterns of L/D enantiomorphs around an SDA, resulting in behavior akin to different rows of the pyramid.

In the example above, the glide reflections (gray dashed lines) and rotation centers (gray ellipses) correspond to the standard symmetry diagram for this group; these features are simply guides to the eye. I have stretched them a bit in different cases for visual clarity, but in principle, the image "behind" them may be regarded as being the same. The three cases shown illustrate different cuts which divide the SAME image but in DIFFERENT ways. The final self-assembled pattern will be the same, but by choosing different cuts you can manipulate how you get there by controlling the chirality of the SDAs at the interface!

Conclusions

Structure-directing agents (SDAs) are typically thought of as (relatively) small molecule additives that can tune properties such as porosity and channel architecture when added during the synthesis of materials like zeolites. However, if we broaden our perspective to include any additive which can be programmed to organize some cargo, it is clear that SDA-driven assembly represents a different route to programmable material design than conventional top-down or bottom-up approaches. I discussed work showing that larger molecules, such as polymers, can tune the relative stability of competing polymorphs in self-assembling colloidal systems by adsorbing in different void spaces selectively. This is similar to the manner in which conventional SDAs perform their task. I subsequently showed how broadening our definition of an SDA leads to a natural generalization that seems almost identical to isohedral tilings in 2D space. This suggests there is an interesting connection between crystallography and the SDA-based programmable assembly paradigm.

Ongoing work seeks to generalize features of these 2D systems to create optimal SDAs to assemble arbitrary cargo with as few defects as possible, how to create other sorts of SDAs, and how to do this in 3D. If you are interested in colloborating or available research positions on these topics, please send me an email.

References

[A] Gruenbaum, B., and Shephard, G. C. Tilings and Patterns. Second Edition. Courier Dover Publications, 2016.

mahynski/research_agent_based_colloidal_self_assembly.md

Table of Contents