get_intersection.py

import sys
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial import ConvexHull

eps = np.random.rand(1)/100


def on_segment(p, q, r):
    return ((q[0] <= max(p[0], r[0])) and (q[0] >= min(p[0], r[0]))
            and q[1] <= max(p[1] , r[1]) and q[1] >= min(p[1], r[1]))

def orientation(p, q, r):
    val = (q[1] - p[1]) * (r[0] - q[0]) - \
          (q[0] - p[0]) * (r[1] - q[1])

    if val == 0:
        return 0
    elif val > 0:
        return 1
    else:
        return -1

def intersect(p1, q1, p2, q2):
    o1 = orientation(p1, q1, p2)
    o2 = orientation(p1, q1, q2)
    o3 = orientation(p2, q2, p1)
    o4 = orientation(p2, q2, q1)

    if (o1 != o2 and o3 != o4):
        return True
    
    if (o1 == 0 and on_segment(p1, p2, q1)):
        return True
    if (o2 == 0 and on_segment(p1, q2, q1)):
        return True
    if (o3 == 0 and on_segment(p2, p1, q2)):
        return True
    if (o4 == 0 and on_segment(p2, q1, q2)):
        return True

    return False

def is_inside(pts, p):
    # taken from https://www.geeksforgeeks.org/how-to-check-if-a-given-point-lies-inside-a-polygon/

    eps = 0.0001
    # to avoid a special case where ray from point to infinity crosses the two vertices of the polygon.
    # and all these three points become collinear.
    p[0] += eps
    p[1] += eps

    n = len(pts)
    extreme = (sys.maxsize, p[1])

    count = 0
    i = 0

    for i in range(n):
        _next = (i + 1) % n

        if intersect(pts[i], pts[_next], p, extreme):
            if orientation(pts[i], p, pts[_next]) == 0:
                return on_segment(pts[i], p, pts[_next])

            count += 1

    return bool(count & 1)

def get_line(pt1, pt2):
    if pt1[0] == pt2[0]:
        return sys.maxsize, pt1[0]
    
    m = (pt2[1] - pt1[1])/(pt2[0] - pt1[0])
    c = (pt1[1]*pt2[0] - pt2[1]*pt1[0]) / (pt2[0] - pt1[0])

    return m, c

def get_line_intersection(m1, c1, m2, c2):
    x = (c2 - c1)/(m1 - m2)
    y = m1 * x + c1

    return x, y

def get_length(pt1, pt2):
    a = pt1[0] - pt2[0]
    a = np.square(a)
    b = pt1[1] - pt2[1]
    b = np.square(b)

    return np.sqrt(a + b)

def is_on_segment(pt1, pt2, pt3, pt4, pt, eps=-0.001):
    x1, y1 = pt1
    x2, y2 = pt2
    x3, y3 = pt3
    x4, y4 = pt4
    x, y = pt
    return eps<=max(y1, y2)-y and y-min(y1, y2)>=eps and eps<=max(y3, y4)-y and y-min(y3, y4)>=eps and \
        eps<=max(x1, x2)-x and x-min(x1, x2)>=eps and eps<=max(x3, x4)-x and x-min(x3, x4)>=eps

def get_intersection(poly1, poly2):
    print("\n\n")
    print(poly1)
    print(poly2)

    intersecting_coords = []
    for c in poly1[:-1]:
        if is_inside(poly2[:-1], c):
            intersecting_coords.append((c[0], c[1]))
            plt.scatter(c[0], c[1])   
            
    for c in poly2[:-1]:
        if is_inside(poly1[:-1], c):
            intersecting_coords.append((c[0], c[1]))
            plt.scatter(c[0], c[1])
            
    for i1, c1 in enumerate(poly1[:-1]):
        for i2, c2 in enumerate(poly2[:-1]):
            pt1, pt2 = (poly1[i1], poly1[(i1+1)%len(poly1)])
            x1, y1 = pt1
            x2, y2 = pt2
            pt3, pt4 = (poly2[i2], poly2[(i2+1)%len(poly2)])
            x3, y3 = pt3
            x4, y4 = pt4
            m1, c1 = get_line(pt1, pt2)
            m2, c2 = get_line(pt3, pt4)

            if m1 == m2 and c1 == c2:
                if get_length(pt1, pt2) < get_length(pt3, pt4):
                    intersecting_coords.append(pt1)
                    intersecting_coords.append(pt2)
                    plt.scatter(pt1, pt2)
                else:
                    intersecting_coords.append(pt3)
                    intersecting_coords.append(pt4)
                    plt.scatter(pt3, pt4)
            elif m1!=m2:

                if m1 == sys.maxsize:
                    x = x1
                    y = m2 * x1 + c2
                    if is_on_segment(pt1, pt2, pt3, pt4, (x, y)):
                        intersecting_coords.append((x, y))
                        plt.scatter(x, y)
                elif m2 == sys.maxsize:
                    x = x3
                    y = m1 * x3 + c1
                    if is_on_segment(pt1, pt2, pt3, pt4, (x, y)):
                        intersecting_coords.append((x, y))
                        plt.scatter(x, y)
                elif m1 == 0:
                    y = y1
                    x = (y1 - c2) / m2
                    if is_on_segment(pt1, pt2, pt3, pt4, (x, y)):
                        intersecting_coords.append((x, y))
                        plt.scatter(x, y)
                elif m2 == 0:
                    y = y3
                    x = (y3 - c1) / m1
                    if is_on_segment(pt1, pt2, pt3, pt4, (x, y)):
                        intersecting_coords.append((x, y))
                        plt.scatter(x, y)
                else:
                    x, y = get_line_intersection(m1, c1, m2, c2) 

                    _m1 = y - pt1[1]
                    _m1 /= (x - pt1[0])
                    _m2 = y - pt2[1]
                    _m2 /= (x - pt2[0])

                    _m3 = y - pt3[1]
                    _m3 /= (x - pt3[0])
                    _m4 = y - pt4[1]
                    _m4 /= (x - pt4[0])
                    if _m1 * _m2 < 0 and _m3 * _m4 < 0:
                        intersecting_coords.append((x, y))
                        plt.scatter(x, y)
            else:
                print('do not intersect parallel')        

    intersecting_coords = np.array(intersecting_coords)
    hull = ConvexHull(intersecting_coords)
    intersecting_coords = intersecting_coords[hull.vertices]
    intersecting_coords = np.append(intersecting_coords, [intersecting_coords[0]], axis=0)
    x, y = intersecting_coords.T

    print(intersecting_coords)
    print(len(intersecting_coords))
    x1, y1 = poly1.T
    x2, y2 = poly2.T
    plt.plot(x1, y1)
    plt.plot(x2, y2)
    plt.plot(x, y, c='k')
    plt.show()

poly1 = np.array([[451.8107,  173.44763],
 [531.7912,  173.45604],
 [533.50757, 222.04575],
 [453.52707, 222.03732],
 [451.8107,  173.44763]])

poly2 = np.array([[449.92476,  172.5057  ],
 [530.552293, 172.5057  ],
 [530.552293, 220.237058],
 [449.92476,  220.237058],
 [449.92476,  172.5057  ]])
get_intersection(poly1, poly2)

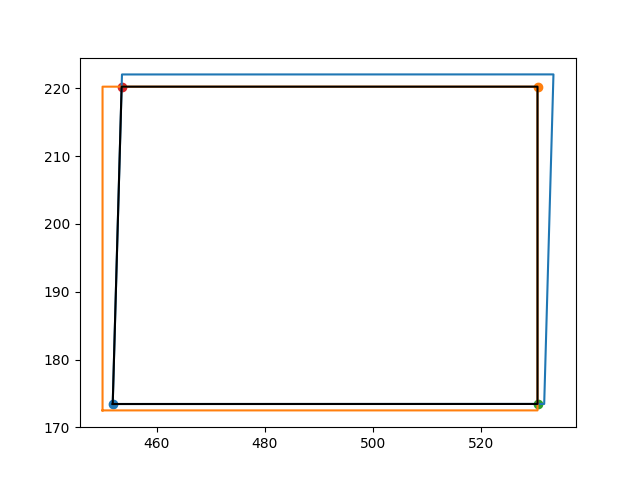
This finds intersection of two quadrilaterals, the intersecting region is bound by black boundary.