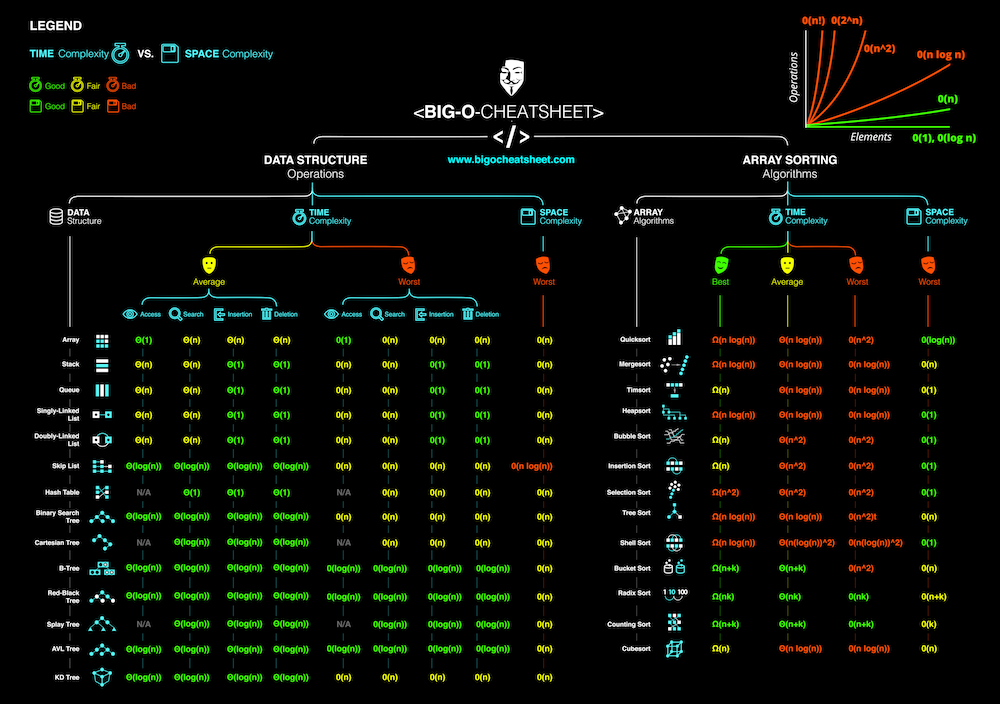
O(1) Constant - no loops
O(log N) Logarithmic - usually searching algorithms have log n if they are sorted (Binary Search)
O(n) Linear - for loops, while loops through n items
O(n log(n)) Log Linear - usually sorting operations
O(n^2) Quadratic - every element in a collection needs to be compared to ever other element. Two nested loops
O(2^n) Exponential - recursive algorithms that solves a problem of size N
O(n!) Factorial - you are adding a loop for every element
Iterating through half a collection is still O(n) Two separate collections: O(a * b)
- Operations (+,-, *, /)
- Comparisons (<, >, ===)
- Looping (for, while)
- Outside Function call (function())
- Rule 1: Always worst Case
- Rule 2: Remove Constants
- Rule 3:
Different inputs should have different variables: O(a + b).
A and B arrays nested would be: O(a * b)
+ for steps in order
* for nested steps
- Rule 4: Drop Non-dominant terms
- Variables
- Data Structures
- Function Call
- Allocations
Pros:
- Fast lookups
- Fast push/pop
- Ordered
Cons
- Slow inserts
- Slow deletes
- Fixed size (if using static array)