Quick and dirty python script to compute the facet sizes for shaping a guitar neck

neck.py

#!/usr/bin/python
# Copyright (c) 2019.
#
# Author(s):
#   Martin Raspaud <[email protected]>

# This program is free software: you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation, either version 3 of the License, or
# (at your option) any later version.
#
# This program is distributed in the hope that it will be useful,
# but WITHOUT ANY WARRANTY; without even the implied warranty of
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
# General Public License for more details.
#
# You should have received a copy of the GNU General Public License
# along with this program. If not, see <http://www.gnu.org/licenses/>.

import numpy as np
import matplotlib.pyplot as plt


def tangent_params(angle, a, b):
    slope = np.tan(angle)
    intercept = np.sqrt(a ** 2 * slope ** 2 + b ** 2)
    return slope, intercept

def tangent(x, angle, a, b):
    slope, intercept = tangent_params(angle, a, b)

    return slope * x + intercept



def plot_neck(ax2, b, title='Neck'):
    # neck shape: oval

    a = ax2 / 2
    x = np.linspace(-a, a, 1000)
    y = b / a * np.sqrt(a ** 2 - x ** 2)

    plt.plot(x, y)

    # axis of symmetry

    plt.plot([0, 0], [0, b * 2], color='grey')

    # first intersection

    inter1 = -a, tangent(-a, np.pi / 4, a, b)
    # print(inter1)
    plt.annotate(('%.2f' % inter1[1]), (-a + 1, inter1[1] / 2))
    plt.annotate(('%.2f' % (b - inter1[1])), (-a + .5, (b + inter1[1]) * 2 / 3), va='center')

    # second intersection

    slope, intercept = tangent_params(np.pi / 4, a, b)
    inter2 = (b - intercept) / slope, b
    # print(inter2)
    plt.annotate(('%.2f' % abs(inter2[0])), (inter2[0] / 2, b + 1), ha='center')
    plt.annotate(('%.2f' % (a - abs(inter2[0]))), ((-a + inter2[0]) / 2, b + 1), ha='center')

    # first tangent
    x = np.array([inter1[0], inter2[0]])
    y = tangent(x, np.pi / 4, a, b)
    plt.plot(x, y, color='orange', linestyle='-')

    # horizontal line

    y = tangent(np.array([-a, inter2[0]]), 0, a, b)
    plt.plot(np.array([-a, inter2[0]]), y, 'g--')
    y = tangent(np.array([inter2[0], 0]), 0, a, b)
    plt.plot(np.array([inter2[0], 0]), y, 'g-')

    # vertical line

    plt.plot([-a, -a], [0, inter1[1]], 'r-')
    plt.plot([-a, -a], [inter1[1], b], 'r--')


    # Second part

    # first intersection

    inter1 = a, tangent(a, -np.pi / 4, a, b)

    # second intersection

    slope, intercept = tangent_params(-np.pi / 4, a, b)
    inter2 = (b - intercept) / slope, b
    slope45 = slope
    intercept45 = intercept

    # third intersection

    inter3 = a, tangent(a, -3 * np.pi / 8, a, b)
    plt.annotate(('%.2f' % inter3[1]), (a - 1, inter3[1] / 2), ha='right')

    # fourth intersection

    slope, intercept = tangent_params(-3 * np.pi / 8, a, b)
    x_inter = (intercept - intercept45) / (slope45 - slope)
    inter4 = x_inter, slope45 * x_inter + intercept45

    plt.plot([inter3[0], inter4[0]], [inter3[1], inter4[1]], color='cyan')

    dst = np.linalg.norm(np.array(inter1) - np.array(inter4))
    plt.annotate('%.2f' % dst, (inter1[0] + 1, inter1[1]), ha='left', va='center')

    # fifth intersection

    slope, intercept = tangent_params(-np.pi / 8, a, b)
    x_inter = (intercept - intercept45) / (slope45 - slope)
    inter5 = x_inter, slope45 * x_inter + intercept45
    dst = np.linalg.norm(np.array(inter2) - np.array(inter5))
    plt.annotate('%.2f' % dst, (inter2[0] + 1, inter2[1]), ha='left', va='center')

    # sixth intersection

    inter6 = (b - intercept) / slope, b
    plt.plot([inter6[0], inter5[0]], [inter6[1], inter5[1]], color='purple')
    plt.annotate(('%.2f' % abs(inter6[0])), (inter6[0] / 2, b + 1), ha='center')

    # vertical line

    plt.plot([a, a], [0, inter3[1]], 'r-')
    plt.plot([a, a], [inter3[1], inter1[1]], 'r--')

    # first tangent
    x = np.array([inter1[0], inter4[0]])
    y = tangent(x, -np.pi / 4, a, b)
    plt.plot(x, y, color='orange', linestyle='--')
    x = np.array([inter4[0], inter5[0]])
    y = tangent(x, -np.pi / 4, a, b)
    plt.plot(x, y, color='orange', linestyle='-')
    x = np.array([inter5[0], inter2[0]])
    y = tangent(x, -np.pi / 4, a, b)
    plt.plot(x, y, color='orange', linestyle='--')

    # horizontal line
    x = np.array([inter2[0], inter6[0]])
    y = tangent(x, 0, a, b)
    plt.plot(x, y, 'g--')
    x = np.array([inter6[0], 0])
    y = tangent(x, 0, a, b)
    plt.plot(x, y, 'g-')





    plt.axis('equal')
    plt.axis([-a * 1.25, a * 1.25, 0, b * 2])
    plt.title('%s, width=%.2f, height=%.2f'%(title, ax2, b))
    plt.show()

plot_neck(42.2, 14.3, 'Nut')
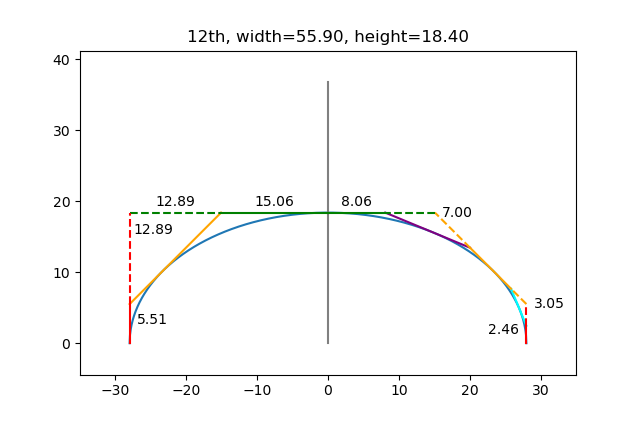
plot_neck(55.9, 18.4, '12th')

example output: