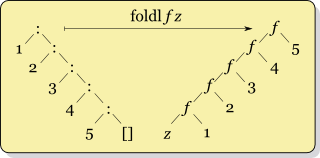
I like to call foldr as "fold from the right", while foldl is "fold from the
left".
This is due to the position of the seed value, and the order of evaluation in
the AST. As you can see, for foldl the position of the seed value is on the left
hand side of the tree, while foldr seed value is on the right hand side of the
tree. In terms of total evaluation order (if we were to strictly evaluate the
entirely cobined result), the foldr would evaluate from the right to left.
While foldl would evaluate from left to right. The deepest node in the AST has
to get evaluated first before the parent nodes can take the recursive value with
the terminal value and apply both to its respective combining operation.
This order of evaluation can be illustrated with a simple left-associative minus combining operation:
foldr (-) 0 [1,2,3,4]
(1 - (2 - (3 - (4 - 0)))) = -2
-
/ \
1 -
/ \
2 -
/ \
3 -
/ \
4 0
foldl (-) 0 [1,2,3,4]
((((0 - 1) - 2) - 3) - 4) = -10
-
/ \
- 4
/ \
- 3
/ \
- 2
/ \
0 1
Another way to remember it is that foldr has a right biased tree, while foldl
is a left biased tree. The tree is the AST. Looking at the tree again, one can
also identify that the foldr preserves the order of the right-recursive list
constructors. While the foldl reverses the order of list constructors.
It is interesting to note that most strict/imperative languages naturally gravitate to
foldl, they obviously mostly call it "array reduce" or some variant of it. Strict
languages don't have much use for foldr, and their reduce functions seem to always
default to foldl. When programming imperatively and strictly, you tend to think
left to right, hence evaluating/combining a list in a left to right manner induces
the foldl bias.
Only foldr is lazy and can be used for codata/infinite streams. While foldl
is tail-recursive (enhanced with strict application foldl' can avoid stack overflow).
This is why foldr should be used by default in Haskellin order preserve laziness
across function composition. However the laziness can only be taken advantage
of, if the combining function is a data constructor, which can be lazily deconstructed.
Refer to https://wiki.haskell.org/Maintaining_laziness for more information!