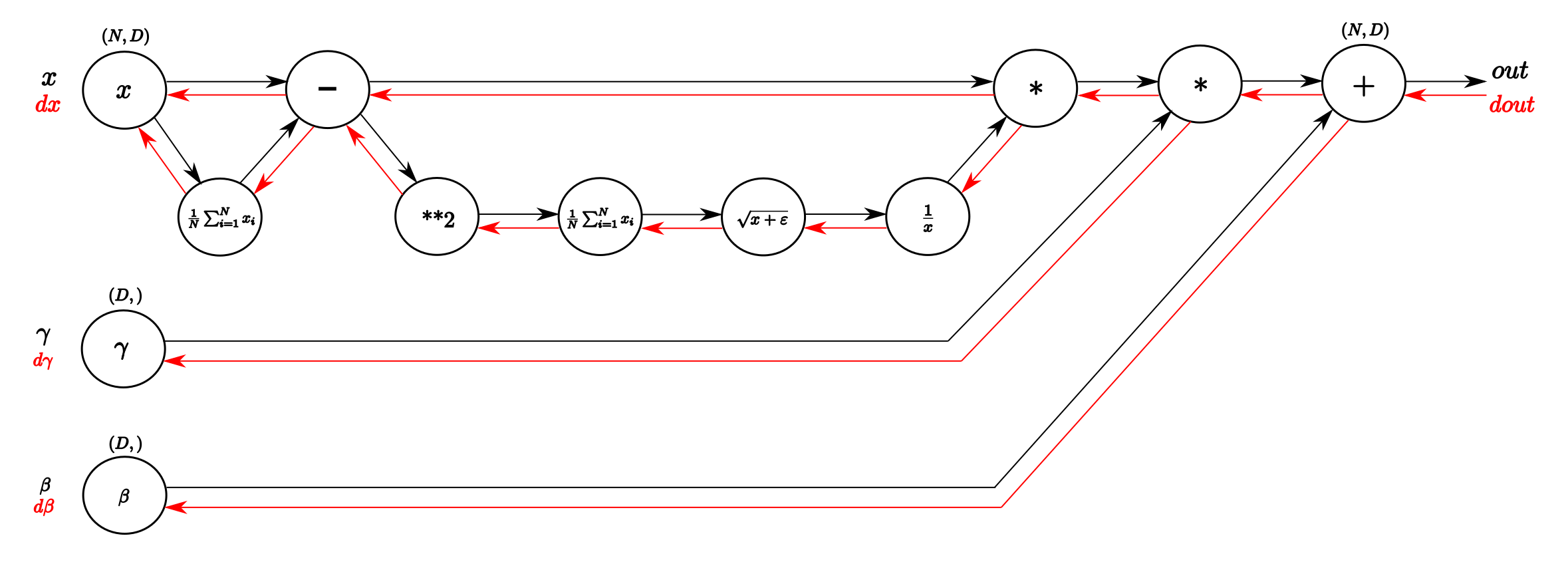
\frac{\partial l}{\partial \beta} = \sum_{i=1}^{m}(\frac{\partial l}{\partial y_i})
\frac{\partial l}{\partial \gamma} = \sum_{i=1}^{m}(\frac{\partial l}{\partial y_i} * \hat{x_i})
\frac{\partial l}{\partial \hat{x_i}} = \sum_{i=1}^{m}(\frac{\partial l}{\partial y_i} * \gamma)
\frac{\partial l}{\partial X_{\mu1}} = \frac{\partial l}{\partial \hat{X}}\odot (ivar)
\frac{\partial l}{\partial ivar} = \sum_{i=1}^{m}(\frac{\partial l}{\partial \hat{x_i}} * x_{\mu i})
\frac{\partial l}{\partial \sqrt{var}} = \frac{\partial l}{\partial ivar}\odot\frac{-1}{{\sqrt{var}}^2}
\frac{\partial l}{\partial var} = \frac{0.5}{\sqrt{var+\epsilon}}\odot\frac{\partial l}{\partial \sqrt{var}}
\frac{\partial l}{\partial sq} = \frac{1}{N} \odot I_{N*D}\odot\frac{\partial l}{\partial var}
\frac{\partial l}{\partial X_{\mu2}} = 2\odot X_{\mu} \odot \frac{\partial l}{\partial sq}
\frac{\partial l}{\partial X_{1}} = \frac{\partial l}{\partial X_{\mu1}} + \frac{\partial l}{\partial X_{\mu2}}
\frac{\partial l}{\partial \mu} = \sum_{i=1}^{N}( \frac{\partial l}{\partial x_{\mu1 i}} + \frac{\partial l}{\partial x_{\mu2 i}})
\frac{\partial l}{\partial X_{2}} = \frac{1}{N} \odot I_{N*D}\odot\frac{\partial l}{\partial \mu}
\frac{\partial l}{\partial X} = \frac{\partial l}{\partial X_{1}} + \frac{\partial l}{\partial X_{2}}Understanding the backward pass through Batch Normalization Layer