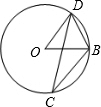Project Kibana

Catalog

Shapes

A / No shape
B / Triangle
C / Quatro
D / Circle
E / Multiple

Methods

I / Direct Rule Apply
II / Transform with geometric features
III / Numerical Calculation
IV / Shape Change & Build
V / Folding, Slicing, Compensating
VI / Multiple Value

        A   B   C   D   E
I       5   5   5   5   5
II      5   5   5   5   5
III     5   5   5   5   7
IV      5   7   5   5   7
V       5   5   6   5   5

Items

I-A

如图，a∥b，若∠1=110°，则∠2的度数是___. [70°]

(19济宁) 如图，直线a，b被直线c，d所截，若∠1=∠2，∠3=125°，则∠4的度数是___. [55°]

如图：AD∥BC，AB=AC，∠ABC=52°，则∠DAC的度数为___. [52°]

(19绵阳) 如图，AB∥CD，∠ABD的平分线与∠BDC的平分线交于点E，则∠1+∠2=__. [90°]

如图，AB∥CD，AF交CD于点O，且OF平分∠EOD，如果∠A=34°，那么∠EOC的度数是___. [112°]

I-B

如图，在△ABC中，D是BC延长线上一点，∠B=50°，∠ACD=110°，则∠A=___. [60°]

(19重庆) 如图，△ABO∽△CDO，若BO=6，DO=3，CD=2，则AB的长是___. [4]

如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若BC=4cm，AD=6cm，则图中阴影部分的面积是___ $cm^2$. [6]

(19重庆) 如图，在△ABC中，AB=AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F．若∠C=36°，则∠BAD=___. [54°]

如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°，则∠BDC=___. [100°]

I-C

如图，在菱形ABCD中，点E，F分别是AB，AC的中点，连接EF，若EF=4，则菱形ABCD的周长为___. [32]

(12南京) 如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角．若∠A=120°，则∠1+∠2+∠3+∠4=___. [300°]

如图，在矩形ABCD中，AC=4，AB=2，则BC的长是___. [2sqrt3]

如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是___. [2.5]

(13南京) 如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为___$cm^2$. [2sqrt3]

I-D

(13成都) 如图，点A，B，C在⊙O上，∠A=50°，则∠BOC的度数为___. [100°]

(19滨州) 如图，AB为⊙O的直径，C，D为⊙O上两点，若∠BCD=40°，则∠ABD的大小为___. [50°]

(11安徽) 如图，⊙O半径是1，A、B、C是圆周上的三点，∠BAC=36°，则劣弧$\overset{\LARGE{\frown}}{BC}$的长是___. [2pi/5]

(11重庆) 如图，⊙O是△ABC的外接圆，∠OCB=40°，则∠A的度数等于___. [50°]

(19怀化) 如图，A、B、C、D、E是⊙O上的5等分点，连接AC、CE、EB、BD、DA，得到一个五角星图形和五边形MNFGH．∠CAD=___. [36°]

I-E

(12济南) 如图，在Rt△ABC中，∠C=90°，AC=4，将△ABC沿CB向右平移得到△DEF，若平移距离为2，则四边形ABED的面积等于___. [8]

(11上海) 如图，点B、C、D在同一条直线上，CE∥AB，∠ACB=90°，如果∠ECD=36°，那么∠A=___. [54°]

(13安徽) 如图，AB∥CD，∠A+∠E=75°，则∠C为___. [75°]

(19重庆) 如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连结OD．若∠C=50°，则∠AOD的度数为___. [80°]

(12无锡) 如图，梯形ABCD中，AD∥BC，AD=3，AB=5，BC=9，CD的垂直平分线交BC于E，连接DE，则四边形ABED的周长等于___. [17]

II-A

(19自贡) 如图，直线 AB、CD 被直线 EF 所截，AB∥CD，∠1=120°，则∠2=___．

如图，直线a∥b，∠1=50°，∠2=40°，则∠3的度数为___. [90°]

如图，直线l1∥l2，AB=BC，CD⊥AB于点D，若∠DCA=20°，则∠1的度数为___. [70°]

如图，AB∥DE，FG⊥BC于F，∠CDE=40°，则∠FGA的度数为___. [130°]

(19滨州) 如图，AB∥CD，∠FGB=154°，FG平分∠EFD，则∠AEF的度数等于___. [52°]

II-B

(19枣庄) 将一副直角三角板按如图所示的位置放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠α的度数是___. [75°]

如图所示，△ABC是等边三角形，且BD=CE，∠1=15°，则∠2的度数为___. [60°]

(13河南) 将一副直角三角板ABC和EDF如图放置（其中∠A=60°，∠F=45°）．使点E落在AC边上，且ED∥BC，则∠CEF的度数为___. [15°]

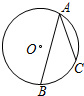
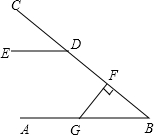
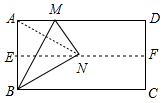
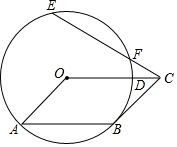
(19衢州) “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动、C点固定，OC=CD=DE，点D、E可在槽中滑动．若∠BDE=75°，则∠CDE的度数是___. [80°]

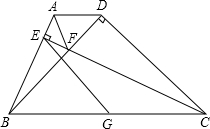
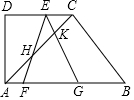
(19衢州) 如图，在Rt△ABC中，∠C=90°，AC=6，∠BAC=60°，AD平分∠BAC交BC于点D，过点D作DE∥AC交AB于点E，点M是线段AD上的动点，连结BM并延长分别交DE，AC于点F、G．若点M是线段AD的中点，则 $\frac{EF}{DF}$=___. [2/3]

II-C

(11武汉) 如图．在梯形ABCD中，AB∥DC，AD=DC=CB，若∠ABD=25°，则∠BAD的大小是___. [50°]

(19达州) 如图，▱ABCD的对角线AC、BD相交于点O，点E是AB的中点，△BEO的周长是8，则△BCD的周长为___. [16]

(11北京) 如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O，若AD=1，BC=3，则$\frac{AO}{CO}$的值为___. [1/3]

(11北京) 如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，CE=4，则四边形ACEB的周长为___． [10+2sqrt13]

(11贵阳) 如图，点E是正方形ABCD内一点，△CDE是等边三角形，连接EB、EA，延长BE交边AD点于点F．∠AFB=___. [75°]

II-D

(19天津) 如图②，已知PA，PB分别与⊙O相切于点A，B，∠APB=80°，C为⊙O上一点，AE为⊙O的直径，AE与BC相交于点D．若AB=AD，则∠EAC=___． [20°]

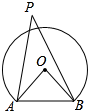
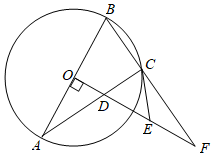
(19聊城) 如图，BC是半圆O的直径，D，E是$\overset{\LARGE{\frown}}{BC}$上两点，连接BD，CE并延长交于点A，连接OD，OE．如果∠A=70°，那么∠DOE的度数为___. [40°]

(11武汉) 如图，OB是⊙O的半径，点C、D在⊙O上，∠DCB=27°，则∠OBD=___. [63°]

(11成都) 如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD=___. [32°]

(13天津) 如图，PA、PB分别切⊙O于点A、B，若∠P=70°，则∠C的大小为___. [55°]

II-E

(11重庆) 如图，梯形ABCD中，AD∥BC，∠DCB=45°，CD=2，BD⊥CD．过点C作CE⊥AB于E，交对角线BD于F，点G为BC中点，连接EG、AF．EG=___. [sqrt2]

(13重庆) 如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，CD=3cm，则AF的长为___cm. [6]

(11兰州) 如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=25°，则∠D等于___. [40°]

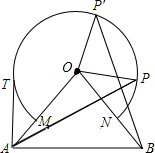
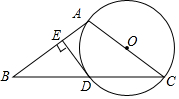
(13河北) 如图，△OAB中，OA=OB=10，∠AOB=80°，以点O为圆心，6为半径的优弧$\overset{\LARGE{\frown}}{MN}$分别交OA，OB于点M，N．点T在左半弧上，若AT与弧相切，则点T到OA的距离为___. [24/5]

(13陕西) 如图，直线l与⊙O相切于点D，过圆心O作EF∥l交⊙O于E、F两点，点A是⊙O上一点，连接AE、AF，并分别延长交直线l于B、C两点．∠ABC+∠ACB=___. [90°]

(13南京) 如图，海边立有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=80°．为了避免触礁，轮船P与A、B的张角∠APB的最大值为___. [40°]

III-A

(19枣庄) 如图，小明为了测量校园里旗杆AB的高度，将测角仪CD竖直放在距旗杆底部B点6m的位置，在D处测得旗杆顶端A的仰角为53°，若测角仪的高度是1.5m，则旗杆AB的高度约为___m．（精确到0.1m．参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33） [9.5]

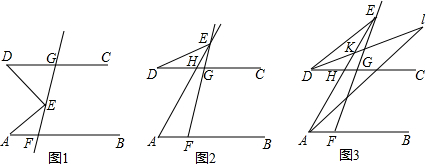
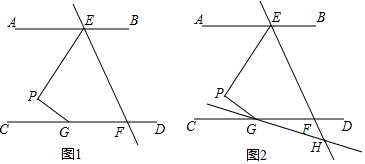
如图3，已知，AB∥CD，点E为射线FG上一点．若∠EAF=30°，∠EDG=40°，DI平分∠EDC，交AE于点K，交AI于点I，且∠EAI：∠BAI=1：2，∠AED=22°，∠I=20°，∠EKD=___. [142°]

如图，已知AM∥BN，∠A=80°，点P是射线AM上动点（与A不重合），BC、BD分别平分∠ABP和∠PBN，交射线AM于C、D．∠CBD=___. [50°]

如图1，AB∥CD，直线EF交AB于点E，交CD于点F，点G在CD上，点P在直线EF左侧、且在直线AB和CD之间，连接PE、PG．连接EG，若EG平分∠PEF，∠AEP+∠PGE=110°，∠PGC=$\frac{1}{2}$∠EFC，∠AEP=___. [40°]

如图1，如果AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF=___. [360°]

III-B

(19自贡) 如图，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，CD∥AB，∠ABC的平分线BD交AC于点E，DE=___．

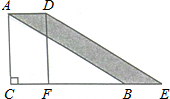
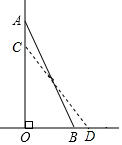
(19德州) 如图，一架长为6米的梯子AB斜靠在一竖直的墙AO上，这时测得∠ABO=70°，如果梯子的底端B外移到D，则梯子顶端A下移到C，这时又测得∠CDO=50°，那么AC的长度约为___米．（sin70°≈0.94，sin50°≈0.77，cos70°≈0.34，cos50°≈0.64） [1.02]

(19衢州) 如图，在Rt△ABC中，∠C=90°，AC=6，∠BAC=60°，AD平分∠BAC交BC于点D，过点D作DE∥AC交AB于点E，点M是线段AD上的动点，连结BM并延长分别交DE，AC于点F、G．CD=___. [2sqrt3]

(19重庆) 为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动．如图，在一个坡度（或坡比）i=1：2.4的山坡AB上发现有一棵古树CD．测得古树底端C到山脚点A的距离AC=26米，在距山脚点A水平距离6米的点E处，测得古树顶端D的仰角∠AED=48°（古树CD与山坡AB的剖面、点E在同一平面上，古树CD与直线AE垂直），则古树CD的高度约为___米.（参考数据：sin48°≈0.73，cos48°≈0.67，tan48°≈1.11） [23.3]

(19枣庄) 如图1，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D．点M，N分别在AD，AB上，且∠BMN=90°，当∠AMN=30°，AB=2时，AM=___. [sqrt2-sqrt6/3]

III-C

(19济宁) 如图1，在矩形ABCD中，AB=8，AD=10，E是CD边上一点，连接AE，将矩形ABCD沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G．CE=___. [3]

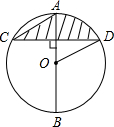
(19绵阳) 公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形的面积是125，小正方形面积是25，则$(sin\theta-cos\theta)^2$=___. [1/5]

(13北京) 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若AB=5，AD=12，则四边形ABOM的周长为___. [20]

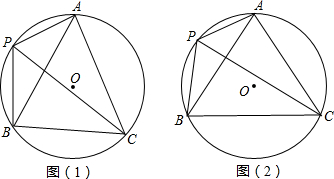
(13重庆) 已知：如图①，在平行四边形ABCD中，AB=12，BC=6，AD⊥BD．以AD为斜边在平行四边形ABCD的内部作Rt△AED，∠EAD=30°，∠AED=90°．则△AED的周长为___. [9+3sqrt3]

(11兰州) 已知：如图所示的一张矩形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连接AF和CE．若AE=10cm，△ABF的面积为24$cm^2$，则△ABF的周长为___cm. [24]

III-D

(19衢州) 一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D．现测得AB=8dm，DC=2dm，则圆形标志牌的半径为___dm. [5]

(19聊城) 如图，△ABC内接于⊙O，AB为直径，作OD⊥AB交AC于点D，延长BC，OD交于点F，过点C作⊙O的切线CE，交OF于点E．如果OA=4，EF=3，则弦AC的长为___. [16sqrt5/5]

(11杭州) 如图，点A，B，C，D都在⊙O上，$\overset{\LARGE{\frown}}{CD}$的度数等于84°，CA是∠OCD的平分线，则∠ABD+∠CAO=___. [48°]

(13河北) 如图，AB是⊙O的直径，弦CD⊥AB，∠C=30°，CD=$2\sqrt{3}$．则$S_{阴影}$=___. [2pi/3]

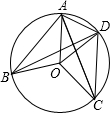
(13武汉) 如图②，已知△ABC是⊙O的内接三角形，AB=AC，点P是$ \overset{\LARGE{\frown}}{AB}$的中点，连接PA，PB，PC. 若sin∠BPC=$\frac{24}{25}$，则tan∠PAB=___． [1/2]

III-E

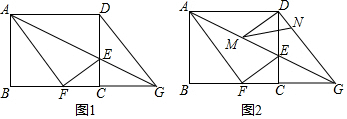
(19滨州) 如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG．若AB=6，AD=10，求四边形CEFG的面积为___. [20/3]

(19滨州) 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F．若⊙O的半径为4，∠CDF=15°，则阴影部分的面积___. [16pi/3-4sqrt3]

(19济宁) 如图，O为Rt△ABC直角边AC上一点，以OC为半径的⊙O与斜边AB相切于点D，交OA于点E，已知BC=$\sqrt{3}$ ，AC=3．则图中阴影部分的面积是___. [pi/6]

(19重庆) 如图，在菱形ABCD中，对角线AC，BD交于点O，∠ABC=60°，AB=2，分别以点A、点C为圆心，以AO的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为___. [2sqrt3-2pi/3]

(19枣庄) 如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置．若四边形AECF的面积为20，DE=2，则AE的长为___. [2sqrt6]

(19枣庄) 如图，在边长为4的正方形ABCD中，以点B为圆心，AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是（结果保留π）___. [8-2pi]

(19枣庄) 如图，在Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上一点，且CD=CB，连接DO并延长交CB的延长线于点E. 若BE=2，DE=4，则AC=___. [3sqrt2]

IV-A

(19德州) 如图，点O为线段BC的中点，点A，C，D到点O的距离相等，若∠ABC=40°，则∠ADC的度数是___. [140°]

如图，直线l1∥l2，∠1=20°，则∠2+∠3等于___. [200°]

如图1，已知，AB∥CD，点E为射线FG上一点．若∠EAF=30°，∠EDG=40°，则∠AED=___. [70°]

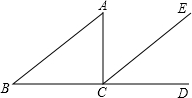
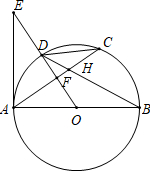
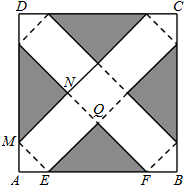
如图，对折长方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开：再一次折叠纸片，使点A落在EF上（设落地为N），并使折痕经过点B，得到折痕BM，连接BN、MN，请你猜想∠MBN的度数是___． [30°]

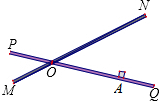
(11武汉) 如图，铁路MN和公路PQ在点O处交汇，∠QON=30°，公路PQ上A处距离O点240米，如果火车行驶时，周围200米以内会受到噪音的影响，那么火车在铁路MN上沿MN方向以72千米/小时的速度行驶时，A处受到噪音影响的时间为___秒. [16]

IV-B

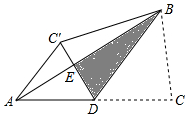
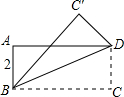
(19重庆) 如图，在△ABC中，D是AC边上的中点，连结BD，把△BDC沿BD翻折，得到△BDC'，DC′与AB交于点E，连结AC'，若AD=AC′=2，BD=3，则点D到BC′的距离为___. [3sqrt21/7]

(19枣庄) 如图，将△ABC沿BC边上的中线AD平移到△A′B′C′的位置．已知△ABC的面积为16，阴影部分三角形的面积9．若AA′=1，则A′D等于___. [3]

(19枣庄) 把两个同样大小含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A，且另外三个锐角顶点B，C，D在同一直线上．若AB=2，则CD=___. [sqrt6-sqrt2]

(19绵阳) 如图，在四边形ABCD中，AB∥DC，∠ADC=90°，AB=5，CD=AD=3，点E是线段CD的三等分点，且靠近点C，∠FEG的两边与线段AB分别交于点F、G，连接AC分别交EF、EG于点H、K．若BG=$\frac{3}{2}$，∠FEG=45°，则HK=___. [5sqrt2/6]

(19聊城) 如图，在Rt△ABC中，∠ACB=90°，∠B=60°，DE为△ABC的中位线，延长BC至F，使CF=$\frac{1}{2}$BC，连接FE并延长交AB于点M．若BC=1，则△FMB的周长为___. [9/2]

如图，在Rt△ABC中，点E在AB上，把这个直角三角形沿CE折叠后，使点B恰好落到斜边AC的中点O处，若BC=3，则折痕CE的长为___. [4sqrt3]

如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=55°，则∠3的度数等于___. [25°]

IV-C

(19天津) 如图，正方形纸片ABCD的边长为12，E是边CD上一点，连接AE、折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上，若DE=5，则GE的长为__. [49/13]

(13重庆) 如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF、BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC．若BC=$2\sqrt{3}$，则AB=___. [6]

(12北京) 如图，在四边形ABCD中，对角线AC，BD交于点E，∠BAC=90°，∠CED=45°，∠DCE=30°，DE=$\sqrt{2}$，BE=$2\sqrt{2}$．四边形ABCD的面积为___. [(3sqrt3+9)/2]

(13河北) 如图，菱形ABCD中，点M，N在AC上，ME⊥AD，NF⊥AB．若NF=NM=2，ME=3，则AN=___. [4]

(13陕西) 如图，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC．若BD=8，AC=6，∠BOC=120°，则四边形ABCD的面积为___. [12sqrt3]

IV-D

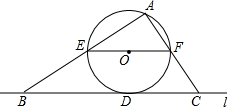
(19德州) 如图，CD为⊙O的直径，弦AB⊥CD，垂足为E， $ \overset{\LARGE{\frown}}{AB} = \overset{\LARGE{\frown}}{BF}$，CE=1，AB=6，则弦AF的长度为___. [48/5]

(19达州) 如图，⊙O是△ABC的外接圆，∠BAC的平分线交⊙O于点D，交BC于点E，过点D作直线DF∥BC. 若AB=6，AE=$\frac{12\sqrt{3}}{5}$，CE=$\frac{4\sqrt{7}}{5}$，则BD=___． [2sqrt21/3]

(19绵阳) 如图，AB是⊙O的直径，点C为$\overset{\LARGE{\frown}}{BD}$ 的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．若AD=BE=2，则 BF=___． [2sqrt3]

(19天津) 如图①，已知PA，PB分别与⊙O相切于点A，B，∠APB=80°，C为⊙O上一点．∠ACB=___. [50°]

(13重庆) 如图，P是⊙O外一点，PA是⊙O的切线，PO=26cm，PA=24cm，则⊙O的周长为___cm. [20pi]

IV-E

(19 自贡) 如图，在由10个完全相同的正三角形构成的网格图中，∠α、∠β如图所示，则cos（α+β）=___．

(19金华) 如图，在▱OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D． $\overset{\LARGE{\frown}}{BD}$ = ___. [45°]

(19金华) 如图，在▱OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D．点E在⊙O上，连结CE与⊙O交于点F，若EF=AB，则∠OCE的度数是___. [30°]

(19衢州) 如图，在等腰△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E．若DE=$\sqrt{3}$ ，∠C=30°，则 $ \overset{\LARGE{\frown}}{AD}$ = ___. [2pi/3]

(19济宁) 如图，AB是⊙O的直径，C是⊙O上一点，D是 $\overset{\LARGE{\frown}}{AC}$ 的中点，E为OD延长线上一点，且∠CAE=2∠C，AC与BD交于点H，与OE交于点F．若DH=9，tanC=$\frac{3}{4}$ ，则直径AB=___. [20]

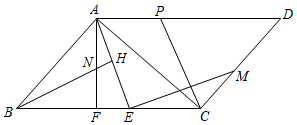
(19重庆) 如图，在平行四边形ABCD中，点E在边BC上，连结AE，EM⊥AE，垂足为E，交CD于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P是AD上一点，连接CP．若DP=2AP=4，CP=$\sqrt{17}$，CD=5，则△ACD的面积为___. [12]

(19绵阳) 如图，在以点O为中心的正方形ABCD中，AD=4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．当点H恰好落在线段BC上时，EH=___. [2sqrt10-5sqrt2]

V-A

如图，已知AM∥BN，∠A=80°，点P是射线AM上动点（与A不重合），BC、BD分别平分∠ABP和∠PBN，交射线AM于C、D．当点P运动时，∠APB:∠ADB=___； [2]

(15鄂州) 如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长取最小值时，四边形PMON的面积为___. [36sqrt3-54]

如图，∠BAC=30°，AP平分∠BAC，GF垂直平分AP，交AC于F，Q为射线AB上一动点，若PQ的最小值为5，则AF的长为___. [10]

如图，是由几个小立方体所搭成的几何体从上方看到的图形，小正方形中的数字表示在该位置小立方块的个数，已知小立方体边长为1，则这个几何体的表面积是___. [36]

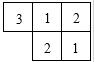
有同样大小的三个立方体骰子，每个骰子的展开图如图1所示，如果把每个骰子点数是4的一面放在桌子上，那么其它五个可以看到的面上的数字的和是17，现在把三个骰子放在桌子上（如图2），凡是能看得到的点数之和最大是___. [51]

V-B

(19金华) 如图2，在等腰Rt△ABC中，∠ACB=90°，AB=$14 \sqrt{2}$，点D，E分别在边AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF，点G为AF的中点.若AD=BD，CE=2，则 DG=___．[5sqrt2/2]

(19绵阳) 如图，△ABC、△BDE都是等腰直角三角形，BA=BC，BD=BE，AC=4，DE=$2\sqrt{2}$．将△BDE绕点B逆时针方向旋转后得△BD′E′，当点E′恰好落在线段AD′上时，则CE′=___. [sqrt2+sqrt6]

(12河南) 如图，在Rt△ABC中，∠C=90°，AC=6，BC=8．把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′，A′C′交AB于点E．若AD=BE，则△A′DE的面积是___. [6]

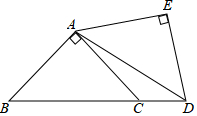
(13成都) 如图，点B在线段AC上，点D、E在AC同侧，∠A=∠C=90°，BD⊥BE，AD=BC．若AD=3，CE=5，点P为线段AB上的动点，连接DP，作PQ⊥DP，交直线BE于点Q；当点P与A、B两点不重合时，$\frac{DP}{PQ}$=___. [3/5]

(11成都) 如图，已知线段AB∥CD，AD与BC相交于点K，E是线段AD上一动点．若BK=$\frac{5}{2}$KC，则$\frac{CD}{AB}$=___. [2/5]

V-C

(19金华) 将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕．若正方形EFGH与五边形MCNGF的面积相等，则 $\frac{FM}{GF}$ 的值是___. [(sqrt5-sqrt2)/2]

(12河南) 如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．当AM的值为___时，四边形AMDN是矩形. [1]

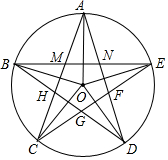
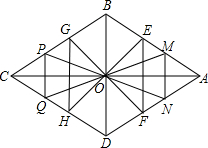
(11杭州) 图形既关于点O中心对称，又关于直线AC，BD对称，AC=10，BD=6，已知点E，M是菁优网线段AB上的动点（不与端点重合），点O到EF，MN的距离分别为h1，h2，△OEF与△OGH组成的图形称为蝶形．蝶形面积S的最大值是___. [15/2]

(13河北) 如图，四边形ABCD中，点M、N分别在AB、BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B=___. [95°]

(13成都) 如图，将矩形ABCD沿对角线BD折叠，使点C和点C′重合，若AB=2，则C′D的长为___. [2]

(12无锡) 如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒（A、B、C、D四个顶点正好重合于上底面上一点）．已知E、F在AB边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x（cm）．某广告商要求包装盒的表面（不含下底面）面积S最大，x应为___. [8]

V-D

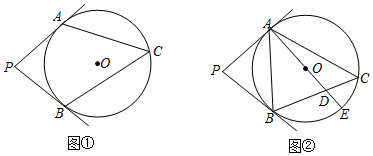
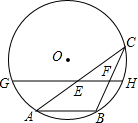
(13陕西) 如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH的最大值为___. [10.5]

(12上海) 如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．DE=___. [sqrt2]

如图，AB是⊙O的弦，AB=$4\sqrt{2}$，点C是⊙O上的一个动点，且∠ACB=45°，若点M、N分别是AB、BC的中点，则MN长的最大值是___. [4]

如图，PA、PB是⊙O的切线，A、B是切点，点C是劣弧AB上的一个动点（点C不与点A、点B重合），若∠P=30°，则∠ACB的度数是___. [105°]

如图，AB是半⊙O的直径，且AB=8．点C是半⊙O上的一个动点（不与点A、B重合），过点C作CD⊥AB，垂足为D．设AC=x，AD=y，则（x-y）的最大值等于___. [2]

V-E

(19衢州) 如图，取两根等宽的纸条折叠穿插，拉紧，可得边长为2的正六边形．则原来的纸带宽为___. [sqrt3]

(19济宁) 如图2，在矩形ABCD中，AB=8，AD=10，E是CD边上一点，连接AE，将矩形ABCD沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G．M，N分别是线段AG，DG上的动点（与端点不重合），且∠DMN=∠DAM，设AM=x，DN=y，则 y 的最小值为___. [2]

(12河北) 如图，在平行四边形ABCD中，∠A=70°，将平行四边形折叠，使点D、C分别落在点F、E处（点F、E都在AB所在的直线上），折痕为MN，则∠AMF等于___. [40°]

(12济南) 如图2，在菱形ABCD中，AC=2，BD=$2\sqrt{3}$，AC，BD相交于点O．将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F，连接EF与AC相交于点G．旋转过程中，当点E为边BC的四等分点时（BE＞CE），CG=___. [3/8]

如图，已知等边△ABC的边长为8，以AB为直径的圆交BC于点F．以C为圆心，CF长为半径作图，D是⊙C上一动点，E为BD的中点，当AE最大时，BD的长为___. [4sqrt5]

VI-E

(19济宁) 如图2，在矩形ABCD中，AB=8，AD=10，E是CD边上一点，连接AE，将矩形ABCD沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G．M，N分别是线段AG，DG上的动点（与端点不重合），且∠DMN=∠DAM，设AM=x，DN=y，当△DMN是等腰三角形时，x 的值为___. [8sqrt5-10;11sqrt5/2]

ronfe/item_set.md

Project Kibana

Catalog

Shapes

Methods

Items

I-A

I-B

I-C

I-D

I-E

II-A

II-B

II-C

II-D

II-E

III-A

III-B

III-C

III-D

III-E

IV-A

IV-B

IV-C

IV-D

IV-E

V-A

V-B

V-C

V-D

V-E

VI-E