債券をキャッシュフローに分解してイールドカーブの形状変化による価値変化をシミュレーションしてみる.
IRRBBは、"Interest Rate Risk in the Banking Book"の略で、銀行勘定の金利リスクのことをいいます。これは、金利水準の不利な変動により、銀行勘定の資産・負債の市場価格あるいは収益が変動することにより生じるリスクを指し、バーゼル銀行監督委員会の自己資本規制の枠組みにおいて、第2の柱(監督上の検証プロセス)の一環として位置付けられており、また「金利リスクの管理と監督のための諸原則(IRR諸原則:2004年制定)」に提示されたガイダンスが適用されます。 IRRBBとは|金融経済用語集
つまり銀行が抱えている金利リスクを明らかにするために, 金利水準が変化した場合のシナリオごとに発生する損益を明らかにせよということ.
シナリオは当局が定める次の6通りを想定する必要がある.
- 上方パラレルシフト
- 下方パラレルシフト
- スティープ化
- フラット化
- 短期金利上昇
- 短期金利低下
いずれのシナリオにおいても金利変化量は通貨ごとに定められており, 日本円の場合は次の計算方法による.
- パラレルシフトは上下100bp
- スティープ化, フラット化, 短期金利変化の場合は以下の式による.(Rshort, Rlongには100bpを与える)
IRRBBはプリンシプル・ベースの規則であるため, 具体的な計算モデルの構築は各金融機関に委ねられているが, 金利ショックに対する経済価値の変化額である⊿EVE(Economic Value of Equity)を公表することが定められている. つまりシナリオに応じた 金利変化後の経済的価値 - 金利変化前の経済的価値 を計算する必要がある.
銀行勘定は通常, 貸出金や有価証券など多様な資産を保有しており, そこから多種多様なキャッシュフローが発生するため, それらのキャッシュフローを対応する期間に分類して金利変化の影響を見ることとなる. ここでは, 代表的な資産として固定利付債を例として, 金利ショックによる価値変化をシミュレートしてみる. なお, 金利変化による債券価格の変化は一般的には修正デュレーションで考えられるが, これは金利のパラレルシフトしか対応できないため, イールドカーブの形状変化による損益を計算するには債券を発生時期別のキャッシュフローに分解する必要がある.
import datetime
import math
import numpy as np
# 基礎数値を設定(オリックス社債第195回)
maturity_date = datetime.datetime(2028, 11, 8)
base_date = datetime.datetime(2019, 3, 8)
coupon = 0.454
freq = 2 # 利払い回数
次に債券を(発生時点, 発生金額)のキャッシュフローに分解する.
zanzon = (maturity_date - base_date).days / 365
# 残存年数から利払い頻度に応じた期間を引いていく
cashflow = []
i = 0
while zanzon - (1 / freq) * i > 0:
cashflow.append(
(zanzon - (1 / freq) * i, coupon / freq + (100 if i == 0 else 0))
)
i += 1
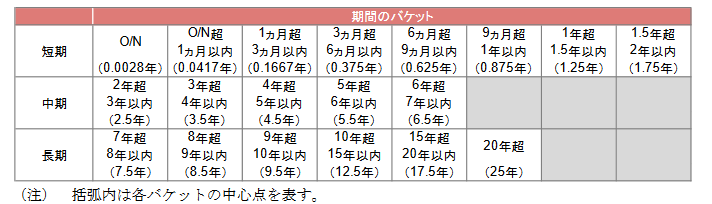
分解したキャッシュフローについて, 当局が定める19期間のバケットに割り当てる.
19期間に割り当てる際に, 期間と金額の加重平均が元々のキャッシュフローと同一になるように, 前後の時点に距離比例で配分する処理を行う.
# バケットの中心時点を設定
buckets_timing = [0.0028, 0.0417, 0.1667, 0.375, 0.625, 0.875, 1.25, 1.75, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 12.5, 17.5, 25]
# バケットへの割当金額を初期化
buckets_amount = [0 for t in buckets_timing]
for t, a in cashflow:
# CFの発生時期を元に前後のバケット時点を取得する
prev_timing = max([b for b in buckets_timing if b < t])
next_timing = min([b for b in buckets_timing if b > t])
# tとの距離に比例して配分率を決める(近いほど配分率が大きい)
prev_bucket_ratio = 1 - (t - prev_timing) / (next_timing - prev_timing)
next_bucket_ratio = 1 - (next_timing - t) / (next_timing - prev_timing)
prev_bucket_cf = a * prev_bucket_ratio
next_bucket_cf = a * next_bucket_ratio
# 前後のバケットに割当CF金額を加算する
buckets_amount[buckets_timing.index(prev_timing)] += prev_bucket_cf
buckets_amount[buckets_timing.index(next_timing)] += next_bucket_cf
キャッシュフローをバケットに割り当てたら次はシナリオ別の金利変化幅を生成する.
# イールドカーブ上の金利を求める関数を作成
# べき乗分母
x = 4.0
# パラレルシフトシナリオ
def change_parallel(parallel):
return parallel
# スティープ化シナリオ
def change_steepner(t, rshort, rlong):
return -0.65 * (rshort * math.e ** (-t / x)) + 0.9 * (rlong * (1 - math.e ** (-t / x)))
# フラット化シナリオ
def change_flattener(t, rshort, rlong):
return 0.8 * (rshort * math.e ** (-t / x)) - 0.6 * (rlong * (1 - math.e ** (-t / x)))
# 短期金利変化シナリオ
def change_short(t, rshort):
return rshort * math.e ** (-t / x)
さて, 当該債券の元々のイールドカーブにシナリオごとの金利変化幅を足せばシミュレートすべきイールドカーブが作成できるが, 債券によってはそもそも特定年限に発行が無くバケットの期間に対応するイールドカーブが描けないことがある. その場合の解決策として以下の方法が想定される.
| 解決策 | メリット | デメリット |
|---|---|---|
| 他の指標金利(国債のイールドカーブなど)で代用する | 全期間のイールドカーブが手に入りやすい | 銘柄固有のクレジットリスクは無視される |
| 当該債券の複利を全期間固定として適用する | 計算が楽 | 期間構造を反映しない仮想のイールドカーブとなる |
さて, 私は当該債券の市場価格が手に入れられず, 期間別の元イールドカーブを入手するのも煩雑であるため, ここでは簡便に長期金利をベースのイールドカーブとして使用することにする. そもそも⊿EVEは金利ショック時における経済価値の変動に着目しているので, 相対的なショック幅が重要なのであり, 絶対的な金利水準はそんなに影響ないのではと思うし, まいっか~.
base_rate = -0.00035
# 長短金利とパラレル変動幅
parallel = 0.01
rshort = 0.01
rlong = 0.01
# 変化量を取得する
senario = [
[(t, 0) for t in buckets_timing], # 変化なし
[(t, change_parallel(parallel)) for t in buckets_timing], # 上方パラレルシフト
[(t, change_parallel(parallel * -1)) for t in buckets_timing], # 下方パラレルシフト
[(t, change_steepner(t, rshort, rlong)) for t in buckets_timing], # スティープ化
[(t, change_flattener(t, rshort, rlong)) for t in buckets_timing], # フラット化
[(t, change_short(t, rshort)) for t in buckets_timing], # 短期金利上昇
[(t, change_short(t, rshort * -1)) for t in buckets_timing] #短期金利低下
]
イールドカーブの金利からシナリオ数ぶんの割引率(discount factor)を求める.
discount_factors = [[ 1 / ((1 + r / freq) ** (t * freq)) for t, r in change ] for change in senario]
バケットに分けた債券のキャッシュフローにディスカウントファクターを乗じて現在価値を求める.
pvs[0]が金利変化なしの場合の現在価値なので, 各シナリオから引いて⊿EVEを算出.
pvs = [ sum(bucket_amount * np.array(df)) for df in discount_factors ]
for i, pv in enumerate(pvs):
print(i, pv - pvs[0])
0 0.0
1 -9.417604340848655
2 10.42500387955431
3 -7.210492083514865
4 4.776781579555461
5 -0.9106947203782738
6 0.9193271935525047
上方パラレルシフトの場合に最大の損失が発生することがわかりました. めでたしめでたし.