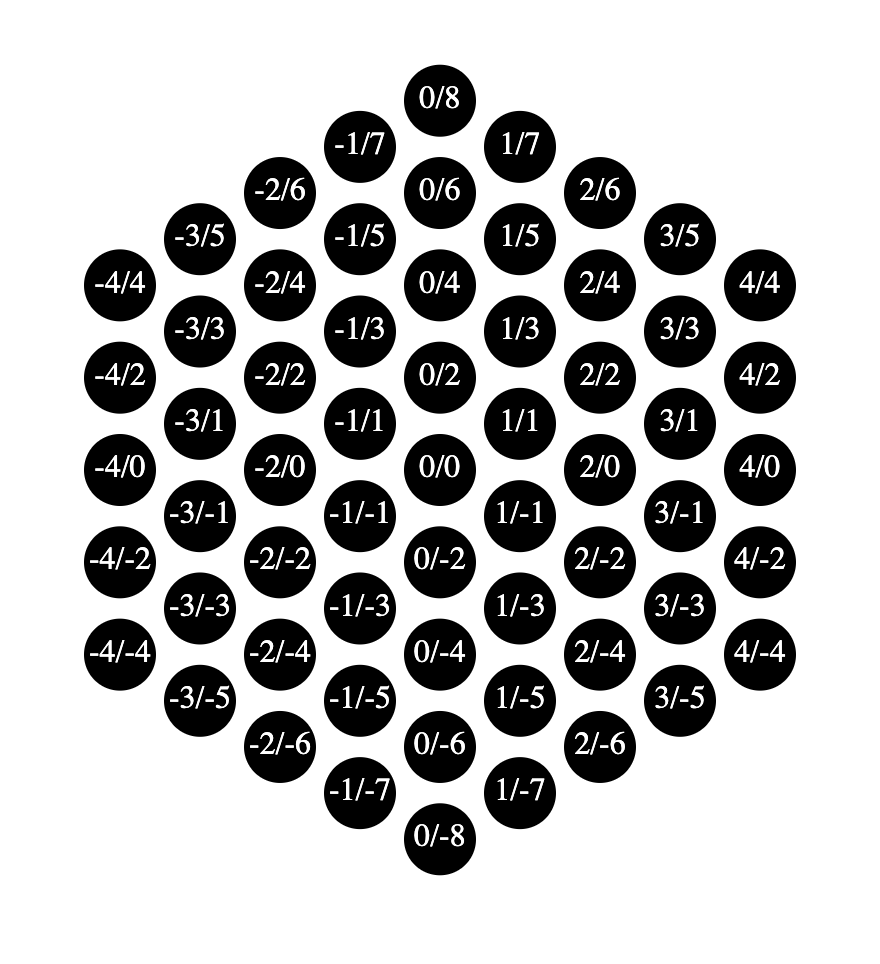
Create hexagon from cube (unusual derivation but clean algorithm) and render with D3

index.html

<!-- Screenshot of how it looks like below -->
<script src="https://cdnjs.cloudflare.com/ajax/libs/d3/7.0.0/d3.min.js" integrity="sha512-0x7/VCkKLLt4wnkFqI8Cgv6no+AaS1TDgmHLOoU3hy/WVtYta2J6gnOIHhYYDJlDxPqEqAYLPS4gzVex4mGJLw==" crossorigin="anonymous" referrerpolicy="no-referrer"></script>

 <div id="output">
 </div>

<script type="text/javascript">
	var svgCanvas = d3.select("#output")
        .append("svg")
        .attr("width", 1000)
        .attr("height", 1000);  

	const center = {
		x: 1000 / 2,
		y: 1000 / 2
	}

	const scale = {
		x: 40,
		y: 40*0.577
	}

	// 57,7% is what it takes to make a line that is 45° normally to be 30° which is what the isometric view is made up of

	// Math style proof:
	// - normal view: tan(45°) = (opposite side) / (adjacent side) = deltaYnormal / deltaX
	// - isometric view: tan(30°) = deltaYiso / deltaX

	// For both adjacent side which I called deltaX is the same because we only scale in y direction which gets us:
	// - normal view:  deltaX = deltaYnormal / tan(45°)
	// - isometric view:  deltaX = deltaYiso / tan(30°)
	// -> deltaYnormal / tan(45°) = deltaYiso / tan(30°)

	// With:
	// tan(45°) = 1
	// tan(30°) = 0.57735

	// deltaYnormal = deltaYiso / 0.57735
	// -> deltaYnormal * 0.57735 = deltaYiso

	const nodes = createNodes(4);
	drawPoints(nodes.array)

	function createNodes(numberOfRings){
		let nodesLUT = {};
		let nodesArray = [];

		const edgeLength = numberOfRings + 1;
		for(let cubeX = 0; cubeX < edgeLength; cubeX++){
			for(let cubeY = 0; cubeY < edgeLength; cubeY++){
				for(let cubeZ = 0; cubeZ < edgeLength; cubeZ++){
					// Idea from https://www.redblobgames.com/grids/hexagons/

					if(cubeX === 0 || cubeY === 0 || cubeZ === 0){
						// If any of the coordinates is 0, that means it's a point on one of 3 sides
						const projectedX = cubeY - cubeX;
						const projectedY = cubeX + cubeY - cubeZ * 2;

						let node = {
							x: projectedX,
							y: projectedY
						}

						const id = node.x + '/' + node.y;
						nodesLUT[id] = node; //Not necessary for drawing, but nice for using later for other purposes
						nodesArray.push(node)
					}
				}
			}	
		}
		return {
			array: nodesArray,
			lut: nodesLUT
		};
	}
	
	function drawPoints(nodesArray){
    	var selection = svgCanvas.selectAll("g")
        .data(nodes.array)
        .enter()
        .append("g")
        .attr("transform", function(d){ return "translate("+(d.x * scale.x+center.x)+","+(-d.y * scale.y+center.y)+")" })
        
       selection.append("circle")
        .attr("r", 18)
        .style("fill", "black")
       
       selection.append("text")
        .text(function(d){ return d.x + "/" + d.y })
        .attr('text-anchor', 'middle')
        .attr('alignment-baseline', 'middle')
        .attr('fill', 'white')
    }
</script>

Result: