gol.adoc

Game Of Life

Game of Life is mathematic toy world that was invented by John Horton Conway in 1970. Game of Life is played on a grid of cells that are either dead or alive by simluating how the world evolves over a series of rounds. In each round cells die, survive, or are reborn depending on the number of neighbours they have. You can find out more about Game of Life by watching the video below or reading up on it in Wikipedia.

This gist shows how to simulate game of life using Cypher.

Make sure we only create one node per grid position

CREATE CONSTRAINT ON (n:O) ASSERT n.id IS UNIQUE;

Let’s start by creating an empty grid of cells connected via horizontal and vertical relationships:

// Setup Grid
FOREACH (x in range(1,5) |
  FOREACH (y in range (1,5) |
    MERGE (a:O {id: [x, y]})
    MERGE (b:O {id: [x+1, y]})
    MERGE (c:O {id: [x, y+1]})
    MERGE (a)-[:X]->(b)
    MERGE (a)-[:Y]->(c)
  )
)
WITH 1 as dummy

FOREACH (x IN range(1,5) |
  MERGE (a:O {id: [x, 5]})
  MERGE (b:O {id: [x, 6]})
  MERGE (a)-[r:Y]->(b)
  DELETE r, b
)
WITH 1 as dummy

FOREACH (y IN range(1,5) |
  MERGE (a:O {id: [5, y]})
  MERGE (b:O {id: [6, y]})
  MERGE (a)-[r:X]->(b)
  DELETE r, b
)

Next, we’ll change the grid to contain one of the most common figures of game of life called a glider.

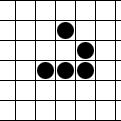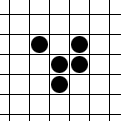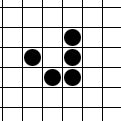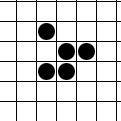
If you don’t like animations, here’s a static version:

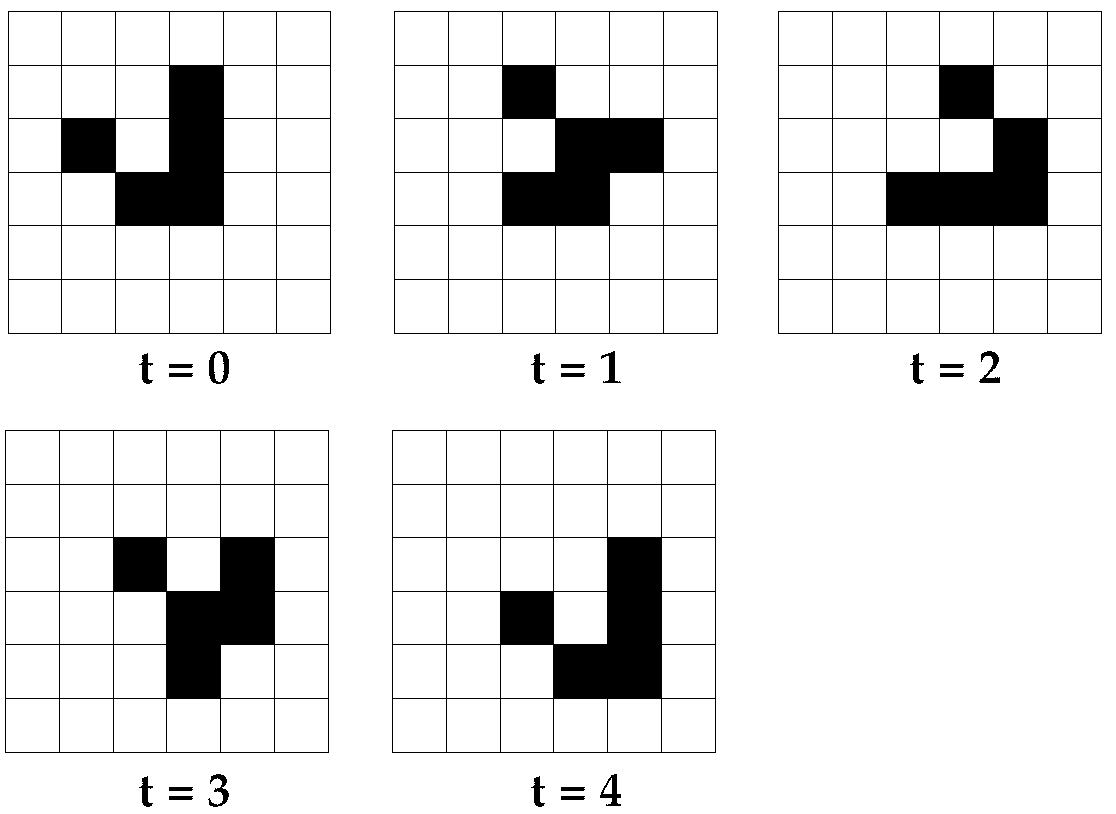
We put a glider in our grid by marking nodes as alive using the label A.

// Set up a game of life example: Glider
MERGE (a:O {id: [4, 4]}) SET a:A
MERGE (b:O {id: [3, 4]}) SET b:A
MERGE (c:O {id: [2, 4]}) SET c:A
MERGE (d:O {id: [4, 3]}) SET d:A
MERGE (e:O {id: [3, 2]}) SET e:A;

Now we are ready to simulate one cycle in the world we created. First we figure out the status of each cell:

MATCH (n:O)
OPTIONAL MATCH (west)-[:X]->(n)
OPTIONAL MATCH (north)-[:Y]->(n)
OPTIONAL MATCH (n)-[:X]->(east)
OPTIONAL MATCH (n)-[:Y]->(south)
OPTIONAL MATCH (northWest)-[:Y]->(west)
OPTIONAL MATCH (northEast)-[:Y]->(east)
OPTIONAL MATCH (southWest)<-[:Y]-(west)
OPTIONAL MATCH (southEast)<-[:Y]-(east)
WITH n, [west, north, east, south, northWest, northEast, southEast, southWest] AS hood
WITH n, filter(hoodie IN hood WHERE hood IS NOT NULL AND (hoodie:A)) AS living
WITH n, length(living) AS count, n:A AS alive, NOT (n:A) AS dead
SET n.count = count
SET n.underpopulation = alive AND (count < 2)
SET n.life = alive AND (count in [2, 3])
SET n.overpopulation = alive AND (count > 3)
SET n.reproduction = dead AND (count = 3)

Now cells die due to over- and underpopulation:

// simulate cell death
MATCH (n:O) WHERE n.underpopulation OR n.overpopulation REMOVE n:A RETURN n

And finally some cells survive this round or are newly born:

// simulate cell life and reproduction
MATCH (n:O) WHERE n.reproduction OR n.life SET n:A RETURN n

It works! We can also compute one cycle with a single Cypher query:

// simulate one cycle of game of life
MATCH (n:O)
OPTIONAL MATCH (west)-[:X]->(n)
OPTIONAL MATCH (north)-[:Y]->(n)
OPTIONAL MATCH (n)-[:X]->(east)
OPTIONAL MATCH (n)-[:Y]->(south)
OPTIONAL MATCH (northWest)-[:Y]->(west)
OPTIONAL MATCH (northEast)-[:Y]->(east)
OPTIONAL MATCH (southWest)<-[:Y]-(west)
OPTIONAL MATCH (southEast)<-[:Y]-(east)
WITH n, [west, north, east, south, northWest, northEast, southEast, southWest] AS hood
WITH n, filter(hoodie IN hood WHERE hood IS NOT NULL AND (hoodie:A)) AS living
WITH n, length(living) AS count, n:A AS alive, NOT (n:A) AS dead
SET n.count = count
SET n.underpopulation = alive AND (count < 2)
SET n.life = alive AND (count in [2, 3])
SET n.overpopulation = alive AND (count > 3)
SET n.reproduction = dead AND (count = 3)
WITH count(*) AS c
MATCH (n:O) WHERE n.underpopulation OR n.overpopulation REMOVE n:A
WITH count(*) AS c
MATCH (n:O) WHERE n.reproduction OR n.live SET n:A
WITH count(*) AS c
MATCH (n:O)
REMOVE n.count
REMOVE n.underpopulation
REMOVE n.life
REMOVE n.overpopulation
REMOVE n.reproduction

It glides!