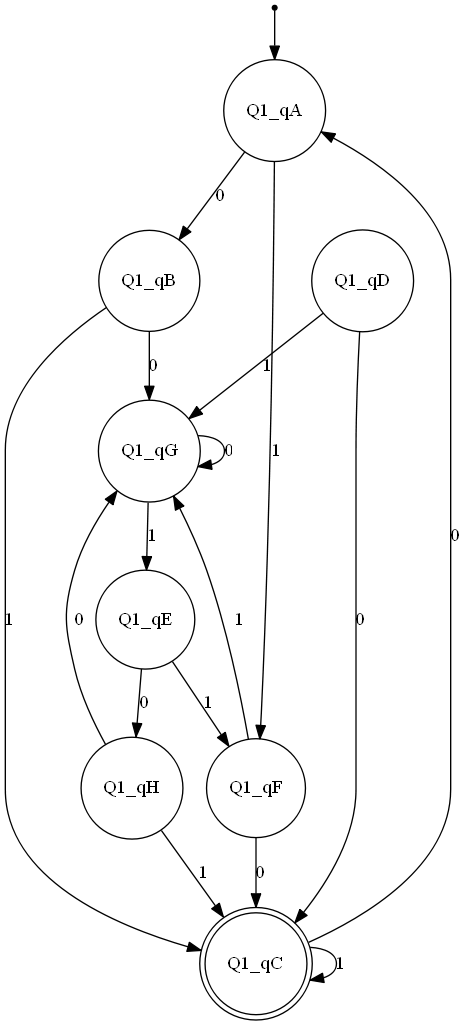
同値な状態のペアを見つける (穴埋めアルゴリズム)

_sandbox4.py

"""
同値な状態を取得する 穴埋めアルゴリズム を使ってみる
"""

from enum import Enum, auto

from graphviz import generate_dot, tweak_q
from nfa import NFA
from states_equivalent import equivalent_pair_set


def run(nfa, input_str):
    print(nfa.run(input_str), f"\t{input_str}")


def print_states(states):
    for pair in states:
        lst = [tweak_q(q) for q in pair]
        print("{" + ','.join(lst) + "}")


class StatesQ1(Enum):
    qA = auto()
    qB = auto()
    qC = auto()
    qD = auto()
    qE = auto()
    qF = auto()
    qG = auto()
    qH = auto()


# 遷移のペア
# 状態が q のときに、a を読みだしたときの遷移先を表す
transition_pair = {
    (StatesQ1.qA, "0"): {StatesQ1.qB},
    (StatesQ1.qA, "1"): {StatesQ1.qF},
    (StatesQ1.qB, "0"): {StatesQ1.qG},
    (StatesQ1.qB, "1"): {StatesQ1.qC},
    (StatesQ1.qC, "0"): {StatesQ1.qA},
    (StatesQ1.qC, "1"): {StatesQ1.qC},
    (StatesQ1.qD, "0"): {StatesQ1.qC},
    (StatesQ1.qD, "1"): {StatesQ1.qG},
    (StatesQ1.qE, "0"): {StatesQ1.qH},
    (StatesQ1.qE, "1"): {StatesQ1.qF},
    (StatesQ1.qF, "0"): {StatesQ1.qC},
    (StatesQ1.qF, "1"): {StatesQ1.qG},
    (StatesQ1.qG, "0"): {StatesQ1.qG},
    (StatesQ1.qG, "1"): {StatesQ1.qE},
    (StatesQ1.qH, "0"): {StatesQ1.qG},
    (StatesQ1.qH, "1"): {StatesQ1.qC},
}


nfa1 = NFA(
    states=set(StatesQ1),
    alphabets={"0", "1"},
    start_state=StatesQ1.qA,
    accept_states={StatesQ1.qC},
    transition_pair=transition_pair,
)

print()
print("NFA1")
run(nfa1, "101")
run(nfa1, "11")
run(nfa1, "100")
run(nfa1, "01000")
run(nfa1, "01000101")


print()
print("同値である状態の対")
# 表示されるものは、同値な状態のペア
print_states(equivalent_pair_set(nfa1))

print()
print(generate_dot(nfa1))

graphviz.py

def tweak_q(q):
    if "States" in str(q):
        return str(q).replace("States", "").replace(".", "_")
    else:
        return f"q{q}"


def generate_dot(nfa, name="sample"):
    """ Graphviz でそのまま出力できるテキスト"""
    result = ""
    result += "digraph sample {\n"
    # すべてを円にする
    result += "\tnode [ shape = circle ];\n"
    result += "\tq0 [ shape = point ];\n"
    # 開始状態
    result += f"""\tq0 -> {tweak_q(nfa.start_state)};\n"""

    from_to_labels = {}
    for tran, states in nfa.transition_pair.items():
        q_from, a = tran
        for q_to in states:
            # １つ状態から同じ遷移先の場合、ラベルを1つにしたいため
            labels = from_to_labels.get((q_from, q_to), [])
            labels += "ε" if a == "" else a
            from_to_labels[(q_from, q_to)] = labels

    # ラベルを結合して、出力
    for from_to_q, labels in from_to_labels.items():
        q_from, q_to = from_to_q
        label = ','.join(labels)
        result += f"""\t{tweak_q(q_from)} -> {tweak_q(q_to)} [label = "{label}"];\n"""

    for q in nfa.accept_states:
        result += f"""\t{tweak_q(q)} [ shape = doublecircle ];\n"""
    result += "}"
    return result

nfa.py

"""
NFA
"""
from functools import reduce


class NFA:
    def __init__(
        self, states, alphabets, start_state, accept_states, transition_pair,
    ):
        self.states = states
        self.alphabets = alphabets
        self.start_state = start_state
        self.accept_states = accept_states

        # 和集合演算するときに使うため、ここで関数を生成するようにしてみた
        # TODO: 空列の遷移を取り除いたあとの状態遷移のdictを生成しておきたい
        self.transition_pair = transition_pair
        # 関数の生成
        # 遷移関数
        self.transition = make_transition(transition_pair)
        # 空列での遷移関数 (開始状態にも使いたいため、こうした)
        self.E = make_E(transition_pair)

    def run(self, input_str: str) -> bool:
        """ 入力文字列を読み出し、受理するかどうかを返す
        """
        # その時時の状態は集合で表す
        # 毎回、リセット
        self.cur_states = self.E(set({self.start_state}))

        for s in input_str:
            # 各状態に対して、遷移関数を適用し、和集合演算する
            # print(f"{s}: {self.cur_states} ==> ", end="")
            _states = set()
            for q in self.cur_states:
                _states = _states.union(self.E(self.transition(q, s)))
            self.cur_states = _states
            # print(self.cur_states)

        # 受理状態が含まれていた場合、True
        return not self.accept_states.isdisjoint(self.cur_states)



def make_transition(tran_pair):
    """ 遷移関数を返す関数 """

    def transition_method(q, a):
        # E を適用
        return tran_pair.get((q, a), {})

    return transition_method


def make_E(tran_pair):
    def E(q_set):
        """ 空列でのみ遷移可能な状態に遷移する遷移関数 """
        q_list = list()
        for q in q_set:
            q_list += [
                states if q_key[0] == q and q_key[1] == "" else set()
                for q_key, states in tran_pair.items()
            ]

        # もし、空列で遷移できたのなら、もう一度呼び出す
        # その遷移先でも、空列で遷移できる可能性もあるため
        result = reduce(set.union, q_list + [q_set])
        if q_set == result:
            return result
        else:
            return E(result)

    return E

states_equivalent.py

"""
DFA の状態の同値性の判定

穴埋めアルゴリズムを使って、計算する
"""


def combinations(set_):
    """ すべての組み合わせの set を生成する """
    result = set()
    for s in set_:
        for t in set_:
            if s != t:
                # 同じものはだめ
                result.add(frozenset({s, t}))
    return result


def equivalent_pair_set(dfa):
    """ 同値な状態の対の集合を返す
    """
    # すべての状態の対の集合
    pair_set = combinations(dfa.states)

    # 区別可能な状態の対の集合
    # 「それ以外の状態」と「それ以外の状態」は空列で区別可能
    disting_pair_set = set()
    for p in dfa.states:
        for q in dfa.accept_states:
            # set の中には set は入れられないため
            if p != q:
                disting_pair_set.add(frozenset({p, q}))

    # 区別可能な状態の対の集合
    disting_pair_set = table_filling(
        pair_set, disting_pair_set, dfa.transition_pair, dfa.alphabets
    )
    # 区別可能なものを取り除いた集合を返す (同値な状態の対の集合を返す)

    return pair_set - disting_pair_set


def table_filling(pair_set, disting_pair_set, trans_pair, alphabets):
    """ 穴埋めアルゴリズム
    区別可能な状態の対を求める

    pair_set:
        すべての状態の対の集合
    disting_pair_set:
        区別可能な状態の対の集合
    trans_pair:
        遷移情報
    alphabets:
        アルファベットの集合
    """
    # 1文字での遷移先の状態の対が区別可能かどうかをチェックし、
    # 区別可能であった場合、その状態の対も区別可能
    # 区別可能ではなかった場合、その状態の対は同値である

    def trans(q, a):
        # DFA のため、必ず遷移が存在するはず
        res = trans_pair.get((q, a))
        if type(res) == set:
            # NFA から DFA に変換した場合、set だから、こうする
            return list(res)[0]
        else:
            return res

    result = set()

    for pair in pair_set:
        p, q = list(pair)
        for a in alphabets:
            r = trans(p, a)
            s = trans(q, a)
            if set(frozenset([r, s])) in disting_pair_set:
                result.add(frozenset({p, q}))
                break

    if disting_pair_set == result:
        # これ以上、新しいペアは見つからないため
        return result
    else:
        # 再帰
        return table_filling(pair_set, result, trans_pair, alphabets)

states_equivalent_better.py

"""
DFA の状態の同値性の判定

穴埋めアルゴリズムを使って、計算する
ちょっといい感じ ver
"""

from queue import SimpleQueue


def combinations(set_):
    """ すべての組み合わせの set を生成する """
    result = set()
    for s in set_:
        for t in set_:
            if s != t:
                # 同じものはだめ
                result.add(frozenset({s, t}))
    return result


def combinations_2(set1, set2):
    """ すべての組み合わせの set を生成する """
    result = set()
    for s in set1:
        for t in set2:
            if s != t:
                # 同じものはだめ
                result.add(frozenset({s, t}))
    return result


def equivalent_pair_set_better(dfa):
    """ 同値な状態の対の集合を返す
    """
    # すべての状態の対の集合
    pair_set = combinations(dfa.states)

    # チェックする状態のペア
    will_trace_pairs = SimpleQueue()

    # 最初は受理状態と受理状態以外の状態がチェック対象となる
    for pair in combinations_2(dfa.states, dfa.accept_states):
        will_trace_pairs.put_nowait(pair)

    # 区別可能な状態の対の集合
    # 「それ以外の状態」と「それ以外の状態」は空列で区別可能
    disting_pair_set = set()

    # 区別可能な状態の対の集合
    disting_pair_set = table_filling_better(
        pair_set, will_trace_pairs, dfa.transition_pair, dfa.alphabets
    )
    # 区別可能なものを取り除いた集合を返す (同値な状態の対の集合を返す)

    return pair_set - disting_pair_set


def table_filling_better(
    pair_set, will_trace_pairs: SimpleQueue, trans_pair, alphabets
):
    """ 穴埋めアルゴリズム
    区別可能な状態の対を求める

    pair_set:
        すべての状態の対の集合
    will_trace_pairs:
        チェック対象のペアの集合
    trans_pair:
        遷移情報
    alphabets:
        アルファベットの集合
    """
    # 1文字での遷移先の状態の対が区別可能かどうかをチェックし、
    # 区別可能であった場合、その状態の対も区別可能
    # 区別可能ではなかった場合、その状態の対は同値である

    def trans(q, a):
        # DFA のため、必ず遷移が存在するはず
        res = trans_pair.get((q, a))
        if type(res) == set:
            # NFA から DFA に変換した場合、set だから、こうする
            return list(res)[0]
        else:
            return res

    # すべての状態のペアに依存するペアのリストを生成する
    dependence_list_dict = dict()

    result = set()

    # 依存する状態のペアのリストを生成
    for pair in pair_set:
        p, q = list(pair)
        for a in alphabets:
            r = trans(p, a)
            s = trans(q, a)

            # 状態が同じではない or
            if r != s:
                lst = dependence_list_dict.get(frozenset([r, s]), [])
                lst += [{p, q}]
                dependence_list_dict[frozenset([r, s])] = lst

    # 依存するリストをたどる必要がなくなるまでループ
    while not will_trace_pairs.empty():
        r, s = will_trace_pairs.get_nowait()
        # 依存する状態をチェック
        for pair in dependence_list_dict.get(frozenset([r, s]), []):
            # 区別可能な状態に含まれていなければ、追加
            # また、そのリストもたどるため、キューに追加する
            if pair not in result:
                will_trace_pairs.put_nowait(pair)
                result.add(frozenset(list(pair)))
    return result

$ py -3 _sandbox4.py
NFA1
True 	101
False 	11
False 	100
False 	01000
True 	01000101

区別可能な状態の対
{Q1_qF,Q1_qD}
{Q1_qH,Q1_qB}
{Q1_qE,Q1_qA}

graphviz の部分は省略した

{F, D}、{H, B}、{E, A} が区別可能な対の状態ということ