A subtle introduction to Lambda Calculus for the JavaScript Developer

lambdajs.md

Lambda (λ) Calculus For Javascript Developers

This article aims at explaining lambda calculus in a more approachable less 'mathy' manner.

Terms That Are Good To Know

• Memoization: Memoization is an optimization technique used primarily to speed up computer programs by caching the result of expensive function calls and returning the cached result when fed with the same input.

• Pure Function: A pure function is a function whose computation does not depend on globally declared variables, it does no I/O or mutations. All it does is return a value after doing a bunch of computations on the arguments it recieves. For a given set of arguments, a pure function will always return the same value. Thus, a pure function is one that is memoizable.

• Functional Programming: This is a programming paradigm that employs the composition of pure functions in solving problems.

• Arity - This refers to the number of arguments a function accepts.

• Unary Function - A unary function is one that accepts only one argument. Lambda functions are unary.

Lambda Calculus is a formal system for expressing computation. Lambda Calculus encapsulates a formalization of the basic aspects of functions' constructions and their uses.

The Grammer rules are divided into two parts namely: Function Absraction and Function Application.

Function Abstraction:

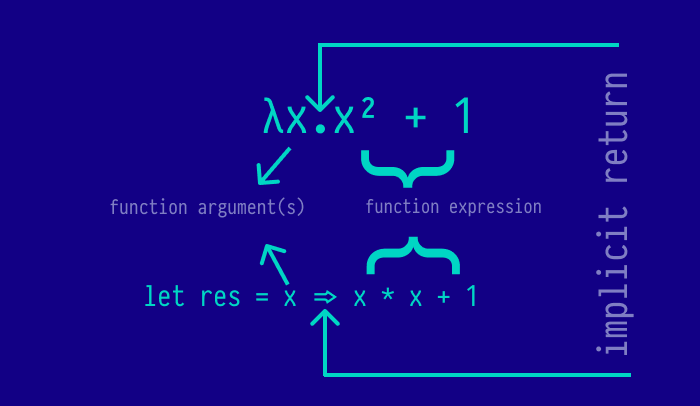
This defines what the function does. Below is a lambda function mapping x to x² + 1

λx.x² + 1

Don't overthink the "λ" symbol. It is only a Greek letter. A Javascript Equivalent should look something like this 👇

let res = x => x * x + 1;

Having expressed the λ expression in Javascript, it is clear that all it does is take an argument 'x' and return the result of increasing the square of 'x' by 1.

Function Application:

Function application computes a function. This can be thought of as calling a JavaScript function with a particular arugument. Application of λx.x² + 1 to 3 gives:

(λx.x² + 1) (3)

In JS

let res = (x => x * x + 1)(3)

The formalization of a function evaluation process is called 'β - reduction' (pronounced 'beta reduction'). β-reduction makes use of substitution. I like to think of this as peeling off of layers. Thinking of β-reduction in terms of peeling off of layers will prove effective when we start dealing with curried functions which as you will see look like an onion of brackets.

Currying

As aforementioned, lambda functions are unary functions. This might seem counterintuitive as we might want to do computations on multiple arguments (variables). This is where Currying comes to play. Lambda functions are powerful enough to not only return simple expressions. They can return Lambdas too!

Supposing we want to write a function that takes two arbitrary numbers, you might be tempted to write a function that looks like this:

λxy.x*y

This violates the grammer rule, as lambda functions can only handle one argument at a time.

Here's how that computation can be expressed:

(λx.(λy.x*y))

This is starting to look like an onion, but don't be dismayed. The above function is a lambda that accepts an argument 'x' and returns another lambda that accepts an argument 'y' that returns the product of x and y.

Note that these brackets can be ommited and the function can be written as:

λx.λy.x*y

To help visualize what is really going on we'll employ those pretty brackets.

How do we go about doing the maths anyways? Supposing we want to supply arguments 5 and 7 for x and y repectively, we do so by peeling off the onion, layer by layer.

We are going to employ β reduction one step at a time.

Supplying '5' as the first argument:

(λx.(λy.x*y)) (5)

The expression is reduced to:

(λy.5*y)

One onion layer has been dealt with.

Supplying '7' as the second argument:

(λy.5*y) (7)

We now have:

5 * 7

And finally with nothing left to peel off:

35

Let us see how this technique plays out in a similar Javascript program. A function that returns the product of two numbers.

  function product(x, y) {
    return x * y;
  }

  product(5, 7) //retuns 35

This function can be rewritten as a generalized curried function.

  function product (x) {
    return function (y) {
      return x * y;
    }
  }

Let's for clarity sake rewrite the above function employing ES6 explicit return.

let product = x => y => x * y;

We are going to call the function with the argument '2' and assign the return value to a variable 'double'.

  let double = (x => y => x * y)(2);

Every occurence of 'x' in the function body is replaced with '2'. The resulting function is thus:

     double = y => 2 * y

I now have a generalized double function that I can call as many times as I want.

double(4) //8
double(8) //16
double(100) //200

In subsequent posts, more practical applications of this technique will be discussed. Stay tuned. Do not fear the Lambda.

Thanks for going over the advantages. Would you recommend currying all functions? If we make curried and uncurried versions of each function, function names would be more cumbersome, so it seems to me that we have to decide whether to curry all functions or none of them, which can lead to bikeshedding.

It boils down to preferred style. At the end of the day, regardless of paradigm, we're only trying to solve problems.
In functional languages like Haskell and Purescript, functions are curried by default.
Javascript's treatment of functions as first class entities that can be passed around like values allows for the use of functional abstractions.
Ramda https://ramdajs.com/ (A practical functional library for JavaScript programmers) might interest you.