モンテカルロ法でtic-tac-toe

mc_tic_tac_toe.py

import gym
import numpy as np
import gym_tic_tac_toe
import random
from math import floor
import matplotlib.pyplot as plt

def random_plus_middle_move(moves, p):
    if ([p, 4] in moves):
        m = [p, 4]
    else:
        m = random_move(moves, p)
    return m
def random_move(moves, p):
    m = random.choice(moves)
    return m

env = gym.make('tic_tac_toe-v0')
n_states = 3**9
n_actions = 9 

rate = []
    
def monte_carlo_policy_iteration(L,M,options):
    T = 10
    
    # initiate lookup table
    Q = np.zeros((n_states, n_actions))

    ####################
    # policy iteration 
    ####################
    for l in range(L):
        visits = np.ones((n_states, n_actions))
        states = np.ones((M, T))
        actions = np.ones((M, T))
        rewards = np.zeros((M, T))
        drewards = np.ones((M, T))
        results = np.zeros(M)
        
        np.random.seed(555)

        # episode
        for m in range(M):
            state = env.reset()
            state3 = state['board']

            done = False
            
            # step
            for t in range(T):
                state3 = encode1(state3)
                state10 = encode2(state3)
                # generate policy
                policy = np.zeros(n_actions)
                
                #####################
                # policy improvement
                #####################
                policy = policy_improvement(options, Q, state10, policy)
            
                action, state, reward, done = action_train(t, state3, policy)
                
                state3 = state['board']
                states[m,t] = state10
                actions[m,t] = action[1]
                rewards[m,t] = reward
                visits[state10, action[1]] += 1
        
                if done or env.move_generator() == []:
                    if reward == 1:
                        fin = 2
                    elif reward == -1:
                        fin = 1
                    elif reward == 0:
                        fin = 3
                    else:
                        fin = None
                    results[m] = fin
                    
                    drewards = calculate_discounted_rewards(m, t, rewards,
                                                            options, drewards)
                    break
                
        #####################
        # policy evaluation
        #####################
        Q = policy_evaluation(M, T, states, actions, drewards, visits)
        
        output_results(l, results, M)
        rate.append( float(len(results[results==2]))/M )
        
###############################################################################
###############################################################################

convert = [[0,1,2,3,4,5,6,7,8],
           [2,1,0,5,4,3,8,7,6],
           [6,3,0,7,4,1,8,5,2],
           [0,3,8,1,4,7,2,5,8],
           [8,7,6,5,4,3,2,1,0],
           [6,7,8,3,4,5,0,1,2],
           [2,5,8,1,4,7,0,3,6],
           [8,5,2,7,4,1,6,3,0]
           ]

power = np.array([ 3**i for i in range(8,-1,-1) ], dtype=np.float64)

def encode1(state3):
    ret = np.empty(len(state3))
    for n, i in enumerate(state3):
        if i == -1:
            ret[n] = 1
        elif i == 1:
            ret[n] = 2
        else:
            ret[n] = 0
    return ret

def encode2(state3):
    cands = [sum(state3[convert[i]]*power) for i in range(len(convert))]
    return int(min(cands))+1

def policy_improvement(options, Q, state10, policy):
    if options['pmode']==0:
        q = Q[state10]
        v = max(q) 
        a = np.where(q==v)[0][0]
        policy[a] = 1
    elif options['pmode']==1:
        q = Q[state10] 
        v = max(q) 
        a = np.where(q==v)[0][0]
        policy = np.ones(n_actions)*options['epsilon']/n_actions
        policy[a] = 1-options['epsilon']+options['epsilon']/n_actions
    elif options['pmode']==2:
        policy = np.exp(Q[state10]/options['tau'])/ \
            sum(np.exp(Q[state10]/options['tau']))
    return policy

def select_npc_action(step, state3, policy):
    a = None
    # first step is always select 0
    if step==0:
        return [1, 0]
    else:
        while 1:
            random = np.random.rand()
            cprob = 0
            for a in range(n_actions):
                cprob += policy[a]
                if random<cprob: 
                    break 
            if state3[a]==0:
                break
    return [1, a]

def select_enemy_action(state3, moves):
    reach = False
    pos = [[0,1,2],[3,4,5],[6,7,8],[0,3,6],[1,4,7],[1,5,8],[0,4,8],[2,4,6]]
    a = None
    for i in range(len(pos)):
        state_i = state3[pos[i]]
        val = sum(state_i)
        num = len(state_i[state_i==0])
        if val==2 and num==1:
            idx = int( state_i[state_i==0][0] )
            a = pos[i][idx]
            if [-1, a] in moves:
                reach = True
                break
    if not reach:
        while 1:
            a = floor(np.random.rand()*8)+1
            if state3[a] == 0:
                break
    return [-1, a]

def action_train(t, state3, policy):
    # select action
    npc_action = select_npc_action(t, state3, policy)

    # action execute
    state, reward, done, _ = env.step(npc_action)

    moves = env.move_generator()
    
    if done or moves == []:
        return npc_action, state, reward, done
        
    state3 = encode1(state['board'])
    enemy_action = select_enemy_action(state3, moves)

    # action execute
    state, reward, done, _ = env.step(enemy_action)
    
    if not done and reward == 0:
        reward = None
    
    return npc_action, state, reward, done

def calculate_discounted_rewards(m, t, rewards, options, drewards):
    drewards[m,t] = rewards[m,t]
    for pstep in range(t-1,-1, -1):
        drewards[m,pstep] = options['gamma']*drewards[m,pstep+1]
    return drewards

def output_results(l, results, M):
        print('l=%d: Win=%d/%d, Draw=%d/%d, Lose=%d/%d' % (l, \
        len(results[results==2]),M, \
        len(results[results==3]),M, \
        len(results[results==1]),M))
        
def policy_evaluation(M, T, states, actions, drewards, visits):
    Q = np.zeros((n_states, n_actions))
    for m in range(M):
        for t in range(T):
            s = states[m,t]
            a = actions[m,t]
            s = int(s)
            a = int(a)
            Q[s,a] += drewards[m,t]        
    return Q/visits

if __name__=='__main__':
    options = {'pmode':1 ,'epsilon':0.05,'tau':2,'gamma':0.9}
    monte_carlo_policy_iteration(10,1000,options)

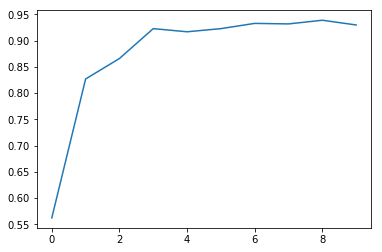
    plt.plot(range(len(rate)), rate)
    plt.show()