merge.js

function mergeSort(arr) {
  //
  // If your array has a length less than 2, congratulations! It's already sorted.
  if(arr.length < 2) {
    return arr;
  }
  // Otherwise, cut your array in half, and consider the two sub-arrays separately.
  var firstLength = arr.length / 2;
  var firstHalf = arr.slice(0, firstLength);
  console.log('firstLength', firstLength);
  firstHalf = mergeSort(firstHalf);
  var secondHalf = arr.slice(firstLength);
  secondHalf = mergeSort(secondHalf);
  // Sort each of your smaller subarrays using merge sort.

  return merge(firstHalf, secondHalf);
  // Merge your two subarrays together, and return the merged array.
}

function merge(arr1, arr2) {

    // 1. declare a new empty array, and pointers corresponding to indices in arr1 and arr2 (set them both to 0)
    var merged = [];
    var firstIndex = 0;
    var secondIndex = 0;

    // 3. Repeat this process until you've gone through one of the arrays
    while(firstIndex < arr1.length && secondIndex < arr2.length) {
      // 2. if the first element in arr1 is less than the first element in arr2,
      if(arr1[firstIndex] < arr2[secondIndex]) {
        // push the first element in arr1 to the new array, and move the pointer for arr1 one spot to the right.
        merged.push(arr1[firstIndex])
        firstIndex++;
      }
      else {
        // Otherwise, do this for arr2.
        merged.push(arr2[secondIndex])
        secondIndex++;
      }
    }

    // return merged.concat(arr1.slice(firstIndex), arr2.slice(secondIndex))
    // OR
    return merged.concat(arr1.splice(firstIndex, arr1.length - firstIndex), arr2.splice(secondIndex, arr2.length - secondIndex))
    // return the new array, concatenated with whatever elements are remaining from the array that you haven't exhausted yet.
}

//
// var nums = [1,5,7,9];
// var nums2 = [3,8,10,99];
//
// console.log(merge(nums, nums2));

var gifNums = [6,5,3,1,8,7,2];
console.log(mergeSort(gifNums));

merge_and_quick_sort.md

"Advanced" Sorting

n²?? We can do better than that!!

---

Objectives

• Implement a merge sort algorithm
• Analyze the Big O of merge sort
• Implement a quicksort algorithm
• Analyze the Big O of quicksort

---

Bubble, Selection, and Insertion sort

These sorting methods are fairly straight forward, but are O(n²)

This is fine for smaller arrays, but for larger arrays, we can (and must) do better.

---

Merge Sort and Quick Sort

Perform better on average as the size of the array grows

---

Merge Sort

---

Merge Sort

Invented by John von Neumann in 1945.

He was a Hungarian-American pure and applied mathematician, physicist, inventor, computer scientist, and polymath.

---

John von Neumann

von Neumann did A LOT in his career, including inventing the Von Neumann Architecture in 1945 which to this day is the basis of modern computer design.

This architecture allows data and a program to co-exist in memory. Before this, computers were programmed by setting switches and inserting patch leads to route data and to control signals between various functional units.

---

Merge Sort was the first program written for the Von Neumann Architecture

Von Neumann's First Computer Program by Donald E. Knuth

---

Merge Sort

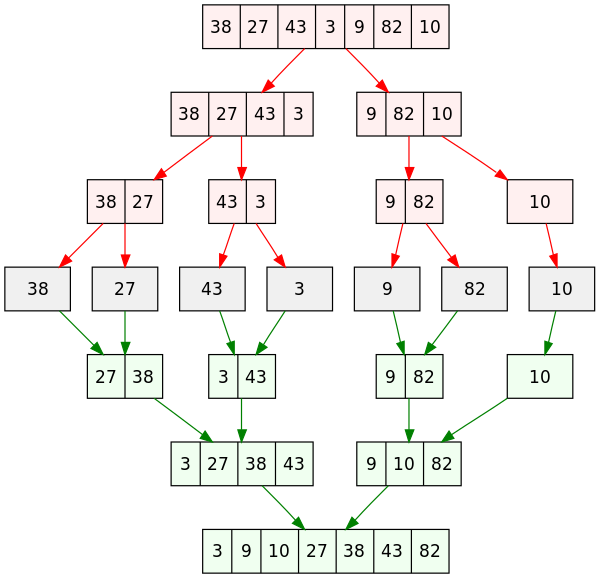
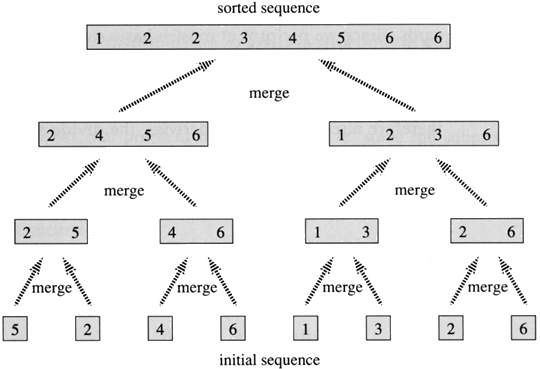
Merge sort works by decomposing the array into smaller chunks, which are then sorted and merged together.

This process goes all the way down to arrays of size 1, which are super easy to sort!

---

Merge Sort Steps:

1. If your array has a length less than 2, congratulations! It's already sorted.
2. Otherwise, cut your array in half, and consider the two sub-arrays separately.
3. Sort each of your smaller subarrays using merge sort.
4. Merge your two subarrays together, and return the merged array.

---

Post It Notes Demonstration

---

Merge: merge two sorted arrays into a single sorted array

In order to implement merge sort, it's useful to have a helper function that takes two sorted arrays and merges them together to create a new, larger sorted array.

Merge Steps:

function merge(arr1, arr2) {

    // 1. declare a new empty array, and pointers corresponding to indices in arr1 and arr2 (set them both to 0)
    // 2. if the first element in arr1 is less than the first element in arr2,
          // push the first element in arr1 to the new array, and move the pointer for arr1 one spot to the right.
          // Otherwise, do this for arr2.
    // 3. Repeat this process until you've gone through one of the arrays
    // return the new array, concatenated with whatever elements are remaining from the array that you haven't exhausted yet.
}

---

Array Merge: Steps to Code

---

<iframe class="stretch" src="http://visualgo.net/sorting"></iframe>

visualgo

---

Example: Splitting an array in half

---

Merge Sort: Steps to Code

---

Merge Sort complexity

n iterations to split the array.

log(n) iterations to merge them back together

O(n) * O(log n) = O(n log(n))

---

---

---

Volunteer?

---

BREAK

Back at 10:45

---

Quick Sort

---

Quick Sort

Invented by Sir Charles Antony Richard Hoare in 1959/1960.

He is a British computer scientist commonly known for inventing the null reference pointer in 1965.

---

Quick Sort

Quick sort works by choosing a pivot, and sorting the rest of the array around the pivot.

---

Quick Sort Steps:

1. Take an element in the array and refer to it as the "pivot." For simplicity, we'll take the first element in the array to be the pivot. (As you'll see, this is a bad choice if the array is already sorted. It makes the algorithm a little easier to reason about though, so we'll take the tradeoff.)
2. Compare every other element to the pivot. If it's less than the pivot value, move it to the left of the pivot. If it's greater, move it to the right. Don't worry about where on the left or right you're putting these values; the only thing that matters is comparisons to the pivot.
3. Once you're done, the pivot will be in the right place, and you can then recursively repeat this process with the left and right halves of the array.

---

Post It Notes Demonstration

---

<iframe class="stretch" src="http://visualgo.net/sorting"></iframe>

visualgo

---

Quick Sort: Steps to Code

---

Quick Sort that returns a new array

function quickSort(arr) {
  /* 1. If the length of the array is less than 2, it is already sorted, so return it.
  2. Otherwise, create two empty arrays (one for the left and one for the right), and set the first value in arr equal to the pivot.
  3. Compare every element in the array to the pivot. If the element is less than the pivot, push it into the left array. Otherwise, push it into the right array.
  4. Recrusively call quickSort on the left array and the right array, then concatenate these arrays together with the pivot value in between them, and return this larger array. */
}

---

Quick Sort in place

The downside to the new array approach, is that is uses more memory.

We can implement quick sort in place with a helper function partition.

---

Partition

// left and right indicate the left and rightmost indices in the sub-array that you're partitioning.
function partition(arr, left, right) {
  // 1. Set the pivot value to be the value at the left index, and set a variable called partitionIndex equal to left.
    // The partitionIndex will help us keep track of where to perform our swaps so that we wind up with values correctly placed on either side of the pivot.
  // 2. For every index greater than left and less than right + 1, compare the array value to the pivot value.
  // 3. If the array value at the given index is less than the pivot value,
    //increment the partition index and swap the array value with the value at the partition index.
  // 4. At the end, swap the pivot value with the value at the partition index
    //(this ensures that the pivot ends up in between values less than it and values greater than it).
  // 5. Return the partition index.
}

---

Quick Sort with Partition

function quickSort(arr, left=0, right=arr.length - 1) {
  // 1. If left is less than right, declare a variable called partitionIndex
      // which is equal to the result of a call to partition, passing in arr, left, and right.
      // After the call to partition, perform a quicksort to the two subarrays to the left and right of the partitionIndex.
  // 2. Return arr.
}

---

Quick Sort complexity

n iterations to choose a pivot.

Best case log(n) iterations to partition around each chosen pivot. Worst case n iterations to partition around each chosen pivot.

O(n) * O(log n) = O(n log(n))

O(n) * O(n) = O(n²)

---

Review

• Implement a merge sort algorithm in Javascript
• Analyze the Big O of merge sort
• Implement a quicksort algorithm in Javascript
• Analyze the Big O of quicksort

quickSort.js

'use strict';

function swap(arr, ind1, ind2) {
  let temp = arr[ind1];
  arr[ind1] = arr[ind2];
  arr[ind2] = temp;
}

function quickSortInPlace(arr, left, right) {
  left = left || 0;
  right = typeof(right) == 'undefined' ? arr.length - 1 : right;
  // 1. If left is less than right, declare a letiable called partitionIndex
  if(left < right) {
    // which is equal to the result of a call to partition, passing in arr, left, and right.
    let partitionIndex = partition(arr, left, right);
    // After the call to partition, perform a quicksort to the two subarrays
    // to the left and right of the partitionIndex.
    quickSortInPlace(arr, left, partitionIndex - 1);
    quickSortInPlace(arr, partitionIndex + 1, right);
  }

  return arr;
  // 2. Return arr.
}

function partition(arr, left, right) {
  // 1. Set the pivot value to be the value at the left index,
  let pivotValue = arr[left];
  // and set a letiable called partitionIndex equal to left.
  let partitionIndex = left;
    // The partitionIndex will help us keep track of where to perform our swaps so that we wind up with values correctly placed on either side of the pivot.

  // 2. For every index greater than left and less than right + 1,
  for (let i = left + 1; i < right + 1; i++) {
    // compare the array value to the pivot value.
    // 3. If the array value at the given index is less than the pivot value,
    if(arr[i] < pivotValue) {
      //increment the partition index and swap the array value with the value at the partition index.
      partitionIndex++;
      swap(arr, i, partitionIndex);
    }
  }

  swap(arr, left, partitionIndex);
  // 4. At the end, swap the pivot value with the value at the partition index
    //(this ensures that the pivot ends up in between values less than it and values greater than it).
  // 5. Return the partition index.
  return partitionIndex;
}

function quickSort(arr) {
  // 1. If the length of the array is less than 2, it is already sorted, so return it.
  if(arr.length < 2) {
    return arr;
  }

  // 2. Otherwise, create two empty arrays (one for the left and one for the right),
  // and set the first value in arr equal to the pivot.
  let left = [];
  let right = [];

  let pivotValue = arr[0];

  // 3. Compare every element in the array to the pivot.
  for (let i = 1; i < arr.length; i++) {
    //If the element is less than the pivot,
    if(arr[i] < pivotValue) {
      // push it into the left array.
      left.push(arr[i]);
    } else {
      // Otherwise, push it into the right array.
      right.push(arr[i]);
    }
  }
  // 4. Recrusively call quickSort on the left array and the right array,
  left = quickSort(left);
  right = quickSort(right);
  // then concatenate these arrays together with the pivot value in between them,
  left.push(pivotValue);
  return left.concat(right);
  // and return this larger array.
}

let gifNums = [6,5,3,1,8,7,2];
// console.log(quickSort(gifNums));
// gifNums = [6,5,3,1,8,7,2];
// console.log(partition(gifNums, 0, gifNums.length - 1))
// console.log(gifNums);
console.log(quickSortInPlace(gifNums));