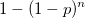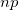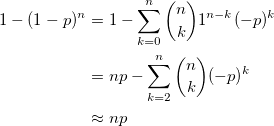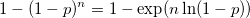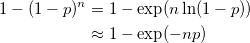pが十分小さい場合の近似として、次の式がよく用いられる:
この式は暗算でも容易に計算できる一方、誤差が大きい。例えば、この式に従えば、1%で成功することは100回繰り返せば必ず成功することになるが、厳密値(63.4%)とは掛け離れた結果である。この近似はどの程度の誤差があるのだろうか?また、どのような近似であればこうしたケースにも対処できるのだろうか?
上の近似は、厳密な値を得るための式を二項展開して得られるものである:
最初の式は、次のようにも変形できる。
ln(1 - p)をp = 0付近でテイラー展開して1次近似することにより、次の式が得られる:
この式は最初に示した1次近似ほど簡単ではないが、一部のケースについては暗算でも計算可能である。例えば、
p = 0.01 として n を変化させた結果をグラフ化したものをここで閲覧可能である。