Created
September 2, 2013 19:50
-
-
Save zhouzhuojie/6416659 to your computer and use it in GitHub Desktop.
Theory of NBRW 9.2
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| # Note | |
| ### Preliminaries | |
| * Definition of asymptotic variance of the estimator $\hat{\mu_n}=\frac{1}{n}\sum_{t=1}^nf(X_t)$ is | |
| $$V_{\infty}(\hat{\mu}) = \lim_{n\rightarrow\infty}nV(\hat{\mu_n}) $$ | |
| ### 1) Peskun's theorem on modifying a reversible chain to avoid staying in the same state | |
| _**Theorem 1 (Peskun 1973):** Let $X_1, X_2, \dots$ and $X'_1, X'_2, \dots$ be two irreducible Markov Chain on the finite state space $\mathcal{X}$, both of which are reversible with respect to the distribution $\pi$, and hence have $\pi$ as their unique invariant distribution. Let the transition probabilities for these chains be_ | |
| $$T(x,y) = P(X_{t+1}=y|X_t=x)\\ T'(x,y) = P(X'_{t+1}=y|X'_t=x) $$ | |
| _Let $f(x)$ be some function of state, whose expectation with respect to $\pi$ is $\mu$. Consider the following two estimators for $\mu$ based on these two chains:_ | |
| $$T'(x,y) \geq T(x,y) \,\,\,\text{for all $x, y\in \mathcal{X}$ with $x\neq y$}$$ | |
| _then the asymptotic variance $\hat{\mu'}$ will be no greater than that of $\hat{\mu}$_. | |
| **Proofs:** | |
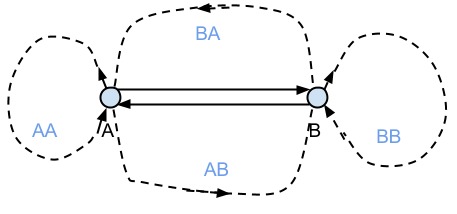
| * (1) Reduce the problem of comparing asymptotic variances when $T$ and $T'$ differ only for transitions involving two states, A and B | |
| * (2) We can divide the chain into blocks of states, which start and end in either state A or state B. | |
|  | |
| For $T$, the blocks may look like: | |
| 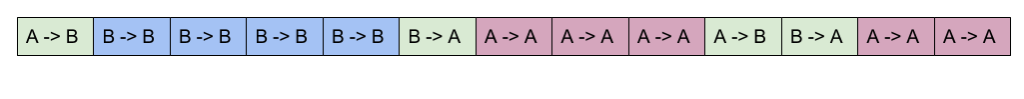 | |
| For $T'$, the blocks may look like: | |
|  | |
| The difference is that in chain $T$, the state stays the same when crossing a block boundary, whereas for the new chain $T'$, it changes from A to B or from B to A. | |
| * (3) We need to prove for both $T$ and $T'$, $$ P(AA)=P(BB) \,\, and \,\, P(AB) = P(BA) $$. | |
| Here, we know that $$T'(x,y) = T(x,y), \,\,\text{when $x\notin \{A, B\}$ or $y\notin \{A, B\}$}$$, and $$ | |
| T'(A,A) = T(A,A) - \delta_A,\,\,\, T'(A,B) = T(A,B) + \delta_A \\ | |
| T'(B,A) = T(B,A) + \delta_B,\,\,\, T'(B,B) = T(B,B) - \delta_B | |
| $$ | |
| Since $\pi_T(B) = \pi_{T'}(B)$, thus $\pi(A)\delta_A = \pi(B)\delta_B$, which yields to $$ P(AA)=P(BB) \,\, and \,\, P(AB) = P(BA) $$. | |
| * blocks starting and ending with A and blocks starting and ending with B are equally likely, but may have different distributions for their contents. | |
| * In contrast, blocks that start with A and end with B have essentially the same distribution of content as blocks that start with B and end with A. | |
| * (4) Comparing the chain $T$ and $T'$, we see that they produce the same sequence of homogeneous/non-homogeneous blocks. However, for the new chain, the homogeneous blocks **alternate** between AA blocks and BB blocks. Although eventually $P(AA) = P(BB)$, but for $T'$, it keeps $|N_{AA} - N_{BB}|\leq 1$ all the time. So for $T'$, it is _'stratified'_ in this respect. According to the lemma in the paper, it is true that this kind of 'stratified' technique will have no greater (typically less) asymptotic variance. | |
| ### 2) Non-backtracking Markov Chain [Neal 2004] | |
| * (1) Change the state as node pairs. | |
| * (2) The modified chain, with transition probability of $T''$ is irreducible. | |
| * (3) The transition probabilities $T''$ leave $\pi$ invariant | |
| * (4) The bias of the estimator of $\hat{\mu_n}'$ is of order $\frac{1}{n}$. | |
| * (5) Start the proof process like the Peskun's theorem. | |
| * $$ | |
| T''((A, O),(O, A)) = T((A, O),(O, A)) - \delta_A \\ | |
| T''((A, O),(O, B)) = T((A, O),(O, B)) + \delta_A \\ | |
| T''((B, O),(O, A)) = T((B, O),(O, A)) + \delta_B \\ | |
| T''((B, O),(O, B)) = T((B, O),(O, B)) - \delta_B | |
| $$ | |
| *  | |
| ### 3) Divide the neighbors into groups | |
| Assume we are looking into the simpler case: we only divide the neighbors into two groups, and all the nodes have even number of neighbors. Denote the transition matrix of the pair of nodes as $T^*$. It is easy to prove that $T^*$ is irreducible, with invariant distribution $\pi$. | |
| * (1) Assume $T^*$ only differs from $T$ on one node O, and we divide O's neighbors into two groups $G$ and $H$. | |
| * (2) $$ | |
| T''((G, O),(O, G)) = T((G, O),(O, G)) - \delta_G\\ | |
| T''((G, O),(O, H)) = T((G, O),(O, H)) + \delta_G\\ | |
| T''((H, O),(O, G)) = T((H, O),(O, G)) + \delta_H\\ | |
| T''((H, O),(O, H)) = T((H, O),(O, H)) - \delta_H | |
| $$ | |
| * (3) The same idea applies. The blocks become GG, GH, HG, HH. _Stratified_ is expected when $|N_{GG} - N_{HH}|\leq 1$. | |
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment