Dances with Factors (Tutorial)

README.md

Dances with Factors (Tutorial)

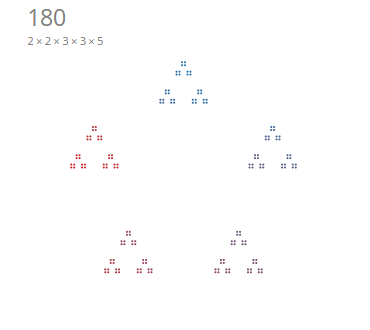
a D3 picture produced by chrisrzhou

Interactive Project Link

---

Contents

• Overview
• Math
  • Prime factorization
  • Adjustments
• D3
  • Generating points
  • Visualization components
  • Updates and transitions
• Adding User Interactions
  • Stop
  • Forward
  • Backward
  • Search
• Samples
• Resources

---

Overview

Dances with Factors is inspired by the creation of Stephen Von Worley, which in turn is based on the original idea by Brent Yorgey.

This visualization helps us track the prime factorization of a number. We can easily identify primes when we arrive at a simple circle (i.e. a prime cannot be composed of smaller divisors). We can also identify common patterns of smaller prime divisors e.g. 2, 3, 5.

This tutorial will explain how we can organize the project workflow into very simple and intuitive parts. A pseudocode workflow is presented:

// generate prime factorization of n e.g. 180 = [2, 2, 3, 3, 5]
factors = primeFactors(n)

// generate an array of point objects from factors eg. points = [point_1, point_2, ... point_n]
points = generatePoints(factors)

// initialize vis object and build update function that contains D3 code to draw and update vis using the points data
init()
var vis = {};
setInterval(update, speed)

// pseudocode for update
function update() {
  vis.number ++;  // update number
  vis.factors = primeFactors(vis.number);  // update factors
  vis.points = generatePoints(vis.factors);  // update factors
  
  // D3 code to draw points and update transitions
  ...
  
}

You can download the files used in this guide in the Github source code.

_{(back to contents)}

---

Math

The fundamental theorem of arithmetic states that every integer greater than 1 is either prime itself or a product of prime numbers.

The fundamental theorem of arithemetic is the basis for this visualization. Given a number n, we are guaranteed an array of prime factors [p1, p2, p3, ... pn], which we use as a foundation for iteratively drawing subgroups of points in the visualization.

Prime factorization

Bulk of the prime factorization code was derived from a previous Python script that I worked on to solve mathematical problems on Project Euler. Porting the implementation to Javascript is fairly easy, and we will build two functions primeFactors and getFactor to generate all prime factors of an integer n in ascending order.

Here is the code for primeFactors:

/**
 * Return array of prime factors (in ascending order) of n.
 * 
 * We will represent even powers of 2 as 4, for ease of plotting
 * 
 * Examples:
 *    primeFactors(1) = []
 *    primeFactors(10) = [2, 5]
 *    primeFactors(5) = [5]
 */
function primeFactors(n) {
  if (n < 1) throw "Argument error";
  var result = [];
  while (n != 1) {
    var factor = getFactor(n); // call getFactor function
    result.push(factor);
    n /= factor;
  }
  return result;
}

• We start with a number n and assert that it is greater than 1.

• Beginning with n, we will obtain the smallest prime factor of n with the helper function getFactor and assign it to factor.

• Divide and update n by factor while collecting the factors in the array result.

• Iteratively repeat the process until we arrive on the termination condition i.e. n = 1.

• An example is provided below:

  // example primeFactors(120) = [2, 2, 2, 3, 5]
  primeFactors(120) = [
      2,  // getFactor(120) = 2, n updates to 60
      2,  // getFactor(60) = 2, n updates to 30
      2,  // getFactor(30) = 2, n updates to 15
      3,  // getFactor(15) = 3, n updates to 5
      5,  // getFactor(5) = 5, n updates to 1
  ]

The implementation for the helper function getFactor is provided below:

/** 
 * Return smallest prime factor of n.
 */
function getFactor(n) {
  if (n < 2) throw "Argument error";
  if (n % 2 == 0) return 2;
  for (var i = 3; i <= Math.floor(Math.sqrt(n)); i += 2) {
    if (n % i == 0) return i;
  }
  return n;
}

• We start with a number n and return 2 if n is even (since 2 is the smallest factor that divides an even number).
• If n is odd, we iteratively check to see if it is divisible by i where i is incremented by 2.

Adjustments

We now have the math code that generates an array of prime factors for any integer n. However, we need to make a small output adjustment to the factors array to simplify subsequent D3 visualizations.

In particular, we wish to visualize groups of 2 and 4 differently. Take a look at the desired outputs of 8 and 16 shown below and notice how they are grouped differently.

We want to group points together in a square (4) rather than sets of pairs (2) whenever possible.

We can accomplish this grouping easily by "cheating" and assume that 4 is a unique "prime" which cannot be broken down into simpler representation of smaller primes.

Mathematically we know that this is not true, but this small change allows for a much simpler D3 visualization implementation since we can ignore special plotting cases for 2 and 4, and rely entirely on the geometry of angles to layout the points.

The code adjustment is as simple as adding a conditionalreturn statement in getFactor:

//function getFactor(n) {
//  if (n < 2) throw "Argument error";
    if (n % 4 == 0) return 4;
//  if (n % 2 == 0) return 2;
//  for (var i = 3; i <= Math.floor(Math.sqrt(n)); i += 2) {
//    if (n % i == 0) return i;
//  }
//  return n;
//}

This prioritizes returning a factor of 4 whenever possible and returning 2 only when necessary. As a result, the outputs of primeFactors is now different. For the same example above:

// previously primeFactors(120) = [2, 2, 2, 3, 5]
primeFactors(120) = [4, 2, 3, 5]  // returning 4 first

Lastly, let's write a function that helps print out a string representation of our prime factors array. We will print "prime" when our factors array has only one element, and iteratively print out a concatenated string of factors otherwise.

/**
 * Print string representation of array of prime factors
 * Examples
 *    printFactors([4, 3, 5]) = "2 × 2 × 3 × 5"
 *    printFactors([3, 5]) = "3 × 5"
 *    printFactors([7]) = "prime"
 */
 function printFactors(factors) {
   var string = "";
   if (factors.length == 1) {
     string = factors[0] == 4 ? "2 × 2" : "prime";
     return string;
   }
   
   factors.forEach(function(factor) {
     stringFactor = factor == 4 ? "2 × 2" : factor;
     string += stringFactor + " × ";
   });
   return string.slice(0, -2);  // remove last two characters
 }

If you have strong opinions to not alter the mathematical sanctity of prime factorization and prefer to delegate logic to their responsible areas, I'm definitely with you on that. But this is one simple tweak that would make our life a lot easier with D3 plotting, as we will now discuss in the next section.

_{(back to contents)}

---

D3

Please refer to the draw.js file for function referenced throughout this section.

Jason Davies has implemented a recursive solution in D3 for this problem, which recursively calls the D3 draw function on subplots to rescale, transform and translate SVGs to achieve the desired visualization. His implementation is elegant and simple to understand, but has a slight drawback on restrictive animation of individual points and transitions.

I wanted to mimic the effect created by Stephen Von Worley, which means that I have to generate all the data and its attributes to allow D3 to work its transition magic on new and old data states.

The ultimate challenge with this approach is to implement a way to describe the geometry, position, size, and angles of all the points from an array of prime factors.

Generating points

In this section, we will assume complete implementation of D3 visualization components (described in the next section) in order to provide a basis to focus the discussion solely on pseudocode and design of the function generatePoints. generatePoints in turn guarantees a dataset of point objects that D3 can rely on for visualization.

The first thing before we start is to ask what does D3 fundamentally require to do its job?

I'm picturing the following D3 pseudocode for drawing a point:

point.enter()
  .append("svg:circle").classed("point", true)
  .attr("r", function(d) { return d.r; })
  .attr("cx", function(d) { return d.x; })
  .attr("cy", function(d) { return d.y; })

Careful mental construction informs us that simply having knowledge on a point's radius and Cartesian coordinates (r, x, y) would be sufficient conditions to handling the visualization.

Given these minimal sufficient parameters, let us first build a helper function to create a point object that we will be reusing throughout this section.

// helper function to create a point
function createPoint(r, x, y) {
  var point = {
    r: r,
    x: x,
    y: y,
  };
  return point;
}

We will use the number 180 = [4, 3, 3, 5] as a sample number in this section to help us organize our implementation for generatePoints.

Recall that we are treating 2 × 2 as 4 for purposes of visualization.

We see that 180 is constructed in rings of 5 -> 3 -> 3 -> 4 (counting from outer rings to inner rings), which is exactly the reverse order of the factors array ([4, 3, 3, 5]) that we generated with primeFactors.

This suggests that we can utilize a loop going through elements in the array in reverse order to iteratively generate points. We would terminate the loop when we exhaust all factors in the array.

A starting template for generatePoints could look like this:

/**
 * Generate and distribute points
 */
function generatePoints(factors) {
  // initialize variables
  var points = [];
  var x, y, r, point;
 
  while (factors.length) {
    n = factors.pop(); // build points from outwards
    // code to update x, y, r and create points
  } 
  return points;
}

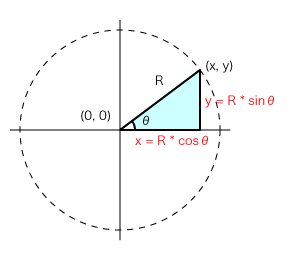
With this template in place, we can try to express the other variables x, y, r in terms of n (i.e. x, y, r, are functions of n).

We first notice that the r should be divided by some factor of n to allow us to fit n points within a unit area. Let's assume for simplicity that r as a function of n can be written as:

r = 1 / n

Next, we observe that n represents the number of vertices of a subgroup, which will allow us to evenly generate angles a to radially distribute the points.

d3.range(n).forEach(function(i) {
  a  = i * 2 * Math.PI / n
}

From basic trigonometry, we know that x and y can be calculated as a function of the angle a:

x = Math.cos(a);
y = Math.sin(a);

We now have a complete set of generated values x, y, and r that satisfies our minimum requirements for plotting points. We can now create a point object using our helper function createPoint(r, x, y).

To recap, generatePoints now looks something along the lines of:

function generatePoints(factors) {
  // initialize variables
  var points = [];
  var a, x, y, r, point;
 
  while (factors.length) {
    n = factors.pop(); // build points from outwards
    r *= 1 / n // scale r smaller by n each loop iteration
    d3.range(n).forEach(function(i) {  // loop through each vertex
	  a  = i * 2 * Math.PI / n  // calculate the angle of the point
	  x = Math.cos(a);  // update x
	  y = Math.sin(a);  // update y
	  point = createPoint(r, x, y);  // create point object
	  points.push(point);  // add to points
	}
  } 
  return points;
}

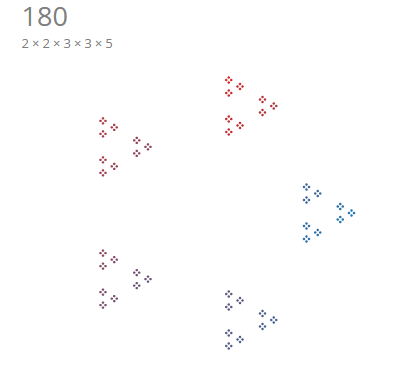
If we try to plot these generated points with D3, we notice something terribly wrong:

We are only generating a total of 4 + 3 + 3 + 5 = 15 points when we need to generate 180 = 4 * 3 * 3 * 5 points.

We need to somehow build points from the outer set of points and for each of those points, multiply out the inner points recursively.

We can achieve this through the use of a temporary variable parentPoints, which holds a list of all current points in the loop that provide a reference to build out more points for each of the parent points. Our general while loop needs to account if we are on the outer loop or within the recursive inner loop, and this can be implemented by providing a check on points.length == 0.

function generatePoints(factors) {
  var parentPoints = [];
  var points = [];
  var a, x, y, r, point;
 
  while (factors.length) {
    n = factors.pop();
    r *= 1 / n
    
    if(!points.length) {  // account for first set of points
      d3.range(n).forEach(function(i) {
        a  = i * 2 * Math.PI / n
		x = Math.cos(a);
		y = Math.sin(a);
		point = createPoint(r, x, y);
		points.push(point);
      });
    } else {  // if we enter the inner loop, we need to create points based on parent points
      parentPoints = points.slice(); // create shallow copy of points
      points = []; // reset points array;
      parentPoints.forEach(function(parentPoint) { // build new points using parentPoints as a template
        d3.range(n).forEach(function(i) {
          a = i * 2 * Math.PI / n + da;
          x = Math.cos(a);
          y = Math.sin(a);
          point = createPoint(r, x, y);
          points.push(point);
        });
      })
    }
  } 
  return points;
}

When we check points.length in the JavaScript console, we see that the dimension of the array now matches up correctly to the number, but a quick look at the visualization shows that the dimensions are all wrong! Here's what it would look like for 180 based on our current implementation of generatePoints.

A number of things are clearly wrong at this point. We notice that the points are all stacked on each other when they should be fanning out from their parent points. The radius scaling is also not correct.

The immediate fix we should make lies in the generation of child points from parent points. We notice that the general trigonometry formulas don't quite work:

x = Math.cos(a);
y = Math.sin(a);

The new child points need to be drawn with the parent point's location as a frame of reference. Luckily, we have access to this from the parentPoint object that we created. A simple change here will be to specify the parentPoint location as the frame of reference:

parentPoints.forEach(function(parentPoint) {
   d3.range(n).forEach(function(i) {
     a = i * 2 * Math.PI / n + da;
     x = parentPoint.x + Math.cos(a) / d;  // refer to x position of parentPoint;
     y = parentPoint.y + Math.sin(a) / d;  // refer to y position of parentPoint;
     point = createPoint(r, x, y);
     points.push(point);
   });
 })

If you are still paying attention, you noticed that we have introduced a variable d, which represents the depth factor that we need to scale as we enter each recursive loop. This scale factor should depend on n since every time we arrive at a nested set of n vertices, we should scale all our dimensions down by a factor of n. We will introduce d at the very start of our while loop.

function generatePoints(factors) {
  var parentPoints = [];
  var points = [];
  var a, x, y, r, point;
  var d = 1;  // initiate d
  var n = 1;  // initiate n
  
  while (factors.length) {
	d *= n  // scale d by n
    n = factors.pop();
    r *= 1 / n
    
    if(!points.length) {
      d3.range(n).forEach(function(i) {
      
        ...
        
		points.push(point);
      });
    } else {  
      parentPoints = points.slice();
      points = [];
      parentPoints.forEach(function(parentPoint) {
        d3.range(n).forEach(function(i) {
          a = i * 2 * Math.PI / n + da;
          x = parentPoint.x + Math.cos(a) / d;  // d applied on child point
          y = parentPoint.y + Math.sin(a) / d;
          point = createPoint(r, x, y);
          points.push(point);
        });
      })
    }
  } 
  return points;
}

Now testing our visualization in D3 yields something that looks much more decent:

We notice that there are slight issues with the orientation/rotation or our current visualization. We will leave this for the user to confirm that a simple introduction of an offset variable da (which is also a function of n) can help fix this problem. In general, the offset should be set as:

• da = -Math.PI / 4 when n == 4 (i.e. rotate 90 degrees)
• da = 0 when n == 2 (i.e. keep at default 0 degrees)
• da = -Math.PI / 2 otherwise (i.e. rotate 180 degrees)

Applying the introduction of the da variable and including this as part of the construction of the angle a yields us our finalized formulation of the function generatePoints:

/**
 * Generate and distribute points
 */
function generatePoints(factors) {
  var parentPoints = [];
  var points = [];
  var a, x, y, da, point;
  var n = 1;
  var r = 1;
  var d = 1;
 
  while (factors.length) {
    d *= n; // scale depth
    n = factors.pop(); // build points from outwards
    da = n === 4 ? -Math.PI / 4 : n === 2 ? 0 : -Math.PI / 2; // apply offset logic here
    r > 1 / 100 ? r *= 1 / n : r *= 0.7;  // aesthetic scale factor to increase size at higher values of n
 
    if (!points.length) { // account for first set of points
      d3.range(n).forEach(function(i) {
        a = i * 2 * Math.PI / n + da;  // apply offset da to angle a
        x = Math.cos(a);
        y = Math.sin(a);
        point = createPoint(r, x, y);
        points.push(point);
      });
 
    } else { // iteratively build points by keeping track of parentPoints
      parentPoints = points.slice();
      points = [];
      parentPoints.forEach(function(parentPoint) {
        d3.range(n).forEach(function(i) {
          a = i * 2 * Math.PI / n + da;  // apply offset da to angle a
          x = parentPoint.x + Math.cos(a) / d;
          y = parentPoint.y + Math.sin(a) / d;
          point = createPoint(r, x, y);
          points.push(point);
        });
      })
    }
  }
  return points;
}

And our visualization is now looking right and great.

That was a heavy section, so let's wrap it up in a quick summary:

• Find a way to generate variables x, y, r (minimal plotting requirements) from knowledge on the factors
• array.
• The factors array encodes information on n vertices, which we found ways to express x(n), y(n), r(n),
• a(n), d(n), da(n) as functions of n.
• We break the generation of points into an generating an initial set of outer points, followed by a recursive logic
• of generating nested inner points while applying the neccessary depth scaling factors.

Visualization components

In the previous section, we made "invisible" mention and displayed images to the visualization without describing its implementation. The goal of the previous section was to focus only on the logic of generating the right points data that D3 can use for plotting.

The goal of this section is to now build on how we inform D3 to take the points data and plot the results.

At the highest of level, our visualization application should run with three simple calls:

// initiate vis object
var vis = {};

// call an initialization function to build vis
init();  

// setup an interval reference to update based on a set speed
var interval = setInterval(update, speed);

You can see this simple call at the top of the draw.js file. What remains now is to implement init and update.

There are a number of things we should initialize in the vis object:

• vis.size: size of the SVG
• vis.speed: to determine how fast setInterval calls update
• vis.number: the number to be factorized and visualized
• vis.factors: the factor array for vis.number
• vis.points: the points generated when vis.factors is passed into the generatePoints i.e. the function we wrote in the previous section
• vis.scale: the scale and domain range of the visualization
• vis.svg: the main SVG object that D3 will build upon
• vis.trackerNumber: the number that we will display in the visualization
• vis.trackerFactors: the string representation of the factorization of vis.number

Following the above requirements, here is our implementation for the init function:

function init() {
  // vis parameters
  vis = {
    size: 250,
    number: 1,
    speed: 1000,
  };
  
  // get prime factors
  vis.factors = primeFactors(vis.number);
 
  // build data points
  vis.points = generatePoints(vis.number);
 
  // build scale
  vis.scale = d3.scale.linear()
    .range([0, vis.size])
    .domain([-1, 1]);
 
  // build vis svg
  vis.svg = d3.select("#vis")
    .append("svg")
    .attr("height", 2 * vis.size)
    .attr("width", 2 * vis.size)
    .append("g")
    .attr("transform", "translate(" + [vis.size / 2, vis.size / 2] + ")");
    
  // build vis tracker number
  vis.trackerNumber = vis.svg
    .append("svg:text").classed("trackerNumber", true)
    .attr("x", -vis.size / 3)
    .attr("y", -vis.size / 3)
    .attr("font-size", "30px")
    .attr("fill", "gray");
 
  // build vis tracker factors
  vis.trackerFactors = vis.svg
    .append("svg:text").classed("trackerFactors", true)
    .attr("x", -vis.size / 3)
    .attr("y", -vis.size / 3 + 25)
    .attr("font-size", "14px")
    .attr("fill", "gray");
}

The next section is to help build the logic of our update function, which will be repeatedly called by setInterval to update numbers and the visualization.

update should handle:

• updating vis.number and vis.factors.
• regenerate vis.points when vis.factors is updated.
• update vis.colorScale since we have to update our color domain range due to changing array size.
• apply transition effects for new data, old data, shifting data

We will first handle updates to vis.number, vis.factors, vis.points, and vis.colorScale:

/**
 * Update function for setInterval
 */
function update(pos) {
  // extend functino with the option to pass a direction
  // to either increment or decrement vis.number
  // i.e. if true, increase vis.number, if false, decrease vis.number
  pos ? vis.number ++ : vis.number > 2 ? vis.number-- : vis.number;
  vis.factors = primeFactors(vis.number);  // update factors
  
  // update tracker
  vis.trackerNumber.transition().text(vis.number);
  vis.trackerFactors.transition().text(printFactors(vis.factors));
 
  // update points
  vis.points = generatePoints(vis.factors); // create new points
  
  // make a reference to each point object
  var point = vis.svg.selectAll(".point").data(vis.points);
 
  // update colorscale
  vis.colorScale = d3.scale.linear()
    .domain([0, vis.points.length])  // rescale since vis.points.length has changed
    .range(["#1f77b4", "#d62728"]);
}

Updates and transitions

In the earlier section, we made a D3 selection reference to point in the update function i.e.

var point = vis.svg.selectAll(".point").data(vis.points);

We can now build on this selection and construct enter, exit, transition animations:

/**
 * Update function for setInterval
 */
function update(pos) {
  
  ...
  
  var point = vis.svg.selectAll(".point").data(vis.points);

  // enter
  point.enter()
    .append("svg:circle").classed("point", true)
    .attr("r", 0)
    .transition().duration(vis.speed / 2)
    .attr("r", function(d) { return d.r * vis.size; })  // scale radius of data point with size of vis
    .attr("cx", function(d) { return vis.scale(d.x); })  // apply vis.scales to x and y
    .attr("cy", function(d) { return vis.scale(d.y); })
    .attr("fill", function(d, i) { return vis.colorScale(i); });  // apply vis.colorScale to index of data points
 
  // update
  point.transition()
    .duration(vis.speed / 2)
    .attr("r", function(d) { return d.r * vis.size; })
    .attr("cx", function(d) { return vis.scale(d.x); })
    .attr("cy", function(d) { return vis.scale(d.y); })
    .attr("fill", function(d, i) { return vis.colorScale(i); });
 
  //exit
  point.exit()
  .transition().duration(vis.speed / 2)
  .attr("r", 0)
  .remove();
}

We are now done with our implementation of init and update and we can initialize our D3 visualization with three simple calls!

var vis = {};
init();
var interval = setInterval(update, vis.speed, true);

_{(back to contents)}

---

Adding User Interactions

We can provide a few interactive options for the users without overcomplicating our D3 code by initiating these interactions in the init function, and pausing and resetting intervals with the use of setInterval and clearInterval.

Let's build out the set of HTML widget controls and tag them with unique ids so D3 can select and reference them:

<!-- controls -->
<div class="btn-group controls">
  <input type="number" class="btn btn-default btn-sm" title="Input a number" id="inputNumber" />
  <a class="btn btn-default btn-sm" title="Search" id="search"><i class="fa fa-search"></i></a>
  <a class="btn btn-default btn-sm" title="Backward" id="backward"><i class="fa fa-chevron-left"></i></a>
  <a class="btn btn-default btn-sm" title="Stop" id="stop"><i class="fa fa-stop"></i></a>
  <a class="btn btn-default btn-sm" title="Forward" id="forward"><i class="fa fa-chevron-right"></i></a>
</div>

Note that we are using an icon set <i></i> from Font Awesome to help add some visuals to our widget :)

Let's now move from the HTML workstation to JavaScript.

Stop

d3.select("#stop")  // select by id
  .on("click", function() {
    clearInterval(interval);  // clear interval
  });

Forward

d3.select("#forward")  // select by id
  .on("click", function() {
    clearInterval(interval);  // clear interval
    interval = setInterval(update, vis.speed, true);  // reinitialize interval
  });

Note that we are passing the parameter true to update, which sets vis.number to increment each time update is called.

Backward

d3.select("#backward")  // select by id
  .on("click", function() {
    clearInterval(interval);  // clear interval
    interval = setInterval(update, vis.speed, false);  // reinitialize interval
  });

Note that we are passing the parameter false to update, which sets vis.number to decrement each time update is called.

Search

d3.select("#search")  // select by id
  .on("click", function() {
    vis.number = document.getElementById("inputNumber").value - 1;  // update vis.number
    clearInterval(interval);  // clear interval
    update(true);  // call update once
  });

For the search implementation, we assume that the user is prompted to pause and reflect on their searched result. We achieve this by stopping the interval using clearInterval, and making one manual call to update to visualize the desired result.

One small thing to pay attention is that update alters vis.number, so we have to pass it n - 1 if we wish to visualize n:

vis.number = document.getElementById("inputNumber").value - 1;

where we have used generic JavaScript to obtain the value of the HTML <input/ > tag.

And there you have it: user interactivity to stop, forward, backward, and search visualizations of various numbers.

Go ahead and test it out!

_{(back to contents)}

---

Samples

Here's a collection of interesting and beautiful samples. Feel free to explore and share any insightful ones you find in the comments below.

_{(back to contents)}

---

Resources

This work would not be possible without the original creative ideas and implementations made by others. I hope that my tutorial and implementation will spark interest in many others to share and expand on the foundations built for us.

• Github source code
• Brent Yorgey's original idea
• Stephen Von Worley's interactive version
• Jason Davies' recursive D3 implementation
• Sierpinski Triangle
• Mike Bostock's General Update Pattern

Thanks for viewing!

_{(back to contents)}

---

thumbnail.png